Решение рациональных уравнений 8 класс онлайн-подготовка на Ростелеком Лицей

 

 

Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями

 

Урок: Решение рациональных уравнений

 

1. Пример решения рационального уравнения, являющегося математической моделью текстовой задачи

 

 

Как вы уже успели заметить на предыдущем уроке, основа решения рациональных уравнений – техника преобразования рациональных выражений. Рассмотрим пример решения рационального уравнения.

 

Пример 1

Решить уравнение: .

Решение:

В первую очередь обратим внимание на то, что в числителях обеих дробей, а также в правой части уравнения стоят чётные числа. То есть, можно упростить уравнение, поделив обе его части на . Этот шаг не является обязательным, но, чем проще уравнение, тем легче его решать, а чем меньше числа, фигурирующие в уравнении, тем легче арифметические вычисления при его решении.

В результате сокращения получаем:

Теперь перенесём все члены уравнения в левую часть, чтобы получить справа , а затем приведём полученные в левой части дроби к общему знаменателю:

Напомним, что дробь равна  тогда и только тогда, когда её числитель равен , а знаменатель не равен . Поэтому наше уравнение превращается в следующую систему:

 

Теперь вспомним ещё один важный факт: произведение равно  тогда и только тогда, когда хотя бы один из его множителей равен , а остальные множители при этом существуют. И наша система превращается в следующую:

.

Оба полученных корня являются решениями данного уравнения, так как при них знаменатель определён.

Ответ: .

 

2. Пример текстовой задачи и решения её с помощью математического моделирования

 

 

Рассмотренное нами уравнение является моделью для такой задачи:

 

Задача 1

Лодка прошла  по течению реки и  против течения реки, затратив на весь путь .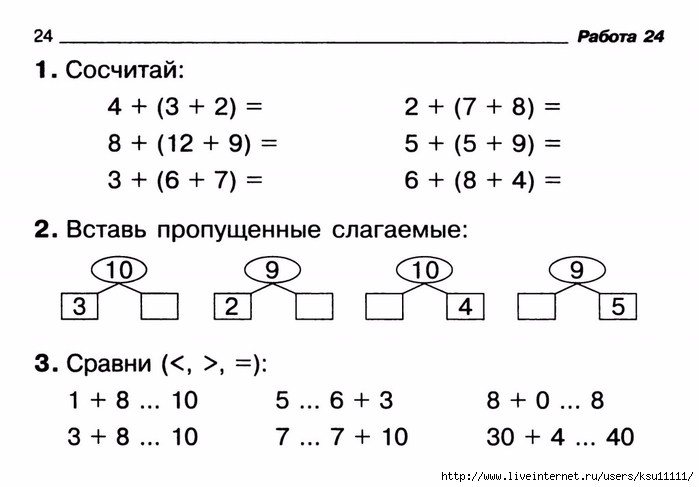 Чему равна собственная скорость лодки, если скорость течения реки равна ?

Решение:

Решение данной задачи осуществим с помощью метода математического моделирования и выделим 3 этапа данного метода.

Этап 1. Составление математической модели

Обозначим через  собственную скорость лодки (это стандартный приём при решении текстовых задач – обозначить с помощью неизвестной ту величину, которая спрашивается в условии задачи). Тогда:

 – скорость движения лодки по течению реки;

 – скорость движения лодки против течения реки.

В этом случае, воспользовавшись формулой: , получаем, что время движения лодки по течению реки выражается как , а время движения лодки против течения реки – . Тогда общее время движения лодки равно , откуда получаем уравнение:

 – это и есть математическая модель данной задачи.

Этап 2. Работа с математической моделью

В данном случае работа с математической моделью сводится к решению данного рационального уравнения, что мы уже сделали в примере 1. При этом получили корни уравнения: .

Этап 3. Ответ на вопрос задачи

Дело в том, что математическая модель потому и является математической, что абстрагирована от реальной жизни. Если брать конкретно данную задачу, то математическая модель – это уравнение, которое может иметь любые корни. Однако неизвестная величина обозначает скорость лодки, поэтому не может быть, к примеру, отрицательной. Или: не может быть меньше скорости течения реки, иначе бы лодка не смогла бы плыть против течения. И такие ограничения могут быть в самых разных задачах. Поэтому, прежде чем записать ответ, необходимо оценить, является ли он правдоподобным.

В данном случае очевидно, что  не подходит, так как лодка не смогла бы с такой скоростью плыть против течения. Поэтому в ответ пойдёт только одна величина: .

Ответ:

 

3. Различные примеры решения рациональных уравнений

 

 

Рассмотрим несколько примеров на решение непосредственно рациональных уравнений.

 

Пример 2

Решить уравнение: .

Решение:

Перенесём все слагаемые в левую часть, а затем приведём дроби к общему знаменателю.

Снова воспользуемся тем фактом, что дробь равна  тогда и только тогда, когда её числитель равен , а знаменатель не равен . Из этого следует, что данное уравнение эквивалентно системе:

Ответ:.

Пример 3

Решить уравнение: .

Решение:

В данном уравнении в правой части уже стоит , поэтому ничего переносить левую часть не нужно. Сразу приведём дроби в левой части к общему знаменателю:

.

Снова воспользуемся тем фактом, что дробь равна  тогда и только тогда, когда её числитель равен , а знаменатель не равен . Из этого следует, что данное уравнение эквивалентно системе:

. Подставив данное значение в знаменатель, убеждаемся, что он не равен . Значит, это значение переменной является ответом.

Ответ:.

Пример 4

Решить уравнение: .

Решение:

Схема решения данного уравнения абсолютно такая же, как и у предыдущих:

Ответ:.

 

4. Решение задачи, сводящейся к рациональному уравнению

 

 

К решению рациональных уравнений часто сводятся различные задачи. Рассмотрим один из таких примеров.

 

Задача 2

Существует ли такое значение , при котором разность дробей  и  равна ?

Решение:

Запишем уравнение, соответствующее условию данной задачи: .

Решим данное рациональное уравнение точно так же, как и в предыдущих примерах.

Приведём подобные слагаемые в числителе (они отмечены одинаковым цветом):

То есть, такое значение  существует.

Ответ: существует:.

Итак, мы рассмотрели примеры решения рациональных уравнений, а также их использование при решении различных задач. На следующих уроках мы перейдём к изучению новой темы, посвящённой различным функциям.

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.

2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Фестиваль педагогических идей «Открытый урок» (Источник).

2. Портал для всей семьи (Источник).

3. Обучающие курсы (Источник).

 

Домашнее задание

1. №№165, 178. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8.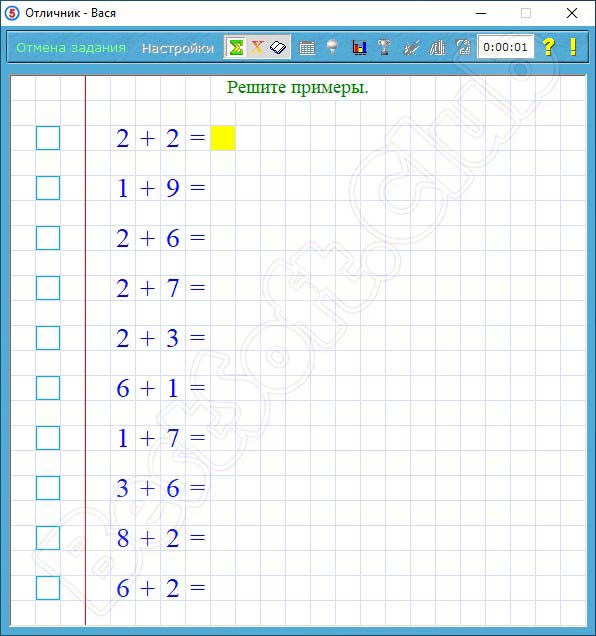 – 5-е изд. – М.: Просвещение, 2010.

2. Решить уравнения: а), б) .

3. Выполнить действия: а) , б) .

4. Два экскаватора могут выкопать котлован за . Первый экскаватор может выкопать котлован в 4 раза быстрее, чем второй. За сколько часов может выкопать такой же котлован каждый экскаватор, работая отдельно?

 

Развитие детей, логические игры и задачи, подготовка к школе, математические тренажёры

Развитие детей, логические игры и задачи, подготовка к школе, математические тренажёры

• Счёт по картинкам
• Ментальная арифметика
• Найди лишнее
• Учить часы со стрелками

• Угадай чья тень
• Задачи на сравнения
• Тренировка устного счёта
• Найди одинаковые картинки

Расширьте границы обучения

вместе с Mathsimple

Определять время по ходу стрелок, считать простые примеры с дробями или складывать цифры в уме — родителям бывает непросто объяснить новую тему ребёнку простым языком

Простые игры помогают школьнику быстрее понять необходимый материал: 15 минут за компьютером могут дать больше, чем несколько часов, проведённых над учебником!

Подготовка к школе

• Познакомим с цифрами
• Научим считать в уме
• Изучим сравнение чисел
• Научим определять время по часам со стрелками

Вперёд к знаниям!

Тренажеры

для 1 и 2 класса

• Запомним таблицу умножения
• Потренируем устный счёт
• Научимся решать простые уравнения

Вперёд к знаниям!

Тренажеры

для детей 3 и 4 класса

• Узнаем, что такое дробные числа
• Изучим римские цифры
• Расскажем про меры измерения
• Научимся вычислять периметр, площадь и объём

Вперёд к знаниям!

Развивайте вашего ребенка

Игры — простая и интересная форма обучения: ребёнку гораздо понятнее, когда знания подаются в форме картинок

Формируя ассоциативное мышление, дошколята и младшие школьники учатся не только запоминать учебный материал, но и понимать его

Почему учиться с Mathsimple классно?

Mathsimple — это постоянно развивающийся интернет-портал
Мы добавляем новые тренажёры раз в месяц, а старые дополняем новыми примерами

Детям понравится игровая форма обучения и понятный сайт, а у родителей появится дополнительный безопасный ресурс для обучения будущих вундеркиндов!

Уникальность

Курсы и тренажеры разработаны по специальной методике

Опыт

Мы совершенствуем свои тренажёры вместе с 2 500 учеников уже 5 лет

Техподдержка

Вы можете обратиться в любой момент: ответим на почту в течение двух дней

Удобство выбора

Занимайтесь с компьютера, телефона или планшета
с Mathsimple вы сами выбираете, как и где учиться!

Выгода

Вы можете оформить подписку — это даст доступ ко всем тренажёрам
А ещё одним аккаунтом могут пользоваться несколько детей!

Всё для детей

Игровая механика помогает ребёнку не просто заучивать материал,
а усваивать новые знания без усилий и стресса

Учебник по математике

онлайн

Математику недаром зовут «царицей наук»: точная, структурная и постоянно совершенствующаяся, математика требует скрупулёзности и внимательности при изучении

Важно понять математику в начальной школе: учиться с пониманием всегда намного легче и интереснее, чем с зубрёжкой.

На Mathsimple мы собрали не только игровые тренажёры, но и статьи, написанные простым и интересным языком. Читайте их вместе с ребёнком — и открывайте математику с новой, захватывающей стороны!

Изучать теорию математики

решений линейного уравнения | Калькулятор

Решения линейного уравнения относятся к набору значений переменных в линейных уравнениях, дающих все возможные решения. Линейные уравнения включают неизвестные величины в виде одной или нескольких переменных для представления реальных задач. Это помогает легко узнать стоимость, пробег, скорость, расстояние и т. Д. Мы все используем линейные уравнения в нашей повседневной жизни, не зная об этом.

В этом уроке мы подробно узнаем о решениях линейных уравнений, типах решений, способах их нахождения и т. д.

1.	Каковы решения линейного уравнения?
2.	Типы решений линейных уравнений
3.	Как найти решение линейного уравнения?
4.	Примеры решений линейного уравнения
5.	Часто задаваемые вопросы о решениях линейного уравнения

Каковы решения линейного уравнения?

Решениями линейных уравнений являются точки, в которых линии или плоскости, представляющие линейные уравнения, пересекаются или встречаются друг с другом. Множество решений системы линейных уравнений — это множество значений переменных всех возможных решений. Например, при решении линейных уравнений можно визуализировать решение системы одновременных линейных уравнений, нарисовав 2 линейных графика и найдя точку их пересечения.

Красная линия представляет все решения уравнения 1, а синяя линия — решения уравнения 2. Пересечение в единственной точке (2,4) — это решение, удовлетворяющее обоим уравнениям.

Типы решений линейных уравнений

Система линейных уравнений может иметь 3 типа решений.

Единственное решение системы линейных уравнений

Единственное решение системы линейных уравнений означает, что существует только одна точка, при подстановке которой левая и правая стороны уравнения становятся равными. Линейное уравнение с одной переменной всегда имеет единственное решение. Например, 3m = 6 имеет единственное решение m = 2, для которого L.H.S = R.H.S. Точно так же для одновременных линейных уравнений с двумя переменными единственным решением является упорядоченная пара (x, y), которая удовлетворяет обоим уравнениям.

Нет решения

Система линейных уравнений не имеет решения, если не существует точки, в которой прямые пересекаются друг с другом, или графики линейных уравнений параллельны.

Бесконечное множество решений

Система линейных уравнений имеет бесконечное множество решений, если существует множество решений, состоящее из бесконечных точек, для которых левая и правая стороны уравнения становятся равными или на графике прямые линии перекрывают друг друга.

Как найти решение линейного уравнения?

Решения для линейных уравнений с одной переменной

Рассмотрим уравнение 2x + 4 = 8

• Чтобы найти значение x, сначала мы удаляем 4 из LHS, поэтому мы вычитаем 4 из обеих частей уравнения. 2x + 4 — 4 = 8 — 4
• Просто. Теперь мы получаем, 2x = 4
• Теперь нам нужно удалить 2 из L.H.S, чтобы получить x, поэтому мы делим уравнение на 2. 2x/2 = 4/2, x=2

Следовательно, решение уравнения 2x + 4 = 8 равно x=2.

Решения линейных уравнений с двумя переменными

Для нахождения решений линейных уравнений с двумя переменными можно использовать следующие методы.

Метод подстановки

Рассмотрим следующую пару линейных уравнений, давайте решим следующие линейные уравнения.

x + y = 4 и x — y = 2

• Преобразуем первое уравнение, чтобы выразить y через x следующим образом: x + y = 4, y = 4 — x
• Теперь это выражение для у можно подставить во второе уравнение, так что у нас останется уравнение только относительно х: х — у = 2, х — 4 + х = 2, 2х = 6 х = 6/2, х = 3
• Получив значение x, мы можем подставить его обратно в любое из двух уравнений, чтобы найти y. Подставим это в первое уравнение: x + y = 4 (3) + y = 4, y = 4 — 3 = 1, y = 1
• Окончательное нетривиальное решение: x = 3, y = 1

Должно быть понятно, почему этот процесс называется заменой. Мы выражаем одну переменную через другую, используя одно из двух уравнений, и подставляем это выражение во второе уравнение.

Метод исключения

Рассмотрим следующую пару линейных уравнений:

2x + 3y — 11 = 0, 3x + 2y — 9 = 0

Коэффициенты x в двух уравнениях равны 2 и 3 соответственно. Умножим первое уравнение на 3, а второе уравнение на 2, чтобы коэффициенты при x в двух уравнениях стали равными:

• 3 {2x + 3y — 11 = 0} 6x + 9y — 33 = 0
• 2 {3x + 2y — 9 = 0} 6x + 4y — 18 = 0

Теперь вычтем два уравнения, это значит, что мы вычтем левые части двух уравнений, а правые части двух уравнений и равенство все равно сохранится.

6x + 9y — 33 = 0 ,6x + 4y — 18 = 0 0 + 5y — 15 = 0, 5y = 15, y = 3 . Получив значение y, мы действуем, как и раньше, — подставляем его в любое из двух уравнений. Подставим это в первое уравнение:

2х + 3у — 11 = 0, 2х + 3 (3) — 11 = 0, 2х + 9 — 11 = 0\, 2х = 2, х = 1

Таким образом, нетривиальное решение: x = 1, y = 3

Графический метод

В качестве примера решим следующее линейное уравнение: x — y + 2 = 0, 2x + y — 5 = 0. Рисуем соответствующие линии на тех же осях:

Точка пересечения (1,3), что означает, что x = 1, y = 3 является решением пары линейных уравнений, заданной (2). Фактически, это единственное решение пары , так как две непараллельные прямые не могут пересекаться более чем в одной точке.

Важные примечания

Вы можете напрямую проверить типы решений, используя следующие условия:

• Уникальное решение (непротиворечивое и независимое) a1/a2 ≠ b1/b2
• Нет решения (противоречивое и независимое) a1/a2 = b1/b2 ≠ c1/c2
• Бесконечное множество решений (непротиворечивых и зависимых) a1/a2 = b1/b2 = c1/c2

Часто задаваемые вопросы о решениях линейных уравнений

Как решить систему линейных уравнений?

У нас есть разные методы решения системы линейных уравнений:

• Графический метод
• Метод замены
• Метод перекрестного умножения
• Метод исключения
• Метод определителей

Что такое уникальное решение линейного уравнения?

Единственным решением системы линейных уравнений является упорядоченная пара или точка, которая делает равенство истинным в уравнении.

Что произойдет, если пара линейных уравнений непротиворечива?

Если пара линейных уравнений непротиворечива, то линии либо пересекаются, либо совпадают (накладываются) друг на друга.

Каковы 3 решения линейных уравнений?

Существует три способа решения систем линейных уравнений: подстановка, исключение и построение графика

Как найти решение линейной системы?

• Сначала решите одно линейное уравнение относительно y через x.
• Затем подставьте это выражение для y в другое линейное уравнение. Вы получите уравнение относительно x .

Линии пересекаются в нулевых точках.
Линии пересекаются ровно в одной точке.
Прямые пересекаются в бесконечном числе точек.

Как найти решение двух линейных уравнений?

Решение систем уравнений путем замены

• Решите одно из двух уравнений для одной из переменных относительно другой.
• Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.

Как решать линейные уравнения с одной переменной?

• Шаг 1: При необходимости упростите каждую сторону.
• Шаг 2: Используйте Доп./Под. Свойства, позволяющие переместить переменный термин в одну сторону, а все остальные термины — в другую.
• Шаг 3: Используйте Mult./Div. …
• Шаг 4: Проверьте свой ответ.

Сколько существует решений линейного уравнения 2x-5y=7?

В данном уравнении 2x – 5y = 7 для каждого значения x мы получаем соответствующее значение y и наоборот. Следовательно, линейное уравнение имеет бесконечно много решений.

Как найти упорядоченные парные решения линейных уравнений?

Чтобы выяснить, является ли упорядоченная пара решением уравнения, вы можете выполнить тест. Определите значение x в упорядоченной паре и подставьте его в уравнение. При упрощении, если полученное вами значение y совпадает со значением y в упорядоченной паре, то эта упорядоченная пара действительно является решением уравнения.

Как найти упорядоченное парное решение линейного уравнения с двумя переменными?

Чтобы убедиться, что упорядоченная пара является решением, подставьте соответствующие значения x и y в каждое уравнение, а затем упростите, чтобы увидеть, получите ли вы верное утверждение для обоих уравнений.

Домашнее задание по упрощению и умножению радикалов. радикалы в вашем ответе. Вопрос: My Drive ДОМАШНЕЕ ЗАДАНИЕ — Упрощение радикалов, множителей и делений …

[PDF] Примечания к радикалам и ключи ответов ws.pdf

www.livingston.org › cms › lib9 › Centricity › Домен › радикалы не…

Упрощение. Дайте точные ответы, без округления. … Рабочий лист по алгебре — Упрощение радикалов. 2) √12. … Рабочий лист по алгебре — Радикалы — Умножение.

[PDF] Умножение подкоренных выражений. Kuta Software — Бесконечная алгебра 1 … Умножение радикальных выражений. Упрощать. 1) 3 12 ∙ 6. 2) 5 ∙ 10,

Результаты для рабочего листа для упрощения и умножения радикалов — TPT

www. teacherspayteachers.com › Обзор › Search:si…

Результаты 1–24 из 240+ · Учащиеся будут практиковаться в упрощении радикалов, сложении, вычитании, умножение и простое деление — все, чтобы решить веселую загадку.

Умножение подкоренных выражений Рабочие листы

www.math-worksheet.org › умножение-2

Упростить. Этот бесплатный рабочий лист содержит 10 заданий, каждое из которых содержит 24 вопроса с ответами. Пример одного вопроса: Radical-Expressions-Multiplying-easy.

[PDF] 7.1 Simplifying Radicals.pdf

www.rcsdk12.org › cms › lib › Centricity › Domain › 7.1 Simplifyin…

Упростите каждое выражение, разложив его на множители, чтобы найти правильные квадраты, а затем извлекая их корень. … калькулятор. Домашнее задание. Упростите каждое подкоренное выражение.

[PDF] 7.1R Simplifying Radicals 020316

www.rcsdk12.org › cms › lib › Centricity › Domain › 7.1R Simplifyi…

LO: Я могу упростить радикальные выражения, включая сложение, вычитание, умножение, деление и .