Объясните, как, используя законы сложения, можно упростить следующие вычисления, и выполните их: 25+65+75 — Знания.site

Ответы

Знаешь ответ? Добавь его сюда!

Последние вопросы

• Информатика

  1 час назад

  Используя связанные таблицы создать:

  — Форму для ввода данных по таблице Студенты.

  — Запрос на выборку по которому из базы данных будут отобраны фамилии, имена, специализация и изучаемый язык:

  Запрос на выборку по которому из базы данных будут отобраны студенты менеджеры и изучающие английский язык;

  — По созданному запросу создать отчет с группировкой по специальности.

• Литература

  2 часа назад

  61 балл по литературе..все очень плохо?
• Математика

  5 часов назад

  какое аниме посмотреть подскажите

• Физика

  1 день назад

  на стройплощадке идет возведение здания на 6 этаже стоит рабочий какие силы действуют на рабочего и на здание если s 100м² вес 70кг

• Химия

  1 день назад

  Помогите пожалуйста

• Геометрия

  2 дня назад

  Помогите пожалуйста

  1. 2.

  2. Напишите уравнение сферы с центром в точке A(-1;1;-1) проходящей через точку N(3;4;2)

• Математика

  2 дня назад

  Помогите решить пример,срочно!!!

  фото прикрепила

• Физика

  3 дня назад

  помогите решить пожалуйста!!!

• Обществознание

  5 дней назад

  47×8:2×2 решите пж этот пример срочно!!! Можно не столбиком
• Английский язык

  5 дней назад

  Помогите пожалуйста очень срочно буду благодарен

• Математика

  6 дней назад

  https://gamejolt. com/invite/Mukhin

• Математика

  7 дней назад

  что делать когда скучно

  не пишите срать через окно и тому подобное

• Геометрия

  7 дней назад

  ПОМОГИТЕ С ГЕОМЕТРИЕЙ ПОЖАЛУЙСТА, желательно с рисунком

• Математика

  7 дней назад

  Ой лето😍😘

• Геометрия

  8 дней назад

  Помогите пожалуйста с геометрией срочно

§ Упрощение выражений. Вынесение общего множителя за скобки

Свойства сложения, вычитания, умножения и деления полезны тем, что позволяют преобразовывать суммы и произведения в удобные выражения для вычислений. Научимся, как можно с помощью этих свойств

упрощать выражения.

Вычислим сумму:

52 + 287 + 48 + 13 =

В этом выражении есть числа, при сложении которых получаются «круглые» числа. Заметив это, легко провести вычисления устно. Воспользуемся переместительным законом сложения.

Также для упрощения вычисления произведений можно использовать переместительный закон умножения.

7 · 2 · 9 · 5 = (2 · 5) · (7 · 9) = 10 · 63 = 630

Сочетательные и переместительные свойства используются и при упрощении буквенных выражений.

• 6 · a · 2 = 6 · 2 · a = 12a
• 2 · a · 4 · b = 2 · 4 · a · b = 8ab
• 5b + 8b = (5 + 8) · b = 13b
• 14y − 12y = (14 − 12) · y = 2y

Распределительный закон умножения часто применяется для упрощения вычислений.

Применяя распределительное свойство умножения относительно сложения или вычитания к выражению «(a + b) · с и (a − b) · c», мы получаем выражение, не содержащее скобки.

В этом случае говорят, что мы раскрыли (опустили) скобки. Для применения свойств не имеет значения, где записан множитель «c» — перед скобками или после.

Раскроем скобки в выражениях.

• 2(t + 8) = 2t + 16
• (3x − 5)4 = 4 · 3x − 4 · 5 = 12x − 20

Запомните!

Если перед буквой не записано число, то подразумевается, что перед буквой стоит числовой множитель 1.

• t + 4t = (1 + 4)t = 5t

Поменяем местами правую и левую часть равенства:

(a + b)с = ac + bc

Получим:

ac + bc = (a + b)с

В таких случаях говорят, что из «ac + bc» вынесен общий множитель «с» за скобки.

Примеры вынесения общего множителя за скобки.

• 73 · 8 + 7 · 8 = (73 + 7) · 8 = 80 · 8 = 640
• 7x − x − 6 = (7 − 1)x − 6 = 6x − 6 = 6(x − 1)

---

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».

Оставить комментарий:

Отправить

25 декабря 2020 в 10:38

Diana Uralbaeva Профиль Благодарили: 0
Сообщений: 1

Раскройте скобки и приведите подобные слагаемые в выражении (ЗАПИШИ ПОДРОБНОЕ РЕШЕНИЕ) -0,8(2у-3х)+(1,6х-1,4у)-2(0,8у+1,7х)

0 СпасибоОтветить

20 января 2021 в 1:40
Ответ для Diana Uralbaeva

Алексей Волошин Профиль Благодарили: 0
Сообщений: 1

-1,6y+2,4x+1,6x-1,4y-1,6y-3,4x=-4,6y+0,6x

0 СпасибоОтветить

30 апреля 2020 в 13:14

Александра Воробьёва Профиль Благодарили: 0
Сообщений: 1

y

x²-xy

  − 

1

x-y

  : 

x + y

x²-xy

−

y

xy-y²

 Надо упростить выражение по строчкам

0 СпасибоОтветить

6 мая 2020 в 16:02
Ответ для Александра Воробьёва

Галина Федотова Профиль Благодарили: 0
Сообщений: 3

1)

1

x-y

*

x(x-y)

x+y

=

   

2)

y

x(x-y)

—

y

y(x-y)

=  

y(y-x)

-xy(y-x)

 =

 

3) —

  —

 =-

x+y+x2

x(x+y)

 

0 СпасибоОтветить

16 сентября 2015 в 14:16

Сабина Ерназарова Профиль Благодарили: 0
Сообщений: 1

бревно длиной 3 м надо распилить на равные части по 60 см.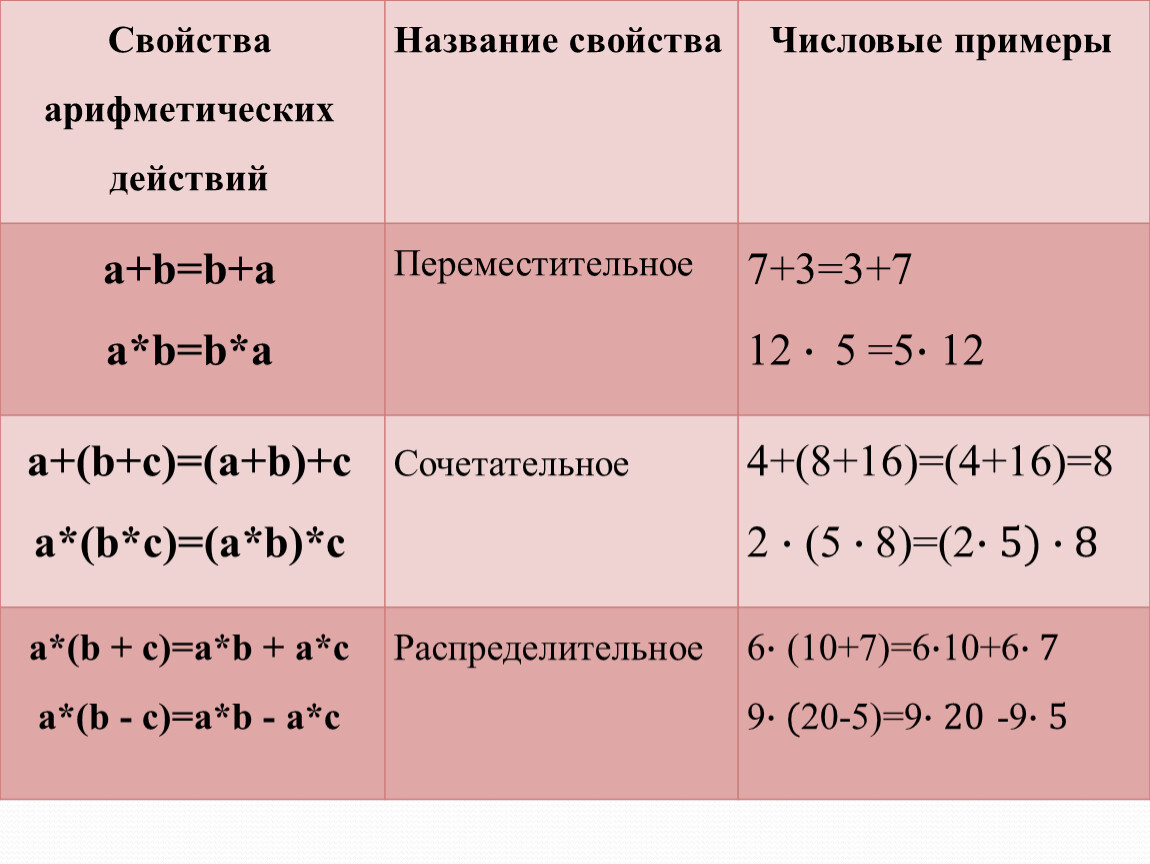 На распил потребуется b мин. Сколько часов понадобится, чтобы распилить на такие же части 15 бревен? Вычислите при b = 7.

0 СпасибоОтветить

16 сентября 2015 в 18:04
Ответ для Сабина Ерназарова

Максим Фатниев Профиль Благодарили: 0
Сообщений: 1

15*7=103=1ч 43 мин

0 СпасибоОтветить

5 сентября 2016 в 14:49
Ответ для Сабина Ерназарова

Евгений Колосов Профиль Благодарили: 12
Сообщений: 197

На распил 15 бревен потрубется в 15 раз больше времени, а именно: 
6мин · 15 бревен = 90 минут = 1,5 часа ( в одном часе 60 минут. 90/60 = 1,5)
При времени равным 7 минутам действия совершаются аналогично:
7 минут · 15 бревен = 105 минут = 1,75 часа.

1 СпасибоОтветить

---

Законы экспоненты (определение, правила экспоненты с примерами)

В математике существуют разные законы экспоненты. Все правила показателей степени используются для решения многих математических задач, связанных с повторяющимися процессами умножения. Законы экспоненты упрощают операции умножения и деления и помогают легко решать задачи. В этой статье мы собираемся обсудить шесть важных законов экспонент с множеством решенных примеров.

Содержание:

• Определение степени
• Законы показателей
  • Полномочия с одинаковым основанием
  • Частное с тем же основанием
  • Сила силы
  • Продукт для повышения мощности
  • Отношение к степени
  • Правило нулевой мощности
  • Правило отрицательного экспонента
  • Правило дробного экспонента
• Практические задачи
• Часто задаваемые вопросы

Что такое экспоненты?

Экспоненты используются для демонстрации многократного умножения числа на себя. Например, 7 × 7 × 7 можно представить как 7 ³ . Здесь показатель степени равен «3», что означает, сколько раз число 7 умножается. 7 — это основание, которое является фактическим числом, которое умножается. Таким образом, в основном показатели степени или степени обозначают, сколько раз число может быть умножено. Если степень равна 2, это означает, что базовое число умножается на себя два раза. Некоторые из примеров:

• 3 ⁴ = 3×3×3×3
• 10 ⁵ = 10×10×10×10×10
• 16 ³ = 16 × 16 × 16

Предположим, что число «а» умножается само на себя n раз, тогда оно представляется как ⁿ  где а — основание, а n — показатель степени.

Экспоненты следуют определенным правилам, помогающим упростить выражения, которые также называются его законами. Остановимся подробнее на законах экспонент.

Правила экспоненты с примерами

Как обсуждалось ранее, для показателей степени определены разные законы или правила. Важные законы показателей приведены ниже:

 

Также читайте:  Теперь давайте обсудим все законы один за другим на примерах здесь.

Продукт с одинаковыми основаниями

Согласно этому закону, для любого ненулевого члена а,

• a ^m ×a ⁿ  = a ^m+n

где m и n — действительные числа.

Пример 1. Как можно упростить 5 ⁵  × 5 ¹  ?

Решение: 5 ⁵  × 5 ¹  = 5 ⁵⁺¹  = 5 ⁶

Пример 2: Как можно упростить (−6) ^-4 × (−6) ^-7 ?

Решение: (−6) ^-4 × (−6) ^-7 = (-6) ^-4-7 = (-6) ^-11

Примечание: Мы можем констатировать, что закон применим и к отрицательным терминам. Следовательно, термин m и n может быть любым целым числом.

Частное с одинаковыми основаниями

Согласно этому правилу,

• а ^м /а ^н = а ^м-н

, где a – ненулевой член, а m и n – целые числа.

Пример 3: Найдите значение, если 10 ^-5 разделить на 10 ^-3 .

Решение: Согласно вопросу;

10 ^-5 /10 ^-3

= 10 ^-5-(-)3

= 10 ^-5+3

= 10 ^-2

= 1/100

Мощность увеличена до мощности

Согласно этому закону, если «а» является основанием, то степень, возведенная в степень основания «а», дает произведение степеней, возведенных в степень основания «а», например;

• (а ^м ) ^н = а ^мн

, где a – ненулевой член, а m и n – целые числа.

Пример 4: Выразите 8 ³ в степени с основанием 2.

Решение: у нас есть 2×2×2 = 8 = 2  ³

Следовательно, 8 ³ = (2 ³ ) ³  = 2 ⁹

Продукт для повышения мощности

По этому правилу, для двух и более разных подставок, если мощность одинаковая, то;

• а ^н б ^н = (аб) ^н

, где a — ненулевой член, а n — целое число.

Пример 5: Упростите и запишите экспоненциальную форму: 1/8 x 5 ^-3

Решение: мы можем написать, 1/8 = 2 ^-3

Следовательно, 2 ^-3 x 5 ^-3  = (2 × 5) ^-3  = 10 ^-3

Отношение к степени

Согласно этому закону, доля двух разных оснований с одинаковой силой представлена ​​как;

•  а ⁿ /b ⁿ = (a/b) ⁿ

, где a и b — ненулевые члены, а n — целое число.

Пример 6: Упростите выражение и найдите значение: 15 ³ /5 ³

Решение: Мы можем записать данное выражение как;

(15/5) ³ = 3 ³  = 27

Нулевая мощность

Согласно этому правилу, когда степень любого целого числа равна нулю, тогда его значение равно 1, например;

a ⁰  = 1

, где «а» — любой ненулевой термин.

Пример 7: Сколько стоит 5 ⁰ + 2 ² + 4 ⁰ + 7 ¹ – 3 ¹  ?

Решение: 5 ⁰ + 2 ² + 4 ⁰ + 7 ¹ – 3 ¹  = 1+4+1+7-3= 10

Правило отрицательного экспонента

Согласно этому правилу, если показатель степени отрицательный, мы можем изменить показатель степени на положительный, записав то же значение в знаменателе, а в числителе будет значение 1.

Правило отрицательного порядка задается как:

а ^-м = 1/а ^м

Пример 8:

Найдите значение 2 ^-2

Решение:

Здесь показатель степени является отрицательным значением (т. е. -2)

Таким образом, 2 ^-2 можно записать как 1/2 ²

2 ^-2 = 1/2 ²

2 ^-2 = 1/4

Другими словами, мы можем сказать, что если «а» является ненулевым числом или ненулевым рациональным числом, мы можем сказать, что 9{\ frac {1} {n}} = \ sqrt [n] {a} \ end {массив} \)

Здесь a называется основанием, а 1/n — показателем степени, который имеет дробную форму. Таким образом, a ^1/n называется корнем n-й степени числа a.

Пример 9:

Упрощение: 4 ^1/2

Решение:

Здесь показатель степени в дробной форме. (т.е. ½)

Согласно правилу дробной экспоненты, 4 ^1/2 можно записать как √4

(т.е.) 4 ^1/2 = √4

4 ^1/2 = 2 (Поскольку квадратный корень из 4 равен 2)

Следовательно, упрощенная форма 4 ^1/2 равна 2.

Практические задачи на законы показателей

Упростите следующие выражения, используя законы показателей:

1. (4 ² ) ³
2. 4 ² ×4 ⁷
3. 3 ^-3
4. 64 ^1/2
5. 7 ⁰ ×2 ³

Часто задаваемые вопросы о законах показателей степени

Q1

Что такое показатели степени?

Показатели степени, также называемые степенями, определяют, сколько раз мы должны умножить базовое число. Например, число 2 нужно умножить 3 раза и представить как 2 ³ .

Q2

Каковы различные законы показателей?

Различные законы показателей:

• a ^m ×a ⁿ = а ^м+п
• а ^м /а ^н = а ^м-н
• (а ^м ) ^н = а ^мн
• а ^н /б ^н = (а/б) ^н
• а ⁰ = 1
• а ^-м = 1/а ^м

Q3

Что такое Сила силового правила?

В силе правила степени мы должны умножить значения экспоненты. Например, (2 ³ ) ² можно записать как 2 ⁶ .

Q4

Объясните правило нулевой мощности.

Согласно правилу нулевой степени, если показатель степени равен нулю, результатом будет 1, каким бы ни было базовое значение. Это означает, что все, что возведено в степень 0, равно 1. Например, 5 ⁰ равно 1.

Q5

Упростим выражение 2

² .2 ⁵

В выражении 2 900 39 2 .2 ⁵ , базовые значения одинаковы, поэтому мы можем добавить показатели степени.
Следовательно, 2 ² .2 ⁵ = 2 ²⁺⁵
2 ² .2 ⁵ = 2 ⁷ .

Следите за обновлениями BYJU’S — The Learning App и загрузите приложение, чтобы получить все понятия математики и учиться простым способом.

Упрощение выражений с помощью различных форм распределительного свойства

Результаты обучения

• Применение распределительного свойства для упрощения алгебраического выражения, включающего целые числа, целые числа, дроби и десятичные дроби
• Применение распределительного свойства в различных формах

Упрощение выражений с использованием свойства распределения

Предположим, трое друзей идут в кино. Каждому из них нужно [латекс]$9,25[/латекс]; то есть [латекс]9[/латекс] долларов и [латекс]1[/латекс] квартал. Сколько денег им нужно всем вместе? Вы можете думать о долларах отдельно от четвертаков.

Им нужно [латекс]3[/латекс] умножить на [латекс]9$[/латекс], поэтому [латекс]27$[/латекс] и [латекс]3[/латекс] умножить на [латекс]1[/латекс] ] квартал, так что [латекс]75[/латекс] центов. Всего им нужно [латекс]$27,75[/латекс].

Если вы думаете о математических вычислениях таким образом, вы используете Распределяющее свойство.

Распределительное свойство

Если [латекс]а,б,с[/латекс] — действительные числа, то

[латекс]а\влево(б+с\вправо)=аб+ас[/латекс]

Назад нашим друзьям в кино мы могли бы показать математические шаги, которые мы предпринимаем, чтобы найти общую сумму денег, которая им нужна, например:

[латекс]3(9,25)\\3(9\quad+\quad0,25)\\ 3(9)\quad+\quad3(0.25)\\27\quad+\quad0.75\\27.75[/latex]

В алгебре мы используем Распределяющее Свойство для удаления скобок при упрощении выражений. Например, если нас просят упростить выражение [латекс]3\влево(х+4\вправо)[/латекс], порядок операций гласит, что сначала нужно работать со скобками. Но мы не можем добавить [латекс]х[/латекс] и [латекс]4[/латекс], так как они не похожи на термины. Поэтому мы используем Распределительное свойство, как показано в следующем примере.

пример

Упростить: [латекс]3\влево(х+4\вправо)[/латекс]

Решение:

[латекс]3\влево(х+4\вправо)[/латекс]
Распределить.	[латекс]3\cdot x+3\cdot 4[/латекс]
Умножить.	[латекс]3x+12[/латекс]

Некоторым учащимся полезно рисовать стрелки, чтобы напомнить им, как использовать Распределительное свойство. Тогда первый шаг в предыдущем примере будет выглядеть так:

[латекс]3\cdot x+3\cdot 4[/латекс]

Теперь попробуйте.

попробуйте

В нашем следующем примере перед переменной y стоит коэффициент. Когда вы используете распределительное свойство, вы перемножаете два числа вместе, точно так же, как упрощаете любой продукт. Вы также увидите еще один пример, где выражение в скобках представляет собой вычитание, а не сложение. Вам нужно быть осторожным, чтобы изменить знак вашего продукта.

пример

Упростить: [латекс]6\влево(5у+1\вправо)[/латекс]

Показать решение

Упростить: [латекс]2\влево(х — 3\вправо)[/латекс]

Показать решение

А теперь попробуй.

попробуйте

Свойство дистрибутивности можно использовать для упрощения выражений, которые выглядят немного иначе, чем [латекс]а\влево(b+с\вправо)[/латекс]. Вот еще две формы.

различных форм распределительного свойства

Если [латекс]а,б,с[/латекс] являются действительными числами, то

[латекс]а\влево(б+с\вправо)=аб+ас[/латекс ]

Другие формы

[латекс]a\left(b-c\right)=ab-ac[/latex]
[латекс]\left(b+c\right)a=ba+ca[/latex]

В следующем видео мы покажем больше примеров использования дистрибутивного свойства.

Использование свойства распределения с дробями и десятичными знаками

Вы помните, как умножать дробь на целое число? Нам нужно будет сделать это в следующих двух примерах. Распределительное свойство бывает всех форм и размеров, а также может включать в себя дроби или десятичные дроби.

пример

Упрощение: [латекс]\большой\фрак{3}{4}\нормальный размер\левый(n+12\правый)[/латекс]

Показать решение

Упрощение: [латекс]8\Большой\левый(\фракция{3}{8}\нормальный размер х+\Большой\фракция{1}{4}\правый)[/латекс].

Показать решение

А теперь попробуй.

попробуй

Использование Распределительного Свойства, как показано в следующем примере, будет очень полезно, когда мы позже будем решать денежные задачи.

пример

Упростить: [латекс]100\влево(0,3+0,25q\вправо)[/латекс]

Показать решение

А теперь попробуй.

попробуй

Распространение переменной

В следующем примере мы будем умножать на переменную. Нам нужно будет сделать это в следующей главе.

пример

Упростить: [латекс]м\влево(n — 4\вправо)[/латекс]

Показать решение

А теперь попробуй.

попробуйте

Обратная форма свойства распределения

В следующем примере будет использоваться ‘обратная’ форма свойства распределения, [латекс]\влево(б+с\вправо)а=ба+ка[/латекс ].

пример

Упростить: [латекс]\влево(х+8\вправо)p[/латекс]

Показать решение

попробуй

Распространение отрицательного термина

Когда вы распространяете отрицательное число, вам нужно быть особенно осторожным, чтобы получить правильные знаки.

пример

Упростить: [латекс]-2\влево(4у+1\вправо)[/латекс]

Показать решение

Упрощение: [латекс]-11\влево(4 — 3а\вправо)[/латекс]

Показать решение

попробуй

В следующем примере мы покажем, как использовать Распределительное свойство, чтобы найти противоположное выражение.