Умножение чисел. Множимое, множитель и произведение

Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.

Пример. Во дворе посадили  3  ряда ёлок, по  4  ёлки в каждом ряду. Сколько ёлок посадили во дворе?

Чтобы ответить на этот вопрос, надо найти сумму  3  слагаемых, каждое из которых равно  4.

4 + 4 + 4 = 12.

Складывая  3  раза по  4  ёлки, мы получим общее количество ёлок во всех трёх рядах.

Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.

Для записи умножения используется знак  х  (косой крест)  или  ·  (точка),  который ставится между числами. Например:

4 х 3   или   4 · 3

Эта запись означает, что  4  надо умножить на  3.  Справа от записи умножения ставится знак  =  (равно),  после которого записывается полученный результат:

4 · 3 = 12.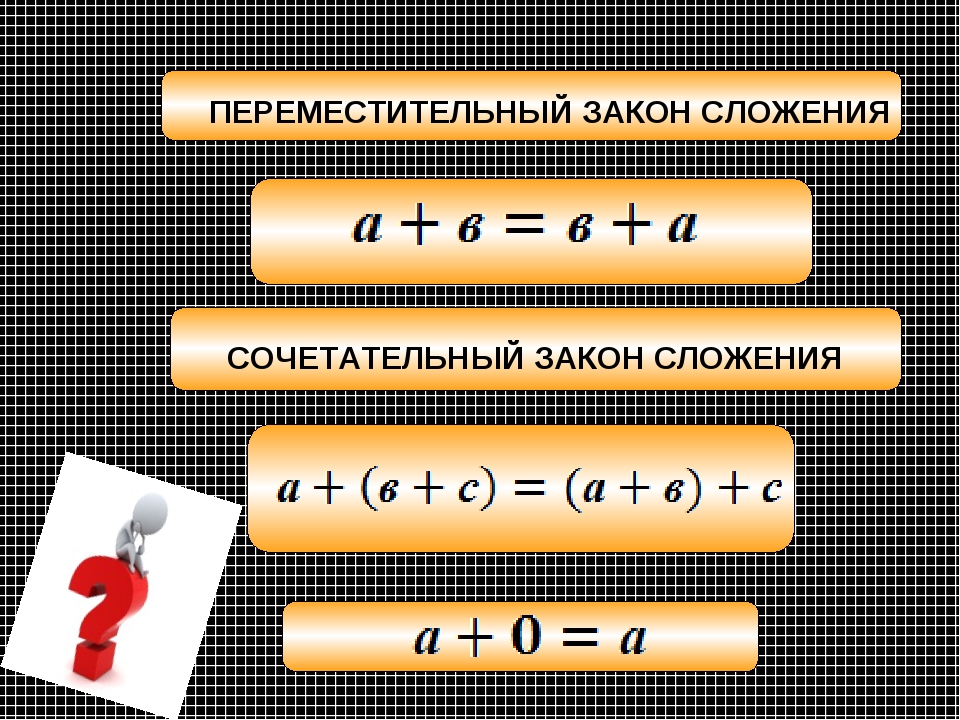

Умножение – это краткая запись сложения одинаковых слагаемых.

Пример. Умножить  6  на  5  — это значит найти сумму пяти слагаемых, каждое из которых равно шести:

6 + 6 + 6 + 6 + 6 = 30.

Сократим запись, заменив сложение на умножение:

6 · 5 = 30.

Оба выражения равны:

6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,

но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.

Множимое, множитель и произведение

Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:

4 · 3,

4  — это множимое,  3  — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.

Произведение — это число, которое получается в результате умножения. Например, в записи:

4 · 3 = 12,

12  — это произведение. При этом сама запись  4 · 3  тоже называется произведением.

Эту запись можно прочитать так:  произведение четырёх и трёх равно двенадцати,  четыре умножить на три равно двенадцати,  по четыре взять три раза, получится двенадцать.

Множимое и множитель иначе называются множителями или сомножителями.

Проверка умножения

Рассмотрим выражение:

4 · 3 = 12,

где  4  — это множимое,  3  — это множитель, а  12  — произведение. Чтобы узнать правильно ли было выполнено умножение, можно:

1. Разделить произведение на множитель, если получится число, равное множимому, то умножение было выполнено верно:
   12 : 3 = 4.

2. Разделить произведение на множимое, если получится число, равное множителю, то умножение выполнено верно:

   12 : 4 = 3.

Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.

Действия с нулём

В математике число ноль занимает особое место. Дело в том, что оно, по сути дела, означает «ничто», «пустоту», однако его значение действительно трудно переоценить. Для этого достаточно вспомнить хотя бы то, что именно с нулевой отметки начинается отсчет координат положения точки в любой системе координат.

 

Ноль широко используется в десятичных дробях для определения значений «пустых» разрядов, находящихся как до, так и после запятой. Кроме того, именно с ним связано одно из основополагающих правил арифметики, гласящее о том, что на ноль делить нельзя. Его логика, собственно говоря, проистекает из самой сути этого числа: действительно, невозможно представить, чтобы некая отличное от него значение (да и само оно – тоже) было разделено на «ничто».

Примеры вычисления

С нулем осуществляются все арифметические действия, причем в качестве его «партнеров» по ним могут использоваться целые числа, обычные и десятичные дроби, причем все они могут иметь как положительное, так и отрицательное значение. Приведем примеры их осуществления и некоторые пояснения к ним.

Сложение

При прибавлении нуля к некоторому числу (как целому, так и к дробному, как к положительному, так и к отрицательному) его значение остается абсолютно неизменным.

Пример 1

Двадцать четыре плюс ноль равняется двадцать четыре.

24 + 0 = 24

Пример 2

Семнадцать целых три восьмых плюс ноль равняется семнадцать целых три восьмых.

Вычитание

При вычитании нуля из некоторого числа (целого, дробного, положительного или отрицательного) оставляет его полностью неизменным.

Пример 1

Две тысячи сто пятьдесят два минус ноль равняется две тысячи сто пятьдесят два.

2152 – 0 = 2152

Пример 2

Сорок одна целая три пятых минус ноль равняется сорок одна целая три пятых.

Умножение

При умножении любого числа (целого, дробного, положительного или отрицательного) на

ноль получается ноль.

Пример 1

Пятьсот восемьдесят шесть умножить на ноль равняется ноль.

586 × 0 = 0

Пример 2

Ноль умножить на сто тридцать пять целых шесть седьмых равняется ноль.

0 × 135 = 0

Пример 3

Ноль умножить на ноль равняется ноль.

0 × 0 = 0

Деление

Правила деления чисел друг на друга в тех случаях, когда одно из них представляет собой ноль, различаются в зависимости от того, в какой именно роли выступает сам ноль: делимого или делителя?

В тех случаях, когда ноль представляет собой делимое, результат всегда равен ему же, причем вне зависимости от значения делителя.

Пример 1

Ноль разделить на двести шестьдесят пять равняется ноль.

0 : 265 = 0

Пример 2

Ноль разделить на семнадцать пятьсот девяносто шестых равняется ноль.

Делить ноль на ноль согласно правилам математики нельзя. Это означает, что при совершении такой процедуры частное является неопределенным. Таким образом, теоретически оно может представлять собой абсолютно любое число.

0 : 0 = 8 ибо 8 × 0 = 0

В математике такая задача, как деление нуля на ноль, не имеет никакого смысла, поскольку ее результат представляет собой бесконечное множество. Это утверждение, однако, справедливо в том случае, если не указаны никакие дополнительные данные, которые могут повлиять на итоговый результат.

Таковые, при их наличии, должны состоять в том, чтобы указывать на степень изменения величины как делимого, так и делителя, причем еще до наступления того момента, когда они превратились в

ноль. Если это определено, то такому выражению, как ноль разделить на ноль, в подавляющем большинстве случаев можно придать некий смысл.

Математики обнаружили идеальный способ перемножения чисел / Хабр

Разбивая крупные числа на мелкие, исследователи превысили фундаментальное математическое ограничение скорости

Четыре тысячи лет назад жители Вавилонии изобрели умножение. А в марте этого года математики усовершенствовали его.

18 марта 2019 два исследователя описали самый быстрый из известных методов перемножения двух очень больших чисел. Работа отмечает кульминацию давнишнего поиска наиболее эффективной процедуры выполнения одной из базовых операций математики.

«Все думают, что метод умножения, который они учили в школе, наилучший, но на самом деле в этой области идут активные исследования», — говорит Йорис ван дер Хувен, математик из Французского национального центра научных исследований, один из соавторов работы.

Сложность множества вычислительных задач, от подсчёта новых цифр числа π до обнаружения крупных простых чисел сводится к скорости перемножения. Ван дер Хувен описывает их результат как назначение своего рода математического ограничения скорости решения множества других задач.

«В физике есть важные константы типа скорости света, позволяющие вам описывать всякие явления, — сказал ван дер Хувен. – Если вы хотите знать, насколько быстро компьютеры могут решать определённые математические задачи, тогда перемножение целых чисел возникает в виде некоего базового строительного блока, по отношению к которому можно выразить такую скорость».

Почти все учатся перемножать числа одинаково. Записываем числа в столбик, перемножаем верхнее число на каждую цифру нижнего (с учётом разрядов) и складываем результат. При перемножении двух двузначных чисел приходится проделать четыре более мелких перемножения для получения итогового результата.

Школьный метод «переноса» требует выполнения n² шагов, где n – количество цифр в каждом из перемножаемых чисел. Вычисления с трёхзначными числами требуют девяти перемножений, а со стозначными – 10 000.

Метод переноса нормально работает с числами, состоящими из нескольких цифр, однако начинает буксовать при перемножении чисел, состоящих из миллионов или миллиардов цифр (чем и занимаются компьютеры при точном подсчёте π или при всемирном поиске больших простых чисел). Чтобы перемножить два числа с миллиардом цифр, нужно будет произвести миллиард в квадрате, или 10¹⁸, умножений, – на это у современного компьютера уйдёт порядка 30 лет.

Несколько тысячелетий считалось, что быстрее перемножать числа нельзя. Затем в 1960 году 23-летний советский и российский математик Анатолий Алексеевич Карацуба посетил семинар, который вёл Андрей Николаевич Колмогоров, советский математик, один из крупнейших математиков XX века. Колмогоров заявил, что не существует обобщённого способа умножения, требующего меньше, чем n

2 операций. Карацуба решил, что такой способ есть – и после недели поисков он его обнаружил.

Анатолий Алексеевич Карацуба

Умножение Карацубы заключается в разбиении цифр числа и повторной их комбинации новым способом, который позволяет вместо большого количества умножений провести меньшее количество сложений и вычитаний. Метод экономит время, поскольку на сложения уходит всего 2n шагов вместо n².

Традиционный метод умножения 25х63 требует четыре умножения на однозначное число и несколько сложений

Умножение Карацубы 25х63 требует трёх умножений на однозначное число и несколько сложений и вычитаний.
a) разбиваем числа
b) перемножаем десятки
c) перемножаем единицы
d) складываем цифры
e) перемножаем эти суммы
f) считаем e – b – c
g) собираем итоговую сумму из b, c и f

При росте количества знаков в числах метод Карацубы можно использовать рекурсивно.

Традиционный метод умножения 2531х1467 требует 16 умножений на однозначное число.

Умножение Карацубы 2531х1467 требует 9 умножений.

«Сложение в школе проходят на год раньше, потому что это гораздо проще, оно выполняется за линейное время, со скоростью чтения цифр слева направо», — сказал Мартин Фюрер, математик из Пенсильванского государственного университета, создавший в 2007 быстрейший на то время алгоритм умножения.

Имея дело с крупными числами, умножение Карацубы можно повторять рекурсивно, разбивая изначальные числа почти на столько частей, сколько в них знаков. И с каждым разбиением вы меняете умножение, требующее выполнения многих шагов, на сложение и вычитание, требующие куда как меньше шагов.

«Несколько умножений можно превратить в сложения, учитывая, что с этим компьютеры будут справляться быстрее», — сказал Дэвид Харви, математик из Университета Нового Южного Уэльса и соавтор новой работы.

Метод Карацубы сделал возможным умножать числа с использованием лишь n^1,58 умножений на однозначное число. Затем в 1971 году Арнольд Шёнхаге и Фолькер Штрассен опубликовали метод, позволяющий умножать большие числа за n × log n × log(log n) небольших умножений. Для умножения двух чисел из миллиарда знаков каждое метод Карацубы потребует 165 трлн шагов.

Йорис ван дер Хувен, математик из Французского национального центра научных исследований

Метод Шёнхаге-Штрассена используется компьютерами для умножения больших чисел, и привёл к двум другим важным последствиям. Во-первых, он ввёл в использование технику из области обработки сигналов под названием быстрое преобразование Фурье. С тех пор эта техника была основой всех быстрых алгоритмов умножения.

Во-вторых, в той же работе Шёнхаге и Штрассен предположили возможность существования ещё более быстрого алгоритма – метода, требующего всего n × log n умножений на один знак – и что такой алгоритм будет наибыстрейшим из возможных. Это предположение было основано на ощущении, что у такой фундаментальной операции, как умножение, ограничение операций должно записываться как-то более элегантно, чем n × log n × log(log n).

«Большинство в общем-то сошлось на том, что умножение – это такая важная базовая операция, что с чисто эстетической точки зрения ей требуется красивое ограничение по сложности, — сказал Фюрер. – По опыту мы знаем, что математика базовых вещей в итоге всегда оказывается элегантной».

Нескладное ограничение Шёнхаге и Штрассена, n × log n × log(log n), держалось 36 лет. В 2007 году Фюрер побил этот рекорд, и всё завертелось. За последнее десятилетие математики находили всё более быстрые алгоритмы умножения, каждый из которых постепенно подползал к отметке в n × log n, не совсем достигая её. Затем в марте этого года Харви и ван дер Хувен достигли её.

Их метод является улучшением большой работы, проделанной до них. Он разбивает числа на знаки, использует улучшенную версию быстрого преобразования Фурье и пользуется другими прорывами, сделанными за последние 40 лет. «Мы используем быстрое преобразование Фурье гораздо более грубо, используем его несколько раз, а не один, и заменяем ещё больше умножений сложением и вычитанием», — сказал ван дер Хувен.

Алгоритм Харви и ван дер Хувена доказывает, что умножение можно провести за n × log n шагов. Однако он не доказывает отсутствия более быстрого метода. Гораздо сложнее будет установить, что их подход максимально быстрый. В конце февраля команда специалистов по информатике из Орхусского университета опубликовала работу, где утверждает, что если одна из недоказанных теорем окажется верной, то этот метод и вправду будет скорейшим из способов умножения.

И хотя в теории этот новый алгоритм весьма важен, на практике он мало что поменяет, поскольку лишь немного выигрывает у уже используемых алгоритмов. «Всё, на что мы можем надеяться, это на трёхкратное ускорение, — сказал ван дер Хувен. – Ничего запредельного».

Кроме того, поменялись схемы компьютерного оборудования. Двадцать лет назад компьютеры выполняли сложение гораздо быстрее умножения. Разрыв в скоростях умножения и сложения с тех пор серьёзно уменьшился, в результате чего на некоторых чипах умножение может даже обгонять сложение. Используя определённые виды оборудования, «можно ускорить сложение, заставляя компьютер умножать числа, и это какое-то безумие», — сказал Харви.

Оборудование меняется со временем, но лучшие алгоритмы своего класса вечны. Вне зависимости от того, как компьютеры будут выглядеть в будущем, алгоритм Харви и ван дер Хувена всё ещё будет самым эффективным способом умножать числа.

Математические действия на английском языке

Даже если ваша учеба, работа или сфера деятельности никак не связана с точными науками, простые математические действия на английском знать важно, т. к. они встречаются не только в академических источниках, но и в фильмах, книгах и в повседневной речи.

Само слово «математика» в английском языке может звучать двумя способами. Первый и самый главный – это термин mathematics [ˌmæθəˈmætɪks]. Такой вариант употребляется, если речь идет о научной дисциплине или предмете изучения.

Mathematics includes the study of many topics. — Математика включает в себя изучение многих тем.

А в разговорной речи более уместен сокращенный вариант – maths [maθs], который принято использовать в Великобритании, а в США широко распространено применение еще более укороченного варианта math [mæθ].

My son has always been good at maths [масс]. — Мой сын всегда был хорош в математике.

Основные математические действия на английском: сложение, вычитание, умножение и деление.

В английском языке, как и в русском, существует 4 арифметических действия: сложение (addition), вычитание (subtraction), умножение (multiplication) и деление (division).

Для удобства можно разделить термины, употребляемые в этих действиях, в небольшие таблицы:

 

сложение (addition)	складывать	to add
	слагаемое	summand/addend
	сумма	sum
	плюс	plus

2+2=4 – Two plus two equals four.

 

вычитание (subtraction)	вычитать	to subtract
	вычитаемое	subtrahend
	уменьшаемое	minuend
	разница	difference / remainder
	минус	minus

 7-2=5 – Seven minus two equals five.

 

умножение (multiplication)	умножать на	multiply by
	умножить, разг.	times
	умножаемое	multiplicand
	множитель	multiplier
	произведение	product

 5×3=15 – Five times three is fifteen.

 

деление (division)	делить на	divide by
	разделить	divided by
	делимое	dividend / numerator
	делитель	divisor / denominator
	частное	quotient

15:3=5 — Fifteen divided by three equals five

 

И термины, которые связаны с результатом действия:

равно	total, equals
ответ	answer
Знак равенства	equal mark
решение	solution

 

Часто вместо equals или is equal to говорят is или get:

23 – 3 = 20 — Twenty-three minus three is twenty.

9 ÷ 3 = 3 – 9 divided by 3 is 3.

6 Х 4 = 24 — Multiply 6 by 4 and you’ll get 24.

Дроби на английском языке.

Простые дроби (common fractions) состоят из числителя (numerator) и знаменателя (denominator).

3/4 – three fourths.

1/8 – one eighth. 

Смешанные дроби или смешанные числа (mixed numeral) включают в себя целое число и дробь, например, 2 ½.

1¼ – one and a quarter.

1½ – one and a half.

1¾ – one and three quarters. 

Числитель в дроби выражается количественным числительным, а знаменатель порядковым. Наиболее употребляемые в речи дроби 1/2, 1/3, 1/4 имеют упрощенные названия: половина, треть, четверть:

1/2 – a half, one half.

1/3 – a third, one third.

1/4 – a quarter, one fourth.

В случаях, когда числитель больше одного, к окончанию добавляется -s, так как знаменатель используется во множественном числе (как и в русском: две третьих, три четвертых).

3/4– three fourths.

Существительное, которое определяется простой дробью, используется с предлогом of:

3/4 mile – Three fourths of a mile.

Существительное, определяемое смешанной дробью, используется без предлога, но во множественном числе:

2 ½ miles – Two and a half miles.

 

Десятичные дроби (decimal fractions, decimals) – дроби, где в английском языке разделителем между целой и дробной частью числа служит точка (point), в отличие от русской запятой. Ноль перед точкой называется zero или в британском варианте nought. Ноль после точки может называться oh (как буква “o”), zero, nought. Если целое число в дроби равно нулю, его часто опускают в речи, начиная говорить сразу с “point”.

1.25 – One point two five.

0.1 – Point one, zero point one.

Целое число читается как обычное количественное числительное, например, 

45. 1 – forty five point one – сорок пять целых одна сотая.

А в дробной части каждая цифра читается отдельно тоже как количественное:

 2.45 – two point four five (не two point forty five) – две целых сорок пять сотых.

Проценты в английском языке

Сотые доли могут выражаться с помощью процентов, тогда используется стандартный значок % и слово percent, всегда использующееся в единственном числе.

1% – One percent.

10% – Ten percent.

17% – Seventeen percent.

Глагол в предложениях с процентами согласуется с существительным, которое употреблено после частицы of:

Единственное число:

The remaining twenty percent of the script has been rewritten — Оставшиеся 20% сценария были переписаны.

Множественное число:

Twenty percent of the students are present — 20% студентов присутствуют.

Возведение в степень в английском.

Для обозначения степени используются выражения to the power of five, to the fifth power, raised to the power of five, raised to the fifth power. Вторая и третья степень имеют упрощенные термины “в квадрате” (squared) и “в кубе” (cubed).

3² – Three squared, three to the second power.

3³ – Three cubed, three to the third power.

10⁴ – Ten to the fourth power, ten to the power of four.

30²⁴ – Thirty to the power of twenty four.

Квадратный корень называется squareroot:

√25 = 5 – The square root of twenty five is five.

Математические выражения со скобками.

Круглые скобки называются parentheses (ед. число parenthesis) или round brackets. Если выражение стоит в скобках, и к нему применяется операция, используется слово quantity.

(2+3)×4=24 – Two plus three quantity times four equals to twenty four.

(3+5)²=64 Three plus five quantity squared is sixty four.  

Карточки с английскими словами на тему “Математика”.

Математические термины из этой статьи можно выучить с  помощью PDF-карточек для распечатки.

10 математических секретов, которые научат легко считать в уме

Те, кто в школе относился к урокам математики с пренебрежением, наверняка хотя бы несколько раз в жизни бывали в неловкой ситуации. Как посчитать, сколько оставить на чай или сумму коммунального платежа? Если знать пару простых приёмов, это займёт у вас буквально секунду. А уж во время экзамена знание правил умножения больших чисел может помочь сэкономить критически недостающее время. «Мел» совместно с Creu делится простыми секретами вычислений.

Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу

1. Умножение на 11

Все мы знаем, что при умножении на десять к числу добавляется ноль, а знаете ли вы, что существует такой же простой способ умножения двузначного числа на 11? Вот он:

Возьмите исходное число и представьте промежуток между двумя знаками (в этом примере мы используем число 52): 5_2

Теперь сложите два числа и запишите их посередине: 5_(5+2)_2.

Таким образом, ваш ответ: 572.Если при сложении чисел в скобках получается двузначное число, просто запомните вторую цифру, а единицу прибавьте к первому числу: 9_(9+9)_9 (9+1)_8_9 10_8_9 1089. Это срабатывает всегда.

2. Быстрое возведение в квадрат

Этот приём поможет быстро возвести в квадрат двузначное число, которое заканчивается на пять. Умножьте первую цифру саму на себя +1, а в конце допишите 25. Вот и всё! 252 = (2x(2+1)) & 25

2×3 = 6

625

3. Умножение на пять

Большинству очень просто даётся таблица умножения на пять, но когда приходится иметь дело с большими числами, сделать это становится сложнее.

Этот приём невероятно прост. Возьмите любое число и поделите пополам. Если в результате получилось целое число, припишите ноль в конце. Если нет, не обращайте внимание на запятую и в конце добавьте пять. Это срабатывает всегда:

2682×5 = (2682 / 2) & 5 или 0

2682 / 2 = 1341 (целое число, поэтому добавьте 0)

13410

Давайте попробуем другой пример:

5887×5

2943,5 (дробное число, пропустите запятую, добавьте 5)

29435

4.

Умножение на девять

Это просто. Чтобы умножить любое число от одного до девяти на девять, посмотрите на руки. Загните палец, который соответствует умножаемому числу (например, 9×3 — загните третий палец), посчитайте пальцы до загнутого пальца (в случае 9×3 — это два), затем посчитайте после загнутого пальца (в нашем случае — семь). Ответ — 27.

5. Умножение на четыре

Это очень простой приём, хотя очевидный лишь для некоторых. Хитрость в том, что нужно просто умножить на два, а затем опять умножить на два: 58×4 = (58×2) + (58×2) = (116) + (116) = 232.

6. Подсчёт чаевых

Если вам нужно оставить 15% чаевых, есть простой способ сделать это. Высчитайте 10% (разделите число на десять), а потом добавьте получившееся число к его половине и получите ответ:

15% от $25 = (10% от 25) + ((10% от 25) / 2)

$2.50 + $1.25 = $3.75

7. Сложное умножение

Если вам нужно умножать большие числа, причём одно из них — чётное, вы можете просто перегруппировать их, чтобы получить ответ:

32×125 всё равно что:

16×250 всё равно что:

8×500 всё равно что:

4×1000 = 4,000

8.

Деление на пять

На самом деле делить большие числа на пять очень просто. Нужно просто умножить на два и перенести запятую:

195 / 5

1. 195 * 2 = 390

2. Переносим запятую: 39,0 или просто 39.

2978 / 5

1. 2978 * 2 = 5956

2. 595,6

9. Вычитание из 1000

Чтобы выполнить вычитание из 1000, можете пользоваться этим простым правилом. Отнимите от девяти все цифры, кроме последней. А последнюю цифру отнимите от десяти:

1000-648

1. От 9 отнимите 6 = 3

2. От 9 отнимите 4 = 5

3. От 10 отнимите 8 = 2

Ответ: 352

10. Систематизированные правила умножения

Умножение на 5: Умножьте на 10 и разделите на 2.

Умножение на 6: Иногда проще умножить на 3, а потом на 2.

Умножение на 9: Умножьте на 10 и отнимите исходное число.

Умножение на 12: Умножьте на 10 и дважды прибавьте исходное число.

Умножение на 13: Умножьте на 3 и 10 раз прибавьте исходное число.

Умножение на 14: Умножьте на 7, а затем на 2.

Умножение на 15: Умножьте на 10 и 5 раз прибавьте исходное число, как в предыдущем примере.

Умножение на 16: Если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2.

Умножение на 17: Умножьте на 7 и 10 раз прибавьте исходное число.

Умножение на 18: Умножьте на 20 и дважды отнимите исходное число.

Умножение на 19: Умножьте на 20 и отнимите исходное число.

Умножение на 24: Умножьте на 8, а потом на 3.

Умножение на 27: Умножьте на 30 и 3 раза отнимите исходное число.

Умножение на 45: Умножьте на 50 и 5 раз отнимите исходное число.

Умножение на 90: Умножьте на 9 и припишите 0.

Умножение на 98: Умножьте на 100 и дважды отнимите исходное число.

Умножение на 99: Умножьте на 100 и отнимите исходное число.

БОНУС: проценты

Вычислить 7% от 300.

Сперва нужно понять значение слова «процент» (percent). Первая часть слова — про (per). Per = для каждого. Вторая часть — цент (cent), это как 100. Например, столетие = 100 лет. 100 центов в одном долларе и так далее. Итак, процент = для каждой сотни.

Итак, получается, что 7% от 100 будет семь. (Семь для каждой сотни, только одной сотни).

8% от 100 = 8.

35,73% от 100 = 35,73

Но как это может быть полезным? Вернёмся к задачке 7% от 300.

7% от первой сотни равно 7. 7% от второй сотни — то же 7, и 7% от третьей сотни — все те же 7. Итак, 7 + 7 + 7 = 21. Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).

Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.

Примеры:

8%200 =? 8 + 8 = 16.

8%250 =? 8 + 8 + 4 = 20,

8%25 = 2,0 (Передвигаем запятую влево).

15%300 = 15+15+15 =45

15%350 = 15+15+15+7,5 = 52,5

Также полезно знать, что вы всегда можете поменять числа местами: 3% от 100 — то же самое, что 100% от 3. А 35% от 8 — то же самое, что и 8% от 35.

Источник: Creu

---

что такое умножение, свойства 0, можно ли делить на 0

Ещё в школе учителя нам всем старались вбить в голову простейшее правило: «Любое число, умноженное на ноль, равняется нулю!», — но всё равно вокруг него постоянно возникает куча споров. Кто-то просто запомнил правило и не забивает себе голову вопросом «почему?». «Нельзя и всё тут, потому что в школе так сказали, правило есть правило!» Кто-то может исписать полтетради формулами, доказывая это правило или, наоборот, его нелогичность.

…

Вконтакте

Facebook

Twitter

Google+

Мой мир

Кто в итоге прав

Во время этих споров оба человека, имеющие противоположные точки зрения, смотрят друг на друга, как на барана, и доказывают всеми силами свою правоту. Хотя, если посмотреть на них со стороны, то можно увидеть не одного, а двух баранов, упирающихся друг в друга рогами. Различие между ними лишь в том, что один чуть менее образован, чем второй.

Это интересно: разрядные слагаемые — что это?

Чаще всего, те, кто считают это правило неверным, стараются призвать к логике вот таким способом:

У меня на столе лежит два яблока, если я положу к ним ноль яблок, то есть не положу ни одного, то от этого мои два яблока не исчезнут! Правило нелогично!

Действительно, яблоки никуда не исчезнут, но не из-за того, что правило нелогично, а потому что здесь использовано немного другое уравнение: 2+0 = 2. Так что такое умозаключение отбросим сразу — оно нелогично, хоть и имеет обратную цель — призвать к логике.

Это интересно: Как найти разность чисел в математике?

Что такое умножение

Изначально правило умножения было определено только для натуральных чисел: умножение — это число, прибавленное к самому себе определённое количество раз, что подразумевает натуральность числа. Таким образом, любое число с умножением можно свести вот к такому уравнению:

1. 25×3 = 75
2. 25 + 25 + 25 = 75
3. 25×3 = 25 + 25 + 25

Из этого уравнения следует вывод, что умножение — это упрощённое сложение.

Это интересно: что такое хорда окружности в геометрии, определение и свойства.

Что такое ноль

Любой человек с самого детства знает: ноль — это пустота, Несмотря на то, что эта пустота имеет обозначение, она не несёт за собой вообще ничего. Древние восточные учёные считали иначе — они подходили к вопросу философски и проводили некие параллели между пустотой и бесконечностью и видели глубокий смысл в этом числе. Ведь ноль, имеющий значение пустоты, встав рядом с любым натуральным числом, умножает его в десять раз. Отсюда и все споры по поводу умножения — это число несёт в себе столько противоречивости, что становится сложно не запутаться. Кроме того, ноль постоянно используется для определения пустых разрядов в десятичных дробях, это делается и до, и после запятой.

Это интересно: какой четырёхугольник называется квадратом?

Можно ли умножать на пустоту

Умножать на ноль можно, но бесполезно, потому что, как ни крути, но даже при умножении отрицательных чисел всё равно будет получаться ноль. Достаточно просто запомнить это простейшее правило и никогда больше не задаваться этим вопросом. На самом деле всё проще, чем кажется на первый взгляд. Нет никаких скрытых смыслов и тайн, как считали древние учёные. Ниже будет приведено самое логичное объяснение, что это умножение бесполезно, ведь при умножении числа на него всё равно будет получаться одно и то же — ноль.

Это интересно: что такое модуль числа?

Возвращаясь в самое начало, к доводу по поводу двух яблок, 2 умножить на 0 выглядит вот так:

• Если съесть по два яблока пять раз, то съедено 2×5 = 2+2+2+2+2 = 10 яблок
• Если их съесть по два трижды, то съедено 2×3 = 2+2+2 = 6 яблок
• Если съесть по два яблока ноль раз, то не будет съедено ничего — 2×0 = 0×2 = 0+0 = 0

Ведь съесть яблоко 0 раз — это означает не съесть ни одного. Это будет понятно даже самому маленькому ребёнку. Как ни крути — выйдет 0, двойку или тройку можно заменить абсолютно любым числом и выйдет абсолютно то же самое. А если проще говоря, то ноль — это ничего, а когда у вас ничего нет, то сколько ни умножай — всё равно будет ноль. Волшебства не бывает, и из ничего не получится яблоко, даже при умножении 0 на миллион. Это самое простое, понятное и логичное объяснение правила умножения на ноль. Человеку, далёкому от всех формул и математики будет достаточно такого объяснения, для того чтобы диссонанс в голове рассосался, и всё встало на свои места.

Это интересно: формулировка и доказательство признаков параллелограмма.

Деление

Из всего вышеперечисленного вытекает и другое важное правило:

На ноль делить нельзя!

Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.

Все просто зазубрили правило и не делят на ноль, не подозревая, что ответ кроется на поверхности. Сложение, умножение, деление и вычитание — неравноправны, полноценны из перечисленного только умножение и сложение, а все остальные манипуляции с числами строятся из них. То есть запись 10: 2 является сокращением уравнения 2 * х = 10. Значит, запись 10: 0 такое же сокращение от 0 * х = 10. Получается, что деление на ноль — это задание найти число, умножая которое на 0, получится 10. А мы уже разобрались, что такого числа не существует, значит, у этого уравнения нет решения, и оно будет априори неверным.

Расскажу тебе позволь,

Чтобы не делил на 0!

Режь 1 как хочешь, вдоль,

Только не дели на 0!

Умножение и его свойства

Определение. Умножение — это действие в результате которого находят сумму одинаковых слагаемых. Умножить число а на число Ь означает найти сумму Ь слагаемых, каждое из которых равно а.

Числа, которые перемножаются, называются множителями (или сомножителями), а результат умножения — произведением.

При умножении натуральных чисел произведение всегда число положительное. Если один из множителей равен 0 (нулю), то произведение равно 0. Если произведение равно нулю, то хотя бы один из множителей равен 0.

Если один из двух множителей равен 1 (единице), То произведение равно второму множителю.

• Например:
• 5 * 6 * 8 * 0 = 0
• 132 * 1 = 132

Законы умножения

Сочетательный закон

Правило. Чтобы произведение двух множителей умножить на третий множитель, можно первый множитель умножить на произведение второго и третьего множителей.

• Например:
• (7 * 6) * 5 = 7 * (6 * 5) = 210
• (a * b) * c = a * (b * c)

Переместительный закон

Правило. От перестановки множителей произведение не изменяется.

• Например:
• 7 * 6 * 5 = 5 * 6 * 7 = 210
• а * Ь * с = с * Ь * а

Распределительным закон

Правило. Чтобы умножить число на сумму, можно умножить это число на каждое из слагаемых и полученные произведения сложить.

• Например:
• 7 * (6 + 5) = 7 * 6 + 7 * 5 = 77
• a * (b + c) = ab + ac

Распределительный закон распространяется и на действие вычитания.

• Например:
• 7 * (6 — 5) = 7 * 6 — 7 * 5 = 7

Законы умножении распространяются на любое количество множителей в числовом или буквенном выражении. Распределительный закон умножения используется для вынесения общего множителя за скобки.

Правило. Чтобы преобразовать сумму (разность) в произведение, достаточно вынести за скобки одинаковый множитель слагаемых, а оставшиеся множители записать в скобках суммой (разностью).

• Например:
• 7 * 8 — 7 * 5 = 7 * (8 — 5)
• аЬ + ас = а * (Ь + с)

Вынесение множителя за скобки для больших числовых или буквенных выражений можно производить по группам слагаемых.

• Например:
• 3 * 6 + 9 * 6 — 4 * 8 = 6 * (3 + 9) — 4 * 8
• ab + bc — df -af = b * (a + c) — f * (d + a)
• c * (a + b) — d * (a + b) = (a + b) * (c — d)

Amazon.com: New Sky Enterprises Монтессори Математическое умножение материала и сложение деления Вычитание (умножение и деление): игрушки и игры

Доска умножения 1. Покажите ребенку материал и попросите его принести его на стол. 2. Покажите ребенку цифры вверху доски. Скажите ребенку: «Эти числа говорят нам, сколько раз брать число». 3. Покажите ребенку, как вставить карточку (4) в прорезь на боковой стороне доски. 4.Скажите ребенку: «Это говорит нам о том, что мы будем выполнять таблицу из четырех». 5. Поместите маленький красный диск над цифрой 1 в верхней части доски. 6. Скажите: «Это говорит нам, что нам нужно взять 4 бусинки по одному разу. 7. Используя красные бусинки, разместите 4 бусинки по вертикальной линии. 8. Попросите ребенка сосчитать, сколько бусинок находится на доске. 9. Скажите ребенок: «4 x 1 равно 4». Попросите ребенка написать ответ на листе рядом с уравнением. 10. Переместите диск над 2. 11. Скажите ребенку: «Теперь нам нужно 4 два раза. Но у нас уже есть 4 раза.12. Попросите ребенка поставить красные бусинки в вертикальную линию рядом с первыми четырьмя. 13. Попросите ребенка подсчитать общее количество бусинок на доске. 14. Скажите: «4 x 2 равно 8». Доска деления 1 . Покажите ребенку материал и попросите его принести его к столу. 2. Посмотрите на доску вместе с ребенком. Покажите ему все места для бусинок. 3. Покажите ему числа в верхней части доски и скажите ему, что они и есть делимое. 4. Скажите ему, что числа сбоку будут ответом. 5. Напишите 27 ¸ 9 = на бумаге в квадрате. 6. Начните с объяснения ребенку двух правил: ответ не может быть больше 9, а остаток не может быть больше делителя. 7. Поместите 27 зеленых бусинок в стеклянную миску. 8. Спросите ребенка, сколько раз мы выдадим 27. (9) 9. Поместите 9 зеленых кеглей на верхнюю часть доски. 10. Дайте каждой кегле по бусинке, пока не останется бусинок. 11. Скажите: «27 ¸ 9 равно 3». Укажите на 3 на вертикальной стороне доски. 12. Попросите ребенка написать ответ на уравнение.

Что не так с «повторным сложением»? — Играем в математику Дениз Гаскинс

[Фото Алехандры Мавроски.]

Миртл назвала это статьей, которая запустила тысячу постов… и подсчет комментариев к этому и нескольким другим блогам, возможно, это не слишком большое преувеличение. Тем не менее, обсуждение кажется неполным — я не смог выразить словами все, что хочу сказать. Таким образом, рискуя еще раз выявить свое математическое невежество, я собираюсь попробовать еще один ответ на статьи Кита Девлина об умножении.

Позвольте мне сразу заявить, что я говорю как учитель, а не как математик.Я не компетентен и не собираюсь спорить о значениях аксиом Пеано. Мой опыт заключается в основном в обучении K-10, от элементарной арифметики до базовой алгебры и геометрии. Я помню только отрывки из уроков математики в колледже, когда мы больше беспокоились о ядерной зиме, чем о глобальном потеплении.

Начну с нескольких вещей, по которым мы все можем согласиться…

Мы все в чем-то согласны

• Ученики начальной школы будут использовать сложение для решения начальных задач умножения.Что еще они могли сделать? Они еще не научились умножению.

• Таблица умножения изначально строится путем повторного сложения , когда наши ученики складывают (или считают) числа в каждой строке и столбце. Даже взрослые, когда их озадачивает математический факт, который они забыли, будут использовать повторное сложение, чтобы найти ответ.

• Повторное сложение дает правильный ответ для любого умножения целых чисел. Иногда это больше проблем, чем того стоит — кто хочет сложить 957 × 842? Но с помощью свойства распределения любое умножение целых чисел можно свести к повторному сложению:
  4 × 3 = (1 + 1 + 1 + 1) × 3 = 3 + 3 + 3 + 3

• Рациональное умножение чисел может быть вычислено как сложение частей. Так египетские книжники умножали дроби. Но будь осторожен! Чтобы вычислить части, нужно умножение, а точнее его обратное деление. Итак, чтобы использовать это как определение, нужно прибегнуть к круговой аргументации.

• Наконец, я думаю, мы все можем согласиться с тем, что повторное добавление является важным инструментом решения проблем. Повторное сложение может помочь учащимся решить простые задачи на умножение слов. Это не всегда работает, но иногда это самый быстрый способ разобраться в ситуации.

Так в чем проблема?

Так что же не так с определением «Умножение — это повторное сложение»? Возможно, неверно. — слишком сильное слово — возможно, в каком-то глубоком теоретическом смысле утверждение верно, по крайней мере, для целых чисел — я оставлю этот аргумент математикам. (См., Например, Как на самом деле определяется умножение в арифметике Пеано.) Но, говоря как учитель, эта фраза определенно может ввести в заблуждение.

Определить умножение как повторное сложение — значит сделать умножение подвидом сложения.

Это как если бы было два типа сложения: обычное, случайное, «дикое» сложение и специально выведенная разновидность сложения, которой мы дали название умножение . Неужели мы действительно хотим, чтобы наши ученики думали именно так? Умножение — это не просто подвид сложения. Умножение — это отдельное животное, самостоятельная операция.

И они не такие.

И они не совпадают.

• Сложение имеет обратную операцию вычитания.
• У умножения есть обратная операция — деление.

И они не совпадают, потому что операции не совпадают.

[Боковой путь: Ой! Я забыл, что у нуля нет обратного мультипликативного числа. Джонатан указал на мою ошибку.]

[Другое примечание: мне интересно, что повторное вычитание может быть полезным инструментом при решении некоторых задач деления, так же как повторное сложение может быть полезным инструментом в понимании умножения. Вычитание играет важную роль в алгоритме деления в столбик.Я полагаю, кто-то возразит, что это доказательство того, что умножение — это все-таки повторное сложение.]

Размерное мышление

Анализ размерностей означает рассмотрение измерений (единиц измерения) величины, чтобы помочь вам решить научную или техническую проблему.

Для добавления требуются идентичные блоки. Сумма всегда должна иметь те же единицы, что и слагаемые:

2 яблока + 3 яблока = 5 яблок

2 яблока + 3 апельсина = ??

Что дает вам это второе уравнение? Фруктовый салат? Чтобы сложить величины с разными единицами, нам нужно найти общий знаменатель. Яблоки и апельсины — это кусочки фруктов, поэтому…

2 яблока + 3 апельсина =

2 фрукта + 3 фрукта = 5 фруктов

Для умножения требуются разные единицы. У продукта разные единицы измерения как у множителя, так и у множимого.

2 корзины × 3 яблока в корзине = 6 яблок

Как сделать так, чтобы умножение получилось таким же, как и повторное сложение? Единственный способ сделать это — изменить единицы измерения.

3 см + 3 см = 6 см

Но…

2 см × 3 см = 6 см ²

Нам нужно…

2 длины × 3 см на длину = 6 см

Обычно мы не думаем об анализе размерностей, когда работаем с простыми числами на уроках математики. Но факт остается фактом: умножение меняет вещи так, как сложение — не .

Сложение одномерное, а умножение многомерное.

Вот почему правила сложения дробей и умножения дробей такие разные.Когда вы складываете положительные рациональные числа, вы всегда получаете сумму, превышающую любое из слагаемых. Но когда вы умножаете рациональные числа, все ставки отменяются — продукт может быть больше, меньше или находится где-то посередине между числами.

Язык имеет значение

Сложение: сложение + сложение = сумма. Дополнения взаимозаменяемы. Это выражается в том, что они имеют одинаковое название.

Умножение: множитель × множимое = произведение. Множитель и множимое имеют разные названия, хотя многие из нас не могут вспомнить, что есть что.

• множитель = «сколько или сколько»
• множимое = размер «единицы» или «группы»

Различные названия указывают на различие в функциях. Множитель и множимое концептуально не взаимозаменяемы. Это правда, что умножение коммутативно, но (2 ряда × 3 стула / ряд) не то же самое, что (3 ряда × 2 стула / ряд), хотя оба набора содержат 6 стульев.

Новый тип числа

В умножении мы вводим совершенно новый тип числа: множимое . В основе умножения лежит странная новая концепция, чего студенты никогда раньше не видели.

Множаемое — это отношение «это к тому».

Коэффициент — это не счетное число, а нечто новое, гораздо более абстрактное, чем все, что студенты видели до этого момента.

Отношение — это номер отношения.

Числа, кроме сложения и вычитания, считают, сколько у вас вещей. Если вы получите больше вещей, цифры станут больше. Если вы потеряете что-то, цифры станут меньше.Цифры измеряют количество печенья, лошадей, долларов, бензина и т. Д.

Множаемое не подсчитывает количество долларов и не измеряет объем бензина. Он говорит о соотношении между ними, в долларах за галлон, который остается неизменным независимо от того, покупаете ли вы много или мало.

Говоря нашим ученикам, что «умножение — это повторное сложение», мы упускаем из виду важность множимого. Но пока наши ученики не начнут ломать голову над концепцией соотношения и не поймут ее, они никогда не смогут полностью понять умножение.

Как же нам учить?

Если мы примем этот аргумент, если мы согласимся больше не определять базовое умножение как повторное сложение, то что тогда? Как это влияет на то, как мы обучаем?

В основном нам нужно сменить фокус с , как , на , почему .

Мы можем обучать умножению почти так же, как и сейчас, используя манипуляторы, расположенные в группы или ряды, изображения ситуаций умножения и прямоугольные массивы точек или блоков.Но вместо того, чтобы привлекать внимание нашего ученика к процессу сложения ответа, мы хотим сосредоточиться на том факте, что элементы расположены в группах равного размера .

Другими словами, мы учим наших студентов распознавать множимое:

• Научите детей использовать полезное слово «за» и узнавать единицу «это за то».
• Попросите их обозначить количество в своей рабочей тетради: 3 печенья на ученика, 5 цветов на вазу, 1 глаз на пришельца или что-то еще.

Если нам нужна простая крылатая фраза элементарного уровня для замены «умножение — это повторное сложение», как насчет этого?

Умножение считается по группам «это за это».

Как и любая подобная фраза, это утверждение не отражает всего, что влечет за собой умножение. Определение необходимо будет расширить по мере того, как учащиеся узнают о рациональных числах. «О, посмотри! Мы можем считать только часть группы, и мы можем измерять с помощью единицы, которая не является целым числом.«Когда-нибудь нашим студентам придется узнать о действительных числах, комплексных числах и умножении матриц. Даже в этом случае фраза отражает важный аспект многих ситуаций умножения, с которыми наши ученики встретятся в K-12: что есть множимое, некоторая величина «это на то».

Этот подход должен быть особенно полезен для тех разочаровывающих студентов — вы знаете, тех, у кого пустой взгляд — которые читают задачу со словом, а затем спрашивают: «Сложить или умножить?»

Полезный инструмент

Завершая круг, я возвращаюсь к своему первому посту «повторное добавление». Я хотел бы, чтобы вы рассмотрели обучающую силу диаграмм гистограмм для представления арифметических операций. Эти диаграммы используются в сингапурских книгах по начальной математике, и, по словам одного из комментаторов, они популярны в России и Австралии. Они даже начинают появляться в новых американских учебниках, где их иногда называют «ленточными диаграммами».

Вот некоторые преимущества модели с гистограммой:

• Столбчатые диаграммы разбивают числовую линию на части и делают числовые отношения менее абстрактными.

• Они предоставляют учащимся начальных классов графическую алгебру, которая может помочь им решить сложные задачи со словами.

• Студентам легко увидеть обратную связь между сложением и вычитанием или между умножением и делением.

• Поскольку они построены на числовой прямой, диаграммы естественным образом расширяются до рациональных и действительных чисел, и их применение увеличивается по мере того, как ваши ученики начинают понимать.

Дополнение — это «это И то»: складывание двух (или более) сумм вместе. Это основная диаграмма сложения / вычитания:

Умножение — это «сколько или сколько ЕДИНИЦЫ»: измерение или подсчет частей заданного размера. Вот схема умножения / деления:

Чтобы узнать больше о моделировании арифметических задач с помощью гистограмм, ознакомьтесь с моделью умножения Ray Gun Mad Scientist’s:

А вот пример гистограммы умножения в действии:

Хорошо, теперь твоя очередь

Я говорил достаточно долго.Как вы думаете:

• Действительно ли есть разница между умножением и повторным сложением, или я тут кланяюсь ветряными мельницами?

• Нужно ли учителям определять умножение ? Или задача учителя — привести множество примеров умножения в действии? Должны ли мы позволить студентам интуитивно воспринимать их собственные определения?

• Поможет ли студентам, если мы сменим фокус внимания с «как получить ответ» и научим их определять множимое, единицу «это на то»? Или это создаст новые трудности, о которых я не думал?

• Или мы уже так учим, только другими словами?

• Если вы учитель начальных классов, как вы научите своих учеников умножению?

• Неужели некоторые студенты невежественны, потому что, как бы мы это ни объясняли, они просто не обращают внимания?

• Пробовали ли вы использовать гистограммы для моделирования элементарных арифметических ситуаций? И если да, то как отреагировали ваши ученики?

Если вы хотите глубже изучить, как дети учатся сложению и умножению, я настоятельно рекомендую книгу Терезины Нуньес и Питера Брайанта « Дети, занимающиеся математикой».

Базовое сложение, вычитание, умножение и деление

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Умножение — Элементарная математика

С помощью рисунка или выражений это не что иное, как чудо, что 4 × 3 = 3 × 4. Дети, конечно, могут переставлять объекты, сгруппированные как 3 + 3 + 3 + 3, чтобы показать эквивалентность 4 + 4 + 4, но требует перестановки и не является «очевидной».

Но если одни и те же печенья разложены на подносе рядами и столбцами, совершенно очевидно, что как бы мы ни держали поднос, количество печений одинаковое. Даже если у нас есть предпочтение в отношении того, как мы помечаем первые два изображения ниже (настаивая, например, на том, что одно имеет размер 4 × 3, а другое — 3 × 4, чего математики не делают), у нас нет способа сделать такое назначение для последнего лотка. 4 × 3 просто равно 3 × 4, хотя обозначения не совпадают.

Если мы описываем картинку «три тарелки, четыре печенья каждая», используя выражение повторного сложения, то 4 + 4 + 4 более «естественное» для использования, чем 3 + 3 + 3 + 3.Но если мы описываем эту картинку выражением умножения, 3 × 4 и 4 × 3 одинаково верны; математически предпочтительного порядка для записи выражений умножения не существует [1].

Молодым ученикам полезно и возможно развить идею умножения, которая выдержит переход от целых чисел к дробям и десятичным дробям. Конечно, также полезно увидеть, как умножение может упростить вычисление, которое в противном случае потребовало бы повторного сложения, но это не должно быть первичным изображением умножения и, по этой причине, предпочтительно не его первым изображением.

В Think Math! Умножение связано в первую очередь с массивами и пересечениями и довольно рано связано с «комбинациями» (включая простые пары) вещей: улиц и проспектов, гласных и согласных в двухбуквенных словах и так далее. Идея повторного сложения также представлена, но позже, как пример другого типа задач, которые решает умножение.

Учитывая количество строк и столбцов в прямоугольном массиве, умножение сообщает нам, сколько элементов находится в массиве, не заставляя нас считать их один за другим или многократно добавлять (или пропускать счет) элементы в каждой строке или столбце.Когда элементы в строках и столбцах оказываются квадратами, выровненными бок о бок, умножение считает эти квадраты и, следовательно, сообщает нам площадь прямоугольника. Это изображение отлично работает даже с дробями и объясняет алгоритм умножения дробей.

Если прямоугольник три на четыре размещен «ровно» в одну сторону, он будет иметь 3 строки и 4 столбца ; если мы повернем его на 90 градусов, строки станут столбцами, а столбцы станут строками, так что у него будет 4 строки и 3 столбца . Если он удерживается под наклоном, не существует правила, которое говорит, какие строки вызывать, а какие столбцы, но в любом случае это не имеет значения; количество квадратов внутри него такое же. Также не имеет значения, в каком порядке мы обозначаем ширину и длину прямоугольника: 3 × 4 и 4 × 3 обозначают один и тот же прямоугольник, независимо от того, как прямоугольник удерживается. Два выражения, 3 × 4 и 4 × 3, называют одно и то же число. Комбинации: сколько возможных блоков можно сделать ровно из трех цветов и четырех форм? (Предположим, что каждый блок имеет один цвет и все блоки одинакового размера.) Вопросы такого рода предлагают другой образ (и использование) умножения.

Фактически, умножение подходит для любой ситуации, когда элементы одного набора объединяются в пары по порядку с элементами другого набора. Здесь элементы одного набора являются началом «слов», а элементы другого набора — окончанием.

Намек на связь с алгоритмом умножения.

См. Статью об умножении и делении для полной разработки алгоритма многозначного умножения, показывающего, как он является точной записью моделей пересечения / площади, показанных здесь.

В отличие от сложения, которое объединяет только одинаковые количества (сотни с сотнями, единицы с единицами), умножение создает все пары (3 × 7, 3 × 40, 3 × 200, 80 × 7, 80 × 40, 80 × 200)

Для выполнения многозначного умножения изображение «пересечений», показанное выше, неудобно, поскольку оно разбрасывает частичные произведения таким образом, что это мешает последнему обязательному этапу сложения. Для понимания того, как организовать вычисление, проще табличное представление комбинаций, а также вводится модель массива / области.

Этот способ размышления о многозначном умножении лежит в основе ведического умножения в Индии. Это может быть увлекательной культурной побочной темой для студентов, которые научились умножать многозначные числа.

Массивы и таблица умножения

В начале второго класса дети могут решать подобные проблемы и получать от них удовольствие.

Вот две красные буквы и три синих буквы: A, I, S, N, T . Сколько двухбуквенных слов можно составить, начиная с красной буквы и заканчивая синей буквой?

Сколько двухблочных башен точно такой формы можно сделать из этих блоков?
Вот два примера: .Сколько еще вы можете сделать?

Дети могут проводить эксперименты, создавая реальные комбинации, и они могут изобретать свою собственную систему для записи этих комбинаций. В случае двухбуквенных слов достаточно просто написать слова. С помощью башен дети могут их нарисовать или указать комбинации цветов более абстрактным способом. Когда количество возможностей достаточно мало, как в случае с двухбуквенными словами, второклассники быстро находят все возможности.

Перекрестки как модель для составления организованного списка

Когда количество возможностей больше, как в случае с проблемой блочной башни, дети склонны пропускать комбинации или составлять их двойные списки, если они не являются систематическими.

Вот один из способов визуализировать пары в этих двух экспериментах. Каждое пересечение представляет собой комбинацию. Сам символ × связан с изображением пересечения, пересечения линий.

Дети могут «водить» пальцем по «улице А» и «проспекту N» и маркировать светофор на этом перекрестке «ан.«Они могут проверить, есть ли у них башня для каждого пересечения: например, пересечение синего низа и красного верха. Когда второклассники впервые проводят эти эксперименты, они учатся составлять систематические списки, а не умножать. Но мы можем видеть, к чему это ведет: пересечения сами по себе перечисляют комбинации, которые ищут дети, и помогают им понять, как организовать эти списки; количество пересечений можно найти путем умножения, и дети получают предварительный обзор этих идей умножения.

Таблицы как модель для составления организованного списка

Таблицы

одинаково хороши для представления комбинаций и организации задачи их перечисления. Ячейки внутри таблицы (и тщательно избегая путаницы с ячейками «заголовка» над каждым столбцом и слева от каждой строки) снова показывают, как умножение отвечает на вопрос «сколько пар можно составить?»

Mathematics широко использует обе структуры — таблицы и пересекающиеся линии.

Умножение часто представлено массивами смежных квадратов — «модель площади» умножения — или массивами точек или других мелких объектов. Первые визуально больше похожи на внутреннюю часть таблиц; последние визуально больше похожи на перекрестки. Якорь

Создание основных фактов

Первые шаги

Когда мы видим одинаковые тройки чисел — 3, 5, 15; 4, 3, 12; 2, 5, 10; 6, 4, 24 — появляясь в разных контекстах, они начинают казаться знакомыми еще до того, как будут предприниматься какие-либо сознательные усилия по их запоминанию.Фактически, целенаправленное, целенаправленное усилие, которое кажется необходимым для некоторых троек (например, 7, 8, 56), может быть связано именно с тем, что существует так мало естественных контекстов, в которых эти тройки иначе появляются. Многие случаи, не связанные с школой, помогают построить пятикратную таблицу: умение определять время в минутах на часах, обращаться с пятаками, замечать свои руки. Следующие ниже идеи представляют несколько контекстов для одних и тех же основных фактов, чтобы разнообразить практику (чтобы сделать ее интересной и создать богатое разнообразие образов), так что к тому времени, когда дети попытаются запомнить факты умножения, они уже настолько знакомы с наиболее распространенными. те, что они знают их «холодно», а количество оставшихся фактов, требующих механического запоминания, совсем невелико (всего пятнадцать!).

Удвоение и деление пополам

В первом классе дети учатся удваивать ([[мысленная арифметика | мысленно]) все целые числа вплоть до 12. Второклассники практикуют эти базовые удвоения дальше, используя их вместе со своими развивающимися представлениями о числовом значении, чтобы удваивать (мысленно) от целых чисел до 50. Дети этих классов также учатся находить половину четных чисел, получаемых в результате такого удвоения.

Малые массивы

В Думай математикой! , вторая половина второго класса дает учащимся большой опыт работы с небольшими массивами, из которых они могут запоминать небольшие факты умножения.В одном задании учитель может поднять такой массив и спросить: «Сколько строк? Сколько столбцов? Сколько квадратов? »

Учащиеся, которые еще не владеют сложением, могут использовать счет сложения или пропуска, чтобы вычислить количество квадратов. Связывание размеров массива — количества строк и столбцов — с количеством маленьких квадратов устанавливает факт умножения.

Затем учитель может держать тот же самый массив в этой ориентации и задавать те же вопросы.

Строки и столбцы меняются местами, но количество квадратов остается прежним.

Учитель может сделать из этого живую игру, варьируя, какой массив удерживается (2 × 3, 3 × 3, 4 × 5 и т. Д., Никогда не с более чем 5 строками или столбцами, потому что большие числа слишком трудно узнавать без утомительного подсчета), и ученики довольно быстро начинают вспоминать, сколько квадратов в этих знакомых прямоугольниках.

Тот факт, что прямоугольник, удерживаемый горизонтально или вертикально, имеет одинаковое количество маленьких квадратов внутри, дает наглядное представление о том, почему умножение коммутативно.

Пересечение вертикальных и горизонтальных линий дает другое изображение для умножения — 2 вертикальные линии пересекают 3 горизонтальные линии в 6 пересечениях — и другой контекст, в котором можно отрепетировать факты. Они могут нарисовать их или поиграть с прозрачными карточками, сначала пытаясь предсказать количество пересечений, а затем перекрывая прозрачные пленки для прямого подсчета, чтобы проверить свои прогнозы. Карты со слотами в них тоже забавны. Дети берут пару и, как и в случае с прозрачными пленками, пытаются представить количество пересечений, прежде чем они начнут экспериментировать, кладя одну карточку на другую, чтобы проверить, верен ли их прогноз.Если карта с 2 вертикальными прорезями помещается поверх карты с 5 горизонтальными прорезями, мы можем видеть сквозь двойной слой только на 10 пересечениях.

Перекрестки для уточнения умножения на 0 и 1. «Представьте себе крошечный город с тремя дорогами, идущими с востока на запад…» Проведите пальцем по воздуху по горизонтали, чтобы лучше понять, что означает «восток-запад». Затем «нарисуйте» еще две дороги с востока на запад прямо в воздухе, чтобы дети могли представить себе их в голове. Позже вы или ребенок нарисуете их на доске.«… И только одна дорога, идущая с севера на юг».

В воздухе укажите пальцем дорогу с севера на юг.

«Давайте нарисуем карту этого крохотного городка. Вот дороги с востока на запад ».

Нарисуйте нерегулярную границу города и нарисуйте на ней три параллельные горизонтальные линии от одной стороны города к другой стороне (и немного выходящие за границу города, чтобы указать, что они продолжают идти в соседние районы).

«На карте дороги выглядят как три горизонтальные линии.Кто хотел бы нарисовать дорогу с севера на юг? »

Вы можете снова указать направление пальцем в воздухе, но не прямо на карте. Пригласите кого-нибудь нарисовать.

«Город установил светофор на каждом перекрестке (указывать на перекрестки). Сколько там светофоров? »

Поиграйте с изображением.

«Что, если бы город построил еще одну дорогу с востока на запад? Сколько будет пересечений? »

Умножение любого числа на 1 дает это число; умножение любого числа на 0 дает 0.Дети, которых учат этим просто как правилам запоминания, без некоторого понимания, часто искажают правила, путая их друг с другом. (Разве 1 ​​умноженное на число дает 1 или число?) Изображение крошечного городка помогает установить, почему 1 умноженное на любое число дает это число. (При наличии только одной вертикальной линии количество пересечений будет таким же, как и количество горизонтальных линий.)

Карты с 0–5 слотами также могут быть особенно полезны. Когда карта с одной вертикальной прорезью помещается поверх карты с тремя горизонтальными прорезями, три пересечения появляются как единственные «окна» в паре карт. Изменение того, какая карта находится сверху, какая вертикальная, а какая горизонтальная, не имеет значения. Если одна карта имеет единственный слот, количество пересечений будет соответствовать количеству слотов на другой карте, когда они накладываются друг на друга (а другие слоты перпендикулярны одному слоту). Изображение слота особенно ясно показывает, почему умножение на 0 всегда дает 0.

Этот урок дает прекрасную возможность использовать слова горизонтальный и вертикальный в контексте и связать их использование в качестве направлений на картах с Востоком, Западом, Севером и Югом как направлениями на земле.(См. Раздел «По горизонтали» и «По вертикали», чтобы увидеть распространенные заблуждения относительно идей, которые представляют эти слова.)

Построение таблицы умножения

Студенческий проект для второго класса: ученики используют сетку, которая устроена как таблица умножения, но не имеет строки или столбца для нуля. Используя лист бумаги в форме буквы «L», они выбирают часть сетки; в правом нижнем углу выделения они пишут количество захваченных квадратов (что совпадает с площадью прямоугольника, если каждый маленький квадрат представляет одну квадратную единицу площади).

Обратите внимание, что число вверху, ближайшее к синей границе, дает ширину зеленого прямоугольника, количество столбцов квадратов; число слева, ближайшее к синей границе, дает высоту зеленого прямоугольника, количество строк в нем.

Если мы переместим границу прямо на один шаг вниз, мы добавим новую строку, не изменяя количество квадратов в строке.

При таком способе мышления скажем, что 6 (количество квадратов в предыдущем прямоугольнике, 2 × 3) плюс 3 (количество квадратов в новой строке) равно 9 (количество квадратов в новом прямоугольнике).Другой способ описать новый прямоугольник — 3 × 3. Итак, 2 × 3 + 3 = 3 × 3.

Этот прямоугольник имеет одинаковую ширину и высоту, поэтому он квадрат. Число в углу (количество крошечных квадратов внутри него) называется квадратным числом.

Перемещение по диагонали — один шаг «на юг» и один шаг «на восток» (или один шаг вниз и один шаг вправо) — дает еще одно квадратное число.

Две диагональные ступеньки на юго-восток дают еще одно квадратное число.

Интересно, что если вы начнете с квадратного числа (в данном случае 16) и сделаете один шаг на северо-восток

или юго-запад

получившееся число ровно на 1 меньше числа в квадрате, с которого вы начали. В этом примере показано, что прямоугольник 3 × 5 содержит на один квадрат меньше, чем прямоугольник 4 × 4. См. Статью о разнице квадратов, чтобы узнать больше об этой интригующей схеме и еще одном особенно эффективном способе для студентов практиковать факты, развивая новые и полезные математические идеи.

Симметрия таблицы умножения

Подсчет квадратов в прямоугольниках дает понять, почему 3 × 4 = 4 × 3. Оба являются способами описания этого прямоугольника . И даже если мы решим зарезервировать одно из этих обозначений для , а другое обозначение для , они все равно будут равны.

Поскольку умножение является коммутативным, то есть потому, что 2 × 6 = 6 × 2, 3 × 5 = 5 × 3 и так далее, таблица умножения симметрична относительно диагонали северо-запад-юго-восток.Эта диагональ, желтая на этих иллюстрациях, содержит квадратные числа.

Избавившись от отвлекающих цифр и стрелок, мы видим три области: диагональ с квадратными числами, зеленую область с другими товарами и белую область с теми же числами, что и в зеленой области.

Это очень хорошая новость для всех, кто пытается запомнить факты умножения! (См. «Сколько фактов нужно узнать?» Ниже.)

Умножение на 10 и 100

Строится: 7 стержней — 70 кубиков

Умножение на 5 и 50

Дети, которые умеют умножать на 10 и могут брать половину, затем могут использовать эти навыки для умножения на 5.Например, 7 × 5 составляет половину от 7 × 10, поэтому это 35. В конечном счете, 7 × 5 следует просто распознать само по себе — один из «основных фактов», но двухэтапная процедура (умножение на 10 и затем взять половину результата), также полезно знать и установить хорошую связь с 5-кратными фактами. Точно так же, зная, что 50 составляет половину от 100, мы можем видеть, что 50 семерок составляют половину от 100 семерок, поэтому 50 × 7 составляет половину 100 × 7: мы можем умножить любое число на 50, умножив на 100, а затем взяв половину. Дети, которые хорошо усвоили это, могут легко умножить в уме 18 × 5, думая «половина от 180.«Поскольку умножение и деление могут выполняться в любом порядке с одним и тем же результатом, мы можем сначала взять половину (из 18), а затем умножить на 10.

Сколько фактов нужно узнать?

Если умножение на ноль и единицу понятно, эти факты (голубой) не нужно запоминать. Если симметрия таблицы понятна (3 × 4 = 4 × 3, коммутативность умножения), эти факты (темно-синий) не нужно запоминать. К тому времени, когда дети работают над практикой фактов, квадратные числа (желтые) уже выучены, а «простые» факты (розовые) уже усвоены (удвоение, умножение на 10 и умножение на 5).На данный момент осталось запомнить только 15 фактов, выделенных зеленым. 2 = 1 \} | & = & 2.\ end {align} \] Обратите внимание, что \ (| \ emptyset | = 0 \), потому что пустой набор не содержит никаких элементов.

Это становится более интересным, когда мы рассматриваем мощность * объединения или пересечения двух или более множеств.

* Эта ссылка мощности приведет вас к не полностью отредактированному, но интересному погружению в мощность бесконечных множеств.

Пример \ (\ PageIndex {2} \)

Определите \ (| A \ cup B | \) и \ (| A \ cap B | \), если \ (A = \ {2,5 \} \) и \ (B = \ {7,9,10 \ } \).

Раствор

Поскольку \ (A \ cup B = \ {2,5,7,9,10 \} \) и \ (A \ cap B = \ emptyset \), ясно, что \ (| A \ cup B | = 5 \) и \ (| A \ cap B | = 0 \).

Пример \ (\ PageIndex {3} \)

Определите \ (| A \ cup B | \) и \ (| A \ cap B | \), если \ (A = \ {2,5 \} \) и \ (B = \ {5,9,10 \ } \).

Раствор

Поскольку \ (A \ cup B = \ {2,5,9,10 \} \) и \ (A \ cap B = \ {5 \} \), ясно, что \ (| A \ cup B | = 4 \) и \ (| A \ cap B | = 1 \).

практическое упражнение \ (\ PageIndex {1} \ label {he: addmult-01} \)

Пусть \ (A = \ {n \ in \ mathbb {Z} \ mid -5 \ leq n \ leq3 \} \) и \ (B = \ {n \ in \ mathbb {Z} \ mid -3 \ leq n \ leq5 \} \). Оцените \ (| A \ cap B | \) и \ (| A \ cup B | \).

Разница между двумя последними примерами состоит в том, имеют ли два набора \ (A \) и \ (B \) непустое пересечение. Два набора \ (A \) и \ (B \) являются непересекающимися , если \ (A \ cap B = \ emptyset \). Набор множеств \ (A_1, A_2, \ ldots, A_n \) называется попарно непересекающимися , если \ (A_i \ cap A_j = \ emptyset \) всякий раз, когда \ (i \ neq j \).

Пример \ (\ PageIndex {4} \)

Пусть \ (A = \ {1,0, -1 \} \), \ (B = \ {- 2,0,2 \} \), \ (C = \ {- 2,2 \} \) и \ (D = \ {3,4,5 \} \). Тогда \ (A \), \ (C \) и \ (D \) попарно не пересекаются, как и \ (B \) и \ (D \), но \ (A \), \ (B \), и \ (C \) нет.

Теорема \ (\ PageIndex {1} \): принцип сложения

Если конечные множества \ (A_1, A_2, \ dots, A_n \) попарно не пересекаются, то \ [| A_1 \ cup A_2 \ cup \ cdots \ cup A_n | = | A_1 | + | A_2 | + \ cdots + | A_n |. \]

Используйте принцип сложения, если мы можем разбить проблемы на случаев и подсчитать, сколько элементов или вариантов выбора у нас есть в каждом случае.Общее количество — это сумма этих индивидуальных подсчетов. Идея состоит в том, что вместо того, чтобы считать большой набор, мы делим его на несколько меньших подмножеств и подсчитываем размер каждого из них. Мощность исходного набора — это сумма мощностей меньших подмножеств. Этот подход «разделяй и властвуй» отлично работает только тогда, когда множества попарно не пересекаются.

Пример \ (\ PageIndex {5} \)

Чтобы найти количество студентов, присутствующих на лекции, учитель подсчитывает, сколько студентов находится в каждой строке, затем складывает числа, чтобы получить общее количество.

Когда множества не пересекаются, принцип сложения не дает нам правильного ответа, потому что элементы, принадлежащие пересечению, считаются более одного раза. Мы должны компенсировать завышенный подсчет, вычитая количество случаев, когда эти элементы были завышены. Самый простой случай охватывает два набора.

Теорема \ (\ PageIndex {2} \ label {pie} \): принцип включения-исключения (PIE)

Для любых конечных множеств \ (A \) и \ (B \) имеем \ [| A \ cup B | = | A | + | B | — | A \ cap B |.\]

Проба

Обратите внимание, что \ (A \ cup B \) — это непересекающееся объединение трех множеств \ [A \ cup B = (AB) \ cup (A \ cap B) \ cup (BA). \] Ясно, что \ (| AB | = | A | — | A \ cap B | \) и \ (| BA | = | B | — | A \ cap B | \). Следовательно, \ [\ begin {align} | A \ cup B | & = & | A-B | + | A \ cap B | + | B-A | \\ & = & (| A | — | A \ cap B |) + | A \ cap B | + (| B | — | A \ cap B |) \\ & = & | A | + | B | — | A \ cap B |, \ end {align} \] что нам и нужно доказать.

Принцип включения-исключения также работает, если \ (A \) и \ (B \) не пересекаются, потому что в таком случае \ (| A \ cap B | = 0 \), сводя PIE к принципу сложения.

Пример \ (\ PageIndex {6} \ label {eg: pie} \)

Предположим, что текущий набор в колледж составляет 4689, с 60 студентами, изучающими MATH 210, 42 изучающими CSIT 260 и 24 изучающими оба. Сколько разных студентов вместе учатся на этих двух курсах? Другими словами, определите количество студентов, которые изучают MATH 210 или CSIT 260.

Раствор

Пусть \ (A \) будет набор студентов, изучающих MATH 210, и \ (B \) набор студентов, изучающих CSIT 260, Тогда \ (| A | = 60 \), \ (| B | = 42 \ ) и \ (| A \ cap B | = 24 \).Мы хотим найти \ (| A \ cup B | \). Согласно PIE, \ [| A \ cup B | = | A | + | B | — | A \ cap B | = 60 + 42-24 = 78. \] Таким образом, 78 студентов сдают MATH 210 или CSIT 260.

Пример \ (\ PageIndex {7} \)

Среди 4689 студентов 2112 из них заработали не менее 60 кредитных часов, а 2678 из них — не более 60 кредитных часов. Сколько студентов набрало ровно 60 часов?

Раствор

Пусть \ (A \) будет набором студентов, заработавших не менее 60 кредитных часов, а \ (B \) будет набором студентов, которые заработали не более 60 кредитных часов. Мы хотим найти \ (| A \ cap B | \). Согласно PIE, \ [4689 = | A \ cup B | = | A | + | B | — | A \ cap B | = 2112 + 2678- | A \ cap B |. \] Следовательно, \ [| A \ cap B | = (2112 + 2678) -4689 = 101. \] 101 студент набрал ровно 60 кредитных часов.

практическое упражнение \ (\ PageIndex {2} \ label {he: addmult-02} \)

Посещаемость двух матчей по футболу колледжей подряд составила 72397 и 69211 человек соответственно. Если 45713 человек посетили обе игры, сколько разных людей смотрели игры?

практическое упражнение \ (\ PageIndex {3} \ label {he: addmult-03} \)

Посещаемость двух матчей по футболу колледжей подряд составила 72397 и 69211 человек соответственно.Если 93478 разных людей посетили эти две игры, сколько человек пришло на обе?

Иногда легко работать с дополнением набора.

Лемма \ (\ PageIndex {3} \)

Для любого конечного множества \ (S \) имеем \ [| \ overline {S} | = | {\ cal U} | — | S |, \], где \ ({\ cal U} \) — универсальное множество, содержащее \ (S \).

Пример \ (\ PageIndex {8} \)

В примере 6, поскольку 78 студентов сдают либо MATH 210, либо CSIT 260, количество студентов, не сдающих ни один из них, равно \ (4689-78 = 4611 \).

Принцип включения-исключения можно распространить на любое количество наборов. Ситуация более сложная, потому что некоторые элементы могут быть подсчитаны дважды, некоторые — троекратно и т. Д. Чтобы дать вам представление об общем результате, вот принцип включения-исключения для трех наборов.

Теорема \ (\ PageIndex {1} \)

Для любых трех конечных множеств \ (A \), \ (B \) и \ (C \), \ [| A \ cup B \ cup B | = | A | + | B | + | C | — | A \ cap B | — | A \ cap C | — | B \ cap C | + | A \ cap B \ cap C |.\ nonumber \]

Проба

Объединение \ (A \ cup B \ cup C \) — это несвязное объединение семи подмножеств: \ [\ displaylines {A- (B \ cup C), \ quad B- (C \ cup A), \ quad C — (A \ чашка B), \ quad (A \ cap B) — (A \ cap B \ cap C), \ cr (B \ cap C) — (A \ cap B \ cap C), \ quad (C \ cap A) — (A \ cap B \ cap C), \ quad \ mbox {и} \ quad A \ cap B \ cap C. \ cr} \ nonumber \] Мы можем применить аргумент, аналогичный тому, который используется в объединение двух наборов для завершения доказательства. Детали оставляем в качестве упражнения.

практическое упражнение \ (\ PageIndex {4} \ label {he: addmult-04} \)

Группа студентов утверждает, что каждый из них видел хотя бы одну часть трилогии Назад в будущее . Быстрое поднятие рук показывает, что

Новая математика: Руководство для родителей | Разобрался

Вас смущает незнакомые математические задачи в домашнем задании вашего ребенка? Подход к обучению математике в последние годы изменился. Приведенные ниже примеры, созданные с помощью специалиста по математике Хайди Коэн, могут помочь вашему ребенку освоить «новую математику».”

Десять рамок — это набор из 10 прямоугольников с точками в некоторых или всех прямоугольниках. Дети могут увидеть, как разные комбинации чисел дают в сумме 10. Десятикадровый просмотр особенно хорош для демонстрации того, как работает вычитание.

В числовой связке линии используются для связывания группы чисел вместе, показывая, как они связаны. На первом рисунке соотношение между числами 3 и 10 показано добавлением числа 7 к пустому кружку (3 + 7 = 10). Это помогает детям понять, как одно число можно разбить на более мелкие части.

В открытой числовой строке нет цифр, которые уже были записаны. Учащийся может использовать любой номер в качестве места начала. (Здесь 37 — это начальная точка, потому что именно столько ярдов прошел Бретт. Затем добавляются 26 ярдов, которые прошел Адам.) Открытая числовая линия позволяет детям складывать или вычитать визуально. Его часто используют для решения словесных задач.

Декомпозиция (также называемая «развернутой формой»)

Декомпозиция — это стратегия решения математических задач путем разбиения числа на его цифровые значения.Например, 37 превращается в 30 и 7. После того, как вы разделите число, вы можете сложить или вычесть отдельные цифровые значения, чтобы получить ответ.

Основание десять — это стратегия решения задач сложения и вычитания с использованием таблицы, разделенной на сотни, десятки и единицы. Вероятно, вы встретите термин «перегруппировка», используемый для этого метода. Каждое число попадает в таблицу в соответствии с его разрядовым значением. Например, 43 будет означать 4 десятка и 3 единицы. Это помогает детям понять, когда «одалживать» и «переносить» числа из одной разряда в другую.

Умножение прямоугольников — это метод разбиения чисел на цифровые значения. В таблице числа разбиты по значениям и отдельно умножены. После умножения каждого числа общие значения складываются. Этот метод может быть полезен для детей, у которых есть проблемы с традиционным умножением с использованием больших чисел.

Модель площади использует длину и ширину прямоугольника или квадрата для решения задачи умножения. Каждая фигура рассчитывается, и ответы складываются.Это еще один способ сделать математику более наглядной для детей.

Как и модель области, массив представляет собой набор объектов, которые представляют собой числа. Эта модель часто используется, чтобы помочь детям увидеть различные качества сложения и умножения.

Столбиковое моделирование (также известное как «ленточная диаграмма»)

Столбиковая модель использует столбцы для визуального представления чисел и неизвестных в словесной задаче. Это может помочь детям увидеть, как количества сравниваются друг с другом. Дети могут адаптировать модель штанги для решения многих задач.

основных математических символов | Словарь

математика (BrE) | по математике (AmE) — это сокращенная форма от по математике

На этой странице перечислены основные математические символы с их названиями и примерами на английском языке.

+
плюс / дополнительный знак

Знак плюс означает:

а. понятие

положительное

Любое число больше нуля является положительным числом и может быть написано со знаком плюс перед ним или без него.

Таким образом, +5 (плюс пять) и 5 ​​(пять) — это одно и то же число.

г. операция сложения

3 + 5 = 8
три плюс пять равняется восьми
пять добавлено к трем дает восемь
три добавлено к пяти дает восемь
если сложить пять к трем, получится восемь

Сложение дает нам сумму . В 3 + 5 = 8 получается восемь.

—

знак минус / знак вычитания

Знак минус представляет:

а.понятие негатива

Любое число меньше нуля является отрицательным числом и записывается со знаком минус перед ним.

-3
минус три

г. операция вычитания

8-5 = 3
восемь минус пять равняется трем
пять вычитаем из восьми равны трем
если вы вычитаете пять из восьми, вы получаете три
, если вы берете пять из восьми, вы получаете три

Вычитание дает нам разницу . В 8-5 = 3 разница в три.

×

знак умножения / знак умножения

Знак раз представляет:

умножение

5 x 6 = 30
пять умножить на шесть равно тридцать
пять умножить на шесть равно тридцать
пять шестерок равно тридцать
если умножить 5 на 6, получится тридцать

Умножение дает нам произведение . В 5 x 6 = 30 получается тридцать.

÷ OR /

разделительный знак

Знак деления означает:

отдел

15 ÷ 3 = 5
15/3 = 5
пятнадцать делить на три равно пять
пять делятся на пятнадцать трижды
если пятнадцать разделить на три, получится пять
если три разделить на пятнадцать, получится пять

Дивизион

дает нам отношение к .При 15 ÷ 3 = 5 частное равно пяти.

Давайте резюмируем вышеупомянутые четыре операции как:

эксплуатация			счет
дополнение	плюс	2 + 2 = 4	сумма
вычитание	«минус»	5–3 = 2	разница
умножение	«раз»	3 х 5 = 15	товар
отделение	«разделить на»	21/7 = 3	частное

=

знак равенства

Знак равенства представляет равенство :

3 + 4 = 7
три плюс четыре равно семь

Обратите внимание, что мы обычно говорим, что равно , НЕ равно:

• два плюс два равно четыре
• два плюс два равны четыре

<
менее

3 <4
три меньше четырех

>

больше

4> 3
четыре больше трех

≠

НЕ равно

x ≠ z
x не равно z

≥

больше или равно

x ≥ z
x больше или равно z

≤

меньше или равно

z ≤ x
z меньше или равно x

¾

дробь

см. Дроби

.

десятичный разделитель | точка

Десятичный разделитель отделяет целое число от дробной части справа:

1,23

В английском языке десятичным разделителем обычно является точка (.). Обратите внимание, что в некоторых языках десятичным разделителем является запятая (,).

см. Десятичные дроби

,

Разделитель тысяч

В английском языке разделитель тысяч разделяет целые числа на группы по три справа.

10 987 654 321

В английском языке разделителем тысяч обычно является запятая (,).Обратите внимание, что в некоторых языках разделителем тысяч является точка (.) Или иногда пробел ().

см. Тыс.

%

знак процента

Знак процентов указывает число или соотношение в виде доли от 100 ( процентов ).

40%
сорок процентов
За нее проголосовало всего сорок процентов людей.
Какой процент проголосовал за нее? Сорок процентов.