|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации… Интересное: Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными. Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Обучение математике по методике Зайцева довольно интересное. Как и методика обучения чтению по Зайцеву, математика не имеет возрастного ограничения. Суть и технология обучения математике по методике Зайцева. Обучение счету проводится по карточкам, с названием «Стосчет», которые состоят из цифр до 100 и их количественного состава. К примеру, все карточки представляют собой таблички 2 строки*5 столбцов. И каждая цифра означает количество закрашенных ячеек. При переходе к изучению «десятков», используют несколько карточек: количество закрашенных карточек, равных первой цифре (десятку) и карточка единиц с аналогично закрашенными ячейками по необходимому вам количеству. Как и с таблицами Зайцева для чтения, располагать их надо по стенам детской на уровне глаз ребенка, а в группах — несколько выше для обзора видимости всем детям. Каждый раз изучая новые числа, вы вывешиваете дополнительные карточки и так у вас получится обучающий паровозик из цифр, благодаря чему будет видно порядок чисел, состав числа. И так, постепенно в игровой ненавязчивой форме закрепляются знания малыша. Что интересно, так автор уже начиная с первого десятка, предлагает познакомить с простыми действиями над числами (сложить и вычесть). Согласитесь, необычно для математики, мы привыкли, что надо изучить минимум 2-3 десятка и лишь потом начинать над ними действия. Все примеры решаются на этой же цифровой цепочке — ребенок просто перемешается вперед или назад на заданное число, тем самым получая ответ. Этапы освоения математики. Ребенок быстро осваивает первый десяток и достаточно в скором времени свободно оперирует в пределах сотни. «Мне в сотне тесно» (изучение до тысячи). «Пять в кубе»(сложные действия с цифрами). «Пифагор (таблица умножения). «Платоновы тела»(геометрические навыки). «Орнамент»(планиметрия и стереометрия). 5. Организация воспитателем самостоятельной деятельности детей по формированию элементарных математических представлений. В соответствии с Федеральными государственными требованиями математическое развитие дошкольников осуществляется через совместную образовательную деятельность воспитателя и детей, а также через самостоятельную познавательно-игровую деятельность самих детей. Ребенок-дошкольник, даже старшего возраста – существо играющее, и наибольший интерес у него вызывает игра, игровые упражнения. Но, очень часто методика обучения элементарным математическим представлениям должна не только дать простейшие знания и умения, но и на их основе развивать у дошкольника мышление, воображение, смекалку, быстроту реакции. На современном этапе, воспитатели дошкольных учреждений осознают важность организации самостоятельной математической деятельности детей, но при этом в реальной практике не уделяют должного внимания созданию условий и использованию специальных приемов руководства этой деятельностью. Критерии эффективности самостоятельной математической деятельности: уровень детской самостоятельности; познавательная активность детей; уровень мотивации. Для реализации цели проводится работа по созданию специальной предметно-развивающей среды, детям предлагаетсяв самостоятельной деятельности комплекс занимательного игрового математического материала, используются специальные приемы руководства. Проводится целенаправленная работа, как с воспитанниками, так и с их родителями. Организуя уголок занимательной математики, воспитатели исходят из принципа доступности игр детям, помещают в уголок такие игры и игровые материалы, освоение которых детьми возможно на разном уровне. Для организации детской деятельности используются разнообразные развивающие игры, дидактические пособия, материалы позволяющие «потренировать» детей в установлении отношений, зависимостей. Соотношение игровых и познавательных мотивов в дошкольном возрасте определяет, что наиболее успешным процесс познания будет в ситуациях, требующих сообразительности детей. В детском саду, в утреннее и вечернее время, проводятся игры математического содержания, настольно – печатные, такие как: «Домино фигур», «Составь картинку», «Арифметическое домино», «Логическое лото», «Лото», «Найди отличие», игры в шашки и шахматы, разгадывание лабиринтов и другие. Ход и результат упражнений в организации самостоятельной математической деятельности детей дошкольного возраста находятся под непосредственным наблюдением и контролем. Вся работа в уголке организовывается с учетом индивидуальных особенностей детей. Игра предлагалась ребенку, ориентируясь на уровень его умственного и нравственно-волевого развития, проявления активности. Воспитатели вовлекают в игры малоактивных, пассивных детей, заинтересовывают их и помогают освоить игру. Таким образом, формирование познавательного интереса у дошкольников к математике успешно осуществляется в процессе использования занимательного математического материала. Создание специальной предметно-развивающей среды, предоставление детям в самостоятельной познавательно-игровой деятельности комплекса занимательного игрового математического материала, использование специальных приемов руководства способствует росту самостоятельности, и познавательной активности детей, а также повышает мотивацию дошкольников в этой деятельности. Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… |
Принципы технологии н.А.Зайцева
Есть несколько основных принципов, которые должны соблюдать при занятии по любому из пособий или методик Зайцева.
1) Первый
принцип касается организаций занятий. Преподавание по Зайцеву — это
преподавание в игре. Раскованность
обстановки (дети могут сидеть на полу,
заниматься на спортивных снарядах, и
это даже поощряется) — непременное
условие занятий. По словам Николая
Зайцева, основу любой учебной игры
составляют поиск и выбор. «Играя»,
дети учатся читать, разбивать слова на
слоги, ставить ударение, делать
звукобуквенный анализ слов, составлять
предложения, считать, писать.
Раскованность
обстановки (дети могут сидеть на полу,
заниматься на спортивных снарядах, и
это даже поощряется) — непременное
условие занятий. По словам Николая
Зайцева, основу любой учебной игры
составляют поиск и выбор. «Играя»,
дети учатся читать, разбивать слова на
слоги, ставить ударение, делать
звукобуквенный анализ слов, составлять
предложения, считать, писать.
2)
Второй принцип касается представления
материала ребёнку. По Зайцеву весь
материал должен быть компактно выражен
и размещён на стене. В любом пособии
Зайцева вы найдёте несколько плакатов
с материалом по заданной теме, которые
и необходимо разместить на стенах вашего
дома или заведения, в котором вы
занимаетесь со своими детьми. Обязательным
условием работы является размещение
сразу всех таблиц комплекта на стенах
учебного помещения.
Софья
Ковалевская рассказывала, что в ее
комнате (ей было 11 лет) делали ремонт,
не хватило обоев, и все стены обклеили
лекциями по дифференциальному исчислению
Остроградского.
3) Следующий принцип касается инструментов, с помощью которых происходит занятие. Весь инструментарий кроме незначительных деталей дается в руки ребёнку сразу с первого дня. Разными будут цели, задачи, приемы, возраст, ситуации — т.е. игры. Они будут служить отправными точками в развитии самой развивающей среды.
4)
И последний принцип — учитывать и
использовать особенности детей в
педагогических целях. Так, например,
Зайцев советует использовать желание
детей подражать взрослым. Взрослые
должны не просто учить ребёнка, а читать
и играть вместе с детьми. Преподаватель
должен обращаться интересы и особенности
ребёнка на пользу обучению. Хочет ребёнок
петь – замечательно. Пусть поёт, а
попутно с помощью взрослых разбирается
в словах песни. Хочет малыш потанцевать
– тоже хорошо. А слово танцы ты написать
сначала сможешь?
Хочет ребёнок
петь – замечательно. Пусть поёт, а
попутно с помощью взрослых разбирается
в словах песни. Хочет малыш потанцевать
– тоже хорошо. А слово танцы ты написать
сначала сможешь?
Вывод: Существует ряд принципов технологии Зайцева Н.А.:
Первый принцип касается организаций занятий;
Второй принцип касается представления материала ребёнку;
Следующий принцип касается инструментов, с помощью которых происходит занятие;
И последний принцип — учитывать и использовать особенности детей в педагогических целях.
Все методики и пособия Зайцева можно разделить на несколько групп: 1. обучение чтению;
2. каллиграфия; 3. общее развитие;
4. грамматика русского языка;
5. математика.
Пособия для обучения чтению по Зайцеву:
• широко распространенные кубики Зайцева;
• складовые картинки;
• читай
и пой.
Кубики на сегодняшний день являются наиболее распространённым пособием Зайцева. Данное пособие представляет собой набор кубиков, на гранях которого написаны всевозможные склады, из которых ребёнку предстоит составлять и читать слова. Кубики различаются по размеру, цвету и звучанию (внутри каждого вида кубика свой наполнитель). Всё это предназначено облегчить восприятие материала детьми. Кроме кубиков в набор пособия входят 6 таблиц с написанными складами, для размещения их на стенах, учебник для родителей и аудиокасетта с попевками.
С
кладовые
картинки – представляют собой
карточки с нарисованными изображениями
по различной тематике. Сверху над каждым
изображением написано название того,
что нарисовано со складами, выделенными
различным цветом. Подразумевается, что
ребёнок не только учится читать, но и
узнаёт полезную информацию об окружающем
его мире. На обратных сторонах карточек
приводятся написание того же слова
строчными буквами, печатными и прописными.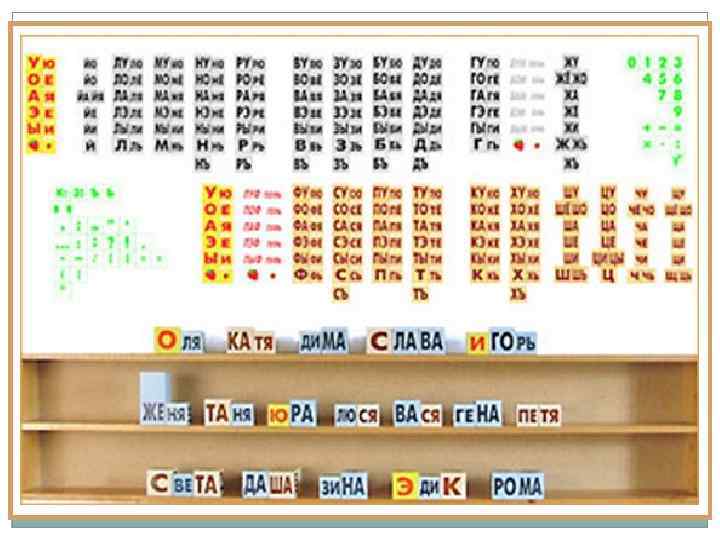 За просмотром карточек ребёнок постепенно
запоминает количество складов в том
или ином слове, находит похожие склады
в разных словах, тем самым, улучшая свою
технику чтения. Пособий со складовыми
картинками достаточно много, среди них:
«Кто вокруг меня живёт?», «Что вокруг
меня растёт?», «Продуктовый магазин» и
т.п.
За просмотром карточек ребёнок постепенно
запоминает количество складов в том
или ином слове, находит похожие склады
в разных словах, тем самым, улучшая свою
технику чтения. Пособий со складовыми
картинками достаточно много, среди них:
«Кто вокруг меня живёт?», «Что вокруг
меня растёт?», «Продуктовый магазин» и
т.п.
П особие «читай и пой» предназначено для организации занятий для обучения чтению в сопровождении музыки. Пособие состоит из 34 таблиц. В таблицах 1-6 русский алфавит представлен в виде шести песенок под марш, вальс, полечку, еще один вальс, «Светит месяц», колыбельную. Цвет букв не случаен: Голубые — Гласные, Синие — Согласные, Зелёные — твёрдый и мягкий Знаки. В таблицах 7-13, представляющих попевки из цепочек складов, зелёным цветом обозначены безударные, чёрным ударные склады. Таблицы с 14 по 34 представляют 21 песенку для закрепления навыков чтения и пения.
З
айцев
предлагает простой и красивый способ
написания букв и тексты для тренировки
письма. Для этого предназначены пособия
«Пишу красиво – печатные буквы» и «Пишу
красиво — пропись». Пособие представлено
на 32 страницах. На обложках и страницах
с 1 по 29 представлены буквы и цифры.
Каждая страница посвящена одной букве.
Страница разделена на три части. В
верхней части страницы показана, как
выглядит буква в разных написаниях.
Верхний ряд — заглавные буквы, нижний
— строчные. Средняя часть каждой
страницы, заключённая между двумя
линиями, представляет буквы в разобранном
на «детали» виде, показывает их количество
и последовательность «сборки». Нижняя
часть страницы представляет собой
обводки. Строчки букв, которые необходимо
обводить карандашом. Страницы 30-32
представляют собой тексты для обводки.
Тексты отличаются от стандартных текстов
в прописях для начальных классов. По
словам Зайцева тексты в прописях весьма
скучны и не представляют интереса для
ребёнка. Зайцев предлагает тренировать
письмо на интересных для детей загадках.
Для этого предназначены пособия
«Пишу красиво – печатные буквы» и «Пишу
красиво — пропись». Пособие представлено
на 32 страницах. На обложках и страницах
с 1 по 29 представлены буквы и цифры.
Каждая страница посвящена одной букве.
Страница разделена на три части. В
верхней части страницы показана, как
выглядит буква в разных написаниях.
Верхний ряд — заглавные буквы, нижний
— строчные. Средняя часть каждой
страницы, заключённая между двумя
линиями, представляет буквы в разобранном
на «детали» виде, показывает их количество
и последовательность «сборки». Нижняя
часть страницы представляет собой
обводки. Строчки букв, которые необходимо
обводить карандашом. Страницы 30-32
представляют собой тексты для обводки.
Тексты отличаются от стандартных текстов
в прописях для начальных классов. По
словам Зайцева тексты в прописях весьма
скучны и не представляют интереса для
ребёнка. Зайцев предлагает тренировать
письмо на интересных для детей загадках.
Обучение
грамматике русского языка Зайцев также
предлагает вести по своей методике. Николай Александрович разработал ряд
таблиц, по которым возможно изучения
правил русского языка.
Николай Александрович разработал ряд
таблиц, по которым возможно изучения
правил русского языка.
Т
еперь
давайте обратимся к методике обучения
счёту. Во-первых, Зайцев призывает не
ограничивать ребёнка узкими рамками
чисел. Он предлагает начинать со счёта
не до десяти, а сразу минимум до сотни.
А возможно и больше — до тысячи или даже
до миллиона. Во-вторых, по Зайцеву
преподнесение материала должно вестись
на 4 уровнях: рисуночном, числовом,
символическим и словесном. Зайцев
разработал ряд карточек и таблиц для
объединения этих уровней. Каждое число
на карточке или на таблице представлено
в нескольких видах – числовом (запись
цифрами), рисуночном и символичном
(представление числа в виде «пирамидок»
сверху над числом и «бочек» под цифровой
записью), и словесном (устный счёт вместе
с преподавателем). Согласитесь, мало
какие другие наглядные материалы могут
использоваться в счёте до сотни и больше.
Вряд ли найдётся столько счётного
материала дома или в детском саду. Представление чисел пирамидами и бочками
кроме всего прочего в будущем призваны
облегчить понимание дробных чисел.
От
пирамидок и бочек ребёнок постепенно
переходит к двухмерному квадрату 10 на
10 клеток и продолжает считать по нему.
Далее следует трёхмерный квадрат,
размерность которого может быть разной
в зависимости от преследуемых целей.
На трёхмерном квадрате осваивается
счёт выше ста, разбираются степени
числа.
Представление чисел пирамидами и бочками
кроме всего прочего в будущем призваны
облегчить понимание дробных чисел.
От
пирамидок и бочек ребёнок постепенно
переходит к двухмерному квадрату 10 на
10 клеток и продолжает считать по нему.
Далее следует трёхмерный квадрат,
размерность которого может быть разной
в зависимости от преследуемых целей.
На трёхмерном квадрате осваивается
счёт выше ста, разбираются степени
числа.
После освоение счёта можно обратиться к другим таблицам, разработанным Зайцевым, которые помогают освоить счёт по числам выше сотни, освоить простейшие арифметические действия, работу с дробями, разобраться в измерении времени и величины углов. Описанные методы представлены в пособиях «Мне в сотне тесно», «Тысяча +», «Миллион +», «Пифагор». Сравнительно недавно Зайцевым был предложен способ обучения счёту по кубикам для ещё детей 2-3 лет. Соответствующее пособие называется «Пять в кубе».
Также
с математической серии методик Зайцева
присутствуют пособия для освоения основ
геометрии. Первое пособие – это игра
«Орнамент». Детям предлагается собирать
различные узоры из геометрических
фигур. Стандартная игра «Орнамент»
содержит 240 элементов 12 цветов и 30
разновидностей. Половина фигур — рамки,
половина — вкладыши. Фигуры разного
цвета с двух сторон. В процессе складывания
различных орнаментов дети знакомятся
с названиями геометрических фигур и их
составляющих.
Второе
пособие – это Платоновы тела. Здесь
детям предлагается собирать различные
объёмные фигуры, а также сложные плоские
фигуры. Данное пособие знакомит детей
с объёмной геометрией и двухмерной
геометрией, а детей по младше учит счёту.
Первое пособие – это игра
«Орнамент». Детям предлагается собирать
различные узоры из геометрических
фигур. Стандартная игра «Орнамент»
содержит 240 элементов 12 цветов и 30
разновидностей. Половина фигур — рамки,
половина — вкладыши. Фигуры разного
цвета с двух сторон. В процессе складывания
различных орнаментов дети знакомятся
с названиями геометрических фигур и их
составляющих.
Второе
пособие – это Платоновы тела. Здесь
детям предлагается собирать различные
объёмные фигуры, а также сложные плоские
фигуры. Данное пособие знакомит детей
с объёмной геометрией и двухмерной
геометрией, а детей по младше учит счёту.
Ну
и заканчивая разговор о методиках и
пособиях Зайцева нельзя не отметить их
направленности на общее развитие
ребёнка. Ни одно пособие не является
узко направленным. Пособия по чтению
направлены не только на обучение чтению,
но и знакомят ребёнка с основами знаний
об окружающем мире. Слоговые картинки
выпущены по множеству тематик — дорожные
знаки, басни Крылова, любимые картины.
Хочется также отметить, что даже сам Николай Александрович Зайцев далеко не настаивает на покупке всех пособий, разработанных им. Более того, он говорит, что специально сделал многие пособия так, что их без труда можно сделать самим. Так, например кубики Зайцева картонные и наполнители у них доступные – пробки и крышки. Поэтому не нужно думать, что развитие ребёнка по Зайцеву это очень дорогое начинание.
Так что, если вы решились использовать в своих занятиях с малышом методики Зайцева, то запаситесь энтузиазмом и вперёд! Однако все хорошо в меру. Познание нового всегда манит детей, приближающихся к возрасту «почемучки». Но если глазки малыша потухли, бросайте все «развивающие» занятия и без сожаления переключайтесь на баюканье любимого медвежонка. Ведь «чудо в самом ребенке, а не в методике».
Вывод:
Пособия для обучения чтению по Зайцеву:
• широко распространенные кубики Зайцева;
• складовые картинки;
• читай
и пой.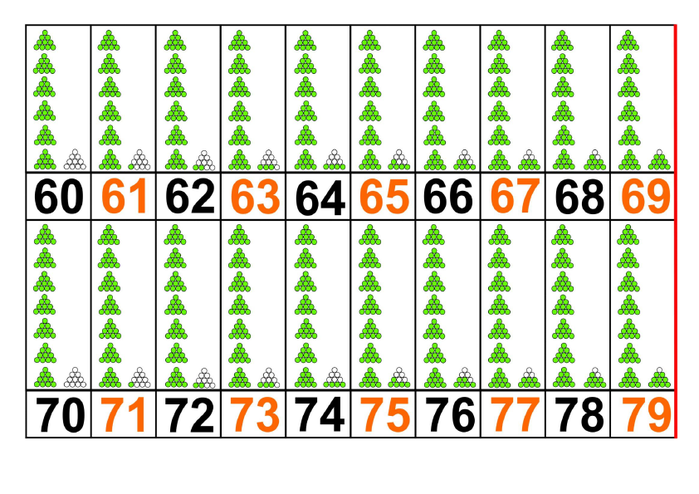
Поздняя античная консервация неопифагореизма | Математические теологии: Николай Кузанский и наследие Тьерри Шартрского
Фильтр поиска панели навигации Oxford AcademicMathematical Theologies: Николай Кузанский и наследие Тьерри ШартрскогоХристианское богословиеИстория христианстваФилософия религииБогословиеКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicMathematical Theologies: Николай Кузанский и наследие Тьерри ШартрскогоХристианское богословиеИстория христианстваФилософия религииБогословиеКнигиЖурналы Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
Cite
Альбертсон, Дэвид,
‘Позднее антикварное сохранение неопитагореанизма’
,
Математические богологии: Николас из Куса и наследие Тьерри Чартр
, Оксфордские исследования в историческом богословии
(
2014;
онлайн,
(
2014;
онлайн,
(
г. Oxford Academic
Oxford Academic
, 19 июня 2014 г.
), https://doi.org/10.1093/acprof:oso/9780199989737.003.0004,
, по состоянию на 5 декабря 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicMathematical Theologies: Николай Кузанский и наследие Тьерри ШартрскогоХристианское богословиеИстория христианстваФилософия религииБогословиеКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicMathematical Theologies: Николай Кузанский и наследие Тьерри ШартрскогоХристианское богословиеИстория христианстваФилософия религииБогословиеКнигиЖурналы Термин поиска на микросайте
Расширенный поиск
Abstract
В этой главе прослеживаются три основных неоплатонических дискурса, унаследованных средневековым латинским христианством: дискурсы Августина, Прокла и Боэция. Каждый из них сложным образом взаимодействовал с никомаховым наследием, но вносил изменения или фальсификации, которые не позволяли средневековому платонизму полностью получить доступ к математическому богословию. Августина изначально привлекало неопифагорейство, и он даже стремился отождествить божественную Мудрость (9).0073 Sapientia ) с номером ( numerus ). Но в последние годы своей жизни Августин рассматривал математическое богословие как угрозу суверенитету посредничества Логоса. Ямвлих довел неопифагорейство Никомаха до такой крайности, что Прокл счел необходимым понизить опосредующую роль числа в своей философии в пользу пространства и движения. Боэций перевел труды Никомаха и окрестил квадривиум, четыре математических пути к Единому. Но его христианские богословские сочинения оставались строго изолированными от таких математических занятий. Таким образом, богословский потенциал неопифагорейства был приглушен, но сохранен в позднеантичных традициях платоника.
Каждый из них сложным образом взаимодействовал с никомаховым наследием, но вносил изменения или фальсификации, которые не позволяли средневековому платонизму полностью получить доступ к математическому богословию. Августина изначально привлекало неопифагорейство, и он даже стремился отождествить божественную Мудрость (9).0073 Sapientia ) с номером ( numerus ). Но в последние годы своей жизни Августин рассматривал математическое богословие как угрозу суверенитету посредничества Логоса. Ямвлих довел неопифагорейство Никомаха до такой крайности, что Прокл счел необходимым понизить опосредующую роль числа в своей философии в пользу пространства и движения. Боэций перевел труды Никомаха и окрестил квадривиум, четыре математических пути к Единому. Но его христианские богословские сочинения оставались строго изолированными от таких математических занятий. Таким образом, богословский потенциал неопифагорейства был приглушен, но сохранен в позднеантичных традициях платоника.
Ключевые слова: Прокл, Августин, Боэций, Ямвлих, неопифагорейство, квадривиум, Никомах, средневековый платонизм
Предмет
История христианстваХристианское богословиеБогословиеФилософия религии
В настоящее время у вас нет доступа к этой главе.
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Войти с помощью личного кабинета
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
д.
Покупка
Наши книги можно приобрести по подписке или приобрести в библиотеках и учреждениях.
Информация о покупке
Полуцикл Собора Парижской Богоматери: готический дизайн и геометрические знания в двенадцатом веке | Журнал Общества историков архитектуры
Исследовательская статья| 01 декабря 2010 г.
Стефан Ван Лифферинге
Журнал Общества историков архитектуры (2010) 69 (4): 490–507.
https://doi.org/10.1525/jsah.2010.69.4.490
- Просмотры
- Содержание артикула
- Рисунки и таблицы
- Видео
- Аудио
- Дополнительные данные
- Экспертная оценка
- Делиться
- Твиттер
- MailTo
- Инструменты
Получить разрешения
Иконка Цитировать Цитировать
- Поиск по сайту
Citation
Стефан Ван Лифферинге; Полуцикл Нотр-Дам де Пари: готический дизайн и геометрические знания в двенадцатом веке. Журнал Общества историков архитектуры 1 декабря 2010 г.; 69 (4): 490–507. doi: https://doi.org/10.1525/jsah.2010.69.4.490
Журнал Общества историков архитектуры 1 декабря 2010 г.; 69 (4): 490–507. doi: https://doi.org/10.1525/jsah.2010.69.4.490
Скачать файл цитаты:
- Рис (Зотеро)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- КонецПримечание
- РефВоркс
- Бибтекс
Полуцикл собора Парижской Богоматери: готический дизайн и геометрические знания в двенадцатом веке анализирует, как расположение четырех постаментов полукруга Нотр-Дам в Париже отражает состояние математических знаний во время первых этапов строительства собора в начале 1160-х годов. В первой половине XII века строительное предприятие сочеталось с интеллектуальной деятельностью в Париже, где архитекторы экспериментировали с новым стилем строительства — готикой, а ученые объясняли геометрию в трактатах.

 Зайцев пришел к выводу, что виною всему упущенное время, когда действительно ребенку было бы интересно учится счету. Ведь так интересно четырехлетке знать, сколько у него будет конфет, если мама к одной добавит другую. Ну не ужели ребенок не проявит интерес? Вот и вывод, что знакомство с цифрами и математическими действиями нужно осуществлять до школы, пока ребенок в игровой форме готов хоть что-то воспринимать.
Зайцев пришел к выводу, что виною всему упущенное время, когда действительно ребенку было бы интересно учится счету. Ведь так интересно четырехлетке знать, сколько у него будет конфет, если мама к одной добавит другую. Ну не ужели ребенок не проявит интерес? Вот и вывод, что знакомство с цифрами и математическими действиями нужно осуществлять до школы, пока ребенок в игровой форме готов хоть что-то воспринимать. Наверно, на словах это звучит сложно, но на деле получается достаточно легко. Слева — десятки, справа — единицы, смотрите рисунок.
Наверно, на словах это звучит сложно, но на деле получается достаточно легко. Слева — десятки, справа — единицы, смотрите рисунок. Уже после этого можно попробовать и другие пособия:
Уже после этого можно попробовать и другие пособия: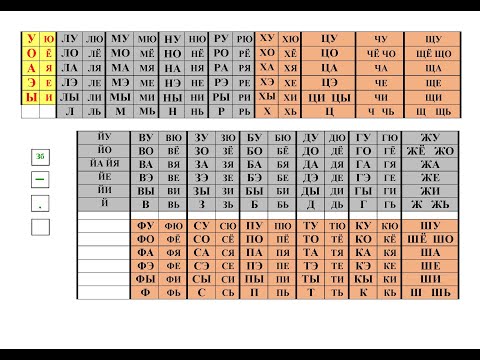 Математика должна быть веселой и занимательной.
Математика должна быть веселой и занимательной. Организация уголка осуществляется с посильным участием детей, что создает у них положительное, эмоциональное отношение к занимательному материалу, интерес и желание играть. Разнообразие занимательного материала позволяет каждому из детей выбрать для себя игру по интересам. Это настольно-печатные игры, игры для развития логического мышления, подводящие детей к освоению игры в шашки и шахматы: «Лиса и гуси», «Мельница», «Волки и овцы» и др. ; головоломки, логические задачи и кубики; лабиринты, игры на составление целого из частей; на воссоздание фигур-силуэтов из специальных наборов фигур; игры на передвижение.
Организация уголка осуществляется с посильным участием детей, что создает у них положительное, эмоциональное отношение к занимательному материалу, интерес и желание играть. Разнообразие занимательного материала позволяет каждому из детей выбрать для себя игру по интересам. Это настольно-печатные игры, игры для развития логического мышления, подводящие детей к освоению игры в шашки и шахматы: «Лиса и гуси», «Мельница», «Волки и овцы» и др. ; головоломки, логические задачи и кубики; лабиринты, игры на составление целого из частей; на воссоздание фигур-силуэтов из специальных наборов фигур; игры на передвижение.
