Ментальная арифметика: чем разнообразить занятия

Час-полтора заниматься арифметикой, даже необычной, — это утомительно и для школьников, а тем более для детей 5-6 лет.

Поэтому у многих преподавателей этого направления встает вопрос: чем разнообразить занятия? Как развлечь детей? И желательно так, чтобы это веселье приносило пользу освоению предмета? Ведь игра в прятки, конечно, внесет бодрую нотку на урок, но вряд ли поможет ментальному счету:)

Вот что мы используем на занятиях в нашем центре.

Кинезиологические упражнения

Кинезиология — это наука о развитии умственных способностей через специальные двигательные упражнения. Они улучшают мыслительную деятельность, развивают межполушарные связи, способствуют развитию памяти, повышают устойчивость внимания.

И… оживляют детей на занятиях по ментальной арифметике:)

Рассмотрим несколько двигательных упражнений. Их можно использовать в качестве разминки в начале нового урока.

«Колечко»

Делаем «колечко» — соединяем большой палец с указательным, потом со средним, с безымянным, с мизинцем. И обратно. Ускоряем темп, меняем положение пальцев как можно быстрее.

«Ухо – нос»

Зажимаем левой рукой кончик носа, правой – левое ухо. Нужно одновременно отпустить руки, хлопнуть в ладоши, поменять положение рук. Очень забавное упражнение?

«Лезгинка»

Нужно сжать левую руку в кулак, большой палец отставить в сторону, кулак развернуть пальцами к себе. Ладонью правой руки прикоснуться к мизинцу левой. Меняем положение правой и левой рук, добиваясь высокой скорости смены положений.

«Кулак-ребро-ладонь»

Сжимаем кулак, потом выпрямляем ладонь ребром к столу (перпендикулярно столу), потом ладонь параллельно столу. Упражнение выполняют сначала правой рукой, потом левой, затем двумя руками.

Игры со счетом

Обычно мы играем в них в конце урока.

---

Вот ссылка ещё на одну статью, которая может вас заинтересовать:

Ментальная арифметика: как объединить в одну группу детей с разным уровнем знаний →

---

Итак, игры со счётом:

«Живой абак»

Дети выступают в роли косточек на абаке.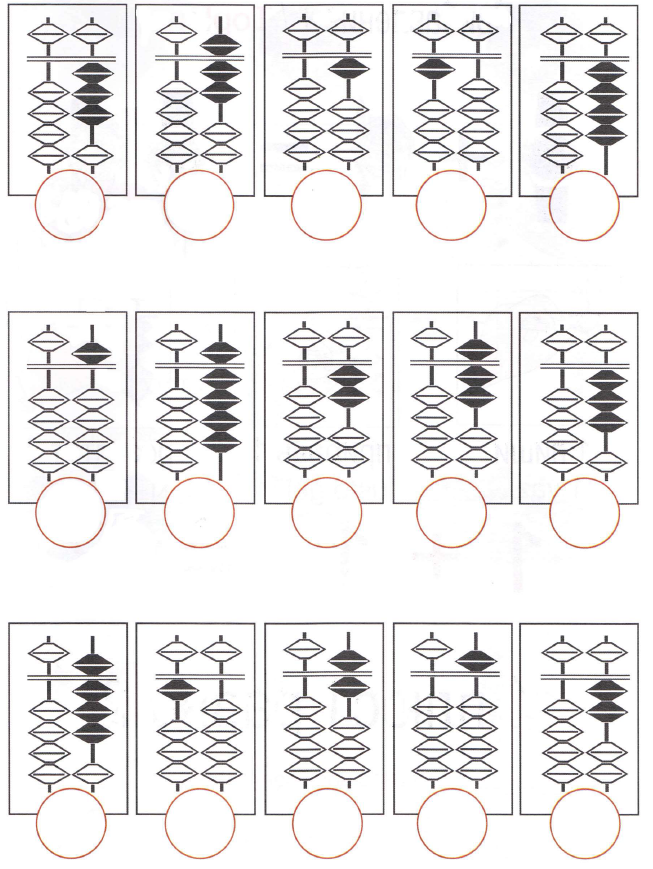 Каждому ребенку присваиваем цифру от 1 до 5. Ребята выстраиваются в линейку, как косточки на спице. На полу между косточкой «5» и остальными проводим воображаемую границу.

Учитель дает команды в виде примера: 1+2+1+5-2-1+3 =?

Дети двигаются либо к границе, либо от нее — в зависимости от команды. Потом спрашиваем у детей ответ. Такая игра развивает у детей командный дух и улучшает понимание счета на абаке.

«Счет с закрытыми глазами»

Считаем на абаке, закрыв глаза повязкой. Такая игра позволяет ребенку улучшить ментальный счет.

«Счет под интенсивную музыку»

Считаем ментально и на абаке под любую ритмичную современную песню. Мои ученики любят мелодию из мультфильма «Гравити Фолз». Такая игра позволят сконцентрироваться на счете и увеличивает темп счета.

«Счет со скакалкой»

Считаем ментально и скачем на скакалке. Такая игра помогает отучиться от использования рук при счете.

«Съедобные абаки»

Можно сделать с детьми съедобные абаки. Нам потребуются: шпажки — это спицы абака, маршмело, сладкая кукуруза — это косточки абака. Нанизываем на шпажку маршмело или кукурузу. Делим на верхнюю и нижнюю часть. Выделяем границу. И считаем  примеры.

После игры можно будет съесть наши косточки.

Физкультминутки

Хотя предпочтительнее разнообразить занятия тематическими играми, все же без самых обыкновенных физкультминуток тоже не обойтись. Они очень нужны после активной умственной деятельности ребенка или перед рассмотрением новой темы.

Расскажу о наших самых любимых. Возможно, вы хорошо их знаете.

Физкультминутка 1

В понедельник я купался (изображаем плавание),
А во вторник — рисовал (изображаем рисование).
В среду долго умывался (умываемся).
А в четверг в футбол играл (бег на месте).
В пятницу я прыгал, бегал (прыгаем),
Очень долго танцевал (кружимся на месте).
А в субботу, воскресенье (хлопки в ладоши)
Целый день я отдыхал (дети садятся на корточки, руки под щеку — засыпают).

Физкультминутка 2

Вышли мышки как-то раз (ходьба на месте или продвигаясь вперед в колонне)
Поглядеть, который час (повороты влево, вправо, пальцы «трубочкой» перед глазами).
Раз, два, три, четыре (хлопки над головой в ладоши).
Мышки дернули за гири (руки вверх и приседание с опусканием рук «дернули за гири»).
Вдруг раздался страшный звон (хлопки перед собой),
Убежали мышки вон (бег на месте или к своему месту).

---

А как вы разнообразите интеллектуальные курсы? Расскажите, пожалуйста, в комментариях.

Ментальная арифметика

Ментальная арифметика – это уникальная методика развития умственных способностей детей от 4 до 16 лет, основанная на системе устного счета. Обучаясь этой методике ребенок может решить любые арифметические задачи за несколько секунд (сложение, вычитание, умножение, деление, вычисление квадратного корня числа) в уме быстрее, чем с помощью калькулятора.

В чем же отличие нашей методики обучения ментальной арифметике от других методик?

1. Наличие методических пособий для инструкторов, содержащих подробно расписанные планы для каждого урока.
2. Каждый урок дети проходят новую тему, поэтому исключено нахождение в одной группе детей с разными уровнями занятий и владений техники ментальной арифметики.
3. Каждая тема объясняется в 6 этапов, а с 3-го уровня — в семь этапов. При этом отрабатываются все каналы восприятия информации у ребенка. Т.е. только одна новая тема отрабатывается в течение 45 минут. Только убедившись, что каждый ребенок на 100% понял и отработал новый материал, ему дается домашнее задание для закрепления полученных знаний и навыков дома.
4. Методика прописана детально и глубоко. При работе над новой темой, обязательно включается материал для повтора и закрепления ранее пройденных тем, чем достигаются прочные знания и навыки. Поэтому исключается добавление новых учащихся в группу на любом этапе обучения и с любым уровнем знаний.
5. Тщательно и детально разработанные книги для обучения. На каждую новую тему отводится не менее 8 страниц. На каждой странице по 4 строчки, по 10 примеров. Что больше обычно предлагаемого другими школами в 2-3 раза.
6. Учитывая наш менталитет, уже с третьего урока в наших школах дети начинают считать ментально. Как только ребенок отработает полученные навыки на абакусе, ему предлагается сделать это уже ментально, используя воображение, сначала на легких примерах без формул, затем постепенно счет усложняется. Это очень сильно мотивирует детей к обучению, т.к. уже с первых шагов в изучении ментальной арифметики они видят результаты, хорошо усвоенный материал и отработанные навыки делают этот процесс максимально несложным. Они пробуют, у них получается и дети приобретают чувство уверенности в себе, в своих способностях и знаниях. Другие методики, как правило, в течение года изучают все формулы на абакусе, и только через год начинают пытаться считать ментально.
7. Уникальный образовательный онлайн портал для учеников, созданный специально для методики ISMA. Дети тренируются на портале ежедневно. Работа портала настроена таким образом, что инструктор контролирует регулярность и правильность выполнения домашнего задания, отслеживает статистику и анализирует развитие ребенка. Если ребенок не тренируется в портале, то это сразу видно, падает его рейтинг. Это является мощным инструментом самоконтроля и мотивации для ребенка, контроля со стороны не только инструктора, но так же и родителей, которые в любой момент могут зайти на портал и проследить динамику развития ребенка. Кроме арифметических заданий, на портале так же есть задания на развитие логики, внимания, фотографической памяти. Данные тренировки очень важны для отработки и закрепления навыков.
8. Дети решают задания с формулами на сложение и вычитание параллельно. Обычные зарубежные методики предлагают задания в основном на сложение. Вычитание они проходят отдельными формулами. Методика ISMA так же учит детей считать отрицательные числа, десятичные дроби, корень квадратный, корень кубический , проценты. Вести подсчеты в денежном выражении, в выражении массы и других мерах.
9. Уникальность методики заключается еще в том, что это наш, казахстанский продукт, который успешно работает в течение 4 лет не только на рынке Казахстана, но и в странах ближнего и дальнего зарубежья. Кроме того, методика постоянно совершенствуется и развивается — в этом ее преимущество перед приобретенными за рубежом, т.к. законодательно невозможно вносить изменения, улучшения в шаблон приобретенной чужой методики, даже если она не совсем подходит для нашего менталитета. Это очень важный аспект. Даже на небольшом примере: во многих методиках число 5 250 пишется, как 5,250. Школы в данном случае не могут отойти от регламентов приобретенной методики. В нашей же системе образования запятая после числа пять означает, что далее идут сотые. И число читается, как пять целых двести пятьдесят сотых. У детей возникает своего рода конфликт восприятия числа, т.к. школа требует одну систему, в школе ментальной арифметики — другую систему.
   Отсюда возникает недовольство и негатив у школьных учителей в отношении ментальной арифметики.

Обучение ментальной арифметике по методике ISMA учитывает требования школы, особенности менталитета и психологии наших детей, что позволяет добиться отличных результатов не только в обучении ментальной арифметике, но существенно повысить общую успеваемость в школе.

Кроме того, знания и навыки детей, обучающихся ментальной арифметике по методике ISMA, соответствуют требованиям крупнейших мировых ассоциаций по ментальной арифметике. В соответствие с международными требованиями в нашей методике увеличено количество рядов, вносятся усовершенствования. Это позволяет нашим детям с блеском выступать на мировых олимпиадах.

Как научить… ментальной арифметике | Учительская сеть

В мире, полном гаджетов и технологий, легко лениться в таких вещах, как сложение чисел в уме. Даже простой калькулятор часто удобнее считать на обеих руках.

Но поощрение учеников к умственной арифметике не только помогает им решать все более сложные математические задачи, но и является очень полезным жизненным навыком — будь то проверка сдачи или определение того, сколько времени вам придется ждать следующего поезда.

Итак, на этой неделе у нас есть множество ресурсов, предназначенных для повышения ловкости ваших учеников в арифметике.

Попытки сделать математику более увлекательной необходимы для вовлечения учащихся в предмет с раннего возраста. Ученикам начальных классов может понравиться викторина по ментальной математике в аудиоформате. Он задает 15 вопросов, которые постепенно усложняются в зависимости от сложения, вычитания, умножения, деления и времени. Если это работает хорошо, и вы хотели бы попробовать больше этого вида деятельности, дополнительные тесты доступны на веб-сайте Teaching Packs.

Учащимся средней школы Мел Малдауни, один из учителей веб-сайта Just Maths, предлагает разместить на доске эти 30 вопросов по арифметике в уме, когда учащиеся входят в класс.

Продолжая тему игр, Малдауни также предлагает: «Если у меня есть несколько минут до звонка, я играю в игру под названием «Вокруг света», где два ученика встают и должны ответить на вопрос, который я задаю (я придумывать их по ходу дела). Если они неверны, они садятся, и я выбираю другого ученика в качестве претендента.

«Мне нравится это делать, и я действительно могу адаптировать вопросы к группе и ученикам. Цель состоит в том, чтобы устоять и победить как можно больше учеников.»

Такие игры, как снэп или бинго, — отличный способ побудить учащихся к быстрым и точным вычислениям в уме. Попробуйте эти карточки с эквивалентными дробями или те, которые проверяют деление, умножение и решение уравнений.

Также есть набор карточек с задачами по математике от Twinkl. В них представлены математические задачи на соотношение и пропорции, которые учащиеся должны решить, используя только свой мозг. Для расширенного занятия вы можете использовать карточки в качестве шаблонов, чтобы учащиеся могли создавать свои собственные.

Элемент жизненных навыков имеет важное значение, особенно сейчас, когда финансовое образование входит в учебную программу. Имея это в виду, ученики начальных классов могут захотеть попрактиковаться в арифметике в контексте классного магазина. Могут ли ученики посчитать в уме стоимость двух-трех предметов? Могут ли они решить, какой должна быть их сдача? Этот рабочий лист о добавлении денег и этот об удвоении стоимости можно использовать для закрепления обучения.

Также имеется широкий выбор рабочих листов по ментальной арифметике. Этот от Mental Arithmetic хорош для проверки числовых связей до 20, в то время как этот касается упорядочения чисел от большего к меньшему. Учитель Дес Хегарти пересматривает умножение на 2, 5 и 10 в этом удобном ресурсе, а в этом заключительном обзоре рассматривается увеличение чисел на 10.

Для старших учеников начальной школы вы можете попробовать набор из 8 тестов по ментальной математике, созданный Primary Leap. Каждый из них содержит 12 вопросов, которые охватывают самые разные темы, от денег и мер до дробей и десятичных знаков. Вот список всех индивидуальных оценок: тест 1; тест 2; тест 3; тест 4; тест 5; тест 6; тест 7; тест 8.

Для вдохновения взгляните на этот постер и эти числа на дисплее, которые помогут вам изучить таблицу умножения от 1 до 12.

Наконец, в The Guardian есть ряд интерактивных уроков, полезных для повторения стратегий ментальной арифметики. . К ним относятся: добавление двойников, оценка и выявление почти двойников. Используйте этот ресурс для создания рабочих листов для проверки быстрого припоминания сложения и вычитания, а этот — для умножения и деления.

Если вы хотите предложить какие-либо другие ресурсы, вы можете поделиться ими в ветке комментариев ниже.

Стратегии и советы по ментальной арифметике, которые должен знать каждый ребенок

Когда мы думаем о стратегиях ментальной арифметики, мы в основном думаем о тех математических навыках, которые мы можем освоить в уме, не используя формальные письменные методы, которые мы использовали бы для более длинных вопросов и стандартные методы алгоритма.

В этой статье мы познакомим вас с некоторыми стратегиями ментальной арифметики, которым вы можете научить своих учеников, чтобы развить их навыки ментальной арифметики в начальной школе.

Что такое математические стратегии в уме?

Стратегии ментальной арифметики — это общепринятые способы решения математических задач в уме, которые помогают нам срезать путь и эффективно находить правильный ответ.

Почему важны математические стратегии в уме?

Стратегии ментальной математики лежат в основе большинства областей математики, в которых используются числа. Без эффективных умственных стратегий дети часто не могут быстро и бегло считать.

Умственные стратегии также являются основой любого письменного или формального метода в математике. Ссылаясь на это как на умственную математику, это не означает, что вы вообще ничего не можете записать, но любая письменная работа будет представлять собой быстрые наброски, помогающие запомнить через многошаговые задачи.

По мере того, как дети начинают использовать более формальные методы, начиная примерно с 3-го класса, и по мере того, как числа, с которыми они работают, становятся все более ценными, навыки счета в уме жизненно важны для обеспечения беглости и точности в математике.

Развитие истинной беглости в математике

Эффективные умственные стратегии важны, если дети хотят развить «истинную» беглость систему счисления для вычисления и решения задач.

Стоит помнить, что свободное владение математикой не ограничивается способностью вспоминать известные факты. Точнее, важно то, как дети могут использовать и применять эти факты, в том числе с помощью ряда умственных математических стратегий.

«Отстающие часто являются отстающими не потому, что знают меньше, а потому, что не умеют гибко использовать числа». – Джо Боалер

Индивидуальное онлайн-обучение Third Space Learning в значительной степени направлено на формирование у учащихся уверенности и беглости в математике. Наши еженедельные уроки с репетиторством, разработанные с учетом индивидуальных потребностей каждого ребенка, направлены на то, чтобы укрепить понимание учениками числовых фактов и способов их применения в широком круге вопросов.

Использование числовых фактов для решения больших вычислений на онлайн-уроке математики 2-го класса Third Space Learning.

Будьте осторожны, чтобы не ошибиться в названиях математических навыков в уме.

При работе над развитием «истинной» беглости речи важно помнить, что точность — это не то же самое, что беглость речи.

Например, рассмотрим следующие сценарии, которые, хотя и являются точными, не обязательно могут быть классифицированы как беглые:

• Первоклассник вычисляет 40 + 8, считая единицами;
• Третьеклассник, вычисляющий 1003 – 998 формальным письменным методом;
• Пятиклассник вычисляет 41,79 + 25,3 + 25,7 – 41,79сложив первые три числа, а затем вычтя четвертое.

Этот отрывок из исследовательской работы «Развитие вычислительной беглости с целыми числами», опубликованной в 2000 году С. Дж. Расселом, остается одним из лучших объяснений беглости:

«Беглость опирается на хорошо построенную математическую основу, состоящую из трех частей:

• понимание смысла операций и их отношений друг к другу — например, обратное отношение между умножением и делением;
• знание большого набора числовых отношений, включая «факты» сложения и умножения, а также другие отношения, например, как 4 × 5 связано с 4 × 50;
• и глубокое понимание системы счисления с основанием 10, того, как числа устроены в этой системе, и как система разрядов ведет себя в различных операциях — например, что 24 + 10 = 34 или 24 × 10 = 240′ .

Быстрое вспоминание и вычисления в уме с заметками

Когда мы обсуждаем вычисления в уме по математике в старших классах начальной школы, нам нужно четко понимать различие между фактами, которые дети должны уметь быстро вспоминать, и типами вычислений, которые дети должны уметь производить в уме, иногда с помощью заметок.

Практика припоминания и быстрого припоминания числовых фактов важна, потому что, если дети способны автоматически вспоминать числовые факты, это позволяет им высвободить свою рабочую память при столкновении с более сложными вопросами.

Они также способны более эффективно и точно решать проблемы, рассуждать и устанавливать связи, если им не приходится постоянно вычислять одни и те же «базовые» факты.

«Обучая процедурным и фактическим знаниям, убедитесь, что учащиеся доходят до автоматизма. Объясните учащимся, что автоматизм [с ключевыми фактами] важен, потому что он освобождает их разум для размышлений о концепциях». – Дэниел Уиллингем – когнитивист, в «Правда ли, что некоторые люди просто не умеют считать?»

Концепция должна быть понята, прежде чем вводить стратегию 

Прежде чем мы сможем ожидать быстрого припоминания и автоматизма числовых фактов с нашими стратегиями ментальной математики, нам необходимо научить основным математическим концепциям. Например, только когда у детей есть надежное концептуальное понимание числовых связей до 10, следует пытаться быстро вспоминать.

Исходя из этого понимания числовых связей до 10, можно использовать стратегию разделения. Например, к 5-му классу большинство детей должны быть в состоянии вычислить в уме 34 х 5 (30 х 5 + 4 х 5), используя разбиение и свои знания закона распределения, подкрепленные базовыми вычислениями.

Хотя учащиеся будут запоминать все больше и больше математических фактов, которые они смогут запомнить «наизусть», жизненно важно, чтобы они понимали концепции. Работа с манипуляторами может помочь в этом, переходя к виртуальным манипуляторам на интерактивной доске, когда числа становятся слишком большими, чтобы удерживать их физически.

Оценка математических стратегий в уме, которые использует ваш класс

Один из действительно интересных способов проверить стратегии в устной арифметике – представить группам разные письменные версии одних и тех же математических задач.

1. Представьте одну задачу

Если вы представите задачу, например 64 + 17, в предложении, подобном этому, те дети, которые уверены в своих математических стратегиях в уме, решат ее в уме.

Обычно они, даже подсознательно, если говорят свободно, разбивают числа и вычисляют 60 + 10, а затем 4 + 7, или 60 + 17, а затем добавляют 4. Некоторые делают 64 + 10, а затем добавляют 7. 

Некоторые могут округлять числа, например, 64 + 20, используя числовые связи, до 20 знаний, а затем минус 3. 

Некоторые могут снова использовать свои числовые связи, чтобы вычислить 64 + 17, добавив 63 + 17, чтобы получить 80, а затем добавить 1.

Вы ожидаете, что ваш класс даст ряд ответов относительно своего метода, но, надеюсь, все говорят бегло. и может найти правильный ответ, не более чем быстро записывая некоторые числа при добавлении нескольких шагов.

2. Создайте две версии одного и того же набора из 10 вопросов

Теперь составьте лист из 10 похожих вопросов с диапазоном сложения и вычитания, которые, как вы ожидаете, ваш класс сможет выполнить в уме. Создайте вторую версию этого, которая излагает те же вопросы, с теми же точными числами и тем же ожидаемым ответом, в стандартном формате метода алгоритма.

Раздайте половине класса первый лист в виде числового предложения, а другой половине — вторую версию, где вопросы представлены в формате стандартного метода алгоритма.

Не говорите группам, что у них разные листы, и раздавайте их за разные столы, чтобы они не видели другой формат тех же вопросов. Дайте им время, чтобы они индивидуально ответили на вопросы и записали свои ответы.

3. Попросите детей поделиться своими методами

Ответьте на первый вопрос и попросите кого-нибудь добровольно поделиться своим методом. Затем попросите кого-нибудь поделиться, затем еще кого-нибудь и так далее. Убедитесь, что вы получили пару примеров из таблиц с горизонтальным расположением вопросов и пару примеров из таблиц с вертикальным расположением столбцов.

Вы, скорее всего, обнаружите, что группы, у которых была горизонтальная схема, с гораздо большей вероятностью просто проработали ее в уме, в то время как группы, у которых была вертикальная схема, потратили время на поиск и запись ответов стандартным методом алгоритма. включая каждый шаг, хотя они могли бы легко решить эти задачи в уме.

Это упражнение является отличным напоминанием о том, что даже когда мы видим формальные вычисления, мы должны использовать наши стратегии ментальной математики, чтобы ускориться там, где мы можем.

Укрепление уверенности в умственных математических стратегиях

При введении любого нового математического понятия — от сложения до процентов и десятичных дробей — детям будет полезно показать физическое представление чисел (с использованием математических манипуляций) и операций перед использованием графических представлений (например, числовые линии или модели столбцов), а затем, наконец, написанные методы с использованием символов числа и операции.

Подробнее: Конкретный иллюстрированный абстрактный метод

По пути вам придется много раз повторять и тренироваться мысленно вспоминать факты. Мы надеемся, что по мере того, как дети становятся старше и переходят в старшие классы начальной школы, переход от физического к письменному будет происходить быстрее для новых концепций, поскольку они строятся на прочном фундаменте.

Разные дети могут переходить к умственным стратегиям в разных точках каждого раздела. Некоторые могут перейти от физического к ментальному, если они быстро схватывают концепцию и уже имеют четкое понимание.

Другие, возможно, не смогут достичь беглости запоминания и применения до тех пор, пока они не попрактикуются в написании своих ответов и не укрепят уверенность в этих новых числовых фактах и ​​стратегиях.

Возможно, вам также придется распаковать любые неправильные представления на этих этапах, и это может включать возвращение «назад» к физическому. Хорошей практикой является всегда иметь под рукой манипуляторы во время выполнения самостоятельных заданий, даже в 5-м классе и для всех способностей. Иногда быстрое сравнение с использованием палочек с основанием 10 или палочек Кюизенера может помочь ребенку «закрепить» эту стратегию в голове.

Также важно не учить детей выполнять математические трюки, например, «прибавлять ноль» при умножении на десять, так как это может вызвать проблемы в более позднем возрасте с пониманием разрядности. Однако можно надеяться, что дети заметят такие закономерности в своих ответах, и это должно привести к обсуждению и сравнению, а также предоставить детям возможность проверить свою теорию там, где они заметили возможную закономерность. Даже если вы знаете, что это неправильно/правильно, они выиграют от возможности проверить и применить это предположение.

Подробнее: Математические приемы, которых следует избегать и умственный труд, арифметика и рассуждение. Они фактически формируют прогрессию, начиная с 3-го класса, поэтому важно, чтобы в детском саду – 2-м классе уже была сделана основа, чтобы дети могли выполнять вычисления в уме.

Таким образом, эти навыки лучше всего рассматривать как прогресс, а не как набор ожиданий годовой группы.

Как улучшать математику в уме год за годом

Наряду с расширением диапазона детских вычислений в уме по мере прохождения ими элементарных предметов, следите за тем, чтобы они каждый год получали достоверные данные.

Как развить в уме математические стратегии, необходимые для сложения и вычитания

В младших классах дети узнают основные сведения о числах, включая сложение и вычитание. Это будет включать количество облигаций до 20 к тому времени, когда они закончат 1-й класс. Они будут много работать с физическими объектами и играть в ролевые игры, поэтому в эти годы хорошей практикой является не только практиковать математические навыки во время уроков математики, но и создавать возможности для вопросов вне этих уроков.

Попросите детей подсчитать, сколько учеников сегодня отсутствовало, посчитав карандаши на каждом столе, чтобы увидеть, достаточно ли у них (или слишком много, или слишком мало), и пополнить словарный запас на уроках математики.

Как только дети усвоят концепцию фактов сложения и фактов вычитания, а также то, что они являются обратными операциями (хотя они могут еще не знать этого конкретного слова), они начнут укреплять свое быстрое запоминание числовых связей и применять их в своей работе.

Никогда не рано вводить различные стратегии для отработки своих расчетов, если базовое понимание правильное. Спросить их, есть ли другой способ, которым они могли бы найти ответ, можно задать на официальных уроках, в ролевой игре или в спорте.

Основные факты сложения, которые дети должны знать ко 2-му классу

Стратегии сложения и вычитания в уме в старших классах 

Счет в прямом и обратном порядке

Счет в прямом и обратном порядке впервые встречается в младших классах, начиная с единицы и считая до единиц .

Чувство числа у учащихся расширяется за счет того, что они начинают с разных чисел и считают в прямом и обратном порядке не только единицы, но и двойки, пятерки, десятки, сотни, десятые и так далее.

Прогресс в счете в прямом и обратном порядке

Вот способы, которыми вы можете помочь своему классу прогрессировать в счете в прямом и обратном порядке:

1. Счет в десятках или в обратном порядке от любого числа (например, вычисление 27 + 60= ? путем подсчета десятками от 27)
2. Счет до пятерок или обратно от любого числа, кратного 5 (например, 35+15=? путем счета с шагом 5 от 35.)
3. Счет до сотен или обратно от любого числа (например, 570 + 300= ?, считая сотни от 570.)
4. Счет вперед или назад в десятых и/или сотых долях (например, 3,2 + 0,6 = ? при счете в десятых долях. 1,7 + 0,55=? в счете в десятых и сотых долях.)

   Разбиение для сложения и вычитания

   Стратегии разбиения учат детей разбивать большие числа на меньшие.

   Важно, чтобы дети знали, что числа могут быть разделены – как по границам разрядного значения (канонически), так и другими способами (неканонически).

   Затем они могут использовать свое разбиение, чтобы помочь им в вычислениях сложения и вычитания. Это может быть расширено по мере того, как дети продвигаются по старшим начальным классам.

   Прогресс в делении на части

   Вы можете помочь своему классу в делении на части:

   1. Вычисления с целыми числами, не требующие пересечения границ разрядных значений. Например. 23 + 45= ? на 40 + 5 +20 + 3 или 40 + 23 + 5
   2. Вычисления с целыми числами, включающие пересечение границ разрядного значения. Например. 49– 32= ? на 49 – 9 – 23 или 57 + 34 = ? на 57 + 3 + 31
   3. Вычисления с десятичными числами, не связанные с пересечением границ разрядного значения 5.6 + 3.7= ? на 5,6 + 3 +0,7 или 540 + 380= ? на 540 + 300 + 80 или 540 + 360 + 20
   4. Вычисления с десятичными числами, которые включают пересечение границ разрядного значения. Например. 1,4 + 1,7= ? на 1,4 + 0,6 + 1,1 и 0,8 + 0,35 = ? на 0,8 + 0,2 + 0,15

   Компенсация и корректировка

   Компенсация заключается в том, чтобы добавить больше, чем нужно, а затем вычесть лишнее.

   Эта стратегия полезна для сложения чисел, близких к кратным 10, например чисел, оканчивающихся на 1 или 2, 8 или 9.

   Добавляемое число округляется до кратного 10 плюс или минус небольшое число.

   Например, добавление 9 выполняется путем прибавления 10, а затем вычитания 1. Аналогичная стратегия работает для добавления десятичных дробей, близких к целым числам.

   Вот как вы можете помочь своему классу добиться прогресса в компенсации и корректировке:

   1. Компенсация и настройка на 10. (например, 34 + 9=? на 34 + 10 – 1 или 34 – 11= ? на 34 – 100 – 1 = ?)
   2. Компенсация и настройка, кратные 10. (например, 38 + 68 = ? на 38 + 70 – 2 или 45 – 29 = 45 – 30 + 1)
   3. Компенсация и корректировка, кратные 10 или 100. (например, 138 + 69= ? на 138 + 70 – 1 или 299 – 48 = 300 – 48 – 1)
   4. Компенсация и корректировка кратных с десятичными дробями. (например, 2 ½ + 1 ¾ на 2½ + 2 – ¼ или 5,7 + 3,9 на 5,7 + 4,0 – 0,1)

   Расчет с использованием почти двойных чисел

   Когда дети автоматически вспоминают основные двойные факты, они могут использовать эту информацию при сложении двух чисел, которые очень близки друг к другу.

   Вот способы, которыми вы можете помочь своему классу прогрессировать в почти двойных числах:

   1. Почти двойные числа до 20. Например. 18 + 16 равно удвоению 18 и вычитанию 2 или удвоению 16 и прибавлению 2.
   2. Почти удваивается до кратного 10. Например. 60 + 70 — это удвоить 60 и прибавить 10, или удвоить 70 и вычесть 10, или 75 + 76 — это удвоить 76 и вычесть 1, или удвоить 75 и прибавить 1.
   3. Десятичное число почти удваивается до целых чисел. Например. 2,5 + 2,6 — это удвоить 2,5, добавить 0,1 или удвоить 2,6, вычесть 0,1.
   
   Как разработать математические стратегии в уме, необходимые для умножения и деления 

   По мере прохождения начальной школы учащиеся узнают факты умножения. Им потребуется свободное владение фактами умножения, чтобы они могли вспомнить их достаточно быстро для проверки сейчас и в высшем образовании. Опять же жизненно важно, чтобы они понимали концепцию умножения, а не просто повторяли факты наизусть.

   Тем не менее, практика имеет решающее значение, так как ежедневное вспоминание известных фактов жизненно важно, чтобы новые факты не вытесняли старые там, где они не полностью укоренились.

   Дети начинают понимать умножение с помощью удвоения и деления пополам в начальной школе. Это вводит понятия как умножения, так и деления, и они должны начать замечать их закономерности и применять это к математическим вопросам.

   Они также узнают факты умножения для 5 и 10, и это начинается со счета вперед и назад в 5s и 10s, что они также должны делать с любого заданного числа, а не только с нуля.

   Умственные математические факты, которые дети должны знать к концу 3-го класса

   К концу 3-го класса учащиеся должны уметь запоминать все произведения двух однозначных чисел. А потом в 4 классе факты умножения 11 и 12. Они также должны применять их к задачам со словами и многошаговым задачам по мере повышения уверенности, чтобы убедиться, что они могут применять числовые факты, а не просто повторять их.

   Эти навыки счета в уме и их беглость будут иметь жизненно важное значение в тестовых ситуациях. К тому времени, когда они пойдут в старшую школу, они должны иметь очень твердое представление о системе счисления, а также о известных фактах и ​​закономерностях.

   38 новых фактов об умножении (и делении), которые дети должны знать к концу 4-го класса. и факты деления на числа, кратные 10 и 100, чтобы мысленно рассчитать увеличивающийся диапазон вопросов на умножение.

   Вот способы, с помощью которых вы можете помочь своему классу повысить разрядность:

   1. Умножить двузначное число на однозначное путем разбиения. Например. 26 х 3 = 20 х 3 + 6 х 3
   2. Умножение десятичного числа, содержащего до 2 знаков после запятой, на одну цифру путем разбиения. Например. 3,42 x 4 = 3 x 4 + 0,4 x 4 + 0,02 x 4

   Стратегии удвоения и деления пополам

   Дети должны уметь распознавать деление пополам как действие, обратное удвоению, и уметь быстро вычислять удвоенные и половинные числа.

   Некоторые двойные и половинчатые факты быстро запоминаются, а не те, которые дети должны вычислять каждый раз, и они описаны в списках выше.

   Вот способы, которыми вы можете помочь своему классу прогрессировать в удвоении и делении пополам:

   1. Найдите двойные и половинные числа любого двузначного числа и любого числа, кратного 10 или 100. (например, половина 680 или двойное 73)
   2. Умножьте и разделите на 4, дважды удвоив/делив пополам, и на 8, снова удвоив/поделив пополам. (например, 34 x 4 = 34 x 2 x 2.)
   3. Найдите двойные числа и половинки любого числа до 10 000 путем разбиения. (например, половина от 32 202 за счет уменьшения вдвое 3000, 2000, 200 и 2)
   4. Умножить на 50 путем умножения на 100 и деления пополам. (например, 8 x 50 = 8 x 100 разделить на 2)
   5. Разделить число, кратное 25, на 25, разделить на 100 и умножить на 4 (путем удвоения и повторного удвоения). (например, 350 ÷ 25 = 350 ÷ 100 x 2 x 2)
   6. Разделите число, кратное 50, на 50 путем деления на 100, а затем удвоения. (например, 450 ÷ 50= 450 ÷ 10 x 2)
   7. Двойное и половинное десятичное число с точностью до одного десятичного знака путем деления на порции. (например, половина 8,4 путем уменьшения вдвое 8 и уменьшения вдвое 0,4)
   
   Стратегии вычисления в уме дробей, десятичных знаков и процентов

   По мере прохождения начальной школы дети должны лучше понимать дроби, десятичные числа и проценты и то, как они связаны с делением.

   Таким образом, к 5-му классу они должны уметь быстро вспоминать факты умножения и деления, чтобы вычислять в уме некоторые вопросы, связанные с дробями, десятичными знаками и процентами.

   Вот как вы можете помочь своему классу освоить дроби, десятичные числа и проценты:

   1. Найдите в уме дроби чисел в таблице умножения на 2, 3, 4, 5 и 10, используя известные факты умножения и деления. (например, 3/5 от 45 на 45 ÷ 5 x 3.)
   2. Вызов процентов эквивалентен ½, 1/3, ⅕, ⅙, 1/10 и 1/100. (например, ¼ = 25%)
   3. Найдите 10% или кратные 10% целых чисел и величин. (например, 30% от 50 на 50 ÷ 10 x 3)
   4. Мысленно найдите 50% путем деления пополам и 25% путем деления чисел и величин на 4 или 2. (например, 25% от 150 на 150 ÷ ​​4)

   Взлом процентных вычислений в уме

   Приведенный ниже твит — это то, что вы, возможно, видели в Твиттере в начале 2019 года, но он представляет собой полезную стратегию, помогающую вычислить сложные проценты.

   Этот вирусный твит — очень хороший пример математического трюка в уме. Это также отличный способ использовать математические трюки в уме, чтобы произвести впечатление на своих друзей!
   
   Лучшие советы по ментальной арифметике: как обучать стратегиям ментальной арифметики

   Мы достаточно подробно рассмотрели вопрос «что», но как мы на самом деле приступаем к обучению стратегиям ментальной арифметики? Вот краткое изложение наших лучших советов:

   1. Обучайте математическим приемам в уме и методам вычисления в уме, а не просто полагайтесь на то, что дети «соберут их».
      Важно, чтобы время урока было посвящено концептуальному обучению стратегиям и оказанию помощи детям в установлении связей между известными им фактами и расчетами в уме. Лучше всего это достигается с помощью моделирования и использования манипулятивных средств и т. д.
   2. Вовлекайте детей в обсуждение. Детей следует поощрять к обсуждению своих умственных стратегий друг с другом и всем классом, а взрослые в классе должны присоединиться к этому обсуждению. Дети будут видеть и подходить к вычислениям в уме разными (и в равной степени обоснованными) способами, и, делясь ими, они знакомят друг друга с разными способами мышления и «видения» вычисления.
   3. Обеспечьте регулярную ментальную арифметику. Дети должны иметь регулярную практику умственного счета, которая фокусируется на стратегиях умственного счета. Наряду с обучением стратегиям на основном уроке математики, школы, где дети имеют высокий уровень компетентности и беглости в умственных стратегиях, часто посвящают 15-20 минут в день практике и развитию умственных стратегий и быстрому воспроизведению вне основного урока математики.
      .
   4. Не думайте, что тестирование по времени — единственный способ добиться быстрого отзыва. Многие исследования показали, что тестирование на время является одним из наименее эффективных способов развития быстрого припоминания. Вместо этого предоставьте детям множество возможностей использовать, применять и вспоминать факты, которые вы хотите, чтобы они могли быстро вспоминать.
   5. Играйте в игры и создавайте возможности для значимой деятельности. Если занятия будут веселыми и осмысленными, дети получат поддержку в развитии чувства числа и беглости в увеличивающемся диапазоне вычислений.
   6. Обеспечьте соблюдение «базовых» числовых фактов. Важно, чтобы вы не пренебрегали «основными» числовыми фактами, например, числовыми связями в пределах 10, 20 и 100 и таблицей умножения 1-12x. Часто такие факты, как числовые связи, практикуются только в начальных классах, но жизненно важно, чтобы они практиковались, и детей поощряют использовать эти факты в своих умственных вычислениях. Помните, если вы не предоставите им возможность ею воспользоваться, они ее потеряют!

   Подробнее:

   • Как учить факты умножения, чтобы ученики быстро запоминали
   • Что такое свободное владение математикой?

   Ссылки:

   Рассел, Сьюзан Джо (2007). Развитие вычислительной беглости с целыми числами в начальных классах

   Есть ли у вас учащиеся, которым нужна дополнительная поддержка по математике?

   
   Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.

   Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.