Умножение на абакусе. Полный разбор ( примеры )

Главная » Ментальная Арифметика

15.04.202120.10.2020

Освоение счётов

Счеты — прекрасный инструмент для решения множества типов арифметических задач, включая умножение. При развитии любого навыка, например использования счётов, требуется практика. Чтобы овладеть инструментом счета абакуса, человек должен попытаться задействовать как можно больше «обучающих» чувств. Это включает рассмотрение визуальных аспектов абака, слуховых сигналов и ответов, а также применение осязания. Если вам приходилось наблюдать за работой мастеров счёта, давно работавших на счетах, вы могли бы увидеть, как эти специалисты перемещают пальцами невидимые бусинки во время процесса вычислений. Вы можете услышать, как они бормочут слова, связанные со счетами, такие как окупаемость, набор и очистка. Я также работал с давними пользователями устройства, которые просто быстро производили вычисления в уме, не говоря ни слова или жестов. Тем не менее,

действительно, счеты абакуса имеют давнюю историю человечества. Счетное устройство по-прежнему является частью обучения математике по определенным причинам в некоторых регионах западного мира и земного шара. Я учил людей решать математические задачи на счетах абакуса, и им очень понравилось изучать счетное устройство. Несомненно, счеты абакуса будут с нами еще долгие годы. Это связано с необходимостью применения разных подходов к изучению математики.

Вот еще несколько причин, по которым счеты абакуса остаются важным инструментом счета во всем мире:

Причины, по которым счеты по-прежнему используются во всем мире

• Счеты прочные. Счеты можно уронить, и они будут продолжать выполнять ту работу, для которой они были предназначены. Кроме того, для работы счеты не требуется электричество или Интернет. Каждый не может позволить себе калькуляторы, а счеты — это недорогая функциональная альтернатива в более бедных странах. Кроме того, люди с потерей зрения часто могут лучше понимать числовые концепции с помощью счетного инструмента.
• Счеты абакуса бывают разных видов, вертикальные и горизонтальные. Счетный инструмент может быть переносным или стационарным. Счеты также могут быть забавным источником разговоров.
• Счеты абакуса можно использовать, чтобы помочь маленьким детям усвоить числовые понятия. Навыки правильного манипулирования бусинками на счетном инструменте развивают понимание математических процессов, таких как деление, умножение, вычитание и сложение. Наконец, не все учатся одинаково или в одинаковом темпе. Использование счеты для математики предлагает альтернативу традиционным карандашным и бумажным методам.

Что нужно знать перед выполнением умножения на счетах

• Как и в случае с любым другим навыком, необходимо развивать знания, чтобы точно и уверенно выполнять все более сложные задачи. То же самое и со счетами. Это навыки, которыми следует овладеть, прежде чем пытаться умножать уравнения с тремя цифрами на счетах:
• Человек должен понимать, как формируются числа на счетах. Это включает в себя установку чисел и очистку счетного инструмента. Человек также должен знать, как перевести счеты в состояние покоя или обнулить показания устройства, как показано на первой фотографии в этой статье.
• Человек должен понимать и уметь проводить сложение задач на счетах абакуса. Человек также должен был выполнить уравнения вычитания на счетах абакуса. Эти проблемы должны были быть однозначными, двухзначными, трехзначными или более.
• Очень важно понимать таблицу умножения. Например, человек должен знать таблицу умножения до девяток. (5 x 3, 6 x 7, 8 x 9 и т. Д.) Человек должен быть знаком с терминологией, относящейся к умножению, такой как «произведение».
• Следует хорошо понимать терминологию, относящуюся к работе со счетами абакуса. Такие термины, как «окупаемость», следует понимать с учетом навыков применения концепции при решении проблемы. Кроме того, поддержание «баланса» по отношению к схемам подсчета по основанию десяти должно быть прочно закреплено в словарном запасе и базе знаний человека. Например: 1 + 9 = 10, 2 + 8 = 10, 10-4 = 6, 3 + 7 = 10 и т. Д.

Исследуй дальше уроки Ментальная Арифметика Умножение

Как считать умножение на абакусе

Изучая счеты, мы замечаем, что имеется не менее тринадцати рядов бусинок. Чтобы произвести умножение, мы должны мысленно представить счеты как разделенные посередине этих рядов, примерно в седьмом ряду бусинок. Это потому, что мы разместим одно число слева от счетчика, а другое — справа.

1. Давайте начнем. Поместите 25 x 7 на счеты.
2. Поместите 25 в самые дальние ряды бусинок.
3. Теперь давайте разместим цифру 7.
4. Для этого мы знаем, что в задаче умножения есть три цифры: 2, 5 и 7.
5. Для умножения нужно дать дополнительный ряд бусинок «для счётов». По сути, мы думаем: три цифры в уравнении плюс ряд бусинок «для счётов».
6. Это означает, что цифра 7 будет размещена в четвертом ряду справа. Важность этого действия заключается в том, что он дает пользователю счетного инструмента некоторое указание на то, что ответ будет в сотнях, оставшиеся три строки справа.
   Задача должна быть настроена как на фото.

Счет «25 X 7».

 

Здесь счет показывает как «7 умножить на два десятка».

Теперь решим уравнение

Умножение: 7 раз первое число, то есть 2, или 2 десятки. Это дает нам ответ 14 или 14 десятков, как показано на рисунке. Не очищайте 7.
Прежде чем продолжить, обратите внимание на ответ. Вы увидите, что первый продукт помещен рядом с 7. Этот результат был предсказан на основании способа постановки проблемы. Первое произведение находится в столбцах сотен, десятков и единиц. Нам еще нужно вычислить число 5.
Теперь умножьте: 7 раз 5. Это дает ответ 35 или 3 десятков и 5 единиц, которые можно добавить к 140. Ваш ответ будет: 175, как показано на фотографии. А теперь остановите счеты абакуса.

На счетах показан расчет «25 X 7».

 

Счеты, показывающие «9 х 50».

Исследуй и практикуйся дальше Онлайн тренажер по Ментальной Арифметике

Проблема нуля на счетах

При вычислении задач с тремя цифрами в уравнении, где ноль является частью двузначного числа, например 80, 90, 40 и т. Д., Мы по-прежнему считаем до четвертой строки, чтобы установить второе число. Например, 50 x 9 потребует такой же процедуры.

Давай попробуем.

Поместите 9 в крайний левый ряд.
Теперь поместите 50 в четвертый ряд справа. Задача должна быть настроена как на фото.
Умножить: 9 х 50.
Ответ будет: 450, которые вы поместите на третий, второй и первый ряды бусинок с правой стороны. После очистки 9 и 50 ответ должен выглядеть как на фото.

Это основные шаги для работы с уравнениями, состоящими из трех цифр, в задаче умножения на счетах. Теперь, когда работа сделана, счеты абакуса можно остановить.
Другая проблема с нулем возникает, когда конечный продукт меньше 100. В этих случаях мы считаем сотни за ноль. Например: 9 x 11 будет считаться таким образом: (0) сотни, 9 десятков и 9 единиц. 3 x 12 будут посчитаны таким образом: (0) сотни, 3 десятки и 6 единиц. Наслаждайтесь счетами абакуса, и вы можете стать экспертом в использовании счетного инструмента в будущем.

На счетах «450».

Ментальная арифметика на пальцах | Сложение и вычитание

Каждый родитель мечтает, чтобы его ребенок рос умным, здоровым, успешным. Но как мы развиваем своих детей? Или надеемся только на занятия в детском саду и школе? Для гармоничного развития, укрепления памяти и уверенности в себе, стимулирования внимания детсадовских занятий мало! Здесь на помощь приходит ментальная арифметика. С этой методикой каждый ребенок полюбит математику, разовьет навыки концентрации внимания, быстрого устного счета, зрительной и слухоречевой памяти, гибкости ума, нестандартного мышления. Что это за система, ее плюсы, назначение и особенности — читайте ниже!

Ментальная арифметика. Что это такое

Это система обучения детей быстрому устному счету: сложению и вычитанию, умножению и делению. Мини-занятия можно начинать с детства, особенно эффективно обучаются дети 4-12 лет. Если ваш ребенок старше этого возраста, учиться тоже можно, но времени и усилий потребуется больше. В основе обучения ментальной математике (менар) лежит практика счета на абакусе — специальном инструменте, который имеет давнюю историю.

Где и когда можно заниматься

Методика ментальной арифметики пошаговая, состоящая из 10 уровней, из которых 5 уровней образуют базовую программу детского развития. Каждый уровень длится 4-6 месяцев, а все обучение базовой программы занимает 2-2,5 года.

Заниматься можно не только в специальных группах с педагогом, но и в домашних условиях с родителями. В группах мини-уроки обычно проходят 1-2 раза еженедельно по 30-45 мин. Дома можно упражняться через день по 15-20 мин.

На начальном уровне достигаются следующие цели:

• знакомство и навык работы с абакусом — специальными счетами;
• тренировка памяти, мелкой моторики;
• освоение ментальных карт, их визуализация;
• развитие логического, пространственного мышления.

Навык визуализации является значимым и переходным на следующий уровень. Если ребенок хорошо разовьет навык визуализации, то в дальнейшем быстро и самостоятельно сможет считать без счет в уме (ментально).

На начальном этапе для облегчения процесса используются специальные флеш-карточки, рабочие тетради, упражнения и игровые примеры. Их цели — стимулировать память, навык обращения с числами, запомнить простейшие действия и примеры, чтобы затем выполнять их в уме.

Счеты для ментальной арифметики. Какие и зачем

Потребность человека в количественном измерении, подсчете и математических расчетах появилась задолго до появления чисел. Первым расчетным инструментом, который природа предоставила в распоряжение человека, была его собственная рука/пальцы. Потом считать стали на ракушках, веточках, камешках и так далее.

Позднее, в Римской Империи, Древней Азии и других частях света, человек изобрел простые и быстрые способы счета и вычисления. Счеты или абакус — это древний азиатский вычислительный инструмент, который и в наше время помогает детям овладеть основными математическими навыками. Существует множество различных типов счетов, и во всем мире используются различные терминологии. Так, в Японии абакус широко распространен под названием японский соробан.

Эти счеты состоят из нескольких частей:

• деревянной или пластиковой рамы;
• горизонтальной линейки-разделителя;
• верхней и нижней части со стержнями, на которые нанизаны косточки/бусины.

Японский соборан или абакус напоминает наши, отечественные счеты, которые перевернули на бок.

Как быстро считать на абакусе. Общие правила

В счетах соробан имеет значение каждый элемент! Так:

• на 1-ой спице у нас единицы;
• на 2-ой — десятки;
• на 3-ей — сотни;
• на 4-ой — тысячи и т. д.

На верхних спицах располагаются «небесные» косточки/бусины, на нижних спицах — «земные». Одна «небесная» косточка = 5 «земных». В примерах это звучит так: если на 3-ей спице верхнего ряда отложена одна бусина к линейке, это 500. Если ни одна бусина не касается расчетной разделительной линейки, это ноль.

Чтобы освоить быстрый счет на абакусе удобно пользоваться двумя пальцами: большим и указательным. Нижние бусины поднимаются большим пальцем, а указательным — опускаются вниз. Верхние бусины опускаются и поднимаются указательным пальцем. Процесс со временем доводится до автоматического, и счет становится очень быстрым и правильным.

Существует история, что в конце 1946 года японский почтовый чиновник, весьма искусный в использовании абакуса, вступил в соревнование с иностранным солдатом, который для счета использовал самый современный калькулятор. В четырех из пяти состязаний японский чиновник со счетами оказался быстрее, уступив лишь в сложных задачах.

Сложение и вычитание на абакусе

Прежде всего, нужно научиться откладывать числа на счетах. Например:

• Если нужно 5, на 1ой верхней спице отпускаем 1-ну бусину.
• Если нужно 7, на 1ой верхней спице отпускаем 1-ну бусину, в это же время на нижней спице поднимаем 2-е вверх.
• Если нужно 73, на 2ой верхней спице опускаем бусину, на 2ой нижней — поднимаем 2-е бусины. Получается 70. Из первой нижней поднимаем три бусины. Образуется 73.

После того как дошкольник освоил цифры на абакусе, практику откладывания чисел, можно переходить к примерам простого сложения. Пошагово это происходит так:

Пример 14+25.

Откладываем число: на 2ой нижней спице поднимаем 1-ну бусину, на 1ой нижней — 4. Затем прибавляем 25: на 2ой нижней спице прибавляем 2, на 1ой спице – верхнюю бусину. Получаем результат 39.

Решение примеров вычитания начинается с наибольшего разряда числа (в трехзначных — с сотен, в двузначных — с десятков). Обязательно задействуется верхний блок косточек.

Пример 23 — 11.

С верхней 2ой спицы опускаем 2 бусины, с 1ой нижней поднимаем 3.

На 2ой и 1ой спицах возвращаем по 1-ной бусине.

Уроки ментальной арифметики по набору чисел, сложению/вычитанию можно предварительно смотреть в видео и сразу повторять с ребенком. Это особенно полезно, если занимаетесь сами, дома.

Умножение и деление на абакусе

После освоения сложения и вычитания можно приступать к действиям посложнее — умножению и делению. Важно не забывать, что подсчет производится двумя пальцами — большим и указательным.

Пример 12 * 21.

Работаем с десятками: с нижней 3ей спицы поднимаем вверх 2-е бусины, 10 * 20 = 200.

Поднимаем на 2ой нижней спице вверх 4-е бусины, умножаем единицы первого числа на десятки, 2 * 20 = 40.

Опускаем на 2ой спице одну верхнюю бусину и все нижние, умножаем десятки первого числа на единицы второго, 10 * 1 = 10.

Поднимаем на 1ой нижней спице вверх 2-е бусины, умножаем единицы первого и второго числа, 2 * 1 = 2.

В результате: 12 * 21 = 252.

По мере тренировки и решения примеров приходит понимание действий, подсчет доводится до автоматизма.

После того, как хорошо усвоено умножение, можно приступать к примерам деления.

Пример 62 : 2.

Выставляем в правой половине счет 62, левая пустая, для ответа.

Делим 6 на 2, получаем 3 и откладываем его на крайней левой спице.

В первой половине на 2ой спице отнимается 6-ть бусин остается 2.

На второй слева спице откладывается 1, которая получилась, когда 2 : 2.

Решение примера получается: 62 : 2 = 31.

Как перейти от абакуса к счету на пальцах

Специальные счеты абакус не всегда будут в ходу. Цель дальнейших этапов — научить ребенка быстро и правильно считать без них, ментально. С помощью методов визуализации ребенок постепенно учится представлять счеты в своем уме, при этом помогая пальцами благодаря мышечной памяти.

Для того, чтобы в последующих уроках начать представлять бусинки, желательно проделывать различные задания, развивающие образное мышление. Например, нахождение различий на картинках, пересказ содержимого в картинке и ответ на вопросы по рисунку, определение фигур на ощупь.

Как правило, обучение ментальной арифметике завершается тем, что ребенок без специальных счет, в уме, быстро решает любые примеры, хорошо запоминает действия, имеет развитое логическое и математическое мышление.

Плюсы и минусы ментальной арифметики

Один из главных плюсов — гармоничное развитие левого и правого полушарий мозга.

Как мы все знаем, наш мозг имеет две части: правое полушарие и левое полушарие Левое управляет логическими, числовыми, аналитическими, последовательными фактами и памятью, в то время как правое отвечает за цвет, музыку, воображение, чувства, рифму, мечтательность и общее мышление. Левое полушарие управляет правыми конечностями, а правое — левыми. И наоборот, действие конечностей также оказывает влияние на развитие мозга.

С помощью магнитно-резонансного теста (МРТ) исследователи доказали, что большинство людей (90%) в мире используют в основном левую сторону мозга для своей повседневной деятельности, включая регулярные школьные занятия. При этом правое полушарие мозга развивается недостаточно, поэтому воображение, фантазия, креативность, гибкость мышления развиты недостаточно.

Таким образом, чтобы повысить общий интеллект головного мозга необходимо межполушарное взаимодействие. Чтобы достичь полного развития мозга, мы и используем ментальную арифметику как средство и счеты как инструмент.

Другие плюсы:

• Обучение ментальной арифметике помогает глубже раскрыть заложенный в детях потенциал, что в дальнейшем станет залогом успешной учебы, творческого развития и счастливого будущего.
• Доказано, что у детей существенно увеличивается качество и скорость усвоения информации и как следствие растет школьная успеваемость, уверенность в собственных силах, самооценка.
• Улучшается усидчивость и концентрация внимания.
• Появляются способности быстро решать задачи.
• Улучшается память.
• Ускоряется понимание других предметов школьной программы и навыки слушания.
• Улучшаются навыки визуализации, воображения.
• Развиваются творческие способности.

Уроки ментальной арифметики разрешены всем, независимо от пола, физической формы, они не имеют медицинских ограничений.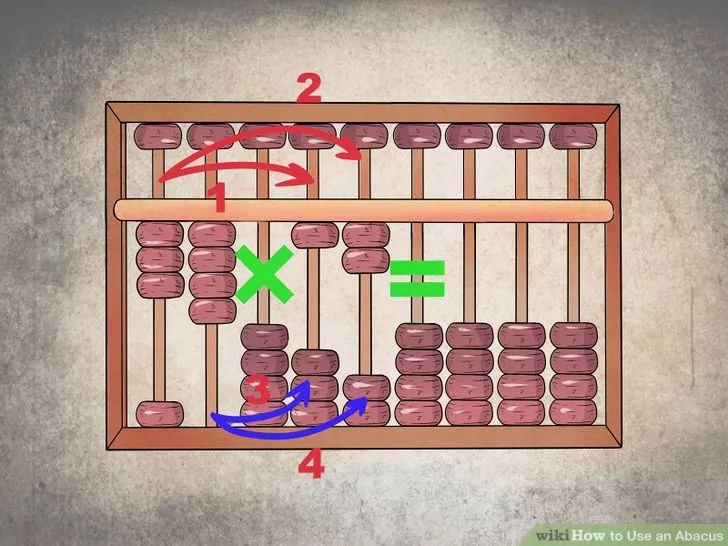 Заниматься можно в группе и одному, дома, с родителями. Малыши с 4-х лет уже могут осваивать интересные счеты абакус и заниматься с игровым раздаточным материалом.

Есть ли минусы у ментальной математики? Многие педагоги подчеркивают важность правильного расписания занятий. Не перегрузить, чтобы не спровоцировать утомление и ухудшение результатов запоминания!

Еще один нюанс состоит в том, чтобы заниматься по плану, не перескакивая с темы на тему. В этом случае можно гарантировать стойкий результат и гармоничное развитие ребенка.

В школу с удовольствием

Подготовьте своего дошкольника к занятиям, используя методику ментальной арифметики. Он научится быстро считать, решать примеры и будет уверенно чувствовать себя на уроках. Учителя наверняка отметят гибкость его мышления, тягу к знаниям, которые вы развили с помощью менара!

Рейтинг: 4.5/5 — 2 голосов

Умножение и деление дробей с помощью Mental Math – World Mental Calculation

Умножение и деление простых дробей более просто, чем сложение и вычитание дробей. Однако при выполнении этих расчетов в уме возникают некоторые проблемы!

Дробь состоит из числа — числителя — деленного на другое число — называемое знаменателем . Обычно оба эти числа должны быть положительными  целых чисел  (целые числа).

Например, в \(\frac{4}{15}\) числитель равен 4, а знаменатель равен 15.

Основное умножение на дробь

Умножение на дробь \(\frac{ a}{b}\), означает умножение на \(a\) и деление на \(b\). Обычно результат представляет собой дробь:

.

\(7 \times \frac{2}{15} = \frac{14}{15}\)

Базовое умножение дробей

При умножении двух или более дробей числители умножаются вместе, а знаменатели умножаются вместе:

\(\frac{a}{b} \times \frac{c}{d}\times \frac{e}{f} = \frac{a \times c \times e}{b \times d \times е}\)

\(\frac{8}{9}\times \frac{5}{7} = \frac{8 \times 5}{9 \times 7} = \frac{40}{63}\)

Упрощенные дроби

Дробь является упрощенной , если нет простых чисел, которые делят на как числитель, так и знаменатель . Например, \(\frac{40}{60}\) — это , а не упрощенно, потому что \(2\) делится на \(40\) и \(60\). На самом деле, то же самое относится и к \(5\), и даже к некоторым большим непростым числам, таким как \(20\). Если вы разделите верх и низ дроби на \(20\), дробь станет \(\frac{2}{3}\), что является упрощенной формой.

На этой странице я предполагаю, что вам нужно умножать или делить уже упрощенные дроби, что обычно для соревнований по ментальной арифметике. В противном случае обычно проще всего сначала упростить их.

Смешанные дроби

Дробь неправильная , если числитель больше знаменателя. Например, \(\frac{14}{3}\) — неправильная дробь. Неправильные дроби можно записать как смешанные дроби — с целой частью и правильной дробной частью. Например, \(\frac{14}{3} = 4 \frac{2}{3}\)

Чтобы умножить или разделить смешанные дроби, обычно гораздо проще сначала преобразовать их в неправильные дроби .

Для этого можно использовать формулу:

\(n \frac{a}{b} = \frac{b \times n + a}{b}\)

Например:

\(2 \frac{3}{4} = \frac{4 \times 2 + 3}{4} = \frac{11}{4}\)

Это верно, потому что если мы разделим целую часть — \(n\) — на \(b\) равных частей, то будет \(n \x b\) этих частей. Добавьте это к \(a\) кусочкам, которые уже были представлены дробью, и всего будет \(n \times b + a\).

В соревнованиях по устному счету вы должны давать все ответы в смешанной форме. Неправильные дроби отмечены как неправильные! Поэтому вы также должны знать, как преобразовать неправильную дробь в смешанную дробь .

Для этого разделите числитель на знаменатель и получите остаток. Например:

\(14 \дел 3 = 4\) остат. \(2\)

Целая часть — это результат деления — \(4\) — а остаток — \(2\) — это числитель смешанной дроби.

\(\frac{14}{3} = 4 \frac{2}{3}\)

Полный пример:

\(2 \frac{3}{4} \times 5 \frac{6}{7} = \frac{11}{4} \times \frac{41}{7}\)

\(= \frac{11 \times 41}{4 \times 7}\)

\(= \frac{541}{28} = 16 \frac{3}{28}\)

Упрощение финальной части

В соревнованиях по устному счету вы должны давать все ответы в упрощенной форме. Неупрощенные дроби отмечены неправильно! Даже вне формальных соревнований дроби лучше представлять в упрощенном виде.

При умножении и делении дробей всегда нужно проверять, можно ли упростить результат. В примерах, которые мы уже видели, упрощение недоступно, поэтому давайте рассмотрим пример с упрощением. Вы можете выбрать два метода:

Способ 1: Упростить в конце

\(1 \frac{1}{15} \times 4 \frac{3}{8}\)

\(= \frac{16}{15} \times \frac{35}{8}\)

\(= \frac{16 \times 35}{15 \times 8}\)

\(= \frac{560}{120}\)

Числитель и знаменатель имеют разные делители, включая 10, 8 и т. д. Самый большой общий делитель равен 40, поэтому разделите обе половины дроби на 40:

\(\frac{560}{120} = \frac{14}{3} = 4 \frac{2}{3}\)

Метод 2: Отмена множителей из неправильных дробей

Этот метод лучше, когда у вас есть большие числа — больше, чем 560 и 120, указанные выше, — и помогает избежать арифметических операций с этими большими числами. Однако следовать этому методу сложнее.

Начните так же, как и раньше:

\(1 \frac{1}{15} \times 4 \frac{3}{8}\)

\(= \frac{16}{15} \times \frac{35}{8}\)

Затем обратите внимание, что при их перемножении дробь будет иметь множитель 8 внизу (от второго знаменателя, 8), а также вверху дроби (от первого числителя, 16 = 8 × 2). Разделите соответствующие числа на 8:

\(= \frac{2}{15} \times \frac{35}{1}\)

Можем ли мы сделать то же самое с любыми другими числами? Фактически, в этом случае мы можем сделать то же самое снова с 5, так как 5 является множителем числителя (35) и знаменателя (15). Итак, разделите обе половины на 5, проверьте, что упрощение невозможно, и завершите:

.

\(= \frac{2}{3} \times \frac{7}{1} = \frac{14}{3} = 4 \frac{2}{3}\)

Обратите внимание: если вы определите все факторы для упрощения до конца, вам гарантированно не придется упрощать окончательную дробь. Но если вы что-то пропустите, например, 5, или если вы разделили на 4, а не на 8, вам придется упростить окончательную дробь.

Также обратите внимание, что часто нет доступного упрощения. В этом случае методы 1 и 2 одинаковы, без шагов упрощения. Во время расчета вы можете столкнуться с большими числами, избежать которых невозможно.

Окончательный итог для устных вычислений (умножение)

При умножении дробей:

• Преобразуйте любые смешанные дроби в неправильные дроби.
• На этом этапе (метод 2) можно дополнительно выполнить некоторое упрощение, найдя числа, являющиеся множителями числителя и знаменателя.
• Умножьте все числители, чтобы получить новый числитель. Перемножьте все знаменатели, чтобы получить новый знаменатель.
• Если возможно, упростите ответ.
• Преобразовать в смешанную дробь.
• Помните, что не следует записывать промежуточные этапы подготовки к соревнованиям!

Деление дробей

Деление на неправильную дробь \(\frac{a}{b}\) противоположно умножению на нее. Следовательно, это означает деления на \(a\) и умножив на \(b\).

Следовательно, \(\div \frac{a}{b}\) можно заменить на \(\times \frac{b}{a}\)

Просто переверните дробь «вверх ногами», затем продолжите, используя Что вы знаете об умножении дробей.

Пример: (с использованием метода 2 для упрощения)

\(4 \frac{5}{6} \div 1 \frac{2}{3}\)

\(= \frac{29}{6} \div \frac{5}{3}\)

\(= \frac{29}{6} \times\frac{3}{5}\)

\(= \фракция{29{2} \times\frac{1}{5}\)

\(= \фракция{29}{10}\)

\(= 2 \фрак{9}{10}\)

Помните, конечно, что если вы тренируетесь для умственного счета, вы должны быть в состоянии выполнить все эти шаги, не записывая ничего, кроме окончательного ответа!

Дополнительная литература

Вам может быть интересно:

• Информация о международных соревнованиях по устному счету.
• Более продвинутые методы вычисления в уме.
• Как складывать и вычитать дроби в уме.

5 быстрых советов по ментальному делению – классная математика

Избегаете ли вы решения задач на деление на длинное деление только потому, что они длинные, трудоемкие и пугающие? Вот 5 советов по умственному делению , которые помогут вам пройти через это!

Совет №1 по умственному делению. Точность не всегда является приоритетом

Очень часто ответы на деление даются с двумя-тремя знаками после запятой. Не тратьте время на подробные расчеты, если вам нужна приблизительная оценка. В таких случаях сделайте быструю общую оценку и получите ответ. Допустим, вам нужно рассчитать среднее количество дней, которое у вас есть для завершения каждого из ваших проектов — 11 проектов за 123 дня. Вот в чем хитрость: 11 близко к 10, а 123 близко к 125. Итак, вместо того, чтобы вычислять 123/11, вычисляйте 125/10! Примерный ответ — 12,5 — будет не сильно далек от 11,1, вашего точного ответа.

Совет № 2 по умственному делению — сначала упростите

Что делать, если приблизительные ответы недостаточно хороши? Вот несколько полезных советов по упрощенному делению :

Если делимое и делитель являются четными числами, попробуйте сначала разделить их на 2. Например, если вам нужно разделить 196/22, сначала разделите их на 2. Когда у вас есть 98/11, вам будет легче вычислить остальную часть с меньшими числами.

Если делитель и делимое нечетные числа, попробуйте разделить их на наименьший множитель. Скажем, например, вам нужно разделить 99 на 21. Разделите их на 3 (наименьший множитель), и вы получите 33/7, что достаточно просто для дальнейшего деления!

Совет №3 по ментальному делению – умножьте, чтобы упростить

Как бы парадоксально не звучал совет по ментальному делению №3 , он чрезвычайно полезен! Секрет в том, чтобы умножить прежде, чем мы разделим. Вместо деления 1525 на 5 умножьте 5 и 1525 на 2! Как только ваш делитель будет равен 10, вам будет легко вычислить остальные.