Ментальная Арифметика Умножение

Урок № 4. Ментальная Арифметика Умножение.

Умножение есть не что иное как многократное сложение. Но вместо того, что бы 23 раза прибавлять одно и тоже число, легче выполнить его умножение. Существует особая техника выполнения умножения в окне соробана. Есть несколько различных методов. Здесь приводится метод, который был рекомендован Японским Комитетом по Абакусу. Этот метод считается дающим меньше ошибок и простым в обучении.

Теперь поставим перед собой задачу умножения 23Х47. Число 23 будет называться множимым, а число 47 — множителем. Прежде всего расположим множимое (а это число 23) вблизи центра счетной доски. Пропустив пустую линейку, число 47 (множитель) расположим слева

Между числами пропущены линейки для лучшей наглядности, при не таких маленьких счетах можно пропускать и больше.

Процесс умножения подобен тому, как мы делаем это на бумаге, но отличается последовательностью выполнения действий

Сначала берем правую цифру множимого ( 3) и умножаем на крайнюю левую цифру множимого 3×4=12.

Число 12 откладываем слева от множимого (на линейках FG)

затем эту же цифру множимого умножаем на следующую слева направо цифру множителя 3×7=21, получившееся число 21 прибавляем к результату, но уже сдвинув вправо на один разряд (линейки GH ) :

Теперь мы не нуждаемся в цифре 3, так как с ней уже все проделано, очистим эту линейку (E ) для дальнейшей работы

Теперь берем следующее число множимого — в нашем случае это 2. Умножаем его на левую крайнюю цифру множителя. Результат (2×4=08) прибавляем к линейкам EF. Поскольку в общем случае результат занимает 2 разряда, одноразрядный результат надо представлять в виде 08, что бы правильно разместить его на линейках, так получается следующая картина:

В заключение мы должны умножить 2 на оставшуюся цифру множителя 7 и получившийся результат 14 прибавить на линейки FG

К линейке F надо прибавить 1, но она полностью заполнена, поэтому по правилам сложения, прибавляется 1 к следующему разряду (E), а здесь отнимается 9. Затем к линейке G прибавляется 4

получившееся число является результатом действия 23×47=1081

Исследуй дальше Умножение на абакусе

Ментальная арифметика. Умножение и деление

Форма проведения :

Дистанционная с автоматической проверкой

Краткое описание:

В процессе обучения Вы: — познакомитесь с целями и задачами методики; — изучите методику по теме «Умножение и деление», освоите технологию преподавания, используя подробный поурочный план; — научитесь выполнять арифметические действия на счётах Абакус и в уме с большей скоростью; — научитесь вести занятия с использованием дистанционных образовательных технологий и ресурсов на сайте УМИУС; — получите все необходимые пособия для успешной работы. В результате прохождения курса слушатели улучшат собственные навыки скорого устного счета, смогут проводить обучение по данной методике. Для этого мы предоставляем планы уроков, методические материалы (рабочие тетради, сборники примеров, тексты, задания).

Для кого этот курс:

методист, воспитатель/педагог дошкольного образования, педагог дополнительного образования, учитель математики, учитель начальных классов

Преподавательский состав:

Кокина Марина Викторовна

Занятия проводятся по дням:

дистанционно

Адрес и место обучения:

ул. Бутлерова, д. 17Б

Рекомендовано Экспертным советом ДПО
ФИО	Место работы	Рекомендация	Рейтинг ОО
Моторо Наталья Павловна	ГАОУ ВО «Московский городской педагогический университет»	рекомендовано	не участвует в рейтинге
Старостина Мария Евгеньевна	ГБОУ Школа № 508	рекомендовано	281
Рощина Наталья Леонидовна	ГБОУ Школа № 37	рекомендовано	не участвует в рейтинге

Ментальная арифметика — уроки на умножение и деление, видео

Развитие ребенка – главная цель родителей. Если на первых порах жизни ему достаточно того, чему научили родители, то со временем потребность знаний возрастает. Так и в ментальной математике. После знакомства с абакусом и полученных навыков сложения и вычитания ребенку хочется чего-то большего. Малыши переходят на новую ступень – ментальная арифметика — уроки на умножение и деление.

Читайте также Ментальная арифметика — уроки на плюс и минус

Сама по себе методика только пробивает дорогу в России, хотя во многих странах мира, в том числе и Казахстане, ее ввели в государственную программу обучения в школе. Ведь умение считать в уме быстро и правильно необходимо каждому человеку.

Польза менара для детей

Как считают исследователи и преподаватели ментальной арифметики, при работе на соробане развиваются одновременно оба полушария головного мозга. Ведь детям приходится работать правой и левой рукой. Ментальная или воображаемая арифметика позволяет расширять возможности мозга, учит выполнять действия в нестандартной ситуации.

В отличие от счета на калькуляторе, который полностью отключает деятельность мозга, абакус, наоборот, призван его тренировать. Начинать занятия менаром лучше с 4-х лет и до 16. Люди старшего возраста не всегда могут научиться быстрому счету посредством новой методики, поскольку пользуются уже имеющимися навыками счета, не могут быстро переключаться на новый вид деятельности.

Читайте также Ментальная арифметика — миф или реальность

Дети, изучающие ментальную математику, как отмечают исследователи, становятся успешными во многих сферах деятельности, учатся лучше и с увлечением. Но главное, у них повышается самооценка.

Выучили таблицу умножения — что дальше

Ментальная арифметика — уроки на умножение и деление

Таблица умножения в школе изучается со 2 класса. Ее заучивали до автоматизма, зачастую не показывали особенности и взаимосвязи. К сожалению, в более взрослом возрасте, когда таблица уходит на второй план, особенно при наличии калькулятора, устно выполнить умножение не всегда могут.

В ментальной арифметике тоже необходимо выучить наизусть таблицу умножения, но учат ее не на автомате, а с объяснением взаимосвязей.

Вам в помощь Таблица умножения для детей

Ведь, по сути, и учить-то много не нужно, если выделить 4 группы примеров на умножение:

1. легкие — таблицы на 2, 5, 9
2. рифмы- 6*4, 5*5, 6*8, 6*6
3. повторяющиеся — с одинаковыми множителями 3*3, 4*4, 7*7
4. сложные — 3*4, 3*6, 3*7, 3*8, 4*7, 4*8, 6*7, 7*8

Заучивают, как правило, на занятиях по менару таблицу в игровой форме. Способов заучивания немало, все они пользуются большим успехом у детей. После того, как ребенок научился выполнять на соробане сложение и вычитание, выучил таблицу умножения, подходит время учиться умножать и делить на инструменте. Позднее переходить к абстрактному счету в уме, воображая перед своими глазами соробан.

Ребенок способен умножать и делить любые многозначные числа. Постараемся разобраться на примерах, как выполняются эти математические действия.

Умножение в ментальной арифметике

Выполнение умножения на соробане отличается от сложения тем, что начинают работу не с первой колонки справа, а со спицы с точкой. Разряды присваивают те же самые.

Давайте рассмотрим сначала простые примеры.

• 34 х 3. Сначала умножим 30 х3 = 90. Откладываем 9 десятков на второй колонке слева от точки. 4 х 3 =12. Это десяток и 2 единицы. Добавляем 1 к десяткам, сбрасываем косточки и переходим в разряд сотен – получается 1 сотня. На колонке с единицами добавляем 2 косточки. В итоге получилось 102.

Умножая двухзначные или трехзначные числа, работу на соробане начинают с крайней левой колонки. Действуют по схеме ab х cd =, то есть набираем первый множитель, оставляем пустую колонку, набираем второй множитель и снова пустая колонка. В работе будут 6 колонок. На оставшихся спицах набирается результат.

• Например, 23 х 14. Набираем 23, пробел и 14. Теперь 2 х 1 = 2, набираем в 7 колонке 2 бусинки. Затем 3 х 1 = 3, набираем это число на 8 спице. Затем 2 х 4 справа, получается 8, но у нас на восьмой спице уже есть три. Сбрасываем косточки, добавляем 1 к сотням и поднимаем 1 косточку на 8-ой. Осталось 3 х 4 = 12. Две косточки поднимаем на 9-ой спице, а одну добавляем на 8-ой. Получилось, что 23 х 14 = 322.

Навык умножения разных чисел отрабатывается ежедневно.

Видео «Ментальная арифметика — умножение»

Суть деления в ментальной арифметике

В делении больше динамики, чем в умножении. Делимое и делитель нужно отделить свободными колонками, чтобы потом ни них набирать ответ. Работу так же начинают с самой крайней колонки слева. На них набирается делитель. Делимое набирают на последних колонках справа.

Как же выполнить деление? Для примера возьмем частное 36: 2. Набираем число 36, оставляем пустые спицы не меньше 3, затем набираем число 2.

Итак, начнем:

• 3 разделить на 2. По 2 можно взять один раз. Откладываем в промежутке для ответа одну косточку на месте десятков.
• Умножим 2 на 1, получим два.
• Отнимаем 3 – 2 = 1 – это остаток.
• Смотрим, какое число еще нужно разделить. Получается 16.
• При делениии 16 на 2 получается 8. Проверяем – 2 х 8 = 16. Вычитаем полученный результат, остается нуль.
• Набираем ответ 8 левее от первого числа. У нас получилось 18.

Видео «Ментальная арифметика — деление»

Несмотря на то, что к ментальной арифметике, в том числе и к урокам на умножения и деления отношение у россиян неоднозначное, можно с уверенностью сказать, что взяв в руки соробан, даже взрослый человек не сможет не заинтересоваться особенностью вычислений.

 

Основы ментальной арифметики

1 день
10. 00-11.20	Знакомство. История возникновения счётных устройств.Теория ментальной арифметики. Цель ментальной арифметики. Какие навыки развивает ментальный счет.	2 часа
11.30 – 12.50	Знакомство с соробаном (абакусом). Постановка рук на соробане (абакусе). Косточки и их значения. Практическое занятие: Работа на соробане (абакусе). Значение цифр на соробане (абакусе). Счёт на соробане (абакусе). Правила сложения и вычитания. Знаки «+», «-» в ментальной арифметике. Одинаковые знаки в ментальной арифметике. Исправление ошибок в ментальной арифметике. Практическая работа. Решение на слух в ментальной арифметике.	2 часа
14.00 – 15.20	Принцип решения примеров на ментальном соробане (абакусе). Практика. Знакомство с упрощенными формулами. Упрощенная формула «-4», «+4» и «-3» и «+3» Практическая работа с использование формулы «-4», «+4» и «-3», «+3».	2 часа
15.30 – 16.50	Упрощенная формула «-2», «+2» и «-1» и «+1» Практическая работа с использование формулы «-2», «+2» и «-1», «+1».	2 часа
Всего:		8 часов
2 день
10.00-11.20	Формулы средней сложности «-7», «+7», «-8», «+8», «-9», «+9».	2 часа
11.30 – 12.50	Принципы решения примеров используя формулы средней сложности «-7», «+7», «-8», «+8», «-9», «+9».	2 часа
14.00 – 15.20	Формулы средней сложности «-4», «+4», «-5», «+5», «-6», «+6».	2 часа
15.30 – 16.50	Принципы решения примеров используя формулы средней сложности «-4», «+4», «-5», «+5», «-6», «+6».	2 часа
Всего:		8 часов
3 день
10. 00 -11.20	Формулы средней сложности «-1», «+1», «-2», «+2», «-3», «+3».	2 часа
11.30 – 12.50	Принципы решения примеров используя формулы средней сложности «-1», «+1», «-2», «+2», «-3», «+3».	2 часа
14.00 – 15.20	Знакомство со сложными формулами. Сложная формула «-6», «+6», «-7», «+7».	2 часа
15.30 – 16.50	Принципы решения примеров, с использованием сложных формул «-6», «+6», «-7», «+7».	2 часа
Всего:		8 часов
4 день
10.00-11.20	Знакомство со сложными формулами. Сложная формула «-8», «+8», «-9», «+9».	2 часа
11.30 – 12.50	Принципы решения примеров, с использованием сложных формул «-8», «+8», «-9», «+9».	2 часа
14.00 – 15.20	Умножение на абакусе.	2 часа
15.30 – 16.50	Практическая работа.	2 часа
Всего:		8 часов
5 день
10.00-11.20	Деление на абакусе.	2 часа
11.30 – 12.50	Практическая работа.	2 часа
14.00 – 15.20	Закрепление умножения и деления на абакусе.	2 часа
15.30 – 16.50	Практическая работа. Решение на слух.	2 часа
Всего:		8 часов
Итого:		40 ч.

Ментальная арифметика педагогам | Rich Brain

Ближайшая запись на курс июнь 2020 г.

Мы являемся партнерами Московского педагогического Университета.

Программа ментальная арифметика прошла экспертные заключения

и рекомендована для преподавания в учебных заведениях.

Записаться можно на нашем сайте, сайтах МГПУ или ДПО МОС

​

Программа 1 уровня Сложение и Вычитание.

День 1. История возникновения счета на Абакусе. Родоначальники и создатели ментальной арифметики. Особенности преподавания в разных школах и отличия методик. Знакомство с  Абакусом, цифры, разряды. Простой счет. Отработка движений на абакусе.

 Принцип работы на онлайн тренажере по ментальной арифметике. 

Простой счет практика. Однозначные двузначные числа. 

Основы простого счета, календарно-тематическое планирование простого счета, его особенности с младшими и старшими детьми. Ментальный счет простых чисел.

Знакомство с формулами 5. Принцип работы. Постановка рук при счете. Методические рекомендации для проведения занятий. Практические занятия на онлайн тренажере. 

Домашняя работа. Все тренера выполняют домашнюю работу на онлайн тренажере, мы контролируем правильность выполнения.

​

День 2. Презентация методики(как мы презентуем конечному потребителю, структура Шоу-урока)

Практическое занятие на абакусе, отработка правил. Особенности ментального счета.

Игры на воображение. Проведение физ. минуток. Способы ментального счета. Особенности ментально счета детей дошкольного возраста, старшего возраста. Как проверять детей на «ментальный счет.

Изучение формул 10 однозначных. Основные движения, принцип работы. Знакомство с тетрадями. Как работать в тетрадях с детьми.

Домашняя работа. Все тренера выполняют домашнюю работу на онлайн тренажере, мы контролируем правильность выполнения.

​

День 3. Тестирование по пройденным темам. Знакомство с тренажерами на платформе. Особенности тренажеров. Проведение шоу-урока участниками тренинга. Разбор частых вопросов от родителей.

Личность тренера(основные роли и функции) Знакомство с формулами 5+10 однозначными.

Тренировка на платформе. Разбор частых ошибок детей. Создание личных кабинетов тестовых учеников, задание домашних заданий на платформе. Принцип работы разрядов+ формул.

​

День 4. Тестирование по пройденным темам. Проверка домашних заданий. Вопрос-ответ. Особенности долгосрочной работы с родителями. Теория и практика двузначных, трехзначных чисел. Методика преподавания двузначных, трехзначных чисел.  Знакомство с методическими материалами для преподавания.

​

​

​

​

После прохождения курса:

-Проводится тестирование, после которого выдается сертификат нашей школы и удостоверение МГПУ.

-Бесплатный доступ на 2 недели к онлайн тренажеру, для тренировок.

-Программа для предоставление в государственное учреждение

-Возможность работать по нашим тетрадям.

-Методические рекомендации.

-Возможность принятия участия в семинарах.

-Поддержка при работе на нашей платформе.

​

​

​

Наши преимущества

Занятия ведет основатель Rich Brain практикующий педагог. 

Собственная онлайн платформа, не требующая дополнительных материалов.

Эффективность занятий на онлайн тренажере в 3-5 раз превышает результаты других школ.

Разработанные нами учебники для детей.

Методика проверенная временем, не теория, а практика.

​

Занятия проходят в Г. Москва, шаговая доступность м. Алма-Атинская, и  м. Тульская здание МГПУ

Программа 2 уровня Умножение и деление

Длительность курса 2 недели по 3 часа. Всего 12 часов.

По прохождению курса выдается сертификат нашей школы.

День.1. Легкое изучение таблицы умножения. Особенности обучения детей не знающих таблицу умножения. Календарно-тематическое планирование. Подготовка детей к умножению.

Умножение двузначных на однозначные числа. Умножение трехзначных на однозначные.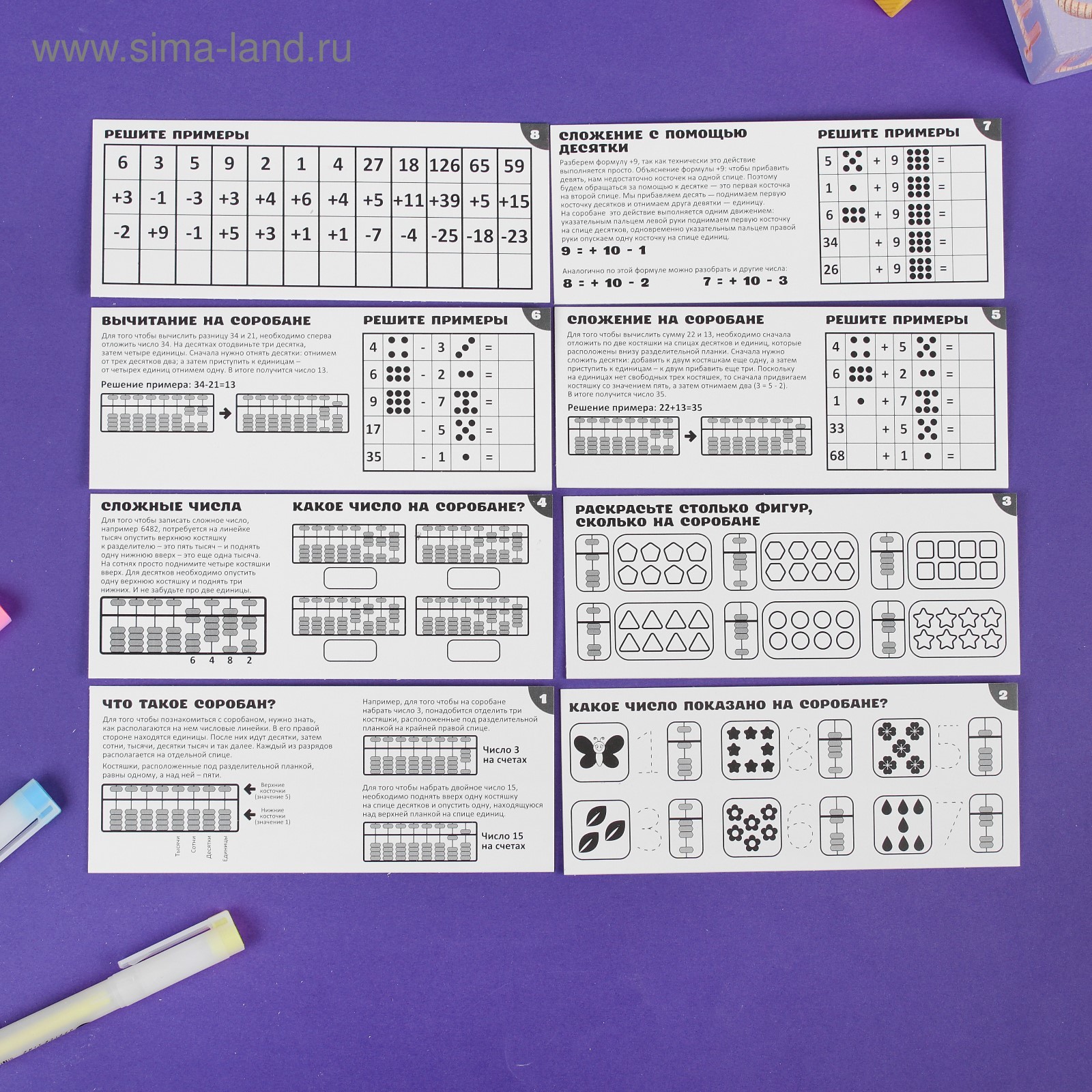 Двузначных на двузначные числа.

Хитрости 11.

День. 2. Хитрости двузначные. Умножение на числа в заданном диапазоне.

Умножение четырехзначных на однозначные. База 100. Отработка правил на онлайн тренажере.

День. 3. База 50, База 200. Повторение. Промежуточное тестирование по пройденным темам. Домашние задания на онлайн-платформе.

 Возведение в квадрат. Секреты возведения в квадрат чисел в диапазоне.

День. 4. Деление Двузначных, Трехзначных, Четырехзначных чисел на однозначное.

Деление на двузначное число. Методика преподавания умножения и деления.

​

​

Методика ментальной арифметики

Дошкольники и школьники: 1 уровень «Просто» Сложение и вычитание на уровне «Просто» (9 недель, 80 страниц) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т. д.) 1-я неделя. Знакомство с абакусом. Сложение и вычитание примеров с числами от 0 до 4 на абакусе и ментально. Флеш-карты. Состав числа 1-4. Развитие обеих рук. Логика. Развития внимания. Нейрогимнастика. 8 листов. 2-я неделя. Сложение и вычитание примеров с числами 0-7 на абакусе и ментально. Флеш-карты. Состав числа 5-7. Развитие обеих рук. Логика. Развитие внимания. Нейрогимнастика. 8 листов. 3-я неделя. Сложение и вычитание примеров с числами 0-9 на абакусе и ментально. Флеш-карты. Состав числа 8-9. Развитие обеих рук. Логика. Развитие внимания. Нейрогимнастика. 8 листов. 4-я неделя. Знакомство с сотней. Сложение и вычитание примеров с круглыми и парными двузначными числами на абакусе и ментально. Флеш-карты. Состав чисел второго десятка. Развитие обеих рук. Логика. Развитие внимания. Нейрогимнастика. 8 листов. 5-я неделя. Сложение и вычитание примеров с двузначными числами на абакусе и ментально. Флеш-карты. Состав числа в сотне. Понятие четных и нечетных чисел. Повторение состава числа 5 и 10 (подготовка к формулам). Развитие обеих рук. Логика. Развитие внимания. Нейрогимнастика. 8 листов. 6-я неделя. Сложение и вычитание примеров с чередованием двузначных и однозначных чисел на абакусе и ментально. Двузначные флеш-карты. Счёт в сотне. Числа соседи. Повторение состава числа 10 (подготовка к формулам). Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов. 7-я неделя. Сложение и вычитание примеров с трёхзначными числами на абакусе. Трёхзначные флеш-карты. Счёт в сотне, состав числа сотни, состав трёхзначного числа. Числа соседи. Последовательность чисел в сотне. Понятие тысячи. Работа с монетной системой. Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов. 8-я неделя. Закрепление. Сложение и вычитание примеров с трёхзначными числами на абакусе и ментально. Трёхзначные флеш-карты. Счёт в сотне, состав числа сотни, состав трёхзначного числа. Числа соседи. Последовательность чисел в сотне. Понятие тысячи. Работа с монетной системой. Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов. 9-я неделя. Итоговое занятие по первому уровню. Сложение и вычитание примеров с одно-, дву- и трёхзначными числами на абакусе и ментально. Замер скорости и правильности решения примеров. Двузначные и трёхзначные флеш-карты. Счёт в сотне, состав числа второго десятка, сотни. Работа с монетной системой. Развитие обеих рук. Логика. Развитие внимания и пространственного мышления. Нейрогимнастика. 8 листов. Дошкольники и школьники: 2 уровень «Помощь брата» Сложение и вычитание на уровне «Помощь брата» (9 недель, 80 страниц) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т. д.) 10-я неделя. Состав числа 5, сложение и вычитание. Формулы +4=+5-3, -4=-5+3. Однозначные, двузначные числа, трехзначные числа. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов. 11-я неделя. Состав числа 5, сложение и вычитание. Формулы +4=+5-3, -4=-5+3. Однозначные, двузначные числа, трехзначные числа. Счёт сотен. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов. 12-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3. Формулы +3=+5-2. Однозначные, двузначные. Трехзначные без новых формул. Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов. 13-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3. Формулы +3=+5-2, -3=-5+2. Однозначные, двузначные, трехзначные. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов. 14-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2. Формулы: +2=+5-3; Однозначные, двузначные; Трехзначные без новых формул. Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов. 15-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2. Формулы: +2=+5-3; -2=-5+3; Однозначные, двузначные, трехзначные. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов. 16-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2, +2=+5-3; -2=-5+3; Формулы: +1=+5-4. Однозначные, двузначные; Трехзначные без новых формул. Понятие умножение. Умножение через сложение. Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов. 17-я неделя. Состав числа 5, сложение и вычитание. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2, +2=+5-3, -2=-5+3, +1=+5-4; Формулы: -1=-5+4. Однозначные, двузначные; Трехзначные без новых формул. Понятие умножение. Умножение через сложение. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов. 18-я неделя. Закрепление формул: +4=+5-3, -4=-5+3, +3=+5-2, -3=-5+2, +2=+5-3; -2=-5+3; Формулы: +1=+5-4, -1=-5+4; Однозначные, двузначные, трехзначные. Умножение через сложение. Логика, основы математических представлений, работа с монетной системой. Графомоторика в клетке. 8 листов. 19-я неделя. Итоговое занятие, получение 2 уровня. Замер скорости и правильности работы с вычислениями на абакусе с формулами «Помощь брата».Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов. Дошкольники и школьники: 3 уровень «Помощь друга» Сложение и вычитание на уровне «Помощь друга» (13 недель, 105 страниц) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т. д.) 20-я неделя. Состав числа 10. Сложение и вычитание с формулой «помощь друга» +9 и -9. Знакомство с переходом через 50. . Закрепление формул «Помощь брата». Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов. 21-я неделя. Сложение и вычитание с формулой «помощь друга» +8 и -8. Закрепление формул «Помощь брата», «Помощь друга +-9», перехода через 50. Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов. 22-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; Новые формулы: +7=+10-3; -7=-10+3; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов. 23-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; Новые формулы: +6=+10-4; -6=-10+4; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов. 24-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; Новые формулы: +5=+10-5; -5=-10+5; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов. 25-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; +5=+10-5; -5=-10+5; Новые формулы: +4=+10-6; -4=-10+6; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов. 26-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; +5=+10-5; -5=-10+5; +4=+10-6; -4=-10+6; Новые формулы: +3=+10-7; -3=-10+7; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов. 27-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; +5=+10-5; -5=-10+5; +4=+10-6; -4=-10+6; +3=+10-7; -3=-10+7; Новые формулы: +2=+10-8; -2=-10+8; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Каллиграфия чисел. 8 листов. 28-я неделя. Состав числа 10, сложение и вычитание. Закрепление формул состава числа 5 и формул состава числа 10: +9=+10-1; -9=-10+1; +8=+10-2; -8=-10+2; +7=+10-3; -7=-10+3; +6=+10-4; -6=-10+4; +5=+10-5; -5=-10+5; +4=+10-6; -4=-10+6; +3=+10-7; -3=-10+7; +2=+10-8; -2=-10+8; Новые формулы: +1=+10-9; -1=-10+9; Использование в примерах однозначных, двузначных, трехзначных чисел. Счет в сотне. Логика. Основы математических представлений. Графомоторика в клетке. 8 листов. 29-я неделя. Интенсив на переход через 50 на абакусе. Повторение всех формул «Помощь брата и друга». Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Каллиграфия чисел. 8 листов. 30-я неделя. Переход через 100 на абакусе. Повторение всех формул «Помощь брата и друга». Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов. 31-я неделя. Закрепление формул друга и переходов через 50, 100. Повторение всех формул «Помощь брата и друга». Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Каллиграфия чисел. 8 листов. 32-я неделя. Итоговое занятие по третьему уровню. Замеры на время и правильность решения примеров со всеми формулами «помощь брата и друга» и переходами через 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов. ями на абакусе с формулами «Помощь брата».Логика, основы математических представлений, работа с монетной системой. Каллиграфия цифр. 8 листов. Дошкольники и школьники: 4 уровень «Микс формулы» Сложение и вычитание на уровне «Формулы Микс» (5 недель, 40 страниц) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т. д.) 33-я неделя. Формула «Микс»: +6=+10-5+1 и -6=-10+5-1. Закрепление формул «Помощь брата и друга» и переходов через 50, 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Каллиграфия чисел. 8 листов. 34-я неделя. Формула «Микс»: +7=+10-5+2 и -7=-10+5-2. Закрепление формул «Помощь брата и друга» и переходов через 50, 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов. 35-я неделя. Формула «Микс»: +8=+10-5+3 и -8=-10+5-3. Закрепление формул «Помощь брата и друга» и переходов через 50, 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов. 36-я неделя. Формула «Микс»: +9=+10-5+4 и -9=-10+5-4. Закрепление формул «Помощь брата и друга» и переходов через 50, 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов. 37-я неделя. Итоговое занятие по миксам формул. Замеры на время и правильность решения примеров со всеми формулами «помощь брата, друга и микс» и переходами через 50 и 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов. Дошкольники и школьники: 5 уровень «Анзан, сложение и вычитание без ограничений» Сложение и вычитание на уровне «Анзан» (4 недели, 48 страниц) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т. д.) 38-я неделя. Счёт АНЗАН — вычисления без ограничений. Замеры на время и правильность решения примеров со всеми формулами «помощь брата, друга и микс» и переходами через 50 и 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. Графомоторика в клетке. 8 листов. 39-я неделя. Счёт АНЗАН. Закрепление. Головоломки и игры на решение примеров со всеми формулами «помощь брата, друга и микс» и переходами через 50 и 100. Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. 8 листов. 40-я неделя. Итоговое занятие по пятому уровню. Замеры на время и правильность решения примеров без ограничений (анзан). Основы математических представлений. Счет в сотне. Логика. Продолжение умножения через сложение. 8 листов. 41-я неделя. (Запасная) Счёт АНЗАН. Решебник. Усложнённый счёт анзан на абакусе. Игровые упражнения и упражнения на повторение тем года. 8 листов. Дошкольники и школьники: 6 уровень «Умножение» Умножение (16 недель, 64 страницы) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.) 6 уровень. Умножение ч.1. 11-й месяц. Умножение двузначного числа на однозначное (x2, 3, 4, 5). Рабочие схемы и правила. Сложение/вычитание анзан. (4 стр.) Умножение двузначного числа на однозначное (x6, 7, 8, 9). Сложение/вычитание анзан. (4 стр.) Умножение трёхзначного числа на однозначное (x 2, 3, 4, 5, 6). Рабочие схемы и правила. Сложение/вычитание анзан. (4 стр.) Умножение трёхзначного числа на однозначное (x7, 8, 9). Сложение/вычитание анзан. (4 стр.) 6 уровень. Умножение ч.2. 12-й месяц. Умножение двузначного числа на двузначное. Рабочие схемы и правила. Сложение/вычитание анзан. (4 стр.) Умножение трехзначного числа на двузначное. Рабочие схемы и правила. Сложение/вычитание анзан. (4 стр.) Умножение трехзначного числа на трехзначное и повторение предыдущих тем. (8 стр.) 6 уровень. Умножение ч.3. 13-й месяц. Умножение трехзначного числа на трехзначное и повторение предыдущих тем. (4 стр.) Практикум умножения и сложения/вычитания анзан. (12 стр.) 6 уровень. Умножение ч.4. 14-й месяц. Практикум умножения и сложения/вычитания анзан. (5 стр.) Умножение четырёхзначного числа на трехзначное и повторение предыдущих тем. (4 стр.) Практикум умножения всех предыдущих тем и сложения/вычитания анзан. (7 стр.) Дошкольники и школьники: 7 уровень «Деление» Деление (12 недель, 48 страниц) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т. д.) 7 уровень. Деление ч.1. 15-й месяц. Деление двузначного числа на однозначное (/2, 3, 4, 5). Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (4 стр.) Деление двузначного числа на однозначное (/2, 3, 4, 5, 6, 7, 8, 9). Умножение и сложение/вычитание анзан. (4 стр.) Деление трёхзначного числа на однозначное (/2, 3, 4, 5). Умножение и сложение/вычитание анзан. (4 стр.) Деление трёхзначного числа на однозначное (/6, 7, 8, 9). Умножение и сложение/вычитание анзан. (4 стр.) 7 уровень. Деление ч.2. 16-й месяц. Деление четырёхзначного числа на однозначное. Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (4 стр.) Деление трехзначного числа на двузначное (/2, 3, 4, 5). Умножение и сложение/вычитание анзан. (4 стр.) Деление трехзначного числа на двузначное (/2, 3, 4, 5, 6, 7, 8, 9). Умножение и сложение/вычитание анзан. (4 стр.) Деление четырехзначного числа на двузначное (/2, 3, 4, 5). Умножение и сложение/вычитание анзан. (4 стр.) 7 уровень. Деление ч.3. 17-й месяц. Деление четырехзначного числа на двузначное. (/2, 3, 4, 5, 6, 7, 8, 9). Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (4 стр.) Практикум умножения, деления и сложения/вычитания анзан. (12 стр.) Школьники: 8 уровень «Дроби» Дроби (4 недели, 16 страницы) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.) 8 уровень. Дроби. 18-й месяц. Понятие и работа с десятичными дробями. Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (16 стр.) Школьники: 9 уровень «Отрицательные числа» Отрицательные числа (4 недели, 16 страниц) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т.д.) 9 уровень. Отрицательные числа. 19 месяц. Понятие и работа с отрицательными числами. Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (16 стр.) Школьники: 10 уровень «Квадратные корни» Квадратные корни (4 недели, 16 страниц) Внимание! Каждая неделя дополняется отдельным конспектом урока для учителя (цели и задачи, ход работы, структура всех необходимых упражнений, тренировок на абакусе и ментально, настройки онлайн платформы для урока и домашних заданий и т. д.) 10 уровень. Квадратные корни. 20 месяц. Понятие и работа с квадратными корнями. Рабочие схемы и правила. Умножение и сложение/вычитание анзан. (16 стр.) Дошкольники: 8-10 уровень решебник «Умножение и деление» Решебник  «Умножение и деление» (12 недель, 30 страниц) Решебник. Для детей дошкольного возраста на умножение и деление сложение/вычитания анзан (30 стр.). Краткосрочный интенсив «Простое сложение и вычитание» Краткосрочный интенсив «Простое сложение и вычитание» (4 недели, 4 темы, 21 страница) Тетрадь дополнена пояснительными записками учителю. Знакомство с абакусом. Простое сложение и вычитание чисел от 1 до 99. Использование монетной системы, флеш-карт, подробное описание работы с абакусом для начинающих. Классическая и ментальная арифметика. Работу с краткосрочным интенсивом можно идеально дополнять работой с онлайн платформой. Экспресс курс «Умножение» Экспресс курс «Умножение» (20 страниц) Тетрадь дополнена пояснительными записками учителю. Умножение двузначного числа на однозначное. Рабочие схемы и правила. Сложение/вычитание анзан. Умножение трёхзначного числа на однозначное. Рабочие схемы и правила. Сложение/вычитание анзан. Умножение двузначного числа на двузначное. Рабочие схемы и правила. Сложение/вычитание анзан. Умножение трехзначного числа на двузначное. Рабочие схемы и правила. Сложение/вычитание анзан. Работу с краткосрочным интенсивом можно идеально дополнять работой с онлайн платформой. Экспресс курс «Деление» Экспресс курс «Деление» (20 страниц) Тетрадь дополнена пояснительными записками учителю. Деление двузначного числа на однозначное. Рабочие схемы и правила. Сложение/вычитание анзан. Деление трёхзначного числа на однозначное. Сложение/вычитание анзан. Деление четырёхзначного числа на однозначное. Сложение/вычитание анзан. Деление трехзначного числа на двузначное. Сложение/вычитание анзан. Деление четырехзначного числа на двузначное. Сложение/вычитание анзан. Работу с краткосрочным интенсивом можно идеально дополнять работой с онлайн платформой.

Ментальная арифметика. Умножение и деление

Я б в нефтяники пошел!

Пройди тест, узнай свою будущую профессию и как её получить.

Химия и биотехнологии в РТУ МИРЭА

120 лет опыта подготовки

Международный колледж искусств и коммуникаций

МКИК — современный колледж

Английский язык

Совместно с экспертами Wall Street English мы решили рассказать об английском языке так, чтобы его захотелось выучить.

15 правил безопасного поведения в интернете

Простые, но важные правила безопасного поведения в Сети.

Олимпиады для школьников

Перечень, календарь, уровни, льготы.

Первый экономический

Рассказываем о том, чем живёт и как устроен РЭУ имени Г.В. Плеханова.

Билет в Голландию

Участвуй в конкурсе и выиграй поездку в Голландию на обучение в одной из летних школ Университета Радбауд.

Цифровые герои

Они создают интернет-сервисы, социальные сети, игры и приложения, которыми ежедневно пользуются миллионы людей во всём мире.

Работа будущего

Как новые технологии, научные открытия и инновации изменят ландшафт на рынке труда в ближайшие 20-30 лет

Профессии мечты

Совместно с центром онлайн-обучения Фоксфорд мы решили узнать у школьников, кем они мечтают стать и куда планируют поступать.

Экономическое образование

О том, что собой представляет современная экономика, и какие карьерные перспективы открываются перед будущими экономистами.

Гуманитарная сфера

Разговариваем с экспертами о важности гуманитарного образования и областях его применения на практике.

Молодые инженеры

Инженерные специальности становятся всё более востребованными и перспективными.

Табель о рангах

Что такое гражданская служба, кто такие госслужащие и какое образование является хорошим стартом для будущих чиновников.

Карьера в нефтехимии

Нефтехимия — это инновации, реальное производство продукции, которая есть в каждом доме.

Ментальная математика: умножение и деление — видео и стенограмма урока

Ментальное умножение

Если вы собираетесь заниматься ментальной математикой, то самый быстрый способ что-то испортить — это забыть о местах расположения единиц. Между 7 умножением на 10 и 7 умножением на 100 существует большая разница. Посмотрим правде в глаза, эти лишние нули могут пугать. Следовательно, при выполнении мысленных вычислений с умножением и делением вы можете делать то, что в противном случае вы не могли бы сделать, складывая или вычитая числа в уме.Вы можете на минуту игнорировать единицы измерения. Обратите внимание, что я сказал на минутку! Возьмем задачу 70 умножить на 100. Теперь вы можете мысленно умножить кучу чисел на ноль, но зачем усложнять себе задачу? Просто посчитайте количество нулей, а затем умножьте ненулевые числа. Затем прибавьте количество нулей в конце, и вы получите ответ: 7000.

Уловки такого рода полезны для задач, где у вас есть хорошие круглые числа, но как насчет чисел, которые немного сложнее. Допустим, вам нужно было умножить 71 на 99.Это уже выглядит менее забавным, не так ли? Иногда достаточно просто приблизиться. Таким образом, вы можете сделать некоторые быстрые настройки. На самом деле нет большой разницы между 99 и 100, так что вы можете подняться до 100 и легко получить 7100. Если вы просто пытаетесь получить приблизительное представление, это дает вам очень хорошее приближение.

Однако, если вам нужно быть точным, еще не все потеряно! Вернитесь к 71 умножению на 99. Теперь, если хотите, вы можете создать задачу в своей голове и умножить единицы, а затем десятки, а затем сложить все вместе.Однако, если вы похожи на меня, это большая работа. Я бы предпочел просто умножить 71 на 100. Это проще, правда? Конечно, но это не совсем так. Ну так что ты делаешь? Вы просто вычтете 71 из 7100. В конце концов, все, что вы делаете, это убираете одно вхождение числа. Кстати, ответ 7029.

Mental Division

Итак, что насчет разделения? Для этого у меня есть две быстрые стратегии. Во-первых, попробуйте найти что-то, что приведет вас к числу, на которое легко разделить.Например, если вам нужно разделить на 8, попробуйте разделить на 2 три раза. Аналогично, для деления на 20 вы можете просто разделить на 2, а затем на 10. С другой стороны, вы можете разделить дивиденд на две части. Предположим, вам нужно выяснить, что такое 354, разделенное на 6. Прежде чем выдергивать волосы, разделите их на 300 и 54. 300/6 = 50, а 54/6 = 9. Добавьте 50 и 9, и вы получите ответ.

Примеры

Давайте попробуем еще одну задачу умножения, чтобы убедиться, что мы понимаем все концепции.Допустим, вы собирались умножить 980 на 130. Это довольно большие числа. Однако давайте сначала избавимся от этих нулей — просто помните, что вы сняли два! Итак, у вас 98 * 13. Это может быть просто 100 * 13, если вычесть 13 дважды, не так ли? Мне эта идея больше нравится. Это означает, что у нас 1,274. Однако у нас все еще есть эти два нуля, так что прикрепите их сзади. Это означает, что у нас 127 400 человек.

Итак, что насчет деления? Возьмите 186, разделив на 4. Что вам нужно сделать в первую очередь? Вы можете просто разделить его на 2 дважды, получив сначала 93, а затем 46.5. Но как насчет этого по-другому? 100/4 = 25, а 86/4 = 21,5. Сложите эти два, и вы получите 46,5.

Краткое содержание урока

В этом уроке мы рассмотрим, как использовать ментальную математику для решения задач умножения и деления. Чтобы выполнить любое из них, требуется определенная умственная гибкость, но как только вы знаете, что делать, вы легко сможете это сделать. Для умножения не бойтесь возвращаться к нулям, и вам не следует беспокоиться об округлении только для вычитания дополнительных значений.При делении не стесняйтесь разбивать делитель или делимое на более мелкие части.

Словарь и определение

ментальная математика

Ментальная математика — это математика, выполненная в вашей голове.

Результаты обучения

После просмотра этого урока вы должны уметь выполнять следующие задачи:

• Обобщите математические приемы в уме для умножения и деления
• Используйте стратегии, обсуждаемые в этом уроке, чтобы правильно вычислить в уме задачи умножения и деления.

Ментальная арифметика | SkillsYouNeed

Ментальная арифметика — это бесценный математический навык, позволяющий производить вычисления в уме без использования каких-либо инструментов, таких как калькулятор, ручка, бумага или пальцы! Он может пригодиться в бесчисленных повседневных ситуациях, от разработки лучшей сделки с несколькими покупками в супермаркете до расчета, как долго вам нужно будет ждать следующего поезда.

Люди, которым необходимо использовать математику в своей работе, будь то бухгалтерский учет, розничная торговля или инженерное дело, например, часто делают довольно сложные и быстрые оценки в своей голове, так что они имеют хорошее представление о том, какой будет ответ, прежде чем они приступят к пора сделать более сложный расчет.

Ментальная арифметика также помогает развить настоящее понимание математических методов арифметики, а не просто выполнять вычисления посредством запоминания.

Практика ментальной арифметики может показаться тяжелым трудом, а некоторым людям, которые находят сложную математику, это даже может показаться пугающей перспективой. Но, как и во всем, чем больше вы это делаете, тем легче становится. Эта страница дает вам несколько полезных советов, которые сделают процесс быстрее, проще и намного менее пугающим.

Каждый может научиться ментальной математике! Они не только для математиков.

---

Умножение чисел на 10, 100 и 1000 и их кратные

Чтобы выполнить простое умножение, вам необходимо иметь базовое представление о значении разряда .Подробнее об этом читайте на нашей странице Numbers . Здесь следует помнить две вещи:

• Нули важны
• Десятичные точки всегда отделяют целые числа от «битов».

Чтобы мысленно умножить любое число на 10:

Оставьте десятичную точку на месте. В уме переместите все цифры на одну позицию влево и при необходимости добавьте в конец ноль.

24 × 10 = 24,0 × 10 = 240
175 × 10 = 175.0 × 10 = 1750
3,56 × 10 = 35,6

Вы можете перемещать десятичную точку вместо цифр, но только то или другое!

---

Некоторым людям легче думать о перемещении десятичной точки, чем о перемещении цифр. В приведенном выше примере десятичная точка остается на том же месте, а все цифры сдвигаются влево.

Это то же самое, что и перемещение десятичной точки вправо !

24 × 10 = 24.0 × 10 = 240
175 × 10 = 175,0 × 10 = 1750
3,56 × 10 = 35,6

Чтобы умножить любое число на 100:

Либо
Оставьте десятичную точку на месте. Переместите цифры на два места влево , добавляя при необходимости нули в конец:
845 × 100 = 845,00 × 100 = 84500
37,64 × 100 = 3764

OR
Переместите десятичную запятую на два разряда вправо:
56,734 × 100 = 5673,4

Чтобы умножить любое число на 1000:

Используйте любой из двух методов, как и раньше, и переместите на три позиции :
Переместите цифры влево:
23.476 × 1000 = 23476
Или переместите десятичную запятую вправо:
8,45692 × 1000 = 8456,92

Умножение на десятки, сотни и тысячи или более:

Основная идея: если вам нужно умножить число на 200, сначала умножьте на 2, а затем переместите цифры. Вы можете сделать это с любым количеством. Например, если вам нужно что-то умножить на 5000, сначала умножьте свое число на 5, а затем переместите три десятичных разряда.

Количество перемещаемых мест всегда равно количеству нулей.

Например, умножьте 25 на 5000. Это кажется довольно сложным в вашей голове, но уловка состоит в том, чтобы разбить это на простые вычисления.

Сначала умножьте 25 на 5:
25 × 5 = 125

Затем переместите цифры на три позиции влево (или десятичную точку на три позиции вправо):
125 × 1000 = 125000.

Деление на 10, 100, 1000 и кратное

Этот процесс точно такой же, как и при умножении, но в обратном порядке.

Чтобы разделить на 10, вы либо

оставьте десятичную точку на месте и переместите цифры на одну позицию вправо,

или

переместите десятичную запятую на одну позицию влево.

За 100 вы перемещаетесь на два места.
Для 1000 вы перемещаетесь на три позиции и так далее.

Примеры:

785 ÷ 100 = 7,85
56 ÷ 1000 = 0,056

Помните, что если ваш ответ меньше 1, слева от десятичной точки всегда должен стоять ноль.0

450 ÷ 1000 = 0,450 = 0,45

Вы можете удалить любые нули справа от чисел после десятичной точки. Однако вы НЕ МОЖЕТЕ сделать это, если нули стоят перед десятичной точкой или между десятичной точкой и другими числами.

Погружения, кратные десяткам, сотням или тысячам (или более):

Основная идея: если вам нужно разделить на 7000, сначала разделите на 7, а затем переместите цифры на три пробела.

Например, 56 ÷ 7000:
56 ÷ 7 = 8
8 ÷ 1000 = 0.008

Ваш ответ такой, как вы ожидаете?

---

Если вы беспокоитесь, что не сможете вспомнить, двигаете ли вы свои цифры влево или вправо, взгляните на свой ответ.

Если вы умножаете исходное число на число больше 1, вы ожидаете, что ваш ответ будет больше, чем число, с которого вы начали.

Аналогично, если вы делите на число больше 1, ваш ответ будет меньше. Если это не так, то вы знаете, что ошиблись!

---

Сложение и вычитание в уме

Так же, как вы делали умножение и деление в уме, вы можете изучить некоторые приемы, которые упростят умственное сложение и вычитание.

Как и раньше, эти уловки не связаны с математическим волшебством, это просто случай разбивки задачи на более мелкие части, которые легче решить в уме.

Лучше всего это сделать с помощью нескольких примеров.

Пример 1:

Разделение вычитания на сотни, десятки и единицы (или более).

Посчитайте 352 — 13 в уме.
Разделите это на два более простых вычитания: отнять 13 — это то же самое, что отнять 10, а затем отнять 3.
352 — 10 = 342
342 — 3 = 339

---

Пример 2:

Вы можете применить тот же принцип, что и в примере 1, к более сложному вычитанию:

Посчитайте 4583 — 333 в уме.
Сначала уберите 300, затем 30, затем 3:
4583 — 300 = 4283
4283 — 30 = 4253
4253 — 3 = 4250

---

Пример 3:

Работа с неудобными числами, близкими к 10:

Посчитайте 77 — 9 в уме.
Убрать 9 — это то же самое, что убрать 10, а затем добавить 1.
77 — 10 = 67
67 + 1 = 68

---

Пример 4:

Работа с неудобными числами, близкими к 100:

Посчитайте 737 + 96 в уме.
Добавление 96 аналогично сложению 100 с последующим вычитанием 4.
737 + 100 = 837
837 — 4 = 833

---

Пример 5:

Работа с неудобными числами, близкими к 1000 (или даже больше):

Посчитайте 5372 — 985 в уме.

Этот выглядит еще сложнее, чем другие, но независимо от того, насколько велики задействованные числа, вы все равно можете разбить расчет на простые части.

Вычитание 985 аналогично вычитанию 1000 с последующим добавлением 15 (поскольку 1000–985 = 15). Вы даже можете добавить 15 поэтапно, добавляя 10, а затем добавляя 5.

5372 — 1000 = 4372
4372 + 10 = 4382
4382 + 5 = 4387

---

Сложение и умножение в голове

Иногда у вас в голове возникает действительно сложный расчет, и это кажется невозможным.Однако, если вы посмотрите на то, как его можно разделить, используя навыки, которые вы усвоили в приведенных выше примерах, что-то действительно сложное может стать намного проще.

Например, посчитайте 97 × 7 в голове .

Есть два способа справиться с этим, и вы можете найти один способ проще, чем другой:

Метод 1:

97 совпадает с (100-3), поэтому вы можете думать о вычислении как
7 × (100-3)
Это то же самое, что
(7 × 100) — (7 × 3)

Теперь вы заменили сложное умножение двумя простыми умножениями и вычитанием:

7 × 100 = 700
7 × 3 = 21
700 — 21 = 700 — 20 — 1 = 679

Следовательно, 97 × 7 = 679

Метод 2:

97 — это почти 100, поэтому вы можете начать с вычисления 7 × 100 = 700.
Следующий шаг — учесть разницу между 97 и 100, которая составляет 3.
Итак, 7 лотов из 3 — это 21.

700 — 21 = 679

---

Применение умственных математических навыков к деньгам и процентам

---

Как вы узнали из приведенных выше примеров, умственная математика заключается в том, чтобы разбить задачу на числа, с которыми легко справиться в уме. Иногда нам нужно перевернуть расчет и подумать о нем по-другому.

Два примера, когда вам могут понадобиться ваши умственные математические навыки, — это когда вы имеете дело с деньгами или когда вам нужно вычислить процент, и то и другое часто случается, когда вы ходите по магазинам.

При работе с деньгами можно округлить сумму до ближайшего целого фунта, а затем обработать пенни отдельно. Вы часто видите цены, отмеченные таким образом, чтобы заставить вас думать, что они дешевле, чем они есть на самом деле. Например, 24,99 фунта стерлингов — это всего лишь один пенни от 25 фунтов стерлингов, но продавец хочет, чтобы вы подумали, что это ближе к 24 фунтам стерлингов.Когда вы делаете мысленные математические вычисления, иметь дело с 25 фунтами стерлингов намного проще, чем с 24,99 фунтами стерлингов.

Полезный мысленный прием для вычисления процентов — это помнить, что они обратимы, поэтому 16% от 25 равно 25% от 16. Неизменно одно из них будет намного легче вычислить в уме… попробуйте!

Заключение

Ментальная арифметика может показаться довольно пугающей, но со временем вы сможете использовать эти приемы ментальной математики, чтобы разбить сложную задачу на более мелкие части, о которых легче думать.Здесь нет никакого волшебства, просто нужно взглянуть на проблему по-другому.

---

Дополнительные материалы по навыкам, которые вам нужны

---

Основы счета
Часть необходимых навыков Руководство по счету

Эта электронная книга содержит рабочие примеры и простые для понимания объяснения, чтобы показать вам, как использовать основные математические операции и начать манипулировать числами. Он также включает в себя примеры из реальной жизни, чтобы прояснить, насколько эти концепции полезны в реальной жизни.

Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.

---

Алгоритм деления как мысленная математика | Бретт Берри | Math Hacks

Серия ментальной математики, часть 14

Знаете ли вы, что алгоритм деления уже представляет собой математический процесс в уме?

Как мы видели, до , алгоритмы слева направо легче реализовать мысленно. К счастью, нам не нужно менять свое мышление, чтобы разделить мысленно, потому что это уже алгоритм слева направо.

Все, что нам нужно делать, это думать о значении каждого шага и практиковать его мысленно.

Позвольте показать вам.

Дивиденд — это число, на которое мы делим. Делитель — это число, на которое мы делим, а частное — это ответ.

Предположим, мы хотим решить 256 ÷ 8.

Шаг 1: Начнем с поиска допустимого диапазона , сколько раз 8 переходит в 256.

Поскольку 8 x 10 = 80 и 8 x 100 = 800 , мы знаем, что 8 превратится в 256 от 10 до 100 раз. Таким образом, мы можем с уверенностью предположить, что наш ответ будет двузначным числом.

Шаг 2 : Определите, какое значение , кратное 10 , умноженное на 8, приближает вас к 256. Поскольку 8 x 30 = 240, 8 переходит в 256 30 с чем-то раз.

Шаг 3 : Подсчитайте, сколько восьмерок от 240 до 256.

Еще две восьмерки помогут.Итак, наш окончательный ответ: 256 ÷ 8 = 32.

Давайте проверим этот процесс с помощью метода карандаша и бумаги. Мы начинаем с того, что вычисляем, сколько восьмерок получается в 250, а затем — в 16.

Оказывается, это идентично процессу мысленных вычислений, который мы использовали выше.

На этот раз попробуем 1012 ÷ 7.

Шаг 1: Найдите допустимый диапазон .

Поскольку 1012 лежит между 700 и 7000, семь должно переходить в 1012 между 100 и 1000 раз.Это означает, что наш ответ будет трехзначным числом .

Шаг 2: Поскольку ответ представляет собой трехзначное число, спросите себя: «семь раз , сколько сотен уместится в 1012?»

Самое близкое, что мы можем получить, это 7 x 100 = 700. Итак, 7 переходит в 1,012 сто с чем-то раз.

Шаг 3: Возьмите разницу между 700 и 1012, которая составляет 312, и спросите себя: «семь раз по , сколько десятков уместится в 312?»

Поскольку 7 x 40 = 280, 4 десятки — это самое близкое, что мы можем получить 312 без перехода.Следовательно, 7 переходит в 1012 сто сорок с чем-то раз.

Шаг 4: Определите, сколько еще семерок нам нужно, чтобы приблизиться к 1012. До сих пор мы обнаружили, что 7 умножить на 140 = 980.

Следовательно, нам нужно найти, сколько семерок в разнице между 1012 и 980, что равно 32.

Поскольку 7 x 4 = 28, мы заключаем, что 7 x 144 = 1008.

Это означает, что 7 переходит в 1,012 сто сорок четыре раза, а 4 остается.

Как и в большинстве случаев, по мере того, как число становится больше, решение проблем мысленно становится все труднее.Не стесняйтесь реализовать тот же процесс с более крупными делителями и дивидендами.

Если эта задача кажется сложной, попробуйте использовать другие приемы деления, чтобы упростить задачу, например:

Следующий урок: Простые числа и решето Эратосфена

5 быстрых мысленных советов по делению — Cool Math

Вы избегаете решения задач с длинным делением и просто потому, что они длительные, трудоемкие и пугающие? Вот 5 быстрых советов по ментальному разделению , которые помогут вам!

Совет ментального отдела №1 — Точность не всегда является приоритетом

Очень часто ответы делятся на два-три десятичных знака.Не тратьте время на подробный расчет, если вам нужна приблизительная оценка. В таких случаях сделайте быструю общую оценку и получите свой ответ. Допустим, вам нужно подсчитать среднее количество дней, в течение которых вы можете завершить каждый из ваших проектов — 11 проектов за 123 дня. Вот уловка: 11 близко к 10, а 123 близко к 125. Итак, вместо вычисления 123/11, вычислите 125/10! Примерный ответ — 12,5 — не будет сильно отличаться от 11,1, ваш точный ответ.

Совет по ментальному разделению № 2 — сначала упростите

Что вы делаете, если приблизительных ответов недостаточно? Вот несколько полезных советов по упрощенному делению :

Если делимое и делитель являются четными числами, попробуйте сначала разделить их на 2.Например, если вам нужно разделить 196/22, сначала разделите их на 2. Когда у вас 98/11, вам будет легче вычислить остальное с меньшими числами.

Если делитель и делимое не являются четными числами, попробуйте разделить их на наименьший множитель. Скажем, например, вам нужно разделить 99 на 21. Разделите их на 3 (наименьший множитель), и вы получите 33/7, что достаточно просто, чтобы разделить их дальше!

Совет ментального деления № 3 — Умножьте, чтобы упростить

Как бы парадоксально ни звучал совет ментального деления № 3 , он чрезвычайно полезен! Секрет в том, чтобы умножать, прежде чем делить.Вместо деления 1525 на 5 умножьте 5 и 1525 на 2! Как только ваш делитель станет 10, вам будет легко вычислить остальное.

Совет ментального подразделения №4 — Разделить дивиденды

Разделите либо делимое (это число, которое вы делите), либо делитель (это число, на которое вы делите), чтобы упростить задачу деления. Если вы имеете дело со сложным делимым, например 54, разделите его на сумму чисел, каждое из которых делится на свой наименьший общий делитель, в данном случае 3 (делитель).Разделите 24 + 30 (сумма равна 54) на 3, и вы получите гораздо более простую задачу деления.

Наконечник ментального деления № 5 — Разделительный делитель

Вместо того, чтобы делить дивиденд на сумму, разделите делитель на произведение. Возьмем для примера 324/6. Разделите 6 на два фактора, в данном случае 2 и 3. После того, как вы разделите делитель, вы можете разделить дивиденд на любой из факторов в любом удобном порядке. Сначала разделите 324 на 3, что равно 108.Разделите 108 на 2, и вы получите 54, ответ на 324/6! Легко, правда?

Разделяй и властвуй с помощью этих простых советов по умственному разделению !

быстрых арифметических советов: быстрое получение результата

Добавление 5
При добавлении 5 к цифре больше 5 легче сначала вычесть 5, а затем прибавить 10.
Например,

7 + 5 = 12.
Также 7-5 = 2; 2 + 10 = 12.

Вычитание 5
При вычитании 5 из числа, заканчивающегося цифрой меньше 5, проще сначала добавить 5, а затем вычесть 10.
Например,

23-5 = 18.
Также 23 + 5 = 28; 28 — 10 = 18.

Деление на 5
Точно так же часто удобнее сначала умножить на 2, а затем разделить на 10.
Например,

1375/5 = 2750/10 = 275,

Дополнительные примеры и пояснения

Умножение на 5
Часто удобнее вместо умножения на 5 сначала умножить на 10, а затем разделить на 2.
Например,

137 × 5 = 1370/2 = 685.

Дополнительные примеры и пояснения

Деление на 5
Точно так же часто удобнее сначала умножить на 2, а затем разделить на 10.
Например,

1375/5 = 2750/10 = 275,

Дополнительные примеры и пояснения

Деление / умножение на 4
Замените либо повторяющейся операцией на 2.
Например,

124/4 = 62/2 = 31.Также
124 × 4 = 248 × 2 = 496.

Деление / умножение на 25
Вместо этого используйте операции с 4.
Например,

37 × 25 = 3700/4 = 1850/2 = 925.

Дополнительные примеры и пояснения

Деление / умножение на 8
Замените либо повторяющейся операцией на 2.
Например,

124 × 8 = 248 × 4 = 496 × 2 = 992.

Деление / умножение на 125
Вместо этого используйте операции с 8.
Например,

37 × 125 = 37000/8 = 18500/4 = 9250/2 = 4625.

Возведение двузначных чисел в квадрат.

1. Вы должны запомнить первые 25 квадратов:

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 1 4 9 16 25 36 49 64 81 100 121 144 169 196 15 16 17 18 19 20 21 22 23 24 25 225 256 289 324 361 400 441 484 529 576 625

2. Если вы забыли запись .
   Скажем, вам нужен квадрат 13. Сделайте следующее: прибавьте 3 (последняя цифра) к 13 (число, которое нужно возвести в квадрат), чтобы получить 16 = 13 + 3. Возведите последнюю цифру в квадрат: 3² = 9. Добавьте результат на сумму: 169.

   В качестве другого примера найдите 14². Сначала, как и раньше, прибавьте последнюю цифру (4) к самому числу (14), чтобы получить 18 = 14 + 4. Затем, как и прежде, возведите последнюю цифру в квадрат: 4² = 16. Вы хотите добавить результат. (16) к сумме (18), получая 1816, что явно слишком велико, например, 14 <20, так что 14² <20² = 400.Вам нужно добавить 6 и перенести 1 к предыдущей цифре (8), получив 14² = 196.

   Дополнительные примеры и пояснения

3. Квадраты чисел от 26 до 50 .
   Пусть A будет таким числом. Вычтем 25 из A, чтобы получить x. Вычтем x из 25, чтобы получить, скажем, a. потом A² = a² + 100x. Например, если A = 26, то x = 1 и a = 24. Следовательно,

   26² = 24² + 100 = 676.

   Дополнительные примеры и пояснения

4. Квадраты чисел от 51 до 99 .
   

   Если A находится между 50 и 100, то A = 50 + x. Вычислите a = 50 — x. Тогда A² = a² + 200x. Например,

   63² = 37² + 200 × 13 = 1369 + 2600 = 3969.

   Дополнительные примеры и пояснения

Любой Квадрат.
Предположим, вы хотите найти 87². Найдите поблизости простое число — число, квадрат которого найти относительно легко. В случае 87 мы берем 90. Чтобы получить 90, нам нужно добавить 3 к 87; Итак, теперь давайте вычтем 3 из 87.Получаем 84. Наконец,

87² = 90 × 84 + 3² = 7200 + 360 + 9 = 7569.

Дополнительные примеры и пояснения

Квадраты можно вычислить последовательно
В случае, если A является преемником числа с известным квадратом, вы найдете A⊃, добавив к последнему самому последнему, а затем A. Например, A = 111 является преемником числа a = 110, квадрат которого равен 12100. Добавляем к этому 110 а затем 111, чтобы получить A²:

111²	= 110² + 110 + 111
	= 12100 + 221
	= 12321.

Дополнительные примеры и пояснения

Квадраты чисел, заканчивающиеся на 5.
Число, оканчивающееся на 5, имеет вид A = 10a + 5, где a на одну цифру меньше A. Чтобы найти квадрат A² числа A, добавьте 25 к произведению a × (a + 1) числа a с его преемником. Например, вычислите 115². 115 = 11 × 10 + 5, так что a = 11. Сначала вычислите 11 × (11 + 1) = 11 × 12 = 132 (так как 3 = 1 + 2). Затем добавьте 25 справа от 132, чтобы получить 13225!

Дополнительные примеры и пояснения

Произведение 10a + b и 10a + c, где b + c = 10.
Аналогично возведению в квадрат чисел, оканчивающихся на 5:

Например, вычислите 113 × 117, где a = 11, b = 3 и c = 7. Сначала вычислите 11 × (11 + 1) = 11 × 12 = 132 (поскольку 3 = 1 + 2). Затем добавьте 21 (= 3 × 7) справа от 132, чтобы получить 13221!

Дополнительные примеры и пояснения

Произведение двух однозначных чисел больше 5.
Это правило помогает запомнить большую часть таблицы умножения. Предположим, вы забыли товар 7 × 9.Сделай это. Сначала найдите превышение каждого из кратных над 5: это 2 для 7 (7-5 ​​= 2) и 4 для 9 (9-5 = 4). Сложите их, чтобы получить 6 = 2 + 4. Теперь найдите дополнение этих двух чисел до 5: это 3 для 2 (5–2 = 3) и 1 для 4 (5–4 = 1). Помните их произведение 3 = 3 × 1. Наконец, объедините полученные таким образом два числа (6 и 3) как 63 = 6 × 10 + 3.

Дополнительные примеры и объяснение

Произведение двух двузначных чисел.

Самый простой случай — когда два числа не слишком далеко друг от друга и их разница четная, например, пусть одно будет 24, а другое 28.Найдите их среднее значение: (24 + 28) / 2 = 26 и половина разницы (28–24) / 2 = 2. Вычтите квадраты:

28 × 24 = 26² — 2² = 676 — 4 = 672.

Древние вавилоняне использовали похожий подход. Они вычислили сумму и разницу двух чисел, вычли их квадраты и разделили результат на четыре. Например,

	33 × 32	= (65² — 1²) / 4
		= (4225 — 1) / 4
		= 4224/4
		= 1056.

Дополнительные примеры и пояснения

Произведение чисел, близких к 100.
Скажем, вам нужно умножить 94 и 98. Возьмите их разности до 100: 100 — 94 = 6 и 100 — 98 = 2. Обратите внимание, что 94 — 2 = 98 — 6, так что для следующего шага не важно, какой из них вы используйте, но вам понадобится результат: 92. Это будут первые две цифры продукта. Последние два — всего 2 × 6 = 12. Следовательно, 94 × 98 = 9212.

Еще примеры и объяснения

Умножение на 11.
Чтобы умножить двузначное число на 11, возьмите сумму его цифр. Если это однозначное число, просто напишите его между двумя цифрами. Если сумма 10 и более, не забудьте перенести 1.

Например, 34 × 11 = 374, поскольку 3 + 4 = 7,47 × 11 = 517, поскольку 4 + 7 = 11.

Более быстрое вычитание.
Вычитание часто выполняется быстрее в два шага вместо одного.

Например,

427 — 38 = (427 — 27) — (38 — 27) = 400 — 11 = 389.

Общий совет может быть таким: «Сначала удалите то, что легко, а потом, что останется».Другой пример:

1049 — 187 = 1000 — (187 — 49) = 900 — 38 = 862.

Более быстрое добавление.
Добавление часто выполняется быстрее в два шага вместо одного.

Например,

487 + 38 = (487 + 13) + (38-13) = 500 + 25 = 525.

Общий совет может быть таким: «Сначала добавь то, что легко, а потом, что осталось». Другой пример:

1049 + 187 = 1100 + (187 — 51) = 1200 + 36 = 1236.

Более быстрое добавление, №2.
Часто быстрее добавлять цифру, начиная с более высоких цифр. Например,

583 + 645	= 583 + 600 + 40 + 5
	= 1183 + 40 + 5
	= 1223 + 5
	= 1228.

Умножьте, а затем вычтите.
При умножении на 9 умножьте вместо этого на 10, а затем вычтите другое число.Например,

23 × 9 = 230 — 23 = 207.

Дополнительные примеры и пояснения

То же самое относится и к другим числам рядом с теми, для которых умножение упрощено:

	23 × 51	= 23 × 50 + 23
		= 2300/2 + 23
		= 1150 + 23
		= 1173.
	87 × 48	= 87 × 50 — 87 × 2
		= 8700/2 — 160 — 14
		= 4350 — 160 — 14
		= 4190 — 14
		= 4176.

Умножение на 9, 99, 999 и т. Д.
Есть еще один способ быстрого умножения на 9, который имеет аналог умножения на 99, 999 и все подобные числа. Начнем с умножения на 9.

Чтобы умножить однозначное число a на 9, сначала вычтите 1 и получите b = a — 1. Затем вычтите b из 9: c = 9 — б . Затем просто напишите b и c рядом друг с другом:

9 a = b c .

Например, найдите 6 × 9 (так что a = 6.) Первое вычитание: 5 = 6 — 1. Вычтите второй раз: 4 = 9 — 5. Наконец, сформируйте произведение 6 × 9 = 54.

Аналогично для 2-значного :

b c	= 100 b + c
	= 100 ( a — 1) + (99 — ( a — 1))
	= 100 a — 100 + 100 — a
	= 99 a .

Попробуйте такой же вывод для трехзначного числа. Например,

543 × 999	= 1000 × 542 + (999 — 542)
	= 542457.

Дополнительные примеры и пояснения

Добавление длинного списка номеров
Как быстро можно рассчитать сумму

97 + 86 + 83 + 95 + 85 + 70 + 84 + 72 + 77 + 81 + 70 + 85 + 84 + 76 + 92 + 66?

На этой странице показано, как это сделать быстро и без особых усилий.

Умножение / деление — 4 класс

Центральная идея

---

«Выбрав подходящую стратегию, мы можем легче мысленно умножать и делить».

Соединение — Различия и сходство между умножением и делением

Изменить — Как манипулировать числами, чтобы упростить умножение и деление в уме

Форма — Различные типы задач со словами, связанные с простым умножением и делением

Теории и вопросы — вместе с классом создайте список вопросов и теорий о центральной идее и концепциях, чтобы добавить их на доску.Со временем добавляйте на доску или проверяйте, были ли даны ответы на предыдущие вопросы, были ли теории доказаны или опровергнуты.

Оценка наших предварительных знаний — Чтобы узнать, что мы уже знаем о мысленных и письменных стратегиях, нам важно показать то, что мы знаем. Используя интеллект-карту и некоторые предложенные вопросы учителя, покажите различные стратегии решения данной проблемы.

Диаграмма Венна — с небольшой группой создайте плакат с перекрывающимися кругами, где один кружок показывает, что такое умножение, а другой показывает деление.Если круги пересекаются, запишите сходства, если таковые имеются, между ними. Когда ваша небольшая группа выполнит задание, присоединитесь к остальной группе, чтобы объединить идеи класса.

Инструменты — Покажите вместе с партнером, как определенные инструменты могут помочь вам конкретным образом визуализировать и моделировать умножение и деление. Какие инструменты помогут вам больше всего? Есть ли какие-то инструменты лучше или хуже других? Что происходит с инструментом, который вы используете, когда вы набираете все больше и больше?

Стратегии ментальных вычислений

---

У нас должен быть автоматический вызов таблиц умножения до 10 x 10, но наши знания умножения и деления не должны останавливаться на достигнутом.Уметь мысленно вычислять большие числа на самом деле не так сложно, как мы могли бы подумать. Хотя у нас может не быть автоматического вызова для всех вопросов, мы можем использовать различные стратегии, чтобы упростить мысленные вычисления. Если мы сможем выбрать правильную стратегию для работы и разбить числа, чтобы найти «дружественные» числа, мы сможем решить даже самые сложные вопросы.

Умножение Разбейте множитель на два или более сложения Для начала мы можем захотеть потренироваться с меньшими двузначными множителями или однозначным умножением на двузначное, 12 x 6 13 x 8 14 x 12 12 x 13 13 x 7 Чтобы бросить вызов самим себе, мы всегда можем двигаться к большим числам. 12 x 14 14 x 25 26 x 48 52 x 18 13 x 26 Эта стратегия также может помочь с умножением и делением дробей и десятичных знаков. 5,5 x 12 12,25 x 12 6,25 x 24 2 1/3 x 12 1 3/4 x 16 3 7/8 x 16 11,75 x 40 5,375 x 24 14 4/5 x 100 Фактор a Коэффициент Когда мы вводим множитель, как мы выбираем, какое число множить? Как это упрощает вопрос? И почему это работает? Можем ли мы сделать это со всеми числами или только с конкретными примерами? 14 x 25 25 x 16 51 x 14 18 x 26 Округлить множитель и отрегулировать Когда мы округляем Фактор и Корректировку, мы всегда хотим попытаться взять «беспорядочные» числа и сделать их более «дружелюбными».»Округление до кратного десяти, когда число довольно близко, всегда является полезной стратегией. Это можно сделать со всеми числами, независимо от их размера. 12 x 9 6 x 19 21 x 7 8 x 13 9 x 23 28 x 13 27 x 18 48 x 26 39 x 23 197 x 56 Это можно сделать даже с дробями и десятичными знаками. 5 3/4 x 7 4 11/12 x 9 8 x 1 5/6 3 x 5,8 6,97 x 8 2 x 11,95 Деление пополам и удвоение Уменьшение вдвое и удвоение также может быть полезной стратегией, но не всегда работает для каждого числа.Как мы узнаем, когда уменьшение вдвое и удвоение может быть хорошей стратегией? Почему так легче думать о некоторых проблемах? 8 x 13 4 x 17 6 ​​x 13 8 x 25 22 x 9 Можем ли мы использовать эту стратегию с десятичными и дробными числами? 0,8 x 1,2 0,64 x 0,08 7 1/4 x 4 3 1/8 x 4 16 x 6 1/4

Деление Вместо умножения Когда мы вместо этого умножаем, мы должны хорошо понимать наши факты умножения.Когда мы видим определенные числа, мы должны быть в состоянии определить, какие числа являются простыми, а какие имеют несколько факторов, которые могут помочь нам решить проблему. 15 ÷ 3 21 ÷ 5 17 ÷ 3 19 ÷ 6 27 ÷ 4 18 ÷ 4 Это можно сделать и с большими числами 50 ÷ 7 154 ÷ 12 84 ÷ 9 66 ÷ 8 60 ÷ 15 29 ÷ 14 Выходной фрагмент Разделение на части — очень полезная стратегия, так как при делении вы можете использовать оценку и работать с дружественными числами.Кроме того, вам не нужно быть «идеальным» в своих догадках с первого раза. Это особенно полезно для вопросов с многозначным делением. 32 ÷ 3 43 ÷ 4 87 ÷ 8 76 ÷ 7 53 ÷ 5 97 ÷ 9 63 ÷ 20 273 ÷ 13 468 ÷ 40 283 ÷ 14 246 ÷ 12 Вы можете даже разбить вопросы с десятичными знаками 134 ÷ 0,5 56 ÷ 0,2 14 ÷ 0,3 18 ÷ 0,4 13,7 ÷ 0,3 14,8 ÷ 0,4 3,75 ÷ 0,6 72,3 ÷ 0,7 Сделать башню Создание башни действительно может помочь, когда у вас мало времени.Иногда мы можем хорошо угадать, какое число попробовать выделить, но в других случаях это не так просто. Когда мы делаем башню, мы можем более четко видеть дружественные числа, с которыми мы можем работать. Деление пополам и деление пополам Так же, как деление пополам и удвоение, деление пополам и деление пополам не работает для всех чисел. Тем не менее, когда мы действительно находим некоторые числа, которые могут быть полезны, нам нужно иметь возможность их идентифицировать. 26 ÷ 4 52 ÷ 4 128 ÷ 8192 ÷ 24 288 ÷ 16 46 ÷ 4 364 ÷ 16 278 ÷ 12 1280 ÷ 24 1464 ÷ 28 321 ÷ 12 Мы также можем использовать эту стратегию с дробями и десятичными знаками 35 ÷ 0.5 2,6 ÷ 0,2 1,35 ÷ 0,03 13,57 ÷ 0,6 1/3 ÷ 1/6 1/2 ÷ 2/3

Стратегии мысленных и письменных вычислений

---

Как мы видим, существует много различных стратегий умножения и деления в уме, и выбор правильной для вопроса, который вы пытаетесь решить, является большой частью процесса. Многие из этих стратегий также можно использовать при написании ответов на вопросы умножения и деления. Если вы не можете держать в голове все числа или если вопросы становятся более сложными, вам также важно уметь записывать свои ответы.

Как и в случае с сложением и вычитанием, также важно записывать вопросы и ответы в понятной для других форме.

Исследование умножения — В таблице ниже представлены несколько различных стратегий умножения, которые варьируются от более простых до более сложных. В этом списке перечислены не все стратегии, поэтому вы можете поискать стратегию, которая подойдет вам. Что у них общего? Насколько они разные? Когда бы вы использовали одну стратегию вместо другой?

Добавление в наш список — По мере изучения мы обнаружим, что существует даже больше стратегий умножения, чем мы ожидали.Найдите другие письменные стратегии однозначного и многозначного умножения, которые мы можем добавить на этот сайт.

Худшие стратегии — Если стратегии, которые мы изучаем, являются лучшими, как бы выглядела худшая стратегия? Создайте задачу, в которой незадачливый математик приходит к правильному ответу, но делает это очень неэффективно.

Объяснение с помощью Google Video — После того, как вы овладеете одной или двумя стратегиями, важно показать большую глубину знаний, имея возможность объяснить свое понимание другим.Используя iPad, создайте видео, объясняющее стратегию, которую вы будете использовать чаще всего.

Запрос в Подразделение — Как и в таблице выше, в таблице ниже представлены различные стратегии Подразделения от более простых до более сложных. Опять же, что у них общего? Насколько они разные? Когда бы вы использовали одну стратегию вместо другой?

Изучите некоторые из приведенных ниже стратегий, а затем используйте шаблон запроса отдела, чтобы показать свое понимание и поделиться с другими.

Добавление в наш список — Как и в случае с умножением, наша цель — добавить в наш список. Какие способы подходят вам лучше всего? Будете ли вы использовать одну и ту же стратегию для письменного разделения во всех ситуациях? Какие стратегии лучше подходят для поиска ответов с остатком? А как насчет ответов с десятичными знаками?

Объяснение с помощью Google Video — После того, как вы овладеете одной или двумя стратегиями, важно показать большую глубину знаний, имея возможность объяснить свое понимание другим.Используя iPad, создайте видео, объясняющее стратегию, которую вы будете использовать чаще всего.

Типы проблем со словами

---

Как и в случае со сложением и вычитанием, существует множество различных форм и способов написания вопросов умножения и деления. Важно, чтобы мы исследовали множество различных типов вопросов, с которыми мы столкнемся, чтобы мы могли как отвечать, так и создавать словесные проблемы в контексте реального мира.

Создание задач Word — Есть много вещей, которые мы можем сделать для создания задач Word, которые сложнее стандартных.Вместе с классом исследуйте различные типы задач умножения и деления слов, а затем создайте свои собственные. Расставьте словесные задачи, которые вы создали, от наименее до наиболее сложных.

Какие переменные вы можете изменить в задаче со словом, чтобы сделать ее более сложной? Какие проблемы вы испытывали в повседневной жизни, которые представляют собой различные типы словесных задач.

Стратегии ментальной математики | Начальная школа королевы Елизаветы

Учебный план требует 10 минут в день

для увеличения скорости отзыва.

Это стратегии, подразумеваемые для строки табеля успеваемости, обозначенной как «Применяет стратегии ментальной математики»

Эти результаты пятого класса рассчитаны на год. В учебном пособии указано, что мастери должен быть до конца июня. Эти стратегии пятого уровня называются:

.

1. разделение фактов до 81 включительно.
2. умножение переднего конца
3. компенсация при умножении
4. умножение на 10, 100 и 1000
5. деление на 10, 100 и 1000
6. умножение на 0.1, 0,01 и 0,001
Весы
7. для постоянной разницы.

Разъяснение стратегий

1. Подразделение Фактов в 81

При окончании четвертого класса ученики должны были усвоить факты умножения до 81 с быстрым воспроизведением, чтобы считаться на уровне класса.

В пятом классе учащиеся должны усвоить факты деления до 81 с быстрым воспроизведением.

2. Оперативное умножение

Эта стратегия включает в себя разложение большего множителя в его разряды и умножение каждого разряда отдельно на меньший множитель.Затем сложите все продукты вместе.

Например, 4 x 352 — это то же самое, что 4 x 300 (1200), 4 x 50 (200) и 4 x 2 (8). Достаточно сложить три произведения, чтобы найти исходное произведение 4 x 352, что составляет 1200 + 200 + 8 или 1408.

3. Вознаграждение при умножении

Эта стратегия включает округление большего множителя до ближайшего умножения 10, 100 или 1000. Затем два множителя умножаются с последующим вычитанием числа, добавленного при округлении, на меньший множитель в исходном уравнении.

Например, 3 x 298 компенсируется до 3 x 300, что составляет 900. Поскольку было добавлено 2 (когда 298 было округлено до 300), нужно вычесть 3 x 2 или 6 из 900, чтобы вернуться к исходное уравнение. Итак, 3 x 298 равно 894 или 900-6 (произведение шага 3 x 2).

4. Умножение на 10, 100 и 1000

Эта стратегия подразумевает увеличение каждой позиции на одну, две или три позиции.

При умножении 657 на 10 каждое разрядное значение увеличивается на 10 или на один ход влево.6 сотен становятся 6 тысячами, 5 десятков становятся 5 сотнями, а 7 единиц становятся 7 десятками. Для более простого метода просто добавьте один ноль в конец исходного множителя.

657 x 10 = 6 570 45 801 x 10 = 458 010 65,5 x 10 = 655,0 или 655 (обратите внимание, что при умножении десятичной дроби на 10 это не так просто, как простое сложение десяти).

Аналогично, при умножении на 100 (или 1000) каждое значение разряда увеличивается на 100 (или 1000) или на два сдвига влево (три хода влево).

При умножении 657 на 100, 6 сотен становятся 6 десятками (двухзначное значение перемещается влево), 5 десятков превращаются в 5 тысяч (двухзначное значение перемещается влево), а 7 сотен становятся 7 сотнями (трехзначное значение значение перемещается влево.) Для более простого метода просто добавьте два нуля в конец исходного множителя.

657 x 100 = 65 700 45 801 x 100 = 4580 100 65,5 x 100 = 6550,0 или 6550

5. Деление на 10, 100 и 1000

Эта стратегия заключалась в уменьшении значения каждой позиции на 10, 100 или 1000.

При делении 657 на 10 6 сотен становятся 6 десятками, 5 десятков становятся 5 единицами, а 7 единиц становятся 7 десятками. Для более простого метода переместите десятичную дробь на одну позицию влево.

(Обратите внимание, что на сайте блога нет символа разделения.)

657 разделить на 10 = 65,7 45 801 разделить на 10 = 4581,0 или 4581

65,5 разделить на 10 = 6,55

При делении на 100 (или 1000) каждое разрядное значение уменьшалось на 100 (или 1000). Каждая цифра перемещается на 2 (или 3) разряда вправо.

657 разделить на 100 = 6,57

657 разделить на 1000 = 0,657

6. Умножение на 0,1, 0,01 и 0,001

Эта стратегия аналогична делению на 10, 100 и 1000. Значение каждой позиции уменьшается на одну, две или три позиции. Как и при делении на 10, 100 и 1000, более простой способ — переместить десятичную дробь на необходимое количество разрядов влево.

7. Баланс на постоянную разницу.

Это стратегия вычитания, когда большее число имеет меньшее значение в разряде единиц.При вычитании 399 из 502 рассмотрите возможность округления 399 до 400, так как вычитание с нулями проще. Однако для того, чтобы разница была постоянной, нужно добавить одинаковую сумму к обоим числам.

Из 502–399 прибавьте 1 к 399, чтобы получилось 400. Чтобы сохранить постоянную разницу, добавьте еще 1 к 502. То, что начиналось как 502–399, теперь составляет 503–400, что является исходным 502 + 1 и оригинал 399 +1.

Итак, для 502 думайте 502 + 1 или 503 для 406 думайте 406 + 3 или 409

— 399 — 399 + 1 — 400 — 297 — 297 + 3 — 300

Нравится:

Нравится Загрузка…