Математические диктанты 2 класс, часть 2
Сложение и вычитание с переходом через разряд
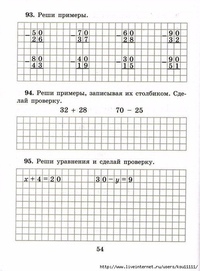
Выполни вычисления столбиком.
Вариант 1
а) 30 – 18; г) 94 – 49; ж) 39 + 39;
б) 61 – 38; д) 38 + 18; з) 96 – 7;
в) 17 + 17; е) 91 – 24; и) 54 + 46.
Какую закономерность в ответах ты видишь?
Вариант 2
а) 46 + 45; г) 18 + 46; ж) 29 + 8;
б) 91 – 9; д) 93 – 38; з) 63 – 35;
в) 36 + 37; е) 18 + 28; и) 52 – 33.
Какую закономерность в ответах ты видишь?
Запиши решение столбиком и вычисли.
45 увеличь на 38.
Найди разность чисел 74 и 36.

На сколько 47 меньше 55?
Найди сумму чисел 46 и 18.
Уменьши 61 на 46.
Уменьшаемое 54, вычитаемое 28. Найди разность.
Из 83 вычти 48.
К 36 прибавь 37.
Первое слагаемое 38, второе – 49. Чему равна сумма?
Сколько получится, если из 60 вычесть 16?
Проверь решение примеров, записывая их в столбик. Найди ошибки.
а) 26 + 35 = 61; е) 35 + 49 = 84;
б) 43 – 15 = 28; ж) 6 + 29 = 89;
в) 18 = 42 = 50; з) 51 – 29 = 22;
г) 38 + 13 = 51; и) 54 + 18 = 72;
д) 74 – 48 = 26; к) 37 + 39 = 76.
Найди ошибки в решении примеров.
 Реши примеры верно.
Реши примеры верно.
1 10
а) _36 б) _92 в) _37 г) _71 д) _35
18 7 5 15 19 54 95 87 64 16
Выполни вычисления, записывая решения столбиком.
_54 _60 _48 _37 _76 _73 _70 _18
37 15 24 4 24 19 26 54
_97 _92 _42 _33 _40 _84 _54 _35
18 29 18 48 29 57 28 48
_14 _60 _37 _52 _44 _62 _17 _34
27 29 44 38 49
Вычисли, записывая решение каждого действия столбиком. Стрелка покажет, какое действие нужно выполнить с полученным результатом.

а) 15 + 37 + 18 – 36 – 17 + 28 – 19 + 74 …
б) 49 + 25 – 18 + 24 – 63 +36 – 28 – 9 …
в) 54 – 18 – 29 + 56 – 48 +37 + 18 – 61 …
г) 95 – 37 – 29 + 57 – 48 +54 – 14 – 58 …
д) 14 + 39 + 38 – 74 + 48 – 26 + 51 – 62 …
е) 90 – 37 – 26 + 45 – 54 +28 + 46 – 78 …
ж) 34 + 16 – 27 + 69 – 73 + 15 + 37 – 35 …
з) 23 + 8 + 29 – 33 + 56 – 45 + 27 – 46 …
и) 96 – 27 – 58 + 39 + 27 – 56 + 75 – 57 …
к) 15 + 37 – 38 + 67 – 33 – 19 + 57 – 38 …
7. Реши круговые примеры. Ответ каждого предыдущего является началом следующего. Начни с примера, обозначенного *.Вариант 1
_94 _91
* _ 35 67 24 _ 13
59 48
94
_53 _32
38 19
_27
26 _74
_61 39
24
_67 _37
35 37
Вариант 2
* _97
28 _ 42
69 13
_ 69 _27
27 63
_29 _ 85
56 36
_73
47 _49
24
_ 90 _ 18
7 56
Уравнение.
 2-й класс
2-й классТип урока: урок введения новых знаний.
Цель: дать учащимся новое математическое понятие «уравнение».
Задачи:
- Образовательная: сформировать представление об уравнении, решение уравнений;
- Развивающая: развивать умение сравнивать, анализировать; совершенствовать вычислительные навыки;
- Воспитательная: формировать культуру общения в классом коллективе.
Оборудование урока:
- Учебник Математика 2 класс 1 часть М.И. Моро и др.
- Мультимедийный проектор, компьютер, презентация.
I.
Самоопределение к деятельности.Психологический настрой: Покажите вашу прямую спинку, покажите правую руку, умные глазки. Подарите мне и друг другу добрые улыбки.
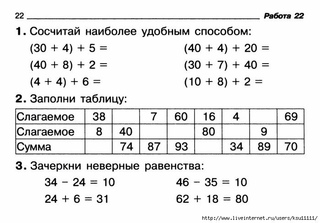
С новой темой познакомится класс.
Сегодня узнаем мы без сомнения
«Имя» этого выражения: х+4=12.
II.
Актуализация знаний и фиксация затруднений в деятельности.– А сейчас нас ждет интересная работа – устный счет.
Назовите действия и компоненты. (Слайд 2)
- 30 + 7 = 37
- 47 – 5 = 42
Найдите значения выражений. (Слайд 3)
- 32 + 2 =
- 13 + 20 =
- 40 – 7 =
- 53 – 20 =
- х + 3 = 33
– Со всеми выражениями справились? (Нет)
– Чем отличается последнее выражение?
III.
Постановка учебной задачи.– Такое выражение называется – уравнением. Умеем ли мы решать уравнение? (Нет) (Слайд 4)
– Чему будем учиться на уроке? (Решать уравнения, составить алгоритм решения уравнений)
IV.
Построение проекта выхода из проблемной ситуации, затруднения.
– Давайте разберемся, что же такое уравнение. Прочтите выражения. (Слайд 5)
- … — 4 = 6
- 2 + … = 8
- … + 3 = 7
- 9 — … = 5
– Что объединяет эти выражения? (Это примеры с неизвестным)
– Что нужно знать, чтобы решить их? (Необходимо знать состав чисел, название действий, название компонентов, нахождение неизвестных компонентов)
– Чтобы открыть новое, нам необходимо хорошо повторить то, что мы уже знаем.
| 1С + 2С = СУММА | У – В = Р | |
| 1С = СУММА – 2С | У = Р + В | |
| 2С = СУММА – 1С | В = У — Р |
Вывод: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое. (Слайд 6)
(Слайд 6)
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое. (Слайд 7)
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.
– В математике принято вместо отсутствующего компонента писать буквы латинского алфавита:
х (икс), а (а), b (бе) c (це) и другие. (Слайд 8)
– Попробуем сделать вывод из всего сказанного.
Вывод: уравнение – это … (х + 3 = 33) равенство, содержащее … (х + 3 = 33) неизвестное число, которое надо найти. (Слайд 9)
– Что надо сделать с неизвестным числом? ( Его надо найти)
– Как обозначается неизвестное число? (Латинскими буквами)
– Молодцы, ваша работа достойна похвалы. А сейчас проверьте себя, прочтите в учебнике на странице 68.
– Давайте составим алгоритм решения уравнения. (Слайд 10)
Алгоритм решения уравнений:
- Прочитай уравнение.

- Назови действие, компоненты.
- Вспомни, как найти неизвестный компонент.
- Запиши и вычисли.
- Проверь.
V.
Первичное закрепление учебного материала.– А теперь давайте решать уравнения. Что нам поможет сделать это? (Алгоритм) (Слайд 11)
VI. Самостоятельная работа.– Пользуясь алгоритмом, решите самостоятельно уравнения на стр. 68 №1.
Вариант 1. Верхнюю строку.
Вариант 2. Нижнюю строку.
– Взаимопроверка работы. (Слайды 12, 13)
VII.
Включение новых знаний в систему и повторение.– Из данных выражений найдите уравнения и запишите их номера: (Слайды 14, 15)
- 8 – 4 = 4
- 6 – х = 4
- 12 + х = 20
- а – 6
- а – 6 = 18
- 13 – 1 = 12
- 10 + у
- 10 + у = 23
VIII.
 Рефлексия деятельности.
Рефлексия деятельности.– Назовите тему урока, над которой работали сегодня.
– Какую цель ставили перед собой?
– Выполнили?
– Так что такое уравнение?
7 способов помочь младшему школьнику с математикой
Предположим, что математика уже в начальной школе ребёнка идёт туго, со скрипом. Трудно и скучно складывать и вычитать, не говоря уже о чём-то более сложном. Новые темы никак не хотят укладываться в голове. Писательница и мама троих детей Ксения Букша рассказывает, основываясь на собственном опыте, как помочь ребёнку освоить математику.
Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу
Раскладываем трудности по полочкам
На уровне 1–5-го классов неспособных к математике детей не бывает. Но бывают дети с конкретными трудностями, которые можно и нужно преодолеть. Подумаем, почему ребёнку трудно с математикой.
Вот возможные варианты или их комбинации.
- Плохо считает, нет навыка счёта.
 Не очень хорошо знаком с числами.
Не очень хорошо знаком с числами. - Не может вникнуть в суть поставленной задачи, с трудом понимает, что надо делать. Пробует все варианты («Так неправильно? Тогда попробую разделить», «В три раза больше — здесь нужен плюс или минус?»).
- Усваивает шаблонное решение, но не может его доработать. Столкнувшись с малейшим изменением условий, впадает в ступор.
- Не умеет читать сложные тексты. В результате не понимает ни описания правил, ни текста задачи. Если на пальцах объяснить, что надо делать, сразу решает нормально.
- В голове не укладываются концепции. С трудом их понимает и быстро забывает. Такой ребёнок может сто раз услышать объяснение, что такое икс (неизвестное), но так и не понять.
- Не развит навык наглядного представления. Не может представить себе, нарисовать схематичную картинку, «увидеть в уме».
- Короткое внимание: всё понимает, но делает кучу ошибок, особенно в длинных сложных примерах.
Как видим, математика раскладывается на множество разных навыков. Когда мы выяснили, в чём проблема, мы можем её решать. Заранее прошу прощения у учителей и методистов: я всего лишь родитель, а мои мысли по этому поводу — всего лишь частное мнение, хотя я стараюсь его обосновывать.
Когда мы выяснили, в чём проблема, мы можем её решать. Заранее прошу прощения у учителей и методистов: я всего лишь родитель, а мои мысли по этому поводу — всего лишь частное мнение, хотя я стараюсь его обосновывать.
Ждём, пока созреет способность абстрактно мыслить
Мозг нейротипичного ребёнка дозревает до абстрагирования и обобщения далеко не сразу. У некоторых это происходит раньше, у других позже. Например, не все дети могут соотнести число и количество. Для очень многих и во 2–3-м классе есть только «15 яблок», а просто «15» нет.
При этом они как-то привыкают оперировать числами, и пробел в базовом понимании не очень заметен, пока речь не заходит о чуть более сложных вещах. Например, именно им трудновато понять, почему не может быть «полтора» в ответе на вопрос «сколько землекопов?». А уж когда начинаются проценты или задачи на скорость и расстояние, становится совсем сложно.
Стоит вернуться назад к конкретике. Возможно, для понимания дробей пока нужно проговаривать «в числителе арбузы, в знаменателе мальчики; 21 арбуз достался 42 мальчикам — каждому по половинке арбуза». Даже в пятом классе почти все концепции ещё можно заземлить до конкретики.
Даже в пятом классе почти все концепции ещё можно заземлить до конкретики.
Развиваем навыки счёта
Просто учиться считать — это скучно. Нам помогут всевозможные игры с числами. Для начала — усложнённые ходилки с 2–3 кубиками (когда за один ход максимум — 18 очков, а не 6), потом — разнообразные игры в кости, где нужно считать очки.
Самая простая игра известна мне под названием «единичка»: игроки по очереди бросают один кубик (или два, или три), пытаясь добраться до сотни очков. Серия прерывается, когда у игрока выпадает хотя бы одна единичка: в этом случае очки за эту серию сгорают, и нужно уметь остановиться вовремя.
Очень рекомендую покер на костях. В этой игре есть ряд комбинаций, каждую из которых надо выбросить за три попытки. Эти попытки можно копить. Игроки делают ходы по очереди, выигрывает тот, кто первым выполнит все комбинации. Помимо простого навыка складывания очков, покер постепенно развивает тонкое понимание случайности и вероятности, просчитываемого риска и шансов. В такой покер может научиться играть даже шести- или семилетка.
В такой покер может научиться играть даже шести- или семилетка.
Для отработки деления и умножения мы с дочкой говорили о числах как о «родственниках». Например, у числа 72 очень большая «семья»: у него есть «детки» 24 и 36, есть «внуки» — 2, 3, 4, 6, 12, 18. А вот число 37 не завело себе никакой «семьи», оно простое. Зато если «поженить» его с другим «одиночкой» — 41, у них получится вместе 78, теперь можно «заводить детей и внуков». Это хорошо помогает ориентироваться в таблице умножения.
Учим видеть и наглядно обобщать задачу
Чтобы хорошо схематизировать, надо уметь выделять именно то, что важно для условия задачи, и схематично изображать это на картинке. Сначала мы учимся выделению главного. Это знаменитые игры «что лишнее?», в которых может быть и несколько ответов. Арбуз, аист, абрикос, виноград — что лишнее? Смотря по какому признаку.
В учебнике Петерсон есть чудесные задачи, загромождённые кучей ненужных данных или лишённые необходимых условий. В задании автор просит найти и выделить только те условия, которые нужны для решения, а если их нет — указать, чего не хватает. Научившись видеть задачу, можно перейти к схематизации.
Научившись видеть задачу, можно перейти к схематизации.
Многие дети вообще не понимают, зачем рисовать схемы к задачам и почему это проще. Всё потому, что схемы эти даны готовыми. Но по какому принципу они строятся? Почему, например, неважно, какой длины сам поезд, если он едет из А в Б? Как нарисовать «3 часа»? А «все груши, посаженные мальчиками»?
Можно вместе рисовать схемы разных задач, а потом предлагать ребёнку придумывать похожие. Такие задания есть и в учебниках, но там их мало. Для некоторых эта трудность вообще определяет все отношения с математикой, да и вообще с упорядочиванием данных, абстрагированием, обобщением, поиском решения.
Оттачиваем логику
Логика — один из инструментов, которые нужны всем. Нет людей, которые были бы не склонны к логике, есть те, у кого она «не поставлена». Это как умение орудовать шуруповёртом: научиться может каждый, у кого есть руки. Вы можете сами оценить, насколько железная у вас логика. Я очень люблю вот этот чудесный тест.
Человека с логикой не способна заморочить никакая пропаганда или реклама, его не запутает недобросовестный банк, он гораздо лучше ориентируется в окружающем мире.
С детьми можно начать с простых силлогизмов, которые иногда звучат смешно, но приводят к пониманию очень важных штук. Например, услышав от кого-нибудь сентенцию «мальчики не плачут», ребёнок может уточнить: «некоторые или все?»
Если дети не проходят понятие множества, стоит хоть немножко вместе с ним порисовать «кружочки» (не обязательно сразу вводить все понятия) и порешать соответствующие задачи: вот мальчики, вот коты, а вот те, кого зовут Вася. Где мальчики, которых зовут не Вася? А где тут девочки? А где кот Барсик?
Развиваем воображение
Воображение необходимо для всего, что связано с математикой и логикой. (Я даже не пишу «как ни странно», потому что это совершенно не странно.) Особенно умение мыслить образами.
Я очень люблю игру, в которой родитель и ребёнок по очереди задают друг другу «графические загадки», не имеющие точного ответа. Каждый рисует серию непонятных геометрических фигур или их комбинаций (точка в треугольнике, молния и круг, несколько кругов, касательные…), а другой дорисовывает их так, чтобы получилась картинка. Чем остроумнее решение, тем больше удовольствия получают оба игрока.
Каждый рисует серию непонятных геометрических фигур или их комбинаций (точка в треугольнике, молния и круг, несколько кругов, касательные…), а другой дорисовывает их так, чтобы получилась картинка. Чем остроумнее решение, тем больше удовольствия получают оба игрока.
Существует много древних и новых игр, в которых нужно складывать узоры из деталей и фрагментов яйца (колумбово яйцо), квадрата, по-разному раскрашенных граней кубика («Сложи узор»). Есть и трёхмерные наборы, например «Пентамино». Речь не о том, чтобы выполнять задания, хотя все эти наборы можно использовать и так, но именно о творчестве из имеющихся деталей и об умении увидеть образ.
А можно ещё вырезать снежинки, дорисовывать симметричных бабочек и человечков, придумывать шифры, рисовать лабиринты и карты. Всё это и есть развитие математического воображения.
Учим ребёнка вычленять, чего конкретно он не понимает (метакогниция)
Я уже не раз писала про неё — и в связи с математикой, и в связи с сочинениями. Вкратце метакогниция — это умение «понимать, как я думаю», «знать, чего именно я не знаю», осознание своего мыслительного процесса. Именно этому почти никогда не учат в школе, а иногда даже портят уже развитую способность. Предполагается ведь, что есть простые и сложные способы решения той или иной задачи. Часто это так и есть, но порой гораздо ценнее умение идти самому и по шагам проверять себя: «Так нужно делать? Я прав?»
Вкратце метакогниция — это умение «понимать, как я думаю», «знать, чего именно я не знаю», осознание своего мыслительного процесса. Именно этому почти никогда не учат в школе, а иногда даже портят уже развитую способность. Предполагается ведь, что есть простые и сложные способы решения той или иной задачи. Часто это так и есть, но порой гораздо ценнее умение идти самому и по шагам проверять себя: «Так нужно делать? Я прав?»
Совместные рассуждения (и я не про математику) ценны и тем, что сближают ребёнка и родителя, и тем, что мы показываем, как проходит процесс думания. Он не должен быть гладким и автоматическим. В нём есть тупики, неожиданные повороты. «Наше первоначальное предположение неверно, а это значит, что нужно идти не по дороге 1, а по дороге 2». Кстати, это пригодится и в школьной математике, когда нужно будет понимать доказательства теорем. Ведь хорошо запоминается только то, что прошёл сам своим умом, когда смог повторить чужие рассуждения и знаешь в них каждый поворот.
Распечатанные рабочие листы для задач по математике для второго класса
Проблемы со словами могут быть сложной задачей для учащихся, особенно для второклассников, которые, возможно, еще учатся читать. Но вы можете использовать базовые стратегии, которые будут работать практически с любым учеником, даже с теми, кто только начинает изучать письменные навыки.
Инструкции и стратегии
Чтобы помочь второклассникам научиться решать задачи со словами, научите их выполнять следующие действия:
- Изучите математическую задачу: Прочтите слово «задача», чтобы понять ее общий характер.Поговорите со своими учениками о проблеме и обсудите, какие части являются наиболее важными.
- Прочтите математическую задачу: Прочтите вопрос еще раз. На этот раз сосредоточьтесь на конкретных деталях проблемы. Какие части проблемы связаны друг с другом?
- Задайте вопросы о задействованных операциях: Поразмышляйте еще раз.
 Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.
Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения. - Спросите себя о предпринятых шагах: Просмотрите каждый сделанный шаг.Определите, кажется ли ваш ответ разумным. Если возможно, сверьте свой ответ с ответами в книге, чтобы определить, на правильном ли вы пути.
- Завершите: Просмотрите текст словесных задач, которые вы будете решать, чтобы определить любые слова, которые вы не узнаете. Перечислите их и определите их значение, прежде чем решать проблемы. Напишите краткие определения терминов для справки при решении проблемы.
Решение проблем
Изучив эти стратегии, используйте следующие бесплатные распечатки задач со словами, чтобы студенты могли практиковать то, что они узнали.Есть только три рабочих листа, потому что вы не хотите перегружать своих второклассников, когда они только учатся решать задачи со словами.
Начните медленно, при необходимости повторите шаги и дайте своим ученикам возможность усвоить информацию и освоить словесные методы решения проблем в расслабленном темпе.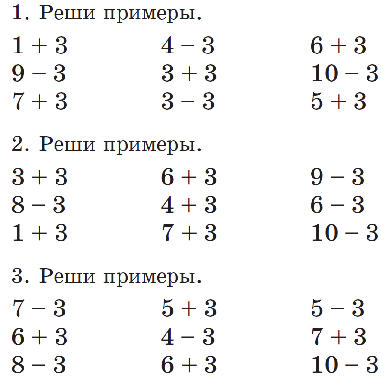 В печатных материалах содержатся термины, которые будут знакомы молодым студентам, такие как «треугольник», «квадрат», «лестница», «десять центов», «пятак» и дни недели.
В печатных материалах содержатся термины, которые будут знакомы молодым студентам, такие как «треугольник», «квадрат», «лестница», «десять центов», «пятак» и дни недели.
В эту распечатку включены восемь математических задач, которые покажутся второклассникам многословными, но на самом деле они довольно просты.Задачи на этом листе включают задачи со словами, сформулированные в виде вопросов, например: «В среду вы видели 12 малиновок на одном дереве и 7 на другом дереве. Сколько всего малиновок вы видели?» и «У всех ваших 8 друзей есть двухколесные велосипеды, сколько всего это колес?»
Если студенты озадачены, прочитайте задачи вслух вместе с ними. Объясните: как только вы вычеркнете слова, это будут простые задачи сложения и умножения, где ответ на первый будет следующим: 12 робинов + 7 робинов = 19 малиновок; а ответ на второй будет: 8 друзей x 2 колеса (для каждого велосипеда) = 16 колес.
Д. Рассел Эта последняя печатная форма в наборе содержит немного более сложные задачи, такие как эта, связанная с деньгами: «У вас есть 3 квартала, и ваша выписка обошлась вам в 54 цента. Сколько денег у вас осталось?»
Сколько денег у вас осталось?»
Чтобы ответить на этот вопрос, предложите учащимся изучить проблему, а затем прочитать ее всем классом. Задайте такие вопросы, как: «Что может помочь нам решить эту проблему?» Если учащиеся не уверены, возьмите три четверти и объясните, что они равны 75 центам. Тогда задача превращается в простую задачу вычитания, поэтому завершите ее, указав числовую операцию на доске следующим образом: 75 центов — 54 цента = 21 цент.
Задачи по обучению словарю во 2-м классе
Если вы ищете лучший способ научить словесным задачам и, что более важно, хотите, чтобы ваши ученики были более успешными в решении словесных задач, я здесь, чтобы помочь. Учить словесные задачи во 2-м классе не должно быть проблемой.
Почему во 2-м классе так сложно учить словесные задачи?
Когда я только начал преподавать, я учил своих учеников использовать ключевые слова, подчеркивать и обводить, выделять и вставлять рамку… и все же это не помогло. Они все еще не знали, когда складывать, а когда убирать.
Они все еще не знали, когда складывать, а когда убирать.
И мои ученики не понимали и не успевали лучше.
Не помогало то, что я постоянно не учил и не позволял своим ученикам практиковаться в решении словесных задач.
Задачи со словом всегда были источником разногласий для моих учеников, независимо от того, в каком классе я преподавал (1-й, 2-й и 4-й), и всегда были тем, что я преподавал наугад в рамках принятой математической программы.
Большинство учебных программ по математике предлагают следующее:
- Задачи на 1 или 2 слова в конце каждого урока, но на самом деле не предлагают способ научить учеников решать задачи со словами
- 1 глава о «решении задач»
И серьезно, ни то, ни другое полезно.
Я хотел, чтобы мои ученики ежедневно практиковались в стратегических задачах.
И знаете что? Когда я начал последовательно и стратегически преподавать задачи со словами во 2-м классе, мои ученики были менее разочарованы и гораздо более искусно решали задачи со словами.
Итак, какое решение?
Сейчас я следую 4-дневному плану обучения и оцениваю его на 5-й день.
Я больше не учу ключевые слова или подчеркивание, обводку, выделение и / или бокс… вместо этого я учу своих учеников искать закономерности в том, как структурированы проблемы со словами… ситуации со словами.
Кроме того, я посвящаю 5-10 минут каждый день обучению и практике словесных задач.
Как я узнаю, чему учить?
Начну со стандарта.
Честно говоря, что бы я ни преподаю, именно здесь я начинаю. Мне нужно точно знать, чего я ожидаю, чтобы потом я мог помочь своим ученикам справиться с этим.
Стандарт Common Core для 2-го класса гласит:
CCSS.MATH.CONTENT.2.OA.A.1
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e.
 g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
Хотя многие штаты больше не используют термин «Common Core», многие принятые ими стандарты совпадают или, по крайней мере, схожи.
MAFS.2.OA.1.1 (стандарты Флориды)
- Используйте сложение и вычитание в пределах 100 для решения одно- и двухэтапных задач со словами, включающих ситуации сложения, взятия из, сложения, разделения и сравнения с неизвестными во всех позициях, e.g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
Итак, второклассники должны уметь решать:
- Сложение / вычитание в пределах 100
- Одно- и двухступенчатое
- Добавить к
- Взять из
- Соединить
- Разобрать
- Сравнить
Когда вы посмотрите на то, что должны делать второклассники, неудивительно, что учить словесные задачи так сложно, не говоря уже о том, что студенты действительно их осваивают.
Как я учу задачи по словам во 2-м классе:
В начале года ученики знакомятся с нашей рутинной задачей со словом после первых двух недель в школе.
Я объясняю, что задачи со словами похожи на истории, которые мы должны читать и понимать, что происходит в рассказе. Мы называем эти слова «проблемными ситуациями».
Затем я учу студентов, что есть 4 вещи, которые они всегда должны делать, решая задачу со словами:
- Напишите числовое предложение
- Используйте стратегию для решения
- Я объясняю студентам, что я не могу залезть в их мозг, чтобы увидеть, что они думают, и если я не знаю, о чем они думают, я не может помочь им лучше решать проблемы со словами.
- Учащиеся могут рисовать картинки, использовать семейство фактов, базовые 10 блоков и / или стандартный алгоритм.
- Вычисление
- Я смотрю, чтобы убедиться, что ученик дал правильный ответ.
- Ответ в предложении
- Например, вместо того, чтобы просто сказать «4», мои ученики пишут: «У Шайенна 4 собаки».
 Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.
Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.
- Например, вместо того, чтобы просто сказать «4», мои ученики пишут: «У Шайенна 4 собаки».
Запуск рутинной задачи со словом — это все о моделировании и рутине. Студентам не нужно много времени, чтобы научиться этому.
Я проделал за вас тяжелую работу — у меня на весь год есть задачи по словам во 2-м классе, готовые для вас!
Что такое рутинная задача для 2-х классов?
По понедельникам я использую слово «проблемная ситуация». Я считаю полезным, чтобы студенты «разыгрывали» ситуацию. Используйте пример на ситуационном плакате / диаграмме привязки, чтобы показать учащимся образец.(Я учу студентов, что подчеркнутые части числового предложения — это известные нам части, а квадрат представляет неизвестное.)
Смоделируйте и решите практическую задачу со словами и поделитесь своими отзывами со студентами.
В течение следующих 3 дней мы моделируем и решаем задачу со словом, которая имеет ту же ситуацию, что и понедельник.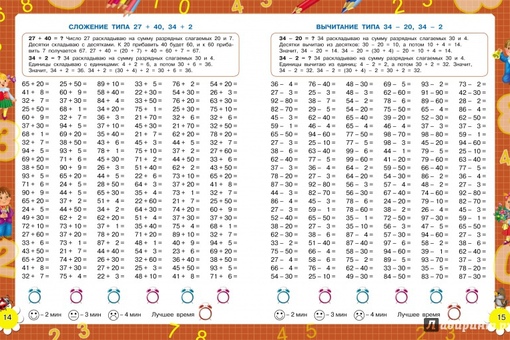 Так что мы не скучаем. Это очень систематично.
Так что мы не скучаем. Это очень систематично.
Наконец, по пятницам ученики самостоятельно решают 2 задачи со словами, следуя той же ситуации, которую мы использовали всю неделю.
Для дифференциации или расширения учащиеся могут написать задачу на обратной стороне своего экзамена, которая соответствует той же ситуации, которую они изучали на этой неделе. Это отличный способ узнать, действительно ли студенты понимают ситуацию, которую мы узнали на той неделе.
Возможно вам понравится:
Давайте подключимся!Instagram // Pinterest // Facebook // Учителя платят учителям
многоступенчатых уравнений | 2-й класс по математике
Научитесь решать многоступенчатые уравнения
😎 Итак, вы научились складывать и вычитать числа.
Что произойдет, если вам нужно будет сложить и вычесть в одном уравнении? 🤔
👉 Давайте посмотрим на пример:
У вас в ланч-боксе 5 печений .Ваш друг дает вам еще 3 файлов cookie. Вы съели 2 печенья. Сколько файлов cookie у вас осталось?
Мы начинаем с , записывая уравнение для задачи.
5 + 3 — 2 =?
Как вы решите это многошаговое уравнение ? 🤔
Решите многоэтапных уравнений с помощью , упрощая одну операцию за раз.
😃 Операция — это слово для сложения или вычитания.
👉 Идем с слева направо . Итак, сначала мы начнем с сложения.
5 + 3 = 8
Теперь мы можем переписать наше исходное уравнение и поместить 8 вместо 5 + 3 .
А теперь вычитаем!
8 — 2 = 6
Отличная работа! 👏 Наш ответ: 6.
Другой пример👉 Давайте попробуем это уравнение.
20-11 + 5 =?
✅ На этот раз вычитание — первая операция, которую мы упростили, .
20-11 = 9
Теперь мы можем поставить 9 вместо первого уравнения.
Все, что нам осталось сделать, это добавить!
9 + 5 = 14
Отличная работа! 👍
Теперь вы можете переходить к практике.
примеров общих основных математических задач для 2-го класса — математический класс [2021]
Примеры операций и алгебраического мышления
Эти стандарты просят студентов работать со сложением и вычитанием различными способами, включая простые вычисления и более сложные решения проблем.
- В классе мисс Винки 24 ученика. Однажды к ним пришли еще трое детей, но четверо из обычных учениц мисс Винки отсутствуют. Сколько детей в классе в этот день? Покажите свое решение как минимум двумя способами.
- Автобус номер три обычно занимает 14 минут, чтобы добраться от автобусной остановки Сьюзи до ее школы. Сегодня автобус застревает в пробке еще на 5 минут. Сколько времени нужно, чтобы добраться от автобусной остановки Сьюзи до школы?
- Карлос и его семья любят гулять.В минувшие выходные собрали 28 желудей! Карлос уронил 6 из них по дороге домой и отдал 2 своему младшему брату. Сколько желудей у него осталось?
- Что на семь больше четырех? Что на четыре меньше семи?
- Джозеф покупает пачки жевательной резинки для своих друзей и семьи.
 Если в каждой пачке есть пять палочек жевательной резинки, а Джозеф покупает три пачки, сколько палочек жевательной резинки покупает Джозеф?
Если в каждой пачке есть пять палочек жевательной резинки, а Джозеф покупает три пачки, сколько палочек жевательной резинки покупает Джозеф?
Числа и операции в десятичных примерах
Эти стандарты основываются на чувстве числа учащихся, предлагая им понять, что представляет каждая цифра в трехзначном числе и как разные числа соотносятся друг с другом.
- Что означает цифра «7» в числе 374? Как можно представить эту «7» цифрами? Используете блоки по основанию десять?
- Если вы пропускаете счет от 10 до 200, сколько раз вам придется считать?
- Что на десять больше, чем 67? Как вы можете ответить на этот вопрос, не производя вычислений?
- Как решить задачу 34 — 17? Покажите свою работу, используя как минимум две разные стратегии.
Примеры измерений и данных
Стандарты в этой области просят ваших учеников измерять длину предметов и работать с длиной в контексте решения проблем.Они также просят ваших второклассников поработать над задачами, требующими времени, денег и базового представления данных.
- Измерьте длину трех разных предметов в классе. Объясните, как вы решили, какой измерительный инструмент использовать для каждого объекта, и запишите их измерения, используя наиболее подходящую единицу измерения.
- Если в прошлом году рост Сисси составлял 48 дюймов, а в этом году она выросла на три дюйма, то какого она роста сейчас?
- Школа начинается в 8:50 каждое утро.Обед — через три часа десять минут после начала учебного дня. Когда будет ланч?
- Если у Лоуренса две четверти и пятак, сколько у него денег?
- Джоди хочет, чтобы ее мама купила ей куклу и кукольное платье. Кукла стоит 36 долларов, а платье — 11 долларов. Сколько денег Джоди просит маму вообще потратить?
- Вместе со своим классом создайте гистограмму, показывающую, сколько букв содержится в именах учащихся в вашем классе. Вместе обсудите график и объясните, что он показывает и что заставляет вас думать.
Примеры геометрии
Эти стандарты требуют, чтобы учащиеся могли рисовать и распознавать формы и разбивать их в соответствии с контрольными дробями.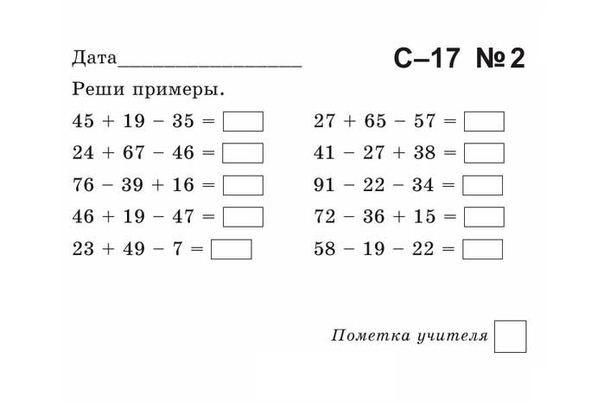
- Как вы называете двухмерную форму с пятью сторонами?
- Нарисуйте прямоугольник. Разделите прямоугольник на три ряда и три столбца квадратов одинакового размера. Сколько всего квадратов в прямоугольнике?
- Нарисуйте круг. Разделите круг на три равные части. Как вы называете эти акции?
Контрольный список навыков для 2-го класса: математика
Контрольные листы подготовки ко второму классу
Математика
Номера, операции и решение проблем
- Считает по 1, 2, 5 и 10 с
- Определяет, упорядочивает и записывает цифры от 0 до 100
- Знает факты сложения и вычитания до 50
- Складывает и вычитает двузначные числа до 99 без перегруппировки
- Показывает начальное понимание разряда
- Делает разумные оценки количеств
- Обозначает целые, половину, трети и четверти
- Называет и использует порядковые номера, такие как первый, второй, третий и т.
 Д.
Д. - Отображает и определяет положительные целые числа в числовой строке
Геометрия и измерения
- Обозначает и рисует основные формы
- Исследует и решает простые пространственные и измерительные задачи, используя манипуляторы (практические объекты, которые можно подсчитать или сортировать) и чертежи.
- Признает и использует стандартные измерительные инструменты, такие как линейки, весы и термометры.
- Понимает основные концепции пространственных отношений, симметрии и отражений.
Математика в действии: определение времени, счет денег, реальная математика
- Распознает и добавляет деньги к 1 доллару.00
- Показывает время с точностью до часа
- Использует рисунки и слова для описания математического мышления
- Собирает и записывает данные с помощью таблиц, списков, диаграмм и графиков
- Считывает график или диаграмму и делает выводы
- Классифицирует, сортирует и сравнивает физические объекты по множеству схем классификации и шаблонов (сходство, различие, звук, цвет, текстура, размер, вес, температура, продолжительность и т.
 Д.).
Д.). - Создает, копирует и расширяет шаблоны с действиями, объектами и словами
Советы для родителей, которые помогут детям чувствовать себя уверенно при решении числовых и числовых задач:
- Создайте банку для монет, в которую вы бросаете мелочь и даете своему ребенку регулярную работу по сортировке и подсчету этих монет (с вашей помощью) на регулярной основе.
- Ведите общий семейный календарь и пусть ваш ребенок отмечает дни, считает дни до предстоящих событий и отслеживает дни рождения.
- Поощряйте ребенка помогать рассортировать банки и коробки в кладовой по размеру или весу.
- Включите ребенка в простые кулинарные упражнения и моделируйте его из мерных чашек или ложек; опишите, что вы делаете, когда используете эти измерительные инструменты.
- Играйте в игры на счет, когда находитесь в машине или на прогулке; выберите «магическое число» и предложите ребенку определить это количество собак, затем магическое количество больших деревьев или красных машин и т.
 д.
д.
навыков математики для 2-го класса, чему научится ваш ребенок
Во втором классе по математике дети начинают работать с большими числами и лучше понимают их значение. Студенты также изучают повседневные навыки, такие как определение времени, работа с деньгами и измерение.
Мы, родители, можем помочь нашим детям преуспеть во втором классе по математике, узнав больше о том, что они собираются изучать.В течение года ваш ребенок научится:
1. Считать в пределах 1000
Второклассники учатся читать и записывать числа до 1000. Они учатся пропускать счет на 5, 10 и 100, поскольку замечают закономерности среди чисел.
Дома: Создайте возможности для чтения и записи трехзначных чисел. Например, попросите ребенка прочитать числа на этикетках с питанием.
Вы также можете попросить ребенка устно пропустить счет на 10 или 100 секунд. Начните с 10 или 100, а затем предложите второкласснику не учитывать другие числа, например 60 или 204.
Начните с 10 или 100, а затем предложите второкласснику не учитывать другие числа, например 60 или 204.
2. Понимание разряда в трехзначных числах
По мере того, как дети учатся считать с точностью до 1000, они будут более внимательно смотреть на трехзначные числа. Глядя на закономерности в числах, дети начинают понимать числовую ценность.
Дома: помогите своему ребенку, спросив, сколько единиц, десятков и сотен в трехзначных числах.
3. Сравните трехзначные числа
Узнав о разрядах и счетах в пределах 1000, второклассники смогут сравнивать трехзначные числа.Они смогут использовать свои знания о числовой стоимости, чтобы посмотреть на два числа и сказать, какое из них больше или меньше другого. Дети узнают, как использовать символы <,> и = для сравнения трехзначных чисел.
Дома. Помогите ребенку отработать навыки сравнения, задав такие вопросы, как «Что больше: 943 или 783?» Развивайте мышление ребенка, спрашивая, почему одно число больше другого.
4. Складывать и вычитать в пределах 1 000
Во втором классе дети привыкают складывать и вычитать числа в пределах 100.Они решают одно- и двухэтапные задачи со словами, например: «У Тимми было 39 игрушечных машинок. Он получил еще 12, затем отдал 18. Сколько машин осталось у Тимми? »
После работы над сложением и вычитанием в пределах 100 дети будут использовать свои знания трехзначных чисел, чтобы практиковать сложение и вычитание в пределах 1000.
Дома: составьте несколько словесных задач, подобных приведенной выше, используя любимые игрушки или еду вашего ребенка.
5. Измерение
Второклассники развивают свое понимание измерения, оценивая длины и измеряя их с использованием различных единиц. Они сравнивают длины, аналогично тому, как они проводят сравнение с числами, и используют сложение и вычитание, чтобы узнать, насколько длиннее или короче объекты.
Они сравнивают длины, аналогично тому, как они проводят сравнение с числами, и используют сложение и вычитание, чтобы узнать, насколько длиннее или короче объекты.
Дома: дайте ребенку линейку и попросите его измерить три разных предмета в доме. Затем попросите ребенка расположить предметы в порядке от самого короткого до самого длинного и объяснить, насколько каждый предмет длиннее или короче других.
6. Определение времени с точностью до ближайших пяти минут
В первом классе учащихся познакомили с функцией определения времени.Теперь второклассники могут расширить свое понимание времени до ближайших пяти минут. Дети также смогут отличить AM от PM.
Попросите вашего ребенка научиться определять время с точностью до пяти минут — напомните ему использовать AM и PM!
7. Задачи со словами, связанные с деньгами
Второклассники решат множество задач со словами, связанных с сложением и вычитанием, в том числе с деньгами.
Дома: дайте ребенку стопку монет и задание посчитать общую сумму.Или поиграйте в «магазин» и попросите ребенка попрактиковаться в покупке предметов на разные суммы денег, а затем вычислить, сколько центов осталось.
8. Картинка и гистограммы
Во втором классе ваш ребенок научится пользоваться картинками и гистограммами до четырех категорий.
Предложите ребенку пройти опросы дома и представить собранные данные в виде графика.
Приятно провести время, погрузившись в математику для второго класса!
Нашли это полезным? Ознакомьтесь с нашими руководствами по математике от детского сада до 5 класса
Написано Лили Джонс, Лили Джонс любит учиться всему.Она была воспитателем детского сада и первого класса, инструктором по обучению, разработчиком учебной программы и наставником учителей. Она любит смотреть на мир с любопытством и вдохновлять людей всех возрастов любить учиться. Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.
Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.
О Komodo — Komodo — это увлекательный и эффективный способ улучшить математические навыки K-5. Komodo, разработанный для детей от 5 до 11 лет для использования в домашних условиях, использует небольшой и частый подход к изучению математики (15 минут, три-пять раз в неделю), который вписывается в напряженный семейный распорядок.Komodo помогает пользователям развить беглость и уверенность в математических вычислениях — , не задерживая их долгое время за экраном .
Узнайте больше о Komodo и о том, как он помогает тысячам детей каждый год лучше учиться по математике — вы даже можете попробовать Komodo бесплатно.
Задачи по математике для 2-го класса — миссис Латс и мисс Уилл
2 класс
GO Math
2016-2017
Цели и учебные цели
Глава 1: Числовые концепции

· Напишите уравнения с равными слагаемыми для представления четных чисел.
· Используйте разряд для описания значений цифр в двузначных числах.
· Напишите 2-значные числа в развернутой форме.
· Записывайте двузначные числа в форме слова, развернутой и стандартной форме.
· Применяйте концепции разряда, чтобы найти эквивалентные представления чисел.
· Решайте проблемы, находя различные комбинации десятков и единиц для представления двухзначных чисел, используя стратегию «найти образец».
· Расширить последовательности подсчета в пределах 100 на 1, 5 и 10
· Расширить последовательности подсчета в пределах 1000 на 1, 5, 10 и 100 секунд.
Глава 2: Числа до 1 000
· Записывайте трехзначные числа в развернутой и стандартной форме.
· Применяйте концепции разряда, чтобы найти эквивалентные представления чисел.
· Определите на 10 больше, на 10 меньше, на 100 больше или на 100 меньше, чем любое заданное число
· Расширьте числовые шаблоны, считая на 10 или 100.
· Решайте проблемы, связанные со сравнением чисел, используя стратегию «создать модель».
· Сравните 3-значные числа, используя символы <, = и>.
Глава 3: Основные факты и взаимосвязи
· Используйте двойные факты как стратегию для нахождения сумм для почти двойных фактов.
· Вспомните суммы основных фактов, используя свойства и стратегии.
· Вызов сумм для сложения фактов, используя стратегию «сделать десять».
· Найдите суммы трех слагаемых, применяя коммутативные и ассоциативные свойства сложения.
· Используйте обратную зависимость сложения и вычитания, чтобы вспомнить основные факты.
· Вспомните различия основных фактов, используя умственные стратегии.
· Найдите различия на числовой прямой, чтобы разработать мысленную стратегию разложения для упрощения фактов.
· Используйте линейчатые модели для представления различных ситуаций сложения и вычитания.
· Решайте проблемы с участием равных групп, используя стратегию «разыграй все».
· Напишите уравнения, используя повторное сложение, чтобы найти общее количество объектов в массивах.
Глава 4: 2-значное дополнение
· Найдите сумму, разделив однозначное сложение, чтобы двузначное сложение стало кратным 10.
· Используйте компенсацию для развития гибкое мышление для сложения двух цифр.
· Применяйте концепцию разряда при использовании стратегии разделения для двухзначного сложения.
· Модель 2-значного сложения с перегруппировкой.
· Нарисуйте быстрые картинки и запишите сложение двух цифр, используя стандартный алгоритм.
· Запишите сложение двух цифр, используя стандартный алгоритм.
· Практикуйте сложение двух цифр с перегруппировкой и без нее.
· Перепишите задачи горизонтального сложения по вертикали в стандартном формате алгоритма.
· Решайте задачи, связанные со сложением двух цифр, используя стратегию «нарисовать диаграмму».
· Представляйте ситуации сложения числовыми предложениями, используя символ для неизвестного числа.
· Найдите суммы трех двузначных чисел.
· Найдите суммы четырех двузначных чисел.
Глава 5: Вычитание двух цифр
· Разделите однозначное вычитание на части, чтобы вычесть его из двузначного числа.
· Разделите 2-значное вычитаемое, чтобы вычесть его из 2-значного числа.
· Модель вычитания двух цифр с перегруппировкой.
· Нарисуйте быстрые картинки и запишите двузначное вычитание, используя стандартный алгоритм.
· Запишите двузначное вычитание, используя стандартный алгоритм.
· Практикуйте вычитание двух цифр с перегруппировкой и без нее.
· Перепишите задачи горизонтального вычитания по вертикали в стандартном формате алгоритма.
· Используйте сложение, чтобы найти различия.
· Решайте задачи вычитанием двух цифр, используя стратегию «нарисовать диаграмму».
· Представляйте ситуации вычитания числовыми предложениями, используя символ неизвестного числа.
· Анализируйте текстовые задачи, чтобы определить, какие операции использовать для решения многоступенчатых задач.
Глава 6: Сложение и вычитание 3-х цифр
- Нарисуйте быстрые картинки для представления 3-значного сложения.
- Примените концепцию разряда при использовании стратегии разделения для 3-значного сложения.
- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки единиц.
- Запишите 3-значное сложение с использованием стандартного алгоритма с возможной перегруппировкой десятков.
- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки единиц и десятков.
- Решайте задачи, связанные с вычитанием трех цифр, используя стратегию «создать модель».
- Запишите сложение трех цифр с использованием стандартного алгоритма с возможной перегруппировкой сотен.

- Запишите сложение трех цифр по стандартному алгоритму с возможностью перегруппировки сотен и десятков.
- Запись вычитания с использованием стандартного алгоритма, когда в уменьшаемом значении есть нули.
Глава 7: Деньги и время
- Найдите общую стоимость коллекций в десять центов, пятак и центов.
- Закажите монеты в коллекции по стоимости, а затем найдите общую стоимость.
- Обозначает денежные суммы меньше доллара с использованием двух различных комбинаций монет.
- Покажите один доллар разными способами.
- Найдите и запишите общую ценность денежных сумм, превышающих доллар.
- Решайте словесные задачи, связанные с деньгами, используя стратегию «разыграй это».
- Сообщите и запишите время с точностью до часа и получаса.
- Сообщите и запишите время с точностью до 5 минут.

- Сообщите и запишите время, используя A.M. и П.
Глава 8: Длина в обычных единицах
- Используйте конкретные модели для измерения длины объектов в дюймах.
- Сделайте дюймовую линейку и используйте ее для измерения длины предметов.
- Оцените длину предметов, мысленно разделив их на дюймы.
- Измерьте длину объектов с точностью до дюйма с помощью дюймовой линейки.
- Решайте задачи сложения и вычитания, связанные с длинами объектов, используя стратегию «рисовать диаграмму».
- Измерьте длину объектов в дюймах и футах, чтобы изучить обратную зависимость между размером и количеством единиц.
- Оцените длину предметов в футах.
- Выберите подходящие инструменты для измерения различной длины.
- Измерьте длину объектов и используйте линейный график для отображения данных измерений.

Глава 9: Длина в метрических единицах
- Используйте конкретную модель для измерения длины объектов в сантиметрах.
- Оцените длину объектов в сантиметрах, сравнив их с известной длиной.
- Измерьте длину предметов с точностью до сантиметра с помощью сантиметровой линейки.
- Измерьте длину объектов в сантиметрах и метрах, чтобы изучить обратную зависимость между размером и количеством единиц.
- Оцените длину объектов в метрах.
- Измерьте, а затем найдите разницу в длине двух объектов.
Глава 10: Данные
· Соберите данные в опросе и запишите эти данные в итоговую таблицу.
· Интерпретируйте данные в графических изображениях и используйте эту информацию для решения проблем.
· Сделайте графические изображения для представления данных.
· Интерпретируйте данные в виде гистограмм и используйте эту информацию для решения проблем.
· Создавайте гистограммы для представления данных.
· Решайте проблемы, связанные с данными, используя стратегию построения графика.
Глава 11: Понятия геометрии и дроби
· Определите трехмерные формы.
· Определите трехмерные формы по количеству граней, ребер и вершин.
· Создавайте трехмерные формы, используя кубы и другие объекты.
· Назовите 3-4-5-6-сторонние формы в соответствии с количеством сторон и вершин,
· Определите углы в двухмерных формах.
· Сортировка двухмерных фигур по их атрибутам.
· Разделите прямоугольники на квадраты одинакового размера и найдите общее количество этих квадратов.
· Определите и назовите равные части кругов и прямоугольников половинками, третями или четвертями.
· Формы разделов для отображения половин, третей или четвертей.
· Определите и опишите одну равную часть как половину трети или четверть целого.

 Реши примеры верно.
Реши примеры верно.

 Не очень хорошо знаком с числами.
Не очень хорошо знаком с числами. Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения.
Определите конкретные математические операции, которые вам нужно выполнить, и перечислите их на бумаге в порядке их выполнения. g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
g., используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему. Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.
Это важно для соединения математики и письма, но также помогает учащимся проверить, действительно ли их ответ отвечает на вопрос, заданный в словесной задаче.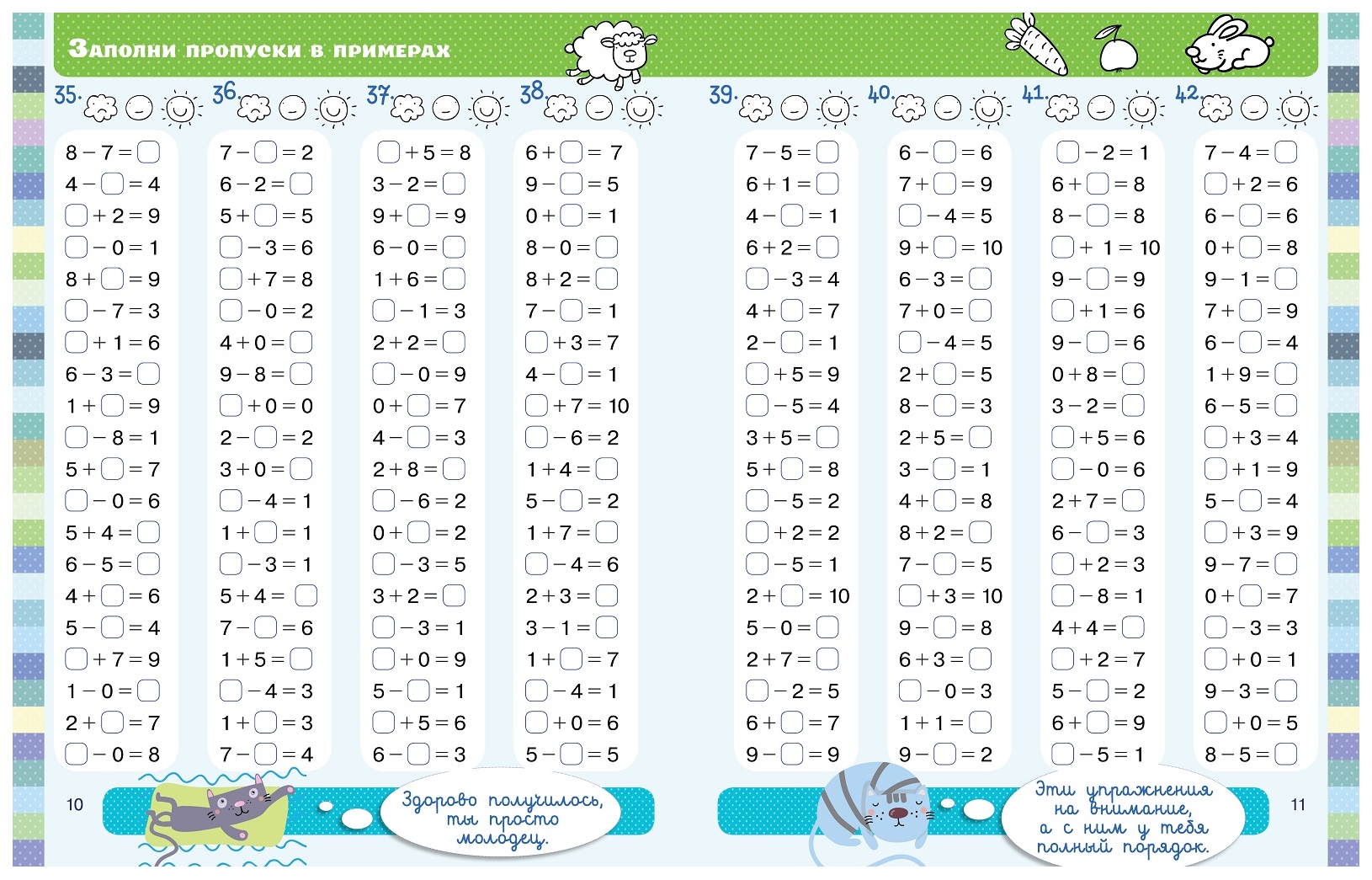 Ваш друг дает вам еще 3 файлов cookie. Вы съели 2 печенья. Сколько файлов cookie у вас осталось?
Ваш друг дает вам еще 3 файлов cookie. Вы съели 2 печенья. Сколько файлов cookie у вас осталось? Если в каждой пачке есть пять палочек жевательной резинки, а Джозеф покупает три пачки, сколько палочек жевательной резинки покупает Джозеф?
Если в каждой пачке есть пять палочек жевательной резинки, а Джозеф покупает три пачки, сколько палочек жевательной резинки покупает Джозеф? Д.
Д. Д.).
Д.). д.
д.