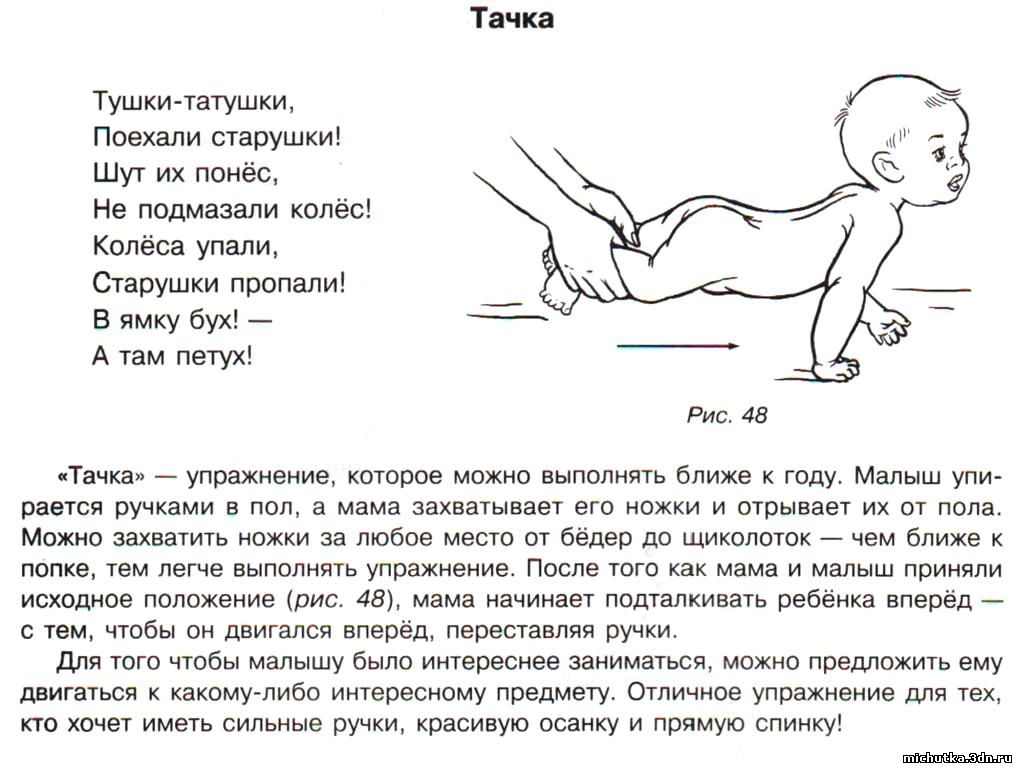
Комплекс номер 1 для грудничков: Гимнастические комплексы упражнений для детей раннего возраста №1-5 (от 1,5 месяцев до 1 года 2 месяцев) — 24 Апреля 2020 — Медицинская профилактика

Содержание

Комплексы массажа и гимнастики для детей

Детям на протяжении первого года жизни показаны 5 комплексов массажа и гимнастики, которые учитывают все физиологические особенности этого возраста. Для детей 1-3 лет разработаны особые 3 комплекса упражнений, которые способствуют развитию у них движений.

Первый комплекс (возраст 1,5-3 мес.)

Массаж ручек и ножек (поглаживание).
Рефлекторные упражнения – выкладывание на животик и ползание.
Массаж спины и живота в виде поглаживаний.
Растирание стоп.
Рефлекторное разгибание и сгибание стоп.
Разгибание позвоночника – проводится на левом и правом боку (рефлекторное упражнение).

Второй комплекс (возраст 3-4 месяца)

Массаж ручек (поглаживание).
Пассивное скрещивание ручек на груди.
Массаж нижних конечностей (растирание, поглаживание, разминание).
Массаж спинки (разминание и поглаживание).
Активно-пассивное упражнение – поворот вправо со спинки на живот.
Рефлекторное упражнение – положение «пловца».
Массаж (растирание и поглаживание) живота.
Массаж (похлопывание и растирание) стоп.
Рефлекторные упражнения для стоп.
«Бокс» — пассивное разгибание и сгибание ручек.

Массаж грудной клетки (вибрационный).
Поворот влево со спинки на живот.

Для всех упражнений исходное положение – горизонтальное.

Третий комплекс (возраст 4-6 месяцев)

Скрещивание ручек на груди.
Массаж ножек.
Пассивное упражнение, имитирующее велосипедные движения («скользящие шаги»).
Поворот вправо со спинки на животик.
Массаж спины (разминание, поглаживание, похлопывание).
Массаж животика.
Рефлекторное «парение» на животе.
Приподнимание туловища и головы при поддержке за отведенные в стороны руки (активное упражнение).
Массаж стоп и упражнение для них.
Разгибание и сгибание ручек или «бокс» (пассивное упражнение).
Попеременное и совместное пассивное разгибание и сгибание ножек

Рефлекторное «парение» на спине.
Поворот влево со спинки на живот.
Массаж (вибрационный) грудной клетки.

Все упражнения проводятся в исходном горизонтальном положении.

Четвертый комплекс (возраст 6-10 месяцев).

Скрещивание ручек на груди при поддержке за кольца.
Попеременное и совместное сгибание ножек и их разгибание (так называемые «скользящие шаги»).
Поворот вправо со спинки на животик без поддержки за ручку.
Массаж животика, спинки.
Ползание.
Присаживание малыша с поддержкой за отведенные в стороны ручки.
Пассивное поднятие выпрямленных ножек.
Круговые движения ручками.
Активное упражнение — напряженное выгибание.
Поворот влево со спинки на животик.
Активное упражнение – приподнимание туловища (положение на животе), поддерживая дитя за выпрямленные ручки.

Присаживание с поддержкой за ручки, которые разводят на ширину плеч (активное упражнение).

Все упражнения этого комплекса выполняются в горизонтальном исходном положении за исключением упражнения «бокс» (его в 8-месячном возрасте, когда ребенок уверенно сидит без опоры, можно выполнять в исходном положении сидя).

Пятый комплекс (возраст 10 месяцев – 1 год 2 месяца)

Сгибание и разгибание ручек («бокс») с кольцами стоя или сидя.
«Скользящие шаги».
Массаж спины.
Поворот в одну и другую сторону со спинки на живот.
Поднятие тела вертикально из положения на животике, при этом дитя поддерживается за ручки.
Наклон и выпрямление туловища.
Поднятие до палочки выпрямленных ножек.
Массаж живота.
Присаживание, поддерживая при этом за разведенные на ширину плеч ручки (с палочкой).
Приседание, поддерживая дитя за ручки с кольцами.
Напряженное выгибание.
Круговые движения ручками с кольцами.
Присаживание самостоятельное, с фиксацией коленок, или при поддержке малыша за одну ручку.

Упражнения 3, 4,7, 8, 9 выполняются в горизонтальном исходном положении. Выполнение 10 и 13 упражнений проходит по речевой инструкции.

Шестой комплекс (возраст 1 год 2 мес. – 1 год 6 мес.)

Сгибание ручек и их разгибание с кольцами. Выполняют с помощью взрослого в исходном положении стоя на полу.
Приседание (ребенок стоит на полу).
Поднятие до палочки выпрямленных ножек (исходное положение — лежа на полу).
Дитя пролезает через обруч, лежа на животике.
Ходьба по ребристой поверхности (к примеру, массажный коврик).

Седьмой комплекс (возраст 1 год 6 мес.

– 2 года)

Ходьба между двумя палками, веревками, по краю коврика или начерченной мелом дорожке и т.п. Ширину такой дорожки постепенно сужают, начиная с 30-25 см и до 10-5 см.

В лежачем положении на полу носками прямых ног нужно достать обруч или из стоячего положения достать предметы, которые лежат на полу, при этом не сгибать колени.
Проползти под обруч, скамейку, стул, палку и т.п., прогибая спину.
Вытянуть ручки вверх и, держась за обруч или палочку, присесть, а затем подняться на носочки («какие мы маленькие и большие»).
Покатать ногой карандаш, палочку и т.п., сидя на стуле.
Перешагнуть через несколько предметов на полу, расстояние между которыми 20-30 см.

Гимнастику нужно проводить каждый день, через 30-40 мин. после завтрака, также можно провести занятие после сна малыша в дневное время. Форма одежды – майка и трусы. Упражнения выполняются на коврике босиком, при этом обязательно нужно открыть форточку или фрамугу.

Длительность занятия – 10-12 минут. Для данного комплекса гимнастики нужно иметь две скакалки или веревки (длина 1-1,5 м), обруч (диаметр 45-50 см), палочка (диаметр 2,5 см, длина 40-50 см), брусочки, кубики, кегли и т.п.

Восьмой комплекс (возраст 2-3 года)

Ходьба вдоль палочки, веревки или по дорожке, ширина которой колеблется в пределах 5-10 см.
Достать предметы, лежащие на полу, при этом, не сгибая колени.
Поднять голову и в лежачем положении посмотреть на игрушку, которая лежит на стульчике или приподнята на высоту 25-30 см.
Перешагнуть через карандаши, палочки, кубики, которые располагаются друг от друга на расстоянии 20-30 см.
Пролезать через палку, веревку, в обруч, под скамейку или стульчик, прогибая при этом спину.
Поднять пальцами ног карандаш, лежащий на полу.

Проводят занятия через день или ежедневно, спустя примерно полчаса после завтрака или дневного сна.

Занятия длятся 12-15 мин, ребенок при этом одет в майку и трусы. Все упражнения выполняются на коврике босиком, при этом нужно держать открытой форточку или фрамугу. Для занятий нужны скакалка или веревка, обруч (диаметр 45-50 см), палка (длина 1-1,5 м, диаметр – 2, 5 см), мяч, кубики, кегли, брусочки.

Детский массаж

Услуги по теме

Записаться на прием прямо сейчас

Записаться на прием в клинику

ЗАПИСАТЬСЯ НА ПРИЕМ

Читайте другие материалы

Детский массаж при пупочной грыже Внешне пупочная грыжа проявляется округлым или овальным выпячиванием в области пупочного кольца, которое легко вправляется в брюшную полость, при легком надавливании на данный участок ощущается бульканье. Часто наряду с грыжей наблюдается расхождение прямых мышц живота, что свидетельствует о слабости мышц передней брюшной стенки.

Противопоказания к детскому массажу Детский массаж противопоказан при всех острых лихорадочных заболеваниях, при тяжелых формах гипотрофии (атрофия), при гнойных и других острых воспалительных поражениях кожи. Теория и практика детского массажа Детский массаж – средство для предупреждения и профилактики многих заболеваний, которые подстерегают малыша на раннем этапе развития. Детский массаж при врожденной косолапости Врожденная косолапость – это тяжелая деформация опорно — двигательного аппарата ребенка. Детский массаж при врожденном вывихе бедра, дисплазии тазобедренного сустава Подвывих бедра возникает на фоне дисплазии тазобедренного сустава. При данной форме вывиха головка бедра смещается кнаружи и кверху, но остается в суставе. Тем не менее, центр головки бедренной кости не соответствует центру вертлужной впадины.

Детский массаж при врожденной мышечной кривошее Фиксированное неправильное положение головы и шеи называется кривошеей. Существует несколько форм кривошеи: костная, неврогенная и мышечная форма. Лечебный детский массаж Cегодня широко известна взаимная тесная связь между всеми органами и частями организма. А наиболее доступными для воздействия являются кожа и поверхностные ткани ребенка. Искусство массажиста в том, чтобы, чувствуя эту связь, «настроить» своими руками организм пациента на нормальную работу. Гигиенические требования для проведения массажа ребенка первого года жизни Массаж необходимо делать мягко и нежно. Очень важно следить за реакцией на массаж ребенка, которая должна быть положительной. Если ребенок по каким-то причинам плохо реагирует на массаж, его следует прервать. Движения при выполнении массажа должны быть направлены по ходу кровеносных сосудов.

Область печени при массировании живота необходимо обходить. Требования к массажисту Требования к массажисту: одежда массажиста должна быть удобной, не стеснять движений, массажист должен быть приветливым, ласковым и терпеливым с ребенком. Детский массаж при перинатальной энцефалопатии Перинатальная энцефалопатия объединяет ряд синдромов. О самых распространённых из них рассказываем в статье. Оздоровительный детский массаж Существуют случаи, когда организм ребёнка нуждается в поддержке и укреплении. Новорождённый организм ещё не успел развить в себе патологии. Но иногда уже имеет к этому предпосылки: мышечная слабость, вялость, ослабление иммунной системы, расстройство работы кишечника и т.п. В такой ситуации ребёнок ещё, по сути, здоров, но болезнь разовьётся, если ничего не предпринимать. Массаж для детей поможет предотвратить нежелательное усугубление проблемы.

СМОТРЕТЬ ВСЕ СТАТЬИ

Комплексы массажа и гимнастики для детей | Методическая разработка на тему:

Комплексы массажа и гимнастики для детей

В течение первого года жизни детям назначают 5 комплексов массажа и гимнастики с учетом возрастных физиологических особенностей ребенка. Для детей от 1 года до 3 лет разработаны свои 3 комплекса упражнений, способствующих развитию движений ребенка.

Первый комплекс (для детей от 1,5 до 3 мес.).
1. Массаж рук (поглаживание). 2. Массаж ног (поглаживание). 3. Выкладывание на живот — упражнение рефлекторное. 4. Массаж спины (поглаживание). 5. Ползание — упражнение рефлекторное. 6. Массаж живота (поглаживание). 7. Массаж стоп (растирание). 8. Упражнение для стоп (сгибание и разгибание рефлекторное). 9. Разгибание позвоночника на правом и левом боку — упражнение рефлекторное.

Второй комплекс (для детей от 3 до 4 мес.).
1. Массаж рук (поглаживание). 2. Скрещивание рук на груди (упражнение пассивное). 3. Массаж ног (поглаживание, растирание, разминание). 4. Поворот со спины на живот вправо — упражнение пассивно-активное. 5. Массаж спины (поглаживание и разминание). 6. Положение «пловца» — упражнение рефлекторное. 7. Массаж живота (поглаживание и растирание). 8. Массаж стоп (растирание и похлопывание). 9. Упражнения для стоп (рефлекторные). 10. Сгибание и разгибание рук («бокс») — упражнение пассивное. 11. Вибрационный массаж грудной клетки. 12. Поворот со спины на живот влево.

Исходное положение для всех упражнений — горизонтальное.

Третий комплекс (для детей от 4 до 6 мес.).
1. Скрещивание рук на груди. 2. Массаж ног. 3. «Скользящие шаги» (имитация велосипедных движений) — упражнение пассивное. 4. Поворот со спины на живот вправо. 5. Массаж спины (поглаживание, разминание, похлопывание). 6. «Парение на животе» — упражнение рефлекторное. 7. Массаж живота. 8. Приподнимание головы и туловища при поддержке за руки, отведенные в стороны — упражнение активное. 9. Массаж стоп. 10. Упражнение для стоп. 11. «Бокс» (сгибание и разгибание рук). 12. Сгибание и разгибание ног вместе и попеременно — упражнение пассивное. 13. «Парение» на спине — упражнение рефлекторное. 14. Вибрационный массаж грудной клетки. 15. Поворот со спины на живот влево.

Исходное положение для всех упражнений — горизонтальное.

Четвертый комплекс (для детей от 6 до 10 мес.).
1. Скрещивание рук на груди, держась за кольца. 2. «Скользящие шаги» (сгибание и разгибание ног вместе и попеременно). 3. Поворот со спины на живот вправо без поддержки за руку. 4. Массаж спины. 5. Ползание. 6. Массаж живота. 7. Присаживание при поддержке за обе руки, отведенные в стороны. 8. Круговые движения руками. 9. Поднятие выпрямленных ног — упражнение пассивное. 10. Напряженное выгибание — упражнение активное. 11. Поворот со спины на живот влево. 12. Приподнимание туловища из положения на животе при поддержке за выпрямленные руки – упражнение активное. 13. Присаживание при поддержке за руки, разведенные на ширину плеч — упражнение активное.

Исходное положение для всех упражнений — горизонтальное, кроме упражнения «бокс», которое в 8 мес. (овладением сидения без опоры) можно выполнять из исходного положения сидя.

Пятый комплекс (для детей от 10 мес. до 1 года 2 мес.).
1. «Бокс» (сгибание и разгибание рук), сидя или стоя с кольцами. 2. «Скользящие шаги». 3. Поворот со спины на живот в одну и другую сторону. 4. Массаж спины. 5. Поднимание тела из положения на животе до вертикального положения при поддержке ребенка за руки с кольцами. 6. Наклон туловища и выпрямление. 7. Массаж живота. 8. Поднятие выпрямленных ног до палочки. 9. Присаживание при поддержке за руки, разведенные на ширину плеч, с палочкой. 10. Напряженное выгибание. 11. Приседание при поддержке за руки с кольцами. 12. Присаживание при поддержке за одну руку или самостоятельно с фиксацией колен. 13. Круговые движения руками с кольцами.

Исходное положение для упражнений 3, 4, 7, 8, 9 — горизонтальное. Упражнения 11 и 12 выполняются по речевой инструкции.

Шестой комплекс (для детей от 1 года 2 мес. до 1 года 6 мес.).
1. Сгибание и разгибание рук с кольцами. Выполняется с помощью взрослого; исходное положение — стоя на полу. 2. Поднятие выпрямленных ног до палочки, лежа на полу. 3. Приседание, стоя на полу. 4. Пролезание через обруч; выполняется лежа на животе. 5. Ходьба по ребристой поверхности, например по массажному коврику.

Седьмой комплекс (для детей от 1 года 6 мес. до 2 лет).
1. Ходьба по дорожке, начерченной мелом, или между двумя веревками, между палками, по краю коврика и т.п. Ширина дорожки постепенно сужается: от 30-25 см до 10-5 см. 2. Лежа на полу на спине достать обруч носками выпрямленных ног или из положения стоя достать лежащие на полу предметы, не сгибая колени. 3. Проползти под стул, скамейку, палку, обруч и т.д. (прогнуть спину). 4. Держась за палочку или обруч, вытянуть руки вверх и подняться на носки, присесть («какие мы большие и маленькие»). 5. Сидя на стульчике, ногой покатать палочку, карандаш и т. п. Перешагнуть через 1-2-3 предмета на полу (расстояние между предметами 20-30 см).

Гимнастика приводится ежедневно, спустя 30-40 мин. после завтрака или сразу после дневного сна. Форма одежды — трусы и майка. Выполняются упражнения босиком на коврике, обязательно при открытой фрамуге, форточке. Продолжительность занятия 10-12 мин. Для проведения занятия необходимы две веревки или скакалки (длиной 1-1,5 м), палочка (длиной 40-50 см, диаметром 2,5 см), обруч (диаметром 45-50 см), кегли, кубики, брусочки и т.п.

Восьмой комплекс (для детей от 2 до 3 лет).
1. Ходьба по дорожке шириной 10-5 см (или вдоль веревки, палочки). 2. Стоя на полу, достать лежащие предметы, не сгибая колени. 3. Лежа, поднять голову и посмотреть на игрушку, приподнятую на высоту 25-30 см (лежащую на стульчике). 4. Перешагивать через кубики, карандаши, расположенные на расстоянии 20-30 см друг от друга. 5. Поднимать пальцами ног лежащий на полу карандаш. 6. Пролезать под стульчик, скамейку, через веревку, палку, в обруч (прогнуть спину).

Занятия проводятся ежедневно или через день, через 30-40 мин. после завтрака или сразу после дневного сна. Длительность занятий 12-15 мин. Форма одежды — трусы и майка. Ребенок выполняет упражнения босиком, на коврике, при открытой форточке (фрамуге). Для занятий необходимы бельевая веревка или скакалка, палка (длиной 1-1,5 м, диаметром 2,5 см), обруч (диаметром 45-50 см), кегли, кубики, брусочки, мяч.

Комплексное число Факты для детей

Детская энциклопедия Факты

Построение правильного пятиугольника с помощью линейки и циркуля

Комплексное число — это число, но оно во многом отличается от обычных чисел. Комплексное число составляется из двух чисел, объединенных вместе. Первая часть — действительное число. Вторая часть комплексного числа — мнимое число. Самое важное мнимое число называется , определяемое как число, которое будет равно -1 при возведении в квадрат («возвести в квадрат» означает «умножить само на себя»). Все остальные мнимые числа умножаются на действительное число точно так же, как все действительные числа можно рассматривать как 1, умноженное на другое число. С комплексными числами можно использовать такие арифметические функции, как сложение, вычитание, умножение и деление. Они также следуют коммутативным, ассоциативным и дистрибутивным свойствам, как и действительные числа.

Комплексные числа были изобретены для решения специальных уравнений, в которых есть показатели степени. Это начало создавать настоящие проблемы для математиков. Для сравнения, используя отрицательные числа, можно найти x в уравнении для всех действительных значений a и b .

С возведением в степень есть проблема. Не существует действительного числа, которое дает -1 при возведении в квадрат. Другими словами, −1 (или любое другое отрицательное число) не имеет реального квадратного корня. Чтобы решить эту проблему, математики ввели мнимое число называется i . Это мнимое число даст -1 при возведении в квадрат.

Вероятно, первыми математиками, додумавшимися до этого, были Джероламо Кардано и Раффаэле Бомбелли. Они жили в 16 веке. Вероятно, Леонард Эйлер ввел запись этого числа.

Все комплексные числа могут быть записаны как (или ), где a называется действительной частью числа ( или ), а b называется мнимая часть ( или ). Комплексный номер также можно записать в виде набора ( a , b ). И a , и b — действительные числа. Любое действительное число можно просто записать как или как множество ( a , 0).

Набор всех комплексных чисел обычно записывается как .

Содержание

Операции над комплексными числами
Другие формы описания комплексных чисел
Заключение
Картинки для детей

Операции над комплексными числами

Сложение, вычитание, умножение, деление, если делитель не равен нулю, и возведение в степень (возведение чисел в степени) возможны с комплексными числами. Некоторые другие вычисления также возможны с комплексными числами.

Правило сложения комплексных чисел довольно простое: пусть , то . Умножение немного отличается:

Другая примечательная операция для комплексных чисел — 9.0011 спряжение . Комплексно-сопряженный есть . Это довольно просто, но важно для расчетов, т.к. к действительным числам относится весь комплекс .

Другие формы описания комплексных чисел

Комплексные числа могут отображаться на так называемой комплексной плоскости. Если у вас есть число, вы можете перейти к точке a на действительной оси и к точке b на воображаемой и нарисовать вектор от до . Вы можете вычислить длину этого вектора, используя теорему Пифагора и угол между действительной осью и этим вектором, считая против часовой стрелки. Длина вектора для числа называется модуль (), а угол аргумент ().

Комплексное число может быть визуально показано как два числа, которые образуют вектор на диаграмме Аргана, представляющей комплексную плоскость.

Это приводит к тригонометрической форме описания комплексных чисел: по определениям синуса и косинуса для всех стоит

Это тесно связано с формулой де Муавра.

Существует даже другая форма, называемая экспоненциальной .

Заключение

С добавлением в математику комплексных чисел каждый корень многочлена с комплексными коэффициентами является комплексным числом. Успешное добавление комплексных чисел в математику также помогло открыть путь к созданию других типов чисел, которые могли бы решить и помочь объяснить множество различных проблем, например: гиперкомплексные числа, седения, гиперреальные числа, сюрреалистические числа и многие другие. другие. См. типы чисел.

Картинки для детей

Все содержимое статей энциклопедии Kiddle (включая изображения статей и факты) можно свободно использовать по лицензии Attribution-ShareAlike, если не указано иное. Процитируйте эту статью:

Комплексное число Факты для детей. 2 = i \times i = -1\[/математика]. Все остальные мнимые числа представляют собой [math]i[/math], умноженные на действительное число, точно так же, как все действительные числа можно рассматривать как 1, умноженное на другое число. С комплексными числами можно использовать такие арифметические функции, как сложение, вычитание, умножение и деление. Они также следуют коммутативным, ассоциативным и дистрибутивным свойствам, как и действительные числа. Набор комплексных чисел часто представляется с помощью символа [math]\mathbb{C}[/math]. ^[1] ^[2]

Комплексные числа были обнаружены при попытке решить специальные уравнения, в которых есть показатели степени. Это начало создавать настоящие проблемы для математиков. В качестве сравнения, используя отрицательные числа, можно найти x в уравнении [math]a + x = b[/math] для всех действительных значений a и b , но если только положительные числа разрешены для x , иногда невозможно найти положительное x 92=-9[/математика]. Чтобы решить эту проблему, математики ввели символ i и назвали его мнимой единицей . ^[1] Это мнимое число, которое даст -1 при возведении в квадрат.

Вероятно, первыми математиками, додумавшимися до этого, были Джероламо Кардано и Раффаэле Бомбелли. Они жили в 16 веке. ^[2] Вероятно, Леонард Эйлер ввел запись [math]\mathrm i[/math] для этого числа.

Все комплексные числа можно записать как [math]a + bi[/math] ^[3] (или [math]a + b \cdot i[/math]), где a называется действительной частью числа, а b называется мнимой частью . Мы пишем [math]\Re (z)[/math] или [math]\operatorname{Re}(z)[/math] для вещественной части комплексного числа [math]z[/math]. Итак, если [math]z = a + bi[/math], мы пишем [math]a = \Re (z) = \operatorname{Re} (z)[/math]. Точно так же мы пишем [math]\Im (z)[/math] или [math]\operatorname{Im} (z)[/math] для мнимой части комплексного числа [math]z[/math]; [math]b = \Im (z) = \operatorname{Im} (z)[/math], для того же z. ^[1] Каждое действительное число также является комплексным; это комплексное число z с [math]\Im (z) = 0[/math].

Комплексное число также можно записать в виде упорядоченной пары ( a , b ), где a и b — действительные числа. Любое действительное число можно просто записать как [math]a + 0 \cdot i[/math] или как пару ( a , 0). ^[3]

Иногда [math]j[/math] пишется вместо [math]i[/math]. Например, в электротехнике [math]i[/math] означает электрический ток, поэтому написание [math]i[/math] может вызвать много проблем, потому что некоторые числа в электротехнике являются комплексными числами.

Набор всех комплексных чисел обычно записывается как [math]\mathbb{C}[/math]. ^[1]