Карточка для проверки таблицы сложения и вычитания в пределах 20 | Картотека по математике (1 класс) на тему:
Опубликовано 19.11.2014 — 13:24 — Лукина Любовь Алексеевна
Карточка для проверки таблицы сложения и вычитания в пределах 20 в двух вариантах.
Скачать:
Предварительный просмотр:
Вариант 1
Ф И______________________
3 + 8 = 9 + 8 = 13 — = 9 8 + 6 =
9 + =12 8 + =12 4 + = 13 14 – 5 =
+7 = 11 +8 = 16 13 – 5 = 9 + = 14
9 + 9 = 8 + 4 = 8 + = 13 8 + 7 =
6 + =12 3 + =12 7 + 6 = 15 — = 6
+5 = 11 +2 = 11 7 + = 14 9 + 7 =
Вариант 2
Ф И______________________
9 + 8 = 3 + 8 = 13 — = 9 8 + 7 =
8 + =12 9 + =12 4 + = 13 13 – 5 =
+7 = 11 +8 = 16 14 – 5 = 9 + = 14
8 + 4 = 9 + 9 = 8 + = 13 8 + 6 =
3 + =12 6 + =12 7 + 9 = 15 — = 6
+2 = 11 +5 = 11 7 + = 14 6 + 7 =
По теме: методические разработки, презентации и конспекты
Урок математики в 1 классе на тему «Таблица сложения и вычитания в пределах 20.
Состав чисел в пределах 10. Закрепление»Урок математики в 1 классе на тему «Таблица сложения и вычитания в пределах 20. Состав чисел в пределах 10. Закрепление»…
«Обобщение и закрепление знаний учащихся по теме «Таблицы сложения и вычитания в пределах 10»
Цели:закрепить изученные таблицы сложения и вычитания в пределах 10;Развивать логическое мышление, творческое воображение ,мелкую моторику;Воспитывать аккуратность, любознательность, бережное от…
Таблицы сложения и вычитания в пределах 10
Конспект урока амтематики в 1 классе закрепление знаний по теме: «Таблицы сложения и вычитания в пределах 10″…
таблица сложения и вычитания в пределах 20
таблица сложения и вычитания в пределах 20 для учащихся 1 класса…
Урок математики по теме:»Закрепление изученного по теме «Сложение однозначных чисел с переходом через разряд и соответствующие случаи вычитания (таблица сложения и вычитания в пределах 20)»
Закрепить знания о приеме сложения однозначных чисел с переходом через разряд.
..
Урок математики в 1, 3 классе- комплекте. Тема урока в 1 классе:«Закрепление знаний таблицы сложения и вычитания в пределах 10» Тема урока в 3 классе: «Приемы умножения и деления в пределах 100. Закрепление»
На уроке ребята отправились в новогоднее путешествие, где познакомились с Дедами Морозами разных стран и узнали, как празднуют Новый год в других частях планеты. За время путешествия закрепили на…
Карточка для проверки таблицы сложения в пределах 20
Карточка для проверки таблицы сложения в пределах 209+ 3=9+ 3=9+ 3=9+ 3=9+ 3=9 + 8=9 + 8=9 + 8=9 + 8=9 + 8=8 + 9=8 + 9=8 + 9=8 + 9=8 + 9=7 + 10=7 + 10=7 + 10=7 + 10=7 + 10=7+6=7+6=7+6=7+6=7+6=8 + 3=8 …
Поделиться:
Таблица сложения и вычитания 2
Тема: Таблица сложения и вычитания 2.
Цель: закрепить знание таблицы сложения и вычитания числа 2, учить применять знания для решения примеров и задач, развивать умения составлять и решать задачи по рисунку, называть компоненты действий вычитания и сложения, определять названия геометрических фигур, воспитывать творческий подход к работе, умение работать в паре и группе.
Оборудование: карточки с заданиями, картинки с примерами, счетный материал, сигнальные карточки, учебник.
Ход урока
1 Сообщение темы урока. Устный счёт.
Ребята, сегодня у нас необычный урок – путешествие в страну Деда Мороза. Мы будем повторять сложение и вычитание числа 2, решать задачи, примеры и ещё много интересного. Пора отправляться: поезд ждет разрешающего сигнала светофора, поможем ему. Красный свет – ответ 8, желтый – 5, зелёный – 3. Приготовьте сигнальные карточки.
Учитель задаёт примеры на сложение и вычитание числа 2, дети показывают ответ цветом карточки.
—8 6+2 8+0
-5 3+2 4+1
-3 1+2 3-0
Светофор дал зеленый свет, пора садиться в вагоны. Чтобы узнать номера вагонов ответьте на задания:
Два снежка у Даши
И пять у Наташи
Вы снежки все эти
Скорей считайте, дети!
Вагон номер – 7.
Семь щенков и мама лайка
Сколько всех, пересчитай-ка!
Вагон номер – 8.
8 храбрых малышей
Перешли по льду ручей.
Один кричит: и я хочу!
Сколько всех идет по льду?
Вагон номер — 9.
7 снегирей на ветку село
3 ещё к ним прилетело
Отвечайте быстро, дети
Сколько снегирей на ветке?
Вагон номер – 10.
Назовите номера вагонов.
7 8 9 10
Какое число лишнее? (10) Почему? ( двузначное) Как назвать все остальные числа? ( однозначные) Какое из этих чисел самое маленькое ?
Самое большое? Какое стоит между числами 7 и 9? Между 8 и 10? Какое стоит перед числом 8, 10? Какое стоит после числа 7, 9?
Откройте тетради – у вас записаны номера вагонов, допишите пропущенные.
1 2 . 4 . 6 7 . 8 . 10
Назовите только те числа, которые записали.
2 Изучение материала урока.
а) работа с геометрическим материалом
Нашему поезду нужен машинист. Чтобы узнать кто это, надо справиться с заданием. Посмотрите на доску: какие геометрические фигуры вы можете назвать?
Сколько здесь фигур? Каким по счету стоит треугольник? Трапеция? Сколько кругов? Они одинакового размера? У вас на парте лежат конверты, в них такие же фигуры, выложите фигуры так же, как на доске. Из этих фигур надо сложить того, о ком пойдет речь в загадке.
Появился во дворе
Он в холодном декабре,
Неуклюжий и смешной
У катка стоит с метлой.
К ветру зимнему привык
Наш приятель … ( снеговик )
б) работа в парах
Дети складывают снеговика, учитель « сажает» снеговика – машиниста в паровоз.
в) физминутка
Поезд готов к отправлению, поможем движению.
г) работа над компонентами действий сложения и вычитания, подбор знаков и составление примеров
Наша первая остановка станция «Снежная». Предлагаю вам поиграть в снежки. Чтобы снежок попал в цель, надо составить пример с помощью знаков – помощников.
2
8
1
2
3
3
2
5
2
2
4
1000
Дети вставляют знаки:
Назовите примеры на сложение, на вычитание. Назовите компоненты сложения, вычитания? Что такое 8, 2, 10 ? 3, 2, 1?
Почему в каждом из примеров прибавляли или вычитали 2? ( повторяем сложение и вычитание 2).
д) решение задач, работа с учебником
Вторая станция – «Задачкино». Откройте учебник на странице 50, задание 3.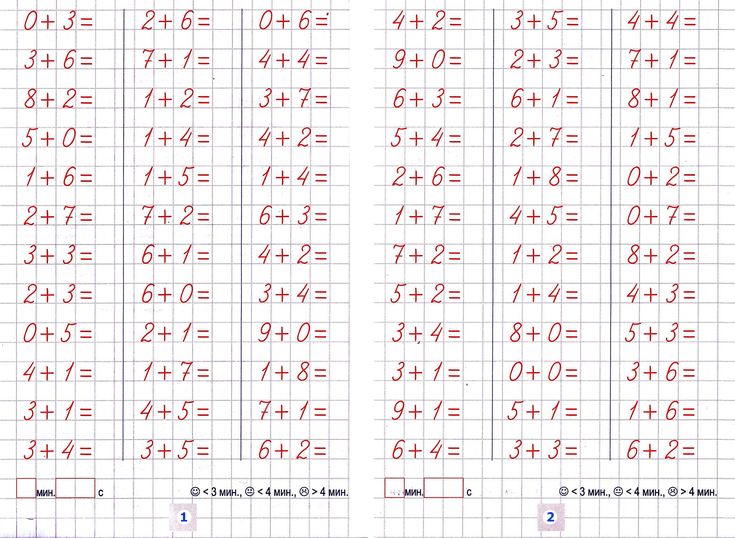
Расскажите, что видите на рисунке, составим условие задачи.
В кормушке было 9 птиц. Одна улетела. Сколько осталось птиц в кормушке?
Запишем задачу в тетради. Сколько клеточек отступим от предыдущей работы? Повторим условие, я буду писать на доске, вы в тетради. Один ученик ведёт класс.
Что нам известно? (Было 9 птиц. Пишем – 9. Улетела 1 птица. Пишем – 1.)
Что надо узнать? (Сколько осталось птиц? Пишем — ?)
Как решить задачу? (9-1=8)
Сколько птиц осталось? (Пишем – 8)
е) физминутка
ё) работа над повторением таблицы сложения и вычитания 2, у доски
Третья станция «Новогодняя ёлка». Надо украсить ёлку шарами. Какой шар повесить, узнаем, решив пример.
3
1+2=3 10-2=8 7-2=5
2+2=4 7+2=9 8+2=10
ж) работа в группах
Мы приближаемся к последней станции – дому Деде Мороза.
Какой снег пошёл, прямо к вам на парты (учитель раздаёт снежинки с примерами). Если дружно, группой решите задание –узнаем код к дому Мороза.
3-2=
0+1=
2-1=
1+1=
3-1=
0+2=
1+1=
3-1=
0+2=
1+1=
3-1=
0+2=
Назовите ответы:
2012
Что это за число? Скольки значное? ( четырех )
3 Итог урока:
Вы так хорошо работали, что Дед Мороз сам вышел вас приветствовать. Давайте вспомним, что мы делали на уроке?
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/245081-tablica-slozhenija-i-vychitanija-2
Свободное владение языком без страха — YouCubed
Скачать PDF
Джо Боулер, профессор математического образования, соучредитель youcubed
С помощью Кэти Уильямс, соучредителя youcubed, и Аманды Конфер, Стэнфордский университет
Обновлено 28 января 2015 г.
Введение
Несколько лет назад британский политик Стивен Байерс допустил в интервью безобидную ошибку. Достопочтенного министра попросили дать ответ на 7 x 8, и он дал ответ 54 вместо правильных 56. Его ошибка вызвала широкомасштабные насмешки в национальных СМИ, сопровождаемые призывами сделать больший акцент на «таблице умножения». заучивание в школах. В сентябре этого года консервативный министр образования Англии, человек без опыта образования, настоял на том, чтобы все учащиеся в Англии запоминали все свои таблицы умножения до 12 x 12 к 9 годам.. Это требование теперь включено в учебную программу по математике в Великобритании и, как я предсказываю, приведет к повышению уровня беспокойства по поводу математики и к рекордному количеству учащихся, отказывающихся от математики. США движутся в противоположном направлении, поскольку новые стандарты Common Core State Standards (CCSS) принижают значение механического запоминания математических фактов. К сожалению, неправильное толкование значения слова «беглость» в CCSS является обычным явлением, и издатели продолжают делать упор на механическое заучивание, поощряя сохранение вредной практики в классе в Соединенных Штатах.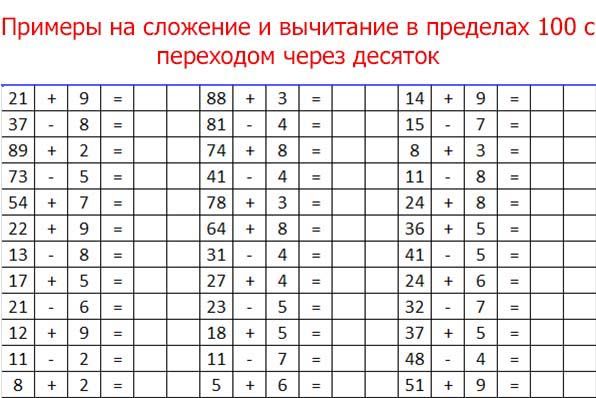
Полезно запомнить некоторые математические факты. Я не останавливаюсь и не думаю об ответе на 8 плюс 4, потому что знаю этот математический факт. Но я изучал математические факты, используя их в различных математических ситуациях, а не практикуя их и проверяя их. Я вырос в прогрессивную эпоху Англии, когда начальные школы были ориентированы на «всего ребенка», и мне не давали таблицы сложения, вычитания или умножения фактов для запоминания в школе. Это никогда не останавливало меня ни в какое время и ни в каком месте моей жизни, даже несмотря на то, что я профессор математического образования. Это потому, что у меня есть чувство числа, что гораздо важнее для учащихся, и это включает в себя изучение математических фактов наряду с глубоким пониманием чисел и того, как они связаны друг с другом.
Чувство числа
В рамках критического исследовательского проекта исследователи изучали студентов, решивших числовые задачи (Gray & Tall, 1994).
Учащиеся в возрасте от 7 до 13 лет были определены учителями как учащиеся с низкой, средней или высокой успеваемостью. Исследователи обнаружили важную разницу между учащимися с низкой и высокой успеваемостью: учащиеся с высокой успеваемостью использовали чувство числа, а учащиеся с низкой успеваемостью — нет. Успешные учащиеся подошли к таким задачам, как 19 + 7, изменив задачу, например, на 20 + 6. Ни один ученик, который был номинирован как слабоуспевающий, не использовал чувство числа. Когда учащимся с низкой успеваемостью давали задачи на вычитание, такие как 21–16, они считали в обратном порядке, начиная с 21 и заканчивая обратным отсчетом, что чрезвычайно сложно сделать. Учащиеся с высокими показателями использовали такие стратегии, как изменение чисел на 20–15, что намного проще. Исследователи пришли к выводу, что малоуспевающие часто являются малоуспешными не потому, что они меньше знают, а потому, что они не используют числа гибко — они были поставлены на неверный путь, часто с раннего возраста, пытаясь запомнить методы вместо того, чтобы взаимодействовать с числами.
Чувство чисел лежит в основе всей высшей математики (Feikes & Schwingendorf, 2008). Когда студенты терпят неудачу по алгебре, это часто происходит потому, что у них нет чувства числа. Когда учащиеся работают над сложными математическими задачами, такими как те, которые мы приводим в конце этой статьи, у них развивается чувство числа, а также они изучают и запоминают математические факты. Когда учащиеся сосредотачиваются на запоминании таблицы умножения, они часто запоминают факты, не имея представления о числах, а это означает, что они очень ограничены в своих возможностях и склонны совершать ошибки, например ту, которая вызвала общенациональные насмешки над британским политиком. Отсутствие чувства числа привело к более катастрофическим ошибкам, например, к тому, что телескоп Хаббл пропустил звезды, которые он должен был сфотографировать в космосе.
Мозг и чувство числа
Некоторые учащиеся не так хорошо запоминают математические факты, как другие. Это то, что нужно праздновать, это часть прекрасного разнообразия жизни и людей. Представьте, как скучно и скучно было бы, если бы учителя давали тесты по математике и все отвечали бы на них одинаково и с одинаковой скоростью, как если бы все они были роботами. В недавнем исследовании мозга ученые исследовали мозг учащихся, когда их учили запоминать математические факты. Они увидели, что некоторые ученики запоминают их гораздо легче, чем другие.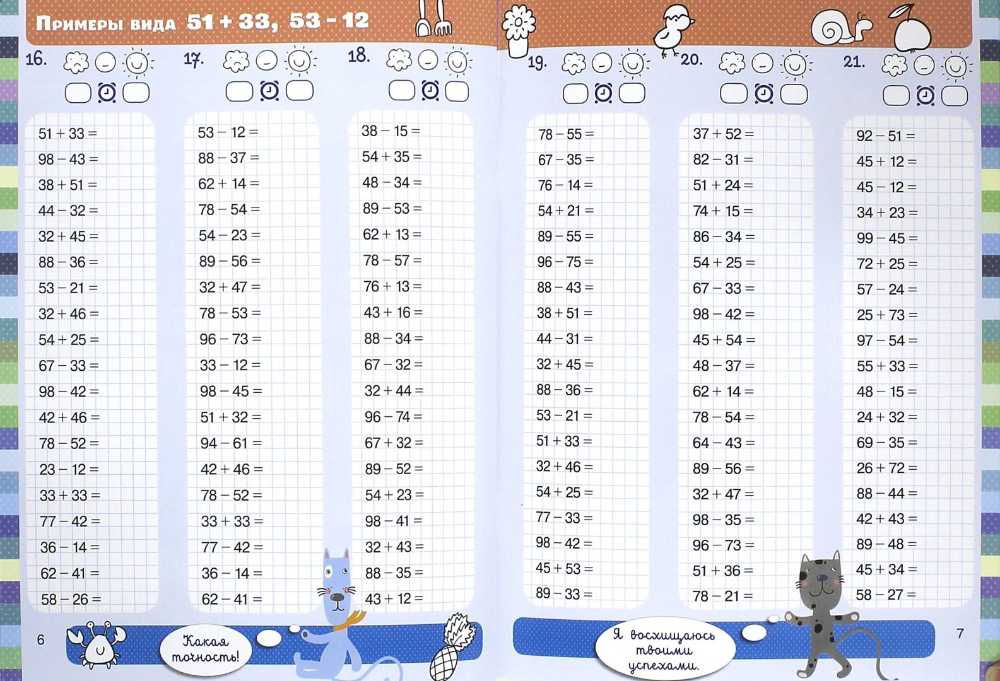
Это не будет сюрпризом для читателей, и многие из нас, вероятно, предположили бы, что те, кто запоминал лучше, были более успешными или «более умными» учениками. Но исследователи обнаружили, что учащиеся, которые лучше запоминали, не имели более высоких достижений, у них не было того, что исследователи назвали более «математическими способностями», и у них не было более высоких показателей IQ (Supekar et al, 2013). Единственные различия, которые обнаружили исследователи, заключались в области мозга, называемой гиппокампом, которая является областью мозга, отвечающей за запоминание фактов (Supekar et al, 2013). Некоторые учащиеся будут медленнее запоминать, но у них все еще есть исключительный математический потенциал. Математические факты составляют очень небольшую часть математики, но, к сожалению, учащиеся, которые плохо запоминают математические факты, часто приходят к выводу, что они никогда не смогут добиться успеха в математике, и отворачиваются от предмета.
Учителя в США и Великобритании просят учащихся запоминать факты умножения, а иногда и факты сложения и вычитания, обычно потому, что в учебных планах указано, что учащиеся должны «свободно обращаться с числами».
Когда учителя делают упор на запоминание фактов и дают тесты для измерения количества фактов, учащиеся страдают двумя важными способами. Примерно для трети учащихся начало тестирования на время является началом математической тревожности (Boaler, 2014). Сиан Бейлок и ее коллеги изучали мозг людей с помощью МРТ и обнаружили, что математические факты хранятся в области рабочей памяти мозга. Но когда учащиеся испытывают стресс, например, когда они отвечают на математические вопросы в условиях дефицита времени, рабочая память блокируется, и учащиеся не могут получить доступ к известным им математическим фактам (Beilock, 2011; Ramirez, et al, 2013).
В настоящее время тревожность по поводу математики регистрируется у учащихся в возрасте от 5 лет (Рамирез и др., 2013 г.), и контрольные работы на время являются основной причиной этого изнурительного состояния, часто сохраняющегося на всю жизнь. Но есть и вторая, не менее важная причина, по которой нельзя использовать временные тесты — они побуждают многих учащихся отворачиваться от математики.
На моих занятиях в Стэнфордском университете я сталкиваюсь со многими студентами, травмированными по математике, хотя они являются одними из самых успевающих студентов в стране. Когда я спрашиваю их, что случилось, что привело к их отвращению к математике, многие ученики говорят о тестах на время во втором или третьем классе как о главном поворотном моменте для них, когда они решили, что математика не для них. Некоторые учащиеся, особенно женщины, говорят о необходимости глубокого понимания, что является очень полезной целью, и о том, что глубокое понимание не ценится и не предлагается, когда тесты на время стали частью урока математики. Возможно, на уроках математики они выполняли другую, более полезную работу, сосредоточившись на осмыслении и понимании, но тесты на время вызывают такие сильные эмоции, что учащиеся могут поверить, что умение быстро справляться с математическими фактами и есть суть математики. Это крайне неудачно. Мы видим результат ошибочного упора школы на заучивание и тестирование в цифрах, выпадающих из математики, и в математическом кризисе, с которым мы сталкиваемся в настоящее время (см.
www.youcubed.org). Когда моя собственная дочь начала запоминать таблицу умножения и тестировать ее в возрасте 5 лет в Англии, она начала приходить домой и плакать из-за математики. Это не та эмоция, которую мы хотим, чтобы учащиеся ассоциировали с математикой, и пока мы продолжаем заставлять учащихся быстро вспоминать факты, мы не сможем избавиться от широко распространенного беспокойства и неприязни к математике, которые пронизывают США и Великобританию (Silva & White, 2013). ; National Numeracy, 2014).
. В последние годы исследователи мозга обнаружили, что учащиеся, которые наиболее успешно справляются с задачами на числа, используют разные мозговые пути: один связан с числами и символами, а другой связан с более интуитивным и пространственным мышлением (Park & Brannon, 2013). . В конце этой статьи мы даем множество упражнений, которые способствуют визуальному пониманию числовых фактов, чтобы задействовать важные мозговые связи. Кроме того, исследователи мозга изучали студентов, изучающих математические факты двумя способами — с помощью стратегий или запоминания.
Они обнаружили, что два подхода (стратегии или запоминание) задействуют два различных пути в мозге и что оба пути идеально подходят для использования на протяжении всей жизни. Важно отметить, что исследование также показало, что те, кто учился с помощью стратегий, достигли «превосходной производительности» по сравнению с теми, кто запоминал, они решали задачи с той же скоростью и лучше переносили новые задачи. Исследователи мозга пришли к выводу, что автоматизм должен быть достигнут через понимание числовых отношений, достигаемое посредством размышлений о числовых стратегиях (Делазер и др., 2005).
Почему к математике относятся по-разному?
Чтобы научиться хорошо изучать английский язык, читать и понимать романы или поэзию, учащиеся должны запомнить значения многих слов. Но ни один изучающий английский язык не скажет и не подумает, что изучение английского языка — это быстрое запоминание и быстрое припоминание слов. Это потому, что мы учим слова, используя их в самых разных ситуациях — в разговоре, чтении и письме.
Учителя английского языка не дают учащимся сотни слов для запоминания, а затем проверяют их в заданных условиях. Все предметы требуют запоминания некоторых фактов, но математика — единственный предмет, по которому учителя считают, что их нужно проверять в условиях времени. Почему мы так относимся к математике?
У математики уже есть огромная проблема с изображениями. Студенты редко плачут по другим предметам, и при этом они не верят, что все остальные предметы связаны с запоминанием или скоростью. Использование методов обучения и воспитания, которые подчеркивают запоминание математических фактов, является основной причиной того, что учащиеся отключаются от математики. Многие люди будут утверждать, что математика отличается от других предметов, и она просто должна быть такой — что математика — это получение правильных ответов, а не интерпретация или смысл. Это еще одно заблуждение. Ядром математики является рассуждение — размышление о том, почему методы имеют смысл, и обсуждение причин использования различных методов (Boaler, 2013).
Математические факты — это небольшая часть математики и, вероятно, наименее интересная часть. Конрад Вольфрам из Wolfram-Alpha, одной из ведущих мировых математических компаний, публично говорит о широте математики и о необходимости перестать рассматривать математику как расчет. Ни Вольфрам, ни я не утверждаем, что в школах не следует обучать счету, но необходимо изменить баланс, и учащиеся должны учиться считать с помощью чувства чисел, а также уделять больше времени слаборазвитым, но важным частям математики, таким как решение задач. и рассуждения.
Важно, обучая студентов смыслу чисел и фактам чисел, никогда не подчеркивать скорость. На самом деле это верно для всей математики. В математике распространено распространенное и вредное заблуждение — представление о том, что сильные ученики-математики — это быстрые ученики. Я работаю со многими математиками, и я замечаю в них одну вещь: они не очень быстро работают с числами, на самом деле некоторые из них довольно медленные. Это неплохо, они медлительны, потому что глубоко и тщательно думают о математике.
Лоран Шварц, выдающийся математик, написал автобиографию о своих школьных годах и о том, как его заставляли чувствовать себя «глупым», потому что он был одним из самых медлительных математических мыслителей в своем классе (Schwartz, 2001). Ему потребовалось много лет ощущения себя неадекватным, чтобы прийти к заключению, что «быстрота не имеет точного отношения к интеллекту». Важно глубоко понимать вещи и их отношения друг к другу. Вот где кроется интеллект. Факт быстрого или медленного на самом деле не имеет значения». (Шварц, 2001) К сожалению, уроки математики, основанные на скорости и тестах, заставляют многих учеников, которые медленно и глубоко мыслят, таких как Шварц, полагать, что они не могут быть хороши в математике.
Математика «Свободное владение» и учебная программа
В США новая учебная программа Common Core включает беглость речи в качестве цели. Беглость возникает, когда у учащихся развивается чувство числа, когда они математически уверены, потому что понимают числа.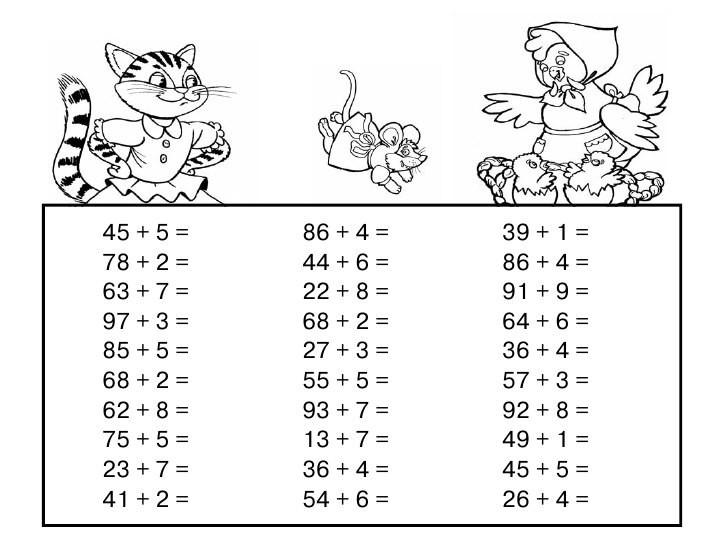
К сожалению, слово «свобода» часто неправильно истолковывается. Учебная программа Engage New York, которая становится все более популярной в США, неправильно интерпретирует беглость речи следующим образом:
Свободное владение языком: Ожидается, что учащиеся будут иметь скорость и точность с простыми расчетами; учителя структурируют время занятий и/или домашнее задание, чтобы учащиеся запоминали посредством повторения основные функции, такие как таблицы умножения, чтобы они лучше понимали и манипулировали более сложными функциями . (Задействуйте Нью-Йорк)
У этой директивы много проблем. Скорость и запоминание — два направления, от которых нам срочно нужно отойти, а не навстречу. Столь же проблематично «Вовлечение Нью-Йорка» связывает запоминание числовых фактов с пониманием учащимися более сложных функций, что не подтверждается данными исследований. Исследования говорят нам, что учащиеся понимают более сложные функции, когда у них есть чувство числа и глубокое понимание числовых принципов, а не слепое запоминание или быстрое припоминание (Boaler, 2009).
). В настоящее время я работаю с аналитиками PISA в ОЭСР. Команда PISA не только выпускает международные тесты по математике каждые 4 года, но и собирает данные о математических стратегиях учащихся. Их данные, полученные от 13 миллионов 15-летних подростков по всему миру, показывают, что ученики с самой низкой успеваемостью — это те, кто сосредотачивается на запоминании и считает, что запоминание важно при изучении математики (Boaler & Zoido, в печати). Эта идея зарождается рано в классах, и нам нужно ее искоренить. Самые высокие достижения в мире — это те, кто сосредотачивается на больших идеях в математике и связях между идеями. У учащихся развивается связанное представление о математике, когда они работают над математикой концептуально, а слепое запоминание заменяется осмыслением.
В Великобритании директивы имеют аналогичный потенциал вреда. В новой национальной учебной программе говорится, что все учащиеся должны «заучить свои таблицы умножения до 12 включительно» к 9 годам, и хотя учащиеся могут запоминать факты умножения до 12 x 12 с помощью насыщенных увлекательных занятий, эта директива побуждает учителей Дайте учащимся таблицу умножения, чтобы они запомнили ее, а затем проверили.
Ведущая группа в Великобритании, возглавляемая детским писателем и поэтом Майклом Розеном, сформировалась, чтобы привлечь внимание к ущербу, наносимому текущей политикой в школах, и к числу детей младшего школьного возраста, которые теперь ходят в школу в слезах из-за стресса, в котором они находятся. — тестирование (Гарнер, The Independent, 2014). Математика является основной причиной беспокойства и страха учащихся, а ненужное сосредоточение внимания на заученных математических фактах в ранние годы является одной из основных причин этого.
Упражнения для развития числовых фактов и числового смысла
Учителя должны помогать учащимся развивать математические факты, не подчеркивая факты ради фактов или используя «тесты на время», а поощряя учащихся использовать числа, работать с ними и исследовать их. По мере того, как учащиеся работают над осмысленными числами, они будут запоминать математические факты одновременно с пониманием чисел и математики. Они будут наслаждаться и изучать важную математику, а не запоминать, бояться и бояться математики.
Телефонные разговоры
Одним из лучших методов одновременного обучения понятию чисел и математическим фактам является обучающая стратегия под названием «Разговоры о числах», разработанная Рут Паркер и Кэти Ричардсон. Это идеальное краткое учебное задание, с которого учителя могут начинать уроки, а родители могут выполнять его дома. Он включает в себя постановку абстрактной математической задачи, такой как 18 x 5, и просьбу учащихся решить ее в уме. Затем учитель собирает различные методы и смотрит, почему они работают. Например, учитель может поставить 18 x 5 и обнаружить, что ученики решают задачу разными способами:
Студенты любят предлагать свои различные стратегии и обычно полностью вовлечены и очарованы различными возникающими методами. Учащиеся изучают математику в уме, у них есть возможность запоминать математические факты, а также они развивают концептуальное понимание чисел и арифметических свойств, которые имеют решающее значение для успеха в алгебре и не только.
Родители могут использовать аналогичную стратегию, спрашивая о методах своих детей и обсуждая различные методы, которые можно использовать. Две книги, одна Кэти Хамфрис и Рут Паркер (в печати), а другая Шерри Пэриш (2014 г.), иллюстрируют множество различных разговоров о числах, над которыми можно работать со учащимися средней и начальной школы соответственно.
Исследования говорят нам, что лучшие классы математики — это те, в которых учащиеся изучают числовые факты и смысл чисел посредством увлекательных занятий, которые сосредоточены на математическом понимании, а не на механическом запоминании. Следующие пять видов деятельности были выбраны для иллюстрации этого принципа; Приложение к этому документу содержит более широкий спектр заданий и ссылок на другие полезные ресурсы, которые помогут учащимся развивать чувство числа.
Дополнительные действия по фактам
Snap It: Это задание, над которым дети могут работать в группах. Каждый ребенок составляет поезд из соединяющихся кубиков определенного числа.
По сигналу «Щелк» дети разбивают свои поезда на две части и держат одну руку за спиной. Дети по очереди ходят по кругу, показывая оставшиеся кубики. Остальные дети отрабатывают полную комбинацию чисел. Например, если у меня есть 8 кубиков в моем числовом поезде, я могу сломать его и положить 3 за спину. Я покажу своей группе оставшиеся 5 кубиков, и они смогут сказать, что трех не хватает и что 5 и 3 составляют 8.
Сколько прячется? В этом задании у каждого ребенка одинаковое количество кубиков и чашек. Они по очереди прячут несколько своих кубиков в чашку и показывают остатки. Другие дети отрабатывают ответ на вопрос «Сколько спряталось» и называют полное числовое сочетание.
Пример: У меня есть 10 кубиков, и я решил спрятать 4 в своей чашке. Моя группа видит, что у меня всего 6 кубиков. Учащиеся должны быть в состоянии сказать, что я прячу 4 кубика и что 6 и 4 дают 10.
Действия по умножению фактов
Насколько близко к 100? В эту игру играют напарники.
Двое детей делят пустую сетку 100. Первый партнер бросает два кубика с числами. Выпадающие числа — это числа, которые ребенок использует для создания массива в сетке 100. Они могут поместить массив в любое место сетки, но цель состоит в том, чтобы заполнить сетку настолько, насколько это возможно. После того, как игрок нарисовал массив на сетке, он записывает числовое предложение, описывающее сетку. Игра заканчивается, когда оба игрока бросили кубики и не могут больше размещать на сетке ряды. Как близко к 100 вы можете получить?
Пицца Пепперони: В этой игре дети дважды бросают кубик. Первый бросок говорит им, сколько пицц нужно вытянуть. Второй рулон говорит им, сколько пепперони положить на КАЖДУЮ пиццу. Затем они пишут числовое предложение, которое поможет им ответить на вопрос: «Сколько всего пепперони?»
Например, я бросаю кости и получаю 4, поэтому я вытягиваю 4 большие пиццы. Я переворачиваю снова, и у меня получается 3, поэтому я кладу по три пепперони на каждую пиццу.
Затем я пишу 4 x 3 = 12, и это говорит мне о том, что всего 12 пепперони.
Математические карточки
Многие родители используют «карточки для запоминания» как способ поощрения изучения математических фактов. К ним обычно относятся 2 бесполезные практики — заучивание без понимания и цейтнот. В нашем задании «Математические карточки» мы использовали структуру карточек, которая нравится детям, но мы сместили акцент на смысл чисел и понимание умножения. Цель игры — сопоставить карточки с одним и тем же числовым ответом, показанным в разных изображениях. Положите все карточки на стол и попросите детей брать их по очереди; выберите столько, сколько они найдут с тем же ответом (показанным через любое представление). Например 9и 4 можно показать с моделью области, наборами объектов, таких как домино, и числовым предложением. Когда учащиеся сопоставляют карточки, они должны объяснить, откуда они знают, что разные карточки эквивалентны. Эта деятельность поощряет понимание умножения, а также повторение математических фактов.
Полный комплект карт приведен в Приложении А.
Заключение: знание — сила
Упражнения, приведенные выше, являются иллюстрациями игр и заданий, в которых учащиеся изучают математические факты одновременно с работой над тем, что им нравится, а не над тем, чего они боятся. Различные упражнения также сосредоточены на понимании сложения и умножения, а не на слепом запоминании, и это очень важно. В Приложении A представлены другие предлагаемые виды деятельности и ссылки.
Как преподаватели, мы все разделяем цель поощрения способных учащихся в математике, которые тщательно обдумывают математику, а также бегло используют числа. Но учителя и составители учебных программ часто не имеют доступа к важным исследованиям, и это означает, что непродуктивные и контрпродуктивные методы работы в классе продолжаются. Эта короткая статья иллюстрирует ущерб, причиняемый практиками, которые часто сопровождают преподавание математических фактов — давление скорости, тестирование на время и слепое запоминание, — а также обобщает результаты исследований чего-то совсем другого — чувства чисел.
Успевающие учащиеся используют чувство числа, и очень важно, чтобы учащиеся с более низкими достижениями вместо того, чтобы работать над упражнениями и запоминанием, также научились использовать числа гибко и концептуально. Запоминание и проверка на время мешают восприятию чисел, создавая у учащихся впечатление, что осмысление не имеет значения. Нам необходимо срочно переориентировать наше преподавание первых чисел и их смысла в нашем преподавании математики в Великобритании и США. Если мы этого не сделаем, то показатели отказов и отсева – уже достигшие рекордно высокого уровня в обеих странах (National Numeracy, 2014; Silva & White, 2013) – возрастут. Когда мы придаем особое значение запоминанию и тестированию во имя беглости, мы наносим вред детям, мы рискуем будущим нашего вечно количественного общества и угрожаем дисциплине математики. У нас есть исследовательские знания, необходимые для того, чтобы изменить это и дать возможность всем детям хорошо учиться математике. Теперь пришло время использовать его.
Ссылки
Бейлок, С. (2011). Дроссель: что раскрывают секреты мозга о том, как сделать все правильно, когда вам нужно . Нью-Йорк: Свободная пресса.
Боалер, Дж. (2015). При чем здесь математика? Как учителя и родители могут помочь преобразовать обучение математике и вдохновить на успех. Нью-Йорк: Пингвин.
Боалер, Дж. (2014). Исследования показывают, что тесты на время вызывают математическую тревогу. Обучение детей математике, 20 (8).
Боалер, Дж. (2013, 12 ноября 2013 г.). Стереотипы, которые искажают то, как американцы преподают и изучают математику. Атлантический океан.
Боалер, Дж. и Зойдо, П. (в печати). Влияние стратегий обучения математике на достижения: тщательный анализ данных Пизы.
Делазер М., Ишебек А., Домахс Ф., Замарян Л., Коппельштеттер Ф., Сидентопф С.М. Кауфманн; Бенке, Т., и Фелбер, С. (2005). Обучение с помощью стратегий и обучение с помощью упражнений — данные исследования фМРТ. НейроИзображение. 839-849
Задействовать Нью-Йорк.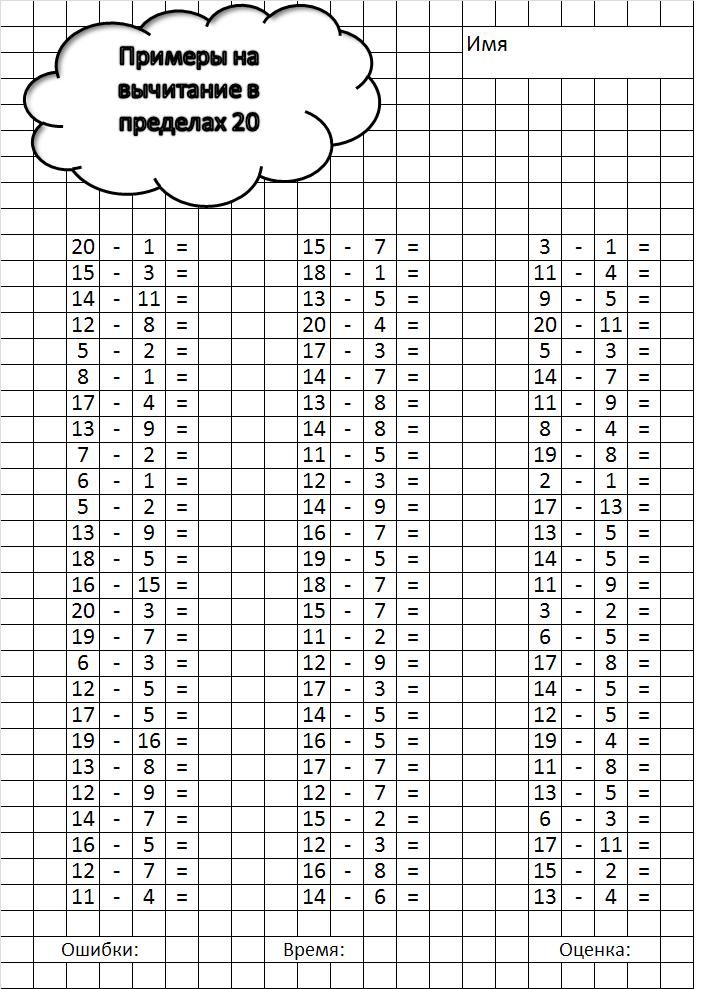
https://schools.nyc.gov/NR/rdonlyres/9375E046-3913-4AF5-9FE3-D21BAE8FEE8D/0/CommonCoreInstructionShifts_Mathematics.pdf
Фейкес, Д. и Швингендорф, К. (2008). Важность сжатия в обучении детей математике и обучении учителей преподаванию математики. Средиземноморский журнал исследований в области математического образования 7 (2).
Фоснот, К., Т. и Долк, М. (2001). Молодые математики за работой: построение умножения и деления. Хайнеманн:
Гарнер, Р. (3 октября 2014 г.). Независимый. (ссылка на статью)
Грей, Э., и Талл, Д. (1994). Двойственность, двусмысленность и гибкость: «процептуальный» взгляд на простую арифметику. Журнал исследований в области математического образования, 25 (2), 116–140.
Хамфрис, Кэти и Паркер, Рут (в печати). Как сделать разговор о числах важным: развитие математических навыков и углубление понимания, 4–10 классы. Портленд, Мэн: Стенхаус.
LA Times (1990) https://articles.latimes.com/1990-05-10/news/mn-1461_1_math-error
Приход, С.
(2014). Разговоры о числах: помощь детям в построении умственной математики и вычислительных стратегий, классы K-5, дополнены общими основными связями. Математические решения.
Парк, Дж. и Браннон, Э. (2013). Обучение приблизительной системе счисления улучшает математические навыки. Ассоциация психологических наук, 1-7
Рамирес Г., Гундерсон Э., Левин С. и Бейлок С. (2013). Математическая тревога, рабочая память и математические достижения в начальной школе. Журнал познания и развития. 14 (2): 187–202.
Супекар, К.; Свигарт А., Тенисон К., Джоллес Д., Розенберг-Ли М., Фукс Л. и Менон В. (2013). Нейронные предикторы индивидуальных различий в реакции на репетиторство по математике у младших школьников. ПНАС, 110, 20 (8230-8235)
Шварц, Л. (2001). Математик, борющийся со своим веком. Биркхойзер
Сильва, Э., и Уайт, Т. (2013). Пути к совершенствованию: использование психологических стратегий, чтобы помочь студентам колледжа освоить развивающую математику: Фонд Карнеги для развития преподавания.
Национальная нумерация (2014). https://www.nationalnumeracy.org.uk/what-the-research-says/index.html
8 забавных математических игр на сложение и вычитание в пределах 20
Примечание редактора:
Это обновленная версия сообщения в блоге, опубликованного 8 января 2020 г.
Легко освойте новый термин с восемью веселыми, но сложными математическими играми, в которых основное внимание уделяется сложению и вычитанию в пределах 20.
At Математика — без проблем! мы любим играть в игры… эм, я имею в виду, что мы очень серьезно относимся к математике.
На самом деле, мы делаем и то, и другое. Математические игры способствуют эффективному обучению и являются отличным способом улучшить беглость речи.
Итак, чтобы начать новый учебный год, вот восемь игр, которые помогут учащимся освоить сложение и вычитание в пределах 20, выработать умственные стратегии для сложения и вычитания и закрепить концепцию числовых связей.
Если вы используете Математика — Нет проблем! , вы можете играть в эти игры вместе с Учебником 1A, Главой 7 или в течение года, чтобы вернуться к теме.
Предложите учащимся найти все числовые связи для числа 20 с помощью этих игр
Если учащиеся знают свои числовые связи для числа 20, они могут использовать факты вычитания, чтобы найти «число, которое составляет 20». Если учащиеся не уверены в своих числовых связях, может быть полезно вспомнить некоторые из числовых связей для числа 20, прежде чем начинать эти игры.
Игра №1: Пары памяти
Вам потребуются: карточки с числами от 1 до 19 и дополнительные 10. Вы также можете играть с двадцатью рамками, чтобы учащиеся могли рассчитывать, что их пара составит 20.
Учащиеся могут играйте парами или тройками.
Как играть
- Перетасуйте карты и разложите их лицевой стороной вниз в четыре ряда на столе. Если учащиеся испытывают затруднения с запоминанием части игры, положите карты 1–10 лицевой стороной вверх.
- Переверните одну карточку и скажите, какая карточка им нужна, чтобы сделать 20. Важно, чтобы учащиеся сделали этот шаг, чтобы подумать о том, какая карточка им нужна. Остальная часть группы должна проверить, что игрок ищет правильную карту.
- Затем переверните еще одну карту.
- Если карточек 20, то соберите карточки.
- Если карты не составляют 20, переверните обе карты.
- По очереди повторяйте шаги 2–5.
- Побеждает игрок, собравший наибольшее количество карт.
Игра №2: Собери карты
Вам понадобятся: жетоны, числовая дорожка от 11 до 19 и девятигранный кубик.
Учащиеся могут играть парами.
Как играть
- Дайте номер трека каждому игроку.
- Бросьте кости и решите, какое число прибавится к счету, чтобы получить 20.
- Поместите жетон на карту, которая дает 20.
- По очереди повторите шаги 2–3.
- Продолжайте играть до тех пор, пока у одного из игроков не будет фишек на каждой карте.
С помощью этой игры учащиеся освоят числовые связи от 10 до 20.
Если учащиеся знают свои числовые связи до 20, они могут использовать факты вычитания, чтобы найти число, которое составляет «цель». Имейте под рукой десять рамок и фишек, если учащимся понадобится дополнительная поддержка.
Игра №3: Кто быстрее?
Вам понадобятся: карты с числами от 10 до 20 и девятигранный кубик.
Учащиеся могут играть парами или тройками.
Как играть
- Положите на стол лицевой стороной вниз карточки с числами.
- Переверните карточку с номером. Это целевой номер.
- Бросьте кости.
- Какое число нужно добавить к очкам на костях, чтобы получить целевое число?
- Игрок, первым назвавший ответ, получает карточку.
- Побеждает игрок с наибольшим количеством карт.
С этими играми учащиеся тренируются в сложении в пределах 20
Учащиеся могут складывать, считая, составляя 10 или складывая единицы.
Имейте под рукой десять рамок и фишек, если учащимся понадобится дополнительная поддержка.
Игра №4: Бросьте кости
Вам понадобятся: жетоны, девятигранный кубик, шестигранный кубик, дорожка чисел 10–15.
Учащиеся могут играть парами или тройками.
Как играть
- Бросьте два кубика.
- Сложите числа.
- Найдите число на числовой дорожке. Поместите счетчик на число. Вы теряете ход, если число меньше 10.
- По очереди повторяйте шаги 1–3.
- Побеждает тот, кто первым закроет все числа.
Игра №5: Кто быстрее?
Вам понадобятся: карточки с номерами 1–5 и 11–15.
Учащиеся могут играть парами.
Как играть
- Положите карты 1–5 и 11–15 лицом вниз на стол.
- Переверните две карты.
- Сколько всего?
- Игрок, первым давший правильный ответ, оставляет себе карты.
- Побеждает игрок с наибольшим количеством карт.
Игра №6: Дополнение к настольной игре
Вам понадобятся: шестигранный кубик и жетоны.
Учащиеся могут играть парами.
Как играть
- Выберите фишку и поставьте ее на 1.
- По очереди бросайте кости, чтобы получить число.
- Добавить, считая от того, где находится счетчик.
- Побеждает тот, кто первым доберется до дома.
Эти игры помогут учащимся попрактиковаться в вычитании в пределах 20.
Учащиеся могут выполнять вычитание, считая в обратном порядке, вычитая единицы или вычитая из 10. Имейте под рукой десять рамок и счетчиков, если учащиеся нуждаются в дополнительной поддержке.
Игра №7: Кто быстрее?
Вам понадобятся: карточки с цифрами 1–9 и 1–20.
Учащиеся могут играть парами.
Как играть
- Разместите 1–20 и 1–9карты лицом вниз на стол.
- Переверните две карты. Вычесть меньшее число из большего числа.
- Игрок, первым давший правильный ответ, оставляет себе карты.
- Побеждает игрок с наибольшим количеством карт.
Игра №8: Настольная игра «Вычитание»
Вам понадобятся: шестигранный кубик и жетоны.
Учащиеся могут играть парами.
Как играть
- Выберите фишку и поставьте ее на 20.
- По очереди бросайте кости, чтобы получить число.
- Вычитание путем обратного отсчета от того места, где стоит счетчик.
- Побеждает тот, кто первым доберется до дома.
Преподавание темы с помощью математических игр — это увлекательный способ дать учащимся возможность изучить то, что они узнали. Но зачем останавливаться на достигнутом?
По прошествии года, когда вы преподаете новые темы, детские воспоминания о предыдущем обучении могут немного смутиться. Вот почему так важно возвращаться к темам в течение года. Игры — отличный способ вернуться к предыдущему обучению, улучшить беглость речи и в то же время немного развлечься.