Урок 4. Изучение чисел
Любое обучение счету и числам всегда должно начинаться с усвоения элементарных количественных понятий, таких как «много», «мало», «больше», «меньше», «поровну» и т.п. И дети легко уясняют их еще в ясельном возрасте. Ваша основная родительская задача – просто помочь им в этом. Формировать же навыки количественного сравнения можно в процессе каждодневной жизни. Так, вместе с малышом можно сравнивать количество конфет или бутербродов, квартир на площадках и ступенек на лесенках, косичек и бантиков у девчушек и т.д. Однако приниматься сразу за большие группы предметов не нужно, ведь все должно начинаться с малого.
После освоения количественных понятий наступает пора знакомства малыша с миром чисел. Как вам уже известно, происходить это должно в интересной и увлекательной для ребенка форме, для чего и следует применять методы, рассмотренные нами в первых уроках.
Рассказывать крохе о числах нужно, не спеша и не стремясь «загрузить» в дитя как можно больше информации.
Когда знакомство с миром чисел будет завершено, можно приступать к разбору состава числа и решению простых задач.
Содержание:
- Как познакомить ребенка с составом числа
- Дополнительные рекомендации и советы
Как познакомить ребенка с составом числа
Как известно, все числа, помимо единицы, можно раскладывать на другие числа. Например, двойку можно разложить на две единицы, тройку – не единицу и двойку и т.д. Под этим и следует понимать состав числа, и объяснять его нужно в тот момент, когда ребенок освоил счет по порядку.
Дело в том, что разбирая числа на составляющие, малыш будет сразу же осваивать навык решения простых примеров.
Когда учите складывать своего малютку, следите, чтобы он не складывал разнородные объекты.
Помимо прочего, научить ребенка составу числа можно и при помощи специальных методов. Об одном из них мы расскажем ниже.
Для реализации метода вам нужно подготовить:
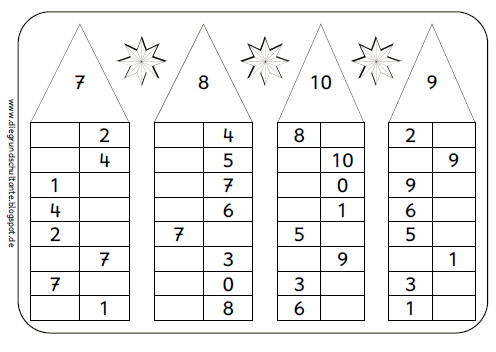
- Карточки на состав числа*
- Большое количество кубиков, шариков или других одинаковых объектов
- Шашки разного цвета (могут подойти и одинаковые разноцветные пуговицы)
*Пример карточки на состав числа
Как только дидактический материал будет готов, можно начинать занятия. Алгоритм таков:
- Для первого занятия подготовьте подобранные ранее объекты счета. Размер и внешний вид не имеют никакого значения. Главное, чтобы объекты относились к одной категории. Начинать занятие нужно с числа «2».
 Попросите своего малыша положить на стол один предмет, а затем поинтересуйтесь, что нужно, чтобы объектов стало два. Если ребенок затрудняется с ответом, обязательно делайте подсказки. Также спрашивайте, из каких чисел можно собрать число «2». Сопровождайте процесс наводящими вопросами.
Попросите своего малыша положить на стол один предмет, а затем поинтересуйтесь, что нужно, чтобы объектов стало два. Если ребенок затрудняется с ответом, обязательно делайте подсказки. Также спрашивайте, из каких чисел можно собрать число «2». Сопровождайте процесс наводящими вопросами. - Возьмите другие объекты и повторите задание с ними. Юный счетовод должен уяснить, что число «2» всегда будет состоять из двух единиц, независимо от того, какими он манипулирует объектами.
- Когда станет понятно, что число «2» освоено, незамедлительно начинайте работать с числом «3». Состав этого числа может быть представлен уже тремя вариантами: «1 + 1 +1», «1 + 2» и «2 + 1». Раскладывайте перед крохой объекты в самых разных вариациях, но с одной особенностью: если рассматриваете вариант сложения трех единиц, путь каждый предмет лежит на одинаковом расстоянии друг от друга; если рассматриваете вариант сложения единицы и двойки, то два предмета должны лежать рядом, а один – на расстоянии от них.
 Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам.
Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам. - Занятия с шашками выполняются параллельно занятиям с игрушками, либо отдельно от них. Задача проста: попросите ребенка положить перед собой (или на доску для шашек) четыре одинаковых шашки. Потом спросите, сколько будет шашек, если сложить две черных и две белых? Смысл в том, чтобы показать, что одно и то же число может быть представлено несколькими вариантами (в данном случае – независимо от цвета).
- Перед работой с карточками на состав числа их нужно приобрести или изготовить самостоятельно. Такие карточки бывают разных модификаций, и будет хорошо, если у вас тоже будет два варианта. Первый комплект состоит из разрезанных на две половинки карточек. На одной половинке изображается один объект, а на другой – 1, 2, 3 – 9 аналогичных объектов (кстати, половинки могут соединяться знаком «+», но полезно иметь и отдельный знак «+», а также отдельный знак «-»).
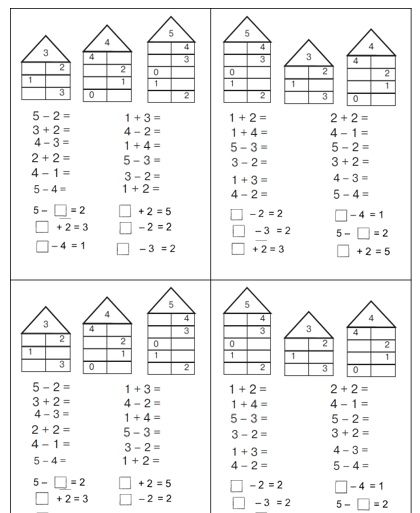
 Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами.
Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами. - Продемонстрируйте малышу карточку, например, с пятью объектами. Попросите подобрать остальные изображения так, чтобы они составляли число пять. Здесь еще удобно меняться ролями, т.е. время от времени просите ребенка давать задания и вам, а вы не ленитесь их выполнять, причем иногда стоит специально ошибаться, чтобы малыш контролировал ваши действия и указывал на то, что вы делаете неправильно.
- Точно такое же задание можно выполнять с использованием карточек с цифрами. К примеру, вы можете показать ребенку карточку с цифрой «7», а он пусть сложит остальные карточки так, чтобы в разных вариантах получить это же число. Впоследствии переходите к более сложным числам (более десяти), объясняя малышу, что чем больше число, тем больше есть вариантов его составления.

Проводить занятия нужно систематически, но не стоит сильно усердствовать. Дважды в день по 20-25 минут будет более чем достаточно. Уже через 1,5-2 месяца таких занятий ваше чадо в достаточной мере освоит состав числа и научится выполнять основные математические операции. Но чтобы повысить шансы на успех, в дополнение к предложенному методу вы можете использовать и составленные нами рекомендации.
Дополнительные рекомендации и советы
Знакомя ребенка с составом числа (и обучая счету вообще), старайтесь обращать как можно больше внимания на поведение своего чада. Наиболее частыми явлениями во время занятий являются отвлекаемость и невнимательность. Практически всегда это свидетельствует о том, что малыш потерял интерес к процессу и новая информация им уже не воспринимается.
Чтобы исправить положение дел, совсем необязательно прекращать домашний урок. Иногда бывает полезно просто повторить то, что уже было изучено. Вспомнив знакомый материал, выполнив несколько заданий и убедившись, что у него все получается, ребенок снова заинтересуется и будет готов к усвоению новых знаний.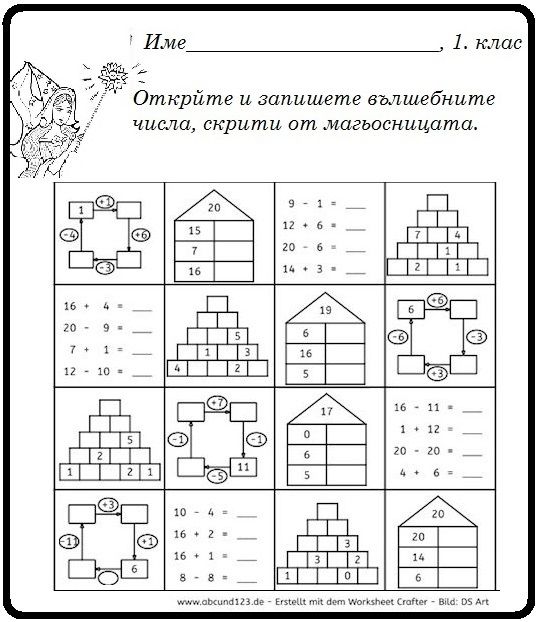
Не гонитесь за результатом – обучайте свое чадо в умеренном темпе и давайте информацию постепенно. Вопреки ошибочному мнению, это вовсе не тормозит развитие маленького ученика, ведь небольшой объем знаний закрепляется прочнее, а это значит, что и переход к новым темам не за горами.
Арифметические задачи становятся для дошколят гораздо интереснее, если использовать в них игрушки, игры, монетки, разноцветные счетные палочки. Сначала считайте их сами, произнося цифры вслух, а затем просите ребенка повторить за вами.
Будет просто супер, если вы сделаете упражнения как можно более зрелищными. Можно выстраивать дорожки из монеток, делать городки и пирамидки из кубиков, разнообразными способами раскладывать карточки и картинки. Добавляя и убирая объекты, вы будете учить свое дитя прямому и обратному счету, сложению и вычитанию, соотнесению чисел и количества. Приобретя такие навыки еще в дошкольном возрасте, а также разобравшись с составом числа, ребенок будет намного легче справляться со школьными заданиями по математике и быстро выучит таблицу умножения (о том, как сделать это еще до школы, мы с вами тоже поговорим в одном из уроков).
Регулярные занятия прекрасно развивают логическое, пространственное, предметное и абстрактно-образное мышление, благодаря чему уже в 3-4 года маленький ученик сможет показывать хорошие результаты.
Тема освоения состава числа и простейших чисел, как вы заметили, совсем небольшая и несложная. Несколько труднее научить ребенка считать до 20 и до 100. В шестом уроке мы познакомим вас с эффективными принципами обучения детей счету и предложим несколько действенных методик, позволяющих научить детей считать до 10, до 20 и до 100, а также производить вычисления столбиком.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.
Cтатистика На весь экран
Кирилл
← 3 Подготовка к счету5 Принципы обучения счету →
Урок математики в 1-м классе. Число 10
Учебные цели, которые будут достигнуты на этом уроке (ссылка на учебную программу) | **Понимать образование натуральных чисел, определять место числа в натуральном ряду чисел. 1.1.1.3 **Определять состав однозначных чисел. | |||||||||||||||||
Цель урока | Все ученики: смогут образовать число 10, определять его место в натуральном ряду чисел; составлять последовательность однозначных чисел. Многие ученики: смогут составлять число 10, используя однозначные числа; соотносить число 10 с предметами окружающего мира. Некоторые ученики: смогут самостоятельно записать состав числа 10 без опоры на образец. | |||||||||||||||||
Языковые цели | Применять математическую терминологию «число», «цифра», | |||||||||||||||||
Прививать ценности | Уважение к сверстникам; сотрудничество; труд и творчество | |||||||||||||||||
Межпредметная связь | В рамках сквозной темы «Моя семья и друзья», «Мир вокруг нас» осуществляется межпредметная связь с предметом познание мира. | |||||||||||||||||
Навыки пользования ИКТ |
| |||||||||||||||||
Начальные знания | Знают цифры и числа в пределах 10, их расположение на числовом луче. | |||||||||||||||||
Ход урока | ||||||||||||||||||
Запланированные этапы урока | Виды запланированных упражнений урока | Метод оценивания |
| |||||||||||||||
Начало урока | Стартер: «Составим математический поезд» | Выявление базовых знаний об образовании последующего числа. |
| |||||||||||||||
«Вопрос-ответ» |
|
| ||||||||||||||||
Самооценка: выявление начального уровня знаний о числе 10. -Отложите шкалу, вернемся к ней в конце урока. | И.Р. направленная на рефлексию «Шкала знаний» |
| ||||||||||||||||
Середина урока | (К) Составление числового ряда из карточек-цифр на доске. (П) «Сравни и расскажи». | Актуализация знаний. |
| |||||||||||||||
Детям, которые испытывают затруднения, предложить критерии: Учитель даёт понятия «однозначные числа» и «двузначные числа». | Вопросы учителя: |
| ||||||||||||||||
(К) «Назови 10…» | Выявление уровня функциональной грамотности. |
| ||||||||||||||||
(П) Работа в паре Пример карточки: | После завершения работы выяснить, у кого из учеников оценка «Д», у кого «С». |
| ||||||||||||||||
(К) Проигрывание ситуации «Разложи число 10» | Наблюдение учителя. Вопросы учителя: |
| ||||||||||||||||
(И) «Составь число 10». Взаимообучение | «Говорящая стена» |
| ||||||||||||||||
Конец урока | Рефлексия учеников в конце урока:
| Обратная связь учителя по листам самооценивания знаний. |
| |||||||||||||||
Дифференциация – как планируете оказать большую поддержку ученикам? | Оценивание – как планируете оценить уровень освоения материалов учениками? | Соблюдение техники безопасности и здоровья | ||||||||||||||||
Дифференциация цели обучения. | Самооценка «Шкала знаний». | Технологии здравоохранения.
| ||||||||||||||||
Карточки и счетчики в математике Монтессори — Удивительный мир Монтессори
Что такое карточки и счетчики?
Карточки и жетоны — увлекательное занятие в области математики в классе Монтессори. Карточки хранятся в деревянном ящике, который содержит набор чисел от 1 до 10 на маленьких деревянных досках. Также есть 55 красных круглых жетонов, которые хранятся в отдельном отсеке в коробке.
Как карты и жетоны представлены в Монтессори
Карточки и счетчики — это занятие по ранней математике Монтессори, которое знакомит ребенка с нечетными и четными числами, а также побуждает ребенка практиковаться в счете.
Директор показывает ребенку, как аккуратно двумя руками нести коробку на коврик. Оказавшись на коврике, она открывает крышку коробки и распаковывает числа на коврик. Затем она просит ребенка найти «номер один» и поместить его в верхнюю левую часть коврика. Затем она спрашивает его, какое число идет после единицы, ребенок говорит «два» и ставит его рядом с числом один. Ребенок продолжает таким же образом, пока все числа от одного до десяти не будут размещены на верхней части коврика.
Сопоставление числовой карточки с правильным количеством жетонов
Воспитатель говорит ребенку, что он будет смотреть на число, а затем отсчитывать правильное количество жетонов, чтобы совпасть с числом. Она указывает на цифру «1» и говорит «один»; Затем она берет одну фишку правой рукой, кладет ее в левую руку и кладет под число 1.
Нечетные и четные числа в
Карты и жетоныОна повторяет то же самое с остальными фишками, обычно до «номер 4». Затем директор размещает их под соответствующими номерами в верхней части коврика. Для четных чисел счетчики помещаются в два столбца под номером, а для нечетных чисел оставшийся счетчик помещается в центр двух нижних столбцов.
Проверка нечетных и четных чисел
После того, как ребенок пересчитал жетоны и разместил их под правильным числом, директор говорит ему, что теперь они будут проверять, какие числа «четные», а какие «нечетные».
Она показывает ребенку, как чувствовать числа, проводя указательным пальцем правой руки по центру двух столбцов. Она показывает ему, что если это четное число, ее палец мягко скользит вниз, но если это нечетное число, ее палец натыкается на дополнительный счетчик в центре двух нижних столбцов. Она продолжает проводить пальцем вниз, чтобы увидеть, какие числа нечетные, а какие четные, повторяя слова «нечетные» для нечетных чисел и «четные» для четных чисел.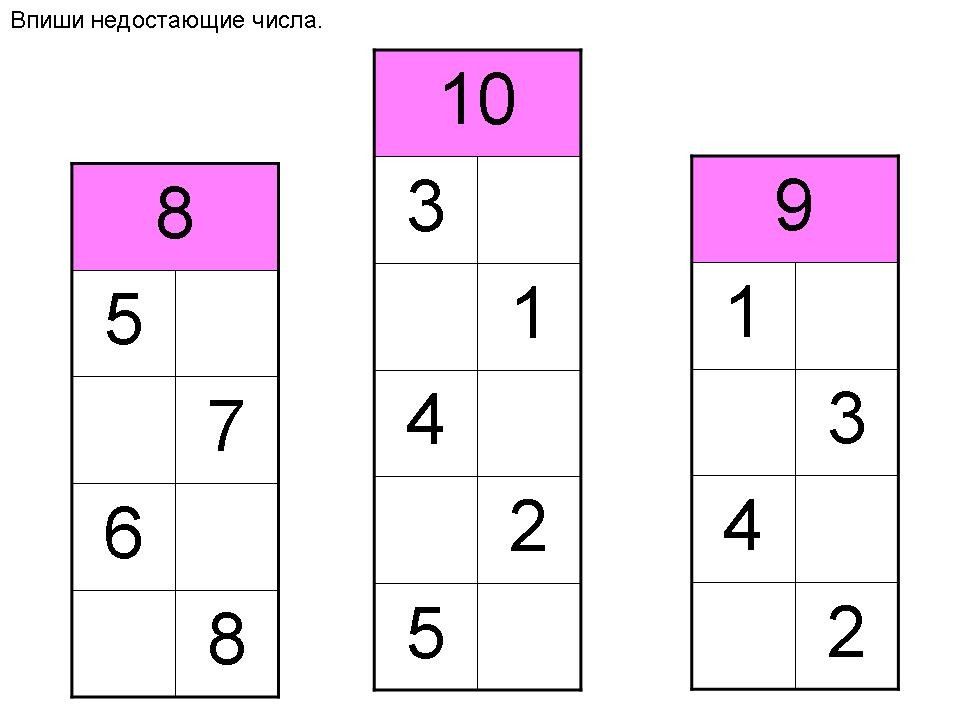
Директор может попросить ребенка показать ей несколько четных и нечетных чисел, как только задание будет выполнено. Затем ребенка попросят упаковать работу.
Чему учится ребенок, работая с карточками и фишками
?Ребенок сможет различать нечетные и четные числа. Эта деятельность помогает ребенку связать реальную величину с числовым символом. Это также развивает слуховое восприятие ребенка, а также дает ребенку дополнительную практику работы с произвольным количеством и произвольными числами.
Хотите узнать больше о занятиях Монтессори?
Вот список всех занятий по математике Монтессори, включая раннюю математику, введение в десятичную систему, доску сегин, доску сотен, короткую лестницу из бисера, цепочки из бисера, игру в змейку, групповые операции, палочки с большими числами, запись. с маленькими числовыми стержнями, короткой лестницей из бусинок, полосовыми досками, досками, игрой в штампы, счетами, игрой в точки и дробями. Просто нажмите на страницу, о которой вы хотите узнать, чтобы перейти на нее.
Ранняя математика
Большое число стержней
Номера наждачных бумаг
Box
Номерные стержни и карты (презентация One)
4050 -й стержни и карты.
Знакомство с десятичной системой счисления
Лоток для презентаций
Карточки с большими числами
Упражнение на переход между лотком для презентаций и карточками с большими числами
Подсчет с Golden Beads
Bring Me Game с Golden Beads
Счет с большими номерами карты
Grout Me с большими карточками
7
. Вид
Банковская игра
Игра «Изменение»
Короткая лестница-бусинка
Короткая лестница-бусинка: упражнение на ориентацию
Доски Seguin
Seguin Board A: Количество обучения
Seguin Board A: Символы обучения
Seguin Board A: Bridging
CEGUIN BOARD B: СОВЕТА
7CEGUIN BOARD BSGUIN BSGUIN BSTURING
7- 9004 CEGUIN BOARD BSGUIN A: Bridging 7
- 9004 CEGUIN BOARD.
 Доска Seguin B: обучающие символы
Доска Seguin B: обучающие символы Доска Seguin B: упражнения для наведения мостов
Доска Seguin B: ассоциация от 11 до 99
Доска сотни
The Stody Board
Чепии бусинок
Цепи бусинок Введение: Укладка и кубики
. номер
Игра в змейку
Игра в змейку: узы десяти
Игра в змейку: переодевание с помощью черно-белой лестницы
Групповые операции
Групповые операции: статическое сложение (без изменения)
Групповые операции: динамическое сложение (с изменением)
Групповые операции: статическое умножение (без изменения)
Группы динамические:
умножение (с изменением)
Групповые операции: Статическое вычитание (без изменения)
Групповые операции: Динамическое вычитание (с изменением)
Групповые операции: Статическое подразделение (без изменения)
Групповые операции: Динамическое разделение (с изменением)
Большое число стержней
Стержни большого числа: Составление (вторая презентация)
Стержни большого числа: Разложение
Запись с помощью стержней с малым числом
Запись с помощью стержней с малым числом
Короткая лестница с короткими бусинками
Дополнение с короткой лестницей.
 Дополнительная полоса (презентация)
Дополнительная полоса (презентация)Дополнительная полоса (вторая)
Вычитающая полоса (презентация)
Плата вычитания (презентация вторая)
Доски
Доска для умножения
. Игра в штампы: формирование числа
Игра в штампы: статическое сложение (без изменения)
Игра в штампы: динамическое сложение (с изменением)
Игра в штампы: статическое умножение (без изменения)
Игра в штампы: динамическое умножение (с изменением)
Игра в штампы: статическое вычитание (без изменения)
9000: Динамическое вычитание (с изменением)
Игра в штампы: Статическое деление (без изменения)
Игра в штампы: Динамическое деление (с изменением)
Счеты
Абакус: мостовое упражнение
Абакус: подсчет на Abacus
Abacus: Формирование числа
The Abacus: подсчет и регистрируя
9007The Abacus: подсчет и регистрируя
- .
 Статическое сложение (без изменений)
Статическое сложение (без изменений) Операции со счетами: Статическое умножение (без изменений)
Операции со счетами: Статическое вычитание (без изменений)
Игра в точки
Игра в точки: статическое сложение (без изменения)
Игра в точки: динамическое сложение (с изменением)
умножение (статическое сложение)
Игра в точки: динамическое умножение (с изменением)
Игра в точки: статическое вычитание (без изменений)
Игра в точки: динамическое вычитание (с изменением)
Фракции
Фракции (презентация ONE)
Фракции (Презентация два)
Фракции (Презентация Три)
Фракции (Презентация четыре)
67Фракции (Презентация четыре)
67Фракции (Презентация четыре)
67(Презентация четыре)
67.
 Интерактивные вопросы| Решенные примеры
Интерактивные вопросы| Решенные примерыМасти, представленные красными карточками, — это черви и бубны, а масти, представленные черными картами, — это пики и трефы.
Масти в колоде карт — это изображения красного и черного цветов на картах.
На этих картах есть числа, а каждая масть равна номеру на числовых картах.
Советы и подсказки
- В каждой масти по 13 карт, включая 1 туз, 3 карты с картинками и 9 карт с числами.
- В колоде из 52 карт 4 туза, 12 лицевых карт и 36 карт с числами.
- Вероятность вытягивания любой карты всегда будет находиться в диапазоне от 0 до 1.
- Количество пик, червей, бубен и треф одинаково в каждой колоде из 52 карт.
Теперь, когда вы знаете все факты о колоде карт, вы можете вытащить карту из колоды и легко найти ее вероятность.
Как определить вероятность вытягивания карты?Давайте сначала научимся находить вероятность.

Теперь вы знаете, что вероятность — это отношение количества благоприятных исходов к общему количеству исходов, давайте применим это здесь.
ПримерыПример 1: Какова вероятность того, что из колоды карт вытащите короля?
Решение: Здесь событие E вытягивает короля из колоды карт.
В колоде карт 52 карты.
Следовательно, общее количество исходов = 52
Число благоприятных исходов = 4 (так как в колоде 4 короля)
Следовательно, вероятность наступления этого события равна
P(E) = 4/52 = 1/13
\(\следовательно\) Вероятность вытащить короля из колоды карт равна 1/13. Пример 2: Какова вероятность вытянуть черную карту из колоды карт?
Решение. Здесь событие E – вытягивание черной карты из колоды карт.
Общее количество исходов = 52
Число благоприятных исходов = 26
Отсюда вероятность наступления события
P(E) = 26/52 = 1/2
\(\ следовательно\) Вероятность вытянуть черную карту из колоды карт равна 1/2. 
Решенные примерыПример 1 Джессика вытянула карту из хорошо перетасованной колоды. Помогите ей найти вероятность того, что карта либо красная, либо король.
Решение
Здесь Джессика знает, что событие E – это вытянутая карта, являющаяся либо красной, либо королем.
Общее количество исходов = 52
Есть 26 красных карт и 4 карты короля.
Тем не менее, 2 из красных карт – это короли.
Если мы добавим 26 и 4, мы будем считать эти две карты дважды.
Таким образом, правильное число исходов, благоприятных для E, равно
26 + 4 — 2 = 28
Следовательно, вероятность события равна
P(E) = 28/52 = 7/13
\(\поэтому\) Вероятность того, что карта либо красная, либо карта короля, равна 7/13. 
Пример 2 Помогите Дайане определить вероятность следующего:
- Рисунок Красной Королевы
- Рисование пикового короля
- Розыгрыш карты с красным номером
Решение
Диана знает здесь события E 1 , E 2 и E 3 : Вытягивание красной королевы, Вытягивание пикового короля и Вытягивание карты с красными числами.
Общее количество исходов в каждом случае = 52
- Розыгрыш Красной Королевы
Красных карточек 26, из них 2 дамы.
Следовательно, вероятность события E 1 равна
P(E 1 ) = 2/52 = 1/26
- Вытягивание пикового короля
В каждой масти по 13 карт, из которых 1 король.
Следовательно, вероятность наступления события E 2 равна
P(E 2 ) = 1/52
- Розыгрыш карты с красным номером
В каждой масти по 9 карточек с числами, и 2 масти красного цвета.

Есть 18 карт с красными номерами.
Следовательно, вероятность события E 3 равна
P(E 3 ) = 18/52 = 9/26
\(\поэтому\) Диана определила, что вероятности E 1 ) = 1/26, P (E 2 ) = 1/52 и P (E 3 ) = 9/26.
Интерактивные вопросыВот несколько упражнений для практики.
Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итогиТеперь вы легко сможете решать задачи на количество карт в колоде, лицевые карты в колоде, колоду из 52 карт, пики, червы, бубны, трефы в колоде карт. Теперь вы можете взять карту из колоды и легко найти ее вероятность.
Мини-урок был посвящен увлекательной концепции вероятности карт.
О Cuemath Математическое путешествие по карточным вероятностям начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, чтобы это было не только понятно и легко для понимания, но и осталось с ними навсегда. В этом заключается магия Cuemath.
Математическое путешествие по карточным вероятностям начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, чтобы это было не только понятно и легко для понимания, но и осталось с ними навсегда. В этом заключается магия Cuemath.В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя изучают тему со всех сторон. Будь то задачи, онлайн-классы, видео или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению.
Часто задаваемые вопросы о вероятности выпадения карты1. Как рассчитать вероятность вытягивания карты?
Находим отношение благоприятных исходов по условию вытягивания карты к общему количеству исходов, т.е. 52.
2.
 Какова вероятность выпадения любой лицевой карты?
Какова вероятность выпадения любой лицевой карты?Вероятность вытянуть любую лицевую карту 6/26.
3. Какова вероятность вытянуть красную карточку?
Вероятность вытянуть красную карточку 1/2.
4. Какова вероятность того, что выпадет король или красная карточка?
Вероятность вытянуть короля или красную карточку 7/13.
5. Какова вероятность того, что выпадет король или ферзь?
Вероятность того, что выпадет король или дама, равна 2/13.
6. Каковы 5 правил вероятности?
5 правил вероятности:
- Правило 1
Для любого события E вероятность наступления E всегда будет находиться в диапазоне от 0 до 1
- Правило 2
Сумма вероятностей каждого возможного исхода всегда будет равна 1
- Правило 3
Сумма вероятности появления Е и вероятности того, что Е не произойдет, всегда будет равна 1
- Правило 4
Когда любые два события не пересекаются, вероятность появления А и В не равна 0, а когда два непересекающихся события, вероятность появления А и В равна 0.

 Попросите своего малыша положить на стол один предмет, а затем поинтересуйтесь, что нужно, чтобы объектов стало два. Если ребенок затрудняется с ответом, обязательно делайте подсказки. Также спрашивайте, из каких чисел можно собрать число «2». Сопровождайте процесс наводящими вопросами.
Попросите своего малыша положить на стол один предмет, а затем поинтересуйтесь, что нужно, чтобы объектов стало два. Если ребенок затрудняется с ответом, обязательно делайте подсказки. Также спрашивайте, из каких чисел можно собрать число «2». Сопровождайте процесс наводящими вопросами. Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам.
Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам. Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами.
Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами.


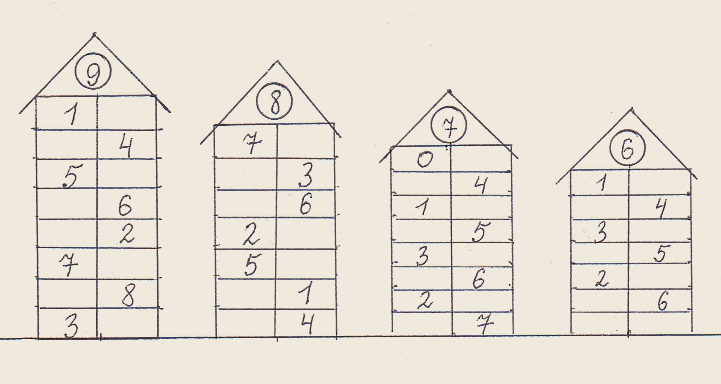

 — Посмотрите на число 10. Сравните его с числами, которые стоят перед числом 10 на числовом луче.
— Посмотрите на число 10. Сравните его с числами, которые стоят перед числом 10 на числовом луче.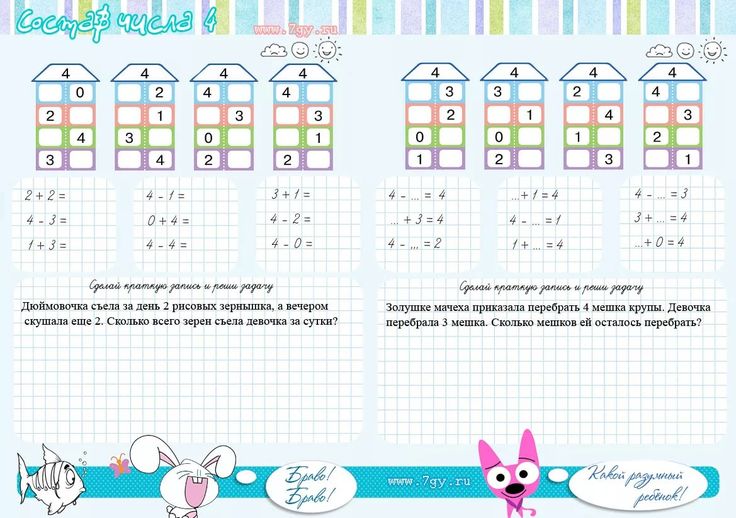
 Дети по указанию учителя движутся по одному или собираются в группы по 3, по 5, по 10.
Дети по указанию учителя движутся по одному или собираются в группы по 3, по 5, по 10. 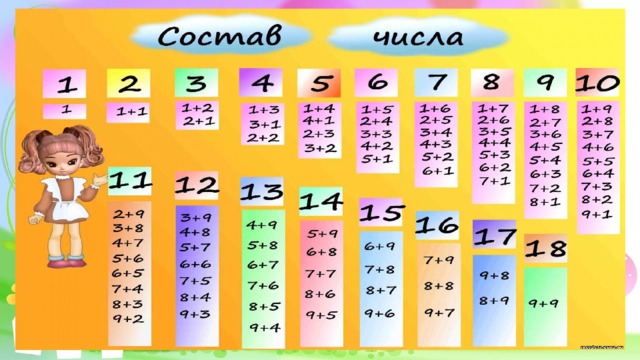
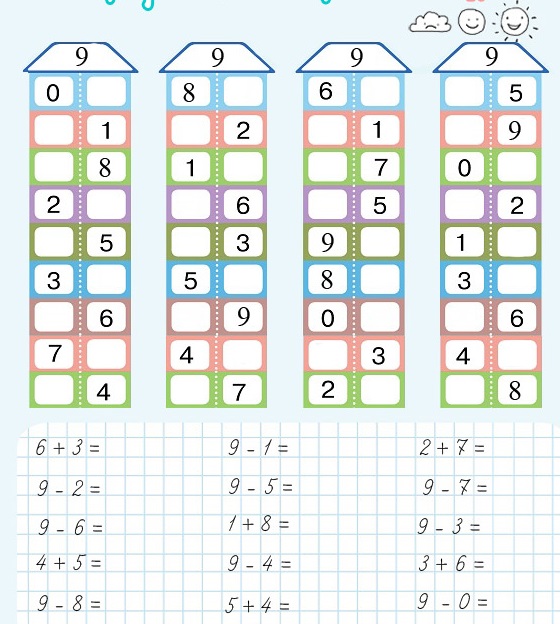
 Доска Seguin B: обучающие символы
Доска Seguin B: обучающие символы Дополнительная полоса (презентация)
Дополнительная полоса (презентация)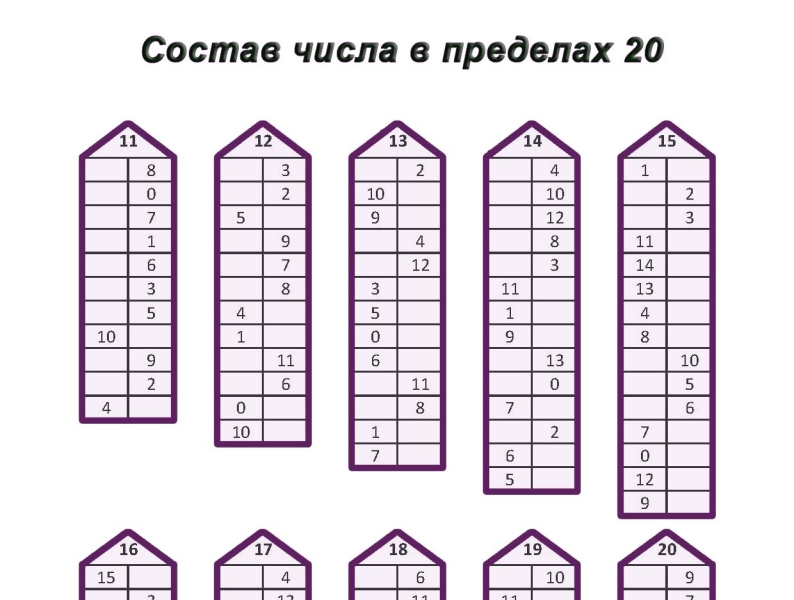 Статическое сложение (без изменений)
Статическое сложение (без изменений) Интерактивные вопросы| Решенные примеры
Интерактивные вопросы| Решенные примеры


 Математическое путешествие по карточным вероятностям начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, чтобы это было не только понятно и легко для понимания, но и осталось с ними навсегда. В этом заключается магия Cuemath.
Математическое путешествие по карточным вероятностям начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, чтобы это было не только понятно и легко для понимания, но и осталось с ними навсегда. В этом заключается магия Cuemath.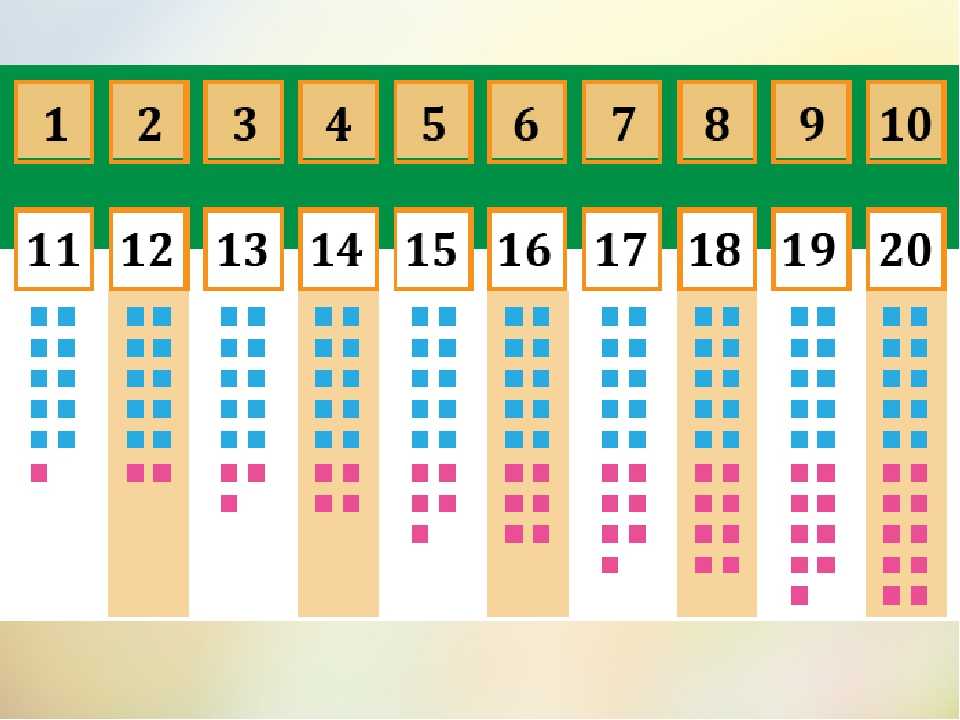 Какова вероятность выпадения любой лицевой карты?
Какова вероятность выпадения любой лицевой карты?