Порядок выполнения действий 5 класс онлайн-подготовка на Ростелеком Лицей
Порядок выполнения действий.
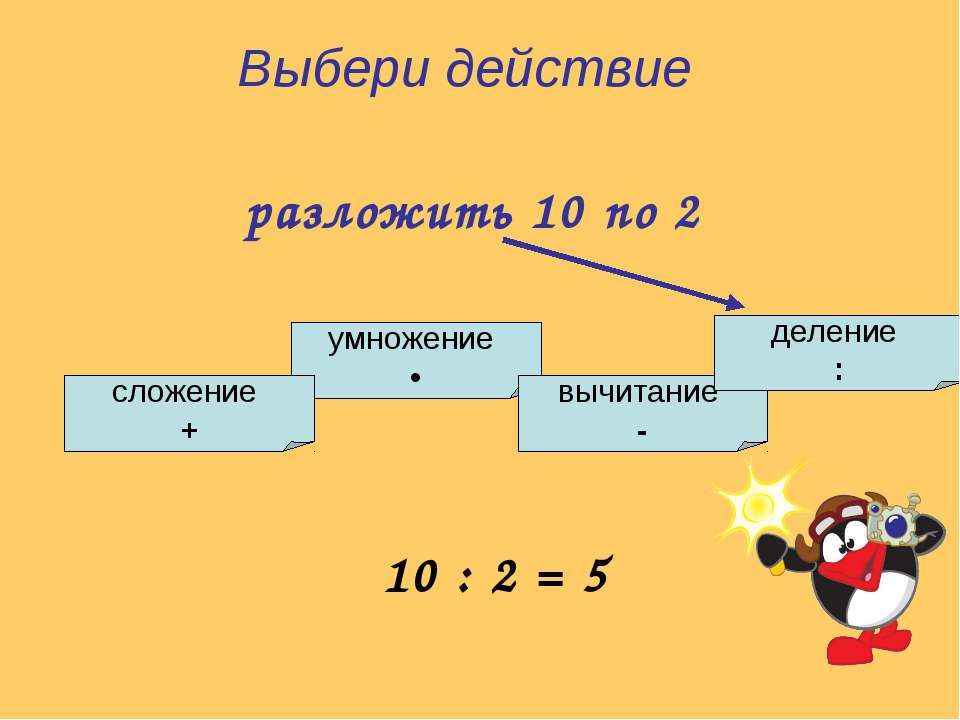
Как ты думаешь, сколько будет «два плюс два умножить на два»?
Давай обсудим полученные результаты. В первом примере получается 8, во втором 6.
(2+2)*2=8;
2+2*2=6.
Поэтому важно поговорить о порядке выполнения действий, и наша цель – закрепить те знания, которые у тебя уже есть и отработать их при решении примеров.
В математике существуют различные арифметические действия: сложение, вычитание, умножение, деление.
Сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.
Порядок выполнения действий:
- Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку, слева направо.
- Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом действия первой ступени.
- Если в выражении есть скобки, то сначала выполняют действия в скобках.
(2+2)*2=8, так как первое действие выполняем в скобке, а потом вычисляем произведение.
2+2*2=6, так как первое действие – произведение, второе действие – сложение.
Пример 1. Найдем значение выражения:
22 + 78 – 56 – 24.
Определим порядок выполнения действий. В выражении отсутствуют скобки, а все
действия первой ступени, значит, будем решать выражение слева направо.
22 + 78 = 100
100 – 56 = 44
44 – 24 = 20
Значит, 22 + 78 – 56 – 24 = 20.
Пример 2. Вычислим:
72 : 8 * 33 : 11 * 2.
Так как в выражении отсутствуют скобки и присутствуют действия только второй ступени, то последовательность выполнения действий будет слева направо.
72 : 8 = 9
9 * 33 = 297
297 : 11 = 27
27 * 2 = 54
Значит, 72 : 8 * 33 : 11 * 2 = 54 .
Пример 3. Вычислим:
25 — 8 * 3 : 2 + 4 * 4.
Последовательность решения определяет наличие действий двух ступеней. Сначала выполним действия второй ступени (умножение и деление) в порядке слева направо:
8 * 3 = 24
24 : 2 = 12
Значит, 8 * 3 : 2 = 12.
4 * 4 = 16
А затем слева направо действия первой ступени:
25 – 12 = 13
13 + 16 = 29
Значит, 25 – 8 * 3 : 2 + 4 * 4 = 29.
Пример 4. Вычислим:
99 : ( 45 – 39 + 5 ) – 25 : 5.
Сначала выполним действия в скобках:
45 – 39 = 6
6 + 5 = 11
Затем действия второй ступени:
99 : 11 = 9
25 : 5 = 5
Затем действия первой ступени:
9 – 5 = 4
Значит, 99 : ( 45 – 39 + 5 ) – 25 : 5 = 4.
Тест Порядок действий (4 класс) по математике
Сложность: новичок.1 человек проходит прямо сейчас.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Какое действие в выражении Вы сделаете первым 110 – (60 + 40) : 10 х 8?
- Правильный ответ
- Неправильный ответ
- Вы и еще 93% ответили правильно
- 93% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопросОтветитьВопрос 2 из 10
Какое действие в выражении 110 – (60 + 40) : 10 х 8 Вы сделаете вторым?
- Правильный ответ
- Неправильный ответ
- Вы и еще 75% ответили правильно
- 75% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
Выберите правильный вариант ответа выражения 110 – (60 + 40) : 10 х 8:
- Правильный ответ
- Неправильный ответ
- Вы и еще 79% ответили правильно
- 79% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
Ответом на выражение 150 : (80 – 60 : 2) х 3 будет:
- Правильный ответ
- Неправильный ответ
- Вы и еще 66% ответили правильно
- 66% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
В каком из выражений последнее действие умножение?
- Правильный ответ
- Неправильный ответ
- Вы и еще 62% ответили правильно
- 62% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
В каком из выражений первое действие вычитание?
- Правильный ответ
- Неправильный ответ
- Вы и еще 81% ответили правильно
- 81% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Выберите верное высказывание: «В выражении без скобок действия выполняются:.
 ..».
..».- Правильный ответ
- Неправильный ответ
- Вы и еще 78% ответили правильно
- 78% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Выберите верное высказывание: «В выражении со скобками действия выполняются:…».
- Правильный ответ
- Неправильный ответ
- Вы и еще 82% ответили правильно
- 82% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
Выберите верный ответ 90 – (50 — 40 : 5) + 30 =
- Правильный ответ
- Неправильный ответ
- Вы и еще 84% ответили правильно
- 84% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Выберите верный ответ 100 — (18 : 3 + 45) =
- Правильный ответ
- Неправильный ответ
- Вы и еще 95% ответили правильно
- 95% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Доска почёта
Чтобы попасть сюда — пройдите тест.
-
Алексей Беляев
10/10
Валерия Усенко
10/10
Полина Кузнецова
10/10
Нелли Непомнящая
9/10
Юлия Слащева
8/10
Мирослав Реутов
9/10
Кристина Шаравьёва
9/10
Юля Шумейкина
10/10
Любовь Латышева
8/10
Тимур Сулякаев
10/10
Рейтинг теста
Средняя оценка: 4. Всего получено оценок: 737.
Всего получено оценок: 737.
А какую оценку получите вы? Чтобы узнать — пройдите тест.
Математика. Составные выражения. Скобки | Сайт Леонида Некина
Главная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Допустим, у Дениса было 5 конфет, мама дала ему еще 3 конфеты, а папа — еще одну конфету. Сколько конфет стало у Дениса? Такая задача решается в два действия.
Первое: 5 + 3 = 8 . Столько конфет стало у Дениса после того, как он получил конфеты от мамы.
Второе: 8 + 1 = 9. Столько конфет стало у Дениса в конечном итоге.
Это же самое решение можно представить в виде одной-единственной строчки. Поскольку « 8 » было получено как « 5 + 3 », то во втором равенстве « 8 » можно заменить на « 5 + 3 »:
До замены: | 8 | + 1 = 9. |
После замены: | ( 5 + 3 ) | + 1 = 9. |
Новую вставку принято заключать в скобки. Таким образом, если в каком-нибудь длинном выражении встречаются скобки, это говорит о том, что в первую очередь следует выполнять действия внутри скобок. В нашем примере порядок выполнения действий таков:
[2] |
| |
( 5 + 3 ) | + | 1 = 8 + 1 = 9. |
На этот раз оказалось, что действия выполняются в самом привычном порядке — слева направо. В этом особом случае скобки можно вообще не писать. Смысл выражения остается тем же самым:
В этом особом случае скобки можно вообще не писать. Смысл выражения остается тем же самым:
[1] | [2] |
|
5 + 3 | + | 1 = 8 + 1 = 9. |
Однако ту же самую задачу можно решить и по-другому.
Первое действие: 3 + 1 = 4 . Столько конфет получил Денис от мамы и папы.
Второе действие: 5 + 4 = 9. Столько конфет оказалось у Дениса.
В одну строку это записывается так:
| [2] | [1] |
|
5 | + | ( 3 + 1 ) | = 5 + 4 = 9. |
Итак, у нас есть два разных решения одной и той же задачи, и им соответствуют два разных выражения, но значения этих выражений одинаковы, поэтому
5 + (3 + 1) = 5 + 3 + 1.
Это равенство показывает, каким образом можно избавиться от скобок, или, выражаясь более грамотно, как можно раскрыть скобки. В данном примере скобки можно просто стереть, а все остальное оставить без изменений. Но так просто дело обстоит далеко не всегда.
Задача 2.2.1. У Дениса было 5 конфет. 3 конфеты он дал маме, и еще одну конфету — папе. Сколько конфет осталось у Дениса? Эту задачу требуется решить двумя способами, причем каждое решение записать в виде одного-единственного выражения.
Решение. Первый способ.
5 − 3 = 2 . Столько конфет осталось у Дениса, после того как он поделился конфетами с мамой.
2 − 1 = 1. Столько конфет осталось у Дениса в конце.
Записываем решение в виде одного выражения:
5 − 3 − 1 = 2 − 1 = 1.
Второй способ.
3 + 1 = 4 . Столько конфет Денис отдал маме и папе.
5 − 4 = 1. Столько конфет осталось у Дениса.
Объединяем решение в одно выражение:
5 − ( 3 + 1 ) = 5 − 4 = 1.
Сравнивая два решения, мы убеждаемся, что
5 − (3 + 1) = 5 − 3 − 1.
На этот раз, для того чтобы раскрыть скобки, недостаточно их просто стереть. Требуется еще и поменять знак «+» на знак «−».
Задача 2.2.2. У Дениса было 7 конфет. Он решил поделиться конфетами с Матвеем. Он протянул Матвею 3 конфеты, однако в последний момент передумал и одну конфету забрал обратно. Сколько конфет стало у Дениса?
Решение. Первый способ.
7 − 3 = 4 . Столько конфет оставалось у Дениса, когда он протянул конфеты Матвею.
4 + 1 = 5. Столько конфет стало у Дениса в конечном итоге.
Единое выражение:
7 − 3 + 1 = 4 + 1 = 5.
Второй способ.
3 − 1 = 2 . Столько конфет досталось Матвею.
7 − 2 = 5. Столько конфет стало у Дениса.
Единое выражение:
7 − ( 3 − 1 ) = 7 − 2 = 3.
Сравнивая два решения, получаем:
7 − (3 − 1) = 7 − 3 + 1.
И на этот раз одного только стирания скобок недостаточно. Нужно еще поменять тот знак «−», который стоял в скобках, на знак «+».
Задача 2.2.3. У Дениса было 5 конфет. Мама подарила ему еще 3 конфеты, из которых одну Денис дал папе. Сколько конфет стало у Дениса?
Рассуждая, как обычно, получаем:
5 + (3 − 1) = 5 + 3 − 1.
Здесь, как и в самый первый раз, нужно просто стереть скобки. Почему же иногда этого оказывается достаточно, а иногда нет? Выпишем все наши наблюдения еще раз:
5 + (3 + 1) = 5 + 3 + 1;
5 + (3 − 1) = 5 + 3 − 1;
5 − (3 + 1) = 5 − 3 − 1;
5 − (3 − 1) = 5 − 3 + 1.
Ага! Теперь всё ясно. Если перед скобкой стоит «+», то скобки можно просто стереть, и больше ничего делать не требуется. Но если перед скобкой стоит «−», то нужно еще поменять тот знак, который стоял внутри скобки.
Дополнение: выражения, содержащие умножение или деление
Разумеется, в составных выражениях могут встречаться не только сложение и вычитание, но также и умножение и деление. Если, решая какую-нибудь задачу, мы составили выражение из двух действий и в этом выражении в первую очередь надо выполнить умножение или деление, а во вторую очередь — сложение или вычитание, то скобки можно не ставить:
10 + (2 ∙ 3) = 10 + 2 ∙ 3;
10 + (6 / 2) = 10 + 6 / 2;
10 − (2 ∙ 3) = 10 − 2 ∙ 3;
10 − (6 / 2) = 10 − 6 / 2.
Точно так же: (2 ∙ 3) + 10 = 2 ∙ 3 + 10
и т.п.
Это означает, что в выражениях без скобок вначале нужно выполнять умножение и деление, а затем — сложение и вычитание:
10 + 2 ∙ 3 = 10 + 6 ≠ (10 + 2) ∙ 3 = 12 ∙ 3.
В выражениях, которые содержат только умножение и деление, скобки можно не ставить в таких случаях:
(3 ∙ 4) ∙ 6 = 3 ∙ 4 ∙ 6;
(3 ∙ 4) / 6 = 3 ∙ 4 / 6.
Примеры на сложение и вычитание в два действия без скобок
Примеры на сложение и вычитание в два действия со скобками
Примеры в два действия, которые легко можно упростить изменением порядка действий
Примеры в два действия на сложение, вычитание, умножение и деление
| Табличка на двери |
Арифметические действия над числами
Советы → Полезные сведения → Арифметика → Арифметические действия
Арифметические действия
Нахождение по нескольким данным числам одного нового числа называется арифметическим действием. В арифметике рассматривается шесть действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.
В арифметике рассматривается шесть действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.
1. Сложение. Это действие состоит в том, что по нескольким числам, называемым слагаемыми, находится число, называемое их суммой.
Пример: 4+3=7, где 4 и 3 – слагаемые, а 7 – их сумма.
2. Вычитание – действие, посредством которого по данной сумме (уменьшаемое) и данному слагаемому (вычитаемое) находят искомое слагаемое (разность).
Это действие обратно сложению.
Пример: 7 – 3 = 4, где 7 – уменьшаемое, 3 – вычитаемое, а 4 – разность.
3. Умножение. Умножить некоторое число (множимое) на целое число (множитель) – значит повторить множимое слагаемым столько раз, сколько единиц содержится в множителе. Результат умножения называется произведением.
Пример: 2 ∙ 3 = 6, где 2 – множимое, 3 – множитель, а 6 – произведение. (2 ∙ 3 = 2 + 2+ 2 = 6)
Если множитель и множимое меняются ролями, то произведение остается тем же. Поэтому множитель и множимое также называются сомножителями.
Пример: 2 ∙ 3 = 3 ∙ 2, то есть (2 + 2 + 2 = 3 + 3)
Полагают, что если множителем является 1, то a ∙ 1 = a.
Например: 2 ∙ 1 = 2, 44 ∙ 1 = 44, 13 ∙ 1 = 13.
4. Деление. Посредством деления по данному произведению (делимое) и данному сомножителю (делитель) находят искомый сомножитель (частное).
Это действие обратно умножению.
Пример: 8 : 2 = 4, где 8 – делимое, 2 – делитель, а 4 – частное.
Проверка деления: произведение делителя 2 и частного 4 дает делимое 8. 2 ∙ 4 = 8
Деление с остатком
Если при делении целого числа на целое число в частном получается целое число, то такое деление целых чисел называется точным, или, что первое число нацело делится (или просто – делится) на второе.
Например: 35 делится (нацело) на 5, частное есть целое число 7.
Второе число при этом называется делителем первого, первое же – кратным второго.
Во многих случаях можно, не выполняя деления, узнать, делится ли нацело одно целое число на другое (см. признаки делимости).
Точное деление возможно далеко не всегда. В таком случае выполняют так называемое деление с остатком. В этом случае находят такое наибольшее число, которое при умножении на делитель даст произведение, не превосходящее делимого. Это число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком от деления.
Делимое равно делителю, умноженное на неполное частное, плюс остаток. Остаток всегда меньше делителя.
Пример: Неполное частное от деления числа 27 на 4 равно 6, а остаток равен 3. Очевидно, 27 = 4∙6 + 3 и 3˂4.
5. Возведение в степень. Возвести некоторое число в целую степень (во вторую, в третью и т.д.) – значит взять это число сомножителем два, три раза и т.д. Иначе говоря, возведение в степень выполняется повторным умножением.
Число, которое берётся сомножителем, называется основанием степени; число, показывающее, сколько раз повторяется основание, называется показателем степени; результат возведения числа в степень называется степенью этого числа.
Пример: 2∙2∙2 = 2³ = 8; где 2 – основание степени, 3 – показатель степени, 8 – степень.
Вторую степень числа иначе называют квадратом, третью степень – кубом. Первой степенью числа называют само это число.
6. Извлечение корня есть действие, посредством которого по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят искомое основание (корень).
Это действие обратно возведению в степень.
Пример: ³√64 = 4; где 64 – подкоренное число, 3 – показатель корня, 4 – корень. 3
3
Формулы возведения выражения больше трех можно при помощи треугольника Паскаля.
Источники:
- формула раскрытия скобок
Заключенные в скобки математические действия могут содержать переменные и выражения разной степени сложности. Для перемножения таких выражений придется искать решение в общем виде, раскрывая скобки и упрощая полученный результат. Если же в скобках содержатся операции без переменных, только с численными значениями, то раскрывать скобки не обязательно, так как при наличии компьютера его пользователю доступны весьма значительные вычислительные ресурсы – проще воспользоваться ими, чем упрощать выражение.
Инструкция
Перемножайте последовательно каждое (или уменьшаемое с ), содержащееся в одной скобке, на содержимое всех остальных скобок, если требуется получить результат в общем виде. Например, пусть исходное выражение записано так: (5+x)∗(6-х)∗(x+2). Тогда последовательное перемножение (то есть раскрытие скобок) даст следующий результат: (5+x)∗(6-х)∗(x+2) = (5∗6-5∗х)∗(5∗x+5∗2) + (6∗x-х∗x)∗(x∗x+2∗x) = (5∗6∗5∗x+5∗6∗5∗2) — (5∗х∗5∗x+5∗х∗5∗2) + (6∗x∗x∗x+6∗x∗2∗x) — (х∗x∗x∗x+х∗x∗2∗x) = 5∗6∗5∗x + 5∗6∗5∗2 — 5∗х∗5∗x — 5∗х∗5∗2 + 6∗x∗x∗x + 6∗x∗2∗x — х∗x∗x∗x — х∗x∗2∗x = 150∗x + 300 — 25∗x² — 50∗x + 6∗x³ + 12∗x² — x∗x³ — 2∗x³.
Упрощайте после результат, сокращая выражения. Например, полученное на предыдущем шаге выражение можно упростить таким образом: 150∗x + 300 — 25∗x² — 50∗x + 6∗x³ + 12∗x² — x∗x³ — 2∗x³ = 100∗x + 300 — 13∗x² — 8∗x³ — x∗x³.
Воспользуйтесь калькулятором, если требуется перемножить , содержащие только численные значения, без неизвестных переменных. Встроенный программный
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя .
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени .
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления — это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
18:2-2*3+12:3=9-6+4=3+4=7
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
30 + 6 * (13 — 9)
Вычислим значение выражения.
30+6*(13-9)=30+6*4=30+24=54
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие — умножение, второе — деление, третье — вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
37 + 9 — 6: 2 * 3 =
18: (11 — 5) + 47=
7 * 3 — (16 + 4)=
Рассуждаем так.
37 + 9 — 6: 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие — деление, второе — умножение. Третье действие должно быть сложение, четвертое — вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
18:(11-5)+47=18:6+47=3+47=50
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие — в скобках, второе — умножение, третье — вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого — вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. — М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. — М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. — М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. — М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. — М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. — М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. — М.: «Экзамен», 2012.
- Festival.1september.ru ().
- Sosnovoborsk-soobchestva.ru ().
- Openclass.ru ().
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
В данной статье мы подробно рассмотрим основные правила такой важной темы курса математики, как раскрытие скобок. 2) * 12 = 1728.
2) * 12 = 1728.
Как раскрыть 3 скобки
Бывают уравнения, в которых перемножаются сразу 3 скобки. В таком случае нужно сначала перемножить между собой слагаемые первых двух скобок, и затем сумму этого перемножения умножить на слагаемые третьей скобки. Пример:
(1 + 2) * (3 + 4) * (5 — 6) = (3 + 4 + 6 + 8) * (5 — 6) = — 21.
Данные правила раскрытия скобок одинаково распространяются для решения как линейных, так и тригонометрических уравнений.
И вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
Сначала умножение и деление, затем сложение и вычитание
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
- действия выполняются по порядку слева направо,
- причем сначала выполняется умножение и деление, а затем – сложение и вычитание.
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Пример.
Выполните действия 7−3+6
.
Решение.
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Ответ:
7−3+6=10 .
Пример.
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Решение.
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
Ответ:
Сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Пример.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Решение.
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
Ответ:
17−5·6:3−2+4:2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Определение.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Пример.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Решение.
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2
. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6
. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2
.
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Ответ:
5+(7−2·3)·(6−4):2=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Пример.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Решение.
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Ответ:
4+(3+1+4·(2+3))=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
На этом уроке вы узнаете, как из выражения, содержащего скобки, путем преобразования получить выражение, в котором скобок нет. Вы научитесь раскрывать скобки, перед которыми стоит знак плюс и знак минус. Мы вспомним, как раскрывать скобки, используя распределительный закон умножения. Рассмотренные примеры позволят связать новый и ранее изученный материал в единое целое.
Тема: Решение уравнений
Урок: Раскрытие скобок
Как раскрыть скобки, перед которыми стоит знак «+».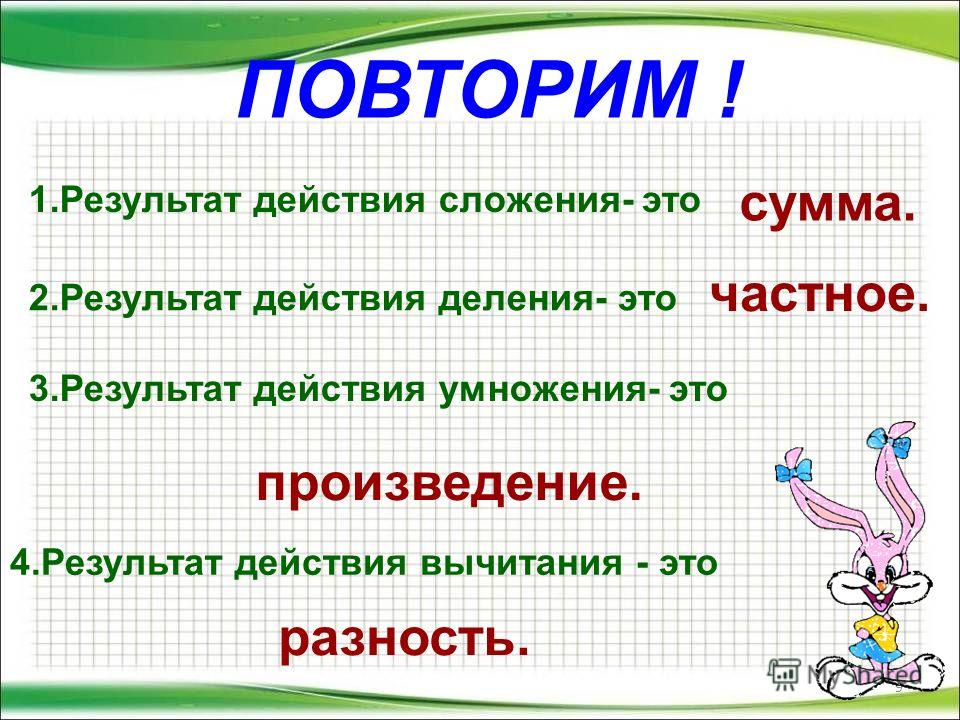 Использование сочетательного закона сложения.
Использование сочетательного закона сложения.
Если к числу нужно прибавить сумму двух чисел, то можно к этому числу прибавить сначала первое слагаемое, а затем второе.
Слева от знака равно выражение со скобками, а справа — выражение без скобок. Значит, при переходе от левой части равенства к правой произошло раскрытие скобок.
Рассмотрим примеры.
Пример 1.
Раскрыв скобки, мы изменили порядок действий. Считать стало удобнее.
Пример 2.
Пример 3.
Заметим, что во всех трех примерах мы просто убирали скобки. Сформулируем правило:
Замечание.
Если первое слагаемое в скобках стоит без знака, то его надо записать со знаком «плюс».
Можно выполнить пример по действиям. Сначала к 889 прибавить 445. Это действие в уме выполнить можно, но это не очень просто. Раскроем скобки и увидим, что изменённый порядок действий значительно упростит вычисления.
Если следовать указанному порядку действий, то нужно сначала из 512 вычесть 345, а затем к результату прибавить 1345. Раскрыв скобки, мы изменим порядок действий и значительно упростим вычисления.
Иллюстрирующий пример и правило.
Рассмотрим пример: . Найти значение выражения можно, сложив 2 и 5, а затем взять полученное число с противоположным знаком. Получим -7.
С другой стороны, тот же самый результат можно получить, сложив числа, противоположные исходным.
Сформулируем правило:
Пример 1.
Пример 2.
Правило не изменяется, если в скобках не два, а три или более слагаемых.
Пример 3.
Замечание. Знаки меняются на противоположные только перед слагаемыми.
Для того чтобы раскрыть скобки, в данном случае нужно вспомнить распределительное свойство.
Сначала умножим первую скобку на 2, а вторую — на 3.
Перед первой скобкой стоит знак «+», значит, знаки нужно оставить без изменения. Перед второй стоит знак «-», следовательно, все знаки нужно поменять на противоположные
Перед второй стоит знак «-», следовательно, все знаки нужно поменять на противоположные
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия, 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс — ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. Библиотека учителя математики. — Просвещение, 1989.
- Онлайн тесты по математике ().
- Можно скачать указанные в п. 1.2. книги ().
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012. (ссылка см. 1.2)
- Домашнее задание: № 1254, № 1255, № 1256 (б,г)
- Другие задания: № 1258(в), № 1248
МОАУ «CОШ №24 г. Орска»|Главная
Официальный сайт школы №24 г.Орска
Школа №24 была основана в 1936 году.
Сейчас в школе учатся 982 человека, работают 42 учителя: 20 — с первой категорией, 12 — со второй категорией.
Руководит дружным педагогическим коллективом Ращупкин Вячеслав Александрович.
Адрес школы: г.Орск, ул.Коммунистов-Большевиков,1
Телефон: (3537)266436
E-mail:[email protected]
Учредитель: муниципальное образование «Город Орск»
Управление образования администрации города Орска: приемная: 21-26-67
Адрес: 462419,3 г. Орск, пр. Ленина, 29
Начальник: Коваленко Вячеслав Александрович, тел. 21-26-67, часы приема: четверг с 14.00ч.
Заместитель начальника: Маслова Светлана Витальевна, тел. 25-01-14
25-01-14
График работы: понедельник — четверг с 8.00 до 17.00; пятница с 8.00 до 16.00; обед с 13.00 до 13.48
Своими мнениями и предложениями по работе сайта вы можете поделиться в гостевой книге.
Вы можете задать интересующий Вас вопрос Администрации и Учительскому составу школы здесь
Сведения о результатах рассмотрения уполномоченным органом МО «Администрация города Орска» результатов независимой оценки качества образовательной деятельности муниципальных образовательных организаций г. Орска: http://bus.gov.ru/pub/info-card/224879
С 23 февраля!
День родной школы 2021
Дорогие выпускники!
В 2021 году День родной школы по Оренбургской области проходит в дистанционном формате. Приглашаем Вас посетить нашу виртуальную видеогалерею! Обучающиеся школы №24 г. Орска подготовили видеоролики на тему: «За что я люблю свою школу?»
Многонациональное Оренбуржье
Депутат Законодательного Собрания Оренбургской области, председатель комитета по законности и правопорядку Алкулов Ермек Кунакбаевич
Шоу профессий «Натуральный продукт»
Телефоны горячей линии
Телефоны «горячей линии»:
8-800-200-56-03
8 (3532) 44-89-38
Горячая линия Роспотребнадзора по коронавирусу в Орске:
8 (3532) 44-23-54 (с 10. 00 до 17.00)
00 до 17.00)
8 (3532) 44-23-51
8 (3532) 77-31-64 (с 9.00 до 16.00)
Единый консультационный центр Роспотребнадзора:
8 (800) 555-49-43
Горячая линия оперативного штаба:
8 (800) 200-01-12
Телефоны «Горячей линии»
по вопросам образования и опеки г. Орска
О коронавирусе и его профилактике
|
На основании письма Управления Роспотребнадзора по Оренбургской области от 03.02.2020 № 01-724 и в связи с началом эпидемического подъема заболеваемости гриппом на территории Оренбургской области и эпидемиологической ситуацией по новой коронавирусной инфекции в Китайской Народной Республике просим ознакомиться с мерами по профилактике указанных заболеваний. |
Сообщи, где торгуют смертью
|
Информируем о том, что в период с 11 по 22 ноября 2019 года проводится Общероссийская акция «Сообщи, где торгуют смертью». Целью акции является объединение усилий органов исполнительной власти и местного самоуправления, общественности и населения в противодействии незаконному обороту и немедицинскому потреблению наркотиков, формирование антинаркотического мировоззрения молодежи. |
Неделя школьной прически
С 1 по 7 марта была объявлена «Неделя школьной прически». В течение этой недели контролировалось посещение занятий девочками с прической, соответствующей положению о внешнем виде учащихся. Также ученицы могли поучаствовать в конкурсе индивидуально. Девочкам было предложено 4 номинации: «Коса – девичья краса», «Весна расцветает в локонах», «Самый нежный образ», «Самая элегантная прическа». Сейчас в группе нашей школы во «ВКонтакте» создан альбом фотографий с этими прическами. Приглашаем вступать в группу и ставить «лайки» девчатам, так вы поможете им одержать победу. Голосование «лайками» продлится с 7 по 10 марта. Победительницы будут награждены почетными грамотами.
В течение этой недели контролировалось посещение занятий девочками с прической, соответствующей положению о внешнем виде учащихся. Также ученицы могли поучаствовать в конкурсе индивидуально. Девочкам было предложено 4 номинации: «Коса – девичья краса», «Весна расцветает в локонах», «Самый нежный образ», «Самая элегантная прическа». Сейчас в группе нашей школы во «ВКонтакте» создан альбом фотографий с этими прическами. Приглашаем вступать в группу и ставить «лайки» девчатам, так вы поможете им одержать победу. Голосование «лайками» продлится с 7 по 10 марта. Победительницы будут награждены почетными грамотами.
Вступить в группу
Перейти к голосованию
Школьная газета. Ноябрь-декабрь 2019
Школьная газета. Сентябрь-октябрь 2019
Информационный интернет проект «Виртуальный университет»
Уважаемые школьники 11 классов, а также их родители!
В январе 2019 года в Орске начинаются 5-месячные подготовительные онлайн курсы по подготовке школьников 11-х классов к успешной сдаче ЕГЭ для поступления в ведущие технические и гуманитарные вузы Урала и Поволжья.
Тест ПДД
Транспорт позволяет экономить время, относительно быстро доставлять грузы и пассажиров. Несмотря на существующие преимущества, он является источником повышенной опасности. Ежегодно по всему миру погибают и получают травмы более миллиона людей.
Всемирный день памяти жертв ДТП отмечается ежегодно в третье воскресенье ноября. Мы призываем Вас пройти по нижеуказанной ссылке и принять участие в тестировании в рамках акции «Повышение безопасности дорожного движения во всем мире».
Всемирный день мира
1 сентября все люди нашей планеты отмечают Всемирный день мира, в знак отказа от насилия и братоубийственных войн. Всем странам, без исключения, поступило предложение в этот день прекратить все военные операции и провести акции, касающиеся проблем мира.
В нашей школе был проведен Школьный конкурс детского рисунка на асфальте «Пусть всегда будет МИР!» .
Популярные материалы
Обзор сложения, вычитания, умножения и деления — математика для 3-го класса
Обзор фактов сложения, вычитания, умножения и деления
В математике есть 4 основных операции: сложение, вычитание, умножение и деление.
🤓 Вы проделали большую работу, изучая каждую из них.
В этом уроке давайте рассмотрим то, что вы узнали. 🤗
Обзор дополнения
Объединение двух или более чисел называется сложением .
✅ Уравнение сложения состоит из двух или более сложений, символа плюса (+), символа равенства (=) и суммы.
Попробуем сложить числа.
Пример добавления 1
4,255 + 3,104 =?
Давайте сложим числа, используя форму столбца .
Итак, каков ответ? 🤓
Верно! Это 7359.
4,255 + 3,104 = 7,359
Отличная работа! 👌
Пример добавления 2
675 + 198 =?
Добавим! (Используйте перегруппировку , при необходимости .)
Какая сумма?
Очень хорошо! Это 873.
675 + 198 = 873
Отлично! 😎
Теперь перейдем к вычитанию.
Обзор вычитания
Вы помните, что такое вычитание? 🤔
Вычитание убирает часть числа.
✅ Уравнение вычитания состоит из , вычитаемого , вычитаемого , , символа минуса (-), символа равенства (=) и разности . Давайте теперь попробуем вычесть несколько чисел.
Пример вычитания 1
497 — 251 =?
Давайте вычтем числа, используя форму столбца .
В чем разница? 🤓
497 — 251 = 246
Отличная работа! 👏
Пример вычитания 2
7 301 — 6 361 =?
Давайте вычесть! Используйте перегруппировку , при необходимости .
Какая разница у тебя? 😃
7 301 — 6 361 = 940
Вперед! 🤗
Давайте теперь рассмотрим умножение и деление.
Обзор умножения
Сложение равных групп снова и снова называется умножением .
👉 Например, когда мы умножаем 2 круга 5 раз, мы получаем 10 кругов.
5 × 2 = 10
✅ Уравнение умножения состоит из множителя , множителя , символа умножения (×), равно символу (=) и произведению .
Множитель и множимое также называются множителями .
Давайте теперь рассмотрим несколько примеров.
Пример умножения 1
9 × 8 =?
Давайте умножим эти числа на повторных сложений.
✅ Мы можем прибавить 9 к себе 8 раз, или прибавить 8 к себе 9 раз.
9 × 8 = 9 + 9 + 9 + 9 + 9 + 9 + + 9000 9 = 72
Итак,
9 × 8 = 72
Отличная работа! 👌
Пример умножения 2
256 × 3 =?
Давайте попробуем умножить эти числа, используя форму столбца .
✅ Сначала мы умножаем цифру в разряде единиц на 3.
✅ Затем мы умножаем цифру в разряде десятков на 3 и складываем перенос.
✅ Наконец, мы умножаем цифру в разряде сотен на 3 и складываем перенос.
Какой ответ вы получили?
256 × 3 = 768
Отличная работа! 👏
Подразделение Обзор
Вы помните, что такое деление? 🤓
Верно!
Раздел разбивает номер на равные группы.
👉 Например, когда мы разбиваем 10 кругов на 5 равных групп, мы получаем по 2 круга в каждой группе.
10 ÷ 5 = 2
✅ Уравнение деления состоит из деления , делителя , символа деления (÷ или ⟌) и частного .
Давайте теперь рассмотрим несколько примеров деления.
Пример отдела 1
30 ÷ 6 =?
Давайте решим эту задачу деления, используя повторное вычитание .
✅ Мы начинаем с 30 и снова и снова вычитаем 6, , пока не дойдем до 0. Наш ответ — это количество раз, которое мы вычитаем.
Сколько раз вы вычитали?
Правильно! 5 раз.
Итак,
30 ÷ 6 = 5
Отлично! 🤗
Совет: Думайте о делении как о противоположности умножения. Если вы видите 30 ÷ 6 =? подумайте: какое число, умноженное на 6, равно 30?
6 х? = 30
И вы получите тот же ответ: 5!
Пример отдела 2
882 ÷ 7 =?
Давайте решим этот вопрос, используя длинное деление .
✅ Начнем с расстановки чисел в виде столбика.
✅ Теперь, посмотрим на первую цифру.
Вы можете сказать, сколько семерок поместится в восьмерку? 🤔
Очень хорошо! 1.
Напишите сверху 1 , как частное и запишите произведение от 1 и 7 под 8.
Теперь вычтите этот продукт из 8 , чтобы получить остаток.
Отлично! 😎
✅ Затем уберите следующую цифру и повторите процесс .
✅ Наконец, опустите последнюю цифру и повторите процесс .
Какой ответ вы получили?
882 ÷ 7 = 126
Отличная работа! 👏
🎉 Вы только что рассмотрели наиболее важные моменты, касающиеся сложения, вычитания, умножения и деления.
А теперь начните свою практику ниже.
Задачи на сложение, вычитание, умножение и деление слов
Не секрет, что задачи на сложение, вычитание, умножение и деление слов представляют собой серьезную проблему для студентов.Студенты часто спешат решить словесные задачи и сразу же пытаются найти ответ, вместо того, чтобы думать о значении проблемы. Учащиеся видят проблему со словами и хотят сразу же взять числа и что-то с ними сделать. К счастью, есть вещи, которые мы можем сделать, что позволит учащимся развить понимание словесных задач.
Как научить решать задачи со словами?
Я обнаружил, что лучше избегать обучения ключевым словам и стратегиям, таким как КУБИКИ. Ключевые слова недостаточны для решения проблемы и часто могут привести учащихся к неправильной операции или единственной операции, когда требуется несколько операций.Другие процедурные стратегии упускают понимание ситуации проблемы.
Для того, чтобы учащиеся полностью понимали текстовые задачи, они должны иметь возможность решать текстовые задачи, используя несколько представлений. Это позволяет учащимся понять действия и отношения в проблеме. Варианты представления включают:
Это позволяет учащимся понять действия и отношения в проблеме. Варианты представления включают:
- Бетон с использованием физических представлений или отыгрыванием посредством моделирования.
- Иллюстрированные изображения и диаграммы могут проиллюстрировать и прояснить действия и отношения так, как слова, даже конкретные представления, не могут.
- Символические символы могут быть знаками операций или переменными.
Когда учащиеся начинают работать с большими числами, представление ситуаций с помощью физической модели становится более сложной задачей, поскольку для этого требуется стратегическая группировка единиц. В этих ситуациях студентам может потребоваться дать ключевое или дополнительное объяснение своих представлений.
Во время работы учащиеся важно замечать, когда они не представляют фактический контекст и количества, а представляют только числа в задаче.Несоответствие проблемной ситуации модели показывает, что студент не проявил практического смысла в решении. Смысл операции — это понимание всей «работы», которую может выполнить каждая операция. Это распространяется на использование соответствующих представлений о действии или взаимосвязи в проблеме, так что они представляют понимание ситуации.
Я начинаю год только с задач на сложение и вычитание. Несмотря на то, что ученики старших классов обычно имеют значительный опыт в решении задач на сложение и вычитание слов, эти уроки невероятно важны.
Действие и бездействие
Один из ключей к пониманию словесной проблемы — распознавать словесные проблемы действия и бездействия. Действие не обязательно относится к движению, но к тому, что что-то происходит с исходным количеством проблемы. Это прекрасное время, чтобы студенты по очереди решали различные словесные задачи. У меня есть ученики сортируют словесные задачи на словесные задачи с действиями и без действий.
В качестве дополнительной практики я прошу студентов заполнить лист «Задача со словом« действие »или« бездействие ». На этой странице практики студенты решают шесть словесных задач на сложение и вычитание. Затем они заштриховывают слова «проблемы», которые показывают действие зеленым, а словесные проблемы «бездействие» — красным.
На этой странице практики студенты решают шесть словесных задач на сложение и вычитание. Затем они заштриховывают слова «проблемы», которые показывают действие зеленым, а словесные проблемы «бездействие» — красным.
Это может показаться чрезмерно упрощенным уроком, но он начинает закладывать основу для более конкретных типов текстовых задач. Лучше не перегружать учеников слишком рано.
Типы проблем со словом действия
Следующий шаг — научить учащихся понимать различные типы задач со словом «действие».На этом уроке ученики могут повторно использовать сортировочные карточки и сортировать карточки действий, объединяя и разделяя проблемы. Для студентов это часто оказывается на удивление сложной задачей.
После того, как учащиеся отсортируют свои карточки, введите термины «результат неизвестен», «изменить неизвестно» и «начать неизвестно». Просмотрите каждую карту, чтобы определить, какой неизвестный тип включает в себя.
Разложите по классу шесть листов диаграммной бумаги. Пометьте каждый лист диаграммной бумаги следующими словами: «Начало соединения неизвестно», «Изменение присоединения неизвестно», «Результат соединения неизвестен», «Удаление неизвестного начала», «Удаление неизвестного изменения», «Результат удаления неизвестен».
Попросите учащихся написать пример каждого типа задачи со словами на отдельной липкой бумаге. После написания словесных задач учащиеся должны поместить стикеры на соответствующий лист диаграммной бумаги. Еще раз, мне нравится следовать этому с дополнительной практикой.
На протяжении многих лет я обнаружил, что один из лучших способов замедлить учеников при решении задач со словами — это обозначить цветом и подчеркнуть каждую часть задачи со словами. Это меняет правила игры! Я сразу рассказываю об этом и пытаюсь сделать цветовое кодирование привычкой для студентов.Это ожидание для каждой решаемой задачи.
Типы проблем со словами бездействия
Затем учащиеся должны узнать о задачах со словами, не являющимися действиями. Я повторяю тот же процесс, чтобы обучать различным типам задач, не связанных с действиями: сравнение разницы неизвестного, сравнение большего количества неизвестного, сравнение меньшего количества неизвестного, часть-часть-целое целое неизвестное и часть-часть-целая часть неизвестного.
Я повторяю тот же процесс, чтобы обучать различным типам задач, не связанных с действиями: сравнение разницы неизвестного, сравнение большего количества неизвестного, сравнение меньшего количества неизвестного, часть-часть-целое целое неизвестное и часть-часть-целая часть неизвестного.
Для дополнительной практики студенты могут заполнить рабочий лист «Типы задач со словами, не связанными с действием».Это единственные задачи со словами, для которых у меня нет цветового кода студентов.
Я не заставляю студентов запоминать каждый тип задач. Но я должен убедиться, что они понимают, какую работу выполняет каждое число в рамках слова «проблема».
Ситуационные уравнения
Часто, когда ученики пишут уравнения, они пишут уравнение, которое можно использовать для решения задачи, но оно не отражает ситуацию со словом «проблема». Ситуационные уравнения представляют действие проблемы. Уравнения решения можно использовать для решения проблемы.
Пример: Некоторые дети играли в жетоны на перемене. Когда другой класс вышел на улицу, к ним присоединились еще восемь учеников. Сейчас в теги играют 14 учеников. Сколько студентов играли в теги с самого начала?
Уравнение решения будет 14-8 = _____. Однако уравнение ситуации ____ + 8 = 14.
Чтобы научить этому, обсудите каждый тип задачи со словом действия и попросите учащихся заметить расположение каждой неизвестной величины для каждой задачи.Студенты должны понимать, что неизвестная величина, называемая словом «проблема», также описывает местонахождение неизвестного в уравнении ситуации.
Затем обсудите, какое решение уравнения будет наиболее эффективным для решения проблемы. Еще раз, выполняйте это с дополнительной практикой.
Каждый из приведенных выше уроков взят из моей единицы сложения и вычитания. Это модуль для 4-го класса, но я создал и включил версию для учеников 3-го класса
Когда я начинаю обучать задачам умножения и деления слов, я не прекращаю повторять задачи на сложение и вычитание слов. Важно сочетать все операции, чтобы учащиеся находили смысл в каждой решаемой ими словесной задаче.
Важно сочетать все операции, чтобы учащиеся находили смысл в каждой решаемой ими словесной задаче.
Ключом к пониманию проблемных ситуаций умножения и деления является определение работы, которую выполняет каждый фактор. Студенты должны учитывать следующее:
- Что означают числа? Что они делают?
- Как я могу представить величины с помощью манипуляторов или картинок?
- Какое числовое предложение лучше всего показывает, что происходит в рассказе?
Равные группы
Чтобы полностью понять равные группы, важно, чтобы учащиеся видели разницу между количеством групп и количеством предметов в каждой группе.Приведенную ниже таблицу можно использовать как отправную точку для размышлений о равных групповых ситуациях. Это также может быть справочник для студентов, когда они пишут свои собственные текстовые задачи.
Хотя свойство коммутативности полезно для запоминания фактов умножения, оно не всегда помогает учащимся развить глубокое понимание смысла операции и значения словесных задач. В текстовых задачах большинство ситуаций не коммутативны, и учащиеся должны быть в состоянии точно представить ситуацию.
Вопросы, подобные приведенному ниже, позволяют увидеть, насколько глубоко учащиеся понимают ситуации умножения, и отлично иллюстрируют, как ситуации не коммутативны.
По мере того, как мы переходим к задачам умножения и деления слов, выделение продолжается. Я выбрал разные цвета, чтобы студенты не путали цветовое кодирование сложения и вычитания с цветовым кодированием умножения и деления. Приведенные ниже слова «проблемы» показывают, как это можно сделать в цифровом виде.
В приведенных выше задачах я уже определил размеры прямоугольников для студентов. Однако, когда все операции объединены, учащимся, возможно, придется изменить размер выделенных прямоугольников.
Сравнение умножения
Задачи мультипликативного сравнения часто представляют собой проблему для учащихся, так как студенты склонны путать аддитивные и мультипликативные сравнения. Студентам нужна возможность разыграть и построить репрезентации для этого типа проблемы.Эти проблемы сравнения должны быть переплетены с задачами равных групп.
Студентам нужна возможность разыграть и построить репрезентации для этого типа проблемы.Эти проблемы сравнения должны быть переплетены с задачами равных групп.
Чтобы дать учащимся время поразмышлять над этими задачами со словами, они могут выполнить сортировку, в которой они различают задачи аддитивного сравнения и задачи мультипликативного сравнения.
Студентам нужно несколько возможностей поработать с умножением в качестве сравнения, и я надеюсь, что на следующей неделе будет готов новый пост для этого!
Во время обучения невероятно полезно, чтобы студенты сами писали задачи со словами.Это выводит их обучение на более глубокий уровень и дает вам лучшее понимание того, что ваши ученики понимают.
Анализ ошибок
Даже используя эти стратегии, Вы все равно будете видеть ошибки и путаницу, особенно с ситуационными уравнениями. Это процесс, и это практическое чутье будет развиваться со временем с последовательной практикой и инструктажем. Когда я учу студентов основам текстовых задач, мне нравится, когда они решают задачи анализа ошибок.Лучше всего решать только одну задачу в день, чтобы можно было глубоко поговорить. Ошибки, обнаруженные в этих задачах, не являются ошибками вычислений. Напротив, это ошибки в представлении проблемы.
Я включил опцию Peardeck для всех действий по анализу ошибок. Конечно, вам не обязательно использовать эту опцию. Это просто способ сделать урок еще более интерактивным.
Все слайды выше взяты из моего ресурса «Задача слова умножения и деления».Вы можете найти этот ресурс здесь.
С ресурсом или без него, я надеюсь, что это помогло предоставить вам идеи и стратегии для обучения задачам со словами. Сообщите мне, как это происходит!
Вычитание — | Основы арифметики
Эта страница посвящена основам арифметики — простейшему способу работы с числами посредством вычитания (-).
См. Другие наши арифметические страницы для обсуждения и примеров: Сложение (+), Умножение ( × ) и Деление ( ÷ ).
Другие наши арифметические страницы для обсуждения и примеров: Сложение (+), Умножение ( × ) и Деление ( ÷ ).
Вычитание
Вычитание — это термин, используемый для описания того, как мы «убираем» одно или несколько чисел у другого.
Вычитаниетакже используется для нахождения разницы между двумя числами. Вычитание противоположно сложению. Если вы еще этого не сделали, мы рекомендуем прочитать нашу дополнительную страницу.
Знак минус «-» используется для обозначения операции вычитания, например, 4–2 = 2. Знак «-» можно использовать несколько раз по мере необходимости: например, 8–2–2 = 4.
Вычисление верное, но его можно упростить, сложив числа, которые мы вычитаем. В нашем примере 8 — 2 — 2 = 4 можно упростить до 8 — 4 = 4 (две двойки были добавлены вместе, чтобы получить 4, которое затем вычитается из 8).
Предупреждение
Будьте осторожны при использовании знака «-». Числа с отрицательным значением записываются с предшествующим «-», поэтому минус два записывается как -2. Это просто означает, что 2 меньше нуля или 2 меньше нуля.
Для получения дополнительной информации см. Нашу страницу Положительные и отрицательные числа .
Остерегайтесь знаков и порядка при вычитании
Когда мы выполняем вычисление сложения , порядок, в котором мы складываем числа, не имеет значения.
Например,
8 + 3 + 5 совпадает с 3 + 8 + 5 и дает нам тот же ответ, 16.
Однако, когда мы выполняем вычитание , нам нужно проявлять особую осторожность с порядком чисел.
Обычно при вычитании мы сначала записываем число, которое мы вычитаем из , , а затем числа, которые мы вычитаем, в любом порядке.
Например,
8-5 = 3
Это НЕ то же самое, что 5-8 = −3
Мы видим, что у нас тот же числовой ответ (3), но его значение другое: 3 в первом вычислении, но минус 3 (−3) во втором.
Аналогично 8-5-3 = 0, но 5-8-3 = −6, что является совершенно другим ответом.
Причина того, что ответы различаются, не в том, что мы поставили числа в «неправильном» порядке, а в том, что мы не позаботились о том, положительные они или отрицательные.
В нашем примере 8 — положительное число, поэтому мы могли бы записать его как «+ 8», и это было бы правильно, но согласно соглашению, нам не нужно писать символ «+». Однако символ «+» очень важен при изменении порядка, как и символы «-», предшествующие 5 и 3.
Вот последний пример, переписанный для правильного ответа:
8 — 5 — 3 = 0, как и раньше, и — 5 + 8 — 3 = 0, что дает тот же ответ. В этом случае мы написали числа в том же порядке, что и раньше, но учли их положительное или отрицательное значение.
Более подробное объяснение и примеры см. В разделе «Вычитание в особых случаях: нулевые и отрицательные числа » ниже.
Выполнение вычитания
Простое вычитание может выполняться так же, как и сложение, путем подсчета или использования числовой строки:
Если у Фиби 9 конфет, а у Люка 5 конфет, какая разница?
Начиная с меньшего числа (5) и считая до большего числа (9).
6 (1), 7 (2), 8 (3), 9 (4).
У Фиби на 4 конфет больше, чем у Люка, разница в конфетах на 4.
Итак: 9-5 = 4 .
Для более сложного вычитания, когда использование подсчета не подходит, полезно записывать наши числа в столбцы один над другим — аналогично вычислению сложения.
Предположим, что Майк зарабатывает 755 фунтов стерлингов в неделю и платит 180 фунтов стерлингов в неделю за аренду. Сколько денег осталось у Майка после того, как он заплатил за квартиру?
В этом примере мы собираемся убрать 180 фунтов стерлингов из 755 фунтов стерлингов.Сначала мы записываем начальное число, а снизу — число, которое мы убираем, следя за тем, чтобы числа были в правильных столбцах.
| Сот | Десятки | Шт. |
| 7 | 5 | 5 |
| 1 | 8 | 0 |
Шаг 1: Сначала мы выполняем вычитание чисел в столбце «Единицы измерения» справа, затем записываем ответ внизу в том же столбце.В этом случае 5 — 0 = 5.
| Сот | Десятки | Шт. | |
| 7 | 5 | 5 | |
| 1 | 8 | 0 | |
| Итого | 5 |
Шаг 2: Используя тот же подход, что и при вычислении сложения, мы работаем по столбцам справа налево.Затем нам нужно вычесть числа в столбце десятков. В нашем примере нам нужно вычесть восемь из пяти (5-8), но 8 больше 5, поэтому мы не можем этого сделать, так как в итоге получим отрицательное число. Нам нужно позаимствовать число из столбца сотен. Это может быть сложной концепцией, и мы рассмотрим ее более подробно ниже: у нас есть 7 в столбце сотен, поэтому мы «заимствуем» 1 для столбца десятков, оставляя нас с 6 в сотнях. Перечеркните 7 и напишите 6 в столбце сотен, чтобы избежать ошибок позже.Переместите 1 в столбец десятков и запишите его перед числом 5. Мы не добавляем «1» к десяткам, мы ссужаем «1 лот из 10». Итак, вместо 5 десятков у нас теперь 15 десятков.
15 больше восьми, поэтому мы можем выполнить вычитание в столбце десятков. Возьмите 8 из 15 и напишите ответ (7) внизу столбца десятков.
| Сот | Десятки | Шт. | |
| | 15 | 5 | |
| 1 | 8 | 0 | |
| Итого | 7 | 5 |
Шаг 3: Наконец, отнимите 1 от 6 в столбце сотен. 6 — 1 = 5, поэтому поставьте 5 в столбце ответов сотен, чтобы дать окончательный ответ. У Майка осталось 575 фунтов стерлингов после того, как он заплатил за квартиру.
6 — 1 = 5, поэтому поставьте 5 в столбце ответов сотен, чтобы дать окончательный ответ. У Майка осталось 575 фунтов стерлингов после того, как он заплатил за квартиру.
| Сот | Десятки | Шт. | |
| | 15 | 5 | |
| 1 | 8 | 0 | |
| Итого | 5 | 7 | 5 |
Заимствование с вычетом
Заимствование , как в приведенном выше примере, может сбивать с толку при вычислениях вычитания.Это похоже на «перенос» в дополнительных вычислениях, но в обратном порядке, потому что вычитание — это обратное (противоположное) сложение.
Повторное заимствование может произойти при вычислении вычитания.
Предположим, у нас есть 10,01 фунта стерлингов, и мы хотим забрать 9,99 фунта стерлингов. Мы можем решить это, не записывая ничего — ответ — 0,02 фунта стерлингов или 2 пенни. Однако, если мы выпишем этот расчет формально, то понятие заимствования станет более ясным.
В этом примере мы проигнорировали десятичную точку и записали числа как 1001 и 999.
Начиная с столбца единиц справа, нам нужно отнять 9 от 1. В наших вычислениях вычитания правило (как в приведенном выше примере) состоит в том, что мы никогда не убираем большее число из меньшего числа, потому что это даст нам отрицательный ответ.
Чтобы расчет заработал, нам нужно « позаимствовать » — число из следующего столбца слева. В столбце десятков стоит 0, поэтому брать нечего, поэтому нам нужно перейти к следующему столбцу слева.В столбце сотен также есть 0, поэтому мы также не можем заимствовать данные из этого столбца, поэтому мы переходим к следующему столбцу слева. Столбец тысяч имеет 1, поэтому мы можем позаимствовать его и переместить в следующий столбец справа, столбец сотен. Мы перечеркнем 1 в столбце тысяч, чтобы избежать ошибок позже.
Одна тысяча равна 10 сотням, поэтому теперь у нас есть 10 в столбце сотен, где раньше было ноль:
| Переносной | 0 | 10 | ||
| | 0 | 0 | 1 | |
| 9 | 9 | 9 |
Однако это не помогает с 1–9 (в столбце единиц), потому что у нас все еще есть ноль для заимствования в столбце десятков, но это первый шаг в процессе.
Теперь, когда у нас есть 10 сотен, мы можем позаимствовать одну из них для столбца десятков. Сто равно 10 десяткам, поэтому мы переносим 10 в столбец десятков. Мы не должны забыть настроить столбец сотен, поэтому мы вычеркиваем 10 и вместо этого пишем 9.
| Переносной | 9 | 10 | ||
| Переносной | 0 | | ||
| | 0 | 0 | 1 | |
| 9 | 9 | 9 |
Наконец, мы можем выполнить вычитание в столбце единиц, заимствовав 1 десятку из столбца десятков.Это оставляет 9 десятков в столбце десятков и 10 + 1, который у нас уже был в столбце единиц, что дает нам 11 единиц.
| Переносной | 9 | 10 | ||
| Переносной | 9 | | ||
| Переносной | 0 | | ||
| | 0 | 0 | 1 | |
| 9 | 9 | 9 |
Теперь мы можем выполнить полный расчет, начиная со столбца единиц, 10 + 1 = 11 — 9 = 2.Тогда в столбце десятков 9 — 9 = 0. То же самое для столбца сотен 9 — 9 = 0. Наконец, в столбце тысяч 0 — 0 = 0.
То же самое для столбца сотен 9 — 9 = 0. Наконец, в столбце тысяч 0 — 0 = 0.
| Переносной | 9 | 10 | ||
| Переносной | 9 | | ||
| Переносной | 0 | | ||
| | 0 | 0 | 1 | |
| 9 | 9 | 9 | ||
| Итого | 0 | 0 | 0 | 2 |
Заимствовав несколько раз, мы пришли к нашему ответу 2.Когда мы заменяем десятичную точку, мы получаем 0,02 фунта стерлингов.
Вычитание в особых случаях: ноль и отрицательные числа
Если бы мы выполняли простое сложение, мы могли бы считать в уме или, возможно, на пальцах. Когда мы выполняем вычитание, особенно если оно включает отрицательные числа, помогает представить себя идущим по линии. Каждый шаг — это номер в этой строке. Если мы начнем с нуля, каждый шаг вперед добавляет число, каждый шаг назад убирает единицу.Самое важное, что нужно помнить, — это то, что мы всегда смотрим в позитивном направлении. Возможно, вам будет полезно думать о своей линии как о подъеме и спуске по лестнице, где каждая ступенька имеет номер. Или, возможно, вы более знакомы с перемещением вверх и вниз по многоэтажному блоку на лифте, где ноль — это первый этаж, положительные числа — над землей, а отрицательные — в подвале.
Если бы мы нарисовали эту линию на листе бумаги, она выглядела бы как линейка. Мы можем перемещать ручку вперед и назад по линии так же, как представляем себе наши шаги вперед и назад.Это называется числовой строкой и является очень полезным инструментом для сложения и вычитания.
Мы собираемся использовать эту аналогию, чтобы помочь нам понять следующие примеры.
Когда числа равного значения вычитаются друг из друга, результат всегда равен нулю: 19-19 = 0.
Используя нашу аналогию, начав с нуля, если мы пройдем 19 шагов вперед по линии, затем 19 шагов назад, мы вернемся к нулю.
При вычитании нуля из любого числа число остается неизменным: 19-0 = 19.
Используя числовую прямую, мы начинаем с 19 и идем назад нулевых шага — мы не двигаемся и остаемся на 19.
Когда мы вычитаем из нуля любое положительное число , получаем отрицательное число : 0–15 = –15
Помните из наших предыдущих примеров, положительное число обычно не нужно записывать с положительным знаком. Когда мы видим число «67», математическое соглашение говорит нам, что оно положительное, т.е.е. «+67».
В этом примере мы вычитаем +15 из нуля: 0 — (+15) = –15. Используя нашу аналогию, мы начинаем с нуля и делаем 15 шагов назад.
Когда мы вычитаем любое положительное число из отрицательного числа , ответ становится « более отрицательный » .
Например, если мы начнем с нашего ответа сверху (–15) и вычтем 6, мы получим: –15 — 6 = –21. Помните, что «6» положительно, поэтому мы можем написать –15 — (+6) = –21, и это означает то же самое.Используя числовую линию, чтобы помочь нам понять, мы начинаем со значения –15. Мы идем назад на шесть шагов, по-прежнему глядя в положительном направлении. В итоге мы делаем 21 шаг назад от нуля, то есть –21.
Но что произойдет, если нам нужно вычесть отрицательное число из любого другого числа?
Начнем с примера: 15 — (–6) = 15 + 6 = 21
Правило : два отрицательных числа дают положительное значение , т.е. вычитание отрицательного числа становится сложением.
Давайте вернемся к нашей числовой прямой, чтобы облегчить нам понимание: начиная с 15, мы знаем, что нам нужно двигаться назад (в отрицательном направлении), потому что мы делаем вычитание. Но нам нужно вычесть отрицательное число, поэтому, чтобы проиллюстрировать это, мы должны повернуть вокруг . Затем мы возвращаемся на 6 позиций назад, чтобы прийти к нашему ответу. При повороте и последующем движении назад (два отрицательных момента) наше общее направление движения находится в положительном направлении , т.е.е. мы выполнили сложение .
Но нам нужно вычесть отрицательное число, поэтому, чтобы проиллюстрировать это, мы должны повернуть вокруг . Затем мы возвращаемся на 6 позиций назад, чтобы прийти к нашему ответу. При повороте и последующем движении назад (два отрицательных момента) наше общее направление движения находится в положительном направлении , т.е.е. мы выполнили сложение .
Вычитание отрицательного числа — это абстрактная концепция, и вы можете подумать, что на самом деле этого не происходит в повседневной жизни. В конце концов, мы не можем удержать отрицательное количество яблок или налить отрицательное количество кофе. Однако это очень важно, когда речь идет о математических понятиях, таких как векторов . Вектор имеет направление и величину звездной величины , поэтому, например, важно не только, как далеко проплыла лодка, но нам также необходимо знать направление, в котором она плыла.
Дополнительные материалы по навыкам, которые вам нужны
Основы счета
Часть необходимых навыков Руководство по счету
Эта электронная книга содержит рабочие примеры и простые для понимания объяснения, чтобы показать вам, как использовать основные математические операции и начать манипулировать числами. Он также включает в себя примеры из реальной жизни, чтобы прояснить, насколько эти концепции полезны в реальной жизни.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Вычитание 4 в строке — Математическая игра с вычитанием
Вычитание 4 в строке — Математическая игра с вычитанием
Навык содержания: Вычитание
Стандарты Common Core State: CCSS.Math.Content.2.OA.B.2 — Свободно вычитайте в пределах 20, используя умственные стратегии. К концу 2 класса выучите по памяти все суммы двух однозначных чисел.
Описание
Вычитание 4 в строке — отличный способ узнать факты умножения. Эта многопользовательская математическая игра сочетает в себе уравнения и стратегию. Дети просто не могут насытиться этой игрой. Играйте против компьютера или против других игроков со всего мира.
Эта многопользовательская математическая игра сочетает в себе уравнения и стратегию. Дети просто не могут насытиться этой игрой. Играйте против компьютера или против других игроков со всего мира.
Предупреждаем, из этой игры сложно бросить! Держись! Не сдавайся. Вы можете обыграть компьютер!
Инструкции
Экран приветствия
Экран приветствия служит отправной точкой игры. Отсюда вы можете отключить все звуки игры. Нажмите пульсирующую кнопку воспроизведения, чтобы начать игру в одиночном или многопользовательском режиме.
Выберите игровой режим
Выберите режим одиночной игры или выберите игру против других игроков. Кнопка слева немедленно запускает одиночную игру. Кнопка справа приведет вас либо к экрану входа в систему, либо к экрану начала матча. Если вы уже вошли в систему, используя систему управления учащимися Multiplication.com, вы уже вошли в систему. Если нет, вам нужно будет указать имя пользователя для входа в систему.
Одиночная игра
В одиночной игре В игре компьютер сразу же выберет ход.Каждый раз, когда наступает ваша очередь, вам будет предложено ответить на один вопрос. После того, как вы ответили на уравнение, вы также сможете выбрать ход. Будьте осторожны, компьютер — очень хороший противник.
Одиночная игра закончилась
Когда одиночная игра окончена, вы увидите этот экран. Кнопка «Домой» вернет вас на экран приветствия. Кнопка «Обновить» запустит новую одиночную игру.
Экран входа в систему
Если вы не вошли в систему как умножение.com студент, вам необходимо войти в игру, чтобы иметь возможность играть против других игроков. Введите имя пользователя, которое вы хотите использовать. Обязательно укажите подходящее имя пользователя.
Экран начала матча
После успешного входа в систему вы увидите экран начала матча. На этом этапе вы вошли в систему и готовы к многопользовательской игре. Если вы решили, что не хотите играть в многопользовательском режиме, вы можете нажать кнопку отмены, чтобы вернуться на экран приветствия. В противном случае нажмите кнопку битвы.
В противном случае нажмите кнопку битвы.
Ожидание экрана соперника
В течение 15 секунд мы будем искать другого игрока, готового начать многопользовательскую игру, чтобы сопоставить вас. Если совпадение найдено, начнется многопользовательская игра. Но сначала вы увидите аватар и имя пользователя оппонента. Если совпадение не найдено, вместо этого начнется одиночная игра.
Многопользовательская игра (ваша очередь)
Пора играть. Каждый раз, когда наступает ваша очередь, у вас будет 20 секунд, чтобы ответить на уравнение и сделать ход.Если вы не сделаете это за 20 секунд, компьютер сделает ход за вас. Просто имейте в виду, что это не будет хорошим ходом, поэтому не рассчитывайте на его победу.
Многопользовательская игра (ход оппонента)
Теперь пришло время подождать, пока ваш оппонент сделает свой ход. У них есть 20 секунд. Так что это ненадолго. Подумайте о своей стратегии. И наслаждаться! Удачи.
Сложение и вычитание чисел с помощью числовой строки
Добавление чисел в числовую строку — отличный способ увидеть, как добавляются числа, с помощью визуальной интерпретации.
I. Действия по сложению чисел в числовой строке
Как показано на схеме ниже:
- Добавление положительного числа означает, что мы перемещаем точку вправо от числовой строки.
- Аналогично, добавление отрицательного числа означает, что мы перемещаем точку влево от числовой строки.
Примеры сложения чисел в числовой строке
Пример 1 : Упростите, добавив числа, 2 + 4 .
Первый шаг — найти первое число, которое составляет два (2) в числовой строке.
Добавление четырех (4) означает, что мы должны переместить точку, четыре (4) единицы вправо .
После этого мы получаем 6. Следовательно, 2 + 4 = 6 .
Пример 2 : Упростите, добавив числа, 3 + (–5) .
Найдите первую точку 3 на числовой прямой.
Теперь мы собираемся к добавить минус 5 (-5) , который говорит нам переместить точку на 5 единиц влево на .
Мы приходим к −2. Поэтому 3 + (–5) = — 2 .
Пример 3 : Упростите, добавив числа, –6 + 5 .
Найдите в числовой строке первое число −6 . К добавьте пять (5) , исходная точка будет перемещена на пять (5) единиц вправо на числовой строки.
Это дает нам –6 + 5 = –1 .
Пример 4 : Упростите, добавив числа, –1 + (–6) .
На этот раз мы складываем два отрицательных числа. Для начала найдите первое число — -1 . Затем добавляет к нему отрицательное число 6 , что означает перемещение существующей точки на 6 единиц влево на числовой прямой.
Следовательно, имеем –1 + (–6) = –7 .
II. Шаги по вычитанию чисел путем преобразования в сложение в числовой строке
Процесс вычитания чисел очень похож на сложение чисел с очень небольшим «поворотом».Уловка состоит в том, чтобы изменить операцию с вычитания на сложение, а затем переключить знак числа, которое следует за ним.
Другими словами, «вычесть» означает « добавить его противоположное ».
Примеры вычитания чисел в числовой строке
Пример 5 : Упростите, вычитая числа, 5 — (+6) .
Как упоминалось ранее, вычитание — это просто сложение. После изменения операции с вычитания на сложение мы должны принять противоположный знак числа, следующего за ним.Это означает, что мы можем переписать задачу как
5 — (+6) → 5 + (–6)
Поскольку мы уже знаем, как добавлять, эта проблема должна быть легкой! Мы находим первое число, которое составляет 5 , а затем перемещаем его на 6 единиц влево на .
Это дает нам ответ 5 — (+6) = 5 + (–6) = –1 .
Пример 6 : Упростите, вычитая числа, –4 — (–7) .
Это пример вычитания двух отрицательных чисел.Давайте превратим это вычитание в задачу сложения. Помните, всегда добавляйте к противоположному.
–4 — (–7) → –4 + (+7)
Начните с поиска первого числа, −4 , а затем переместите его на 7 единиц вправо на числовой строки.
Получаем 3. Поэтому –4 — (–7) = –4 + (+7) = 3 .
Деление как повторное вычитание — полное занятие для 3 класса
Это законченный урок с обучением и упражнениями, показывающий, как деление можно рассматривать как повторное вычитание.Он предназначен для третьего класса.
Учащиеся решают деления, «вычитая» или вычеркивая группы одинакового размера из общей суммы в визуальной модели, пока ничего не останется. Примеры показывают, как можно решить деление, многократно вычитая одно и то же число (делитель). Часто на самом деле проще сложить множитель или вычесть и выяснить, сколько раз вы будете складывать число (делитель), пока не достигнете делимого.
Урок также показывает, как переходы числовые линии связаны с этой концепцией: мы прыгаем назад от делимого, делая прыжки одинакового размера (размер является делителем), пока не достигнем нуля.На уроке также есть несколько задач со словами.
Вы нарисовали _____ групп по четыре человека. |
20-4-4-4-4-4-4 = 0 Это повторяется
вычитание.Вы вычитаете 4 несколько раз, пока не дойдете до нуля. |
1. Создавайте группы, но мысленно «отодвиньте их» или вычесть. Напишите предложение на вычитание.
DIVISION можно решить путем повторного вычитания : | |||||||||||||||||||||||||||||
20 ÷ 4 = ?? 20-4-4-4-4-4-4 = 0. | 75 ÷ 25 = ??
Я трижды вычитал 25, | 84 ÷ 21 = ??
Я вычел 21 четыре раза, | |||||||||||||||||||||||||||
Часто удобнее добавить вместо вычесть:
Поскольку 13 + 13 = 26, | Поскольку 25 + 25 + 25 = 75, | Поскольку 21 + 21 + 21 + 21 = 84, |
2. Напишите предложение умножения И предложение деления, которое подходит факты сложения / вычитания.
а. 15-5-5-5 = 0 ___ × ___ = ______ _____ ÷ ___ = ____ | б. ____ — 20-20-20-20-20-20 = 0 ___ × ___ = ______ ___ ÷ ___ = ___ |
с. _____ — 23-23-23 = 0 ___ × ___ = ______ ___ ÷ ___ = ___ | г. ____ — 14 — 14 — 14 — 14 — 14 = 0 ___ × ___ = ______ ___ ÷ ___ = ___ |
3. Напишите предложение на вычитание для каждого предложения деления.
а. 45 ÷ 15 = _______ 45 — | б. 32 ÷ 8 = _______ 32 — |
с. 100 ÷ 20 = _______ 100 — | г. 50 ÷ 10 = _______ 50 — |
e. 50 ÷ 25 = _______ 50 — | ф. 78 ÷ 26 = _______ 78 — |
| Умножение как
прыгает на числовую строку. 5 × 4 = 20. Пять прыжков из 4 получают вы к 20. |
| Отдел есть
нравится делать прыжки
из четырех назад от 20 до 0: 20 ÷ 4 = 5. 20 — 4 — 4 — 4 — 4 — 4 = 0 Пять прыжков из 4 дают вам от 20 до 0. |
Какое деление изображено здесь? |
4. Нарисуйте прыжки назад, чтобы проиллюстрировать разделение предложений.
Нарисуйте прыжки назад, чтобы проиллюстрировать разделение предложений.
| а. |
| б. |
| г. |
| г. |
| e. |
| ф. |
| г. |
| ч. |
| i. |
5. Решите, используя повторное вычитание ИЛИ сложение разделенный.
а. 90 ÷ 30 = ______ 30 ÷ 15 = ______ | б. 34 ÷ 17 = ______ 69 ÷ 23 = ______ | г. 32 ÷ 16 = ______ 72 ÷ 18 = ______ | г. 90 ÷ 15 = ______ 90 ÷ 18 = ______ |
6. Если 12 × 2 = 24,
тогда 13 × 2 — это _____. Как насчет разделения? Используйте предыдущий
проблема, чтобы помочь вам решить следующую.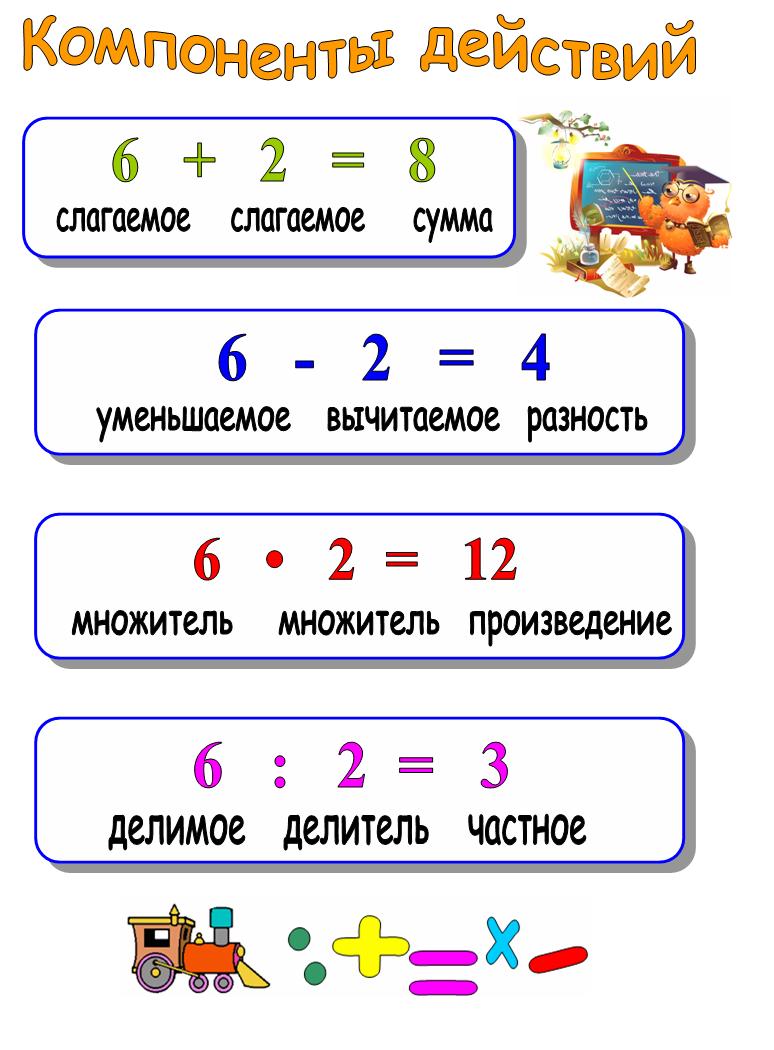
а. 26 ÷ 2 = ______ 28 ÷ 2 = ______ 30 ÷ 2 = ______ | б. 36 ÷ 2 = ______ 38 ÷ 2 = ______ 42 ÷ 2 = ______ | г. 50 ÷ 2 = ______ 52 ÷ 2 = ______ 58 ÷ 2 = ______ | г. 66 ÷ 2 = ______ 70 ÷ 2 = ______ 78 ÷ 2 = ______ |
7. Попробуйте сделать то же самое при делении на 3.
а. 36 ÷ 3 = ______ 39 ÷ 3 = ______ | б. 45 ÷ 3 = ______ 51 ÷ 3 = ______ | г. 69 ÷ 3 = ______ 72 ÷ 3 = ______ | г. 90 ÷ 3 = ______ 99 ÷ 3 = ______ |
8. Устраните проблемы.
а. Заполните таблицы расписания чтения Алисы, если
Если в ее книге 235 страниц, и она хочет прочитать ее через две недели, что расписание чтения она должна выбрать? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
б. Джерри читает 25 страниц
день. Сколько страниц он читает Джерри читает 25 страниц
день. Сколько страниц он читает | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| с. В книге Джерри 325 страниц. Сколько дней ему нужно, чтобы это прочитать? Используйте предыдущее упражнение, чтобы помочь. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| г. В книжном магазине есть
много копий одной и той же книги на полке. Одна книга толщиной 2 см.Заполните Таблица:
Сколько книг поместится на полку длиной 66 см? |
Этот урок взят из книги Марии Миллер Math Mammoth Division 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
В каком порядке студенты должны быстро изучать математические факты?
Базовый, Дополнительный и Альтернативный — существует множество различных программ Rocket Math. Но какую программу следует использовать в первую очередь? И в каком порядке вы должны учить математическим фактам? Ну, все зависит от класса, который вы преподаете, и быстрых математических фактов, которые ваши ученики уже запомнили.
Но какую программу следует использовать в первую очередь? И в каком порядке вы должны учить математическим фактам? Ну, все зависит от класса, который вы преподаете, и быстрых математических фактов, которые ваши ученики уже запомнили.
Обзор быстрых математических программ фактов Rocket Math
Rocket Math предлагает несколько программ, потому что это несколько способов быстро научить математике. Вот ссылка на версию для печати различных программ Rocket Math, показанных здесь .
Основная программа
Основная программаRocket Math включает сложение, вычитание, умножение и деление (от 1 до 9). Базовую программу должны освоить все студенты.
Альтернативная программа: Fact Families
Есть еще один способ познания фактов — математика семейства фактов. Вместо того, чтобы изучать все факты сложения, учащиеся могут одновременно изучать факты сложения и вычитания.Семейство фактов состоит из четырех связанных фактов, например: 3 + 2 = 5, 2 + 3 = 5, 5 — 3 = 2, 5 — 2 = 3. В качестве альтернативы использованию базовой программы учащиеся могут изучать группы фактов. до 10 в первом классе. Затем учащиеся могут перейти в высшие семьи от 11 до 18 во втором классе. Нет четких доказательств того, что этот способ лучше или способ отдельных операций лучше. Поэтому мы предлагаем оба варианта.
Дополнительные программы
Остальные программы быстрой математической обработки фактов, такие как Rocket Writing for Numerals или Skip Counting, не являются обязательными.Вы должны предлагать эти программы студентам только после того, как они запомнят быстрые математические факты с помощью базовой программы или альтернативной программы.
Единственное исключение — школа, где ученики детского сада не имели возможности научиться быстро и легко писать цифры. В этом случае вы можете потратить первые два месяца первого года обучения на то, чтобы познакомить учащихся с ракетным письмом для цифр, прежде чем приступить к сложению (от 1 до 9).
Давайте подробнее рассмотрим, как реализовать каждую программу в разных классах.
Факты по математике для первого класса: Дополнение
Программа быстрой математики для первоклассников Rocket Math включает:
- Основная программа
- Альтернативная программа
- Фактические семейства (1-10) Сложить и вычесть
- Дополнительные программы
- Ракетный ввод цифр
- Добавить к 20
Если учащиеся первого класса тратят весь год на прохождение комплектов от А до Я в дополнение к базовой программе, им нужна дополнительная помощь.Вы должны вмешаться, чтобы помочь студентам, которым требуется больше недели, чтобы пройти уровень. Часто им нужно тренироваться лучше или тренироваться с лучшим партнером. Некоторым, возможно, потребуется практиковать второй раз в течение дня или дома вечером. Учащиеся первого класса, закончившие 1–9 баллов, могут перейти к дополнительной программе «Добавить к 20» на оставшуюся часть года.
Аналогичным образом, если вы решите преподавать «Фактические семьи» (1-10) «Сложение и вычитание из альтернативной программы» вместо использования базовой программы, ваши ученики могут использовать дополнительные программы для дополнительного обучения.
Математические факты для второго класса: сложение и вычитание
Программа быстрой математики для второклассников Rocket Math включает:
- Основная программа
- (1s-9s) Дополнение
- (1s-9s) Вычитание
- Альтернативная программа
- Фактические семейства (1-10) Сложить и вычесть
- Факт Семейства Часть вторая (11-18) Сложить и вычесть
- Дополнительные программы
- Вычесть из 20
- Подсчет пропусков
Ученики второго класса должны пройти сложение перед тем, как приступить к вычитанию (1–9).Они также могут протестировать добавление через Зонды размещения. Второклассники, которые не могут сдать экзамен по сложению в первом классе или не сдали его в первом классе, должны сосредоточиться на добавлении. Только после прохождения набора Z сложения они могут перейти к вычитанию.
Второклассники, которые не могут сдать экзамен по сложению в первом классе или не сдали его в первом классе, должны сосредоточиться на добавлении. Только после прохождения набора Z сложения они могут перейти к вычитанию.
Вы можете заменить Базовая программа (1s-9s) сложением и (1s-9s) вычитанием для фактических семейств альтернативной программы (1-10) Add & Subtract и Fact Families Part Two (11-18) Add & Subtract.
Ученики второго класса, выполнившие сложение и вычитание 1s-9 (или альтернативную программу), могут перейти к вычитанию из 20.Учащиеся, закончившие «Вычесть из 20», могут выполнять «счетчик пропусков», который отлично подготовит учащихся к изучению фактов умножения.
Математические факты для третьего класса: умножение
Нет альтернативных программ для третьеклассников от Rocket Math. Есть только базовые и дополнительные программы. К ним относятся:
- Основная программа
- (1s-9s) Умножение (приоритет)
- (1s-9s) Дополнение
- (1s-9s) Вычитание
- Дополнительные программы
- 10s, 11s, 12s Умножение
- Факторы
В третьем классе умножение имеет приоритет, даже если учащиеся не освоили сложение и вычитание. Факты умножения настолько важны для остальной части высшей математики, что без фактов умножения учащиеся становятся еще более искалеченными, чем им приходится пересчитывать на пальцах задачи сложения и вычитания. Так что сначала сделайте умножение. Затем, если есть время, учащиеся, которым это необходимо, могут вернуться и освоить сложение и вычитание. Как только все три из этих основных операций будут выполнены, учащиеся могут переходить к 10, 11, 12 в умножении (одна из дополнительных программ).Если учащиеся успешно проходят каждую программу и в учебном году остается достаточно времени, введите следующую программу «Факторы».
Математические факты для четвертого класса: умножение и деление
Как и программы для третьеклассников, для четвероклассников нет альтернативных программ.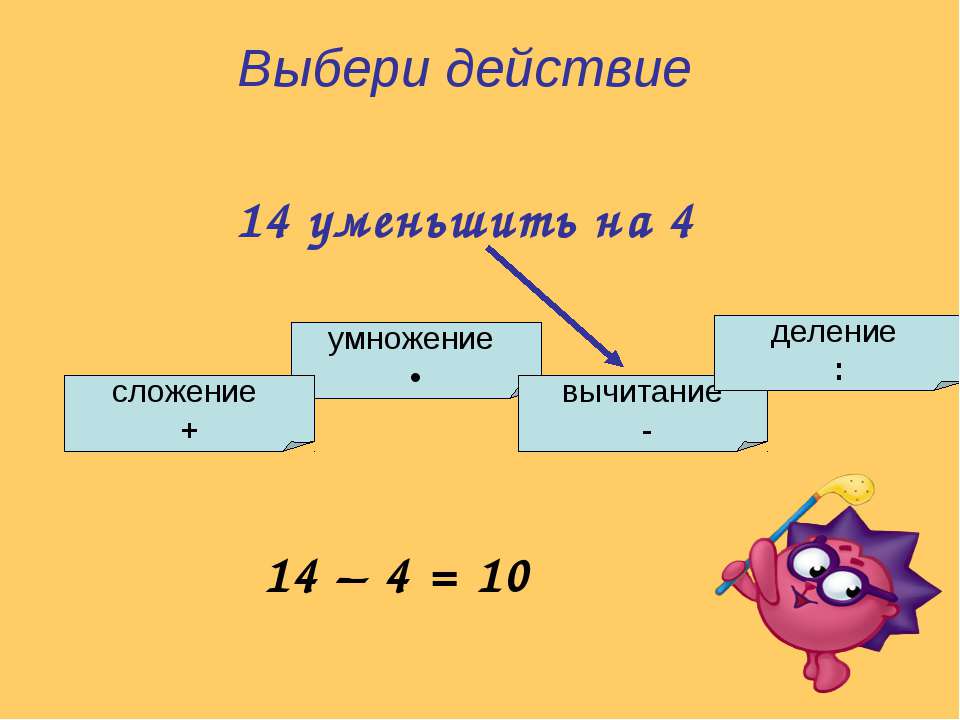
 ..».
..».



 Вот как она звучит:
Вот как она звучит:

 ..
..

 Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи. 

 действия, записанные в скобках;
действия, записанные в скобках; Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие — в скобках, второе — деление, третье — сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения. 3 класс. — М.: Просвещение, 2012.
3 класс. — М.: Просвещение, 2012.
 Сейчас расстояние между собакой и кошкой 30 м. Через сколько секунд собака догонит кошку, если скорость собаки 10 м/с, а кошки — 7 м/с?
Сейчас расстояние между собакой и кошкой 30 м. Через сколько секунд собака догонит кошку, если скорость собаки 10 м/с, а кошки — 7 м/с? 5 × 4 = 4 + 4 + 4 + 4 + 4 = 20.
5 × 4 = 4 + 4 + 4 + 4 + 4 = 20.
