Порядок действий в примерах по математике

Опубликовано 30.04.202221.09.2022 от Admin — Оставить комментарий

В статье рассмотрим порядок действий в примерах по математике, которые содержат скобки, умножение, деление, сложение и вычитание. В статье также приведены примеры, начиная от простых и заканчивая сложными.

Правила выполнения действий для решения примеров:

1. Сначала вычислить то, что находится в скобках. Если скобок нет, то переходим к следующему пункту.
2. Читаем выражение слева направо. Если встретится умножение или деление, то сразу же выполняем эту операцию. Если нет умножения или деления, то переходим к следующему пункту.
3. Читаем выражение слева направо. Если встретится сложение или вычитание, то сразу же выполняем эту операцию.

 

Пример 1.    12 –  3 + 2 + 5  

Читаем его слева направо:
1) 12 — 3 = 9. Запишем число 9 в главном выражении ➜  9+2+5

2) 9 + 2 = 11. Запишем число 11 в главном выражении ➜  11+5
3) 11 + 5 = 16.
Ответ: 12 — 3 + 2 + 5 = 16

Иногда удобно расставить порядок действий над самим выражением. Для этого над операцией, которую необходимо выполнить, указывают её очередь. К примеру, в выражении 10 − 1 + 2 + 3 все действия выполняются последовательно слева направо, поэтому для него можно определить следующий порядок:

1          2           3

12  – 3  +  2  +  5  =  16

Также, можно поставить знак равенства и сразу начать вычислять выражение в порядке приоритета действий:

1          2           3

12  – 3  +  2  +  5  =  9 + 2 + 5 = 11 + 5 = 16

 

Пример 2.    12 – (7 + 2) + 5 × 3  

Применим правила порядка действий. Прочитаем правила в порядке их приоритета.
1) сначала вычислить то, что находится в скобках: 7+2=9. Запишем полученное число 9 в главном выражении вместо выражения в скобках ➜  12-9+5×3

2) вычислить умножение и деление: 5×3=15. Запишем полученное число 15 в главном выражении ➜  12-9+15
3) вычислить сложение и вычитание: 12-9+15.

3         1          4       2

12 – (7 + 2) + 5 × 3  =   12 – 9 + 5 × 3 = 12 – 9 + 15 = 3 + 15 = 18

 

Пример 3.   20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7)  

Расставим порядок действий.

6       3         7          4        1          5        8             2

20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7)

1) Действие в скобках будет первым. Так как в примере скобки встречаются два раза, то выполняем действия в скобках по порядку 7-3=4 и 12-7=5
2) далее выполняется умножение и деление в порядке следования
3) и последним выполняется умножение и деление в порядке следования

6        3        7         4         1          5       8             2

1) 20 – 5 × 3 + 24 : (7 – 3) × 2 + (12 – 7) = 20 – 5 × 3 + 24 : 4 × 2 + 5 = 2) 20 – 5 × 3 + 24 : 4 × 2 + 5 = 20 – 15 + 6 × 2 + 5 = 20 – 15 + 12 + 5 = 3) 20 – 15 + 12 + 5 = 5 + 12 + 5 = 17 + 5 = 22

Таким образом, для правильного решения примеров по математике необходимо правильно определить порядок действий в примерах.

Для тренировки решения примеров по математике на порядок действий можно скачать программы:

• Порядок действий в пределах 20 (сложение и вычитание)
• Порядок действий в пределах 100 (все действия)
• Порядок действий в пределах 1000 (все действия)
• Сложные примеры на порядок действий

Для освоения темы вам также могут понадобится темы: раскрытие скобок и законы математики.

Рубрика: Для школьников

Метка Математика

Внимание! Математическое Действие Начинается Только с…

Главная » Ментальная Арифметика

15.04.2021

01.03.2019

Если вас попросят решить что-то вроде « 4 + 2 × 3 », то естественно возникает вопрос: «Как мне это сделать? Потому что есть два варианта!» Я мог бы добавить сначала:

4 + 2 × 3 = (4 + 2) × 3 = 6 × 3 = 18

… или я мог бы умножить сначала:

4 + 2 × 3 = 4 + (2 × 3) = 4 + 6 = 10

Какой ответ правильный?

Разберем аналогичные примеры:

Для того  чтобы решить пример с примерами чисел,нужно прежде всего знать правила

Если в выражении скобок нет, то:

• сначала выполняем слева направо все действия умножения и деления;
• а потом слева направо все действия сложения и вычитания.

Пример:

( 10+6) — 38=

Порядок выполнения действий:
1) в скобках: 10 + 6 = 16;
2) вычитание: 38 – 16 = 22.

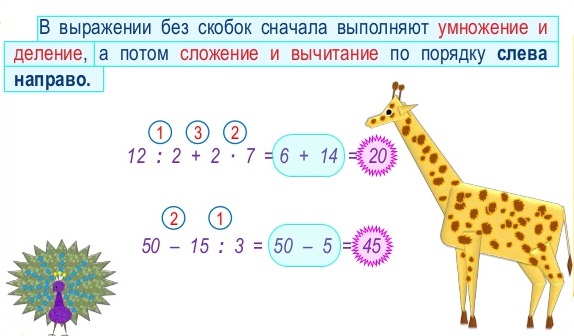
Если в выражение без скобок входит только сложение и вычитание, или только умножение и деление, то действия выполняются по порядку слева направо.

10 ÷ 2 × 4 = 20;

Порядок выполнения действий:
1) слева направо, сначала деление: 10 ÷ 2 = 5;
2) умножение: 5 × 4 = 20;

10 + 4 – 3 = 11, т. е.:

1) 10 + 4 = 14;
2) 14 – 3 = 11.

Если в выражении без скобок есть не только сложение и вычитание, но и умножение или деление, то действия выполняются по порядку слева направо, но преимущество имеет умножение и деление, их выполняют в первую очередь, а за ними и сложение с вычитанием.

Рассмотрим порядок действийв следующем примере.

Напоминаем вам, что порядок действий в математикерасставляется слева направо (от начала к концу примера).

При вычислении значения выражения можно вести запись двумя способами.

Первый способ

• Каждое действие записывается отдельно со своим номером под примером.
• После выполнения последнего действия ответ обязательно записывается в исходный пример.

Запомните! При расчёте результатов действий с двузначными и/или трёхзначными числами обязательно приводите свои расчёты в столбик.

Второй способ

• Второй способ называется запись «цепочкой». Все вычисления проводятся в точно таком же порядке действий, но результаты записываются сразу после знака равно.

Запомните!Если выражение содержит скобки, то сначала выполняют действия в скобках.

Внутри самих скобок действует правило порядка действий как в выражениях без скобок.

Если внутри скобок находятся ещё одни скобки, то сначала выполняются действия внутри вложенных (внутренних) скобок.

Порядок действий и возведение в степень

Если в примере содержится числовое или буквенное выражение в скобках, которое надо возвести в степень, то:

• Сначала выполняем все действия внутри скобок
• Затем возводим в степень все скобки и числа, стоящие в степени, слева направо (от начала к концу примера).
• Выполняем оставшиеся действия в обычном порядке

Теперь решаете вы:

18 ÷ 2 – 2 × 3 + 12 ÷ 3 =

Проверяем как вы решали…

Порядок выполнения действий:

1) 18 ÷ 2 = 9;
2) 2 × 3 = 6;
3) 12 ÷ 3 = 4;
4) 9 – 6 = 3;

т.е. слева направо – результат первого действия минус результат второго;

5) 3 + 4 = 7;

т.е. результат четвертого действия плюс результат третьего;

Если в выражении есть скобки, то сначала выполняются выражения в скобках, затем умножение и деление, а уж потом сложение с вычитанием.

30 + 6 × (13 – 9) = 54, т.е.:

1) выражение в скобках: 13 – 9 = 4;
2) умножение: 6 × 4 = 24;
3) сложение: 30 + 24 = 54;

Итак, подведем итоги. Прежде чем приступить к вычислению, надо проанализировать выражение: есть ли в нем скобки и какие действия в нем имеются. После этого приступать к вычислениям в следующем порядке:

1) действия, заключенные в скобках;
2) умножение и деление;
3) сложение и вычитание.

Значение PEMDAS с примерами — Mashup Math

Сообщение от: Энтони Персико

В математике есть нечто, называемое порядком операций , которое является правилом для решения математических задач, которые имеют более одной операции (сложение, вычитание, умножение и т. д.). ). Изучая математику и изучая, как правильно использовать порядок операций, многие люди полагаются на общую мнемонику, известную как PEMDAS, в качестве средства памяти для запоминания порядка операций.

PEMDAS Значение:

P = Saxesis

E = Экспоненты

M = Умножение

D = разделение

A = Добавление

S = подложка

Эти операции должны выполняться слева

S = подложка

. вправо, где самая левая операция выполняется первой. Но это только общее правило для запоминания порядка операций и есть ключевые нюансы связи между умножением/делением и сложением/вычитанием, которые необходимо помнить помимо мнемоники, PEMDAS, иначе она становится очень ненадежной инструмент, который часто приводит к получению неправильных ответов на, казалось бы, математические задачи. Эти ключевые нюансы выделены в разделе примеров ниже.

PEMDAS Значение: Ключевые идеи

PEMDAS существует уже давно, и многие студенты-математики учат фразу «Пожалуйста, извините, моя дорогая тетя Салли», чтобы запомнить порядок математических операций.

Тем не менее, PEMDAS не является идеальной мнемоникой для запоминания того, как правильно выполнять

порядок операций , но может быть полезным инструментом, доказавшим, что вы помните несколько чрезвычайно важных нюансов:

• Всегда выполняйте скобки и /или группы первых

• После круглых скобок и группировок выполнить операции сложения и/или вычитания ( в зависимости от того, что наступит раньше слева направо)

PEMDAS Значение: Примеры

 Одно дело помнить порядок операций, и совсем другое — знать, как его использовать для правильного решения математических задач. На самом деле, многие старожилы могут легко вспомнить фразу «Пожалуйста, извините, моя дорогая тетя Салли» спустя десятилетия после окончания школы, но понятия не имеют, что означает PEMDAS и как правильно ее использовать.

 Опять же, PEMDAS полезен только как мнемоника, если вы также помните ранее упомянутые ключевые идеи и нюансы. Теперь давайте рассмотрим несколько примеров того, как правильно использовать PEMDAS для выполнения порядка операций.

PEMDAS Пример 01: (3+1) x 4

Сначала решите, что находится в скобках. В этом случае 3+1=4.

 Затем выполните умножение: 4 x 4 = 16

PEMDAS Пример 02: 92=9. Наконец, 27÷3 = 9 

.

PEMDAS Пример 03: 10 x 6 + 1

Для начала, когда нет скобок/группировок и/или показателей степени, вы можете пропустить P и E в PEMDAS.

Согласно PEMDAS, вы должны выполнить умножение/деление перед сложением/вычитанием, поэтому вы можете решить эту задачу слева направо:

 10×6 = 60 и 60 + 1 = 61

PEMDAS Пример 04: 75 — 10 x 5

Опять же, PEMDAS требует выполнения умножения/деления перед сложением/вычитанием, поэтому в этом примере; вы не выполняете операции слева направо.

В этом случае сначала выполните 10 х 5 = 50, а затем выполните 75 – 50 = 25.

PEMDAS Пример 05: 8 x 8 ÷ 16

Этот пример подчеркивает ght s, где ключевые нюансы PEMDAS имеют огромное значение. Помните, что PEMDAS требует, чтобы вы решали умножение/деление слева направо в зависимости от того, что наступит раньше.

В этом примере при движении слева направо сначала идет умножение, поэтому сначала вы должны выполнить 8 x 8 = 64.

Затем вы должны выполнить деление: 64 ÷ 16 = 4

Примечание: Если бы вы строго следовали PEMDAS, двигаясь слева направо в этом примере, вы бы получили правильный ответ, но давайте рассмотрим пример, когда деление идет первым, а умножение — вторым.

PEMDAS Пример 06: 42 ÷ 7 x 3

Чтобы правильно решить эту задачу, вы должны помнить, что ключевой нюанс значения PEMDAS заключается в том, что вы выполняете умножение/деление и сложение/вычитание на основе какая операция идет первой слева направо.

 Тот факт, что M (умножение) стоит перед D (деление) в PEMDAS, не означает, что вы всегда выполняете умножение первым.

Обратите внимание, что в этом примере есть только две операции — деление и умножение. В отличие от предыдущего примера, на этот раз сначала идет деление, поэтому вам нужно выполнить 42 ÷ 7=6 сначала, а затем 6×3=18 секунд.

Примечание: Многие учащиеся неправильно используют PEMDAS в таких примерах и сначала выполняют умножение 42 / 21 = 2. Обратите внимание, что 2 не является правильным ответом.

PEMDAS Значение: Почему это важно

 

Правильное применение порядка операций и использование PEMDAS стало очень популярным в последние годы из-за вирусных математических задач, которые появляются в социальных сетях. Такие сообщения популярны, потому что люди предполагают, что правильный способ применить порядок операций — выполнять каждую операцию слева направо. Поскольку большинство людей неправильно решают эти, казалось бы, простые математические задачи, им предлагается комментировать и делиться ими, что быстро распространяет пост и носит вирусный характер.

 

Однако, если бы люди могли помнить (A) порядок операций с использованием мнемоники, такой как PEMDAS (или еще более полезной, известной как GEMS), и (B) нюансы правильного применения порядка операций (а именно отношения между умножением/делением и сложением/вычитанием), то такие вирусные задачи можно было бы легко решить без особых споров.

 

PEMDAS Значение: Заключение

  PEMDAS является распространенным, но лишь отчасти полезным мнемоническим знаком для запоминания порядка операций в математике. PEMDAS относится к порядку операций следующим образом: скобки, возведения в степень, умножение, деление, сложение и вычитание. В то время как многие люди помнят PEMDAS, используя известную фразу «Пожалуйста, извините, моя дорогая тетя Салли», они часто забывают о важном нюансе, что умножение не выполняется автоматически перед делением, а сложение не выполняется автоматически перед вычитанием (умножение/деление и сложение/вычитание выполняются автоматически). слева направо в зависимости от того, какая операция наступит раньше). Это распространенное заблуждение обесценивает PEMDAS как надежный инструмент для запоминания и является основной причиной того, что, казалось бы, простые математические задачи становятся вирусными в социальных сетях, потому что большой процент взрослых может помнить мнемонические правила спустя десятилетия после окончания школы, но не может получить правильный ответ.

PEMDAS по-прежнему используется как стратегия для запоминания порядка операций больше из-за ностальгии и сопротивления изменениям, чем из-за того, что это самая эффективная стратегия. И хотя использование мнемоники редко бывает хорошей стратегией для понимания математических концепций и развития навыков рассуждения, существуют гораздо лучшие альтернативы PEMDAS, включая GEMS, которые значительно надежнее.

Дополнительные бесплатные математические ресурсы для классов K-8:

Комментарий

Порядок операций Java :: K-State Computational Core

Ресурсы

• Слайды

Сценарий видео

Наверное, все мы выучили аббревиатуру PEMDAS, обозначающую порядок операций в математике. Он обозначает круглые скобки, показатели степени, умножение и деление, сложение и вычитание. Столкнувшись с большим математическим уравнением, мы можем использовать этот список, чтобы понять, какие операции следует выполнять в первую очередь.

Языки программирования, такие как Java, также определяют порядок операций. Фактически, он очень похож на тот, с которым мы уже знакомы из математики. Как и в математике, мы должны сначала оценить все в скобках. Затем мы выполняем любые префиксные действия или символы перед переменными, такие как увеличение, уменьшение или отрицание, когда они помещаются перед числом. После этого мы имеем дело с любыми постфиксными действиями, такими как увеличение или уменьшение после переменных. Наконец, мы можем выполнять умножение, деление и операции по модулю, а затем сложение и вычитание слева направо, как мы это делаем в математике. Наконец, оператор присваивания обрабатывается последним, сохраняя результат из правой части в переменную слева.

Чтобы действительно понять, как это работает, давайте рассмотрим пример. Вот простой фрагмент кода, взятый прямо из учебника, который может помочь нам проиллюстрировать, как порядок операций работает в Java.

Во-первых, мы устанавливаем значение x равным 1. Это довольно просто.

Далее мы доходим до этой второй строки, которая будет определять значение y . Давайте сломаем это. Поскольку в этом выражении нет скобок, нам не нужно беспокоиться об этом шаге.

Следующим шагом являются префиксные операторы, такие как здесь оператор приращения. Так как этот оператор ставится перед переменной, мы должны сначала выполнить эту операцию. Итак, мы продолжим и обновим значение x до 2, прежде чем делать что-либо еще.

Далее мы будем обрабатывать любые постфиксные операторы, которые здесь будут операцией декремента. Поскольку он помещается после переменной, мы фактически должны выполнить эту операцию после того, как остальная часть выражения будет вычислена. Итак, мысленно нам нужно добавить новую строку кода ниже этой, которая обновит значение 9. 0207 x после того, как мы закончим.

Теперь можно разобраться с самими операторами. Сначала идут мультипликативные операторы: умножение, деление и по модулю. Мы работаем с ними слева направо, как и в математике. Итак, первая — это операция деления. Мы заменяем переменные их текущими значениями, затем вычисляем результат. Поскольку оба они являются целыми числами, Java будет производить целое число при выполнении деления.

Затем мы можем сделать то же самое для оператора умножения. Мы заменяем любые переменные их текущими значениями, затем выполняем расчет.

Наконец, здесь мы также выполним операцию по модулю.

Далее мы проделаем тот же процесс для любых операторов сложения и вычитания, также слева направо. Итак, сначала мы выполним сложение, а затем вычитание, чтобы получить окончательный результат.

Наконец, мы обработаем оператор присваивания, который присвоит значение 4 y .

Но подождите, мы также должны помнить, что у нас был постфиксный оператор декремента, который представлен этой новой строкой кода, которую мы мысленно добавили в код.