Что сначала — сложение или умножение: правила, порядок выполнения действия и рекомендации — OneKu

Содержание статьи:

• Сложение и вычитание
• Умножение
• Что сначала — умножение или сложение
• Деление
• Скобки
• «Вишенка на торте&raquo
• «Совсем вишня&raquo

С самого начала следует напомнить, чтобы потом не путаться: есть цифры – их 10. От 0 до 9. Есть числа, и они состоят их цифр. Чисел бесконечно много. Точно больше, чем звезд на небе.

Математическое выражение − это записанное с помощью математических символов наставление, какие действия нужно произвести с числами, чтобы получить результат. Не «выйти» на искомый результат, как в статистике, а узнать, сколько их точно было. А вот чего и когда было − уже не входит в сферу интересов арифметики. При этом важно не ошибиться в последовательности действий, что сначала — сложение или умножение? Выражение в школе иногда называют «пример».

Вам будет интересно:Консилиум — это не приговор

Сложение и вычитание

Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.

Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.

Вам будет интересно:Остеоны или система Гаверсова

Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.

Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.

Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.

Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.

Вам будет интересно:Тореро — это… Значение слова

Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.

Сложение столбиком −­­­­­­ это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр.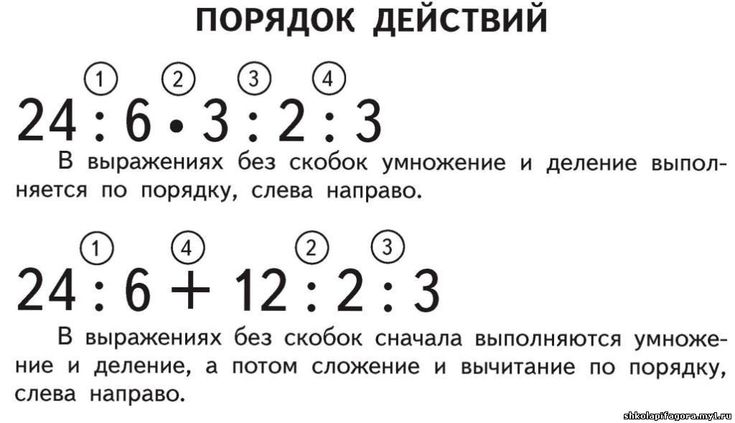 При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.

Умножение

Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.

Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».

Что сначала — умножение или сложение?

Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:

• 5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
• 2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все помидоры сдавали учетчику, он укладывал их по кучкам.

Запишем результат «сбора» урожая в виде выражения:

• 500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
• 50 + 50 – это кучки малолетних работников;
• 70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).

Получаем пример для школы, запись учетчика результатов работы:

500 + 500 +500 +500 +500 + 50 +50 + 70 =?;

Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.

Две кучки по 50 – это тоже можно записать через умножение.

И одна кучка 70 помидоров.

5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?

И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры.

Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.

2500 + 100 + 70 = 2 670

При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.

Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.

Деление

Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.

Скобки

Большое значение в решении примеров имеют скобки. Скобки в арифметике – математический знак, используемый для регулирования последовательности вычислений в выражении (примере).

Умножение и деление имеют приоритет выше, чем сложение и вычитание. А скобки имеют приоритет выше, чем умножение и деление.

Все, что записано в скобках, вычисляется в первую очередь. Если скобки вложенные, то сначала вычисляется выражение во внутренних скобках. И это непреложное правило. Как только выражение в скобках вычислено, скобки пропадают, а на их месте возникает число. Варианты раскрытия скобок с неизвестными здесь не рассматриваются. Так делают до тех пор, пока все они не исчезнут из выражения.

((25-5) : 5 + 2) : 3 =?

Это как коробочки с конфетами в большом мешке. Сначала нужно раскрыть все коробочки и ссыпать в большой мешок: (25 – 5 ) = 20. Пять конфет из коробочки сразу заслали отличнице Люде, которая приболела и в празднике не участвует. Остальные конфеты − в мешок!

Потом связать конфеты в пучки по 5 штук: 20 : 5 = 4.

Потом добавить в мешок еще 2 пучка конфет, чтобы можно было поделить на троих детей без драки. Признаки деления на 3 в данной статье не рассматриваются.

(20 : 5 + 2) : 3 = (4 +2) : 3 = 6 : 3 = 2

Итого: трем детям по два пучка конфет (по пучку в руку), по 5 конфет в пучке.

Если вычислить первые скобки в выражении и переписать все заново, пример станет короче. Метод не быстрый, с большим расходом бумаги, зато удивительно эффективный. Заодно тренирует внимательность при переписывании. Пример приводится к виду, когда остается только один вопрос, сначала умножение или сложение без скобок. То есть к такому виду, когда скобок уже и нет. Но ответ на этот вопрос уже есть, и нет смысла обсуждать, что идет сначала — умножение или сложение.

«Вишенка на торте»

И напоследок. К математическому выражению не применимы правила русского языка – читать и выполнять слева направо:

5 – 8 + 4 = 1;

Это простенький пример может довести до истерики ребенка или испортить вечер его маме. Потому что именной ей придется объяснять второкласснику, что бывают отрицательные числа. Или рушить авторитет «МарьиВановны», которая сказала, что: «Нужно слева направо и по порядку».

«Совсем вишня»

В Сети гуляет пример, вызывающий затруднения у взрослых дяденек и тетенек. Он не совсем по рассматриваемой теме, что сначала — умножение или сложение. Он вроде как про то, что сначала выполняете действие в скобках.

От перестановки слагаемых сумма не изменяется, от перестановки множителей тоже. Нужно просто записывать выражение так, чтобы не было потом мучительно стыдно.

6 : 2 ∙ (1+2) = 6 ∙ ½ ∙ (1+2) = 6 ∙ ½ ∙ 3 = 3 ∙ 3 = 9

Теперь точно все!

Урок по математике на тему: «Порядок выполнения действий в выражениях»

Конспект открытого урока Охрименко Айны Алексеевны

Предмет: математика

Дата: 14. 12.16

Тема: «Порядок выполнения действий в выражениях»

Тип урока: урок закрепления знаний

Цели урока:

• Деятельностная : учиться применять правила порядка выполнения действий в выражениях.

• Содержательная: продолжить формирование системы понятий в разделе «Арифметические действия»

Задачи:

-создать условия для усвоения учащимися правила порядка выполнения действий в выражениях;

— продолжить отработку изученных приёмов устных вычислений ( таблица умножения, деления, сложения, вычитания), учить применять на практике правило нахождения значений выражений;

— развивать наблюдательность, умение сравнивать, анализировать, делать выводы;

— содействовать воспитанию активной личности, воспитывать доброжелательное, уважительное отношение друг к другу.

Планируемые результаты урока:

Личностные — личностная мотивация к познавательной деятельности

Предметные — развитие умений решать учебные и практические задачи, учиться применять правило порядка выполнения действий.

Метапредметные — (регулятивные УУД, познавательные УУД, коммуникативные УУД)- овладение навыками осознанного построения речевых высказываний в соответствии с задачами коммуникации; овладение логическими действиями анализа, синтеза, классификации, причинно-следственных связей, построения рассуждений, отнесения к известным понятиям; готовность слушать собеседника, излагать свое мнение и аргументировать свою точку зрения и оценку событий.

Дидактическое обеспечение: сигнальные карточки, карточки для оценивания, презентация Microsoft Office PowerPoint.

Оборудование: компьютер с мультимедийным проектором.

Ход урока.

1.Организационный момент.

Все услышали звонок ,

Поспешили на урок .

Всех я рада видеть вас ,

Мой любимый 3 класс.

Улыбнемся же друг другу .

Добрый день и добрый час.

— Поприветствуем наших гостей, пожелаем им доброго дня.

— Ребята, а кто из вас любит математику? Почему вы её любите?

— Слайд 1 Начать наш урок мне хотелось бы с высказывания русского учёного, поэта Михаила Васильевича Ломоносова «Математику уже затем изучать нужно, что она ум в порядок приводит». Я думаю, что эти слова будут отличным девизом нашего сегодняшнего урока. 

2. Актуализация опорных знаний.

Устный счёт

А) Игра «Да или нет»

— Поиграем в игру «Да или нет». У каждого из вас на парте лежат сигнальные карточки. Если вы согласны с моим высказыванием, то показываете зелёную карточку, если не согласны – красную.

— При умножении любого числа на 1, получается 1 (нет).

— Чтобы разделить на 10, достаточно дописать 0 (нет, отбросить).

— Умножать на 0 нельзя (нет, можно).

— Чтобы найти делимое, нужно значение частного умножить на делитель (да).

— Чтобы найти неизвестный множитель, нужно значение произведения умножить на известный множитель (нет, разделить).

— В выражениях без скобок все действия выполняются по порядку слева направо (нет, сначала умножение и деление, потом вычитание и сложение).

— С каждым уроком у вас получается всё лучше! Просто замечательно!

Б) Логические упражнения

Слайд 2— Предлагаю выполнить логические задания. Вы готовы?

— Какие два числа, если их перемножить, дают такой же результат, что и при их сложении? (2 и 2)

— Из-под забора видно 6 пар лошадиных ног. Сколько этих животных во дворе? (3)

— Петух, стоя на одной ноге весит 5кг. Сколько он будет весить, стоя на двух ногах? (5кг)

— На руках 10 пальцев. Сколько пальцев на 6 руках? (30)

— Ребята, именно такой работы я и ждала от вас: вы были активны, внимательны, сообразительны.

В) Слайд 3 Работа с геометрическим материалом

— Посмотрите на геометрические фигуры.

— Какая лишняя?

Г) Слайд 4 Математический диктант

— Ребята, предлагаю повторить таблицу умножения. А сделаем мы это необычно.

— Посмотрите на экран. Там изображена таблица. Вам нужно заполнить свободные ячейки таблицы.

— Откройте тетрадочки. Запишите число классная работа. Приступайте к выполнению задания.

— Слайд 5 Давайте проверим. Обменяйтесь, пожалуйста, своими тетрадями. И смотрим внимательно на экран. ( беру несколько тетрадей на оценку)

3.Сообщение темы и целей урока

— Ребята, посмотрите, пожалуйста, на экран. Слайд 6

: ( + ) +

— Что поможет нам правильно решить пример?

— Посмотрите на схему этого выражения, постройте алгоритм работы над этим выражением.

— Сформулируйте тему нашего урока («Порядок выполнения действий в выражениях»). Слайд 7

— Какие цели поставим на урок? (закрепить, повторить порядок выполнения действий в выражениях)

— Все ли хорошо и правильно научились выполнять порядок действий?

— Давайте вспомним правило.

Порядок действий в выражениях особый. 
И в каждом случае, помни, он свой. 
В порядке все действия ты выполняй.

Сначала в скобках все посчитай.

Потом чередом, умножай или дели.

И, наконец, вычитай или сложи.

— Сегодня мы с вами продолжим изучать, как же правильно выполнять порядок действий.

4. Работа над темой урока

А) Фронтальная работа

— Посмотрите, пожалуйста, на экран: Слайд 8

Пример объяснения: 70 : (3+7) + 24( ученик комментирует с места)

1. Смотрю, есть ли в этом выражении скобки.

2. Первым буду выполнять действие в скобках. Над скобками ставлю цифру 1.

3. Дальше выполню деление. Над знаком деления ставлю цифру 2.

4. Последним действием выполняю сложение. Над знаком сложения ставлю цифру 3.

Б) Работа в парах

— Ребята, поработаем в парах.

— Посмотрите внимательно на доску. Правильно ли решены примеры?

— Что нужно сделать?

— Ваша задача записать выражение и поставить скобки так, чтобы равенство было верным.

5+3 ∙ 2 = 16

0 + 24: 3 = 8

(одного ученика вызываю к доске)

В) Физкультминутка

Г) Работа с учебником.

— № 328

Ученик у доски решает задачу на оценку. Записываем задачу в виде выражения.

— № 332 (1). Первый пример – первый ряд

Второй пример – второй ряд

Третий пример – третий ряд.

— Почему у вас всех разные ответы? Несмотря на то, что числа везде одинаковые.

5. Закрепление изученного.

Дифференцированная работа по карточкам.

— Сейчас посмотрим, как вы умеете определять порядок действий в выражениях. В карточках вам надо расставить порядок выполнения действий на каждой схеме.

… + … : … + … * … — …

… : … + … — … — … *(… + …)

… + … (… * … + …) : … — … : … * …

… * … * … — …(… * … — …) + … : …

1. Рефлексия

— Ребята, давайте подведем итог нашего урока.

— Какие цели ставили?

— Цели выполнены?

— Давайте оценим свою работу на уроке. У каждого на парте лежит лист самооценки. Пожалуйста, оцените свою работу на уроке.

7. Д.з.

— Запишем домашнее задание. Откройте свои дневники № 320, № 332 (2).

8. Организационный момент.

— Ребята, встали все ровненько возле своих парт. Большое спасибо за урок! Можете отдыхать.

Порядок операций

Горячая математика

В математике порядок операций — это набор правил, определяющих, какие процедуры следует выполнять в первую очередь, так что, оценивая данное математическое выражение, мы все приходим к одному и тому же ответу.

1 ^ул. : Делайте какие-либо расчеты внутри п арентезы или другие группирующие символы, начиная с самых внутренних и заканчивая разработкой.

2 ^й : Упростить любой

е экспоненциальный выражения.

3 ^рд : Работа все м умножения и г видения, слева направо, по мере их появления.

4 ^й : Работа все а дополнения и с вычитания, слева направо, по мере их появления.

Чтобы вы не запутались, помните ПЕМДАС что означает Скобки, Экспоненты, Умножение-Деление, Сложение-Вычитание.

В Калифорнии мы говорим п великолепный Е землетрясения М да Д Эливер А после- С скакательные суставы

Пример :

Упрощать 3 + 2 × ( 5 − 7 ) 2 .

Сначала выполните операцию в скобках.

знак равно 3 + 2 × ( − 2 ) 2

Затем оцените показатель степени. Поскольку знак минус находится внутри скобок, это означает ( − 2 ) × ( − 2 ) .

знак равно 3 + 2 × 4

Умножьте, а затем добавьте.

знак равно 3 + 8

знак равно 11

Будьте особенно осторожны с такими проблемами, как следующие.

( 3 × 4 ) 2 знак равно 12 2 знак равно 144 потому что круглые скобки стоят перед показателями степени, НО 3 × 4 2 знак равно 48 потому что показатели степени стоят перед умножением.

( − 4 ) 2 знак равно ( − 4 ) ( − 4 ) знак равно 16 НО − 4 × 4 знак равно − 16

3 + 4 ( 5 + 6 ) ≠ 7 ( 5 + 6 ) потому что круглые скобки — это операция, с которой нужно начинать.

Так, 3 + 4 ( 5 + 6 ) знак равно 3 + 4 ( 11 ) знак равно 3 + 44 знак равно 47 .

Также будьте осторожны с дробями. Дробная черта действует как символ группировки, поэтому сначала упростите числитель и знаменатель.

5 + 4 8 − 5 знак равно 93 знак равно 3

Вы можете думать об этом так: если вы переписали дробь в одной строке, используя символ деления, вам понадобятся круглые скобки.

5 + 4 8 − 5 знак равно ( 5 + 4 ) ÷ ( 8 − 5 ) знак равно 9÷ 3 знак равно 3

Объяснение урока: Порядок действий: десятичные дроби

В этом эксплейнере мы научимся вычислять выражения, включающие десятичные дроби, в разных арифметические операции с использованием порядка операций.

Порядок операций является важным соглашением, обеспечивающим правильность числовых выражений. только одно значение. Порядок операций дает нам определенный порядок решения задачи. операции в выражении. Напомним порядок действий.

Порядок операций

Решаем отдельные операции в расчете в следующем порядке очередности.

• Круглые скобки (или группировка): мы всегда сначала решаем элементы в круглых или квадратных скобках, например, (𝑥+3) или [𝑥+3]. Мы также можем иметь группы например 5+34. При дробной группировке мы всегда оцениваем все числителя и всего знаменателя до выполнения деления.
• Показатель степени: например, 10 и 𝑥.
• Умножение и деление: Оба они имеют одинаковый приоритет, поэтому, когда у нас есть выражение, которое имеет более одного умножения и/или деления, мы выполняем порядок операций слева направо.
• Сложение и вычитание: Оба они имеют одинаковый приоритет, поэтому, когда у нас есть выражение, которое имеет более одного сложения и/или вычитания, мы выполняем порядок операции слева направо.

Аббревиатура PEMDAS часто используется для обозначения этого приказа, где буквы обозначают скобки, показатели степени, умножение/деление и сложение/вычитание.

Точно так же, как мы используем порядок операций с целыми числами, мы также применяем их в точно так же и с десятичными числами. Вспомним стратегии, которые мы используем для арифметика с десятичными числами.

Арифметика с десятичными числами

Сложение и вычитание

• Мы можем использовать те же методы сложения и вычитания десятичных дробей, которые мы используем для целые числа; однако метод столбца может быть наиболее полезным, поскольку он сохраняет десятичные разряды четко. Может быть полезно добавить нули в качестве заполнителей в расчетах. если необходимо.

Умножение

• Чтобы умножить десятичные дроби, удалите десятичные точки из чисел, которые нужно умножить, и выполнить умножение. Поставьте в ответе запятую так, чтобы он имел как количество знаков после запятой как сумма знаков после запятой в исходных числах.

Деление

• Чтобы разделить десятичные дроби, сделайте делитель целым числом, умножив его на степень 10, например 10, 100 и 1‎ ‎000. Умножьте делимое на это же число. Мы можем тогда разделить эти числа, что дает тот же ответ, как если бы мы разделили десятичные дроби.

Давайте теперь рассмотрим несколько примеров того, как использовать порядок операций с десятичными числами. числа.

Пример 1. Вычисление десятичного выражения с использованием порядка операций

Определите значение 2×1,3+1,5, используя порядок операции.

Ответ

Чтобы начать использовать порядок операций, мы сначала проверяем, есть ли скобки или группировки. Поскольку в выражении 2×1,3+1,5 нет скобок, мы переходим к следующей категории в порядке операций, которая экспоненты. Поскольку их нет, мы можем перейти к следующему шагу — умножению или разделение. Поскольку есть только одно умножение, 2 × 1,3, мы делаем это первый.

Напомним, что для умножения десятичных дробей 2×1,3 мы рассматриваем числа как целые числа, удалив десятичную точку, что даст 2×13=26. Затем мы заменяем десятичную точку так, чтобы в ответе было столько знаков после запятой, сколько сумма десятичных знаков в исходных числах. Здесь это будет один десятичный знак, так что у нас есть 2 × 1,3 = 2,6, что мы можем заменить в исходном расчете, чтобы получить 2 × 1,3 + 1,5 = 2,6 + 1,5.

Далее мы добавляем 2,6+1,5, что дает следующее: 2,6+1,54,1

Итак, наш ответ: 2×1,3+1,5=4,1.

Пример 2. Вычисление десятичного выражения с использованием порядка операций

Вычислить 68,7−9,9÷3,3−2,5.

Ответ

Чтобы начать использовать порядок операций, мы сначала проверяем, есть ли скобки. Как в выражении 68,7−9,9÷3,3−2,5 скобок нет, мы перейти к следующей категории в порядке операций, которая является показателями. как есть нет, мы можем перейти к следующему шагу в порядке операций, который является умножением или разделение. Поскольку есть только одно деление, 9.9÷3, делаем так первый.

Чтобы разделить десятичные дроби 9,9÷3,3, мы должны умножить делимое, 9,9, и делитель 3,3 на 10, чтобы делитель стал целым числом. Итак, у нас есть 9,9÷3,3=9,93,3=9,9×103,3×10=9933=3.

Тогда получаем 68,7−9,9÷3,3−2,5=68,7−3−2,5.

Теперь у нас осталось только два вычисления вычитания, поэтому следуя порядку операций, мы выполняем их слева направо, начиная с 68,7−3. Мы можем использовать столбчатый метод вычитания. Может быть полезно добавить дополнительную десятичную точку и ноль к нашему значению 3, чтобы помочь в наших вычислениях: 68,7−3,065,7

Мы можем заменить это в нашем расчете, чтобы получить 68,7−3−2,5=65,7−2,5.

Наш окончательный расчет, 65,7−2,5, можно выполнить с помощью столбца метод дает следующее: 65,7−2,563,2

Следовательно, окончательный ответ: 68,7−9,9÷3,3−2,5=63,2.

Пример 3. Вычисление десятичного выражения с использованием порядка операций

Вычислить (0,2)×4(13+7)−5.

Ответ

В этом вычислении у нас есть два набора скобок. Мы можем заметить, что скобки вокруг (0,2) помогают сохранить ясность того, какая часть выражение является основанием экспоненты. (0.2) имеет тот же смысл, что и 0,2. Поскольку это показатель степени, мы оценим его на следующем шаге, после любых других скобок.

Используя порядок операций, первой операцией для вычисления является сложение, содержащееся в скобках (13+7).

Поскольку у нас 13+7=20, мы можем заменить это в вычисление дает 0,2×4(13+7)−5=0,2×4(20)−5.

Поскольку член 4(20) представляет 4×20, мы можем записать вычисление как 0,2×4(13+7)−5=0,2×4(20)−5=0,2×4×20−5. 

Следующим шагом в порядке операций является вычислить показатели. С 0,2=0,2×0,2, вспомните, что при умножении десятичных дробей мы убери запятую и считай числа целыми числами и умножай. Мы тут вычислить 2×2=4. Чтобы найти ответ на 0,2 × 0,2, мы ставим десятичную точку в ответ, 4, так что он имеет то же самое количество знаков после запятой как сумма знаков после запятой в исходных числах. Этот означает, что наш ответ должен иметь два знака после запятой, поэтому цифра 4 будет в сотый столбик.

Следовательно, 0,2=0,2×0,2=0,04.

Заменив это в нашем вычислении, мы получим 0,2×4×20−5=0,04×4×20−5.

У нас есть еще два показатели степени для расчета, 20 и 5. Так как у нас есть 20 = 4005 = 25,   и мы имеем 0,04 × 4 × 20−5 = 0,04 × 4 × 400−25. 

В порядке операций после показателей степени мы имеем умножение и деление. С тех пор, как мы есть 0,04×4×400, мы вычисляем это в порядке слева направо правильно. Чтобы оценить 0,04 × 4, мы удалим десятичную точку от 0,04. и рассмотрим расчет 4×4=16. Поскольку наш ответ будет иметь два десятичных знака, мы имеем 0,04×4=0,16.

Мы можем заменить это в нашем расчете, чтобы получить 0,04×4×400−25=0,16×400−25.

Чтобы вычислить 0,16×400, снова убираем десятичную точку до вычислить 16×400=6400 и поставить запятую так, чтобы 6‎ ‎400 имеет 2 десятичных знака, что дает 0,16 × 400 = 64,00 = 64.

Заменив это в нашем расчете, мы получим 0,16×400−25=64−25.

Таким образом, мы можем оценить это последнее вычисление, чтобы получить 64−25=39.

Это дает нам окончательный ответ: (0,2)×4(13+7)−5=39..

В следующем примере мы увидим, что группировка внутри вычисления имеет тот же приоритет, что и скобки.

Пример 4. Вычисление десятичного выражения, включающего группировку

Вычислить 3,4+9,24,2−0,3×2.

Ответ

Поскольку мы начинаем использовать порядок операций для вычисления этого вопроса, важно обратите внимание, что первая группа, 3. 4+9.24.2, попадет в категория скобок в порядке операций, так как эта часть будет вычисляться первый. Скобки здесь подразумеваются, но так как мы вычисляем все числители и знаменатель сначала, мы могли бы вставить скобки следующим образом: 3,4+9.24,2=((3,4+9,2)÷4,2). Итак, чтобы начать решать 3,4 + 9,24,2−0,3 × 2, мы сначала рассчитать ((3,4+9,2)÷4,2). Когда у нас есть два набора скобок, сначала вычисляем самое внутреннее; здесь мы должны сначала добавить 3.4 и 9.2, что дает следующее: 3,4+9,212,6

Итак, мы имеем 3,4+9,24,2=12,64,2.

Напомним, что для деления десятичных дробей 12,6÷4,2 мы делаем делитель целое число, умножив его на степень 10, а делимое умножим на такое же количество.

Это даст нам 12,64,2=12,6×104,2×10=12642.

Для вычисления 12642 имеем следующее:

Поскольку мы оценили 3,4+9,24,2=3, мы можем ввести это в исходный расчет, что даст 3,4+9,24,2-0,3×2=3-0,3×2.

Поскольку у нас осталось умножение и вычитание, порядок операций означает что мы должны сначала вычислить часть умножения, 0,3 × 2. Мы уберите десятичную точку и считайте, что это 3×2=6, и наш ответ будет иметь столько знаков после запятой, сколько сумма знаков после запятой в числах умножается, в данном случае, на 1 десятичный знак.

Таким образом, мы имеем 0,3×2=0,6, что мы можно заменить в нашем расчете как 3−0,3×2=3−0,6.

Наконец, мы можем вычислить 3−0,6, используя метод столбцов. Это может быть полезно добавить десятичную точку и 0 к нашему значению 3, чтобы сделать вычитание более понятным: 3,0−0,62,4

Итак, наш окончательный ответ: 3,4+9,24,2−0,3×2=2,4.

Пример 5. Поиск пропущенных операторов в десятичном вычислении

Вставьте соответствующие символы из +, −, × и ÷, чтобы расчет был правильным: 8□0,5□40=28.

Ответ

Часто лучший подход к этому типу проблем — проверить более простые варианты сначала сложение и вычитание. Мы видим, что комбинации двух сложений нет. или сложение и вычитание, которое даст ответ 28. Обратите внимание, что два вычитания дали бы отрицательный ответ, а не положительное значение 28.

Если мы проверим два умножения, мы могли бы считать, что множители 28 равны 4 и 7, 14 и 2, и 1, и 28. Мы не можем составить эти множители из чисел 8, 0,5 и 40.

Теперь попробуем выполнить однократное умножение. Чтобы вычислить 0,5×40, напомним, что мы удаляем десятичную точку, чтобы вычислить 5×40=200 и вставьте десятичную точку так, чтобы в ответе было то же количество знаков после запятой, что и сумма десятичных знаков в исходных числах. Следовательно, 0,5×40=20,0=20.

Глядя на первоначальный расчет, мы видим, что добавление дополнительного значения 8 даст нужный ответ. Следовательно, имеем 8+0,5×40=28.

Обратите внимание: поскольку порядок операций означает, что мы будем выполнять умножение во-первых, нет необходимости добавлять круглые скобки к какой-либо части вычисления.