Порядок действий в Математике
Основные операции в математике
Основные операции, которые используют в математике — это сложение, вычитание, умножение и деление. Помимо этих операций есть ещё операции отношения, такие как равно (=), больше (>), меньше (<), больше или равно (≥), меньше или равно (≤), не равно (≠).
Операции действия:
- сложение (+)
- вычитание (-)
- умножение (*)
- деление (:)
Операции отношения:
- равно (=)
- больше (>)
- меньше (<)
- больше или равно (≥)
- меньше или равно (≤)
- не равно (≠)
Сложение — операция, которая позволяет объединить два слагаемых.
- Запись сложения: 5 + 1 = 6, где 5 и 1 — слагаемые, 6 — сумма.
Вычитание — действие, обратное сложению.
- Запись вычитания: 10 — 1 = 9, где 10 — уменьшаемое, 1 — вычитаемое, 9 — разность.

Если разность 9, сложить с вычитаемым 1, то получится уменьшаемое 10. Операция сложения 9 + 1 = 10 является контрольной проверкой вычитания 10 — 1 = 9.
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.
- Запись: 3 * 4 = 12, где 3 — множимое, 4 — множитель, 12 — произведение.
- 3 * 4 = 3 + 3 + 3 + 3
В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же. Например: 5 * 2 = 5 + 5 = 10.
Поэтому и множитель, и множимое называют сомножителями.
Деление — арифметическое действие обратное умножению.
- Запись: 30 : 6 = 5 или 30/6 = 5, где 30 — делимое, 6 — делитель, 5 — частное.
В этом случае произведение делителя 6 и частного 5, в качестве проверки, дает делимое 30.
Если в результате операции деления, частное является не целым числом, то его можно представить в виде дроби.
Возведение степень — операция умножения числа на самого себя несколько раз. 4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
4 = 81 — возведение числа 3 в четвертую степень дает 81 (проверка извлечения корня).
При знаке квадратного корня показатель корня принято опускать: √16 = 4.
3√8 = 2 — корень третьей степени называется — кубическим.
Сложение и вычитание, умножение и деление, возведение в степень и извлечение корня попарно представляют обратные друг другу действия. Далее узнаем порядок выполнения арифметических действий.
Порядок вычисления простых выражений
Есть однозначное правило, которое определяет порядок выполнения действий в выражениях без скобок:
- действия выполняются по порядку слева направо
- сначала выполняется умножение и деление, а затем — сложение и вычитание.
Из этого правила становится яснее, какое действие выполняется первым. Универсального ответа нет, нужно анализировать каждый пример и подбирать ход решения самостоятельно.
Что первое, умножение или деление? — По порядку слева направо. Сначала умножение или сложение? — Умножаем, потом складываем. |
Порядок выполнения действий в математике (слева направо) можно объяснить тем, что в нашей культуре принято вести записи слева направо. А необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Рассмотрим порядок арифметических действий в примерах.
Пример 1. Выполнить вычисление: 11- 2 + 5.
Как решаем:
В нашем выражении нет скобок, умножение и деление отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычтем два из одиннадцати, затем прибавим к остатку пять и в итоге получим четырнадцать.
Вот запись всего решения: 11- 2 + 5 = 9 + 5 = 14.
Ответ: 14.
Пример 2. В каком порядке выполнить вычисления в выражении: 10 : 2 * 7 : 5?
Как рассуждаем:
Чтобы не ошибиться, перечитаем правило для выражений без скобок. У нас есть только умножение и деление — значит сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Сначала выполняем деление десяти на два, результат умножаем на семь и получившееся в число делим на пять.
Запись всего решения выглядит так: 10 : 2 * 7 : 5 = 5 * 7 : 5 = 35 : 5 = 7.
Ответ: 7.
Пока новые знания не стали привычными, чтобы не перепутать последовательность действий при вычислении значения выражения, удобно над знаками арифметический действий расставить цифры, которые соответствуют порядку их выполнения.
Например, в такой последовательности можно решить пример по действиям:
Действия первой и второй ступени
В некоторых учебниках по математике можно встретить разделение арифметических действий на действия первой и второй ступени.
- Действиями первой ступени называют сложение и вычитание, а умножение и деление — действиями второй ступени.
С этими терминами правило определения порядка выполнения действий звучит так:
Если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем — действия первой ступени (сложение и вычитание).
Порядок вычислений в выражениях со скобками
Иногда выражения могут содержать скобки, которые подсказывают порядок выполнения математических действий. В этом случае правило звучит так:
Сначала выполнить действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем — сложение и вычитание.
Выражения в скобках рассматриваются как составные части исходного выражения. В них сохраняется уже известный нам порядок выполнения действий.
Рассмотрим порядок выполнения действий на примерах со скобками.
Пример 1. Вычислить: 10 + (8 — 2 * 3) * (12 — 4) : 2.
Как правильно решить пример:
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, которые заключены в эти скобки.
Начнем с первого 8 — 2 * 3. Что сначала, умножение или вычитание? Мы уже знаем правильный ответ: умножение, затем вычитание. Получается так:
8 — 2 * 3 = 8 — 6 = 2.
Переходим ко второму выражению в скобках 12 — 4. Здесь только одно действие – вычитание, выполняем: 12 — 4 = 8.
Подставляем полученные значения в исходное выражение:
10 + (8 — 2 * 3) * (12 — 4) : 2 = 10 + 2 * 8 : 2.
Порядок действий: умножение, деление, и только потом — сложение. Получится:
10 + 2 * 8 : 2 = 10 + 16 : 2 = 10 + 8 = 18.
На этом все действия выполнены.
Ответ: 10 + (8 — 2 * 3) * (12 — 4) : 2 = 18.
Можно встретить выражения, которые содержат скобки в скобках. Для их решения, нужно последовательно применять правило выполнения действий в выражениях со скобками. Удобнее всего начинать выполнение действий с внутренних скобок и продвигаться к внешним. Покажем на примере.
Пример 2. Выполнить действия в выражении: 9 + (5 + 1 + 4 * (2 + 3)).
Как решаем:
Перед нами выражение со скобками. Это значит, что выполнение действий нужно начать с выражения в скобках, то есть, с 5 + 1 + 4 * (2 + 3). Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
Но! Это выражение также содержит скобки, поэтому начнем сначала с действий в них:
2 + 3 = 5.
Подставим найденное значение: 5 + 1 + 4 * 5. В этом выражении сначала выполняем умножение, затем — сложение:
5 + 1 + 4 * 5 = 5 + 1 + 20 = 26.
Исходное значение, после подстановки примет вид 9 + 24, и остается лишь выполнить сложение: 9 + 26 = 35.
Ответ: 4 + (3 + 1 + 4 * (2 + 3)) = 35.
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции — их значения нужно вычислить до выполнения остальных действий. При этом важно учитывать правила из предыдущих пунктов, которые задают очередность действий в математике.
Другими словами, перечисленные функции по степени важности можно приравнивать к выражению в скобках.
И, как всегда, рассмотрим, как это работает на примере.
Пример 1. Вычислить (4 + 1) * 3 + 62 : 3 — 7.
Вычислить (4 + 1) * 3 + 62 : 3 — 7.
Как решаем:
В этом выражении есть степень 62. И нам нужно найти ее значение до выполнения остальных действий. Выполним возведение в степень: 62 = 36.
Подставляем полученное значение в исходное выражение:
(4 + 1) * 3 + 36 : 3 — 7.
Дальше нам уже все знакомо: выполняем действия в скобках, далее по порядку слева направо выполняем сначала умножение, деление, а затем — сложение и вычитание. Ход решения выглядит так:
(4 + 1) * 3 + 36 : 3 — 7 = 3 * 3 + 36 : 3 — 7 = 9 + 12 — 7 = 14.
Ответ: (3 + 1) * 2 + 62 : 3 — 7 = 14.
У нас есть статья «знаки больше, меньше или равно», она может быть полезной для тебя!
Еще больше практики — в детской школе Skysmart. Ученики занимаются на интерактивной платформе, в комфортном темпе и с поддержкой внимательных учителей.
Чтобы ребенок занимался математикой в удовольствие и чувствовал себя увереннее в школе, запишите его на бесплатный вводный урок.
Что сперва умножение или деление
Вот вам очень простой математический пример:
8 / 2(2 + 2)
Вы удивитесь, но большинство людей не смогут правильно это посчитать. Посчитайте сами и потом смотрите правильный ответ:
В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:
- То, что в скобках, выполняется в первую очередь. Если скобок несколько, они выполняются слева направо.
- При отсутствии скобок математические действия выполняются слева направо, сначала умножение и деление, потом — сложение и вычитание.
- Между множителем и скобкой (или двумя скобками) может опускаться знак умножения.
Разберём подробнее, что это значит в нашем случае.
1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:
8 / 2(2 + 2) → 8 / 2(4)
2. Между числом и скобкой можно опустить знак умножения. У нас перед скобкой двойка, то есть можно сделать такую замену:
3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.
Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:
8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16
Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.
А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами 🙂
Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:
«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
Ф., 1967 год. (стр. 43)
Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!
А вот как на это отвечают те, кто действительно в теме и не ленится полностью посмотреть первоисточник:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».
Если апеллировать к Фриде Максовне Шустеф, то выходит, что:
- В. Л. Гончаров говорит так: «Ребята, используйте черту и ставьте скобки, чтобы ни у кого не было вопросов про приоритет».
- Если у нас всё же битва арифметики и алгебры, то, по П.
 С. Александрову и А. Н. Колмогорову, пример нужно решать слева направо, как обычно. Они, конечно, предложили решать такое по-другому, но научное сообщество их не поддержало.
С. Александрову и А. Н. Колмогорову, пример нужно решать слева направо, как обычно. Они, конечно, предложили решать такое по-другому, но научное сообщество их не поддержало.
Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя.
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
Вычислим значение выражения.
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Выполнение тренировочных заданий на изученное правило
Рассмотрим выражения, установим порядок действий и выполним вычисления.
Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Узнаем, правильно ли определен порядок действий в следующих выражениях.
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.
 И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012. - М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Если производить действия в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
- в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
- в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:
- сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
- затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 – 9 = 1
Сначала выполняем действия в скобках:
16 – 2 · 7 + 4 = 16 – 14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43
Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Выполняем действия в круглых скобках, имеем:
8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4
действия в квадратных скобках дают:
14 – 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29
Порядок действий:
30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150
Какие действия нужно выполнять. Порядок выполнения действий в выражениях без скобок и со скобками. Вставь пропущенное число
Числовые,буквенные выражения и выражения с переменными в своей записи могут содержать знаки различных арифметических действий. При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
При преобразовании выражений и вычислении значений выражений действия выполняются в определенной очередности, иными словами, нужно соблюдать порядок выполнения действий .
В этой статье мы разберемся, какие действия следует выполнять сначала, а какие следом за ними. Начнем с самых простых случаев, когда выражение содержит лишь числа или переменные, соединенные знаками плюс, минус, умножить и разделить. Дальше разъясним, какого порядка выполнения действий следует придерживаться в выражениях со скобками. Наконец, рассмотрим, в какой последовательности выполняются действия в выражениях, содержащих степени, корни и другие функции.
Навигация по странице.
В школе дается следующее правило, определяющее порядок выполнения действий в выражениях без скобок :
Озвученное правило воспринимается достаточно естественно. Выполнение действий по порядку слева направо объясняется тем, что у нас принято вести записи слева направо. А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
А то, что умножение и деление выполняется перед сложением и вычитанием объясняется смыслом, который в себе несут эти действия.
Рассмотрим несколько примеров применения этого правила. Для примеров будем брать простейшие числовые выражения, чтобы не отвлекаться на вычисления, а сосредоточиться именно на порядке выполнения действий.
Выполните действия 7−3+6 .
Исходное выражение не содержит скобок, а также оно не содержит умножения и деления. Поэтому нам следует выполнить все действия по порядку слева направо, то есть, сначала мы от 7 отнимаем 3 , получаем 4 , после чего к полученной разности 4 прибавляем 6 , получаем 10 .
Кратко решение можно записать так: 7−3+6=4+6=10 .
Укажите порядок выполнения действий в выражении 6:2·8:3 .
Чтобы ответить на вопрос задачи, обратимся к правилу, указывающему порядок выполнения действий в выражениях без скобок. В исходном выражении содержатся лишь действия умножения и деления, а согласно правилу, их нужно выполнять по порядку слева направо.
сначала 6 делим на 2 , это частное умножаем на 8 , наконец, полученный результат делим на 3.
Вычислите значение выражения 17−5·6:3−2+4:2 .
Сначала определим, в каком порядке следует выполнять действия в исходном выражении. Оно содержит и умножение с делением, и сложение с вычитанием. Сначала слева направо нужно выполнить умножение и деление. Так 5 умножаем на 6 , получаем 30 , это число делим на 3 , получаем 10 . Теперь 4 делим на 2 , получаем 2 . Подставляем в исходное выражение вместо 5·6:3 найденное значение 10 , а вместо 4:2 — значение 2 , имеем 17−5·6:3−2+4:2=17−10−2+2 .
В полученном выражении уже нет умножения и деления, поэтому остается по порядку слева направо выполнить оставшиеся действия: 17−10−2+2=7−2+2=5+2=7 .
На первых порах, чтобы не перепутать порядок выполнения действий при вычислении значения выражения, удобно над знаками действий расставить цифры, соответствующие порядку их выполнения. Для предыдущего примера это выглядело бы так: .
Этого же порядка выполнения действий – сначала умножение и деление, затем сложение и вычитание — следует придерживаться и при работе с буквенными выражениями.
Действия первой и второй ступени
В некоторых учебниках по математике встречается разделение арифметических действий на действия первой и второй ступени. Разберемся с этим.
Действиями первой ступени называют сложение и вычитание, а умножение и деление называют действиями второй ступени .
В этих терминах правило из предыдущего пункта, определяющее порядок выполнения действий, запишется так: если выражение не содержит скобок, то по порядку слева направо сначала выполняются действия второй ступени (умножение и деление), затем – действия первой ступени (сложение и вычитание).
Порядок выполнения арифметических действий в выражениях со скобками
Выражения часто содержат скобки, указывающие порядок выполнения действий. В этом случае правило, задающее порядок выполнения действий в выражениях со скобками , формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.
Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.
Выполните указанные действия 5+(7−2·3)·(6−4):2 .
Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3 . В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1 . Переходим ко второму выражению в скобках 6−4 . Здесь лишь одно действие – вычитание, выполняем его 6−4=2 .
Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2 . В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6 . На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2 .
Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6 .
Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.
Выполните действия в выражении 4+(3+1+4·(2+3)) .
Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3) . Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5 . Подставив найденное значение, получаем 3+1+4·5 . В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24 . Исходное значение, после подстановки этого значения, принимает вид 4+24 , и остается лишь закончить выполнение действий: 4+24=28 .
Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.
Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1 . Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1 , то после этого исходное выражение примет вид (4+(4+1)−1)−1 . Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Опять выполняем действие во внутренних скобках, так как 4+1=5 , то приходим к следующему выражению (4+5−1)−1 . Опять выполняем действия в скобках: 4+5−1=8 , при этом приходим к разности 8−1 , которая равна 7 .
Порядок выполнения действий в выражениях с корнями, степенями, логарифмами и другими функциями
Если в выражение входят степени, корни, логарифмы, синус, косинус, тангенс и котангенс, а также другие функции, то их значения вычисляются до выполнения остальных действий, при этом также учитываются правила из предыдущих пунктов, задающие порядок выполнения действий. Иными словами, перечисленные вещи, грубо говоря, можно считать заключенными в скобки, а мы знаем, что сначала выполняются действия в скобках.
Рассмотрим решения примеров.
Выполните действия в выражении (3+1)·2+6 2:3−7 .
В этом выражении содержится степень 6 2 , ее значение нужно вычислить до выполнения остальных действий. Итак, выполняем возведение в степень: 6 2 =36 . Подставляем это значение в исходное выражение, оно примет вид (3+1)·2+36:3−7 .
Дальше все понятно: выполняем действия в скобках, после чего остается выражение без скобок, в котором по порядку слева направо сначала выполняем умножение и деление, а затем – сложение и вычитание. Имеем (3+1)·2+36:3−7=4·2+36:3−7= 8+12−7=13 .
Другие, в том числе и более сложные примеры выполнения действий в выражениях с корнями, степенями и т.п., Вы можете посмотреть в статье вычисление значений выражений.
cleverstudents.ru
Онлайн игры,тренажеры,презентации,уроки,энциклопедии,статьи
Post navigation
Примеры со скобками, урок с тренажерами.
Мы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
Это происходит потому, что во втором и третьем примере есть скобки.
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20.
 Онлайн тренажер.
Онлайн тренажер.2) Примеры со скобками в пределах до 100. Онлайн тренажер.
3) Примеры со скобками. Тренажер №2
4) Вставь пропущенное число — примеры со скобками. Тренажер
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.
А теперь закрепляем решение примеров на порядок действий на тренажерах!
1.
 Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.
Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.2. Тренажер по математике 2 — 3 класс «Расставь порядок действий (буквенные выражения).»
3. Порядок действий (расставляем порядок и решаем примеры)
Порядок действий в математике 4 класс
Начальная школа подходит к концу, скоро ребёнок шагнёт в углубленный мир математики. Но уже в этот период школьник сталкивается с трудностями науки. Выполняя простое задание, ребёнок путается, теряется, что в результате приводит к отрицательной отметке за выполненную работу. Чтобы избежать подобных неприятностей, нужно при решении примеров, уметь ориентироваться в порядке, по которому нужно решать пример. Не верно распределив действия, ребёнок не правильно выполняет задание. В статье раскрываются основные правила решения примеров, содержащих в себе весь спектр математических вычислений, включая скобки. Порядок действий в математике 4 класс правила и примеры.
Перед выполнением задания попросите своё чадо пронумеровать действия, которые он собирается выполнить. Если возникли затруднения – помогите.
Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:
Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем сложение. Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.
Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.
27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).
Научите ребёнка всегда планировать и нумеровать выполняемые действия.
Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.
Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:
Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.
Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.
Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?
Решение примеров со скобками
Разберём конкретный пример:
Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:
Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.
Ребёнку останется только выполнить непосредственно решение.
Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.
7*3-5*4+(20-19) 14+2*3-(13-9)
17+2*5+(28-2) 5*3+15-(2-1*2)
24-3*2-(56-4*3) 14+12-3*(21-7)
Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.
Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий. Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.
Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.
detskoerazvitie. info
info
Урок по математике 2 класс Порядок действий в выражениях со скобками.
Успейте воспользоваться скидками до 50% на курсы «Инфоурок»
Цель: 1.
2.
3. Закрепить знание таблицы умножения и деления на 2 – 6, понятия делителя и
4. Учить работать в парах с целью развития коммуникативных качеств.
Оборудование * : + — (), геометрический материал.
Раз, два – выше голова.
Три, четыре – руки шире.
Пять, шесть – всем присесть.
Семь, восемь – лень отбросим.
Но сначала придется узнать его название. Для этого нужно выполнить несколько заданий:
6 + 6 + 6 … 6 * 4 6 * 4 + 6… 6 * 5 – 6 14 дм 5 см… 4 дм 5 см
Пока мы вспоминали о порядке действий в выражениях, с замком происходили чудеса. Мы были только что у ворот, а теперь попали в коридор. Смотрите, дверь. А на ней замок. Откроем?
1. Из числа 20 вычесть частное чисел 8 и 2.
2. Разность чисел 20 и 8 разделить на 2.
— Чем отличаются результаты?
— Кто сможет назвать тему нашего урока?
(на массажных ковриках)
По дорожке, по дорожке
Скачем мы на правой ножке,
Скачем мы на левой ножке.
По тропинке побежим,
Наше предположение было полностью правильно7
Где выполняются действия сначала, если в выражении есть скобки?
Смотрите перед нами «живые примеры». Давайте «оживим» их.
* : + — ().
m – c * (a + d) + x
k: b + (a – c) * t
6. Работа в парах.
Для их решения вам понадобиться геометрический материал.
Учащиеся выполняют задания в парах. После выполнения проверка работы пар у доски.
Что нового вы узнали?
8. Домашнее задание.
Тема: Порядок действий в выражениях со скобками.
Цель: 1. Вывести правило порядка действий в выражениях со скобками, содержащих все
4 арифметических действия,
2. Формировать способность к практическому применению правила,
Формировать способность к практическому применению правила,
4.Учить работать в парах с целью развития коммуникативных качеств.
Оборудование : учебник, тетради, карточки со знаками действий * : + — (), геометрический материал.
1 .Физминутка.
Девять, десять – тихо сесть.
2. Актуализация опорных знаний.
Сегодня мы с вами отправляемся в очередное путешествие по стране Знаний городу математика. Нам предстоит посетить один дворец. Что-то я забыла его название. Но не будем расстраиваться, вы сами сможете мне подсказать его название. Пока я переживала, мы подошли к воротам дворца. Войдем?
1. Сравните выражения:
2. Расшифруй слово.
3. Постановка проблемы. Открытие нового.
Так как же называется дворец?
А когда в математике мы говорим о порядке?
Что вы уже знаете о порядке выполнения действий в выражениях?
— Интересно, нам предлагают записать и решить выражения (учитель читает выражения, учащиеся записывают их и решают).
20 – 8: 2
(20 – 8) : 2
Молодцы. А что интересного в этих выражениях?
Посмотрите на выражения и их результаты.
— Что общего в записи выражений?
— Как вы думаете, почему получились разные результаты, ведь числа были одинаковые?
Кто рискнет сформулировать правило выполнения действий в выражениях со скобками?
Правильность этого ответа мы сможем проверить в другой комнате. Отправляемся туда.
4. Физминутка.
И по этой же дорожке
До горы мы добежим.
Стоп. Немножко отдохнем
И опять пешком пойдем.
5. Первичное закрепление изученного.
Вот мы и пришли.
Нам нужно решить еще два выражения, чтобы проверить правильность нашего предположения.
6 * (33 – 25) 54: (6 + 3) 25 – 5 * (9 – 5) : 2
Для проверки правильности предположения откроем учебники на стр. 33 и прочитаем правило.
Как нужно выполнять действия после решения в скобках?
На доске написаны буквенные выражения и лежат карточки со знаками действий * : + — (). Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.
Дети выходят к доске по одному, берут карточку с тем действием, которое нужно сделать сначала, потом выходит второй ученик и берет карточку со вторым действием и т. д.
а + (а –в)
а * (в +с) : d – t
m – c * ( a + d ) + x
k : b + ( a – c ) * t
(a – b) : t + d
6. Работа в парах.
Знание порядка действий необходимо не только для решения примеров, но и при решении задач мы тоже сталкиваемся с этим правилом. Сейчас вы в этом убедитесь работая в парах. Вам нужно будет решить задачи из № 3 стр. 33.
 Согласно статье 4 Федерального закона «О порядке рассмотрения […]
Согласно статье 4 Федерального закона «О порядке рассмотрения […]Примеры со скобками, урок с тренажерами. — Kid-mama
Мы рассмотрим в этой статье три варианта примеров:
1. Примеры со скобками (действия сложения и вычитания)
2. Примеры со скобками (сложение, вычитание, умножение, деление)
3. Примеры, в которых много действий
1 Примеры со скобками (действия сложения и вычитания)
Рассмотрим три примера. В каждом из них порядок действий обозначен цифрами красного цвета:
Мы видим, что порядок действий в каждом примере будет разный, хотя числа и знаки одинаковые. Это происходит потому, что во втором и третьем примере есть скобки.
Это происходит потому, что во втором и третьем примере есть скобки.
Запомните правило:
|
*Это правило для примеров без умножения и деления. Правила для примеров со скобками, включающих действия умножения и деления мы рассмотрим во второй части этой статьи.
Чтобы не запутаться в примере со скобками, можно превратить его в обычный пример, без скобок. Для этого результат, полученный в скобках, записываем над скобками, далее переписываем весь пример, записывая вместо скобок этот результат, и далее выполняем все действия по порядку, слева направо:
В несложных примерах можно все эти операции производить в уме. Главное — сначала выполнить действие в скобках и запомнить результат, а затем считать по порядку, слева направо.
А теперь — тренажеры!
1) Примеры со скобками в пределах до 20. Онлайн тренажер.
Перейти на страницу с тренажером
2) Примеры со скобками в пределах до 100. Онлайн тренажер.
Перейти на страницу с тренажером
3) Примеры со скобками. Тренажер №2
Перейти на страницу с тренажером
4) Вставь пропущенное число — примеры со скобками. Тренажер
Перейти на страницу с тренажером
2 Примеры со скобками (сложение, вычитание, умножение, деление)
Теперь рассмотрим примеры, в которых кроме сложения и вычитания есть умножение и деление.
Сначала рассмотрим примеры без скобок:
Запомните правило:
|
Есть одна хитрость, как не запутаться при решении примеров на порядок действий. Если нет скобок, то выполняем действия умножения и деления, далее переписываем пример, записывая вместо этих действий полученные результаты. Затем выполняем сложение и вычитание по порядку:
Если в примере есть скобки, то сначала нужно избавиться от скобок: переписать пример, записывая вместо скобок полученный в них результат. Затем нужно выделить мысленно части примера, разделенные знаками «+» и «-«, и посчитать каждую часть отдельно. Затем выполнить сложение и вычитание по порядку:
3 Примеры, в которых много действий
Если в примере много действий, то удобнее будет не расставлять порядок действий во всем примере, а выделить блоки, и решить каждый блок отдельно. Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Для этого находим свободные знаки «+» и «–» (свободные — значит не в скобках, на рисунке показаны стрелочками).
Эти знаки и будут делить наш пример на блоки:
Выполняя действия в каждом блоке не забываем про порядок действий, приведенный выше в статье. Решив каждый блок, выполняем действия сложения и вычитания по порядку.
А теперь закрепляем решение примеров на порядок действий на тренажерах!
1. Примеры со скобками в пределах чисел до 100, действия сложения, вычитания, умножения и деления. Онлайн тренажер.
Перейти на страницу с тренажером
Перейти на страницу с тренажером
3. Порядок действий (расставляем порядок и решаем примеры)
Перейти на страницу с тренажером
3 класс. Моро. Учебник №1. Ответы к стр. 24
Числа от 1 до 100
Умножение и деление
Порядок выполнения действий
Ответы к стр.
 24
24Узнаем, в каком порядке выполняются действия в числовых выражениях.
1. Сравни выражения каждой пары: какие действия в них выполняются? В каком порядке выполняются эти действия и почему?
38 — 10 + 6 = 28 + 6 = 34 24 : 3 • 2 = 8 • 2 = 16
38 — (10 + 6) = 28 + 6 = 34 24 : (3 • 2) = 8 • 2 = 16
Прежде чем приступить к вычислениям, надо рассмотреть выражение: выяснить, есть ли в нём скобки, какие действия в нём имеются.
1) Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняются в том порядке, в каком они записаны: слева направо.
Если в выражение без скобок входят не только сложение и вычитание, но и умножение или деление или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
3) Если в выражении есть скобки, то сначала выполняют действия, записанные в скобках, по правилам пунктов 1 и 2.
Действия в числовых выражениях выполняют в следующем порядке:
1) действия, записанные в скобках;
2) умножение и деление;
3) сложение и вычитание.
В первой паре выполняется сложение и вычитание, во второй — деление и умножение. В первой случае сначала выполняется вычитание, а затем деление. Но при наличии скобок сначала выполняются действия в скобках — сложение, а затем вычитание.
Во втором случае сначала выполняется деление, а затем умножение. Но при наличии скобок сначала выполняются действия в скобках — умножение, а затем деление.
2. Объясни, как надо выполнять действия.
3 2 1
30 + 6 • (13 — 9) = 30 + 6 • 4 = 30 + 24 = 54
1 4 2 5 3
18 : 2 — 2 • 3 + 12 : 3 = 9 — 6 + 4 = 7
В первом выражении сначала выполняется действие в скобках — вычитание, затем умножение, а потом сложение.
Во втором выражении сначала выполняются действия деления и умножения, а затем действия вычитания и сложения — слева направо.
ГДЗ по математике. Учебник. 3 класс. Часть 1. Моро М. И., Бантова М. А., Бельтюкова М. А., Волкова С. И., Степанова С. В.
Математика. 3 класс
3 класс. Моро. Учебник №1. Ответы к стр. 24
3.9 (78.46%) от 13 голосующихСложение, вычитание, умножение и деление. ереместительное, сочетательное свойства. Примеры решение задач.
Арифметические операции
Сложение:
Умножение:
Вычитание:
Деление:
Переместительное свойство
Это свойство относится только к двум операциям: сложение и умножение, так как только в этих операциях каждое из слагаемых или множителей имеет одинаковое значение.
Cочетательное свойство.
Следующее свойство – сочетательное. Это свойство рассматривается для сложения и умножения.
Переместительное и сочетательное свойства для сложения и умножения позволяют объединять слагаемые и множители в группы, менять их местами. Эти свойства позволяют считать быстрее и без ошибок.
Распределительные свойства
Следующие свойства раcпределительные. Они показывают, как можно вычислить выражение, если в нем используются операция умножение вместе со сложением или вычитанием (распределяют порядок вычисления):
Противоположный элемент
Нейтральный элемент – 0.
Ноль — это нейтральный элемент относительно сложения целых чисел:
Также обрати внимание на порядок действий, если скобки не расставлены. Итак, у нас есть 4 операции, они выполняются в следующем порядке:
- Умножение и деление – в порядке следования слева направо;
- Сложение и вычитание – в порядке следования слева направо.
- При наличии скобок сначала выполняются действия в скобках в указанном выше порядке, а затем все остальные действия вне скобок опять же с соблюдением указанного выше порядка.

Задача 1. Вычислить \(-55+(-7)+18+7.\)
Решение.
- Воспользуемся переместительным свойством для удобства вычисления: \(-7+7-55+18\)
- \(-7\) и \(7\) противоположные элементы, итого: \(-55+18=-37\)
Ответ:\(-37\)
Задача 1. Вычислить \((-7+9)+7*2-56\).
- Первое действие выполняем в скобках и умножение: \(2+ 7*2\)
- выполняем умножение, затем сложение и вычитание: \(2+14-56=16-56=-40.\)
Ответ:\(-40.\)
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Что сначала делают умножение или деление
Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.
В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.
Порядок вычисления простых выражений
В случае выражений без скобок порядок действий определяется однозначно:
- Все действия выполняются слева направо.
- В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.
Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.
Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.
Условие: вычислите, сколько будет 7 − 3 + 6 .
Решение
В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:
7 − 3 + 6 = 4 + 6 = 10
Ответ: 7 − 3 + 6 = 10 .
Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?
Решение
Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.
Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.
Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .
Решение
Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:
17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2
Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:
17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7
Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .
Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:
.
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.
Что такое действия первой и второй ступени
Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.
К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.
Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:
В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).
Порядок вычислений в выражениях со скобками
Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:
В таком случае нужное правило можно записать так:
Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.
Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.
Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .
Решение
В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :
7 − 2 · 3 = 7 − 6 = 1
Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .
Теперь нам нужно подставить получившиеся значения в первоначальное выражение:
5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2
Начнем с умножения и деления, потом выполним вычитание и получим:
5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6
На этом вычисления можно закончить.
Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .
Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.
Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .
Решение
У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .
Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .
Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.
Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 – 1 , результатом которой будет 7 .
Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями
Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.
Разберем пример такого вычисления.
Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .
Решение
У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .
Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.
( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13
Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .
В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).
Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя.
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.
Выполняем действия слева направо по порядку (рис. 2).
Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).
Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
Вычислим значение выражения.
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
Рис. 4. Порядок действий
Выполнение тренировочных заданий на изученное правило
Рассмотрим выражения, установим порядок действий и выполним вычисления.
Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Узнаем, правильно ли определен порядок действий в следующих выражениях.
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.
 И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012. - М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.
Если несколько действий выполняются одно за другим, то результат, зависит от порядка действий.
Если производить действия в порядке их записи.
Если же сначала сложить 2 и 1 и вычесть полученную сумму из 4, то получим 1.
Чтобы указать, в каком порядке нужно выполнять действия (в тех случаях, когда результат зависит от порядка действий), пользуются скобками. Действия, заключенные в скобки, выполняются раньше других. В нашем случае:
Чтобы не загромождать чрезмерно записи, условились не писать скобок:
- в том случае, когда действия сложения и вычитания, следуя друг за другом, должны выполняться в том порядке, в каком они записаны;
- в том случае, когда внутри скобок производятся действия умножения или деления; например, вместо 2 + (4 · 5) = 22 пишут 2 + 4 · 5 = 22.

При вычислении таких выражений, которые либо совсем не содержат скобок, либо содержат лишь такие скобки, внутри которых больше нет скобок, нужно производить действия в таком порядке:
- сначала выполняются действия, заключенные в скобки; при этом умножение и деление делаются в порядке из следования, но раньше, чем сложение и вычитание;
- затем выполняются остающиеся действия, причем опять умножение и деление делаются в порядке из следования, но раньше сложения и вычитания.
Сначала выполняем умножения:
2 · 5 = 10
3 · 3 = 9
затем вычитание:
10 – 9 = 1
Сначала выполняем действия в скобках:
16 – 2 · 7 + 4 = 16 – 14 + 4 = 6
2 + 5 = 7
Теперь выполняем остающиеся действия:
9 + 16 : 4 – 2 · 6 + 6 · 7 =
= 9 + 4 – 12 + 42 =
= 43
Часто для указания порядка действий необходимо заключать в скобки такие выражения, которые сами уже содержат скобки. Тогда, кроме обычных (круглых), применяют скобки иной формы, например квадратные []. Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Если в скобки нужно заключить выражение, содержащее уже круглые и квадратные скобки, пользуются фигурными скобками <>. Вычисление подобных выражений производится в следующем порядке: сначала производятся вычисления внутри всех круглых скобок в вышеуказанной последовательности. Затем — вычисления внутри всех квадратных скобок по тем же правилам. Далее — вычисления внутри фигурных скобок и т.д.. Наконец, выполняются остающиеся действия.
Выполняем действия в круглых скобках, имеем:
8 – 6 = 2
10 – 2 · 3 = 10 – 6 = 4
действия в квадратных скобках дают:
14 – 3 · 2 = 8
выполняя остающиеся действия скобках находим:
5 + 2 · 8 + 32 : 4 = 5 + 16 + 8 = 29
Порядок действий:
30 – 20 = 10
35 – 10 = 25
100 – 25 = 75
75 · 2 = 150
Порядок операций
Когда у вас есть математическая задача, которая включает более одной операции, например, сложение и вычитание или вычитание и умножение ? Что вы делаете в первую очередь?
Пример № 1 : 6? 3 х 2 =?
- Вы делаете сначала вычитание (6? 3 = 3), а затем умножение (3 x 2 = 6 )?
- Или вы начнете с умножения (3 x 2 = 6), а затем вычтите (6? 6 = 0 )?
PEMDAS
В подобных случаях мы следуем порядку операций . Порядок выполнения операций сокращен до PEMDAS :
Порядок выполнения операций сокращен до PEMDAS :
- P arentheses
- E xponents
- M ultiplication и D ivision (слева направо)
- A ddition и S ubtraction (слева направо)
(Один из способов запомнить это — вспомнить фразу P lease E xcuse M y D ear A Unt S союзник.)
- В приведенном выше примере мы имеем дело с умножением и вычитанием. Ультипликация M идет на шаг перед убиранием S , поэтому сначала мы умножаем 3 x 2, а затем вычитаем сумму из 6, получая 0.
Пример № 2 : 30 5 x 2 + 1 =?
- Нет арентезов P .
- Нет компонентов E .
- Начнем с ultiplication M и ivision D , работая слева направо.
ПРИМЕЧАНИЕ: Несмотря на то, что умножение предшествует делению в PEMDAS, они выполняются в одном шаге слева направо. Сложение и вычитание также выполняются на одном этапе.
Сложение и вычитание также выполняются на одном этапе. - 30 5 = 6 , в результате чего 6 x 2 + 1 =?
- 6 x 2 = 12 , в результате чего 12 + 1 =?
- Затем мы выполняем A ddition: 12 + 1 = 13
Обратите внимание, что если бы мы выполняли умножение до деления, то получили бы неправильный ответ:
- 5 x 2 = 10 , оставляя 30 10 + 1 =?
- 30 10 = 3 , оставляя 3 + 1 =?
- 3 + 1 = 4 (на 9! Меньше!)
Последний пример для продвинутых студентов, использующий все шесть операций:
Пример № 3 : 5 + (4? 2) 2 х 3 6? 1 =?
- Начать с P аренцев: 4? 2 = 2 .(Хотя вычитание обычно выполняется на последнем шаге, потому что оно указано в скобках, мы делаем это в первую очередь.) Остается 5 + 2 2 x 3 6? 1 =?
- Тогда E xponents: 2 2 = 4 .
 Теперь у нас 5 + 4 x 3 6? 1 =?
Теперь у нас 5 + 4 x 3 6? 1 =? - Затем M ultiplication и D ivision, начиная слева: 4 x 3 = 12 , оставляя нас с 5 + 12 6? 1 =?
- Затем двигаемся вправо: 12 6 = 2 , что делает задачу 5 + 2? 1 =?
- Затем A ddition и S ubtraction, начиная слева: 5 + 2 = 7 , оставляя 7? 1 =?
- И, наконец, вправо: 7? 1 = 6
(Для большей практики попробуйте нашу игру Operation Order!)
| Десятичные эквиваленты обыкновенных дробей | Числа и формулы |
.com / ipa / 0/9/3/3/3/4 / A0933340.html
Порядок операций — ChiliMath
Фундаментальная концепция порядка операций — выполнять арифметические операции в «правильном» порядке или последовательности. Давайте посмотрим, как Роб и Пэтти пытались упростить данное числовое выражение, применяя порядок или правило операций.
В чем ошибка Роба?
- Он небрежно упростил числовые выражения, применив арифметические операции слева направо.
Пэтти получила правильный ответ, потому что она правильно применила правила порядка операций.
- Сначала она выполнила умножение и деление, а затем сложение и вычитание.
Каков порядок действий?
Порядок операций — это просто набор правил, устанавливающих приоритет последовательности операций , начиная от наиболее важных до наименее важных.
Это правило о том, как правильно упрощать числовые выражения, также известно как правило PEMDAS (сокращение от P lease E xcuse M y D ear A Unt S ally).
Шаг 1: Сделайте все возможное, чтобы упростить все, что находится внутри скобок или символа группировки.
Шаг 2: По возможности упрощайте экспоненциальные числа в числовом выражении.
Шаг 3: Умножение и деление слева направо в зависимости от того, что наступит раньше.
Шаг 4: Сложите и вычтите в зависимости от того, что наступит раньше, слева направо
Примеры применения порядка операций для упрощения числовых выражений
Пример 1: Упростите приведенное ниже выражение, используя Порядок операций.
- Рассматривая числовые выражения с несколькими операциями слева направо, мы видим, что сначала мы должны выполнить деление, что составляет 5 \ div 5 = 1.
- На данный момент у меня есть три (3) возможных операции. В Порядке операций умножение имеет приоритет перед сложением и вычитанием. Следовательно, мы должны дальше размножаться. У нас 6 \ умножить на 2 = 12.
- Что нам делать дальше, складывать или вычитать? В зависимости от порядка операций сложение и вычитание имеют одинаковое значение.
 Чтобы определить, какую операцию выполнить в первую очередь, мы добавляем или вычитаем слева направо в зависимости от того, что идет первым, что в этой ситуации должно сложить, 1 + 3 = 4.
Чтобы определить, какую операцию выполнить в первую очередь, мы добавляем или вычитаем слева направо в зависимости от того, что идет первым, что в этой ситуации должно сложить, 1 + 3 = 4.
- Осталась одна операция — вычитание. На первый взгляд сложное числовое выражение сводится к окончательному ответу — 8.
Пример 2: Упростите приведенное ниже выражение, используя Порядок операций.
В следующих примерах будет задействовано скобок .Помните, что вам нужно сначала упростить все, что указано в скобках, прежде чем двигаться дальше.
Пример 3: Упростите приведенное ниже выражение, используя Порядок операций.
- Обратите внимание на выражения в скобках. Правило говорит нам сначала делить, а затем вычитать.
- Мы можем избавиться от скобок, вычтя 7 на 2.
- Умножение — это гораздо более «сильная» операция, чем вычитание, поэтому мы должны сначала умножить 5 и 4.

- Закончите, вычтя 25 на 20.
Пример 4: Упростите приведенное ниже выражение, используя Порядок операций.
- Сначала упростите выражения в круглых скобках. Умножьте на первую скобку и разделите на вторую.
- Сложите числа в первой скобке, затем вычтите числа внутри второй.
- Здесь есть умножение и деление.Поскольку умножение предшествует делению, мы собираемся сначала умножить.
- Между вычитанием и делением приоритет имеет деление, поэтому мы делим 5 на 5, чтобы получить 1.
- Последняя оставшаяся операция — вычитание, поэтому мы и займемся этим.
Последние примеры будут включать экспоненты, поэтому будьте осторожны на каждом шаге, потому что в них происходит очень много всего. Пока вы сосредотачиваетесь на соблюдении правил, регулирующих порядок действий, это не должно быть так сложно! Поехали…
Пример 5: Упростите числовое выражение ниже, используя правила Порядка операций.
- Упростите выражения в круглых скобках. Но, более конкретно, упростите числа с помощью показателей.
- Для упрощения заключены две круглые скобки. Мы упростим второй, \ left ({30 — 27} \ right), потому что он намного проще. Здесь разница 30 и 27 составляет 3.
- Теперь обратим внимание на другую скобку. Порядок действий говорит нам делить, прежде чем вычитать.
- Наконец, мы можем избавиться от скобок, выполнив вычитание, потому что больше нечего делать.
- Глядя на то, что мы оставили, упрощение экспоненциальных чисел имеет приоритет перед операциями умножения, сложения и вычитания.
- Просматривая слева направо, очевидно, что мы должны умножать перед сложением и / или вычитанием.
- В зависимости от порядка операций сложение и вычитание имеют одинаковое значение. Сначала мы должны вычесть, потому что операция вычитания предшествует сложению, если смотреть слева направо.
 3} первый.
3} первый.
- Заглянув в круглые скобки, мы должны сначала разделить, прежде чем умножать и вычитать.
- Сохраняя внимание в круглых скобках, порядок операций говорит нам умножать, прежде чем мы будем вычитать.
- Последняя операция внутри скобок — вычитание. Давай сделаем это!
- Здесь сделаем паузу. На данный момент ясно, что мы можем выполнить три (3) упрощения одновременно.2}.
- Кажущаяся сложной проблема теперь сведена к чему-то, что очень легко упростить. Если смотреть слева направо, деление имеет приоритет перед вычитанием и сложением.
- Потому что вычитание и умножение находятся на одном уровне в иерархии операций. Способ, которым мы разрываем связь, как вы уже должны были знать, — это выполнять ту, которая идет первой, если смотреть слева направо. В этой ситуации мы будем вычитать, а затем прибавлять.Это оно!
Практика с рабочими листами
Возможно, вас заинтересует:
Порядок действий Проблемы с ответами
Правило PEMDAS
Что такое порядок операций?
Что такое порядок действий? В математике порядок операций — это правила, устанавливающие последовательность, в которой должны выполняться несколько операций в выражении.
Способ запоминания порядка операций — PEMDAS, где каждая буква обозначает математическую операцию.
| п. | Круглые скобки |
| E | Показатель |
| M | Умножение |
| D | Дивизия |
| А | Дополнение |
| S | Вычитание |
Правила PEMDAS, устанавливающие порядок, в котором должны выполняться операции в выражении, следующие:
1. Круглые скобки — они имеют приоритет над всеми другими операторами. Первый шаг — выполнить все операции в скобках. Проработайте все группировки изнутри наружу. (Все, что указано в скобках, является группировкой)2. Экспоненты — Найдите все экспоненциальные выражения.
3. Умножение и деление — Затем, двигаясь слева направо, умножайте и / или делите в зависимости от того, что наступит раньше.
4. Сложение и вычитание — Наконец, двигаясь слева направо, складывайте и / или вычитайте в зависимости от того, что наступит раньше. Почему следует соблюдать порядок действий?
Умножение и деление — Затем, двигаясь слева направо, умножайте и / или делите в зависимости от того, что наступит раньше.
4. Сложение и вычитание — Наконец, двигаясь слева направо, складывайте и / или вычитайте в зависимости от того, что наступит раньше. Почему следует соблюдать порядок действий? Следуйте правилам порядка операций для решения выражений, чтобы все пришли к одному и тому же ответу.
Вот пример того, как мы можем получить разные ответы, если НЕ соблюдаем правильный порядок операций.
| Выражение решено слева направо | Выражение решено с использованием порядка операций (PEMDAS) |
6 х 3 + 4 х (9 ÷ 3) 6 х 3 + 4 х (9 ÷ 3) 18 + 4 x (9 ÷ 3) 22 х (9 ÷ 3) 198 ÷ 3 = 66 ✘ | 6 х 3 + 4 х (9 ÷ 3) 6 х 3 + 4 х (9 ÷ 3) → пол. 6 х 3 + 4 х 3 → М 18 + 4 x 3 → М 18 + 12 → А = 30 ✔ |
Интересные факты
|
Все дело в операциях,
Решайте по порядку, иначе будет напряженность.
Начните с открытия скобок.
Прыгайте с экспонентами.
Куб или Квадрат — это все очень честно!
Далее, Умножение или Разделение — переход слева направо.
Сложение и вычитание идут последними, но они просты.
наконец, это так просто, как A B C D!
Давайте сделаем это! Вместо того, чтобы раздавать ребенку рабочие листы, составляйте словесные задачи из реальных жизненных ситуаций. Это поможет им писать и решать выражения, а также использовать порядок операций для упрощения выражений в предалгебре и алгебре.
Это поможет им писать и решать выражения, а также использовать порядок операций для упрощения выражений в предалгебре и алгебре.
Например, возьмите ребенка за покупками. Попросите их выбрать 2 дюжины яиц, 3 пакета булочек для хот-догов, 2 пакета конфет и 2 коробки хлопьев.Затем попросите их положить обратно одну коробку хлопьев. Теперь спросите у ребенка количество яиц в дюжине, количество булочек в пачке, количество конфет в пачке и подсчитайте общее количество купленных предметов. Попросите их составить выражение и использовать порядок действий, чтобы найти ответ.
Сопутствующий математический словарьПравило PEMDAS: понимание порядка операций
Каждый, кто посещал математические курсы в США, раньше слышал аббревиатуру «PEMDAS».Но что именно это означает? Здесь мы подробно объясним значение PEMDAS и то, как он используется , прежде чем дать вам несколько примеров задач PEMDAS, чтобы вы могли практиковать то, что вы узнали.
PEMDAS Значение: что это означает?
PEMDAS — это аббревиатура, призванная помочь вам запомнить порядок операций, используемых для решения математических задач. Это обычно произносится как «пем-дасс», «пем-дозз» или «пем-досс».
Вот что означает каждая буква в PEMDAS:
- P аренцев
- E xponents
- M ultiplication и D ivision
- A ddition и S ubtraction
Порядок букв показывает порядок, в котором вы должны решать различные части математической задачи , причем выражения в скобках идут первыми, а сложение и вычитание — последними.
Многие ученики используют этот мнемонический прием, чтобы помочь им запомнить каждую букву: Пожалуйста, извините, моя дорогая тетя Салли .
В Великобритании и других странах студентов обычно изучают PEMDAS как BODMAS . Значение BODMAS такое же, как значение PEMDAS — просто используется пара разных слов. В этом аббревиатуре B обозначает «скобки» (то, что мы в США называем круглыми скобками), а O обозначает «порядки» (или показатели).
Значение BODMAS такое же, как значение PEMDAS — просто используется пара разных слов. В этом аббревиатуре B обозначает «скобки» (то, что мы в США называем круглыми скобками), а O обозначает «порядки» (или показатели).
Итак, как именно вы используете правило PEMDAS? Давайте взглянем.
Как вы используете PEMDAS?
PEMDAS — это аббревиатура, используемая для напоминания людям о порядке операций.
Это означает, что вы не просто решаете математические задачи слева направо; скорее, вы решаете их в заранее определенном порядке, который дается вам через аббревиатуру PEMDAS . Другими словами, вы начнете с упрощения любых выражений в круглых скобках, прежде чем упрощать любые показатели и переходить к умножению и т. Д.
Но это еще не все.Вот что означает PEMDAS для решения математических задач:
- Круглые скобки: Все, что указано в скобках, необходимо сначала упростить
- Показатели: Все, что имеет показатель степени (или квадратный корень), должно быть упрощено после все в скобках было упрощено
- Умножение и деление: После того, как разобрались со скобками и показателями степени, решите любое умножение и деление слева направо
- Сложение и вычитание: После того, как разобрались со скобками, экспонентами, умножением и делением, решите любое сложение и вычитание слева направо
Если какой-либо из этих элементов отсутствует (например,g. , у вас есть математическая задача без показателей), вы можете просто пропустить этот шаг и перейти к следующему.
, у вас есть математическая задача без показателей), вы можете просто пропустить этот шаг и перейти к следующему.
Теперь давайте рассмотрим пример задачи, чтобы помочь вам лучше понять правило PEMDAS:
4 (5 — 3) ² — 10 ÷ 5 + 8
У вас может возникнуть соблазн решить эту математическую задачу слева направо, но это приведет к неправильному ответу! Итак, вместо этого давайте использовать PEMDAS, чтобы помочь нам приблизиться к правильному подходу к .
Мы знаем, что сначала нужно разобраться со скобками.В этой задаче заключены одни скобки: (5 — 3). Упрощение дает 2 , поэтому теперь наше уравнение выглядит так:
4 (2) ² — 10 ÷ 5 + 8
Следующая часть PEMDAS — экспоненты (и квадратные корни). В этой задаче есть один показатель степени, который возводит в квадрат число 2 (то есть то, что мы нашли, упростив выражение в скобках).
Это дает нам 2 × 2 = 4. Итак, теперь наше уравнение выглядит так:
4 (4) — 10 ÷ 5 + 8 ИЛИ 4 × 4 — 10 ÷ 5 + 8
Далее идет умножение и деление слева направо .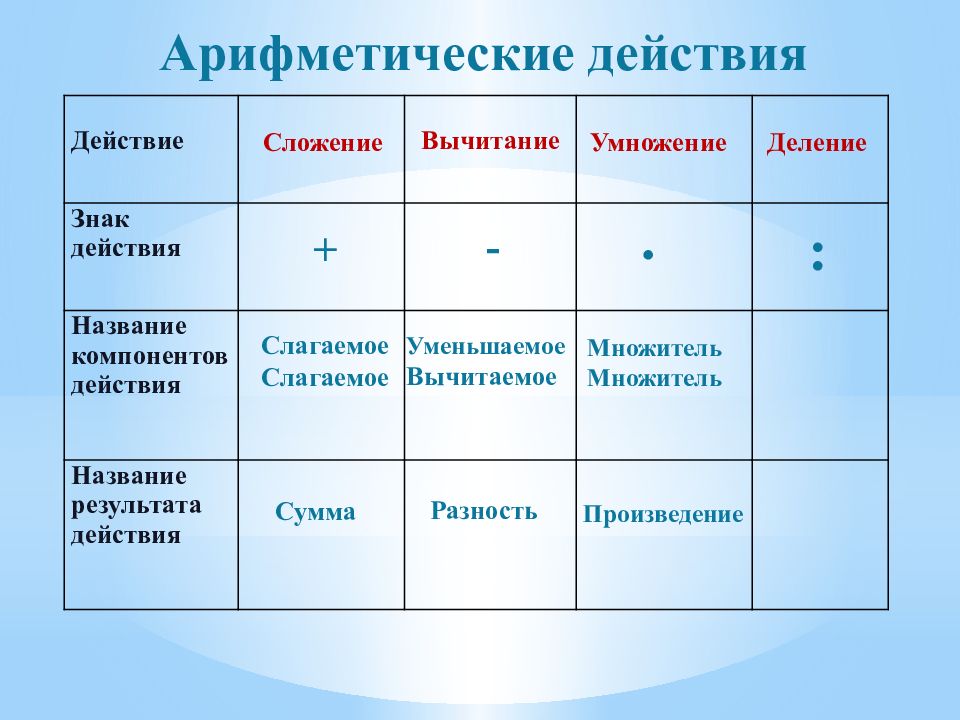 Наша задача содержит как умножение, так и деление, которые мы будем решать слева направо (сначала 4 × 4, а затем 10 ÷ 5). Это упрощает наше уравнение следующим образом:
Наша задача содержит как умножение, так и деление, которые мы будем решать слева направо (сначала 4 × 4, а затем 10 ÷ 5). Это упрощает наше уравнение следующим образом:
16-2 + 8
Наконец, все, что нам нужно сделать, это решить оставшееся сложение и вычитание слева направо :
16-2 + 8
14 + 8
= 22
Окончательный ответ: 22. Не верите? Вставьте все уравнение в свой калькулятор (написанное в точности так, как указано выше), и вы получите тот же результат!
Дэвид Геринг / Flickr
Примеры математических задач с использованием PEMDAS + ответы
Посмотрите, сможете ли вы правильно решить следующие четыре проблемы, используя правило PEMDAS.Мы рассмотрим ответы позже.
Пример проблем PEMDAS
- 11-8 + 5 × 6
- 8 ÷ 2 (2 + 2)
- 7 × 4 — 10 (5 — 3) ÷ 2²
- √25 (4 + 2) ² — 18 ÷ 3 (3 — 1) + 2³
Ответы
- 33
- 16
- 23
- 176
Ответ объяснения
Здесь мы рассмотрим каждую проблему, указанную выше, и то, как вы можете использовать PEMDAS, чтобы получить правильный ответ.
# 1 Объяснение ответа
11-8 + 5 × 6
Эта математическая задача представляет собой довольно простой пример PEMDAS, который использует сложение, вычитание и умножение только , поэтому здесь не нужно беспокоиться о скобках или показателях степени.
Мы знаем, что умножение предшествует сложению и вычитанию , поэтому вам нужно начать с умножения 5 на 6, чтобы получить 30:
.11–8 + 30
Теперь мы можем просто работать слева направо над сложением и вычитанием:
11-8 + 30
3 + 30
= 33
Это приводит нас к , правильный ответ — 33 .
# 2 Объяснение ответа
8 ÷ 2 (2 + 2)
Если эта математическая задача кажется вам знакомой, вероятно, это связано с тем, что стал вирусным в августе 2019 года из-за своей неоднозначной настройки . Многие люди спорили о том, был ли правильный ответ 1 или 16, но, как все мы знаем, в математике есть (почти всегда!) Только один истинно правильный ответ .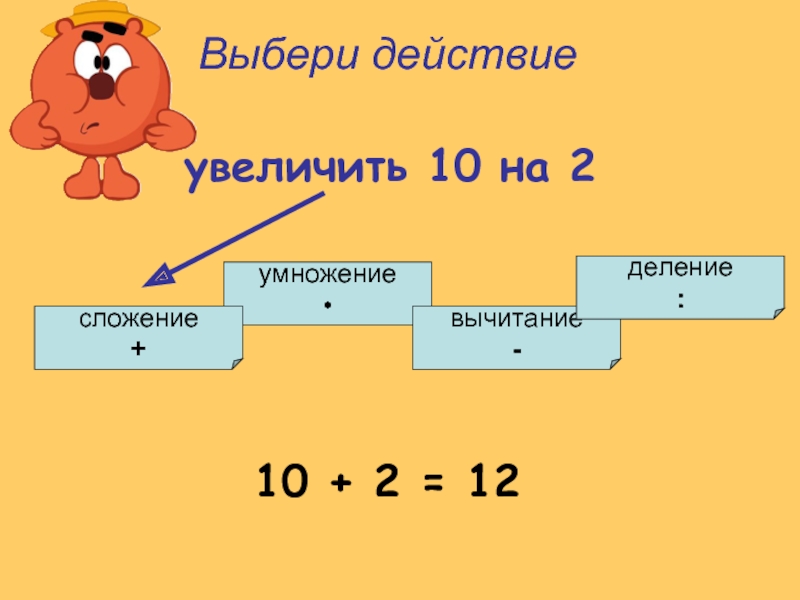
Так что это: 1 или 16?
Давайте посмотрим, как PEMDAS может дать нам правильный ответ.В этой задаче есть скобки, деление и умножение. Итак, мы начнем с упрощения выражения в скобках, согласно PEMDAS:
.8 ÷ 2 (4)
Хотя большинство людей в сети до этого момента соглашались, многие не соглашались с тем, что делать дальше: умножить ли 2 на 4 или разделить 8 на 2?
PEMDAS может ответить на этот вопрос: когда дело доходит до умножения и деления, вы всегда работаете слева направо. Это означает, что вы действительно должны разделить 8 на 2, прежде чем умножить на 4.
Было бы полезно взглянуть на проблему таким образом, поскольку люди склонны запутаться в круглых скобках (помните, что все, что находится рядом с круглыми скобками, это , умноженное на на значение, указанное в скобках):
8 ÷ 2 × 4
Теперь решим уравнение слева направо:
8 ÷ 2 × 4
4 × 4
= 16
Правильный ответ — 16.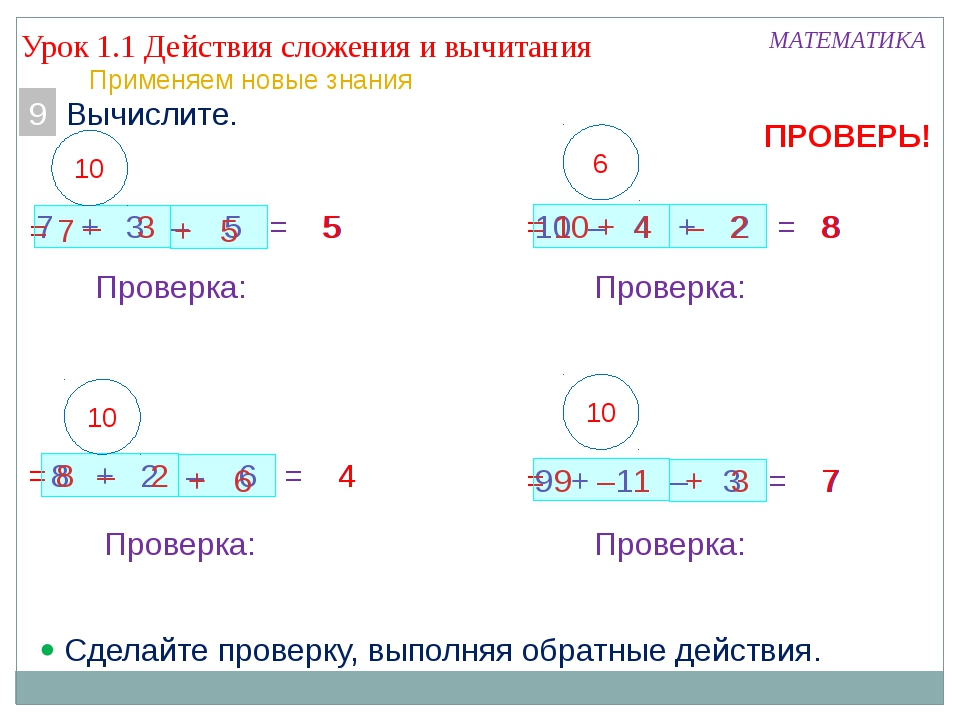 Любой, кто утверждает, что это 1, определенно неправ — и явно неправильно использует PEMDAS!
Любой, кто утверждает, что это 1, определенно неправ — и явно неправильно использует PEMDAS!
Если бы только эти примеры проблем PEMDAS были такими простыми…
# 3 Ответ Объяснение
7 × 4 — 10 (5 — 3) ÷ 2²
Теперь все становится немного сложнее.
В этой математической задаче есть скобки, показатель степени, умножение, деление, вычитание и . Но не расстраивайтесь — давайте поработаем над уравнением, шаг за шагом.
Во-первых, согласно правилу PEMDAS, мы должны упростить то, что в скобках :
7 × 4 — 10 (2) ÷ 2²
Легко и просто, правда? Затем давайте упростим показатель степени :
7 × 4 — 10 (2) ÷ 4
Теперь осталось только умножение, деление и вычитание.Помните, что с умножением и делением мы просто работаем слева направо:
7 × 4-10 (2) ÷ 4
28-10 (2) ÷ 4
28-20 ÷ 4
28-5
После того, как вы умножили и разделили, вам просто нужно , выполнить вычитание , чтобы решить его:
28–5
= 23
Это дает нам правильный ответ 23 .
# 4 Объяснение ответа
√25 (4 + 2) ² — 18 ÷ 3 (3 — 1) + 2³
Эта проблема может показаться пугающей, но я обещаю, что это не так! Если вы подходите к ней по одному шагу за раз, используя правило PEMDAS , вы сможете решить ее в кратчайшие сроки.
Сразу видно, что эта задача содержит все компонента PEMDAS : круглые скобки (два набора), показатели степени (два и квадратный корень), умножение, деление, сложение и вычитание. Но на самом деле это не отличается от любой другой математической задачи, которую мы решали.
Во-первых, мы должны упростить то, что заключено в два набора круглых скобок:
√25 (6) ² — 18 ÷ 3 (2) + 2³
Затем мы должны упростить все экспоненты — , включая квадратные корни :
5 (36) — 18 ÷ 3 (2) + 8
Теперь мы должны произвести умножение и деление слева направо:
5 (36) — 18 ÷ 3 (2) + 8
180-18 ÷ 3 (2) + 8
180-6 (2) + 8
180-12 + 8
Наконец, решаем оставшееся сложение и вычитание слева направо:
180 — 12 + 8
168 + 8
= 176
Это приводит нас к и правильному ответу 176 .
Что дальше?
Еще одна математическая аббревиатура, которую вам следует знать — SOHCAHTOA. В нашем экспертном руководстве рассказывается, что означает аббревиатура SOHCAHTOAH и как вы можете использовать его для решения задач, связанных с треугольниками.
Готовитесь к разделу SAT или ACT Math? Тогда вы обязательно захотите ознакомиться с нашим полным руководством по SAT Math / ACT Math, которое дает вам множество советов и стратегий для этого сложного раздела.
Заинтересованы в действительно больших цифрах? Узнайте, что такое гугол и гуголплекс, а также почему невозможно выписать одно из этих чисел.
Что такое PEMDAS? — Определение, правила и примеры — Видео и стенограмма урока
Почему PEMDAS важен?
Без PEMDAS нет указаний для получения только одного правильного ответа. В качестве очень простого примера, чтобы вычислить 2 * 4 + 7, я мог бы сначала умножить, а затем сложить, чтобы получить 15. У меня также есть возможность сначала сложить, а затем умножить и получить 22. Какой ответ правильный? Используя PEMDAS, единственный правильный ответ — 15, потому что порядок букв в PEMDAS говорит мне, что умножение M должно выполняться перед сложением A.
У меня также есть возможность сначала сложить, а затем умножить и получить 22. Какой ответ правильный? Используя PEMDAS, единственный правильный ответ — 15, потому что порядок букв в PEMDAS говорит мне, что умножение M должно выполняться перед сложением A.
Вот объяснение правил, приведенных в PEMDAS:
- P, поскольку первая буква означает, что вы сначала выполняете любые вычисления с группировкой символов.
- Затем найдите показатели степени, E. Игнорируйте любые другие операции и возьмите любые числа с показателями степени в соответствующие степени.
- Несмотря на то, что M для умножения в PEMDAS стоит перед D для деления, эти две операции фактически имеют одинаковый приоритет. Выполняйте только эти две операции в порядке их следования слева направо.2) + 10
- 36 — 2 (20 + 12/4 * 3-4) + 10
- 36 — 2 (20 + 3 * 3-4) + 10
- 36 — 2 (20 + 12/4 * 3-4) + 10
- Осознайте важность PEMDAS и произнесите фразу, которая поможет вам запомнить порядок действий
- Использование PEMDAS в математических выражениях
- Понять, как PEMDAS применяется к выражениям дробей и абсолютных значений
Игнорируя сложение и вычитание, я завершаю следующую операцию умножения. 2} + 12/4.3 |, шаги будут следующими:
2} + 12/4.3 |, шаги будут следующими:
Краткое содержание урока
PEMDAS — это аббревиатура слов скобка, показатель степени, умножение, деление, сложение, вычитание. Для любого выражения сначала следует упростить все показатели, затем умножить и разделить слева направо и, наконец, сложить и вычесть слева направо. Слово «круглые скобки» стоит первым в этом аббревиатуре, чтобы указать, что любое выражение в символе группировки, такое как круглые скобки, должно быть сначала упрощено.Этот приказ также можно запомнить, используя фразу «Прошу прощения, моя дорогая тетя Салли».
Результаты обучения
Изучив этот урок на PEMDAS, откройте для себя свою способность:
Порядок операций
Поделитесь этой страницей!
После изучения 4 основных операций сложения, вычитания, умножения и деления пора научиться использовать их в различных комбинациях. Чтобы сделать это правильно, нам нужно понять некоторые правила того, как операции соотносятся друг с другом.
Чтобы сделать это правильно, нам нужно понять некоторые правила того, как операции соотносятся друг с другом.
Мы делаем это, понимая порядок важности каждой операции относительно других.
Правило: сложение и вычитание одинаково важны.
Это означает, что мы выполняем сложение и / или вычитание в том порядке, в котором они появляются (слева направо).
Пример 1
10 + 4-8
= 14-8 (тренировка 10 + 4 вначале)
= 6
Пример 2
10-7 + 8
= 3 + 8 (сначала тренировка 10-7)
= 11
Если вы выполните расчет в другом порядке, в большинстве случаев вы получите другой результат.Так что навести порядок в правильной последовательности жизненно важно.
Пусть ваш ребенок или ученик сначала поработает с двумя операциями, прежде чем переходить к более сложным выражениям, включающим три, четыре или более операций.
Правило: умножение и деление имеют одинаковое значение.
Это означает, что мы выполняем умножение и / или деление в том порядке, в котором они появляются (слева направо).
Правило: умножение и деление важнее сложения и вычитания.
Это означает, что нам нужно сначала выполнить умножение и деление, прежде чем мы сможем выполнять сложение и вычитание.
Правило: круглые скобки или квадратные скобки () более важны, чем каждая из 4 операций.
Это означает, что мы должны выполнить все, что находится в круглых скобках (), прежде чем следовать другим правилам.
Примеры
Это приводит нас к правилу BODMAS :
Скобки, порядки (степени и корни), деление и умножение, сложение и вычитание
Или правило PEMDAS :
Круглые скобки, экспоненты, умножение и деление и сложение и вычитание
Для облегчения запоминания: Прошу прощения, моя дорогая тетя Салли
Практические вопросы
ОТВЕТЫ
Термины для уравнений сложения, вычитания, умножения и деления — математика для 3-го класса
Изучите термины для уравнений сложения, вычитания, умножения и деления
Итак, вы научились решать уравнения сложения, вычитания, умножения и деления. 👏
👏
Давайте рассмотрим терминов для каждого из них.
Совет: Термины — это имен различных частей уравнения.
Условия добавления
Слагаемые — это числа, которые складываются вместе.
Сумма — это ответ, который вы получите, сложив числа.
Мы пишем плюс ( +) между двумя слагаемыми и знак равенства перед суммой.
Совет: Знак равенства (=) означает, что элементы слева и справа от него равны.
Термины для вычитания
Minuend — это число, из которого вычитается. Это большее число.
Subtrahend — это число, которое убирается из убываемого. Это меньшее число.
Это меньшее число.
Вычитаемое всегда предшествует вычитаемому.
Наконечник для запоминания:
Разница — это ответ, который мы получаем в уравнении вычитания.
Мы используем знак минус (-) между минусом и вычитаемым.
Запишем знак равенства перед разностью.
Условия умножения
Умножаемое — это число, которое нужно умножить.
Умножитель — это число, указывающее, сколько раз следует умножить множимое.
Множаемое и множитель также называются коэффициентами .
Множитель часто записывается первым, но положение этих чисел не имеет особого значения. Это называется коммутативным свойством умножения.
Это называется коммутативным свойством умножения.
Ответ в уравнении умножения называется произведением .
Знак умножения ( ×) записывается между двумя множителями. Его также называют знаком раз.
Условия для подкласса
Дивиденд — это делимое число.
Делитель — это число, которое указывает, сколько раз следует разделить дивиденд.Он отвечает на вопрос «На сколько равных групп делится число?».
Ответ, который мы получаем в уравнении деления, называется частным .
Знак деления (÷) помещается между делимым и делителем. Это короткая горизонтальная линия с точками над и под ней.
Совет: Вы также можете увидеть /, используемые как знак деления. То же, что и ÷.
То же, что и ÷.
Смотри и учись
Отличная работа по изучению этих терминов.👏
А теперь попробуйте практиковаться, чтобы убедиться, что вы помните, что они означают.
.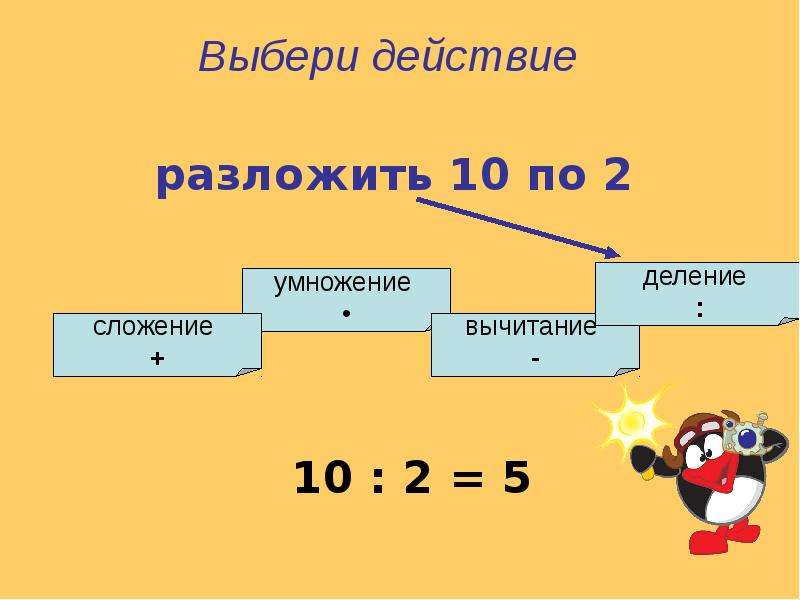


 С. Александрову и А. Н. Колмогорову, пример нужно решать слева направо, как обычно. Они, конечно, предложили решать такое по-другому, но научное сообщество их не поддержало.
С. Александрову и А. Н. Колмогорову, пример нужно решать слева направо, как обычно. Они, конечно, предложили решать такое по-другому, но научное сообщество их не поддержало. И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.


 И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
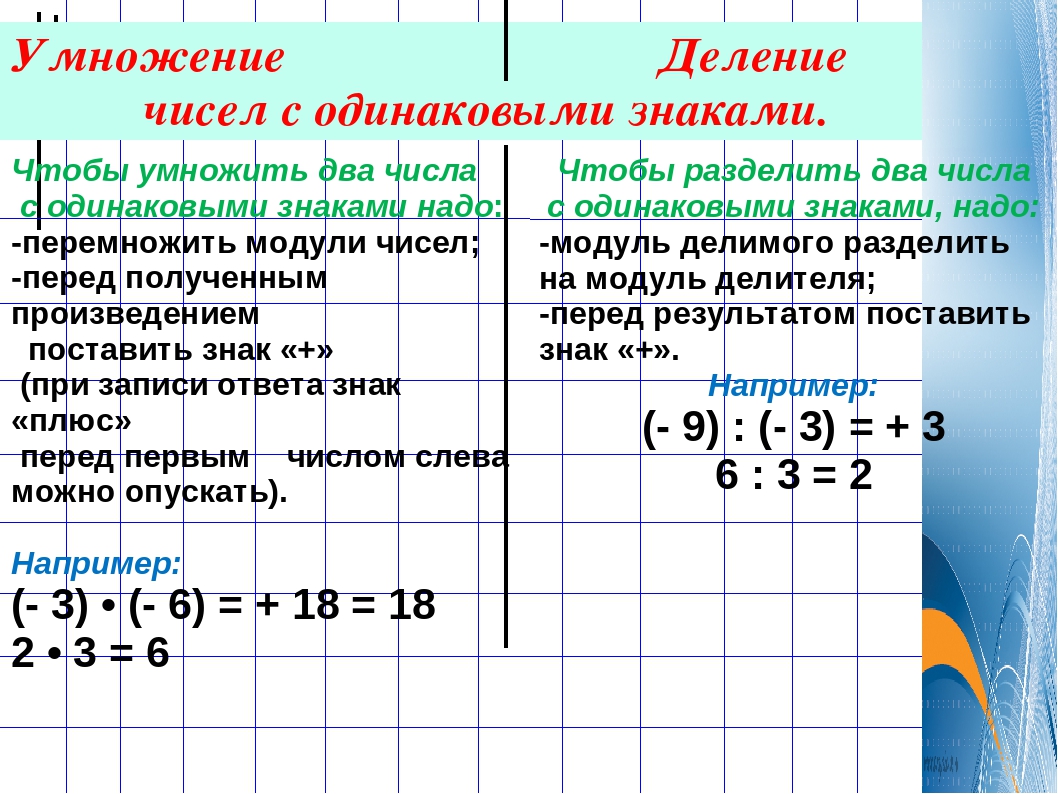 Сложение и вычитание также выполняются на одном этапе.
Сложение и вычитание также выполняются на одном этапе. Теперь у нас 5 + 4 x 3 6? 1 =?
Теперь у нас 5 + 4 x 3 6? 1 =?  Чтобы определить, какую операцию выполнить в первую очередь, мы добавляем или вычитаем слева направо в зависимости от того, что идет первым, что в этой ситуации должно сложить, 1 + 3 = 4.
Чтобы определить, какую операцию выполнить в первую очередь, мы добавляем или вычитаем слева направо в зависимости от того, что идет первым, что в этой ситуации должно сложить, 1 + 3 = 4.
 3} первый.
3} первый.