Снова «Морской бой». Считаем число возможных расположений кораблей / Хабр

Раз уж неделя «Морского боя» на Хабре продолжается, добавлю и я свои два цента.
При попытке найти оптимальную стратегию для игры за компьютер довольно быстро приходим к такому приближению:

Допустим, что состояние некоторых клеток нам уже известно, и мы хотим сделать ход, максимально приближающий нас к победе. В таком случае имеет смысл выбирать клетку, которая занята кораблём противника в наибольшем числе возможных размещений кораблей, не противоречащих имеющейся информации

В самом деле. Если возможная конфигурация только одна, то мы заканчиваем игру за один ход, расстреливая его корабли по очереди (ведь конфигурация нам известна!) Если же конфигураций больше, то нам нужно уменьшить их число как можно сильнее, тем самым увеличив имеющееся у нас количество информации. Если мы попадём в корабль, то ничего не потеряем (ведь ход остаётся у нас!), а если промахнёмся — то число оставшихся комбинаций будет минимальным из возможных после этого хода.

Понятно, что это только приближение к отпимальной стратегии. Если противник будет знать о нашем плане, он постарается разместить корабли так, чтобы они не попадали в те клетки, куда мы будем стрелять в начале игры. Правда, ему это поможет мало — мы всё равно в конце концом зажмём его в угол — но возможно, что определённая гибкость нам не помешала бы. Кроме того, не исключено, что продуманная серия ходов, первый из которых не является оптимальным, привела бы к лучшему результату. Но не будем пока усложнять и без того сложную задачу, а попытаемся просчитать все конфигурации и построить карту вероятности заполнения поля.

На первый взгляд, задача кажется неподъёмной. Число конфигураций представляется порядка 10²⁰ (на самом деле их несколько меньше — ближе к 10¹⁵), так что на полный перебор времени уйдёт слишком много. Перебирать раскраски поля и оставлять только допустимые — не лучше: всё равно нам каждую комбинацию придётся просмотреть.

Что же ещё попробовать? Любой олимпиадник тут же ответит — динамическое программирование. Но как его организовать?

Идём сверху вниз. Какая информация нам нужна?

Итак, будем идти сверху вниз. Предположим, что поле у нас разделено на две части — часть A состоит из первых k строк, а часть B — из всех остальных. Заполнением части поля назовём любую раскраску его клеток в два цвета. Заполнение всего поля называется корректным, если чёрные клетки образуют набор кораблей, удовлетворяющий правилам (корабли прямые, не соприкасаются, их длины образуют нужный набор). Два заполнения S1 и S2 части A мы будем называть эквивалентными, если для любого заполнения T части B объединенные заполнения всего поля S1|T и S2|T будут корректными или некорректными одновременно.

Для решения задачи нам достаточно:

• Описать все классы эквивалентности заполнений для части A
• Для каждого класса вычислить число различных заполнений, и для каждой клетки области A указать, в каком числе заполнений она была чёрной (назовём эту информацию картой данного класса)
• Описать пересчёт классов и их карт при добавлении к области A новой строки.

Пусть у нас есть неизвестное заполнение S области A и известное заполнение T области B. Что нам достаточно знать про S?

Во-первых, неплохо иметь полное состояние последней строки. Только в этом случае мы сможем определить, какие клетки первой строки области B мы ещё можем занимать, а какие — нет.

Во-вторых, надо знать, сколько и каких законченных кораблей в области A уже есть. Законченным мы называем корабль, который уже нельзя продлить в область B. В нашем случае это либо корабли, не имеющие клеток в последней строчке, либо корабли, целиком лежащие в ней (и занимающие две или более клетки).

В-третьих, про каждый корабль, который ещё можно продлить в область B, нам нужно знать его текущую длину. Сами эти корабли легко узнать по последней строчке: они занимают в ней одну чёрную клетку, окруженную белыми полями.

И всё. Класс эквивалентности целиком определяется этими данными, причём даже не все их комбинации являются допустимыми. Посчитаем, сколько получилось:

• Последняя строчка: 10 бит, причём не все варианты возможны: не может идти более 4 единиц подряд, и не может быть двух групп по 4 единицы (0111101111). Всего получается 909 вариантов.
• Уже выставленные корабли. От 0 до 4 однопалубных, от 0 до 3 двухпалубных, от 0 до 2 трёхпалубных, 0 или 1 четырёхпалубный. Всего 120 вариантов.
• Для каждого изолированного бита строчки — число клеток в соответствующем вертикальном корабле, попавших в A: от 1 до 4. Таких кораблей не более 5, итого не более 1024 вариантов.

Каждый класс, таким образом, описывается 27 битами, а их общее количество — не более 120 миллионов. В действительности, эта оценка сильно завышена, и программа смогла найти 1053612 классов.

Добавляем новую строку

Пусть у нас есть заполнение S, про которое нам известна только описанная выше информация. Мы хотим продлить его ещё на одну строку: перечислить все заполнения, которые можно получить, определить классы для них, и для каждого нового класса построить карту плотности заполнений.

Сначала посмотрим, какие строки мы можем добавлять к нашему заполнению. Основной критерий известен всем: черная клетка новой строчки не может быть соседней по диагонали с чёрной клеткой последней строчки S. Далее, как мы уже знаем, в новой строчке не может быть слишком длинных кораблей. И еще, если один из вертикальных кораблей имеет длину 4, то продолжаться на новую строку он тоже не может. Остальные ограничения связаны с набором кораблей, и их удобнее проверять потом.

Переберём все строки, которые можно добавить. Если в строке есть более одной единицы подряд, то они образуют горизонтальный корабль — его сразу учитываем в счётчиках законченных кораблей. С изолированными единицами есть три ситуации:

• В последней строке S изолированная единица была, а в новой строке в этом месте её нет. Значит, корабль закончен, и его длина добавляется к счётчику.
• В новой строке изолированная единица есть, а в последней строке S в этом месте её не было. Значит, появился новый вертикальный корабль, и его длина сейчас равна 1.
• Изолированная единица есть и в последней строке S, и в новой строке.
  Значит, вертикальный корабль продолжается, и его длина увеличивается на 1.

Теперь проверим, допустим ли набор длин. Пусть s1, s2, s3, s4 — число законченных кораблей длины 1,2,3,4 соответственно, а n1, n2, n3, n4 — число незаконченных кораблей с соответствующими длинами. Чтобы набор не противоречил условиям, необходимо следующее:

s1<=4 && s2<=3 && s3<=2 && s4+n4<=1 && (s3+s4+n3+n4)<=3 && (s2+s3+s4+n2+n3+n4)<=6 && (s1+s2+s3+s4+n1+n2+n3+n4)<=10

Информация для нового класса готова. Чтобы построить для него карту, достаточно скопировать первые строки старой карты, а в следующую строку вписать добавленную битовую строчку, умноженную на число комбинаций. Карты одного и того же класса, полученные из разных конфигураций, складываются.

Концовка

После того, как мы добавили к исходной пустой конфигурации 10 строк, у нас получился список из 1053612 классов, каждый — со своей картой. Чтобы получить карту всех конфигураций поля, нам надо пройтись по всем этим классам,«закончить» незаконченные корабли, посчитать число получившихся кораблей каждого размера, и если оно правильное — то прибавить карту класса к общей сумме.

Для пустого поля 10×10 получилось 1855545978831780 конфигураций, а карта заполнения выглядит так (все числа поделены на 10⁹):

438487 418064 475795 466986 459000 459000 466986 475795 418064 438487
418064 273993 311381 287231 287065 287065 287231 311381 273993 418064
475795 311381 378334 357367 361127 361127 357367 378334 311381 475795
466986 287231 357367 330652 334756 334756 330652 357367 287231 466986
459000 287065 361127 334756 338709 338709 334756 361127 287065 459000
459000 287065 361127 334756 338709 338709 334756 361127 287065 459000
466986 287231 357367 330652 334756 334756 330652 357367 287231 466986
475795 311381 378334 357367 361127 361127 357367 378334 311381 475795
418064 273993 311381 287231 287065 287065 287231 311381 273993 418064
438487 418064 475795 466986 459000 459000 466986 475795 418064 438487

То, что она симметрична, косвенно подтверждает, что грубых ошибок в программе нет 🙂 Самая заполненная клетка — С1, самая незаполненная — B2.
После хода в С1 карта примет такой вид:

334039 316782 362205 354834 348680 348723 354859 362278 316825 334105
316847 204441 234170 214857 214919 214952 214721 234125 204338 316830
362174 234066 286949 270246 273421 273609 270199 287338 234109 362286
354993 215372 270082 249099 252049 252445 248433 270251 214694 354875
347443 215675 272189 252807 255040 256554 252272 273744 214941 348764
344351 216423 272030 253365 252114 255722 251441 273431 214746 348625
351029 226597 265572 262005 251178 255339 249502 271093 215027 354867
347356 238783 245635 276238 258889 268837 266947 286297 234182 362174
342552 273993 227511 287231 237138 226857 216325 233431 204620 316794
292453 231475      0 269650 316361 349490 359545 360275 316193 333632

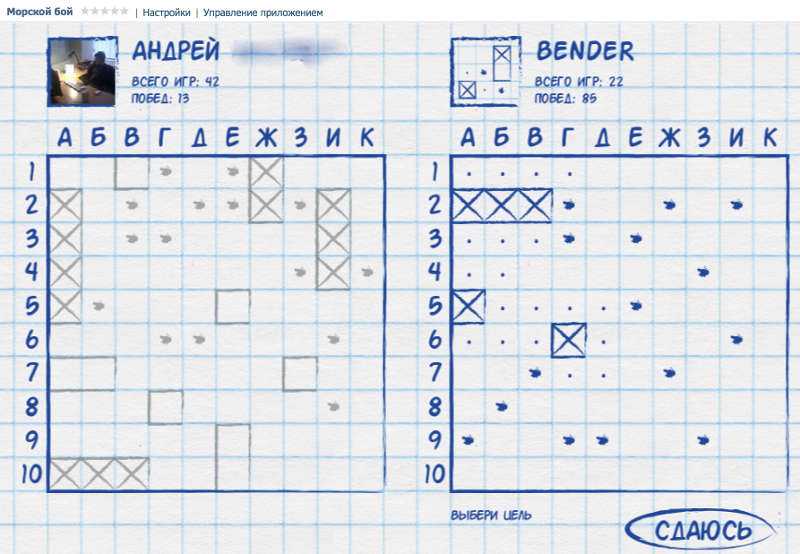
Последовательность «лучших ходов» при постоянных промахах выглядит так (см. рисунок):
C1, J8, A8, h2, A4, J4, D10, G10, E1, D2, B3, A2, C9, B10, H9, I10, I7, J6, I5, H6, J2, I3, h5, G5, G2, F3, E4, B7, A6, B5, C6, C3, D4, D5, F6.
Видно, что программа не торопится ловить линкоры. К 24-му ходу, когда «диагональному» алгоритму остался бы последний ход до гарантированного попадания, число оставшихся расположений кораблей составляет примерно 240*10

9, а у «диагонального» алгоритма оно составляет 260*10⁹. Разница невелика. Надо будет устроить турнир между этими алгоритмами, чтобы выяснить, насколько она существенна.

Неделя Морского Боя

Оптимальный алгоритм игры в морской бойGORKOFF
Алгоритм игры в «морской бой»: обстрел противникаimpersonalis

И более старые публикации:
Теория и практика игры «Морской бой» — по-честному born2fly
Морской бой с искусственным интеллектом — по-честному michurin

Морской бой: задачка для олимпиадников

Когда мы берем ребёнку репетитора, то каждый по-своему представляет себе, как будут проходить эти прекрасные занятия, ведущие к светлому будущему олимпиад и ЕГЭ. И далеко не каждый допускает мысль, что ребёнок и репетитор будут просто играть. О том, почему это полезно и работает только на пользу, рассказывает наш блогер, репетитор Яна Полянских.

Я играю с детьми на занятиях. В комментариях к одной из моих старых статей на «Меле» был чудесный вопрос: мол, занятие оплачено, за чей счёт вы играете с детьми в морской бой? За счёт сокращения основной, содержательной части?

Сейчас будет страшное. Игра в морской бой — это и есть основная, содержательная часть занятия. И не у младших школьников, а у олимпиадников… Жесть, правда? Мне бы стоило не смущать людей, которые платят за занятия, лучше просто выкинуть из образовательного процесса целый раздел математики, который называется «теория игр». А лучше вообще его из математики выкинуть. Или переименовать. Во что-то посерьёзнее, ну? Игр. Игр. И что это слово делает в такой адской науке?

Ладно, проехали, рассказываю, зачем и как играть с детьми в морской бой. Игра старая и известная, но если забыли классические правила, напомню. Два игрока рисуют каждый по два поля 10*10 с буквенно-числовыми координатами. На одном из них расставляют свои корабли, второе поле будет необходимо для стрельбы по противнику. Корабли делятся на классы: одноклеточные (катер) — их будет 4, двухклеточные (эсминец) — их будет 3, трёхклеточные (крейсер) — их будет 2, и четырёхклеточные (линкор) — он будет… конечно, 1. Корабли не могут касаться друг друга даже в точке, в классической версии не могут и изгибаться (т. е. четырёхклеточный корабль всегда представляет собой этакую палочку, расположенную вертикально или горизонтально).

Игра заключается в том, что игроки по очереди называют координаты клеток (а8, з4, и3…), где, по их мнению, может располагаться корабль противника. Эти ходы отмечают на втором, свободном поле. При удачном выстреле в клеточке с нужной координатой рисуется крестик (убит или ранен), при промахе ставится точка. Игра продолжается до тех пор, пока все корабли противника не будут уничтожены.

На первый взгляд, игра носит глупый вероятностный характер: стреляй себе по полю, авось попадёшь. Кому-то даже везёт. Но, приобретая некоторый опыт игры, ты понимаешь, что у неё (как и у большинства) есть стратегия.

Очень простая мысль: вероятность попасть по кораблю противника тем выше, чем меньше непроверенных клеток осталось на его поле (логично, правда?). Аналогично вероятность попадания по вашим кораблям тем ниже, чем больше непроверенных клеток осталось на вашем поле. А значит, для эффективной игры нужно научиться сразу двум вещам: оптимальной стрельбе по противнику и оптимальному размещению своих кораблей.

Как вы понимаете, сложнее всего искать однопалубные корабли. Существуют определенные стратегии расстановки кораблей, которые ещё больше уменьшают вероятность попадания в последний одноклеточный корабль. Например, можно расположить весь флот кучкой в одном месте так, чтобы он занимал как можно меньше места, а на оставшемся свободном поле расположить пару своих маленьких кораблей. Эта игра отлично тренирует внимательность, учит рациональному мышлению и умению принимать свои ошибки, перерабатывая их в опыт.

В поиске кораблей тоже есть много смысла, если к ней подходить с точки зрения математики.

В правилах четко оговорено, что корабли не соприкасаются друг с другом, а значит, если вы нашли корабль с координатами в4-г4-д4-е4, то по каким клеткам стрелять бесполезно? Верно, по всем, которые непосредственно окружают этот корабль, сразу ставим на них точки: б3-б4-б5, в3-г3-д3-е3-ж3, ж4-ж5, в5-г5-д5-е5. Какой теперь стала вероятность попасть в корабль? Насколько уменьшилось количество свободного пространства? Уничтожив вражеский линкор в лучшем случае (если он одиноко стоял посреди поля), мы получили информацию аж о 14 клетках поля, а пошедший ко дну трёхпалубный корабль даст нам информацию о 12 клетках.

Ого. 14 клеток. И ещё два раза по 12. Нехило, правда? Получается, удобнее всего вначале искать крупные корабли. Как это сделать? Давайте рассмотрим поле 4*4. За сколько выстрелов вы гарантированно найдёте четырёхпалубный корабль? Правильно, не более чем за 4 хода. Для этого надо стрелять так, чтобы на каждой горизонтали и вертикали было ровно по одной проверенной клетке.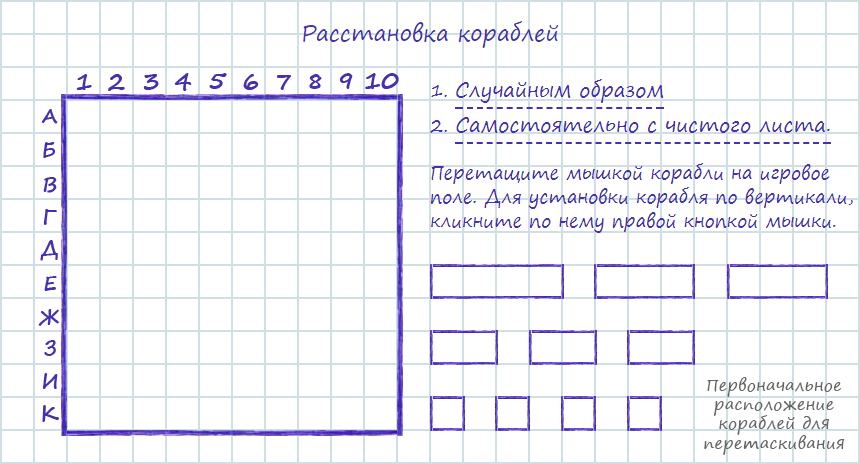

Снова посмотрим на поле 10*10. Попробуйте понять, сколько ходов вам гарантированно потребуется для того, чтобы, используя эту стратегию, найти этот самый неповоротливый корабль. Сколько получилось ходов? Проверим в комментариях? Мои олимпиадники не с первого раза нашли минимальное количество ходов, а что у вас получилось?

Аналогично поступим с трехпалубным. Для этого рассмотрим поле 3*3, поймём, как надо стрелять, и снова перенесёмся на наше большое поле с этим знанием. Причём по многим из клеток вы уже стреляли, пока искали линкор. Двухпалубные искать будем так же. А вот для самых маленьких кораблей стратегии нет. Надо лишь надеяться на теорию вероятностей и на то, что вы внимательно расставляли точки «мимо», когда заполняли поле противника.

Мало математики и слишком понятно. Конечно, на занятиях математикой ученик должен плакать от безысходности, это всем известно. Тогда можно поискать одноклеточный корабль с помощью страшных слов. Итак, если на поле из 100 (или n) клеток расположен 1 однопалубный корабль, то вероятность попасть в него равна… здесь не нужны страшные формулы, чтобы понять, что 1/100 (1/n). Тогда определим вероятность уничтожения этого корабля за k выстрелов. Это событие может произойти как сразу (уничтожен первым выстрелом), так и последним, то есть благоприятная выборка состоит из всех клеток, включая клетку с кораблем.

Количество благоприятных стратегий вычисляется как число неупорядоченных выборок из множества 99 клеток (n-1) по k-1 (клетка, занятая кораблем, не учитывается), умноженное на число перестановок в самой выборке k! и число перестановок клеток, оставшихся за выборкой (n-k)! Pk = [k! C из (n-1) по (k-1) (n-k)!]/n! = [C из (n-1) по (k-1)]/C из n по k…

Упрощая выражение, получаем, что вероятность попадания в корабль за k выстрелов равно k/n. Логично? Логично.

Полегчало, правда? Ну, если так, то пусть дитятко играет на занятиях в морской бой.

Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.

Фото: Shutterstock (shinobi)

Список кораблей, участвовавших в битве в Коралловом море

1942

 » 

Битва в Коралловом море

 » 

Список кораблей, участвовавших в битве в Коралловом море

• Последняя битва за USS Houston

Батаан и Коррехидор

Ранние морские рейды

Рейд Дулиттла

Битва в Коралловом море

• Американо-австралийское сотрудничество
• Список кораблей в битве в Коралловом море

Битва за Мидуэй

Боевые патрули подводных лодок

Битва за Атлантику

• Арктические конвои: «Конвой врассыпную»
• Испытание PQ-17
• Битва за Атлантику: обзор
• Необычайный героизм и выдающееся мужество

Кампания Соломоновых островов: Гуадалканал

• Гуадалканал и пристань Тулаги
  • Снимки: начальные операции, август – сентябрь 1942 г.
• Битва за остров Саво
  • Битва за остров Саво Боевые порядки
• Битва у Восточных Соломоновых островов
• Битва у мыса Эсперанс
  • Снимки: Битва у мыса Эсперанс
• Битва за острова Санта-Крус
• Морское сражение за Гуадалканал
  • Гуадалканал Историческая справка
  • Гуадалканал Хронология
  • Боевой орден Гуадалканала
• Битва при Тассафаронге
  • Снимки: Битва при Тассафаронге
• Выход Японии

Операция Факел: Вторжение в Северную Африку

• Рабочий фонарь Галерея изображений

Создание инфраструктуры для войны

• Морским пчелам 75 лет

Комплектование ВМС США

• Афроамериканцы на службе общего назначения, 1942 г.
• 75 лет со дня рождения WAVES
• ВОЛНЫ Общая информация
• Программа подготовки офицеров V-12

Тема

• Лодки-Корабли-Крейсеры
• Лодки-Корабли—Эсминец

Тип документа

• Судовая история

Войны и конфликты

• Вторая мировая война 1939-1945

Сообщества военно-морского флота

Форматы файлов

Местонахождение архивных материалов

Имя автора

Место события

Имя получателя

Корабли в битве в Коралловом море

---

Сноски

Пн. :11 по восточноевропейскому времени 2017 г.

Ютландия: Смерть в море — Национальный архив

• Задания
• Фон
• Заметки учителя
• Внешние ссылки
• Связь с учебным планом

31 мая 1916 года у берегов Ютландии в Дании произошло крупнейшее морское сражение Первой мировой войны. Погибло более 6000 британских моряков.

Эти большие потери частично были вызваны неожиданным затоплением трех больших кораблей: HMS Invincible, HMS Queen Mary и HMS Indefatigable. В то время погибших моряков прославляли как доблестных товарищей, славно павших в бою. Однако некоторые историки считают, что большинство этих моряков погибли из-за того, что люди допустили ошибки по неосторожности. Используйте этот урок, чтобы изучить оригинальные документы, касающиеся потерь в битве при Ютландии.

---

Задания

1. Посмотрите Исходник 1. Сначала узнайте из послужного списка матроса, участвовавшего в бою, следующую информацию:

• Как полное имя матроса?
• Дата и место его рождения?
• Кем работал моряк до поступления на флот?
• Когда он поступил на флот?
• Сколько ему было лет, когда он присоединился?
• На скольких кораблях и казармах он служил?
• На каком корабле он погиб и когда?
• Есть ли в послужном списке какая-либо информация о том, почему затонул HMS Indefatigable?

Скачать стенограмму послужного списка ВМФ Джона Экрилла (ADM 188/464) (19. 50 Kb)

Скачать стенограмму послужного списка ВМФ Джона Экрилла (ADM 188/464) (PDF, 44,6 КБ)

2. Посмотрите на Источник 2. Это телеграмма, сообщающая о затоплении «Неутомимого».

• Как по телеграмме был потоплен «Неутомимый»?
• Был ли «Неустанный» единственным кораблем, который был потоплен таким образом?
• Что такое корабельный журнал? (Подсказка: это не публикация!)

3. Посмотрите на Источник 3. Это отчет о потере Indefatigable, опубликованный в London Gazette. Его сделал адмирал Битти, морской офицер, командовавший 1-й эскадрой линейных крейсеров во время сражения.

• Приведена ли в этом заявлении какая-либо причина «серьезных потерь»?
• Что адмирал думает о погибших?
• Есть ли какие-либо признаки того, что Адмирал обеспокоен причинами потерь этих кораблей?

4. Посмотрите на Источник 4. Это частный меморандум ВМФ о гибели «Неутомимого».

• Какой «вывод» был сделан о том, почему «Неустанный» взорвался?
• Заряды взрывчатые. Что не так с тем, как заряды подносились к пушкам?
• Какой еще фактор способствовал взрыву?
• Был смертью Джозефа Джона Акрилла и многих других на «Неустанном»:
  • славный?
  • ненужная потеря?
  • объясните свой ответ
• Напишите газетный репортаж на основе одного из следующих заголовков.
  • Потопление «Неутомимого»: славная и благородная жертва для защиты короля и страны
  • Неутомимый погибает! Жизни потрачены впустую из-за ошибок, допущенных на борту корабля

---

Предыстория

До 1916 года не было крупных морских сражений между крупнейшими военно-морскими державами мира, Германией и Великобританией, несмотря на гонку вооружений, создававшую большие флоты в ожидании великих морских сражений между новыми боевыми кораблями-дредноутами и более совершенными линейными крейсерами.

В январе 1916 года у немцев появился новый командующий флотом, адмирал Шеер, и он рвался в бой. В немецком флоте было менее 100 кораблей по сравнению с Великим британским флотом, насчитывающим около 150. Шир планировал заманить британский флот в бой и заманить его в ловушку, но немецкие планы были перехвачены британцами, которые в ответ приготовились заманить немецкий флот в ловушку. Около 16:00 31 мая быстрые британские линейные крейсера заманили немцев к Великому флоту, понеся тяжелые потери в первых боях.

Незадолго до 18:00 все великие флоты Британии и Германии вступили в контакт. Весь вечер шел ожесточенный бой, осколочно-фугасные снаряды врывались в толстую броню. Моряки сгорели заживо или утонули в ледяном море. С наступлением темноты Шеер попытался вернуться в порт, но обнаружил, что британцы маневрировали, чтобы преградить им путь. После очередной стычки между линейными крейсерами Шееру удалось отступить, в то время как британский флот, обеспокоенный вражескими подводными лодками и минными полями, решил не преследовать его.

Обе стороны заявили о своей победе. Немцы заявили, что потопили больше кораблей, но британцы заявили, что Шеер сдался первым и скрылся с места сражения. Однако при подсчете потерь Британия, похоже, потеряла больше. Великобритания потеряла 14 кораблей против 11 немецких, и в то время как Германия потеряла 2551 человека, Великобритания потеряла 6097 человек.

Немецкий флот открытого моря оставался в порту до конца войны, став «флотом в состоянии», чтобы угрожать, но не вступать в бой с британским флотом. Вместо этого они предпочли полагаться на подводные лодки (подводные лодки). Немецкие подводные лодки доставили британцам большие проблемы, поскольку они потопили огромное количество импортных товаров и припасов. Британцы в конечном итоге победили угрозу подводных лодок, применив систему конвоев, в которой противолодочные корабли защищали другие корабли в группе.

---

Заметки учителя

Этот урок помогает учащимся оценить ценность изучения различных источников и опасность основывать вывод на одном источнике. Учащиеся исследуют четыре источника. Первый источник — послужной список моряка, участвовавшего в Ютландском сражении. Второй источник — телеграмма о потоплении линкора «Неутомимый». Третий источник — выдержка из газеты «Ведомости» о гибели линкора. Четвертый источник — военно-морской меморандум, из которого следует, что потерь можно было бы избежать.

Первой реакцией на гибель линкора «Неутомимый» были героические потери. Согласно источнику 4, потеря могла быть связана с магазином на корабле. Магазин на корабле был местом хранения боеприпасов. Следовательно, боеприпасы должны были быть физически доставлены матросами к орудиям из этих складских помещений (погребов). Они довольно часто взрывались в бою — если корабль попадал прямо в магазин, это вызывало мощный взрыв. Однако в данном случае выясняется, что, поскольку боеприпасы к орудиям не находились в негорючих корпусах, они загорелись отчасти из-за следа пороха, который привел к магазину и, в свою очередь, вызвал взрыв.

• Обсудите со студентами, считают ли они, что правду нужно было рассказать родственникам моряков или скрыть, чтобы избежать смущения и ненужных страданий.
• Обсудите, как такое откровение повлияет на боевой дух. Затем это может привести к общей дискуссии о важности морального духа в военное время.
• Учащиеся могут продолжить расследование битвы за Ютландию, используя блог с дополнительными документами ниже
.
• Дебаты о том, кто «выиграл» битву на основании улик.
• Были ли потери важнее того, кто первым покинул поле боя?
• Используйте источники, чтобы написать газетный репортаж о Ютландской битве

Источники

Иллюстрация: MFQ 1/366/4

Источник 1 – ADM 188/464

Источник 2 – ADM 137/1642

Источник 3 – ADM 137/301 – ADM7 Источник 4

3 9 / 308

---

Внешние ссылки

Ютландская битва Информация
Этот веб-сайт предоставляет вам информацию о предыстории битвы, участвующих кораблях и результатах.

https://blog.nationalarchives.gov.uk/clash-titans/
Прочтите этот блог о Ютландской битве, в котором обсуждаются дополнительные оригинальные документы

Связь с учебным планом

Ключевой этап 3
Первая мировая война и мирное урегулирование

Ключевой этап 4
AQA GCSE History: Конфликт и напряженность: История Первой мировой войны, 1894–1910 Eceldex 2 : с 1900 г.