Конспект урока ««Порядок выполнения действий в выражениях без скобок и со скобками».»

Тема урока: «Порядок выполнения действий в выражениях без скобок и со скобками».

Цель урока: создать условия для закрепления умений применять знания о порядке выполнения действий в выражениях без скобок и со скобками в различных ситуациях, умений решать задачи выражением.

Задачи урока.

Образовательные:

— закрепить знания учащихся о правилах выполнения действий  в  выражениях без скобок и со скобками; формировать у них умение пользоваться этими  правилами при вычислении конкретных выражений; совершенствовать  вычислительные навыки; повторить табличные случаи умножения и деления;

Развивающие:

— развивать вычислительные навыки, логическое мышление, внимание, память, познавательные способности учащихся,

коммуникативные навыки;

Воспитательные: 

— воспитывать толерантное  отношение друг к другу, взаимное сотрудничество,

культуру поведения на уроке, аккуратность, самостоятельность,  воспитывать интерес к занятиям  математикой.

Формируемые УУД:

Регулятивные УУД:

работать по предложенному плану, инструкции;

выдвигать свои гипотезы на основе учебного материала;

 осуществлять самоконтроль.

Познавательные УУД:

знать правила порядка выполнения действий:

уметь разъяснить их содержание;

понимать правило порядка выполнения действий;

находить значения выражений согласно правилам порядка выполнения;

действий, используя для этого текстовые задачи;

 записывать решение задачи выражением;

 применять правила порядка выполнения действий;

уметь применять полученные знания при выполнении контрольной работы.

Коммуникативные УУД:

слушать и понимать речь других;

 выражать свои мысли с достаточной полнотой и точностью;

 допускать возможность различных точек зрения, стремиться понимать позицию собеседника;

работать в команде разного наполнения (паре, малой группе, целым классом), участвовать в обсуждениях, работая в паре;

Личностные УУД:

устанавливать связь между  целью деятельности и её результатом;

определять общие для всех правила поведения;

  уметь осознанно и внимательно читать задания;

выражать способность к самооценке на основе критерия успешности учебной деятельности.

Планируемый результат:

Предметные:

Знать правила порядка выполнения действий.

Уметь разъяснить их содержание.

Уметь решать задачи с помощью выражений.

Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.

Метапредметные:

Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану;  оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки;  планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение(Регулятивные УУД).

Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им  (Коммуникативные УУД).

Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД).

Ход урока

1. Организационный  момент. 

Чтоб урок наш стал светлее,

Мы поделимся добром.

Вы ладони протяните,

В них любовь свою вложите,

Ей с друзьями поделитесь

И друг другу улыбнитесь.

— Займите свои рабочие места.

Открыли тетради, записали число и классная работа.

2. Актуализация знаний.

— На уроке нам с вами предстоит подробно рассмотреть порядок выполнения арифметических действий в выражениях без скобок и со скобками.

Устный счёт.

Игра «Найди правильный ответ».

( У каждого ученика лист с числами)

55	56	57	58	59	60	61
62	63	64	65	66	67	68
69	70	71	72	73	74	75
76	77	78	79	80	81	82
83	84	85	86	87	88	89
90	91	92	93	94	95	96
97	98	99	100	101	102	103

— Я читаю задания, а вы, выполнив в уме действия, должны полученный результат, т. е. ответ, зачеркнуть крестиком.

1. Я задумала число, из него вычла 80, получила 18. Какое число я задумала? (98)

2. Я задумала число, к нему прибавила 12, получила 70. Какое число я задумала? (58)

3. Первое слагаемое 90, второе слагаемое 12. Найдите сумму. (102)

— Соедините полученные результаты.

— Какую геометрическую фигуру вы получили? ( Треугольник)

— Расскажите, что вы знаете о данной геометрической фигуре. (Имеет 3 стороны, 3 вершины, 3 угла)

— Продолжаем работать по карточке.

1. Найдите разность чисел 100 и 22. (78)

2. Уменьшаемое 99, вычитаемое 19. Найдите разность. (80).

3. Возьмите число 25 4 раза. (100)

— Начертите внутри треугольника еще 1 треугольник, соединяя полученные результаты.

— Сколько треугольников получилось? (5)

3. Работа над темой урока. Наблюдение за изменением значения выражения от порядка выполнения арифметических действий

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Давайте проверим

Сравним выражения: 
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Запишем.

8-3+4=5+4=9

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

8-3+4=8-7=1

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя.

Порядок выполнения арифметических действий в выражениях без скобок

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

Потренируемся.

Рассмотрим выражение

38-10+6

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

24:3*2

В этом выражении имеются только действия умножения и деления – это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассмотрим выражение.

18:2-2*3+12:3

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

    1   4  2  5    3

18:2-2*3+12:3

Вычислим значение выражения.

    1   4  2  5    3

18:2-2*3+12:3=9-6+4=3+4=7

Порядок выполнения арифметических действий в выражениях со скобками

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Рассмотрим выражение.

30 + 6 * (13 — 9)

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

     3   2      1

30 + 6 * (13 — 9)

Вычислим значение выражения.

3    2   1

30+6*(13-9)=30+6*4=30+24=54

Правило выполнения арифметических действий в выражениях без скобок и со скобками

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

4. Закрепление Выполнение тренировочных заданий на изученное правило

Потренируемся.

Рассмотрим выражения, установим порядок действий и выполним вычисления.

43 — (20 — 7) +15

32 + 9 * (19 — 16)

2 * 9 — 18:3

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

2*9-18:3=18-6=12

Узнаем, правильно ли определен порядок действий в следующих выражениях.

     4    3    1   2

37 + 9 — 6 : 2 * 3 =

    3       1     2

18 : (11 — 5) + 47=

   1  3       2

7 * 3 — (16 + 4)=

Рассуждаем так.

     3     4   1   2

37 + 9 — 6 : 2 * 3 =

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

     3 4  1  2

37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37

Продолжаем рассуждать.

    3    1    2

18:(11-5)+47=

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

    2    1    3

18:(11-5)+47=18:6+47=3+47=50

Рассуждаем далее.

  1  3     2

7*3-(16+4)=

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

 

   2  3   1

7*3-(16+4)=7*3-20=21-20=1

Выполним задание.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

5. Подведение итогов.

— Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками. В ходе выполнения заданий определяли, зависит ли значение выражений от порядка выполнения арифметических действий, узнали, отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренировались в применении изученного правила, искали и исправляли ошибки, допущенные при определении порядка действий.

Скобки / Порядок выполнения действий / Справочник по математике для начальной школы

1. Главная
2. Справочники
3. Справочник по математике для начальной школы
4. Порядок выполнения действий
5. Скобки

В данном разделе мы познакомимся с выражениями со скобками в примерах первой ступени, то есть в тех примерах, в которых всего два действия: сложение и вычитание.

Мы научимся читать выражения со скобками и вычислять значения выражений со скобками.

Скобки

Знаки ( и ) называются скобками.

Скобки показывают, какие действия выполняются первыми, а какие потом.

Если скобок нет, то действия выполняются по порядку слева направо.

Например, 15 — 7 + 4.

Сначала производим вычитание, а потом сложение.

---

Рассмотри два примера. Что в них общего и чем они отличаются?

Общее: одинаковые математические знаки + и -, одинаковые числа: 16, 6 и 7.

Различие: во втором примере есть скобки.

---

В первом примере прямой порядок действий: 

Во втором примере сначала выполняется действие в скобках (сложение) и только потом — вычитание.

Рассматриваю примеры, порядок действий и результаты вычислений:

---

Как читать выражения со скобками?

15 — (6 + 7) = 2

Из числа 15 вычесть сумму чисел 6 и 7.

8 + (19 — 11)

К числу 8 прибавить разность чисел 19 и 11.

Советуем посмотреть:

Порядок выполнения действий

Правило встречается в следующих упражнениях:

2 класс

Страница 58, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 69, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 38, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 48. ПР 4. Вариант 1, Моро, Волкова, Проверочные работы

Страница 68. Тест 1. Вариант 1, Моро, Волкова, Проверочные работы

Страница 10, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 74, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 33, Моро, Волкова, Рабочая тетрадь, часть 2

3 класс

Страница 8, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 25, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 52, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 65, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 46, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 71, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 11. ПР 1. Вариант 2, Моро, Волкова, Проверочные работы

Страница 34. ПР 3. Вариант 1, Моро, Волкова, Проверочные работы

Страница 15, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 59, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

4 класс

Страница 6, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 14, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 18, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 62, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 73, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 92, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 5, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 13, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 78, Моро, Волкова, Рабочая тетрадь, часть 1

Страница 36, Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

---

абстрактная алгебра — Порядок операций — почему они в том порядке, в котором они находятся?

Просматривая посты, посвященные математике в r/askcience, я наткнулся на тот же вопрос!

---

u/KyleG подтверждает этот комментарий:

Это произвольно, потому что вся письменная математика является произвольным символом обозначения, изобретенные людьми. Существует множество языков программирования и другие типы систем обозначений, которые не следуют PEMDAS. Для Например, обратная польская нотация (которую предпочитали ранние компьютерные ученые) записывается как «операнд-операнд-оператор». Так, например, 3 4 + 7 / оценивается как 1, потому что слева направо 3 4 + оценивается как 3+4=7. Тогда у вас есть 7 /, поэтому 7, полученное из 3 4 + вы делите на 7.

http://en.wikipedia.org/wiki/Reverse_polish_notation

Как бы то ни было, и показатели степени, и скобки относительно недавние дополнения к математической нотации, поэтому имеет смысл, что наша произвольно определенная система письма будет адаптироваться к новым символам путем говоря «все работает точно так же, как и раньше, но прежде чем делать что мы должны делать что-то новое и убрать это с дороги».

---

Тем не менее, u/paolog предлагает причину для PEDMAS:

По сути, мы используем PEDMAS, потому что мы обнаружили, что он полезен в арифметике и алгебре (хотя есть области математики, где это не всегда так). Ничто не мешает нам использовать, скажем, ~~SAMDEP~~ PSAMDE, если бы мы захотели, но если бы мы это сделали, то все стало бы очень грязно.

Давайте просто рассмотрим бит DMAS. Почему умножение и деление предшествуют сложению и вычитанию? Потому что это имеет смысл делать именно так. Я мог бы послать вас купить мне три полдюжины коробок яиц и две коробки по дюжине. Общее количество яиц равно 3 x 6 + 2 x 12. Описываемая здесь реальная ситуация требует, чтобы мы интерпретировали это как (3 x 6) + (2 x 12), или всего 42 яйца, а не 3 x (6). + 2) x 12. Умножение перед сложением всегда происходит естественным образом, поэтому имеет смысл выполнять операции именно в таком порядке. 92 + 5б + 1$

 = 4 х (3 х 3) + б + б + б + б + б + 1
  = 3 х 3 + 3 х 3 + 3 х 3 + 3 х 3 + б + б + б + б + б + 1
  = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + б + б + б + б + б + 1
 

Теперь у нас есть только одна операция, поэтому мы можем выполнять сложения в любом порядке, но вы можете видеть, что если мы вернемся к исходному выражению, то каждый раз, когда мы собираем слагаемые в умножение, мы получим один продукт, который нужно добавить к другому результату. Таким образом, мы в конечном итоге складываем продукты, то есть умножение должно предшествовать сложению. Возведение в степень объединяет множимые, готовые к умножению на другие члены, поэтому возведение в степень необходимо выполнить до умножения.

Если рассматривать только целые числа, деление можно рассматривать как просто повторяющееся вычитание, а вычитание — просто сложение отрицательных членов, следовательно, деление происходит на том же уровне, что и умножение, а вычитание — на том же уровне, что и сложение.

Круглые скобки дают нам способ переопределить существующий порядок, поэтому P должен стоять перед всем остальным, чтобы нам было легче решать текстовые задачи, такие как: «Сколько унций овощей в трех пакетах с овощами, каждый из которых содержит четыре унций моркови и шести унций гороха?» (Ответ: $3 \times (4 + 6)$ oz = 3 x 10 унций = 30 унций.) Без круглых скобок нам пришлось бы писать $3 \times 4 + 3 \times 6$, существенно расширяя скобки. Представьте, если бы скобки содержали какое-то гораздо более сложное выражение — нам пришлось бы писать его полностью несколько раз, если бы скобки были недоступны.

TL;DR: Для целых чисел возведение в степень представляет собой повторное умножение и собирает множимые, готовые для умножения или добавления к другим терминам, в то время как умножение представляет собой повторное сложение и собирает слагаемые для добавления к другим терминам. Следовательно, полезно возводить в степень перед умножением (и делением) и умножением перед сложением (и вычитанием). Круглые скобки позволяют изменить порядок.

---

u/DirichletIndicator выдвигает другую причину — многочлены. 92$ и 3 по х. Затем вы добавляете все вместе.

На самом деле это не более чем правило набора текста, например, «всегда ставить точку перед кавычками». В какой-то момент это был самый удобный способ делать что-то, но в какой-то момент он был формализован.

Расширение термина, умножение выражений с помощью Пошагового решения математических задач

Язык алгебры

Использование букв для представления чисел является фундаментальной алгебра.
В этой главе буквы будут обозначать числа арифметики. Когда вы станете знаком с символами и терминологией алгебры, операциями по арифметике номера будут пересмотрены.
 

НЕКОТОРЫЕ СИМВОЛЫ ДЛЯ ОПЕРАЦИЙ
 

ЗАДАЧИ

По завершении этого раздела вы должны уметь:
1. Определять символы операций арифметики.
2. Выполните эти операции над целыми числами, дробями и десятичными дробями.

Помните, что при сложении или вычитании дробей необходимо найти общий знаменатель.

При добавлении или вычитании десятичных знаков выравнивайте десятичные точки.

При умножении дробей умножьте числители, чтобы получить числитель произведения и умножить знаменатели, чтобы получить знаменатель произведения.

Символ + используется для обозначения суммы. a + b (читается как «a плюс b») используется для укажите сумму a и b.

 

Символ — используется для обозначения операции вычитания, a — b (читается как «a минус b») указывает на разницу чисел a и b.

Операцию умножения (произведение двух чисел) можно представить несколькими способами. Вам следует ознакомиться с каждым из них.
 

1. Символ X часто используется для обозначения умножения, a X b (читается как «a умноженное на b») представляет собой произведение двух чисел a и b.

Символ X обычно не используется с буквами в алгебре, потому что он может можно спутать с буквой X.

2. a * b (читается как «a умножить на b») также используется для представления произведения числа а и б.
Символ * обычно не используется с цифрами, потому что его можно спутать с десятичная точка.
 

3. Если две буквы или цифра и буква написаны вместе без знак операции, указано умножение.

 

Процесс написания двух букв или числа и буквы вместе без признак операции называется сопоставлением. Этот способ указания умножение нельзя использовать для двух чисел, так как 52 не означает «5 раз 2.»

4. Когда между двумя наборами скобок нет знака операции, указано умножение, (a)(6) означает «a, умноженное на b». Также буква или цифра предшествующая скобке без знака между ними указывает на умножение. а{б) означает «а умножить на 6», а 7(x) означает «7 умножить на х».

4.2 * 5.1 может привести к путанице при указании произведения 4.2 и 5.1.
Обратите внимание, что сумма или произведение двух чисел не изменится, если мы реверсируем порядке, в котором они написаны. Например,
3 + 5 = 8; также 5 + 3 = 8
4 * 6 = 24 и 6 * 4 = 24. Эта характеристика называется коммутативной свойство.
Справедливо ли это свойство для вычитания?
(рассмотрите 7-2 и 2-7.)

(4.2)(5.1) — гораздо лучший способ указать произведение этих двух чисел. чем способы, показанные ранее.
Напомним, что деление — это операция, обратная умножению. Следовательно,

 

Выполните следующие действия:

Является ли деление коммутативным?

Эту информацию будет полезно помнить при работе с задачами в следующий комплекс упражнений.
Не забывайте сокращать дроби.

Из этих нескольких методов обозначения продукта последние два являются наиболее обычно используется.
Частное двух чисел, a и b, можно записать двумя способами, и — оба указывают на то, что «число а делится на число б.»

Дробное представление деления чаще всего используется в алгебре.

Напомним из арифметики, что дробь, числитель которой больше знаменатель называется неправильной дробью .
Следовательно,

 

— неправильная дробь.
Напомним также, что неправильную дробь можно записать как смешанное число.

Точно так же смешанное число может быть записано как неправильная дробь.

Форма неправильной дроби обычно более удобна для работы. Если нужно выполнить деление или умножение, то получится неправильная дробь почти необходимость.

Некоторые проблемы могут касаться только одного операция, в то время как другим может потребоваться два или более.

Важно знать символы для различных операций. Это также Важно знать, какую операцию или ряд операций использовать при решении задачи. конкретный Мы сталкиваемся с этими проблемами каждый день.

Решение Операция сложения. Мы бы указали общую стоимость как
1,89 доллара + 0,65 доллара + 0,59 доллара.
Затем складываем, получаем
1,89$ + 0,65$ + 0,59$ = 3,13$.
 

Операция вычитания часто используется в задачах, связанных с выполнением изменение, балансировка чековых книжек и снижение цен. При подготовке к дальнейшей работе привыкайте использовать круглые скобки для обозначения умножение.

Решение Операцией в этом примере является вычитание. Нам нужно вычесть стоимость заказа от $5.00.
$5,00 — $3,13 = $1,87

Решение Это задача на умножение. Умножаем почасовую оплату на количество отработанных часов.
5 X 4,50$
0r 5(4,50$) = 22,50$
 

Решение Это задача на деление. Мы должны разделить стоимость лодки на число людей.
 

4 200 долл. США -5- 3 = 1 400 долл. США
 

Часто задачи включают более одной арифметической операции.
 

Мы могли бы также записать это как

 

Решение Эта задача включает в себя как умножение, так и вычитание. Мы первые нужно найти 20% от $529. Для этого умножаем 529 долларов на десятичный эквивалент 20%.
.20(529$) = 105.80$

Помните, что для замены процента на десятичную дробь переместите десятичную точку на два знака влево

Это размер скидки. Чтобы найти цену продажи, мы теперь должны вычесть 105,80 доллара из обычной цены.
529,00 долл. США — 105,80 долл. США = 423,20 долл. США

СИМВОЛЫ ГРУППИРОВАНИЯ
 

ЗАДАЧИ
По завершении этого раздела вы должны уметь:
1. Выполнять операции в правильном порядке, указанном символами группировки.
2. Выполнять операции в определенном порядке, когда символы группировки не используются.
 

Круглые скобки ( ), квадратные скобки [ ] и фигурные скобки j } используются для группировки символы в алгебре. Числовое выражение, заключенное в символ группировки, обрабатывается как если бы это было одно число.

Пример 1 12 — (3 + 4) означает, что сумма (3 + 4) вычитается из 12. 12 — (3 + 4) = 12 — 7 = 5. Обратите внимание, что без скобки, 12 — 3 + 4 = 13.

Пример 2 7(5 + x) указывает, что сумма (5 + x) умножается на 7.
Обычно сначала выполняются операции внутри символов группировки. Кронштейны а фигурные скобки можно использовать вместо скобок.
12 — [3 + 4] и 12 — {3 + 4} означают то же, что и 12 — (3 + 4).
В некоторых приложениях может потребоваться использование группирующих символов.
 

Пример 3 Баланс банковского счета составляет 567,19 долларов США. Чеки выписываются на 18,50, 24,95 и 129,40 долларов. Что нового баланс?

Скобки чаще всего используются, когда не используются другие символы группировки.
 

Решение Нам нужно сложить суммы трех чеков и вычесть сумму от первоначального баланса. Таким образом, мы пишем
567,19 долл. США — (18,50 долл. США + 24,95 долл. США + 129,40 долл. США) = 567,19 долл. США — 172,85 долл. США = 394,34 долл. США.

Первый шаг — упростить то, что находится внутри скобок.

Как упоминалось ранее, выражение может иметь другое значение, если скобки не используются. Мы видели, что
12 — (3 + 4) = 5,
 

, но было указано, что без скобок
12 — 3 + 4 = 13.
 

Это обусловлено следующим правилом: выражение без группирующих символов содержит только дополнения и вычитания, эти операции выполняются в порядке слева направо.

 

Если выражение содержит операции, отличные от простого сложения и вычитания, мы используем следующее правило:
 

Если в выражении не встречаются символы группировки, умножение и деление выполняются слева направо, а затем сложение и вычитание слева направо верно.
 

Обратите внимание, что при добавлении трех чисел порядок их добавления меняется. не влияет на сумму.
3 + (8 + 4) = 3 + 12 = 15 (3 + 8) + 4 = 11 + 4 = 15 Эта характеристика называется ассоциативным свойством. Является ли умножение ассоциативным?

Иногда в выражении требуется более одного набора символов группировки. Когда это происходит, мы используем скобки или фигурные скобки вместе со скобками для уточнение. Например, 5 + [7 — (2 + 1)] можно записать, используя только скобки, а 5+(7-(2+1)) не так ясно на первый взгляд. Поэтому, мы чередуем символы, чтобы избежать путаницы. Чтобы вычислить такое выражение, мы используйте следующее правило:

При упрощении выражения, содержащего символы группировки внутри группировки символы, сначала удалите самый внутренний набор символов.

При использовании этого правила не пытайтесь выполнять более одной операции за раз.

Пример 10 Чтобы вычислить 5 + [7 — (2 + 1)] мы упростить самый внутренний набор символов, а именно (2 + 1). Записав (2 + 1) как 3, мы теперь получите

Помните, что все разные символы используются для одной и той же цели — группировать числа.
Опять же, убедитесь, что вы выполняете только одну операцию за раз. Это очень важно в во избежание ошибок.
Обратите внимание, что мы начинаем с (5 — 2), так как это самый внутренний набор символов.

 

АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
 

Когда буквы используются для представления чисел, они называются буквенными числами. Если числовое выражение содержит одно или несколько буквенных чисел, оно называется буквальное выражение или алгебраическое выражение.
 

ЗАДАЧИ
По завершении этого раздела вы должны уметь:
1. Писать буквенные выражения, включающие арифметические операции.
2. Определите термины и факторы выражения.

Пример 1 x + 5 представляет «сумму x и 5.» a — b представляет собой «разность a и b». 4y представляет собой «произведение 4 и у. »
Когда мы говорим о разности двух чисел, второе число всегда вычитается из первого.
 

Пример 2 Напишите буквальное выражение для «сумма х и 5, деленная на 7».
Решение
(x + 5) представляет «сумму x и 5», поэтому мы имеем (x + 5) / 7. Обратите внимание, что круглые скобки необходимы, если мы запишем приведенное выше как (x + 5) / 7.
Обратите внимание, что запятая очень важна в примере 2. Без запятой утверждение будет читаться как «сумма х и 5, деленная на 7». Буквальный выражение будет

Пример 3 Напишите алгебраическое выражение для «разности a и b, умноженной на сумму a и b».
х + (5 -4 — 7) или .V + -y .
Решение. Разность a и b равна (o — b)\ сумма a и b равна (a + b), поэтому мы имеем (а — b) (а + b).

Еще раз обратите внимание на важность использования запятой в примере 3.

Пример 4 Выразите c — (a + b) словами.
Решение Поскольку (a + b) заключено в скобки, это «сумма a и b». Итак, мы запишите c — (a + b) как «разность c и суммы a и b»

Когда алгебраическое выражение состоит из частей, соединенных сложением или знаки вычитания, эти части называются членами выражения.
 

Пример 5 a + b имеет два члена.

В а + б термины а и б.

Пример 6 2x + 5y + 3 имеет три члена: 2x, 5y и 3.
 

Когда алгебраическое выражение состоит из частей, подлежащих умножению, эти части называются факторами выражения.

Пример 7 ab имеет два фактора, a и b.

Очень важно уметь различать термины и факторы. Правила , применимые к терминам, как правило, не применяются к факторы. При именовании терминов или факторов важно необходимо учитывать все выражение.

Отныне через всю алгебру ты будет использовать слова термин и фактор. Убедитесь, что вы понимаете определения.

Пример 8 Выражение 3x + 2y + 7 имеет три термина. Обратите внимание, что термин может содержать факторы (например, первый термин этого выражения, 3x, содержит два множителя), но все выражение состоит сроков.

Следует отметить, что в выражении более четырех множителей 5xyz. Очевидными факторами являются 5, x, y и z. Но 5x тоже фактор. Другой факторы 5xy, xy, 5yz, xz, 5z и так далее.

Показатель степени иногда называют степенью. Например, 5 ³ можно обозначить как «пять в третьей степени».
Если не используются круглые скобки, показатель степени влияет только на коэффициент напрямую. предшествующий ему.

Пример 9 5xyz — это один термин, состоящий из факторы.

Пример 10 3(a + b) — один член, имеющий два факторы. Заметим здесь, что множитель (a + b) состоит из двух членов, но весь выражение состоит из факторов.
Показатель степени — это число, используемое для указания того, сколько раз следует использовать коэффициент. в продукте.
Показатель степени обычно записывается как меньшая (по размеру) цифра чуть выше и справа от множителя, на который влияет показатель степени.

Здесь остановились

Обратите внимание на разницу между 2x ³ и (2x) ³ . От использования скобок в качестве группирующих символов мы видим, что
2x ³ означает 2(x)(x)(x), тогда как (2x) ³ означает (2x)(2x)(2x) или 8x ³ .
 

В таком выражении, как 5x ⁴

1. 5 , числовой коэффициент или коэффициент ,
2. х это база ,
3. 4 — это показатель степени .
    

Многие студенты совершают ошибку, умножая основание на показатель степени.
Например, они скажут
3 ⁴ = 12 вместо правильного ответа
3 ⁴ = (3)(3)(3)(3) = 81.

Обратите внимание, что показатель степени влияет только на основание.

Пример 13 В выражении ax ³
 

1. а — коэффициент,
2. х это база,
3. 3 — показатель степени.

ax ³ означает (a)(x)(x)(x).

Пример 14 (ax) ³
 

Решение 1 — коэффициент (понятно), ax — основание круглые скобки), 3 — показатель степени.
(ax) ³ означает (ax)(ax)(ax).

Когда мы пишем буквальное число, такое как x, будет понятно, что коэффициент равен единице, а показатель степени равен единице. Это может быть очень важно во многих операции.
 

x означает 1x ¹ .

Если в выражении есть символы группировки, операции в нем выполняются первый.

Коэффициент 1 понятен, и обычно мы не утруждаем себя его записью. выражение.
Напомнить порядок операций.
 

ОЦЕНКА ЛИТЕРАЛЬНЫХ ВЫРАЖЕНИЙ

ЦЕЛИ
По завершении этого раздела вы должны уметь:
1. Заменять буквы цифрами в буквенных выражениях.
2. Оцените выражение после внесения замен.
 

Принцип подстановки гласит, что любое количество может быть заменить его равным в любом процессе. Этот принцип широко используется в алгебры, и мы будем использовать его здесь для вычисления литеральных выражений. В этом процессе подставляем цифры вместо букв и находим числовое значение.

Пример 1 Оценить x + 3, если x = 5.
Подставим 5 вместо x в выражение, получив
5 + 3 = 8.
 

Пример 2 замените 3 на a в выражении, получив
4(3) -1 = 12-1
= 11.

Помните, что в буквальном выражении буквы просто занимают место для различные номера, которые могут быть присвоены им. По этой причине эти буквы иногда называемые заполнителями или переменными.
 

Чтобы найти периметр прямоугольника, нам нужно сложить все четыре стороны, но так как противоположные стороны равны, нам нужно только удвоить длину и удвоить ширину, а затем найти их сумму.
Высота треугольника называется высотой треугольника. Это перпендикулярное расстояние от основания до противоположного угла, которое называется вершина.

Одно из наиболее распространенных применений вычисления литеральных выражений — работа с формулы.

Пример 7 Периметр (расстояние вокруг) прямоугольник находится по формуле P = 2l + 2w, где l представляет собой длина, а w представляет ширину.
 

 

Если длина прямоугольника равна 10, а ширина равна 6, мы можем найти периметру, подставив 10 вместо l и 6 вместо w.
 

P = 2(10) + 2(6)
P = 2(10) + 2(6) = 20+12 = 32.
 

Пример 8 по формуле

 

, где b — основание треугольника, а h — высота.

Если мы хотим найти площадь треугольника, в котором основание равно 10, а высота равна 8, мы бы положили b = 10 и h = 8. Подставляя эти значения в формулу, мы получить

 

ОБЪЕДИНЕНИЕ ПОДОБНЫХ ТЕРМИНОВ
 

ЦЕЛИ
По завершении этого раздела вы должны уметь:
1. Идентифицировать похожие термины.
2. Соедините одинаковые термины.
 

В предыдущих разделах мы представили символы, используемые в алгебраических выражения. Теперь приступим к операциям сложения и вычитания на некоторые из этих выражений.

Подобные термины — это термины, которые имеют точно такие же буквальные факторы.

Пример 1 5x и 3x похожи, так как они имеют одинаковые буквальные множители (x — буквальный множитель в каждом термине).

Пример 2 5x и 3y не похожи на термины, поскольку буквальные коэффициенты не совпадают (x и y — буквальные коэффициенты). подобны терминам, поскольку они имеют одинаковые буквальные
множителей (x ² и y).

Пример 4 3x ² y ² и 2xy не похожи на термины. У них разные буквальные факторы. (Обратите внимание, что x ² и x не совпадают.)

Комбинировать можно только одинаковые термины. Когда два термина похожи на термины, объедините числовые коэффициенты для получения коэффициента подобных общих коэффициентов.

Пример 5 Если мы добавим одинаковые члены 5x + 3x, мы объединяем коэффициенты 5 и 3, получая
5x + 3x = (5 + 3)x = 8x.

 

Многие учащиеся делают ошибку, меняя строчные и заглавные буквы местами.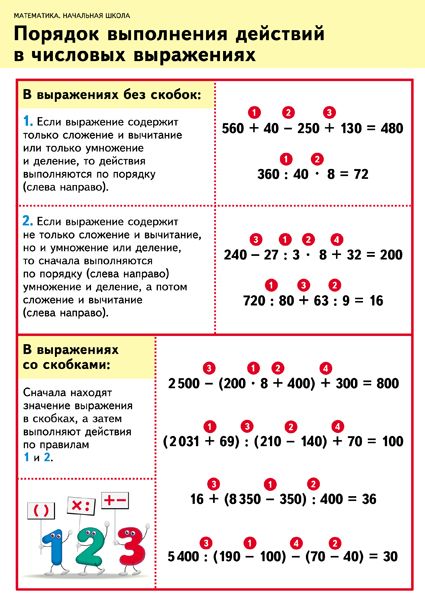 в выражении. В алгебре считается заглавная «А» и строчная «а». так же различны, как x и y. Следовательно, такие термины, как 5А и 3а, не будут считаются как термины. Будь осторожен. Будьте последовательны с буквами, которые вы используете.

Обратите внимание, что числовой коэффициент x равен 1 и в этом примере должен быть добавлено в 7 лк.
 

Пример 11 12 ab + 4 ba — 6 ab = 10 ab
По коммутативному закону умножения 4ba = 4ab.

Ключевые слова

• Скобки ( ), скобки [ ] и скобки { } все используются в качестве группирующих символов в алгебре.
• Буквенные числа — это буквы, используемые для представления чисел.
• Алгебраическое выражение или буквальное выражение является числом выражение, содержащее одно или несколько литеральных чисел.
• Термины — это те части алгебраического выражения, которые добавляются или вычитано.
  Коэффициенты — это те части алгебраического выражения, которые умноженный.