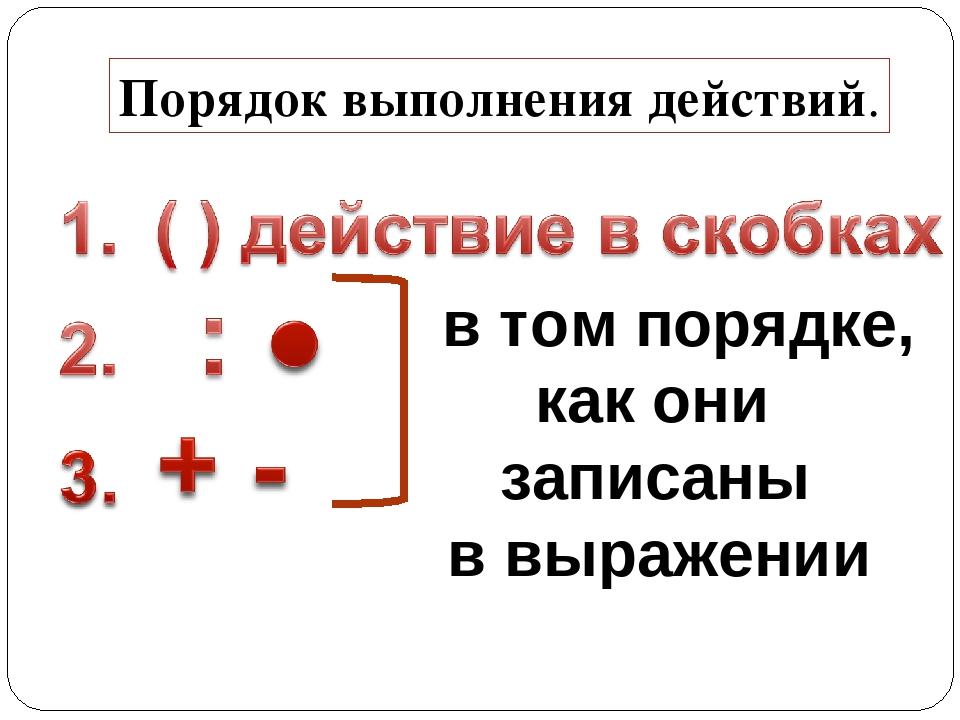
Порядок действий в примерах со скобками: попробуйте решить простой пример

Англоязычный Twitter облетела старая задачка по математике, которая разделила пользователей на несколько враждующих лагерей. Однако, ничего удивительного здесь нет, ведь правильное решение примеров по действиям со скобками всегда непросто отыскать, особенно если вы давно закончили школу. Хватит ли у вас смекалки и знаний базовой математики, чтобы пройти это испытание, посильное для младшеклассника, но непреодолимое для взрослого?

Юлиана Качанова Отвечаю за тесты

Twitter: 1RealMir

Решить пример со скобками по действиям пытались многие комментаторы твиттера, при этом используя самые разные, в том числе и несуществующие, математические приемы.

Известный новозеландский актёр Тайка Вайтити, знакомый отечественным кинозрителям по фильму «Реальные упыри», принял участие в данном интернет-споре, но к сожалению, не стал «отличником», решившим задачу правильно. Его, как и большинство других участников, подвело знание порядка действий сложных примеров со скобками.

Если вы считаете что хорошо помните последовательность действий в примерах со скобками, то попробуйте дать правильный ответ:

Не торопитесь давать ответ: правила хотя бы вспомните!

ВОПРОС 1 ИЗ 1

3

17

21

Главное – не торопитесь! В математике порядок действий примеров со скобками имеет огромное значение. «Дорожная карта» для того, чтобы правильно решить тот, или иной пример выглядит следующим образом:

• Внимательно посмотрите на пример и сначала произведите действие, которое указано в скобках.
• Запомните: порядок выполнения действий в примерах со скобками отдаёт предпочтение умножению и делению. Их называют действиями первой ступени.
• Последними выполняются сложение и вычитание. Это действия второй ступени.

Такая последовательность действий в примере со скобками выбрана не случайно и позволяет без особых затруднений получить правильный ответ.

Для закрепления рассмотрим следующий пример действия со скобками:

5+(7−2⋅3)⋅(6−4):2

В этом сложном примере со скобками порядок действий будет точно таким же.

Сначала мы вычислим значение первой скобки. Для этого сначала нужно выполнить умножение 2 на 3, как действие первой ступени, а затем вычесть из 7 полученное произведение. Получится 7-6=1
После этого мы переходим ко второй скобке. Если в первой скобке у нас был пример с умножением и вычитанием в ней, то здесь у нас только вычитание: 6-4=2

Давайте подставим решение примеров в скобках в первоначальное выражение:

5+(1)⋅(2):2 . 

Здесь уже сложных примеров со скобками нет, мы оставили их просто для визуального понимания, какое число по итогам наших манипуляций получилось.

Порядок действий в примерах со скобками (как впрочем и без них) требует от нас сначала выполнения умножения и деления, а затем сложения и вычитания. Продолжаем соблюдать его и получаем что сначала мы должны умножить 1 на 2, а затем поделив её на 2 прибавить разность к 5:

5+1⋅2:2=6

Таким образом первоначальный пример со скобками также будет равняться 6

5+(7−2⋅3)⋅(6−4):2=6.

Большая энциклопедия школьника

Большая энциклопедия школьникауникальное издание, содержащее весь свод знаний, необходимый ученикам младших классов. Для детей, собирающихся в 1-й класс, она послужит незаменимым помощником для подготовки к школе. В этой энциклопедии ребенок сможет найти любую интересующую его информацию, в понятном и простом для него изложении. Вы подбираете слова и определения для простых вещей, которые надо объяснить ребенку? Сомневаетесь в формулировках? Просто возьмите

«Большую энциклопедию школьника» и найдите нужный ответ вместе с малышом!

Математика в стихах
Развитие речи
Азбука в картинках
Игры на развитие внимания
Как правильно выбрать школу
Ваш ребенок левша
Как готовить домашнее задание
Контрольные и экзамены

Большая энциклопедия школьника — это твой надёжный путеводитель в мире знаний. Она проведёт сквозь извилистые лабиринты наук и раскроет завесу великих тайн Вселенной. С ней ты поднимешься высоко к звёздам и опустишься на дно самых глубоких морей, ты научишься видеть мельчайшие организмы и осязать огромные пространства Земли. Отправившись в это увлекательное путешествие, ты значительно расширишь свой кругозор и поднимешься на новую ступень развития. Отныне никакие вопросы учителей не смогут поставить тебя в тупик, ты сможешь найти выход из любой ситуации. Мир знаний зовёт тебя. В добрый путь!

Ребенок не хочет учить буквы Ребенок не хочет учить буквы — Понимаете, ведь надо что-то делать! — с тревогой говорила мне полная, хорошо одетая дама, едва умещающаяся на стуле. Ее ноги в аккуратных лодочках были плотно сжаты (юбка до середины колена казалась слегка коротковатой для такой монументальной фигуры), руки сложены на коленях. — Ей же на тот год в школу, все ее сверстники уже читают, а она даже буквы …

Past continuous passive Страдательный залог образуется с помощью вспомогательного глагола ‘to be’. Страдательный залог глагола ‘to repair’ в группе ‘continuous’ : To be repaired = Быть исправленным. The road is being repaired = Дорогу чинят. The road is not being repaired = Дорогу не чинят. Is the road being repaired? = Чинят ли дорогу? The road was being repaired = Дорогу чинили. The road was not being repaired = Дорогу не чинили. Was the road being repaired? = Чинили ли дорогу? Страдательный …

Определение формулы органического вещества по его молярной массе Задание: Определить формулу углеводорода, если его молярная масса равна 78 г. № п/п Последовательность действий Выполнение действий 1. Записать общую формулу углеводорода. Общая формула углеводорода СхНу 2. Найти молярную массу углеводорода в общем виде. М(СхНу)=12х +у 3. Приравнять найденное в общем виде значение молярной массы к данному в …

У У ЗВУК (У). 1) Удобная буква! Удобно в ней то, Что можно на букву Повесить пальто. У – сучок, В любом лесу Ты увидишь букву У. 2) ФОНЕТИЧЕСКАЯ ЗАРЯДКА. — Как воет волк! ( у – у – у ) 3) ЗАДАНИЯ. а) Подними руку, если услышишь звук (у): паук, цветок, лужа, диван, стол, стул, голуби, курица. б) Где стоит (у)? Зубы, утка, наука, кенгуру …

Эффективное преподавание математики. Практика 1: постановка целей по математике, чтобы сфокусировать обучение

Перейти к основному содержанию

You are here

Home

Меню поддержки обучения

• Лучшая первая инструкция по математике
• Эффективная практика преподавания математики NCTM
• Практика преподавания математики на основе долевого участия
• Планирование урока для обучения и размышлений
• Научно-практические руководства для преподавания математики
• Поддержка учащихся, испытывающих затруднения в изучении математики
• Подготовка к математике на 2020-2021 год

---

Постановка целей по математике для фокусировки обучения

Первая эффективная практика преподавания NCTM — постановка целей для фокусировки обучения

. Самый острый аспект этой педагогической практики заключается в том, что учителя математики должны быть более сосредоточены на значимых изменениях в понимании учениками, а не только на том, что ученики должны делать. В этом разница между целью обучения и целью производительности. Сравните следующие формулировки цели:

Цель A: Учащиеся узнают, что площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах, и предположат, что c ² =а ² +б ² .
Цель B: Учащиеся смогут (SWBAT) использовать теорему Пифагора (c ² =a ² +b ² ) для решения ряда задач с пропущенными значениями.

Цель A является целью обучения, поскольку она описывает рассуждения и понимание, которые мы хотим, чтобы учащиеся усвоили в результате обучения. Цель B — это цель производительности, поскольку она не описывает, что именно изучается, а вместо этого, по сути, говорит: «Студенты будут решать задачи, используя теорему».

Хотя часть занятий на уроке может включать решение ряда задач, наши цели должны быть сосредоточены на развитии обучения, а не на задачах, которые необходимо выполнить. Это задает все для остальной части урока: выбранные задачи, представления, которые используют учащиеся, вопросы, которые необходимо задать, фокус обсуждения в классе и стратегии оценивания.

• Посмотреть все 8 эффективных методик преподавания математики

---

Практика в действии

Одним из способов, которым NCTM (2014, стр. 16) обобщает практику установления математических целей для фокусировки обучения , является описание набора действий, ожидаемых от учителей и учащихся, которые указывают на участие в этом преподавательская практика.

Внимание! Не переоценивайте собственное понимание, основанное на этих кратких описаниях педагогической практики. Профессиональные преподаватели должны более глубоко изучить ресурсы NCTM, присоединиться к исследовательским группам и профессиональным сетям, а также стремиться к профессиональному развитию и обучению, чтобы обеспечить качественное участие в практике.

Чем занимаются учителя?

• Постановка четких целей, которые формулируют математику, которую учащиеся изучают в результате обучения на уроке, в течение серии уроков или в течение всего раздела.
• Определение того, как цели вписываются в процесс обучения математике.
• Обсуждение и ссылка на математическую цель и цель урока во время обучения, чтобы убедиться, что учащиеся понимают, как текущая работа способствует их обучению.
• Использование целей по математике для планирования урока и размышлений, а также для принятия сиюминутных решений во время обучения.

Чем занимаются студенты?

• Участие в обсуждении математической цели и задач, связанных с их текущей работой в классе математики (например, Что мы изучаем? Почему мы это изучаем?)
• Использование целей обучения, чтобы сосредоточиться на своем прогрессе в улучшении понимания содержания математики и навыков использования математических методов.
• Связать свою текущую работу с математикой, которую они изучали ранее, и увидеть, куда движется математика.
• Оценка и мониторинг собственного понимания и прогресса в достижении целей обучения математике.

---

Ресурсы

• Принципы действий: обеспечение математического успеха для всех (NCTM, 2014, стр. 12-16)
• Принятие мер: внедрение эффективных методов преподавания математики в K-классе 5 (NCTM, 2017, стр. 17–35)
• Принятие мер: внедрение эффективных методов преподавания математики в 6–8 классах (NCTM, 2017, стр. 15–27)
• Принятие мер: внедрение эффективных методов преподавания математики в 9–12 классах (NCTM, 2017, стр. 15–27)
• Улучшение практики в классе с помощью исследований, лежащих в основе принципов действий (NCTM, 2017, стр. 1–11)
• Катализация изменений в математике средней школы (NCTM, 2020, стр. 59)

Первая математическая онлайн-практика 9 по математике0001

С момента закрытия школ учащиеся решили 2 877 196 805 задач.

Решено 28 042 466 934 математических задач — и их число продолжает расти!

«Я был по-настоящему поражен интересом и решимостью, проявленными в моих учениках First in Math, с мотивацией не было проблем! Они не только изучили математику и улучшили свою способность концентрироваться, они также узнали о важности постановки и достижения ежедневных целей. долгосрочные цели, чтобы в конечном итоге достичь того, что вначале было только мечтами».

Джоэл Стоктон — учитель 5-го класса начальной школы Кавасос, La Joya ISD, TX    УЗНАТЬ БОЛЬШЕ

First In Math охватывает всех учащихся K-8, от интерактивных до одаренных, а также всех демографических групп, что делает его бесценным дополнение к любой учебной программе.
УЗНАТЬ БОЛЬШЕ >>

Более 200 заданий для самостоятельного обучения предлагают немедленную обратную связь, чтобы помочь учащимся овладеть процедурными навыками и помочь педагоги оценивают, где необходимо вмешательство.
УЗНАТЬ БОЛЬШЕ >>

«У программы «Первые в математике» есть такая ценность. Она дает детям, которым нужна небольшая дополнительная помощь, возможность поработать над своими навыками, а также позволяет детям, которые преуспевают, выйти за рамки того, чему учат в классе. »

Доктор Франк Фишель — Директор начальной школы Маунтин-Вью, Фландрия, Нью-Джерси

Постановка и достижение целей, а также постоянные возможности для признания дают учащимся энергию для поддержания ускоренных усилий с течением времени.
УЗНАТЬ БОЛЬШЕ >>

Первая демонстрация математики

Учителя, запишитесь на один класс бесплатно! Если вам нравится программа First In Math и вы решите ее купить, ваши ученики смогут продолжить, не упустив ни одной детали.

Истории успеха в математике

Прочтите информативные статьи из нашей библиотеки, в том числе образовательные теории о том, почему First In Math работает, тематические исследования, Истории успеха, свидетельства, и полученные результаты.