детская математика: сложение и вычитание дробей

Поначалу сложение и вычитание дробей может показаться сложным, но если вы выполните несколько простых шагов и решите множество практических задач, вы быстро научитесь этому.

Вот несколько шагов, которые нужно выполнить:

• Убедитесь, что у дробей одинаковый знаменатель.
• Если у них разный знаменатель, преобразуйте их в эквивалентные дроби с тем же знаменателем.
• Как только у них будет одинаковый знаменатель, сложите или вычтите числа в числителе.
• Запишите свой ответ, поставив новый числитель над знаменателем.

Примечание: знаменатель мог измениться, когда вы преобразовали дроби к одному и тому же общему знаменателю.

Простой пример

Простой пример — знаменатели уже совпадают:

Поскольку знаменатели в каждом вопросе одинаковы, вы просто складываете или вычитаете числители, чтобы получить ответы.

Более сложный пример

Здесь мы попробуем решить задачу, в которой знаменатели не совпадают.

Как видите, у этих дробей разные знаменатели. Прежде чем мы сможем сложить дроби, мы должны сначала создать эквивалентные дроби с общими знаменателями.

Найдите общий знаменатель

Чтобы найти общий знаменатель, мы должны умножить каждую дробь на знаменатель другой дроби (тот, что внизу). Если мы умножим верхнюю и нижнюю части дроби на одно и то же число, это будет похоже на умножение на 1, поэтому значение дроби останется прежним. См. Пример ниже:

Добавьте нумераторы

Теперь, когда знаменатели совпадают, вы можете сложить числители и поставить ответ над тем же знаменателем.

Пример вычитания дробей

Вот пример вычитания дробей, когда нужно изменить только один знаменатель:

Уменьшите окончательный ответ

Иногда ответ нужно будет сократить. Вот пример:

Первоначальный ответ после сложения числителей был 10/15, однако эту дробь можно дополнительно уменьшить до 2/3, как показано на последнем шаге.

Советы по сложению и вычитанию дробей

• Всегда проверяйте, чтобы знаменатели были одинаковыми, прежде чем прибавлять или вычитать.
• Если вы умножите верхнюю и нижнюю часть дроби на одно и то же число, значение останется прежним.
• Обязательно потренируйтесь переводить дроби в общий знаменатель. Это самая сложная часть сложения и вычитания дробей.
• Возможно, вам придется упростить ответ после того, как вы закончите складывать и вычитать. Иногда ответ может быть сокращен, даже если исходные дроби не могут быть уменьшены.
• Тот же процесс используется и для сложения, и для вычитания: если вы можете складывать дроби, вы можете их вычитать.
• Если вы добавляете или вычитаете смешанные числа, не забудьте преобразовать их в неправильные дроби, прежде чем начинать процесс.

Вычитание алгебраических дробей | Алгебра

Рассмотрим вычитание алгебраических (рациональных) дробей в теории и на практике.

Чтобы вычесть алгебраические дроби, нужно:

1) Найти наименьший общий знаменатель этих дробей.

2) Найти дополнительный множитель к каждой дроби.

3) Дополнительный множитель  умножить на числитель и знаменатель.

4) Выполнить вычитание дробей с одинаковыми знаменателями (при вычитании дробей с одинаковыми знаменателями числители вычитают, а знаменатель оставляют тем же).

Примеры вычитания алгебраических дробей.

   

Наименьший общий знаменатель для чисел равен 18. Из степеней в общий знаменатель включаем каждый множитель, взяв его с наибольшим показателем. Таким образом, наименьший общий знаменатель данных дробей равен 18m²n².

Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый.

18m²n²:( 9mn²)=2m, 18m²n²:( 6mn²)=3m.

   

   

   

   

   

В знаменателях дробей стоят многочлены. Раскладываем их на множители. Для этого выносим за скобки общий множитель: в первом знаменателе — y, во втором — 5:

   

Наименьший общий знаменатель состоит из всех множителей и равен 5y(5x-y). Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый:

5y(5x-y):(y(5x-y))=5, 5y(5x-y):(5(5x-y))=y,

то есть, дополнительный множитель к первой дроби равен 5, ко второй — y. Затем умножаем числитель и знаменатель каждой дроби на дополнительный множитель.

Числитель раскладываем по формуле разности квадратов, после чего сокращаем дробь на (5x-y):

   

   

Многочлены, стоящие в знаменателях, раскладываем на множители по формулам сокращенного умножения. В знаменателе первой дроби — квадрат разности, в знаменателе второй дроби — разность квадратов:

   

Выражения (x-2) и (2-x), стоящие в знаменателях, отличаются только знаками. Изменим знаменатель второй дроби.

(2-x)= -(x-2). «Минус» вынесем перед дробью, соответственно, знак изменится на «+»:

   

Наименьший общий знаменатель состоит из всех входящих в знаменатели множителей, взятых в наибольшей степени. Он равен (x-2)²(2+x).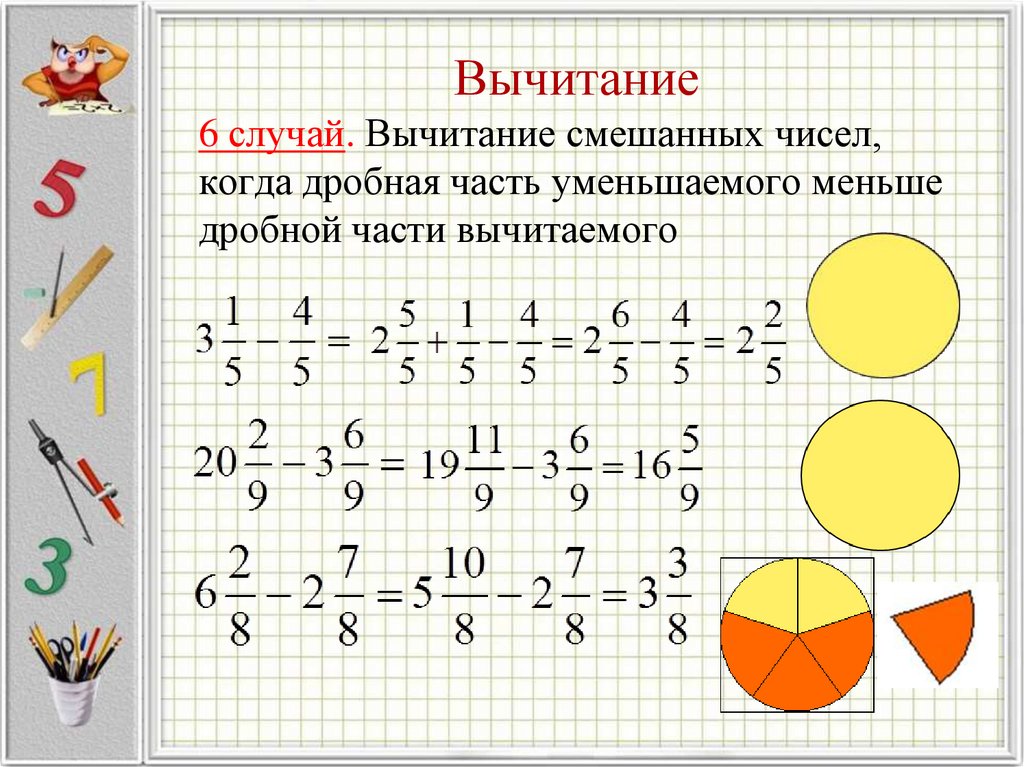 Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем дроби с одинаковыми знаменателями.

   

   

В знаменателе второй дроби — формула разности кубов:

   

Приводим дроби к общему знаменателю и упрощаем:

   

   

Выносим из знаменателя «минус» и сокращаем дробь на (1+x+x):

   

В алгебре складывать и вычитать дроби с разными знаменателями сложнее, чем их умножать и делить (при умножении и делении дроби не нужно приводить к общему знаменателю).

Умножение и деление алгебраических (рациональных) дробей — следующие темы для изучения.

Рубрика: Алгебраические дроби | Комментарии

Быстрые и простые пошаговые примеры

Вычитание дробей проще, чем вы думаете, так как это очень похоже на сложение дробей. Как и при сложении дробей, вам необходимо помнить о следующих четырех важных правилах.

• Вы не можете вычитать знаменатели, также называемые нижними числами!
• Вы можете вычитать только числители, также называемые старшими числами!
• Вычитать числители можно только тогда, когда знаменатели совпадают!
• Если знаменатели не совпадают, найдите общий знаменатель перед вычитанием числителей.

Как вычитать дроби с одинаковыми знаменателями

Как показано на рисунке выше, вычитание 2/8 из 5/8 выполняется просто. Поскольку знаменатель тот же, просто вычтите числители.

5/8 — 2/8 = (5 — 2)/8 = 3/8

Еще пара примеров, показывающих, как вычитать дроби с одинаковым знаменателем

−

1 / 2

«=»

Нет необходимости искать общий знаменатель, потому что они и так одинаковы.

Так, 5 / 2

− 1 / 2

«=» 5 − 1 / 2

«=» 4 / 2 = 2

− 1 / 2 «=»

Нет необходимости искать общий знаменатель, потому что они и так одинаковы.

Так, 5 / 2

− 1 / 2

«=» 5 − 1 / 2

«=» 4 / 2 = 2

Пример #2:

9/4 — 3/4 = (9 — 3)/4 = 6/4

Как вычитать дроби с разными знаменателями

Как и при сложении дробей, если знаменатели разные, вы сначала найдете эквивалентные дроби, которые дают общий знаменатель для обеих дробей.

Пример №3:

− 3 / 6 «=»

Здесь знаменатели не совпадают, поэтому умножьте 3 на 2, чтобы получить тот же знаменатель.

Помните, что мы должны умножить 7 на 2, чтобы не изменить задачу.

Так, 7 / 3

− 3 / 6

«=» 7 × 2 / 3 × 2

− 3 / 6

«=» 14 / 6

− 3 / 6

«=» 11 / 6

Пример №4:

− 2 / 4 «=»

Так, 3 / 5

− 2 / 4

«=» 3 × 4 / 5 × 4

− 2 × 5 / 4 × 5

«=» 12 / 20

− 10 / 20

«=» 2 / 20

Пример №3:

− 3 / 6 «=»

Здесь знаменатели не совпадают, поэтому умножьте 3 на 2, чтобы получить тот же знаменатель.

Помните, что мы должны умножить 7 на 2, чтобы не изменить задачу.

Так, 7 / 3

− 3 / 6

«=» 7 × 2 / 3 × 2

− 3 / 6

− 3 / 6

«=» 14 / 6

− 3 / 6

«=» 11 / 6

Пример №4:

− 2 / 4 «=»

Так, 3 / 5

− 2 / 4

«=» 3 × 4 / 5 × 4

− 2 × 5 / 4 × 5

− 2 / 4

«=» 12 / 20

− 10 / 20

«=» 2 / 20

Как вычитать дроби с целыми числами

Вот три простых шага, которые необходимо выполнить при вычитании дробей с целыми числами.

Шаг 1

Преобразуйте целое число в дробь. Вы делаете это, используя 1 в качестве знаменателя для целого числа.

Шаг 2

Найдите наименьший общий знаменатель. Вам просто нужно умножить 1 и другой знаменатель, чтобы получить наименьший общий знаменатель.

Шаг 3

Умножьте числитель и знаменатель дроби на шаге 1 на наименьший общий знаменатель.

Шаг 4

Вычтите дроби.

Пример #5:

Вычесть: 5 — 1/3

5 — 1/3 = 5/1 — 1/3 = 15/3 — 1/3 = (15 — 1)/3 = 14 /3

Вычитание дробей и смешанных чисел

При вычитании дробей со смешанными числами просто преобразуйте смешанное число в неправильную дробь перед вычитанием.

Пример #6:

7/3 — 1 2/3 = 7/3 — [(3 × 1 + 2) / 3]

7/3 — 1 2/3 = 7/3 — (5/3)

7/3 — 1 2/3 = (7 — 5)/3

7/3 — 1 2/3 = 2/3

Тест на вычитание дробей. Посмотрите, как хорошо вы можете вычитать дроби.

Все еще боретесь с дробями? Избавьтесь от страхов и разочарований раз и навсегда!

Если вы не очень хорошо знаете дроби, вам, вероятно, будет трудно хорошо сдать большинство математических тестов. Создайте прочную основу в математике сегодня, пока не стало слишком поздно!

Купите электронную книгу «Мои дроби». Он предлагает полное покрытие фракций!

1. Квадратичная формула: простые шаги

   26, 23 января 11:44

   Узнайте о квадратной формуле, дискриминанте, важных определениях, связанных с формулой, и приложениях.

   Подробнее

2. Формула площади — список важных формул

   25, 23 января 05:54

   Что такое формула площади для двумерной фигуры? Вот список тех, которые вы должны знать!

   Подробнее

Вычитание дробей с разными знаменателями

Мы можем использовать один из следующих методов для вычитания двух дробей с разными знаменателями.

1. Метод перекрестного умножения

2. Метод НОК.

Метод перекрестного умножения

Если знаменатели дробей взаимно просты или взаимно просты, мы должны применить этот метод.

Для примера рассмотрим вычитание двух дробей, приведенное ниже.

1/3 — 1/8

В этих двух дробях знаменатели равны 3 и 8.

Для 3 и 8 нет общего делителя, кроме 1.

Таким образом, числа 3 и 8 взаимно просты.

Здесь мы должны применить метод перекрестного умножения, чтобы найти вычитание двух дробей 1/3 и 1/8, как показано ниже.

Метод НОК (метод наименьшего общего кратного)

Если знаменатели дробей не взаимно просты (есть общий делитель, отличный от 1), мы должны применить этот метод.

Для примера рассмотрим вычитание двух дробей, приведенное ниже.

5/12 — 1/20

В этих двух дробях знаменатели равны 12 и 20. -основной.

Для 12 и 20 у нас есть следующие общие делители, отличные от 1.

2 и 4

Итак, 12 и 20 не взаимно просты.

На следующем шаге мы должны найти НОК (наименьшее общее кратное) чисел 12 и 20.

12 = 2 ²  x 3

20 = 2 ²  x 5

Когда мы разложим 12 и 20 на простые числа, мы найдем 2, 0 3 и 5 как простые множители 20,12.

Чтобы получить L.C.M 12 и 20, мы должны взять 2, 3 и 5 с максимальными степенями, указанными выше.

Таким образом, НОК чисел 12 и 20 равен

= 2 ² х 3 х 5

= 4 х 3 х 5

= 60

Теперь умножьте 60, используя знаменатель каждой дроби. вычтите их, как показано ниже.

Практические задачи

Проблема 1:

Найдите значение:

3/5 — 2/3

Решение:

В вышеупомянутых двое деноминаторы — 5 и 3.

2

. Для чисел 5 и 3 нет других общих делителей, кроме 1.

Таким образом, числа 5 и 3 взаимно просты.

Здесь мы должны применить метод перекрестного умножения, чтобы найти вычитание двух дробей 1/8 и 1/3, как показано ниже.

3/5 — 2/3 = (9- 10)/15

3/5 — 2/3 = — 1/15

Задача 2:

Найдите значение:

7/12 — 5/18

Решение:

В приведенных выше двух дробях знаменателями являются 12 и 18.

Для 12 и 18, если есть хотя бы один общий делитель, отличный от 1, то 12 и 18 не взаимно просты.

Для 12 и 18 у нас есть следующие общие делители, кроме 1.

2, 3 и 6

Итак, числа 12 и 20 не взаимно просты.

Здесь мы должны применить метод НОК, чтобы найти вычитание двух дробей.

Найдите НОК числа 12 и 18.

НОК числа (12, 18)  =  36

Теперь умножьте знаменатель каждой дроби на 36 и вычтите дроби с одинаковыми знаменателями.

Тогда имеем

12/07 — 18/5  = 36/21 — 36 10

12/7 — 18/5  = (21 — 10) / 36

12/07 18  =  11/36

Помимо материала, указанного выше, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь.