Сложение и вычитание смешанных чисел (Вольфсон Г.И.). Вычитание смешанных дробей

Решение сложных примеров правильно – непосильная задача для тех, кто не понимает в математике элементарных правил и законов. Сложение и вычитание смешанных чисел по праву можно отнести к сложным примерам. Однако, при правильном разборе самих чисел можно легко проводить любые действия.

Что это такое?

Смешанное число – это комбинация целой части и дробной. К примеру, имеется 2 и 3, из них 2 – это простое число, а вот 3 – это уже смешанное, где 3 – целая часть, а – дробная. Представленные разновидности складываются и вычитаются по-разному, но не влекут сложностей в самостоятельном решении примеров.

Полноценный разбор примера

Для полноценного представления сущности смешанного значения следует привести в пример задачу, которая поможет отобразить смысл повествования задуманного. Итак, Вася проехал круг вокруг школы на велосипеде за 1 минуту и 30 секунд, а потом еще круг прошел пешком за 3 минуты и 30 секунд. Сколько времени затратил Вася на всю прогулку вокруг школы?

Этот пример направлен на сложение смешанных чисел, которые предварительно в данном случае даже не придется переводить в секунды. Получается, что сложение осуществляется путем отдельного прибавления минут и секунд. В результате получим следующий результат:

1. Сложение минут – 1+3=4.
2. Сложение секунд = 30+30=60 секунд = 1 минута.
3. Общее значение 4 минуты+1 минута = 5 минут.

Если исходить из математического отображения, то представленные действия можно выделить в одном выражении:

Из представленного выше становится понятным, что складывать смешанные числа следует в отдельности по частям – сначала целые части, а затем дробные. Если дробное число дает еще целое значение, его также складывают с целым полученным ранее значением. К полученному целому значению прибавляют дробную часть – получается смешанное число.

Правила сложения

Для закрепления изученного следует привести правило сложения смешанных чисел. Здесь следует воспользоваться следующей последовательностью:

1. Для начала отделить от значения части – на целую и дробную.
2. Теперь сложить целые части.
3. Далее сложить дробные.
4. Если из дробного числа можно извлечь еще целую часть – перевести в смешанное значение – значит, проводят подобную разбивку.
5. Полученную целую часть из дробного значения складывают с целым ранее полученным значением.
6. К целой части прибавляют дробную.

Для пояснения следует привести несколько примеров:

Сложение смешанных чисел происходит по тому же алгоритму, что и вычитание, поэтому далее будет подробно рассмотрено следующее действие.

Правила вычитания

Как и в первом случае, для вычитания смешанных значений существует правило, но оно в корне отличается от предыдущей последовательности. Итак, здесь следует придерживаться последовательности:

1. Пример на вычитание представляется в виде: уменьшаемое – вычитаемое = разность.
2. В связи с приведенным уравнением следует предварительно сравнить дробные части представленных чисел.
3. Если у уменьшаемого дробная часть больше, значит, вычитание проводится по тому же признаку, что и при сложении – сначала вычитаются целые, а затем дробные значения. Оба результата складывают.
4. Если у уменьшаемого дробное значение меньше, значит, их предварительно переводят в неправильную дробь и осуществляют стандартное вычитание.
5. Из полученной разницы определяют целую часть и дробную.

Для пояснения следует привести следующие примеры:

Из представленной статьи стало понятным, как проводить сложение и вычитание смешанных чисел. В описанном выше примере видно, что не всегда приходится видоизменять числа – переводить их из простых дробей в сложные. Зачастую достаточно просто сложить или вычесть целые и дробные значения по отдельности, что для человека с большим опытом можно легко провести в уме.

В статье подробно рассмотрены примеры, решение которых представлено в полном соответствии с математическими правилами и основами. Разобраны отдельные ситуации, для каждого приведен пример видоизменений, с которыми можно столкнуться в решении задач и сложных примеров.

Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Подписи к слайдам:

Учитель математики Кузнецова Марина Николаевна Сложение и вычитание смешанных чисел

Домашнее задание

Астрид Линдгрен

Устный счет 1 0

На какие группы мы можем разделить данные дроби?

На какие группы мы можем разделить данные дроби? Правильные дроби Неправильные дроби

Найдите лишний пример:

Сложение и вычитание смешанных чисел. Цель урока: Научится выполнять сложение и вычитание смешанных чисел.

Справка 1. К целой части прибавить целую часть. К полученной целой части прибавить дробную часть. Сформулировать правило сложения смешанного числа с натуральным. 2. К целой части прибавить целую часть. К дробной части прибавить дробную часть К полученной целой части прибавить полученную дробную часть. Сформулировать правило сложения смешанных чисел. 3. Из целой части вычесть целую часть. Из дробной части вычесть дробную часть К оставшейся целой части прибавить оставшуюся дробную часть. Сформулировать правило вычитания смешанных чисел. 4. Если дробная часть уменьшаемого меньше дробной части вычитаемого. Занимаем у целой части уменьшаемого единицу и представляем ее в виде неправильной дроби. Полученную дробь складываем с дробной частью уменьшаемого. Вычитаем отдельно целые части и дробные части. К оставшейся целой части прибавляем оставшуюся дробную часть. Сформулировать правило вычитания из смешанного числа дроби, причем дробь уменьшаемого больше дроби вычитаемого.

Чтобы сложить два смешанных числа, нужно сложить отдельно их целые и дробные части, сложить полученные результаты. Чтобы вычесть из смешанного числа смешанное число, нужно отдельно вычесть их целые и дробные части, сложить полученные результаты.

= (3 + 2) + () = 5 + = 5 – = (5 – 3) + ()= 2 + = 2

Физкультминутка Потрудились — отдохнём, Встанем, глубоко вздохнём. Руки в стороны, вперёд, Влево, вправо поворот. Три наклона, прямо встать. Руки вниз и вверх поднять. Руки плавно опустили, Всем улыбки подарили.

4 – В 7 – О 3 – У 4 – Е 5 – Х 4 – П 5 – С У С П Е В Х О

Решение задач Стр. 175, № 1115 Стр. 175, № 1116

Что такое смешанное число? Чему вы сегодня научились? Как сложить смешанные числа? Как вычесть смешанные числа?

Домашнее задание: П. 29 (учить правила) Стр. 178, № 1136, 1137

Спасибо за урок!

Предварительный просмотр:

Учитель математики Кузнецова М.Н.

Урок в 5 классе по теме:

Сложение и вычитание смешанных чисел.

Цели:

Учебные:

1. Познакомить учащихся с алгоритмами сложения и вычитания смешанных чисел путем включения учащихся в практическую деятельность.
2. Продолжить работу по развитию вычислительных навыков.

Развивающие:

1. Развитие умения решать задачи изученных видов.
2. Создание условий для формирования мыслительных операций.

Воспитательная:

1. Воспитывать чувство товарищества и взаимовыручки.

Ход урока

I. Организационный момент.

Посмотрите, все ль в порядке:

Книжка, ручки и тетрадки.

Прозвенел сейчас звонок.

Начинается урок.

II. Проверка домашнего задания.

Дата, классная работа.

Дома вы выполнили задание. Вы разгадали ребус. (Слайд 1)И какой же ответ? (Астрид Линдгрен) (Слайд 2)

Д/з. 1. Выделить целую часть и расположить в порядке возрастания. 18 -И 7 -А 14 -Р 11 -Т 9 -С 21 -Д 5 5 5 5 5 5 1 2/5 1 4/5 2 1/5 2 4/5 3 3/5 4 1/5 А С Т Р И Д 2. Запиши в виде неправильной дроби и расшифруй. 41/2-Д 2 3/7-Н 4 9/10-Р 32/5-И 14/6-Г 2 2/8-Е 3 ¾ -Л 5 1/6-Н 15 4 17 5 17 7 9 2 10 6 49 10 20 8 31 6 Л И Н Д Г Р Е Н

А кто такая Астрид Линдгрен? Какую сказку написала эта шведская писательница? («Малыш и Карлсон») (Слайд 3)

Но к сожалению Карлсон улетел, но оставил письмо.

Письмо: Ребята, я полетел искать старательных, внимательных, трудолюбивых, дружных, умеющих придти на помощь ребят. Найду – вернусь.)

Ребята, давайте быстрее встретимся с другом, для этого выполним математические задания. Если мы их выполним правильно, то у нас к возвращению Карлсона — сладкоежки получится большой общий торт. И у каждого – свой маленький.

Первое задание.

III. Устный счет

1. Решение цепочек (стр. 175, № 1111).

2/5 + 1/5 + 2/5 – 3/7 – 1/7 = 3/7

5/17 + 7/17 – 12/17 + 7/9 – 4/9 = 3/9

2. На какие группы мы можем разделить данные дроби: (правильные и неправильные дроби) (Слайд 6)

9 5 8 10 24 15 7 12

8 12 11 6 13 16 7 25

Какие дроби называются правильными?

Какие дроби называются неправильными?

Как по-другому представить неправильные дроби?

Из чего состоит смешанное число?

(Кусок торта.)

IV. Актуализация знаний.

Найдите лишний пример:

2/8 + 3/8 14/12 – 7/12 7/9 + 1/9 3 1/7 + 2 3/7 18/27 -5/27

Попробуйте сформулировать тему урока (Сложение смешанных чисел) (Слайд8)

Сегодня на уроке мы научимся выполнять сложение и вычитание смешанных чисел, для достижения этой цели сформулируем правила.

V. Исследование

Учащиеся работают в группах, выполняя задания различной сложности. Все учащиеся делятся на 4 группы. На парту каждой группы раздается задание и справочный материал. Для решения задания нужно выбрать соответственное правило.

Задание 1 . Выполнение сложения 2 ½ + 3

Задание 2. Выполнение сложения 2 1/4 + 1 2/4

Задание 3 . Выполнение вычитания 3 5/6 – 3/6

Задание 4. Выполнение вычитания 5 1/4 — 3 2/4

Справка

1. К полученной целой части прибавить дробную часть.
2. Сформулировать правило сложения смешанного числа с натуральным.

1. К целой части прибавить целую часть.
2. К дробной части прибавить дробную часть
3. К полученной целой части прибавить полученную дробную часть.
4. Сформулировать правило сложения смешанных чисел.

1. Из целой части вычесть целую часть.
2. Из дробной части вычесть дробную часть
3. К оставшейся целой части прибавить оставшуюся дробную часть.
4. Сформулировать правило вычитания смешанных чисел.

1. Если дробная часть уменьшаемого меньше дробной части вычитаемого.
2. Занимаем у целой части уменьшаемого единицу и представляем ее в виде неправильной дроби.
3. Полученную дробь складываем с дробной частью уменьшаемого.
4. Вычитаем отдельно целые части и дробные части.
5. К оставшейся целой части прибавляем оставшуюся дробную часть.
6. Сформулировать правило вычитания из смешанного числа дроби, причем дробь уменьшаемого больше дроби вычитаемого.

VI. Обмен информацией .

Вы рассмотрели правила сложения и вычитания смешанных чисел. Что общего у них? (Действия выполняются сначала с целыми числами, затем с дробными частями.)

Сформулируйте правило сложения смешанных чисел. (Слайд 9)

Сформулируйте правило вычитания смешанных чисел. (Слайд 10)

Стр. 174 учебника, правило

(Кусок торта.)

VII. Применение

— Вернемся к примеру:

3 1/7 + 2 3/7= (3+2)+(1/7+3/7)=5+4/7=54/7

Как убедиться, что сложение выполнено правильно? (Вычитанием). Сделать проверку.

54/7-31/7=(5-3)+(4/7-1/7)= 2+3/7= 23/7

(Кусок торта.)

VIII. Физкультминутка (Слайд)

Потрудились — отдохнём,

Встанем, глубоко вздохнём.

Руки в стороны, вперёд,

Влево, вправо поворот.

Три наклона, прямо встать.

Руки вниз и вверх поднять.

Руки плавно опустили,

Всем улыбки подарили.

IX. Закрепление изученного материала

1. Карлсон прислал телеграмму, но все слова перепутались. Давайте решим примеры и соотнесем их с ответами. (Слайд 11)

3 7/13 – 4/13= 4 – В

5 2/5+1/5= 7 4/6 – О

10 2/3-6= 3 3/13 – У

2 2/7+2 4/7= 4 6/7 – Е

8 5/9-3= 5 5/9 – Х

3/6+7 1/6 = 4 2/3 – П

7 4/5-3 4/5= 5 3/5 – С

(Кусок торта.)

«Охота за пятерками»

2. Работа над задачами.

а) Стр. 175, №1115.

1. Прочитайте задачу.
2. Сколько конфет в одной коробке?
3. Сколько конфет в другой коробке?
4. Как ответить на вопрос задачи?
5. Решите задачу. Прочитайте ответ. (В двух коробках 4 4/8 кг конфет.)

б) Стр. 175, № 1116.

1. Чему равна длина красной ленты?
2. Что сказано про длину белой?
3. Что значит на 2 1/5 м короче?
4. Как будете решать эту задачу?

Решите. Прочитайте ответ. (Длина белой ленты 1 2/5 метра.)

(Кусок торта.)

Вы – замечательные ученики: старательные, внимательные, дружные, помогаете друг другу.

(прилетел Карлсон) Карлсон увидел, что вы такие ребята, каких он искал, и вернулся. Мы дарим ему торт.

X. Итог урока (вопросы Карлосона).

1. Что такое смешанное число?
2. Чему вы сегодня научились? (Складывать и вычитать смешанные числа.)
3. Как сложить смешанные числа?
4. Как вычесть смешанные числа?

Это вам поможет справиться с домашним заданием.

XI. Домашнее задание: Стр. 178, № 1136,1137

XII. Рефлексия.

Соберите заработанные кусочки в тортик. (3-5 частей – «5»)

Учитель оценивает работу учащихся. (Мордашка). (Слайд 13)

Смешанные дроби также, как и простые дроби можно вычитать. Чтобы отнять смешанные числа дробей нужно знать несколько правил вычитания. Изучим эти правила на примерах.

Вычитание смешанных дробей с одинаковыми знаменателями.

Рассмотрим пример с условием, что уменьшаемое целое и дробная часть больше соответственно вычитаемого целой и дробной части. При таких условиях вычитание происходит отдельно. Целую часть вычитаем из целой части, а дробную часть из дробной .

Рассмотрим пример:

Выполните вычитание смешанных дробей \(5\frac{3}{7}\) и \(1\frac{1}{7}\).

\(5\frac{3}{7}-1\frac{1}{7} = (5-1) + (\frac{3}{7}-\frac{1}{7}) = 4\frac{2}{7}\)

Правильность вычитания проверяется сложением. Сделаем проверку вычитания:

\(4\frac{2}{7}+1\frac{1}{7} = (4 + 1) + (\frac{2}{7} + \frac{1}{7}) = 5\frac{3}{7}\)

Рассмотрим пример с условием, когда дробная часть уменьшаемого меньше соответственно дробной части вычитаемого. В таком случае мы занимаем единицу у целого в уменьшаемом.

Рассмотрим пример:

Выполните вычитание смешанных дробей \(6\frac{1}{4}\) и \(3\frac{3}{4}\).

У уменьшаемого \(6\frac{1}{4}\) дробная часть меньше чем у дробной части вычитаемого \(3\frac{3}{4}\). То есть \(\frac{1}{4}

\(\begin{align}&6\frac{1}{4}-3\frac{3}{4} = (6 + \frac{1}{4})-3\frac{3}{4} = (5 + \color{red} {1} + \frac{1}{4})-3\frac{3}{4} = (5 + \color{red} {\frac{4}{4}} + \frac{1}{4})-3\frac{3}{4} = (5 + \frac{5}{4})-3\frac{3}{4} = \\\\ &= 5\frac{5}{4}-3\frac{3}{4} = 2\frac{2}{4} = 2\frac{1}{4}\\\\ \end{align}\)

Следующий пример:

\(7\frac{8}{19}-3 = 4\frac{8}{19}\)

Вычитание смешанного дроби из целого числа.

Пример: \(3-1\frac{2}{5}\)

Уменьшаемое 3 не имеет дробной части, поэтому сразу отнять мы не сможем. Займем у целой части у 3 единицу, а потом выполним вычитание. Единицу мы запишем как \(3 = 2 + 1 = 2 + \frac{5}{5} = 2\frac{5}{5}\)

\(3-1\frac{2}{5}= (2 + \color{red} {1})-1\frac{2}{5} = (2 + \color{red} {\frac{5}{5}})-1\frac{2}{5} = 2\frac{5}{5}-1\frac{2}{5} = 1\frac{3}{5}\)

Вычитание смешанных дробей с разными знаменателями.

Рассмотрим пример с условием, если дробные части уменьшаемого и вычитаемого с разными знаменателями. Нужно привести к общему знаменателю, а потом выполнить вычитание .

Выполните вычитание двух смешанных дробей с разными знаменателями \(2\frac{2}{3}\) и \(1\frac{1}{4}\).

Общим знаменателем будет число 12.

\(2\frac{2}{3}-1\frac{1}{4} = 2\frac{2 \times \color{red} {4}}{3 \times \color{red} {4}}-1\frac{1 \times \color{red} {3}}{4 \times \color{red} {3}} = 2\frac{8}{12}-1\frac{3}{12} = 1\frac{5}{12}\)

Вопросы по теме:
Как вычитать смешанные дроби? Как решать смешанные дроби?
Ответ: нужно определиться к какому типу относиться выражение и по типу выражения применять алгоритм решения. Из целой части вычитаем целое, у дробной части вычитаем дробную часть.

Как из целого числа вычесть дробь? Как от целого числа отнять дробь?
Ответ: у целого числа нужно занять единицу и записать эту единицу в виде дроби

\(4 = 3 + 1 = 3 + \frac{7}{7} = 3\frac{7}{7}\),

а потом целое отнять от целого, дробную часть отнять от дробной части. Пример:

\(4-2\frac{3}{7} = (3 + \color{red} {1})-2\frac{3}{7} = (3 + \color{red} {\frac{7}{7}})-2\frac{3}{7} = 3\frac{7}{7}-2\frac{3}{7} = 1\frac{4}{7}\)

Пример №1:
Выполните вычитание правильной дроби из единицы: а) \(1-\frac{8}{33}\) б) \(1-\frac{6}{7}\)

Решение:
а) Представим единицу как дробь со знаменателем 33. Получим \(1 = \frac{33}{33}\)

\(1-\frac{8}{33} = \frac{33}{33}-\frac{8}{33} = \frac{25}{33}\)

б) Представим единицу как дробь со знаменателем 7. Получим \(1 = \frac{7}{7}\)

\(1-\frac{6}{7} = \frac{7}{7}-\frac{6}{7} = \frac{7-6}{7} = \frac{1}{7}\)

Пример №2:
Выполните вычитание смешанной дроби из целого числа: а) \(21-10\frac{4}{5}\) б) \(2-1\frac{1}{3}\)

Решение:
а) Займем у целого числа 21 единицу и распишем так \(21 = 20 + 1 = 20 + \frac{5}{5} = 20\frac{5}{5}\)

\(21-10\frac{4}{5} = (20 + 1)-10\frac{4}{5} = (20 + \frac{5}{5})-10\frac{4}{5} = 20\frac{5}{5}-10\frac{4}{5} = 10\frac{1}{5}\\\\\)

б) Займем у целого числа 2 единицу и распишем так \(2 = 1 + 1 = 1 + \frac{3}{3} = 1\frac{3}{3}\)

\(2-1\frac{1}{3} = (1 + 1)-1\frac{1}{3} = (1 + \frac{3}{3})-1\frac{1}{3} = 1\frac{3}{3}-1\frac{1}{3} = \frac{2}{3}\\\\\)

Пример №3:
Выполните вычитание целого числа из смешанной дроби: а) \(15\frac{6}{17}-4\) б) \(23\frac{1}{2}-12\)

а) \(15\frac{6}{17}-4 = 11\frac{6}{17}\)

б) \(23\frac{1}{2}-12 = 11\frac{1}{2}\)

Пример № 4:
Выполните вычитание правильной дроби из смешанной дроби: а) \(1\frac{4}{5}-\frac{4}{5}\)

\(1\frac{4}{5}-\frac{4}{5} = 1\\\\\)

Пример №5:
Вычислите \(5\frac{5}{16}-3\frac{3}{8}\)

\(\begin{align}&5\frac{5}{16}-3\frac{3}{8} = 5\frac{5}{16}-3\frac{3 \times \color{red} {2}}{8 \times \color{red} {2}} = 5\frac{5}{16}-3\frac{6}{16} = (5 + \frac{5}{16})-3\frac{6}{16} = (4 + \color{red} {1} + \frac{5}{16})-3\frac{6}{16} = \\\\ &= (4 + \color{red} {\frac{16}{16}} + \frac{5}{16})-3\frac{6}{16} = (4 + \color{red} {\frac{21}{16}})-3\frac{3}{8} = 4\frac{21}{16}-3\frac{6}{16} = 1\frac{15}{16}\\\\ \end{align}\)

Сложение и вычитание смешанных чисел

Урок 12.

Математика 6 класс

В этом уроке мы повторим понятие смешанного числа. Сформируем представления о сложении и вычитании смешанных чисел. Выведем правило сложения смешанных чисел и правило вычитания смешанных чисел. Закрепим полученные знания при решении примеров.

Конспект урока «Сложение и вычитание смешанных чисел»

Сегодня на уроке мы научимся складывать и вычитать смешанные числа.

Напомним, сумму натурального числа и правильной дроби принято записывать без знака «+». Такую сумму называют смешанным числом. То есть «смешали» натуральное число и правильную дробь, и назвали эту запись смешанным числом.

Натуральное число называют целой частью смешанного числа, а дробь – дробной частью смешанного числа.

То есть запись  является сокращённым вариантом записи .

Складывать смешанные числа помогают свойства сложения: переместительное и сочетательное.

Пример

Найдём сумму чисел  и .

При выполнении записи в тетрадях, не нужно записывать смешанное число как сумму натурального числа и дроби, затем подробно расписывать, как вы складываете целые и дробные части смешанных чисел.

Пример

Найдём сумму смешанных чисел  и .

Таким образом, если при сложении дробных частей получилась неправильная дробь, выделяют целую часть этой дроби и добавляют к уже имеющейся целой части.

Пример

Теперь найдём сумму чисел  и .

Задача

На столе лежало  пиццы. Если принести ещё  пиццы. Сколько пицц окажется на столе?

Чтобы решить задачу, надо сложить числа  и .

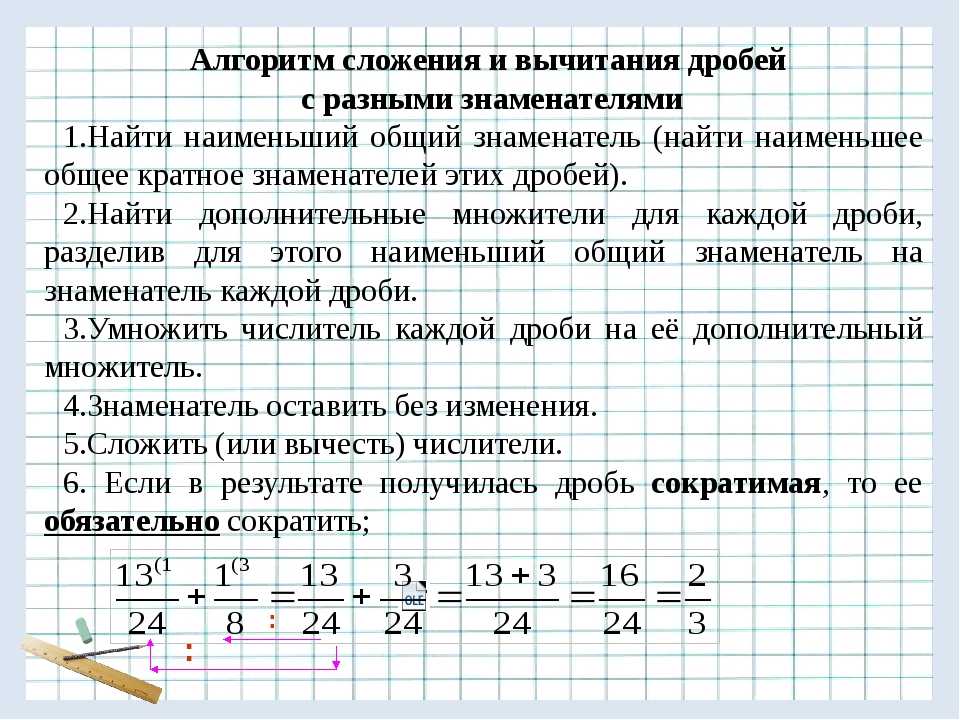
Чтобы найти разность смешанных чисел, нужно найти отдельно разность целых частей и отдельно разность дробных частей.

Пример

Вычтем из дроби  дробь .

Есть в вычитании «коварные» примеры.

Пример

Запомните! Не начинайте выполнять вычитание, пока не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби.

А вот если вычесть нельзя, «занимаем» у целой части уменьшаемого одну целую единицу.

Иногда в примерах нужно вычесть из натурального числа смешанную дробь.

Пример

Найдём значение выражения .

Итоги

Чтобы сложить смешанные числа, надо: привести дробные части этих чисел к наименьшему общему знаменателю; отдельно выполнить сложение целых частей и отдельно дробных частей.

Если при сложении дробных частей получилась неправильная дробь, выделить целую часть из этой дроби и прибавить её к полученной целой части.

Чтобы выполнить вычитание смешанных чисел, надо: привести дробные части этих чисел к наименьшему общему знаменателю; если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть; отдельно выполнить вычитание целых частей и отдельно дробных частей.

Предыдущий урок 11 Сравнение, сложение и вычитание дробей с разными знаменателями

Следующий урок 13 Умножение дробей

Получите полный комплект видеоуроков, тестов и презентаций Математика 6 класс

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Как вычитать смешанные дроби из целых чисел?

Подмножество чисел, включающее ноль и все положительные целые числа, называется целыми числами. Общее число идет от 0 до бесконечности. Эти числа используются в повседневных вычислениях, в основном для измерения фундаментальных величин. Натуральные числа состоят исключительно из целых чисел, включая ноль. Числа 0, 1, 2, 3, 4, 5, 6, 7… обозначают подмножество. Подмножество исключает дроби, десятичные числа и отрицательные целые числа.

Положительные целые числа, также называемые счетными числами, представляют собой части целых чисел, содержащие ноль, например 0, 1, 2, 3, 4, 5, 6, 7 и т. д., исключая отрицательные целые числа, дроби и десятичные дроби. 10, 11, 12, 22, 28, 100, 1000 и т. д. — примеры целых чисел.

Смешанные дроби 

Смешанная дробь – это форма дроби, которая имеет как целое число, так и дробную часть. Например, 3(5/2) — смешанная дробь, здесь 3 — целое число, а 5/2 — дробная часть. 2(4/3) — смешанная дробь, здесь 2 — целое число, а 4/3 — дробная часть.

Как вычитать смешанные дроби из целых чисел?

Решение:  

Чтобы вычесть смешанную дробь с целым числом 

Выполните несколько шагов,

• Шаг 1: Составьте неправильную дробь из смешанной дроби.
• Шаг 2: Выразите целое число в виде дроби с 1 в знаменателе.
• Шаг 3: Вычитание дробей

Это правильный способ вычитания смешанной дроби с целым числом.

Примеры вопросов

Вопрос 1: Вычесть 3(4/5) – 8?

Решение:  

Дано: 3(4/5) – 8

Здесь смешанная дробь 3(4/5)

Шаг 1:  Составь из смешанной дроби неправильную дробь.

Следовательно, 3(4/5)

= 19/5 в виде неправильной дроби

Шаг 2: Выразите целое число в виде дроби с 1 в знаменателе. Таким образом, 8 можно записать как 8/1

Шаг 3: Вычесть дробь, т.е. 19/5 – 8/1

= Здесь lcm знаменателей равны 5

= (19 – 8)/5

= 11/ 5

Вопрос 2. Вычесть 8–5 (2/3)?

Решение:   

Дано: 8 – 5(2/3)

Здесь смешанная дробь 5 (2/3)

Шаг 1. Из смешанной дроби составьте неправильную дробь.

Следовательно, 5(2/3)

= 17/3 в виде неправильной дроби

Шаг 2: Выразите целое число в виде дроби с 1 в знаменателе. Таким образом, 8 мы можем записать как 8/1

Шаг 3: Вычтите дробь, т.е. 17/3 – 8/1

= Здесь lcm знаменателей равны 3

= (17 – 8)/3

= 9/3

= 3, что является целым числом.

Вопрос 3: Вычесть 7 – 2(8/5)?

Решение:  

Дано: 7 – 2(8/5)

Здесь смешанная дробь 2(8/5)

Шаг 1. Из смешанной дроби составить неправильную дробь.

Следовательно, 2(8/5)

= 18/5 в виде неправильной дроби

Шаг 2: Выразите целое число в виде дроби с 1 в знаменателе. Итак, 7 мы можем записать как 7/1 9.0003

Шаг 3: Вычтите дробь, т.е. 18/5 – 7/1

= Здесь lcm знаменателей равны 5

= (18 – 7)/5

= 11/5

Вопрос 4: Вычесть 8/5 – 9/6?

Решение:

Дано: 8/5 — 9/6

= Здесь LCM знаменателя 5 и 6 — 30

= (48 — 45)/30

= 3/30

= 1/10

Вопрос 5: Вычесть 2(8/5) – 4(9/6)?

Решение:  

Дано: 2(8/5) – 4( 9/6)

= 18/5 – 33/6

= (108 – 165)/30

= -57/30

= -19/10

Вопрос 6: Вычесть 2 – 3(7/2)?

Решение:  

Дано: 2 – 3(7/2)

Здесь смешанная дробь 3(7/2)

Шаг 1. Из смешанной дроби составьте неправильную дробь.

Следовательно, 3(7/2)

= 13/2 как неправильная дробь

Шаг 2. Выразите целое число в виде дроби с 1 в знаменателе.

= 2/1 -13/2

= Здесь lcm знаменателей равны 2

= (2 – 13)/2

= – 11/2

Рабочие листы | TPT

by

Simply Kinder

972,00 $

25,00 $

Идеальный набор учебников для детского сада, игр, раскрашивания по коду и многого другого для 200+ высокочастотных слов! ЛУЧШИЙ ПРОДАВЕЦ на TpT с более чем 7000 отзывов учителей! Оцените эту невероятную стоимость всего, что вам нужно для практики словесного зрения! Ваша практика словесного зрения стала намного лучше благодаря этому огромному файлу печатных форм, занятий, центров и многого другого. Каждое включенное прицельное слово имеет отдельный файл с 67 страницами действий! Идеально подходит для детского сада, первого класса

Предметы:

Английский язык, чтение

Классы:

PreK — 1st

Типы:

Занятия, распечатки, рабочие листы

CCSS, RF. 3.9002. .K.3c

by

My Nerdy Teacher от Алины В. Спешите, время истекает! Ваши ученики могут практиковаться в чтении весело и увлекательно, используя эти декодируемые тексты. Наука чтения AlignedLow Требуется подготовка. Просто распечатайте и идите. Эти декодируемые отрывки помогут вашим ученикам практиковать фонетические модели, которым вы их учите. Идеально подходит для центров, домашних заданий, утренней работы и многого другого. Печатные и цифровые (Google Slides™) Идеально подходит для дошкольного детского сада, 1-й класс

Предметы:

Акустика, Чтение, Письмо

Классы:

К — 2-й

Виды:

Занятия, Центры, Печатные формы

CCSS, RF.K.3.K. .K.3c, RF.1.2c, RF.1.2d…

by

Специально для образования

Если вы ищете индивидуальную книгу расписаний, наглядные расписания или сначала доску, этот ресурс поддержки позитивного поведения найдет для вас все! Обратите внимание: все редактируемые файлы совместимы с Microsoft PowerPoint. Некоторые страницы теперь можно редактировать с помощью Google Slides. В эту загрузку включены: — Варианты флипбука с 6 и 2 вкладками — Более 200 визуальных значков расписания (они не редактируются) — Сначала доска (отдельно от флипбука) — Сначала затем доска (отдельно от флипбука) — доски жетонов (wi

Предметы:

Снова в школу, Специальное образование, Логопедия

Классы:

PreK — 2-й

Типы:

Расписание занятий

Также включено в: НАБОР: First Book Then Boards & Visual настоящие фотографии)

на

Искусство с Дженни К.

Мои знаменитые лица® из афроамериканской истории Проект «Одеяло» — это идеальное занятие для всего класса во время Месяца черной истории или в любое время года! Он соединяет человека с группой с помощью шестиугольников, которые будут складываться, чтобы создать большой совместный плакат «лоскутное одеяло», на котором изображены 40 влиятельных афроамериканцев и их биографии. После завершения финальный постер вызывает массу «вау-фактора», и я надеюсь, что он окажет большое влияние на ваших учеников, когда они узнают об этих 40 влиятельных

субъекты:

Месяц черной истории, искусство английского языка, общественные науки — история

Оценки:

1 -й — 8 -й

Типы:

Мероприятия, печатные изделия, проекты

на

My Teaching Pal

$ 12.509

.

8,00 $

Bundle

Предложите своим ученикам попрактиковаться во всем, что связано с алфавитом, с помощью этого ОГРОМНОГО комплекта рабочих листов по алфавиту. Студенты будут работать над идентификацией букв, начальными звуками, формированием букв, различением строчных и прописных букв и многим другим. В этот пакет включены 4 различных типа рабочих листов, которые охватывают каждую букву алфавита. Всего включено 104 рабочих листа. Что включено: ♥ Рабочие листы по алфавиту — Работа с буквами ♥ Рабочие листы для начальных звуков — цвет по моему звуку ♥ Алфавит M

Предметы:

Английский языковой искусство, Фоника, написание

Оценки:

Prek — K

Типы:

Мероприятия, печатные изделия, рабочие листы

на

Shelly Rees

Interactive Noteppeak практический опыт для учащихся. Этот интерактивный блокнот «Карты, континенты и формы рельефа» не является исключением! Пакет удобен в использовании как для ученика, так и для учителя. ✅ Нажмите ЗДЕСЬ, чтобы СЭКОНОМИТЬ 20% на этом ресурсе с блоком «Карты, континенты и формы рельефа» и комплектом плакатов! ✅ Нажмите ЗДЕСЬ, чтобы сэкономить еще больше, купив ВСЕ 15 интерактивных тетрадей по общественным наукам и мини-блоков в одном годовом комплекте. Нажмите на кнопку ПРЕДПРОСМОТР выше, чтобы увидеть все t

Предметы:

География, Другое (Обществоведение — История), Обществознание — История

Классы:

3-5

Типы:

Самостоятельные рабочие пакеты, печатные формы, рабочие листы

Также включены в классы Комплект социальных исследований и интерактивных тетрадей для 4-го класса

by

Мой друг-учитель

22,00 $

15,00 $

Комплект

Этот комплект содержит 263 ОГРОМНЫХ математических листа для первого класса! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время. Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для занятий в классе, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D

Предметы:

Базовые операции, математика, числа

Классы:

Типы:

Печатные издания, рабочие тетради, рабочие листы

by

Патриция Пэт Написание предложения как трудная задача для ваших учащихся

3 9 Если это так, вам понравится, как эти рабочие листы для построения предложений помогут вам научить писать полные предложения. ✏️ Многочисленные изображения в рабочем листе помогут вашим ученикам ПОНЯТЬ и ЗАПОМНИТЬ правильную структуру предложения. ✏️ Это ресурс без подготовки, который понравится даже неохотным писателям, плюс вы сэкономите много времени с помощью ТРЕХ дифференциаций и строительных лесов, сделанных за вас. ✏️ Эти практические рабочие листы будут

Предметы:

EFL — ESL — ELD, английский язык, специальное образование

Классы:

K — 2nd

Типы:

Центры, Домашнее обучение, Домашнее задание

9.1002 CCSS3: SL.1.6, L.K.1f, L.1.1c, L.1.2b

Также включено в: Центр написания предложений | Полные предложения | Структура предложения | Небольшие группы

по

Образование в основе

20,00 долл. США

12,00 долл. США

Основы образования услышали ваши призывы и разработали целый ресурс, посвященный основанным на фонетике занятиям по программе I SPY, обновленный и включающий 84 страницы с заданиями! эти рабочие листы помогут вашим ученикам укрепить их зрительное различение, развивая при этом их внимание и навыки фокусировки. (Потребуется некоторое время и терпение, чтобы найти все изображения в каждом упражнении.) Только представьте, как тихо будет в вашем классе! Это такое увлекательное занятие, что ваши ученики будут б

субъекты:

Фоника, орфография, словарь

Оценки:

K — 2 -й

Типы:

Мероприятия, печатные изготовления, рабочие листы

на

Pathway 2. ‘ навыки самоконтроля в форме! Действия сосредоточены на понимании самоконтроля, импульсивного контроля, остановке и обдумывании, чтобы принять решение, ожидании своей очереди, соблюдении правил и указаний, сохранении мотивации, выполнении нашей работы наилучшим образом, управлении эмоциями, использовании стратегий преодоления и практике самоконтроля для укрепления. навыки со временем. Также рассматриваются другие навыки, влияющие на самоконтроль, включая планирование, управление временем и настойчивость. Цифровая версия обновлена ​​до 9.0003

Тема:

Школьное консультирование, социальное эмоциональное обучение, специальное образование

Оценки:

4 -й — 8 -е

Типы:

Урок, печатные издания

на

Эшли

. эти 50 печатных форм! Никакой подготовки не требуется Все, что вам нужно сделать, это распечатать, и вы готовы к работе! Эти печатные формы периметра и площади — отличный способ дополнить существующую учебную программу по математике. Эти рабочие листы были созданы для моих учеников, которым нужна дополнительная помощь с площадью и периметром. Они были разработаны для третьего класса и полностью соответствуют Common Core.*************************************** ******************************************* Что

Предметы:

Классы:

3-4

Типы:

Упражнения, Печатные формы

CCSS:

3.MD.C.5, 3.MD.3MD.5a, 3.MD.C.5a. 5b, 3.MD.C.6, 3.MD.C.7…

Также включено в: Пакет «Без подготовительной математики» | Печатные и цифровые материалы для дистанционного обучения

на

Lucky Little Learners

34,00 долл. США

23,00 долл. США

Bundle

Отрывки для чтения по фонетике, или Phonics Mats, представляют собой идеальный изолированный ресурс, помогающий учащимся, не требующий подготовки, распечатайте и приступайте к работе навыки чтения текста! Учащиеся практикуют изолированные фонетические навыки, декодирование, беглость речи и понимание в одном ресурсе. *** НОВОЕ ОБНОВЛЕНИЕ *** Этот ресурс обновлен новой версией 2022 года! В новых ковриках для фонетики есть декодируемые отрывки, вопросы на понимание, практика написания слов и страница для разминки для каждого навыка. Обязательно загрузите превью

Предметы:

Акустика, чтение, письмо

Классы:

Типы:

Печатные формы, рабочие листы

CCSS:

RF.2.3, RF.2.3c, RF.2.2.2 .2.3d…

by

Rockin Resources

18,98 $

11,99 $

Bundle

Ваши учащиеся испытывают затруднения при написании полных предложений и абзацев? Эти пошаговые письменные модули для составления структуры предложений и написания абзацев загружены увлекательными уроками, чтобы дать вашим учащимся прочную основу структуры предложений и написания абзацев. Вы увидите, как учащиеся начнут писать полные предложения и строить эффективные абзацы, что также поможет в написании эссе! Следующие навыки помогут вам научить писать предложения и абзацы!

Предметы:

Английский язык искусства, написание

Оценки:

3 -е — 6 -е

Типы:

Урок, печатные изготовления

на

Lucky Little Cecuriers

Эта упаковка порта им нужно в увлекательной форме. Они будут развивать выносливость при письме, повторять построение букв и цифр и практиковаться в словах, изучая новые шутки и забавные факты! и почерк, который не является «детским»? Глупые шутки и забавные факты привлекут ваших учеников, пока они

субъекты:

Сбалансированная грамотность, почерк, написание

. делать выводы и делать выводы, анализируя различные текстовые сообщения. Студенты должны привести доказательства для каждого ответа. Цифровые и печатные варианты: этот продукт теперь включает опцию Google Slides, а также печатный PDF-файл. Этот продукт также включает страницу с двумя пустыми телефонными разговорами. Студентам нравится макет текстового сообщения! Это отличный способ для старших школьников попрактиковаться в выводах и цитировании доказательств в форме для 9.0003

Субъекты:

Чтение

Оценки:

5 -й — 7 -й

Типы:

печатные изготовления, рабочие листы

CCSS:

RL.5.1, RL.6.1, RL.7.1

Также включены в: rl. Анализ Bundle Создание выводов и цитирование доказательств

по

Читать Написать Средний

35,00 $

$20,00

Bundle

Вы ищете способ, чтобы ваши ученики были вовлечены и готовы к занятиям, как только они входят в дверь? Мои ежедневные отрывки для понимания прочитанного могут помочь вам сделать это! Эти печатные и цифровые звонари специально разработаны для улучшения навыков чтения учащихся средних школ. Этот ресурс включает в себя короткие и увлекательные отрывки для ежедневного чтения, которые обеспечивают содержательную практику с контекстными подсказками, основной идеей, выводами, определением темы и многим другим! Эти отрывки отлично подходят для: H

субъекты:

Английский язык, информационный текст, чтение

Оценки:

6 -й — 8th

Типы:

Рабочие листы

CCSS:

RL.6.1, RL.6.2, RL.6.4, RL. 7.1, RL.7.2…

на

Обучаемый учитель

Редактируемые рабочие листы для чтения слов обеспечивают учащимся детского сада, первого и второго классов эффективную и увлекательную практику словесного чтения. Волшебная часть этих действий со словами-визуалами заключается в том, что они эффективны и для вас! Были ли у вас рабочие листы со словами для зрения, но затем вы изменили классы или ваша школа изменила свой список слов для зрения,

Субъекты:

EFL — ESL — ELD, орфография, словарь

Оценки:

K — 2 -й

Типы:

Мероприятия, печатные изделия, рабочие листы

по

The Moffatt Girls

. Пакет для 2-го класса НАПОЛНЕН практическими, увлекательными и ВЕСЕЛЫМИ ресурсами, которые охватывают основные навыки для 2-го класса! Занятия в этом пакете можно использовать для повторения во 2-м классе, «Снова в школу» для 3-го класса (обзор подоконников во 2-м классе или ознакомления с новым материалом для высоколетящих первоклассников! САМОЕ ЛУЧШЕЕ в том, что НЕТ ПОДГОТОВКИ! НИКАКИХ дорогостоящих цветных чернил) , БЕЗ ламинирования, БЕЗ вырезания… просто РАСПЕЧАТАЙТЕ!⭐️ Версия для дошкольников: ЗДЕСЬ⭐️ Версия для детского сада: ЗДЕСЬ⭐️ Версия для 1-го класса: ЗДЕСЬ

субъекты:

Английский язык искусства, математика, лето

Оценки:

1 -й — 2 -й

Типы:

Центры, печатные изготовления, рабочие листы

на

Caren Jones

$ 10. 00

OT

. фонетические ресурсы! Этот пакет содержит более 100 страниц готовых к использованию листов для печати по фонетике! Никаких подготовительных работ не требуется, просто распечатайте и скопируйте! Каждая страница представляет собой отдельное задание, над которым ваши ученики могут работать самостоятельно. Они отлично подходят для практики работы со словами, утренней работы, центров грамотности или домашних заданий. Каждая страница включает в себя какой-либо интерактивный элемент вырезания и склейки, раскрашивания или сортировки. Версия PowerPoint и файлы изображений также включены для загрузкиi

Предметы:

Английский язык, акустика

Классы:

K — 1-й

Типы:

Мероприятия, Центры, Печатные формы

CCSS:

, RF.K.2a

.K.2c, RF.K.2d, RF.K.3…

на

Crystal McGinnis

Вашим ученикам понравится эта игра с рифмованными словами, включая рабочие листы по рифмовке для практики! Эта деятельность по сортировке карманных таблиц Центра грамотности рифмующих слов поможет вашим детям освоить рифмование на практике. Этот набор включает в себя 30 пар рифмующихся слов, которые можно отсортировать в карманной таблице, и 3 листа с рифмующимися словами. Учащиеся решают, рифмуются слова или нет. Затем они кладут карточки под знак «большой палец вверх» или «большой палец вниз». Я также предоставил 3 распечатки для самостоятельной практики f

субъекты:

Сбалансированная грамотность, чтение

Оценки:

Prek — 1st

Типы:

, Центры, печатные изделия

CCSS:

RF.K.2A

Также включены в: Доллар ПУЧОК! (ВСЕ МОИ ДОЛЛАРОВЫЕ СДЕЛКИ)

на

WholeHearted School Counseling

$10,75

В нашем наборе Calm Down Corner есть ВСЕ, что вам нужно, чтобы помочь вашим ученикам в саморегуляции, и он изменит правила игры в вашем классе. Это идеальный инструмент социально-эмоционального обучения и управления поведением, необходимый для каждого начального класса! Вы сможете создать красивое место для отдыха, где учащиеся смогут самостоятельно использовать стратегии выживания, чтобы контролировать свои сильные чувства и управлять ими. В то же время сокращая перерывы в работе в классе, облегчая вам задачу

Предметы:

Управление классом, школьное консультирование, социально-эмоциональное обучение

Классы:

K — 6th

Типы:

Занятия, плакаты, рабочие листы

, SEL Уроки, игры и декор

by

The Moffatt Girls

Этот пакет «Простые дроби НЕТ ПОДГОТОВКИ» НАПОЛНЕН увлекательными заданиями, которые помогут учащимся освоить простые дроби! УДОВОЛЬСТВИЕ, практический и интерактивный подход позволяет преподавателям учить несколькими способами! ЛУЧШЕЕ в этом пакете то, что НЕТ ПОДГОТОВКИ! БЕЗ ламинирования, БЕЗ дорогостоящих цветных чернил, БЕЗ резки… просто ПЕЧАТАЙТЕ и УЧИТЕСЬ!0003

Субъекты:

Фракции, математика, задачи слов

Оценки:

1 -й — 3 -й

Типы:

Центры, печатные изготовления, рабочие листы

на

Обучение с горой. Карточки с заданиями по чтению для проверки навыков понимания Привлекайте своих читателей интересными отрывками для понимания прочитанного и соответствующими вопросами! Этот ресурс включает в себя 32 карточки с информационными текстовыми заданиями на полстраницы с 4 вопросами на понимание и заданиями на КАЖДОЙ карточке, всего 128 информационных текстовых вопросов! Вовлеките своих учащихся в осмысленную практику внимательного чтения и просмотрите ключевые навыки чтения, связанные с информационным и научно-популярным текстом

Субъекты:

ELA PREP TEST PREP, АНГЛИЙСКОЕ ЯЗЫКИ, информационный текст

Оценки:

3 -е — 5 -е

Типы:

Центры, Зачитанные карты

CCS:

RI.