Записывают десятичные выражения, используя в качестве разделителя запятую. Например, 1/10 = 0,1.

С дробями, так как по факту это числа, разрешено выполнять любые математические действия. Самые простые из них — это умножение и деление, немного сложнее сложение и вычитание. Чтобы вычитать обыкновенные дроби, нужно знать их основное свойство. Сформулировать его можно следующим образом: если делитель и делимое умножить или разделить на одну и ту же величину, то результат отношения не изменится. Причём такую операцию можно выполнять сколько угодно раз.

Естественно, это не должен быть ноль, иначе выражение потеряет смысл. Например, ¾ = (3 * n)/(4 * n). Это свойство позволяет не только преобразовывать выражение, делая вычисления проще и удобнее, но и выполнять вычитание.

Всё дело в том, что при выполнении действия находят так называемые дополнительные множители, которые можно определить, опираясь на основное свойство.

Нахождение общего знаменателя

Основная сложность, которая может возникнуть при нахождении разности дробей, — это правильное определение общего знаменателя.

В качестве него выступает положительное число, делящееся на делители вычитаемых выражений без остатка. Искомый параметр можно находить как для двух дробей, так и сразу для нескольких.

В простейшем понимании такое число можно получить простым перемножением знаменателей.

Но такой подход будет нерациональным, хотя назвать его в корне неправильным нельзя.

Общее правило для вычисления наименьшего общего знаменателя (НОЗ):

1. Из чисел, стоящих в делимых, выбрать наибольшее и исследовать его на возможность деления с оставшимися. Если такое действие возможно, то выбранное значение и будет НОЗ. В ином случае переходят ко второму пункту.
2. Наибольший знаменатель умножают на два и проверяют делимость полученного числа на все остальные.
3. На этом шаге наибольший знаменатель умножают на три и повторяют проверку.
4. Если НОЗ не найден, делители раскладывают на простые множители. В результате повторяющиеся числа убирают, а оставшиеся перемножают. Получившееся произведение и будет НОЗ.

Таким образом, чтобы найти нужный знаменатель, необходимо уметь раскладывать простые числа на множители. Эта операция является тождественным преобразованием. Выполняется она в несколько этапов.

Сначала ищется наименьшее число, на которое можно разделить исходное без остатка. Затем выполняют деление и повторяют действие, но уже для полученного значения. Операцию повторяют до тех пор, пока в ответе не получится единица.

Понять процедуру проще на примере. Пусть нужно выполнить вычитание двух дробей, у которых в знаменателях стоит 15 и 40. Следуя алгоритму, нужно наибольшее из этих чисел умножить на два и попробовать выполнить деление.

Это значение можно было найти и пойдя путём разложения. Так, 15 можно представить как 5 * 3, а 40 в виде произведения 2 * 2 * 2 * 5. При сравнении записей видно, что и в первой, и во второй стоит цифра пять. Поэтому в одной из них её нужно убрать, а оставшиеся члены перемножить: 3 * 2 * 2 * 2 * 5 = 120. Ответ идентичен.

Алгоритм вычитания

Следует отметить, что сложение и вычитание дробей выполняется по одинаковому алгоритму. Единственное отличие в арифметическом знаке действия. Если нужно из одного дробного выражения вычесть другое, рекомендуется придерживаться

• если в многочлене стоит смешанная дробь, то преобразовать её в неправильную;
• исследовать вычитаемое и уменьшаемое на возможность упрощения;
• найти наименьшее общее кратное среди знаменателей;
• вычислить дополнительные множители;
• домножить числители на найденные для них значения;
• записать в знаменатель НОЗ, а в числитель разницу произведений делимых;
• при возможности сократить дробь;
• привести ответ к виду смешанного числа в случае получения неправильной дроби.

Как можно заметить, алгоритм простой. Но может возникнуть вопрос по нахождению дополнительных множителей, несмотря на то что действие относят к простым операциям. После того как найден общий знаменатель, нужно делитель вычитаемого и уменьшаемого разделить на это число. Полученные значения и будут являться искомыми аргументами, предназначенными для домножения.

Кроме этого, необходимо обратить внимание на вычитание дробей разного типа. Чтобы правильно их вычесть, желательно вначале выполнить преобразование. Смешанное выражение можно довольно просто представить в виде неправильного числа. Для этого следует умножить целую часть на знаменатель и к полученному произведению добавить делимое. Затем результат сложения записать в числитель, а знаменатель оставить неизменным.

Существует и другой путь, обратный, то есть неправильную дробь превратить в смешанное число.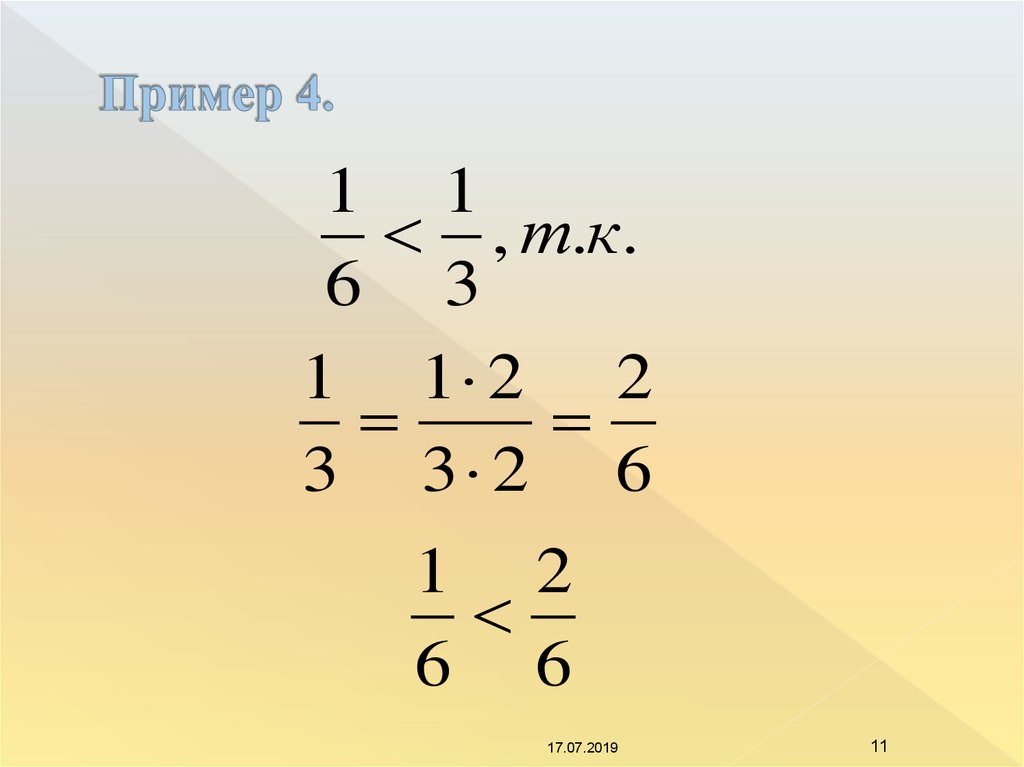 Для этого числитель нужно разделить на знаменатель. По результату операции остаток записывают в делимое, а делитель оставляют без изменения. Целую же часть прибавляют к дробной. После того как два числа будут смешанными, алгоритм вычитания немного изменяется. Так, целые части вычитают отдельно от дробных чисел, а затем результаты просто складывают.

Какой алгоритм использовать для того, чтобы отнять дроби друг от друга, не принципиально. Всё дело в привычке и навыках решающего.

Но, пожалуй, способ, заключающийся в переводе смешанного числа в неправильное выражение, проще. Другой же метод лучше использовать, когда надо вычесть из целого числа дробное или же наоборот.

Решение примеров

Чтобы научиться правильно вычитать дроби с разными знаменателями, нужно самостоятельно решить несколько задач. Обычно хватает проработать порядка пяти примеров, чтобы получить необходимый опыт. Вот некоторые наиболее интересные задания:

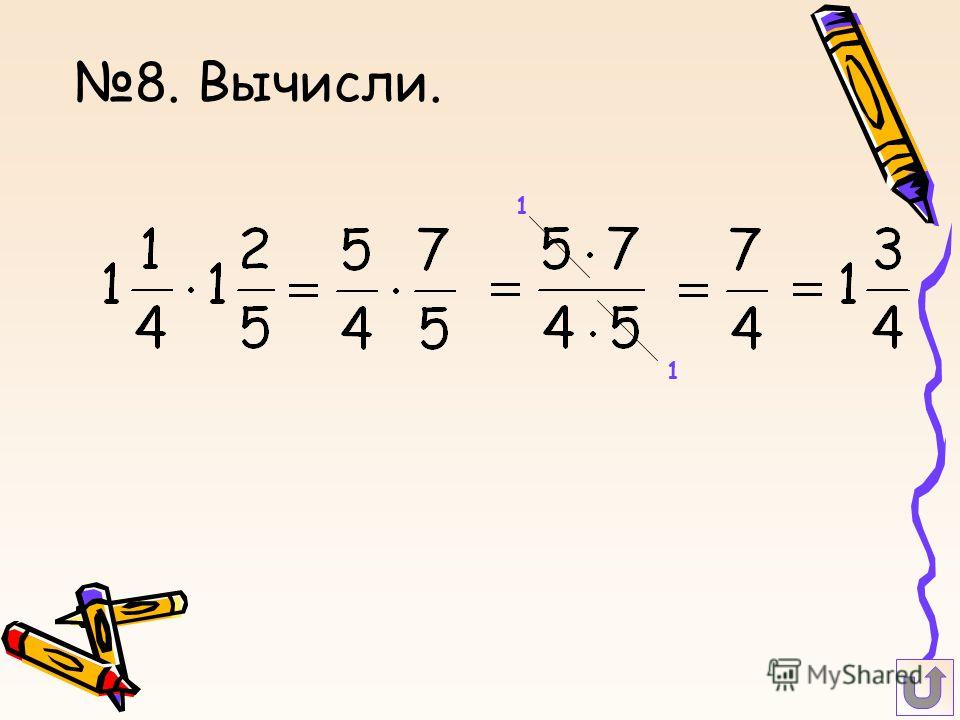
1. Вычислить разницу: (4 / 7) — (2 / 21). Придерживаясь алгоритма, вначале нужно найти общий знаменатель. Число в вычитаемом можно разделить на делитель уменьшаемого без остатка. Поэтому оно и будет искомым выражением. Далее, для первого члена дополнительным множителем будет 21: 7 = 3, а для второго 21: 21 = 1. Значит, решение примет следующий вид: (4 / 7) — (2 / 21) = ((3 * 4) — 2) / 21 = 10 / 21.
2. Определить результат действия: 4 (1 / 3) — 1 / 7. Перед началом выполнения вычитания нужно смешанную дробь привести к неправильному виду, а уже после действовать по алгоритму. Итак, 4 (1 / 3) = ((4 * 3) + 1) / 3 = 13 / 3. Отсюда (13 / 3) — 1 / 7 = ((7 * 13) — (3 * 1)) / 21 = (91 — 3) / 21 = 88 / 21. Полученный ответ нужно представить в виде смешанного выражения: 88 / 21 = (4 + 4 * 21) / 21 = 4 (4 / 21).
3. Сравнить два выражения по модулю: 4 / 5 — 12 / 4 — 4 (5 / 6) и 11 — 3 (1 / 3) + 8 / 7. Чтобы определить, какое из них больше, необходимо выполнить действия. Первый многочлен будет равен: 4 / 5 — 25 / 4 — 4 (5/6) = 4 / 5 — 12/ 4 — (4 * 6 + 5) / 6 = 4 / 5 — 25 / 4 — 29 / 6 = ((12*4) — (15 * 25) — (29 * 10)) / 60 = (48 — 375 — 290) / 60 = — 617 / 60 = -(17 + 10 * 60) / 60 = -10 (17 / 60). Второе выражение можно вычислить так: 11 — 3 (1 / 3) — 8 / 7 = 11 — 3 + 1 / 3 — 8 / 7 = 8 + 1 /3 — 8 / 7 = 8 + ((1*7) — (8 * 3)) / 21 = 8 + (7 — 24) / 21 = 8 — 17 / 21 = (8 / 1) — (17 / 21) = (168 — 17) / 21 = 151 / 21 = 74 / 21. Полученные ответы нужно сравнить без учёта знака. Поэтому можно утверждать, что первое выражение будет больше второго.

Таким образом, отнимать дроби с разными знаменателями не так уж и сложно. Нужно просто найти общий знаменатель, дополнительные множители и выполнить вычитание. При этом следует упомянуть так называемые онлайн-калькуляторы. Это веб-сервисы, которые в автоматическом режиме выполняют вычитание.

Их довольно удобно использовать не только для проверки самостоятельно решённых примеров, но и на стадии обучения.

Всё дело в том, что, кроме быстрого решения, эти сайты могут предоставить пользователям подробные решения того или иного примера.

Как из целого числа вычесть дробь?

Дробь — это числовая цифра, представляющая часть целого. Дробь состоит из двух частей: числителя и знаменателя. Здесь дробь делится на две части, верхняя часть дроби представляет собой числитель, а знаменатель — нижнюю часть дроби. Например, 5/8 — это дробь. В этом случае числитель равен 5, а знаменатель — 8. Натуральные числа — это набор счетных чисел, начинающихся с 1. С другой стороны, натуральные числа с нулем (0) образуют набор, известный как целые числа. Ноль, с другой стороны, является неопределенной идентичностью, которая представляет нулевой набор или вообще отсутствие результата. Целые числа — это в основном числа, которые не содержат дробей, десятичных знаков или даже отрицательных целых чисел. Целые числа — это множество положительных чисел и нулей. Альтернативно, целые числа представляют собой набор неотрицательных целых чисел. Набор целых чисел в математике задается как {0, 1, 2, 3, 4, 5, …}, что обозначается символом W.

W = {0, 1, 2, 3, 4, 5, 6, 7 …}

Как из целого числа вычесть дробь?

Решение: 

Чтобы вычесть дробь из целого числа. Мы должны выполнить несколько шагов,

• Шаг 1: Сделайте знаменатель 1, чтобы преобразовать целое число в дробь.
• Шаг 2: Сравните знаменатели и возьмите lcm, чтобы сделать их похожими на дроби.
• Шаг 3: В последнем вычтите числители дроби

Пример: научимся вычитать х – у/z,

Решение: фракция. Поэтому здесь выше преобразуйте x в дробь; мы можем записать это как x/1 в дроби.

Шаг 2: Сравните знаменатели и возьмите lcm, чтобы сделать их похожими на дроби. Теперь это x/1 – y/z, мы возьмем lcm знаменателей z и 1, lcm равно z, так что дроби будут = (xz – y)/z

Шаг 3: В последнем вычтите числители дроби, так что дробь будет

= (xz – y)/z

Примеры вопросов

Вопрос 5: Вычесть целое число от 3/4?

Решение: 

Выполните описанные выше шаги,

Шаг 1. Сделайте знаменатель равным 1, чтобы преобразовать целое число в дробь. Поэтому здесь выше целое число равно 5, мы можем записать его как 5/1 дробью.

Шаг 2: Сравните знаменатели и возьмите lcm, чтобы сделать их похожими на дроби. Теперь это 3/4 — 5/1, мы возьмем lcm знаменателей 4 и 1, lcm равно 4, поэтому дроби будут = (3 — 20) / 4

Шаг 3: В конце вычтите числители дроби

Сейчас = (3 – 20)/4

= -17/4

Вопрос 2: Вычесть 3/2 из 8?

Решение:  

Мы можем записать целое число 8 как 8/1 в дроби, а другое число у нас есть 3/2, теперь вычтем 3/2 из 8/1.

= 8/1 – 3/2 

Взяв lcm из 1 и 2, мы получим 2,

= {(8 × 2) – (3 × 1)}/2

= (16 – 3) /2

= 13/2

Вопрос 3: Вычесть 25 из 10/8?

Решение:  

Мы можем записать целое число 25 как 25/1 в дроби, а другое число у нас есть 10/8, теперь вычтем 25 из 10/8.

= 25/1 – 10/8

Взяв lcm из 1 и 8, мы получим 8,

= {(25 × 8) – (10 × 1)}/8

= (200 – 10)/8

= 190/8

= 95/4

Вопрос 4: Вычесть 1/5 из 4?

Решение:  

Мы можем записать целое число 4 как 4/1 в дроби, а другое число у нас есть 1/5, теперь вычтем 1/5 из 4/1.

= 4/1 – 1/5 

Взяв lcm из 5 и 1, мы получим 5,

= {(4 × 5) – (1 × 5)}/5

= (20 – 5) /5

= 15/5

= 3

Вопрос 5: Вычесть 100 из 10/8?

Решение:  

Мы можем записать целое число 100 как 100/1 в дроби, а другое число у нас есть 10/8, теперь вычтем 100 из 10/8.

= 10/8 – 100/1

Взяв lcm из 8 и 1, мы получим 8,

= {(10 × 1) – (100 × 8)}/8

= (10 – 800) /8

= -790/8

= -395/4

Вопрос 6: Вычесть 5/3 из 55?

Решение:  

Мы можем записать целое число 55 как 55/1 в дроби, а другое число у нас получится 5/3, теперь из 55/1 вычтем 5/3.

= 55/1 – 5/3

Взяв lcm из 1 и 3, мы получим 3,

= {(55 × 3) – (1 × 3)}/3

= (165 – 3) /3

= 162/3

= 54

Как вычитать дроби с разными знаменателями0005 Если вы хотите вычитать дроби с разными знаменателями, у вас есть выбор методов: простой способ, быстрый прием и традиционный способ.

Простой способ всегда работает, и вы должны использовать этот метод для большинства ваших потребностей в вычитании дробей. Быстрый трюк отлично экономит время, поэтому используйте его, когда можете. А что касается традиционного способа — ну, ваш учитель и другие сторонники чистоты математики, вероятно, предпочитают, чтобы вы использовали его таким образом.

Вычитание дробей простым методом

Этот способ вычитания дробей работает во всех случаях, и он прост. Вот простой способ вычитания дробей с разными знаменателями:

1. Перемножьте две дроби и вычтите второе число из первого, чтобы получить числитель ответа.

   Например, предположим, что вы хотите вычесть 6/7 – 2/5. Чтобы получить числитель, перемножьте две дроби, а затем вычтите второе число из первого числа:

   .

   (6 5) – (2 7) = 30 – 14 = 16

   После перекрестного умножения обязательно выполняйте вычитание в правильном порядке. (Первое число равно произведению числителя первой дроби на знаменатель второй.)

2. Умножьте два знаменателя, чтобы получить знаменатель ответа.

   7 5 = 35

3. Поставив числитель над знаменателем, вы получите ответ.

Вот еще один пример для работы:

Этот пример объединяет все шаги:

При такой постановке задачи вам просто нужно упростить результат:

В этом случае вы можете уменьшить дробь:

Вычитание дробей методом быстрого трюка

Простой способ лучше всего работает, когда числители и знаменатели малы. Когда они больше, вы можете срезать путь.

Прежде чем вычитать дроби с разными знаменателями, проверьте знаменатели, чтобы увидеть, кратен ли один из них другому. Если это так, вы можете использовать быстрый трюк:

1. Увеличьте члены дроби с меньшим знаменателем, чтобы она имела больший знаменатель.

   Например, предположим, что вы хотите найти 17/20 – 31/80. Если вы перемножите эти дроби, ваши результаты будут намного больше, чем вы хотите работать. Но, к счастью, 80 кратно 20, так что можно воспользоваться быстрым способом.

   Сначала увеличьте члены 17/20 так, чтобы знаменатель был равен 80:

   ? = 80 ÷ 20 17 = 68

2. Перепишите задачу, подставив эту увеличенную версию дроби, и вычтите.

   Вот задача на вычитание дробей с одинаковым знаменателем, которую решить гораздо проще:

   В этом случае не нужно приводить к самым низким условиям, хотя в других задачах, возможно, придется.

Вычитание дробей традиционным методом

Вы должны использовать традиционный способ только в крайнем случае, когда числитель и знаменатель слишком велики, чтобы использовать простой способ, и когда вы не можете использовать быстрый прием.

правила с разными и одинаковыми знаменателями, как происходит, примеры с решениями

Вычитание дробей является важной темой при изучении арифметических операций. Чтобы его выполнять, нужно понять и изучить несколько простых правил, которые изложены далее. Знания о вычитании дробей могут пригодиться не только на уроке математики, но и в повседневной жизни. Например, при расчете процента за кредит или при разделении объекта на несколько частей.

Особенности темы дробей в программе обучения

Вычитание – действие в арифметике, когда от одного числа (не обязательно большего) отнимают второе. Его на практике применяют очень часто, и не только в отношении дробей, но и простых цифр. Проводить подобную операцию учат еще в младших классах школы, постепенно совершенствуя навыки. Но с вычитанием дробей не все так просто. Мало просто понять одно число от другого. Нужно понять принципы этого процесса и выучить правила.

Дробь – термин, который обозначает количество, определяемое как доля от некоторого числа. Дробное число состоит из числителя и знаменателя. Его можно выразить несколькими способами: 1/2 = 2/4 = 3/6. Если оба умножить на одно и то же, то изменений не произойдет. Для этого может быть использован десятичный вид – 0,5 = 1/2.

В некоторых случаях для выражения потребуется десятичная форма с бесконечным количеством цифр после запятой.

Если необходимо вычитать дроби с разными знаменателями, вместо них используют эквивалентные, но с одинаковыми нижними показателями.

Как происходит вычитание

Эта операция обратна по отношению к сложению. Проще всего осуществлять вычитание обыкновенных дробей, нижние значения которых равны. Для решения подобных уравнений достаточно от первого числителя отнять второй. Можно рассмотреть это на примере:

7/15 — 3/15 = 4/15

Отнимая 3 из 7 получают числитель.

Если нижние части различаются, следует сделать так, чтобы свести вычисления к первому случаю. Для этого используют тот факт, что для каждой ситуации существуют эквивалентные варианты. Умножая верхнюю и нижнюю часть на одно и то же число, значение изменить нельзя. Вычитание дробей с разными знаменателями основано на правильном выполнении эквивалентных преобразований уменьшаемого и вычитаемого.

Воспользовавшись этим правилом, можно привести дробные числа к виду, когда нижние показатели у них равны. После этого осуществляют действие обычным образом. Сказанное можно лучше понять, решив простое задание – сколько будет из 2/3 вычесть 4/7?

Для того, чтобы привести их к эквивалентному виду, оба числа умножают одинаковым образом. Вот несколько возможных вариантов:

2/3 = 4/6 = 6/9 = 8/12 = 10/15= 12/18 = 14/21

Теперь проводят аналогичные действия со вторым операндом. Здесь получают:

4/7= 8/14 = 12/21

Сравнивая полученные показатели видно, что в обоих случаях есть величины с использованием 21. После эквивалентного преобразования ранее сформулированное задание получило следующую формулировку – сколько будет из 14/21 вычесть 12/21?

Чтобы получить числитель, надо от первого отнять второй: 14 — 12 = 2. Результат равен 2/21.

Можно решать такие уравнения и не обязательно искать эквивалентные значения до тех пор, пока не получиться наткнуться на подходящее. Нужный цифры получают перемножением.

Для решения предложено задание – сколько будет из 15/17 вычесть 5/7?

Нужный ответ получается при умножении 17 на 7. Он равен 119. Таким образом, выражение преобразуется:

15/17 — 5/7 = 15х7/17х7 — 5х17/7х17 = 105/119 — 85/119 = (105 — 85)/119 = 20/119

Если делается вычитание десятичных дробей, то действия происходят аналогичным способом. У них знаменатель равен 10, 100, 1000 или аналогичным значениям. Работа с ними будет рассмотрена в задании – чему равно 0,56 — 0,32?

Здесь речь идет о 56/100и 32/100. В этом случае выполняют вычитание величин, у которых одинаковая нижняя часть. Осуществляется это так:

0,56 — 0,32 = 56/100 — 32/100 = (56 — 32)/100 = 24/100 = 0,24

Иногда используется различное количество цифр после запятой.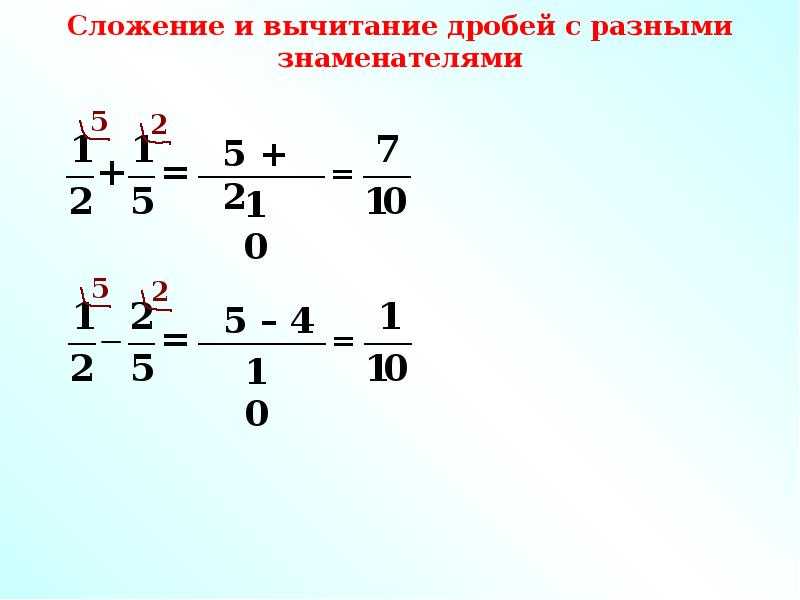 Вот пример – сколько будет из 0,71 вычесть 0,335 ?

Для начала надо преобразовать десятичные величины в обычные. При этом будет результат такой: 0,71 = 71/100, 0,335 = 335/1000. Здесь поступают в соответствии с правилами работы с величинами с различными знаменателями. Однако нужное значение определяется более легким способом. Если первый операнд умножить на 10, то будет использована 1000.

Теперь делают подсчеты так:

0,71 — 0,335 = 71х10/100х10 — 335/1000 = 710 — 335/1000 = 375/1000 = 0,375

С десятичными дробными величинами работают обычным способом. При этом ту, в которой меньше знаков после запятой, дополняют нужным количеством нулей, чтобы уравнять количество цифр после запятой. Операцию выполняют приведенным ранее способом.

В рассмотренном выше примере решение будет выглядеть та:

0,71 — 0,335 = 0,710 — 0,335 = 0,375

Если в результате подсчета требуется получить положительное значение, необходимо сделать так, чтобы уменьшаемое было больше вычитаемого. Это проверяют, приведя обе цифры к обычной форме. У уменьшаемого числитель должен быть больше.

При выполнении операций при наличии целого и дробного значения, их сначала преобразуют в неправильную дробь, затем поступают так, как указано выше. Чтобы их вычитать, нужно сначала привести к общему знаменателю. Затем от одного числителя отнимают второй.

Вычитание дробей – не слишком легкая и доступная тема в математике. Чтобы понять, как проводить подобные подсчеты, следует потренироваться сначала на более простых примерах и обязательно изучить правила. Тогда никаких проблем точно не возникнет. Случаются ли у вас проблемы при вычитании? С чем они были связаны? Напишите в комментариях. Поделитесь статьей в социальных сетях и сохраните ее в закладках, чтобы не потерять полезную информацию и основные правила.

Также рекомендуем посмотреть подобранные видео по нашей теме.

Вычитание дробей с разными знаменателями

Сложение и вычитание дробей с одинаковыми знаменателями.

Как вычитать дроби за 3 простых шага — Mashup Math

Бесплатное пошаговое руководство: Как вычитать дроби?

Знание того, как вычитать дроби, является важным и фундаментальным математическим навыком, который должен освоить каждый учащийся, поскольку он служит основой для понимания более сложных математических идей, с которыми вы можете столкнуться в будущем.

(Хотите узнать, как сложить дроби ? Нажмите здесь, чтобы получить доступ к нашему бесплатному руководству)

К счастью, вычитание дробей, независимо от того, совпадают ли знаменатели (похожие) или разные (непохожие), можно выполнить с помощью простой и несложный трехэтапный процесс.

Это бесплатное пошаговое руководство по вычитанию дробей проведет вас через процесс вычитания дробей с одинаковыми и разными знаменателями, включая подробные примеры для каждого сценария.

В этом пошаговом руководстве основное внимание уделяется обучению вас следующим математическим навыкам:

Прежде чем мы расскажем, как вычитать дроби, и поработаем с несколькими примерами, давайте кратко повторим некоторые ключевые характеристики и словарные термины, связанные с вычитанием. дроби.

Начнем!

Прежде чем вы научитесь вычитать дроби, важно знать два ключевых словарных термина (и разницу между ними):

Определение: Верхнее число дроби называется числителем . Например, дробь 5/6 имеет числитель 5.

Определение: Нижнее число дроби называется знаменателем . Например, дробь 5/6 имеет знаменатель 6.

Опять же, числитель — это верхнее число дроби, а знаменатель — нижнее число. Эти термины дополнительно проиллюстрированы на рисунке 01 ниже. Хотя эти два термина математической лексики просты, крайне важно, чтобы вы могли понимать и правильно определять числитель и знаменатель дробей, чтобы овладеть навыком вычитания дробей.

Рисунок 01: Вычитание дроби Ключевые термины: Числитель дроби — это верхнее число, а знаменатель — нижнее число.

Двигаясь дальше, вы готовы сделать следующий шаг к освоению вычитания дробей. Далее вам нужно будет уметь определять, когда задача вычитания дроби попадает в одну из следующих двух категорий:

Дроби с одинаковыми знаменателями имеют нижние числа, равные одному и тому же значению.

В качестве альтернативы дроби с разными знаменателями имеют нижние числа, которые делают , а не равными одному и тому же значению.

Оба примера (один с одинаковыми знаменателями и один с разными знаменателями) проиллюстрированы на Рисунок 02 ниже.

Рисунок 02: Как вычитать дроби? Первый шаг заключается в том, чтобы определить, имеют ли рассматриваемые дроби одинаковые знаменатели или разные знаменатели.

Эта концепция может показаться несложной, но важно освежить ваше понимание, поскольку вы должны уметь распознавать, имеют ли задача на вычитание дробей одинаковые или разные знаменатели, чтобы найти правильное решение.

Теперь, когда у вас есть важные базовые навыки, вы готовы решить несколько задач на вычитание дробей.

Шаг третий: Вычтите числители и найдите разницу. 03 ниже иллюстрирует, как вы пришли к такому выводу.

Рисунок 03: Как вычитать дроби с одинаковыми знаменателями: Вычтите числители и сохраните знаменатель.

Первый пример показывает, что вычитание дробей с одинаковыми знаменателями довольно просто.

Чтобы вычесть дроби с одинаковым знаменателем, вычтите числители и оставьте тот же знаменатель.

Теперь давайте перейдем к еще одному примеру вычитания дробей с одинаковыми знаменателями, прежде чем перейти к примерам вычитания дробей с разными знаменателями.

Пример № 2: 8/9 — 5/9

В следующем примере вы будете применять тот же трехэтапный метод, что и в примере № 1, следующим образом:

Шаг Один: Определите, одинаковы ли знаменатели (подобные) или разные (непохожие).

В этом примере дроби имеют одинаковые знаменатели. Они оба равны 9.

Шаг второй: Если в примере используются одинаковые знаменатели, переходите к третьему шагу. Если они отличаются знаменателями, найдите общий знаменатель.

Опять же, поскольку знаменатели одинаковы, вы можете перейти к третьему шагу.

Шаг третий: Вычтите числители и найдите разницу.

Чтобы выполнить эту задачу на вычитание дробей, вычтите числители следующим образом:

В этом случае правильный ответ — 3/9, но эту дробь можно упростить. Поскольку и 3, и 9 делятся на 3, 3/9 можно упростить до 1/3.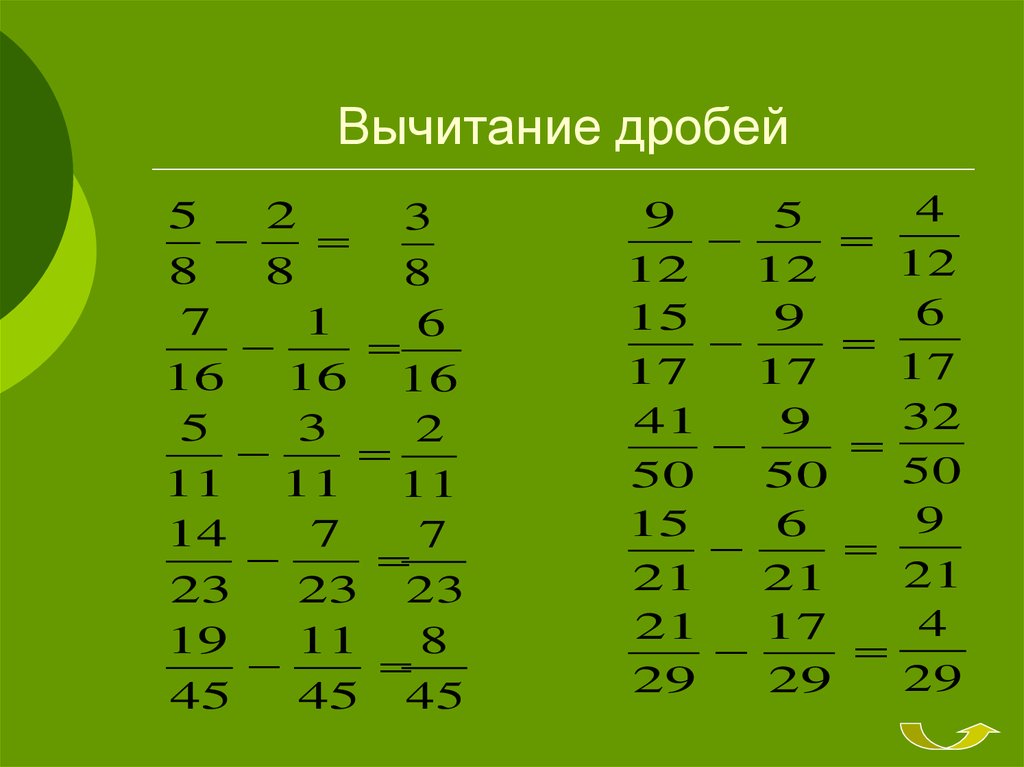

Окончательный ответ: 1/3

Рисунок 04 ниже иллюстрирует, как вы только что решили пример № 2.

Рисунок 04: Вычитание дробей: 3/9 можно упростить до 1/3

Теперь давайте перейдем к изучению того, как вычитать дроби с разными знаменателями.

Пример #1: 1/2 — 3/7

Шаг первый: Определите, одинаковы ли знаменатели (подобны) или различны ( В отличие от).

В этом примере дроби имеют разные знаменатели (они разные). Знаменатель первой дроби равен 2, а второй — 7.

Шаг второй: Если в примере используются одинаковые знаменатели, переходите к третьему шагу. Если они отличаются знаменателями, найдите общий знаменатель.

Так как дроби имеют разные знаменатели, вы не можете пропустить вперед.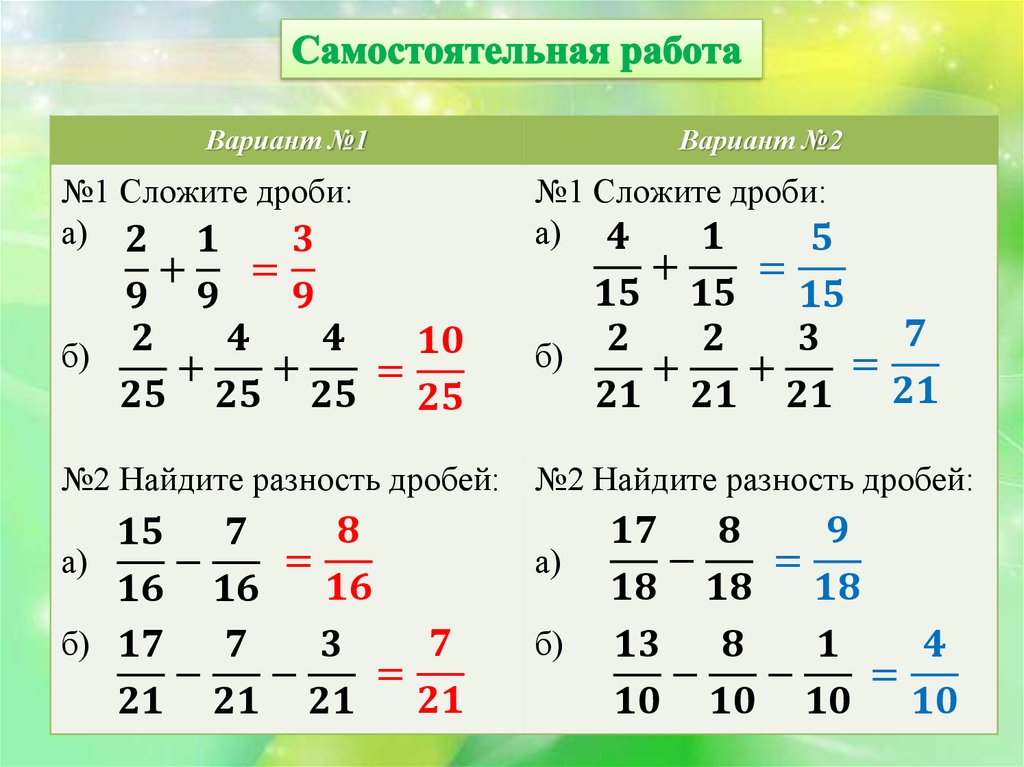

Прежде чем перейти к третьему шагу, вам нужно найти число, на которое оба знаменателя можно разделить без остатка. это называется общий знаменатель .

Очень простой и эффективный способ найти общий знаменатель между двумя дробями — перемножить знаменатели вместе (т. е. умножить знаменатель первой дроби на вторую дробь и умножить знаменатель второй дроби на первую дробь).

Этот процесс вычитания дроби показан на рис. 05 ниже.

Рис. 05: Как вычитать дроби с разными знаменателями: Найдите общий знаменатель, перемножив знаменатели вместе.

(Если вам нужна дополнительная помощь в умножении дробей, щелкните здесь, чтобы получить доступ к нашему бесплатному руководству для учащихся).

Теперь, когда второй шаг завершен, вы можете видеть, что исходный вопрос был преобразован, и теперь вы работаете с эквивалентными дробями, которые имеют общие знаменатели, а это означает, что тяжелая работа была проделана, и теперь вы можете решить задачу, вычитая числители и оставить тот же знаменатель:

Поскольку 1/14 не может быть уменьшено дальше, вы решили задачу…

Окончательный ответ: 1/14

Рисунок 06: Получив общие знаменатели, просто вычтите числители, чтобы сохранить тот же знаменатель.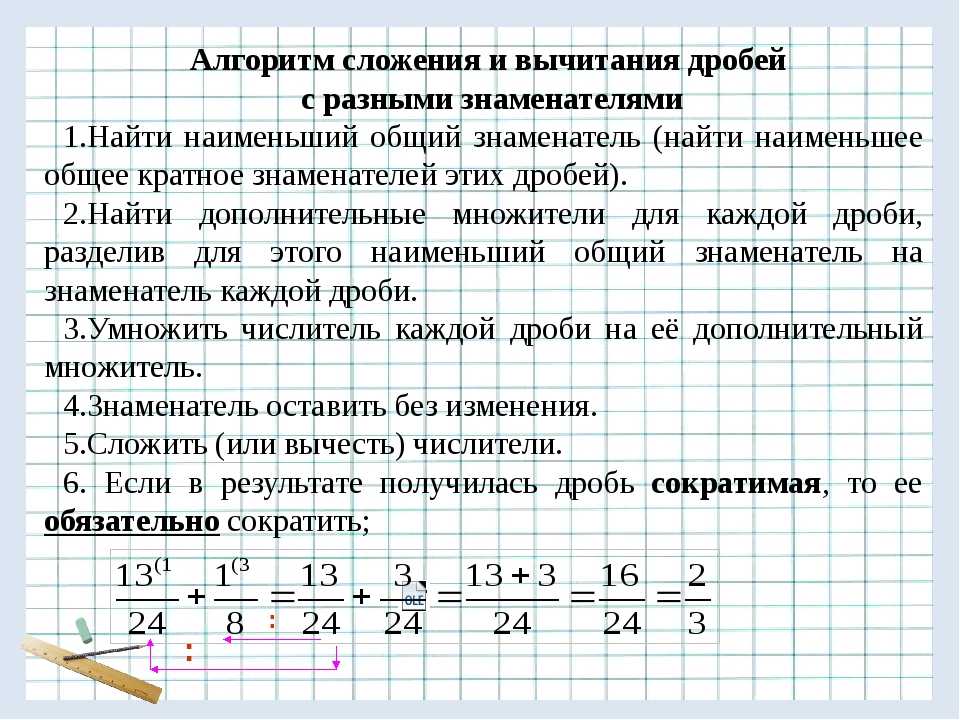

Готовы ли вы к еще одной практической задаче на вычитание дробей с разными знаменателями?

Пример № 1: 2/3 — 8/15

В этом последнем примере вычитания дробей вы снова будете использовать трехэтапный метод следующим образом:

Шаг первый: Определить одинаковы ли знаменатели (похожие) или разные (непохожие).

Дроби имеют разные знаменатели (одна 3, другая 5).

Второй шаг: Если в примере используются одинаковые знаменатели, перейдите к третьему шагу. Если они отличаются знаменателями, найдите общий знаменатель.

Как и в предыдущем примере, вам нужно будет найти общий знаменатель , так как дроби имеют разные знаменатели. Вы можете найти общий знаменатель, перемножив знаменатели следующим образом:

Этот процесс показан на Рисунок 07 ниже.

Рисунок 07: Как вычитать дроби с разными знаменателями

Теперь, когда дроби имеют общий знаменатель, вы можете решить задачу на вычитание дробей следующим образом:

Поскольку и 6, и 45 делятся на 3, вы можете упростить эту дробь как…

Окончательный ответ: 15/2

Рисунок 08: Вычитание дробей с разными знаменателями

Вычитание дробей с одинаковыми знаменателями требует простого нахождения разности числителей (верхние значения) без изменения знаменателя (нижнее значение).

Вычитание дробей с разными знаменателями требует, чтобы вы нашли общий знаменатель, то есть число, на которое оба знаменателя делятся поровну.

Как вычитать дроби? Вы можете решить любую задачу на вычитание дробей, применяя следующий трехэтапный метод:

• Шаг первый: Определите, одинаковы ли знаменатели (похожие) или разные (непохожие).

• Второй шаг: Если в примере используются одинаковые знаменатели, перейдите к третьему шагу. Если они отличаются знаменателями, найдите общий знаменатель.

• Шаг третий: Вычтите числители и найдите разницу.

Поиск Метки: как вычитать дроби, вычитание дробей, как вычитать дроби с разными знаменателями, вычитание дробей, вычитание дробей с разными знаменателями, как вычитать дроби?

Комментарий

Дроби: Сложение и вычитание дробей

Урок 3: Сложение и вычитание дробей

/en/fractions/comparing-and-reduction-fractions/content/

Сложение и вычитание дробей

На предыдущих уроках вы узнали, что дробь является частью целого. Дроби показывают, сколько у вас есть чего-то, например, 1/2 бака бензина или 1/3 стакана воды.

В реальной жизни вам может понадобиться складывать или вычитать дроби. Например, вы когда-нибудь проходили 1/2 мили на работу, а затем шли еще 1/2 мили обратно? Или слить 1/4 литра бензина из бензобака, в котором было 3/4 литра? Вы, наверное, не думали об этом в то время, но это примеры сложение и вычитание дробей.

Просмотрите слайд-шоу, чтобы узнать, как решать задачи на сложение и вычитание с дробями.

• Представим, что в рецепте торта сказано добавить в тесто 3/5 стакана масла.

• Вам также понадобится 1/5 стакана масла, чтобы смазать сковороду. Чтобы узнать, сколько всего масла вам понадобится, вы можете сложить вместе этих дробей.

• Когда вы складываете дроби, вы просто добавляете верхних чисел или числителей .

• Это потому, что нижних чисел или знаменателей показывают, сколько частей составит целое.

• Мы не хотим менять количество частей, составляющих целую чашку (5). Мы просто хотим выяснить, сколько частей нам нужно всего.

• Итак, нам нужно только сложить числители наших дробей.

• Мы можем сложить дробей так, чтобы числители выстроились. Это облегчит их добавление.

• И это все, что нам нужно сделать, чтобы настроить пример сложения с дробями. Теперь наши фракции готовы к добавлению.

• Мы сделаем то же самое, чтобы настроить пример вычитания. Допустим, у вас было 3/4 бака бензина, когда вы приступили к работе.

• Если вы используете 1/4 бака, чтобы добраться до дома, сколько у вас останется? Мы можем вычесть этих дробей, чтобы узнать.

• Точно так же, как при добавлении, мы будем сложите наших дробей, чтобы числители были выровнены.

• Это потому, что мы хотим вычесть 1 часть из 3 частей.

• Теперь, когда наш пример настроен, мы готовы к вычитанию!

Попробуйте!

Попробуйте решить эти задачи на сложение и вычитание с дробями. Не пытайтесь их решить!

Утром вы пробегаете 4/10 мили. Позже вы бежите 3/10 мили.

У вас было 7/8 пачки сливочного масла, и вы использовали 2/8 пачки во время приготовления обеда.

Ваш бензобак заполнен на 2/5, и вы заправляете еще 2/5 бака.

Решение задач на сложение с дробями

Теперь, когда мы знаем, как писать задачи на сложение с дробями, давайте попрактикуемся в решении некоторых из них. Если вы можете складывать целые числа, вы готовы складывать дроби.

Щелкните слайд-шоу, чтобы узнать, как складывать дроби.

• Продолжим наш предыдущий пример и добавим следующие части: 3/5 стакана масла и 1/5 стакана масла.

• Помните, что когда мы складываем дроби, мы не складываем знаменатели.

• Это потому, что мы находим, сколько всего частей нам нужно. Числители показывают, какие части нам нужны, поэтому мы добавим 3 и 1.

• 3 плюс 1 равно 4. Убедитесь, что 4 выровнены с числами, которые вы только что добавили.

• Знаменатели останутся прежними, поэтому мы напишем 5 внизу нашей новой дроби.

• 3/5 плюс 1/5 равно 4/5. Итак, вам понадобится 4/5 стакана масла всего , чтобы сделать свой торт.

• Возьмем другой пример: 7/10 плюс 2/10.

• Как и прежде, мы будем добавлять только числители. В этом примере числители 7 и 2.

• 7 плюс 2 равно 9, поэтому мы напишем это справа от числителей.

• Как и в нашем предыдущем примере, знаменатель остается прежним.

• Итак, 7/10 плюс 2/10 равно 9/10.

Попробуйте!

Попробуйте решить некоторые из приведенных ниже задач на сложение.

Решение задач на вычитание с дробями

Вычитание дробей очень похоже на обычное вычитание. Если вы можете вычитать целые числа, вы можете вычитать и дроби!

Просмотрите слайд-шоу, чтобы узнать, как вычитать дроби.

• Давайте воспользуемся нашим предыдущим примером и вычтем 1/4 бака бензина из 3/4 бака.

• Как и в дополнение, мы не собираемся менять знаменатели.

• Мы не хотим менять количество деталей, составляющих целый бак бензина. Мы просто хотим знать, сколько деталей у нас останется.

• Начнем с вычитания числителей. 3 минус 1 равно 2, поэтому мы напишем 2 справа от числителя.

• Как и при сложении, знаменатель нашего ответа будет таким же, как и другие знаменатели.

• Итак, 3/4 минус 1/4 равно 2/4. Когда вы вернетесь домой, у вас останется 2/4 бака бензина.

• Попробуем решить другую задачу: 5/6 минус 3/6.

• Начнем с вычитания числителей.

• 5 минус 3 равно 2. Итак, мы поставим 2 справа от числителя.

• Как обычно, знаменатель остается прежним.

• Итак, 5/6 минус 3/6 равно 2/6.

Попробуйте!

Попробуйте решить некоторые из приведенных ниже задач на вычитание.

После сложения или вычитания дробей иногда может получиться дробь, которую можно сократить до более простой дроби. Как вы узнали из раздела «Сравнение и сокращение дробей», всегда лучше сократить дробь до ее простейшей формы , когда это возможно. Например, 1/4 плюс 1/4 равно 2/4. Поскольку 2 и 4 можно разделить на 2, мы можем уменьшить 2/4 до 1/2.

Сложение дробей с разными знаменателями

На прошлой странице мы научились складывать дроби с одинаковым знаменателем, например 1/4 и 3/4. Но что, если вам нужно сложить дроби с различными знаменателями? Например, в нашем рецепте торта можно сказать, что нужно медленно смешать 1/4 стакана молока, а затем добавить еще 1/3 стакана.

В разделе «Сравнение и сокращение дробей» мы сравнили дробей с другим нижним числом или знаменателем. Нам пришлось изменить дроби, чтобы их знаменатели были одинаковыми. Для этого мы нашли наименьший общий знаменатель или LCD .

Мы можем складывать или вычитать дроби, только если они имеют одинаковые знаменатели. Поэтому нам нужно найти наименьший общий знаменатель, прежде чем складывать или вычитать эти дроби. Когда дроби имеют одинаковый знаменатель, мы можем складывать или вычитать, как обычно.

Просмотрите слайд-шоу, чтобы узнать, как складывать дроби с разными знаменателями.

• Добавим 1/4 и 1/3.

• Прежде чем мы сможем сложить эти дроби, нам нужно изменить их, чтобы они имели одинаковые знаменатель .

• Для этого нам нужно найти LCD , или наименьший общий знаменатель чисел 4 и 3. и 4, так что 12 это наш LCD .

• Поскольку 12 — это LCD, это будет новый знаменатель наших дробей.

• Теперь изменим числители дробей так же, как мы изменили знаменатели.

• Во-первых, давайте посмотрим на дробь слева: 1/4.

• Чтобы преобразовать 4 в 12, мы умножаем его на 3.

• Поскольку знаменатель был умножен на 3, мы также умножим числитель на 3.

• 1/4 равно 3/12.

• Теперь посмотрим на дробь справа: 1/3. Мы также изменили его знаменатель на 12.

• Наш старый знаменатель был 3. Мы умножили его на 4, чтобы получить 12.

• Мы также умножим числитель на 4. 1 умножить на 4 равно 4.

• Итак, 1/3 равно 4/12.

• Теперь, когда наши дроби имеют одинаковый знаменатель, мы можем сложить их, как обычно.

• 3 плюс 4 равно 7. Как обычно, знаменатель остается прежним. Таким образом, 3/12 плюс 4/12 равно 7/12.

Попробуйте!

Попробуйте решить приведенные ниже задачи на сложение.

Вычитание дробей с разными знаменателями

Мы только что видели, что дроби можно складывать, только если у них один и тот же знаменатель. То же самое верно, когда мы вычитаем дроби. Прежде чем мы сможем вычитать, нам нужно изменить наши дроби, чтобы у них был один и тот же знаменатель.

Просмотрите слайд-шоу, чтобы узнать, как вычитать дроби с разными знаменателями.

• Попробуем вычесть 1/3 из 3/5.

• Во-первых, мы изменим знаменатели обеих дробей, чтобы они были одинаковыми, найдя наименьший общий знаменатель .

• Похоже, 15 — это наименьшее число, которое можно разделить без остатка на 3 и 5, поэтому 15 — это наш ЖК-дисплей.

• Теперь изменим нашу первую дробь. Чтобы изменить знаменатель на 15, мы умножим знаменатель и числитель на 3.

• 5 умножить на 3 равно 15. Итак, наша дробь теперь равна 9/15.

• Теперь изменим вторую дробь. Чтобы изменить знаменатель на 15, мы умножим оба числа на 5, чтобы получить 5/15.

• Теперь, когда наши дроби имеют одинаковый знаменатель, мы можем вычитать, как обычно.

• 9 минус 5 равно 4. Как всегда, знаменатель остается прежним. Итак, 9/15 минус 5/15 равно 4/15.

Попробуйте!

Попробуйте решить приведенные ниже задачи на вычитание.

Сложение и вычитание смешанных чисел

На последних нескольких страницах вы практиковались в сложении и вычитании различных дробей. Но для некоторых проблем потребуется один дополнительный шаг. Например, можете ли вы сложить приведенные ниже дроби?

В разделе «Введение в дроби» вы узнали о смешанных числах . Смешанное число имеет как дробь , так и целое число . Например, 2 1/2, или два с половиной . Другой способ записать это будет 5/2, или пять половин . Эти два числа выглядят по-разному, но на самом деле они одинаковы.

5/2 — это неправильная дробь . Это просто означает, что верхнее число на больше, чем нижнее число на . Несмотря на то, что неправильные дроби выглядят странно, их можно складывать и вычитать так же, как обычные дроби. Смешанные числа складывать непросто, поэтому сначала вам придется преобразовать их в неправильные дроби.

• Сложим эти два смешанных числа: 2 3/5 и 1 3/5.

• Нам нужно преобразовать этих смешанных чисел в неправильные дроби. Начнем с 2 3/5.

• Как вы узнали из Урока 2, мы умножаем целое число 2 на нижнее число 5.

• 2 умножить на 5 равно 10.

• Теперь добавим 10 к числителю. , 3.

• 10 + 3 равно 13.

• Точно так же, как если вы сложите дробей, знаменатель останется прежним. Наша неправильная дробь 13/5.

• Теперь нам нужно преобразовать наше второе смешанное число: 1 3/5.

• Сначала умножим целое число на знаменатель.