Калькулятор онлайн — Сокращение дробей

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Обыкновенные дроби. Деление с остатком

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления. В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело.

Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.

Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление. Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а знаменатель п — делитель:

\( m:n = \frac{m}{n} \)

Верны следующие правила:

Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:

\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.

Два последних преобразования называют сокращением дроби.

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.

Правильные и неправильные дроби. Смешанные числа

Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют

неправильными дробями. Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями.

Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.

Если число состоит из целой части и дроби, то такие дроби называются смешанными.

Например:

\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.

Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)

Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её знаменатель умножить на это число:
\( \large \frac{a}{b} : n = \frac{a}{bn} \)

Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.

Действия с дробями. Сложение дробей.

С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \). Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.

Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)

Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.

Сложение смешанных дробей

Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями

. При этом число 2 называют целой частью смешанной дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».

При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)

Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть.

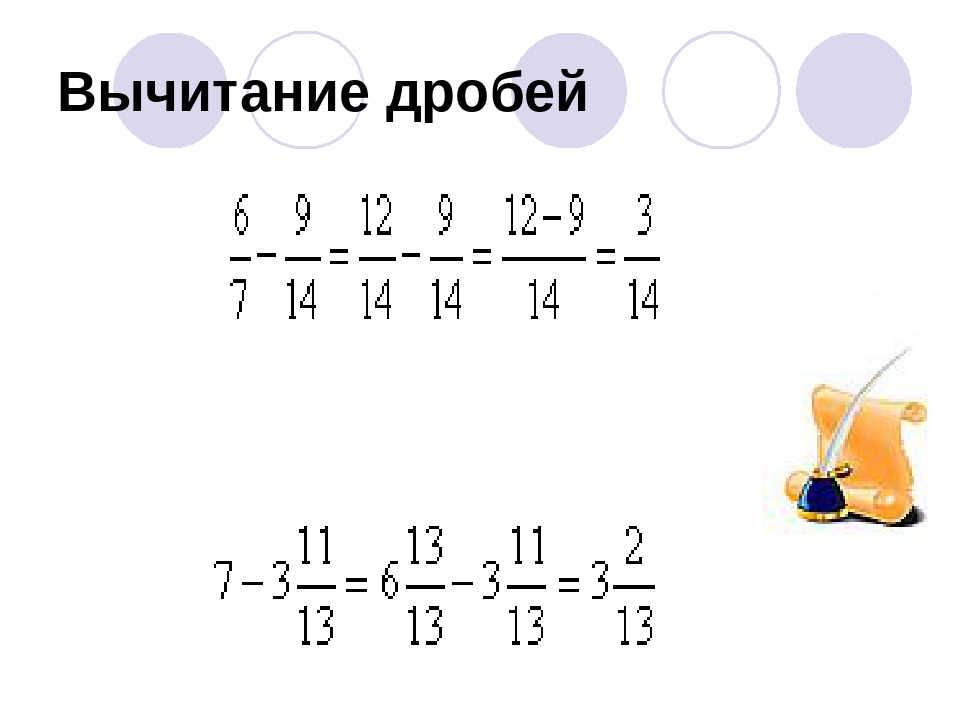
Вычитание дробей (дробных чисел)

Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит найти такое число, которое при сложении со вторым дает первое. Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)

Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель оставить прежним.

С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)

Умножение дробей

Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.

С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)

Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.

Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.

Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.

Деление дробей

Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \). Эту дробь называют обратной дроби \( \frac{2}{3} \).

Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как \( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.

Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).

С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)

Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)

Используя взаимно обратные дроби, можно деление дробей свести к умножению.

Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.

Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)

Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.

Преобразование числа в дробь, дроби из одного вида в другой. Десятичное число, смешанная, неправильная, периодическая дробь

Тестирование онлайн

• Преобразование дробей

Преобразование десятичного числа в дробь

Десятичные числа, такие как 0,2; 1,05; 3,017 и т.п. как слышатся, так и пишутся. Ноль целых две десятых, получаем дробь . Одна целая пять сотых, получаем дробь . Три целых семнадцать тысячных, получаем дробь . Цифры до запятой в десятичном числе — это целая часть дроби. Цифра после запятой — числитель будущей дроби. Если после запятой однозначное число — в знаменателе будет 10, если двухзначное — 100, трехзначное — 1000 и т. д. Некоторые полученные дроби можно сократить. В наших примерах

Преобразование дроби в десятичное число

Это обратное предыдущему преобразованию. Десятичная дробь чем характерна? У неё в знаменателе всегда стоит 10, или 100, или 1000, или 10000 и так далее. Если ваша обычная дробь имеет такой знаменатель, проблем нет. Например, или

Если дробь, например . В этом случае необходимо воспользоваться основным свойством дроби и преобразовать знаменатель до 10 или 100, или 1000 … В нашем примере, если домножить числитель и знаменатель на 4, получим дробь , которую возможно записать в виде десятичного числа 0,12.

Некоторые дроби проще разделить, чем преобразовать знаменатель. Например,

Некоторые дроби невозможно преобразовать в десятичные числа!
Например,

Преобразование смешанной дроби в неправильную

Смешанную дробь, например , легко преобразовать в неправильную. Для этого необходимо целую часть умножить на знаменатель (низ) и сложить с числителем (верх), знаменатель (низ) оставить без изменения. То есть

При преобразовании смешанной дроби в неправильную, можно вспомнить, что Можно использовать сложение дробей

Преобразование неправильной дроби в смешанную (выделение целой части)

Неправильную дробь можно перевести в смешанную, выделив целую часть. Рассмотрим пример, . Определяем, сколько целых раз «3» вмещается в «23». Или 23 делим на 3 на калькуляторе, целое число до запятой — искомое. Это «7». Далее определяем числитель уже будущей дроби: полученную «7» умножаем на знаменатель «3» и из числителя «23» вычитаем полученное. Как бы находим то лишнее, что остается от числителя «23», если изъять максимальное количество «3». Знаменатель оставляем без изменения. Все сделано, записываем результат

Из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и сделать эту разность числителем; в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после девяток дописать столько нулей, сколько цифр между запятой и первым периодом.

Сложение и вычитание отрицательных дробей.

Отрицательные дроби складываются и вычитаются также как и отрицательные числа, только по правилам сложения дробей. Мы можете добавлять только половинки к половинкам, четверти к четвертям или десятые к десятым и так далее. Вычитание отрицательных дробей следует тем же правилам. Для того чтобы сложить или вычесть две дроби нам нужно привести их к общему знаменателю. Если дробь отрицательная мы можем знак минус поставить в числитель и наоборот. Ниже расписано сложение \(-\frac{7}{6}+\frac{5}{7}\):

При сложении двух отрицательных дробей результат будет отрицательным. Когда мы вычитаем две отрицательные дроби, то мы к первой отрицательной дроби прибавляем положительную вторую, так как минус на минус дает плюс.

 

 

Рассмотрим сложение и вычитание следующих отрицательных дробей.

Задача 1. Вычислите \(\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2}).\).

Решение. Приводим к наименьшему общему знаменателю:

\(\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2})=\frac{5-3*2+10}{20}=\frac{9}{20}\)

Ответ: \(\frac{9}{20}\).

Задача 2. Вычислите \(\frac{1}{7}-(-\frac{5}{6})-(-\frac{1}{3})\).

Решение. Приводим к наименьшему общему знаменателю:

\(\frac{6-35+14}{42}=-\frac{15}{42}=-\frac{5}{14}\)

Ответ: \(-\frac{5}{14}\).

Задача 3. Вычислите \(\frac{1}{4}+\frac{5}{3}-(-\frac{1}{12})\).

Решение. Приводим к наименьшему общему знаменателю:

\(\frac{3+20+1}{12}=\frac{24}{12}=2.\)

Ответ: \(2.\).

Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.

 

 

 

 

 

 

 

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

01Math — онлайн учебник по математике.

Для того, чтобы найти сумму  \(\displaystyle 0,(3)+1,4,\) сперва распишем периодическую дробь:

\(\displaystyle 0,(3)=0,3333\ldots\)

 

Далее произведем сложение десятичных дробей, записывая одну дробь под другой так, чтобы одинаковые разряды располагались друг под другом, и запятая была под запятой:

\(\displaystyle +\)	\(\displaystyle 0\)	\(\displaystyle ,\)	\(\displaystyle 3\)	\(\displaystyle 3\)	\(\displaystyle 3\)	\(\displaystyle 3\)	\(\displaystyle \ldots\)
	\(\displaystyle 1\)	\(\displaystyle ,\)	\(\displaystyle 4\)
	\(\displaystyle ?\)	\(\displaystyle ,\)	\(\displaystyle ?\)	\(\displaystyle ?\)	\(\displaystyle ?\)	\(\displaystyle ?\)	\(\displaystyle ?\)

 

Вначале сносим все цифры, стоящие над пустыми ячейками:

\(\displaystyle +\)	\(\displaystyle 0\)	\(\displaystyle ,\)	\(\displaystyle 3\)	\(\displaystyle \color{red}{3}\)	\(\displaystyle \color{red}{3}\)	\(\displaystyle \color{red}{3}\)	\(\displaystyle \ldots\)
	\(\displaystyle 1\)	\(\displaystyle ,\)	\(\displaystyle 4\)
	\(\displaystyle ?\)	\(\displaystyle ,\)	\(\displaystyle ?\)	\(\displaystyle \color{red}{3}\)	\(\displaystyle \color{red}{3}\)	\(\displaystyle \color{red}{3}\)	\(\displaystyle \ldots\)

 

Далее складываем обычные десятичные дроби:

\(\displaystyle +\)	\(\displaystyle \color{blue}{0}\)	\(\displaystyle ,\)	\(\displaystyle \color{blue}{3}\)	\(\displaystyle 3\)	\(\displaystyle 3\)	\(\displaystyle 3\)	\(\displaystyle \ldots\)
	\(\displaystyle \color{blue}{1}\)	\(\displaystyle ,\)	\(\displaystyle \color{blue}{4}\)
	\(\displaystyle \color{blue}{1}\)	\(\displaystyle ,\)	\(\displaystyle \color{blue}{7}\)	\(\displaystyle 3\)	\(\displaystyle 3\)	\(\displaystyle 3\)	\(\displaystyle \ldots\)

 

Таким образом,

\(\displaystyle 0,(3)+1,4=1,7333\ldots\)

и

\(\displaystyle 1,7333\ldots=1,7(3). \)

Ответ: \(\displaystyle 1,7(3).\)

Вычитание алгебраических дробей | Алгебра

Рассмотрим вычитание алгебраических (рациональных) дробей в теории и на практике.

Чтобы вычесть алгебраические дроби, нужно:

1) Найти наименьший общий знаменатель этих дробей.

2) Найти дополнительный множитель к каждой дроби.

3) Дополнительный множитель  умножить на числитель и знаменатель.

4) Выполнить вычитание дробей с одинаковыми знаменателями (при вычитании дробей с одинаковыми знаменателями числители вычитают, а знаменатель оставляют тем же).

Примеры вычитания алгебраических дробей.

   

Наименьший общий знаменатель для чисел равен 18. Из степеней в общий знаменатель включаем каждый множитель, взяв его с наибольшим показателем. Таким образом, наименьший общий знаменатель данных дробей равен 18m²n².

Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый.

18m²n²:( 9mn²)=2m, 18m²n²:( 6mn²)=3m.

   

   

   

   

   

В знаменателях дробей стоят многочлены. Раскладываем их на множители. Для этого выносим за скобки общий множитель: в первом знаменателе — y, во втором — 5:

   

Наименьший общий знаменатель состоит из всех множителей и равен 5y(5x-y). Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый:

5y(5x-y):(y(5x-y))=5, 5y(5x-y):(5(5x-y))=y,

то есть, дополнительный множитель к первой дроби равен 5, ко второй — y. Затем умножаем числитель и знаменатель каждой дроби на дополнительный множитель.

Числитель раскладываем по формуле разности квадратов, после чего сокращаем дробь на (5x-y):

   

   

Многочлены, стоящие в знаменателях, раскладываем на множители по формулам сокращенного умножения. В знаменателе первой дроби — квадрат разности, в знаменателе второй дроби — разность квадратов:

   

Выражения (x-2) и (2-x), стоящие в знаменателях, отличаются только знаками. Изменим знаменатель второй дроби.

(2-x)= -(x-2). «Минус» вынесем перед дробью, соответственно, знак изменится на «+»:

   

Наименьший общий знаменатель состоит из всех входящих в знаменатели множителей, взятых в наибольшей степени. Он равен (x-2)²(2+x). Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем дроби с одинаковыми знаменателями.

   

   

В знаменателе второй дроби — формула разности кубов:

   

Приводим дроби к общему знаменателю и упрощаем:

   

   

Выносим из знаменателя «минус» и сокращаем дробь на (1+x+x):

   

В алгебре складывать и вычитать дроби с разными знаменателями сложнее, чем их умножать и делить (при умножении и делении дроби не нужно приводить к общему знаменателю).

Умножение и деление алгебраических (рациональных) дробей — следующие темы для изучения.

Дроби и рациональные числа (ЕГЭ — 2021)

В данном случае от целого куска в сторонке отделенная одна доля, одна из четырех, одна четвертая.

Это простая дробь.

Простые дроби принято записывать одним из следующих способов: \(\displaystyle \frac{1}{4}\), \(\displaystyle {1}/{4}\;.\)

Ты не поверишь, все эти записи означают одно и то же – одна четвертая. А что останется если забрать эту \(\displaystyle 1/4?\) Было \(\displaystyle 4\) из \(\displaystyle 4\), или \(\displaystyle 4/4\), забрали \(\displaystyle 1/4\).

Верно, останется \(\displaystyle 3\) дольки, \(\displaystyle 3\) из \(\displaystyle 4\). Запишем, как полагается, \(\displaystyle 3/4\).

Можно даже вот так: \(\displaystyle 4/4-1/4=3/4\)

То, что находится выше черты – это числитель (ну или слева от черты в такой записи как тут), то, что ниже – знаменатель.

Можно запомнить так: Ч – чердак. Числитель сверху 🙂

Примеры простых дробей: \(\displaystyle 1/5,\text{ }2/4,\text{ }3/10,\text{ }17/3.\)

В этом ряду все дроби правильные, в них числитель меньше знаменателя. Кроме одной. Да-да, ты не ошибся, бывает и такое, что числитель больше знаменателя, как в этой дроби, например: \(\displaystyle 17/3\).

Если числитель больше знаменателя, то дробь называется неправильной.

Вне зависимости от того правильная дробь или неправильная, она будет простой.

Давай остановимся на неправильной дроби \(\displaystyle 17/3\). Что же это она неправильная?

Вспоминай пример с пирогом, там была \(\displaystyle 1/4\) – одна часть из четырех, а тут что получается? \(\displaystyle 17\) частей из \(\displaystyle 3\)?

Бред какой-то! У нас в знаменателе число, которое означает, что весь пирог состоит из стольки частей! Берем \(\displaystyle 4\) части и поучаем целый ровненький пирог. Но числитель говорит, что на данный момент у нас есть лишь одна из этих частей.

А \(\displaystyle 17/3\)?

Что же, у нас есть \(\displaystyle 17\) частей, а для целого пирога в данном случае надо \(\displaystyle 3\) части. Ну так давай соберем из кусочков целые пироги и отдельно их поставим.

Как узнать сколько пирогов мы можем получить из \(\displaystyle 17\) частей? Верно, надо на \(\displaystyle 3\) как раз и поделить.

Если попробовать составить \(\displaystyle 6\) пирогов, т.е. \(\displaystyle 3\cdot 6=18\), надо \(\displaystyle 18\) частей. Не хватает. А \(\displaystyle 3\cdot 5=15\), о, хватило! Получается \(\displaystyle 5\) целых пирогов собрали, положили в сторону. Осталось \(\displaystyle 17-3\cdot 5=2,2\), \( \displaystyle  2\) куска.

А для целого пирога надо \( \displaystyle  3\) части. В итоге у нас \( \displaystyle  5\) целых и \( \displaystyle  2/3\) (две третьих) пирога.

Много места занимает такое обозначение. А что если убрать лишние слова и оставить только \( \displaystyle  5\frac{2}{3}\) (пять целых и две третьих).

То, что у нас получилось (\( \displaystyle  5\frac{2}{3}\)),называют смешанная дробь – дробь, записанная в виде целого числа и правильной дроби и понимается как сумма этого числа и дроби.

То, что между \( \displaystyle  5\) пирогами и \( \displaystyle  2/3\) пирога нет никакого знака не говорит о том, что там знак умножения, как если бы мы писали \( \displaystyle  2x\)!!! Запомни, между целой и дробной частями можно поставить знак плюс, вот так: \( \displaystyle  5\frac{2}{3}=5+\frac{2}{3}\).

Так же можно проделать и обратное действие, т.е. преобразование из смешанной дроби в неправильную дробь. Ты же знаешь, как это сделать? Конечно, нужно умножить знаменатель дроби (в случае с , \(\displaystyle5\frac{2}{3}\) знаменатель равен \( \displaystyle  3\)), умножить знаменатель…, верно, на \(\displaystyle5\) и прибавить нецелую часть, а именно – \( \displaystyle  2\) . В результате получим исходное \( \displaystyle  17/3\).

Преобразуй следующие неправильные дроби:

Действия с дробями

Условимся считать, что под «действиями с дробями» на нашем уроке будут пониматься действия с обыкновенными дробями. Обыкновенная дробь — это дробь, обладающая такими атрибутами, как числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается из обыкновенной путём приведения знаменателя к числу, кратному 10. Десятичная дробь записывается с запятой, отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби особых затруднений не вызывают. Итак, вперёд!

Две дроби и называются равными, если .

Например, , так как

Равными также являются дроби и (так как ), и (так как ).

Очевидно, равными являются и дроби и . Это означает, что если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной: .

Это свойство называется основным свойством дроби.

Основное свойство дроби можно использовать для перемены знаков у числителя и знаменателя дроби. Если числитель и знаменатель дроби умножить на -1, то получим . Это означает, что значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:

;

.

Пользуясь основным свойством дроби, можно заменить данную дробь другой дробью, равной данной, но с меньшим числителем и знаменателем. Такую замену называют сокращением дроби.

Пусть, например, дана дробь . Числа 36 и 48 имеют наибольший общий делитель 12. Тогда

.

В общем случае сокращение дроби возможно всегда, если числитель и знаменатель не являются взаимно простыми числами. Если числитель и знаменатель — взаимно простые числа, то дробь называется несократимой.

На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.

Итак, сократить дробь — это значит разделить числитель и знаменатель дроби на общий множитель. Всё вышесказанное применимо и к дробным выражениям, содержащим переменные.

Пример 1. Сократить дробь

.

Решение. Для разложения числителя на множители, представив предварительно одночлен — 5xy в виде суммы — 2xy — 3xy, получим

Для разложения знаменателя на множители используем формулу разности квадратов:

.

В результате

.

Далее, изменяя знаки в числителе и знаменателе дроби, получим

Пусть даны две дроби и . Они имеют разные знаменатели: 5 и 7. Пользуясь основным свойством дроби, можно заменить эти дроби другими, равными им, причём такими, что у полученных дробей будут одинаковые знаменатели. Умножив числитель и знаменатель дроби на 7, получим

.

Умножив числитель и знаменатель дроби на 5, получим

.

Итак, дроби приведены к общему знаменателю:

.

Но это не единственное решение поставленной задачи: например, данные дроби можно привести также к общему знаменателю 70:

,

и вообще к любому знаменателю, делящемуся одновременно на 5 и 7.

Рассмотрим ещё один пример: приведём к общему знаменателю дроби и . Рассуждая, как в предыдущем примере, получим

,

.

Но в данном случае можно привести дроби к общему знаменателю, меньшему, чем произведение знаменателей этих дробей. Найдём наименьшее общее кратное чисел 24 и 30: НОК(24, 30) = 120.

Так как 120:4=5, то чтобы записать дробь со знаменателем 120, надо и числитель, и знаменатель умножить на 5, это число называется дополнительным множителем. Значит .

Далее, получаем 120:30=4. Умножив числитель и знаменатель дроби на дополнительный множитель 4, получим .

Итак, данные дроби приведены к общему знаменателю.

Наименьшее общее кратное знаменателей этих дробей является наименьшим возможным общим знаменателем.

На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.

Для дробных выражений, в которые входят переменные, общим знаменателем является многочлен, который делится на знаменатель каждой дроби.

Сложение дробей определяется следующим образом:

.

Например,

.

Если b = d, то

.

Это значит, что для сложения дробей с одинаковым знаменателем достаточно сложить числители, а знаменатель оставить прежним. Например,

.

Если же складываются дроби с разными знаменателями, то обычно приводят дроби к наименьшему общему знаменателю, а потом складывают числители. Например,

.

На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.

Теперь рассмотрим пример сложения дробных выражений с переменными.

Пример 3. Преобразовать в одну дробь выражение

.

Решение. Найдём наименьший общий знаменатель. Для этого сначала разложим знаменатели на множители:

1) ;

2) ;

3) .

Наименьший общий знаменатель:

Дополнительные множители, на которые умножаются числители дробей:

1) 6;

2) ;

3) .

Результат этого умножения:

.

Далее, раскрывая скобки и выполняя тождественные преобразования, получаем

.

Произведение двух дробей и равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей, т. е. .

Например,

.

При делении дроби на дробь числитель делимого умножается на знаменатель делителя, а знаменатель делимого — на числитель делителя, т. е. .

Например,

.

1. Произведение крайних членов пропорции равно произведению её средних членов, т. е. если , то .

2. Из пропорции вытекают следующие пропорции: , , , то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.

3. Чтобы найти неизвестный средний (крайний) член пропорции, нужно произведение крайних (средних) членов пропорции разделить на известный средний (крайний) член пропорции: и .

В высшей математике это действие с дробями чаще всего применяется при интегрировании рациональных функций. Поэтому оно подробно разобрано в уроке Интегрирование рациональных функций и метод неопределённых коэффициентов.

Другие темы в блоке «Школьная математика»

Вычитание дробей — методы и примеры

Как вычитать дроби?

Как и при сложении дробей, при вычитании дробей с общим знаменателем числители вычитаются, а знаменатель остается.

Аналогичным образом, в случае дробей, имеющих разные знаменатели, сначала следует получить наименьшее общее кратное (НОК), а затем преобразовать дроби в эквивалентные дроби с НОК в качестве знаменателя. Но эти условия применимы только в том случае, если дроби не являются смешанными числами.

Пример 1

а. Решить: 2/5 — 1/4

Решение
Во-первых, сделайте знаменатели одинаковыми.

Умножьте числитель и знаменатель 2/5 и 1/4 на 4 и 5 соответственно.

2/5 × 4/4 = 8/20

1/4 x 5/5 = 5/20

Теперь выполните вычитания:

8/20 — 5/20 = 3/20

b. Вычтем 3/8 из 7/8

Решение
7/8 — 3/8
= (7 — 3) / 8

= 1/2

c. Вычтем 5/6 из 11/6

Решение
11/6 — 5/6
= (11-5) / 6
= 6/6
= 1/1
= 1

г. Вычтем 7/9 из 9/11

Решение
9/9 — 7/9
= (11-7) / 9
= 4/9

e. Вычтем 4/6 из 16/6

Решение
16/6 — 4/6
= (16-4) / 6

= 2/1

= 2

f. 1 — 2/3

Решение

• Мы начинаем с предположения, что целое число совпадает с числом над одним i.е. 1 равно 1/1

Таким образом, наше уравнение будет выглядеть так:

1 / 1-2 / 3

• Затем мы продолжаем получать L.C.M. двух знаменателей, которые будут равны 3, поскольку L.C.M. числа, и один становится этим числом.
• Затем мы делим этот L.C.M. на первый знаменатель, который равен 1, чтобы получить ответ 3, затем умножьте 1 на первый числитель, который равен 1, чтобы получить = 3
• Затем мы разделим L.C.M. на второй знаменатель, равный 3, чтобы получить ответ 1, затем умножьте 1 на второй числитель, который равен 2, чтобы получить = 2
• Затем вычтем два результата над L. СМ.

= 1 / 1-2 / 3

= (3-2) / 3

= 1/3

Как вычесть смешанные числа?

Смешанные дроби можно вычитать так же, как и правильные дроби. Правила вычитания смешанных фракций такие же, как и для правильных фракций. Есть два метода вычитания смешанных дробей.

Метод 1:

Ниже приведены шаги, предпринимаемые при вычитании смешанных дробей:

• Сначала преобразуйте все смешанные дроби в неправильные дроби.
• Проверьте, имеют ли неправильные дроби общий знаменатель, если нет, найдите общий знаменатель для дробей.
• Попробуйте создать эквивалентную дробь.
• Вычтите числитель, сохраняя знаменатель прежним.
• Если результат вычитания является неправильной дробью, преобразуйте его обратно в смешанную дробь или уменьшите, если это правильная дробь

Пример 2

6 ^1// ₃ — 3 ¹ / ₁₂

= (6 × 3) + 1/3 + (3 × 12) + 1/12

= 19/3 — 37/12

= 19 × 4/3 × 4 — 37 × 1/12 × 1, (Л. СМ. из 3 и 12 = 12)

= 76/12 — 37/12

= 76 — 37/12

= 39/12

= 13/4

= 3 ¼

Метод 2

В этом методе смешанные фракции разделяются на целые и части.

• Вычтите целые части дробей.
• Проверьте, совпадают ли знаменатели дроби, и если нет, найдите общий знаменатель.
• При необходимости создайте эквивалентную дробь.
• Вычтите числители дробной части, оставив знаменатель неизменным.
• Сложите разности целого числа и дробной части.

Пример 3:

6 ¹ / ₃ — 3 ¹ / ₁₂

= (6 — 3) + (1/3 — 1/12)

= 3 + (1/3 — 1/12)

= 3 + (1 × 4/3 × 4 — 1 × 1/12 × 1) (НОК 12 и 3 = 12)

= 3 + 4/12 — 1/12

= 3 + (4 — 1) / 12

= 3 + 3/12

= 3 + ¼

= 3 ¼

Как вычесть дроби с разными знаменателями?

Вычитание дробей с разными знаменателями очень похоже на сложение дробей. При вычитании дробей с разными знаменателями важно вычислить общий знаменатель для всех дробей. Затем вычтите числители, сохраняя знаменатель постоянным.

• Выберите общий знаменатель дробей, найдя наименьшее общее кратное знаменателей.
• Записываем дроби с новым общим знаменателем.
• Вычтите числитель, сохраняя знаменатель постоянным.

Пример 4:
5/6 — 3/4
Решение :

• Найдите НОК 6 и 4, перечислив их факторы, как показано ниже,
  4, 8, 12, 16, 20, 24, 28, 32,….
  6, 12, 18, 24, 30, 36, 42, 48, …
• В этом случае наименьшее общее кратное 4 и 6 равно 12,
• Умножьте каждую дробь на НОК как:

5 / 6 = 5/6 x 2/2 = 10/12 и 3/4 = 3/4 x 3/3 = 9/12.

• Теперь вычтите числители, сохраняя знаменатели постоянными.

10/12 — 9/12 = 1/12

И, следовательно, 5/6 — 3/4 = 1/12

Пример 5
4/5 — 1/3

Решение

• Перечислить числа, кратные 5 и 3.

5, 10, 15, 20, 25, 30,….
3, 6, 9, 12, 15, 18, 21, …

Из кратных, НОК 3 и 5 равно 15.

4/5 = 4/5 X 3/3 = 12/15 и 1/3 = 1/3 x 5/5 = 5/15

12/15 — 5/15 = 7/15

Таким образом,

4/5 — 1/3 = 7/15

Практические вопросы

1: 3 ¹ /8 — 1 ⁵ /8

2: 1 ¹ /6 — 5/7

3: 3 / 4-4 / 7

4: Джеймс имел 1 / 6 кг мяса и он дал сестре 1/9 кг мяса.Со скольким он остался?

5: У Мэри в миске 2/5 литра молока. Ее ребенок будет пить 1/4 литра молока. Сколько молока останется в миске?

Предыдущий урок | Главная страница | Следующий урок

Что такое вычитание дробей? — Определение, факты и примеры

Вычитание дробей

Нравится дробь

Дроби с одинаковыми знаменателями называются дробями.

Например:

Пример 1- На рисунке ниже все дроби похожи на дроби.

В отличие от дробей

Дроби с разными знаменателями называются разнородными дробями.

Вычитание дробей

Легче складывать или вычитать одинаковые дроби, потому что либо они являются равными частями одного целого, либо являются частями одного размера.

Случай 1 — Вычитание подобных дробей

• Вычтите числитель, и он даст нам ответ.
• При необходимости упростите дробь.

Например:

Пример 2- Вычтем из 3 15 из 12 15.

Решение: В обоих случаях дроби подобны дробям

∴ 1215-315 = 12-3 15 = 9 15

Поскольку 9 15 можно упростить, окончательный ответ — 3 5.

Случай 2 — Вычитание непохожих дробей

Ниже приведены шаги для вычитания непохожих дробей:

• Найдите наименьшее общее кратное знаменателей.
• Измените знаменатель на НОК, умножив числитель и знаменатель на одно и то же число.
• Как только у дробей будут одинаковые знаменатели, вычтите числители дробей.
• Разница между числителем и НОК будет числителем и знаменателем ответа соответственно.
• При необходимости упростите дробь.
• Например:

Пример 3 — Вычтем 4 7 из 3 5.

Решение — Мы должны найти, 3 5 — 4 7

Поскольку обе дроби не похожи на дроби (разные знаменатели), нам нужно сделать знаменатели одинаковыми для вычитания.

Наименьшее общее кратное 7 и 5 равно 35.

Чтобы сделать знаменатели 35, дробь 3 5 может быть записана как 3×7 5×7 = 21 35, а дробь 4 7 может быть записана как 4×5 7×5 = 20 35.

Теперь вопрос можно переписать как 21 35 — 20 35.

Поскольку знаменатели те же, & там 21 35 — 20 35 = 1 35

Так как 1 35 находится в простейшей форме, окончательный ответ — 1 35.

Интересные факты: Мы не можем складывать или вычитать дроби, не преобразовав их в аналогичную дробь.

Как складывать и вычитать дроби: 3 простых шага

На первый взгляд сложение и вычитание дробей может показаться устрашающим. Вы не только работаете с дробями, которые, как известно, сбивают с толку, но и внезапно сталкиваетесь с преобразованием числителей и знаменателей.

Но сложение и вычитание дробей — полезный навык. Как только вы выучите словарный запас и основы, вы с легкостью сможете складывать и вычитать дроби. Это руководство проведет вас через все, что вам нужно знать для сложения и вычитания дробей , включая некоторые примеры задач для проверки ваших навыков.

Ключевые слова для сложения и вычитания дробей

Прежде чем мы перейдем к математике сложения и вычитания дробей, вам необходимо знать терминологию. Мы будем использовать эти термины на протяжении всего , так что освежите их, чтобы быть уверенным, что вы всегда знаете, какую часть дроби мы имеем в виду.

Дробь : число, не являющееся целым числом; часть целого. Для наших целей дробь будет относиться к числу, записанному с числителем и знаменателем , например 1/5 $ или 147/4 $.

Числитель : верхнее число в дроби, отражающее количество частей целого, например 1 в 1/5 $.

Знаменатель : нижнее число в дроби, представляющее общее количество частей, например 5 в 1/5 $.

Общий знаменатель : Когда две дроби имеют один и тот же знаменатель, например, $ 1/3 $ и $ 2/3 $.

Наименьший общий знаменатель : Наименьший знаменатель, который могут разделить две дроби. Например, наименьший общий знаменатель для $ 1/2 $ и $ 1/5 $ равен 10, потому что наименьшее число, в которое входят 2 и 5, равно 10.

Пироги образуют большие фракции.

Как складывать и вычитать дроби?

Теперь, когда у вас есть словарный запас, пора применить его на практике. Вы не можете просто складывать или вычитать дроби, как, например, целое число $ 1 / 4–1 / 2 $ не равно $ 0/2 $.

Вместо вам нужно будет найти общий знаменатель, прежде чем прибавлять или вычитать . Есть много способов найти общий знаменатель, некоторые из которых проще или эффективнее других.

Один из самых простых способов найти общий знаменатель, хотя и не обязательно лучший, — это просто перемножить два знаменателя вместе.

Например, возможный наименьший общий знаменатель для 1/2 $ и 1/12 $ будет равен 24, что вы найдете, умножив знаменатель 2 на знаменатель 12. Вы можете решить проблему, используя общий знаменатель 24, выполнив следующие действия, но если вы это сделаете, вы столкнетесь с проблемой — вашу дробь нужно будет уменьшить.

Чтобы избавиться от необходимости уменьшать после сложения или вычитания, вместо этого попытайтесь найти наименьший общий знаменатель. Иногда это то же самое, что умножение двух знаменателей вместе, но часто это не так.

Однако найти наименьший общий знаменатель несложно — , вам просто нужно ознакомиться с таблицей умножения .Например, давайте попробуем найти наименьший общий знаменатель, а не просто общий знаменатель для тех же дробей, которые мы использовали выше:

$$ 1/2 \: \ и \: 1/12 $$.

Для этого перечислите несколько значений, кратных каждому знаменателю

Кратное 2 : 2, 4, 6, 8, 10, 12 , 14, 16, 18, 20, 22, 24

Кратное 12 : 12 , 24, 36, 48, 60

Затем просмотрите оба списка кратных и найдите наименьшее число, общее для обоих.В этом случае и 2, и 12 делят кратное 12. Если мы продолжим, мы получим другие кратные, которые они разделяют, например 24, но 12 является наименьшим, что означает, что это наименьшее общее кратное .

Вы можете сделать это с любой парой чисел, хотя большие числа могут представлять большую проблему. Для сложения или вычитания вы всегда можете вернуться к простому умножению одного знаменателя на другой, если у вас возникнут проблемы с нахождением наименьшего общего знаменателя , но имейте в виду, что вам, вероятно, придется уменьшить.

Дроби — самая вкусная часть математики.

Как сложить дроби — метод 1

Теперь, когда вы знаете, как найти общий знаменатель, вы готовы приступить к сложению и вычитанию.

Вернемся к примеру с 1/2 $ и 1/12 $ — в данном случае давайте рассмотрим эту задачу:

$$ 1/2 + 1/12 $$

Помните, что нельзя складывать прямо поперек; $ 1/2 + 1/12 $ не равно $ 2/14 $.

# 1: Найдите общий знаменатель

Сначала мы найдем наименьший общий знаменатель, так как это, как правило, лучший способ решить эту проблему.

Мы уже выполнили описанную выше работу, но напомним, , вам нужно записать серию кратных каждому числу, пока не найдете совпадение . В этом случае и 2, и 12 кратны 12.

# 2: Умножьте, чтобы получить каждый числитель по одному знаменателю

Всегда помните, что все, что вы делаете со знаменателем, должно происходить и с числителем. Итак, давайте посмотрим на эти две дроби, которые нам нужно преодолеть знаменатель 12.

$ 1/12 $ — это просто — оно уже превышает знаменатель 12, поэтому нам не нужно ничего с этим делать.

$ 1/2 $ потребует доработки. Какое число, умноженное на 2, будет равно 12?

Перефразируя этот вопрос как проблему, которую мы можем решить, $ 2 *? = 12 $. Или, что еще проще, , мы можем инвертировать операцию , чтобы получить $ 12/2 =? $, Что мы можем легко решить.

Итак, теперь мы знаем, что для перехода от знаменателя 2 к знаменателю 12 нам нужно умножить на 6. Опять же, помните, что все, что вы делаете со знаменателем, нужно делать и с числителем, поэтому умножьте верхнюю и снизу на 6, чтобы получить $ 6/12 $.

# 3: Добавьте числители, но оставьте знаменатели в покое

Теперь, когда у вас те же знаменатели, вы можете складывать числители прямо поперек.

В данном случае это будет означать, что $ 6/12 + 1/12 = 7/12 $. Спросите себя, можно ли уменьшить дробь, разделив числитель и знаменатель на одно и то же число. В этом случае вы не можете, поэтому ваш ответ — 7 долларов / 12 долларов.

Как сложить дроби — метод 2

В качестве альтернативы, мы могли бы просто умножить два знаменателя вместе, чтобы найти другой общий знаменатель. Это другой способ решения проблемы, но ответ будет таким же.

# 1: Умножаем знаменатели вместе

Никаких хитростей — просто умножьте 2 на 12, чтобы получить 24. Это будет ваш общий знаменатель.

# 2: Умножьте, чтобы получить каждый числитель по одному знаменателю

Так же, как мы это сделали, когда нашли наименьший общий знаменатель, нам нужно будет умножить верхнее и нижнее число каждой дроби. В этом случае используйте обратные операции, чтобы узнать, какое число вам нужно умножить.

Если $ 1/2 $ должно быть $? / 24 $, вы можете сделать $ 24 ÷ 2 $, чтобы вычислить, какое число вам нужно умножить на -12. Умножьте верхнюю и нижнюю часть на 12, чтобы получить $ 12/24 $.

Повторите процесс с $ 1/12 $. Если $ 1/12 $ должно быть $? / 24 $, решите $ 24 ÷ 12 $, чтобы получить 2. Теперь умножьте числитель и знаменатель $ 1/12 $ на 2, чтобы получить $ 2/24 $.

# 3: сложите числители вместе

Теперь вы можете просто добавлять прямо поперек.$$ 12/24 + 2/24 = 14/24 $$.

# 4: Уменьшить

Вот здесь-то и появляется дополнительный шаг. 14 $ / 24 $ не является дробью в самой низкой форме, поэтому нам нужно уменьшить ее. Чтобы уменьшить, нам нужно разделить числитель и знаменатель на одно и то же число.

Для этого нам нужно найти наибольший общий множитель. Подобно поиску наименьшего общего кратного, это означает перечисление чисел до тех пор, пока мы не найдем два общих множителя и числитель, и знаменатель, исключая 1, например:

14 : 2 , 7

24 : 2 , 3, 4, 6, 8, 12

Какое число у них общего? 2. Это означает, что 2 — наш наибольший общий делитель, и поэтому число, на которое мы будем делить числитель и знаменатель.

$ 14 ÷ 2 = 7 $ и 24 ÷ 2 = 12 $, что дает нам ответ 7/12 $.

Ответ такой же, как и в случае, когда мы решили использовать наименьшее общее кратное, и не может быть сокращен дальше, так что это наш окончательный ответ!

Если вы когда-нибудь обнаружите, что записываете множество факторов без особой удачи, есть несколько быстрых способов выяснить потенциальные факторы.

• Если число четное, его можно разделить на 2.
• Если вы можете сложить цифры числа, число, которое делится на 3, число делится на 3, например 96 (9 + 6 = 15 $ и 1 + 5 = 6 $, что делится на 3).
• Если число заканчивается на 5 или 0, оно делится на 5.
• Если вы не уверены, когда прекращать поиск факторов, вычтите меньшее число из большего. Это число будет наибольшим общим множителем из возможных , но не наибольшим общим множителем.

  Например, возьмем 50 и 32.Конечно, мы могли бы просто разделить оба значения на 2 и продолжать уменьшать оттуда, но если вы сделаете 50-32 доллара, вы получите 18, что говорит нам прекратить искать наибольший общий фактор, когда мы достигнем 18.

  На практике это выглядит так. это:

  50 : 2 , 5, 10

  32 : 2 , 4, 8, 16

  выше, не позволяя нам тратить больше времени на выяснение факторов, которые нам не нужны. Мы можем намного быстрее увидеть, что наибольший общий множитель равен 2, и приступить к решению проблемы!

$ 1/1 — 1 /? = ням $

Как вычислить дроби

Как только вы научитесь складывать дроби, вычитание дробей станет проще простого! Процесс точно такой же, хотя вы, естественно, будете вычитать, а не складывать.

# 1: Найдите общий знаменатель

Давайте посмотрим на следующий пример:

$$ 2 / 3-3 / 10 $$

Нам нужно найти наименьшее общее кратное для знаменателей, которое будет выглядеть так:

3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30

10 : 10, 20, 30

Первое общее число — 30, поэтому мы поставим оба числителя над знаменателем 30.

# 2: Умножьте, чтобы получить оба числителя над одним знаменателем

Во-первых, нам нужно выяснить, на сколько нам нужно умножить числитель и знаменатель каждой дроби, чтобы получить знаменатель 30. Для 2/3 доллара какое число, умноженное на 3, равно 30? В форме уравнения:

$$ 30 ÷ 3 =? $$

Наш ответ — 10, поэтому мы умножим числитель и знаменатель на 10, чтобы получить 20/30 долларов.

Затем мы повторим процесс для второй дроби.Какое число нам нужно умножить на 10, чтобы получить 30? Итак, $ 30 ÷ 10 = 3 $, поэтому мы умножим верхнюю и нижнюю часть на 3, чтобы получить $ 9/30 $.

Это делает нашу задачу $ 20 / 30-9 / 30 $, а это значит, что мы готовы продолжить!

# 3: вычесть числители

Так же, как мы это делали со сложением, мы вычтем один числитель из другого, но знаменатели оставим в покое.

$$ 20 / 30-9 / 30 = 11/30 $$.

Так как мы нашли наименьшее общее кратное, мы уже знаем, что проблему нельзя решить дальше.

Однако предположим, что мы просто умножили 3 на 10, чтобы получить знаменатель 30, поэтому нам нужно проверить, можем ли мы уменьшить. Давайте воспользуемся этим маленьким трюком, чтобы найти наибольший общий множитель из возможных . Независимо от того, какие делят множители 11 и 30, они не могут быть больше, чем $ 30-11, или 19.

11 : 11

30 : 2, 3, 5, 6, 10, 15

Поскольку у них нет общих факторов, ответ не может быть сокращен дальше.

$ 1/10 $ пицца по-прежнему остается вкусной 10 $ / 10 $.

Примеры сложения и вычитания дробей

Давайте рассмотрим еще несколько примеров задач!

$$ 8 / 15-4 / 9 $$

# 1: Найдите общий знаменатель

15 : 15, 30, 45 , 60

9 : 9, 18, 27, 26, 45

# 2: Умножьте, чтобы получить оба числителя с одним и тем же знаменателем

$$ 45/15 = \ bo3 $$

$$ 8 ÷ 3 = 24 $$

$$ 15 * 3 = 45 $$

$$ 24/45 $$

$$ 45 ÷ 9 = \ bo5 $$

$$ 4 * 5 = 20 $$

$$ 9 * 5 = 45 $$

$$ 20/45 $$

# 3: вычесть числители

$$ 24 / 45-20 / 45 = \ bo4 / \ bo45 $$

$$ 6/11 + 3/4 $$

# 1: Найдите общий знаменатель

11 : 11, 22, 33, 44

4 : 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44

# 2: Умножьте, чтобы получить оба числителя с одним и тем же знаменателем

$$ 44 ÷ 11 = \ bo4 $$

$$ 6 * 4 = 24 $$

$$ 11 * 4 = 44 $$

$$ 24/44 $$

$$ 44 ÷ 4 = \ bo11 $$

$$ 3 * 11 = 33 $$

$$ 4 * 11 = 44 $$

$$ 33/44 $$

# 3: сложить числители

$$ 24/44 + 33/44 = \ bo57 / \ bo44 $$ или $$ \ bo1 \ bo13 / \ bo44 $$

$$ 4 / 7-11 / 21 $$

# 1: Найдите общий знаменатель

7 : 7, 14, 21

21 : 21 , 42, 63

# 2: Умножьте, чтобы получить оба числителя с одним и тем же знаменателем

$$ 21 ÷ 7 = \ bo3 $$

$$ 3 * 4 = 12 $$

$$ 3 * 7 = 21 $$

$$ 12/21 $$

$ 11/2 $ уже старше 21, поэтому нам не нужно ничего делать.

# 3: вычесть числители

$$ 12 / 21-11 / 21 = \ bo1 / 21 $$

$$ 8/9 + 7/13 $$

# 1: Найдите общий знаменатель

9 : 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117

13 : 13, 26, 39, 52, 65, 78, 91, 104, 117

# 2: Умножьте, чтобы получить оба числителя с одним и тем же знаменателем

$$ 117 ÷ 9 = \ bo13 $$

$$ 8 * 13 = 104 $$

$$ 9 * 13 = 117 $$

$$ 104/117 $$

$$ 117 ÷ 13 = \ bo9 $$

$$ 7 * 9 = 63 $$

$$ 13 * 9 = 117 $$

$$ 63/117 $$

# 3: сложить числители

$$ 104/117 + 63/117 = \ bo167 / \ bo117 $$

Что дальше?

Сложение и вычитание дробей станет еще проще, если вы начнете преобразовывать десятичные дроби в дроби!

Если вы не знаете, какие уроки математики в старшей школе вам следует посещать, это руководство поможет вам составить расписание и убедиться, что вы готовы к поступлению в колледж!

Теперь, когда вы являетесь экспертом в сложении и вычитании дробей, испытайте себя, научившись переводить градусы Цельсия в градусы Фаренгейта!

Обзор дробей: сложение и вычитание дробей

Purplemath

Для сложения дробей у вас должны быть «общие» (общие) знаменатели. Как гласит пословица, можно добавлять только яблоки к яблокам, а не яблоки к апельсинам. В контексте сложения дробей нельзя комбинировать, скажем, 1/4 и 2/5. Поскольку это фракции разных типов (одна четвертая, другая пятая), они являются «яблоками и апельсинами». Чтобы добавить их, вам сначала нужно преобразовать в знаменатель, состоящий только из яблок; в этом случае вы конвертируете в двадцатые, получая 5/20 и 8/20 в качестве целых яблочных дробей.

Хотите верьте, хотите нет, но многие высокоразвитые древние цивилизации (например, древние египтяне) никогда не понимали концепцию общего знаменателя.Так что не расстраивайтесь, если у вас возникнут проблемы с вычислениями!

MathHelp.com

Основная идея преобразования к общему знаменателю — умножение дробей на полезные формы 1. Что это значит? Взгляните:

• Упростить

Прежде чем я смогу сложить эти дроби, я должен найти их общий знаменатель. Наименьший (наименьший) общий знаменатель — это просто наименьшее общее кратное (НОК) двух знаменателей, 4 и 5. Разложение на простые множители и НОК знаменателей 4 и 5 равны:

 4: 2 * 2
  5: 5
---: -----------
НОК: 2 * 2 * 5 = 20 

Другими словами, я должен преобразовать четвертые и пятые доли в двадцатые.Я сделаю это умножением на полезную форму 1. В случае первой дроби, ¹ / ₄ , 4 должно стать 20, поэтому мне нужно умножить 4 на 5. Чтобы сохранить дробь равна исходному значению, верхнюю часть тоже надо умножить на 5. Другими словами, я умножу дробь на ⁵ / ₅ , что является просто полезной формой числа 1:

.

Поскольку я умножил на (полезную форму) 1, я не изменил фактическое значение дроби.Все, что я изменил, — это то, как указано значение.

В случае второй дроби, ² / ₅ , 5 должно стать 20, поэтому мне нужно умножить 5 на 4. Чтобы дробь оставалась равной той же величине, мне также нужно умножить верх на 4 тоже. Другими словами, я умножу на ⁴ / ₄ , что является просто полезной формой 1:

.

Четвертые и пятые теперь обе двадцатые; Я наконец-то оказался в ситуации «все яблоки».Только теперь я могу складывать дроби. Чтобы сложить эти «яблоки», складываю числители:

Числитель 13 — простое число и не множитель 20, поэтому я не могу ничего отменить.

Мой упрощенный окончательный ответ:

¹³ / ₂₀ .

---

Кстати, ваш калькулятор может сделать все это за вас; проверьте свое руководство. Но убедитесь, что вы понимаете хотя бы основную идею, потому что этот процесс вам понадобится позже в алгебре, когда вы дойдете до дробей с многочленами, называемых «рациональными выражениями».

---

• Упростить

Сначала я найду НОК двух знаменателей:

 15: 3 * 5
  5: 5
---: ---------
НОК: 3 * 5 = 15 

Поскольку 5 — это множитель 15, то НОК равно 15; в частности, одна из фракций уже находится в форме НОК.Я конвертирую другую дробь в этот общий знаменатель, добавляю и, если возможно, упрощаю:

Общих множителей нет, поэтому ничего не упрощает.

Мой окончательный ответ:

⁸ / ₁₅ .

---

• Упростить

Сначала я найду НОК двух знаменателей:

 8: 2 * 2 * 2
  6: 2 * 3
---: -------------
НОК: 2 * 2 * 2 * 3 = 24 

Обратите внимание, что 8 и 6 имеют коэффициент 2.Смысл аккуратного и аккуратного выстраивания факторов в столбцы, как я сделал выше, заключается в том, чтобы избежать дублирования факторов при нахождении LCM. Будьте осторожны: в LCM всего три двойки, а не четыре.

Чтобы преобразовать первую дробь в знаменатель 24, я умножу верхнюю и нижнюю часть на 3. Чтобы преобразовать знаменатель второй дроби, я умножу верхнюю и нижнюю часть на 4.

В инструкциях не говорится, что нужно выражать ответ в виде смешанных чисел, поэтому я оставлю его как неправильную дробь. Между числителем и знаменателем нет общих множителей, поэтому я не могу больше упрощать.

---

Партнер

---

• Упростить

Сначала я найду НОК трех знаменателей:

 7: 7
 52: 2 * 2 * 13
  4: 2 * 2
---: ---------------
НОК: 2 * 2 * 7 * 13 = 364 

Теперь я переведу три дроби к общему знаменателю, сложу и посмотрю, смогу ли я упростить.

Поскольку 4 было общим множителем 1072 и 364, я смог отменить это и упростить, чтобы получить окончательный ответ:

⁵ / ₇ + ²⁵ / ₅₂ + ⁷ / ₄ = ²⁶⁸ / ₉₁

---

• Упростить

Сначала я найду НОК двух знаменателей:

 25: 5 * 5
 35: 5 * 7
---: ------------
НОК: 5 * 5 * 7 = 175 

Чтобы преобразовать в НОК, я умножу первую дробь, верхнюю и нижнюю, на 7, а вторую дробь, верхнюю и нижнюю, на 5.

Числитель 106 множит 2 × 53, а 53 — простое число, поэтому я ничего не могу отменить; дробь не подлежит дальнейшему упрощению.

Тогда мой окончательный ответ:

¹⁰⁶ / ₁₇₅ .

---

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в сложении и вычитании дробей. Попробуйте выполнить указанное упражнение или введите свое собственное.Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)

---

URL: https://www.purplemath.com/modules/fraction4.htm

вычитание дробей

Covid-19 привел мир к феноменальному переходу.

Электронное обучение — это будущее уже сегодня.

Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!

Вычитание дробей такое же, как и сложение дробей. Вычитание подобных дробей: Поскольку знаменатели (нижние числа) такие же, просто вычтите числители (верхние числа).

Вычитание одинаковых дробей 12 8 —— — —- 5 5 12-8 4 ———- = —- 5 5

При вычитании разнородных дробей используйте следующие шаги.
1) Найдите НОК знаменателя.
2) Сделайте знаменатель таким же, как у LCM (LCD).
3) Новые дроби подобны дробям.
4) Вычтите числители, сохраняя общий знаменатель.

Например:

Вычитание разнородных дробей 12 5 —— — —- 5 6 НОК 5 и 6 = 30 12 x 6 5 x 5 — ——- — ——- 5 x 6 6 x 5 72 25 72-25 —— — —- = ——— 30 30 30 47 = —— 30

Вычитание смешанных дробей:
1) преобразовать их в неправильные дроби
2) затем вычесть их (используя вычитание дробей)
3) затем преобразовать обратно в смешанные фракции Примеры:
1) У молочника было 2 2/3 литра молока в банке. Он продал покупателю 1 1/4 литра. Сколько молока осталось в банке?
Решение:
2 2/3 — 1 1/4
• Замена на неправильные дроби ——> 8/3 — 5/4
• Используя НОК, сделайте знаменатели одинаковыми —-> 32 / 12 — 15/12 = 17/12
• Замените ответ на смешанную дробь ———> 1 5/12.
В емкости осталось 1 5/12 л молока.
————————————————- ————————
2) Вы получаете пятую часть бутылки сока, а ваша сестра — треть бутылки сока.Кто получит больше? На сколько больше?
Решение:
Вы получаете одну пятую бутылки сока = 1/5
ваша сестра получает треть бутылки сока = 1/3
1/5 и 1/3
(1 x3) < (1 x 5) [путем перекрестного умножения] 3 <5
∴ ваша сестра получает больше.
1/3 — 1/5
НОК 3 и 5 равно 15. Итак, сделайте знаменатели такими же, как и НОК.
(1×5) / (3×5) — (1×3) / (5×3)
⇒ 5/15 — 3/15
⇒ (5-3) / 15 = 2/15
Итак, ваша сестра получит 2/15 бутылки сок побольше.

---

Дробь

• Типы дробей
• Преобразование неправильной дроби в смешанную
• Эквивалентные дроби
• Дроби в простейшей форме
• Подобные и непохожие дроби
• Сложение дробей
• Вычитание дробей
• Умножение дробей

Вычитание дробей на главную страницу Fractions

Covid-19 повлиял на физическое взаимодействие между людьми.

Не позволяйте этому влиять на ваше обучение.

Вычитание дробей с общим знаменателем

Результаты обучения

• Используйте круги с дробями, чтобы найти разницу между двумя дробями с одинаковыми знаменателями
• Вычесть дроби с одинаковым знаменателем без кружков дробей

Модель вычитания дроби

Вычитание двух дробей с общим знаменателем во многом похоже на сложение дробей.Представьте себе пиццу, нарезанную [латексными] 12 [/ латексными] ломтиками. Предположим, на обед съедено пять штук. Это означает, что после ужина в коробке осталось семь кусочков (или [латекс] {\ Large \ frac {7} {12}} [/ latex] пиццы). Если Леонардо съест [латекс] 2 [/ latex] из этих оставшихся кусков (или [латекс] {\ Large \ frac {2} {12}} [/ latex] пиццы), сколько останется? Осталось бы [latex] 5 [/ latex] частей (или [latex] {\ Large \ frac {5} {12}} [/ latex] пиццы).

[латекс] {\ Large \ frac {7} {12}} — {\ Large \ frac {2} {12}} = {\ Large \ frac {5} {12}} [/ latex]

Давайте использовать дробные круги для моделирования того же примера, [latex] {\ Large \ frac {7} {12}} — {\ Large \ frac {2} {12}} [/ latex].

Начните с семи частей [латекса] {\ Large \ frac {1} {12}} [/ latex]. Уберите две части [латекса] {\ Large \ frac {1} {12}} [/ latex]. Сколько двенадцатых осталось?

Опять же, у нас пять двенадцатых, [латекс] {\ Large \ frac {5} {12}} [/ latex].

Пример

Используйте дробные круги, чтобы найти разницу: [latex] {\ Large \ frac {4} {5}} — {\ Large \ frac {1} {5}} [/ latex]

Решение:
Начните с четырех частей [латекса] {\ Large \ frac {1} {5}} [/ latex]. Уберите один кусок [латекса] {\ Large \ frac {1} {5}} [/ latex].Посчитайте, сколько осталось пятых. Осталось три [латексных] {\ Large \ frac {1} {5}} [/ latex] куска.

Вычесть дроби с общим знаменателем

Мы вычитаем дроби с общим знаменателем почти так же, как складываем дроби с общим знаменателем.

Вычитание дроби

Если [латекс] a, b, \ text {и} c [/ latex] — числа, где [latex] c \ ne 0 [/ latex], то

[латекс] {\ Large \ frac {a} {c}} — {\ Large \ frac {b} {c}} = {\ Large \ frac {a-b} {c}} [/ latex]

Чтобы вычесть дроби с общим знаменателем, мы вычитаем числители и помещаем разницу над общим знаменателем.

Пример

Найдите разницу: [латекс] {\ Large \ frac {23} {24}} — {\ Large \ frac {14} {24}} [/ latex]

Показать решение

Решение:

[латекс] {\ Large \ frac {23} {24}} — {\ Large \ frac {14} {24}} [/ latex]
Вычтите числители и поместите разницу над общим знаменателем.	[латекс] {\ Large \ frac {23–14} {24}} [/ латекс]
Упростим числитель.	[латекс] {\ Large \ frac {9} {24}} [/ латекс]
Упростите дробь, удалив общие множители.	[латекс] {\ Large \ frac {3} {8}} [/ латекс]

Посмотрите следующее видео, чтобы увидеть больше примеров вычитания дробей с одинаковыми знаменателями.

Пример

Найдите разницу: [латекс] {\ Large- \ frac {10} {7} — \ frac {4} {7}} [/ latex]

Показать решение

Решение:
Помните, дробь [латекс] {\ Large- \ frac {10} {7}} [/ latex] может быть записана как [latex] {\ Large \ frac {-10} {7}} [/ латекс]

[латекс] — \ frac {10} {7} — \ frac {4} {7} [/ latex]
Вычтите числители.	[латекс] {\ Large \ frac {-10 — 4} {7}} [/ латекс]
Упростить.	[латекс] {\ Large \ frac {-14} {7}} [/ латекс]
Запишите дробь со знаком минус.	[латекс] {\ Large- \ frac {14} {7}} [/ латекс]

Теперь давайте рассмотрим пример, который включает в себя как сложение, так и вычитание.

Пример

Упростить: [латекс] {\ Large \ frac {3} {8}} + \ left (- {\ Large \ frac {5} {8}} \ right) — {\ Large \ frac {1} {8} } [/ латекс]

Показать решение

Решение:

	[латекс] \ Large \ frac {3} {8} + \ left (- \ frac {5} {8} \ right) — \ frac {1} {8} [/ latex]
Объедините числители над общим знаменателем.	[латекс] {\ Large \ frac {3+ \ left (-5 \ right) -1} {8}} [/ latex]
Упростите числитель, работая слева направо.	[латекс] {\ Large \ frac {-2 — 1} {8}} [/ латекс]
Вычтите члены в числителе.	[латекс] {\ Large \ frac {-3} {8}} [/ латекс]
Запишите дробь со знаком минус.	[латекс] {\ Large- \ frac {3} {8}} [/ латекс]

Калькулятор вычитания дробей

Как вычитать дроби?

Результат вычитания чисел — \ underline {разница}. Разница двух чисел зависит от их порядка, т.е. вычитание — некоммутативная операция. Например, $ \ frac 53- \ frac 13 \ ne \ frac 13- \ frac 53 $. Как и свойство коммутативности, свойство ассоциативности не выполняется для вычитания чисел.
Когда мы имеем дело с дробями, существует два типа вычитания:

• Когда знаменатели равны

Когда знаменатели дробей равны, то их разность будет разницей числителей над общим знаменателем.При необходимости результат можно упростить. Это можно выразить алгебраически:

$$ \ frac {a} {b} — \ frac {c} {b} = \ frac {a-c} {b}, \ quad \ mbox {for} \; b \ ne0 $$

• Если знаменатели разные

Если знаменатели дробей различны, чтобы вычесть две такие дроби, необходимо выполнить следующие шаги:

1. Найдите НОК знаменателей;
2. Перепишите дроби над НОК;
3. Вычесть новые числители;
4. Результат — разница числителей в НОК;
5. При необходимости упростите результат.

Этот метод можно выразить алгебраически:

$$ \ frac {a} {b} — \ frac {c} {d} = \ frac {a \ times \ frac {LCM (b, d)} {b} -c \ times \ frac {LCM (b , d)} {d}} {LCM (b, d)}, \ quad \ mbox {for} \; b, d \ ne0 $$

Если $ LCM (b, d) = b \ times d $, то предыдущая формула принимает вид

$$ \ frac {a} {b} — \ frac {c} {d} = \ frac {a \ times dc \ times b} {b \ times d}, \ quad \ mbox {for} \; b, d \ ne0 $$

Например, найдем разницу между $ \ frac 76 $ и $ \ frac 3 4 $. Поскольку $ LCM (6,4) = 12 $, то

$$ \ frac 76- \ frac 3 4 = \ frac {7 \ times 2-3 \ times 3} {12} = \ frac {8} {12} $$

Чтобы записать разницу в простейшей форме, найдите GCF числителя и знаменателя разницы.$ GFC (8,12) = 4 $, поэтому, разделив числитель и знаменатель разницы на 4, окончательный результат будет

$$ \ frac {8 \ div4} {12 \ div 4} = \ frac 23 $$

Аналогичное соображение можно применить при вычитании алгебраических дробей.
Работа по вычитанию дробей с пошаговыми инструкциями показывает полное пошаговое вычисление для нахождения разности двух дробей $ \ frac {7} {6} $ и $ \ frac {3} {4} $ с использованием правила вычитания дробей.