Умножение дробей: простая инструкция — Лайфхакер

15 января 2021 Ликбез Образование

Простая шпаргалка для тех, кто подзабыл школьную программу по математике.

Умножение дробей друг на друга

Обыкновенные дроби

Всё просто: числитель умножьте на числитель, а знаменатель на знаменатель. Потом проверьте, можно ли сократить дробь. Например:

Правило работает для дробей и с разными, и с одинаковыми знаменателями. Если дробь большая, допустим ²⁴/₃₅, постарайтесь сразу сократить её — так будет легче вести подсчёты.

Если в примере есть смешанное число, сначала преобразуйте его в неправильную дробь, а потом умножайте способом, описанным выше. Полученный результат переведите обратно в смешанное число.

Вспомните основы 💡

• Какие бывают дроби и как их складывать

Десятичные дроби

Процесс умножения происходит в три шага:

1. Запишите дроби в столбик и умножьте как натуральные числа, пока не думая о запятых.
2. Посмотрите, сколько знаков после запятой было в каждой дроби, и сложите их количество.
3. Двигаясь справа налево, отсчитайте в результате умножения столько же цифр, сколько получилось в предыдущем шаге. Поставьте там запятую. Это и есть ответ. Например:

Если умножаете на 0,1, 0,01, 0,001 и так далее, то переместите запятую влево на столько знаков, сколько их после запятой в множителе: 0,18 × 0,1 = 0,018; 0,5 × 0,001 = 0,0005.

Освежите знания 👈

• Как перевести обычную дробь в десятичную

Умножение дробей на натуральные числа

Обыкновенные дроби

Нужно умножить только числитель, а знаменатель оставить без изменений. Если результат — неправильная дробь, выделите из неё целую часть, чтобы получить смешанное число. Например:

Если нужно умножить смешанное число, переведите его в неправильную дробь и умножайте по тому же принципу. То есть:

Есть и второй способ: разделить знаменатель на данное вам натуральное число, а числитель не трогать. Этот способ удобнее применять, когда знаменатель делится на это натуральное число без остатка. Например:

Сравните этот метод с первым — результат одинаковый.

Десятичные дроби

В этом случае используйте такой же способ, как для умножения дроби на дробь. Перемножьте числа столбиком, потом отсчитайте столько цифр, сколько их было после запятой в десятичной дроби, и там поставьте запятую. То есть:

Если нужно умножить десятичную дробь на 10, 100, 1 000 и так далее, просто переместите запятую вправо на столько знаков, сколько нулей после единицы. Например: 0,045 × 10 = 0,45; 0,045 × 100 = 4,5.

Читайте также 🧮👌🤓

• Умножать, делить, складывать как Шелдон Купер? Математические хаки…
• Как научить ребёнка считать играючи
• 6 способов посчитать проценты от суммы с калькулятором и без
• Как выучить таблицу умножения легко и быстро
• Как освоить устный счёт школьникам и взрослым

Как умножить обыкновенную дробь на десятичную дробь

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel. ru Математика Алгебра Умножение обыкновенной дроби на десятичную: правило, примеры

В данной публикации мы рассмотрим, каким образом обыкновенную (простую) дробь можно умножить на десятичную. Также разберем примеры для закрепления теоретического материала.

• Произведение обыкновенной и десятичной дробей
• Примеры

Произведение обыкновенной и десятичной дробей

Чтобы умножить обыкновенную дробь на десятичную (и наоборот, т.к. от перестановки множителей результат не меняется), необходимо одну из дробей представить в виде другой.

Примечания:

1. Бесконечные десятичные дроби сначала требуется округлить, т.е. оставить конечное количество цифр после запятой.
2. Смешанные обыкновенные дроби сперва необходимо превратить в неправильные.

Примеры

Пример 1

Давайте найдем результат произведения дроби 

3/20

 и 2,19.

 
Решение 1

Переведем обыкновенную дробь в десятичную:

3/20

=

3⋅5/20⋅5

=

15/100

= 0,15

 
Теперь выполним умножение десятичных дробей:

0,15 ⋅ 2,19 = 0,3285.

Решение 2

Преобразуем десятичную дробь в обыкновенную:

2,19 = 2

19/100

=

2 ⋅ 100 + 19/100

=

219/100

 
Остается только найти произведение двух обыкновенных дробей:

219/100

⋅

3/20

=

219 ⋅ 3/100 ⋅ 20

=

657/2000

 
Пример 2

Умножим 6,24 на дробь 2

4/9

.

 
Решение

Преобразуем заданную смешанную дробь в неправильную:

2

4/9

=

2 ⋅ 9 + 4/9

=

22/9

 
Далее у нас есть выбор: либо мы переводим десятичную дробь в обыкновенную, либо наоборот. Выберем первый вариант.

6,24 = 6

24/100

=

6 ⋅ 100 + 24/100

=

624/100

 
Теперь разделим одну простую дробь на другую:

624/100

:

22/9

=

624/100

⋅

9/22

=

624 ⋅ 9/100 ⋅ 22

=

5616/2200

= 2

1216/2200

= 2

152/275

≈ 2,5528

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Как умножать смешанные числа

Что такое смешанные числа

Смешанное число — это целое число и правильная дробь, представленные вместе. Обычно представляет собой число между любыми двумя целыми числами.

Посмотрите на данное изображение, оно представляет собой дробь, которая больше 1, но меньше 2. Таким образом, это смешанное число.

Некоторые другие примеры смешанных чисел: 

Части смешанного числа

Смешанное число образуется путем объединения трех частей: целого числа, числителя и знаменателя. Числитель и знаменатель являются частью правильной дроби, составляющей смешанное число.

Родственные игры

Преобразование смешанных чисел в неправильные дроби

• Умножьте целое число на знаменатель дроби.
• Прибавьте ответ, полученный на шаге 1, к числителю дроби.
• Запишите ответ, полученный на шаге 2, над знаменателем.

Предположим, нам нужно преобразовать $2\frac{2}{3}$ в неправильную дробь.

Шаг 1 : Умножаем 3 на 2, получаем 3$\умножить на 2 = 6$.

Шаг 2 : Складываем 6 и 2, получаем $6 + 2 = 8$

Шаг 3: Полученная дробь равна $\frac{8}{3}$.

Связанные рабочие листы

Умножение смешанного числа на целое число

Шаг 1: Преобразуйте смешанное число в неправильную дробь.

Шаг 2: Перепишите целое число в виде дроби со знаменателем 1.

Шаг 3: Умножьте две дроби, умножая числители и знаменатели отдельно.

Шаг 4: При необходимости преобразуйте его в упрощенную форму.

Предположим, нам нужно умножить 3 и $2\frac{1}{2}$.

$2\frac{1}{2}=\frac{2\times2+1}{2}=\frac{5}{2}$

$3\times\frac{5}{2}=\frac {3}{1}\times\frac{5}{2}=\frac{15}{2}=7\frac{1}{2}$

Умножение смешанного числа на дробь

Шаг 1 : Преобразуйте смешанное число в неправильную дробь.

Шаг 2: Умножьте числители дроби и умножьте знаменатели дроби.

Шаг 3: При необходимости преобразуйте его в упрощенную форму.

Предположим, нам нужно перемножить $\frac{2}{5}$ и $3\frac{1}{2}$.

$3\frac{1}{2}=\frac{3\times2+1}{2}=\frac{7}{2}$

$\frac{2}{5}\times\frac{ 7}{2}=\frac{14}{10}=\frac{7}{5}=1\frac{2}{5}$

Умножение двух смешанных чисел

Шаг 1: Преобразование смешанных чисел числа в неправильные дроби.

Шаг 2: Умножьте две дроби, раздельно умножив числители и знаменатели.

Шаг 3: При необходимости преобразуйте его в упрощенную форму.

Например: умножьте $4\frac{1}{2}$ и $3\frac{1}{3}$.

$4\frac{1}{2}=\frac{4\times2+1}{2}=\frac{9}{2}$

$3\frac{1}{3}=\frac{3 \times3+1}{3}=\frac{10}{3}$

$4\frac{1}{2}\times3\frac{1}{3}=\frac{9}{2}\times \frac{10}{3}=\frac{90}{6}=15$ 

Заключение

В этой статье мы узнали об умножении смешанных чисел. Смешанные числа также известны как смешанные дроби. Чтобы прочитать больше таких информативных статей о других концепциях, посетите наш веб-сайт. Мы в SplashLearn стремимся сделать обучение интересным и интерактивным для всех учащихся.

Решенные примеры

1. Умножьте $5\frac{3}{7}$ на мультипликативное значение, обратное $7\frac{3}{5}$ .

Решение: $5\frac{3}{7}=\frac{5\times7+3}{7}=\frac{38}{7}$

$7\frac{3}{5} =\frac{7\times5+3}{5}=\frac{38}{5}$

Мультипликативное значение, обратное $\frac{38}{5}$ равно $\frac{5}{38} $ .

Продукт $= \frac{38}{7}\times\frac{5}{38}=\frac{5}{7}$

2. Эмма идет 5 2 3 миль в день. Какое расстояние она преодолеет за 9 дней?

Решение: Расстояние, пройденное Эммой за 1 дней $= 5\frac{2}{3}$ миль $=\frac{17}{3}$ миль.

Расстояние, пройденное Эммой за 9 дней $= 9\times\frac{17}{3}= 51$ миль 

3. Умножьте $6\frac{2}{5}\times\frac{3} {4}$ .

Решение: $6\frac{2}{5}=\frac{6\times5+2}{5}=\frac{32}{5}$

$\frac{32}{5}\times \frac{3}{4}=\frac{32\times3}{5\times4}=\frac{96}{20}=\frac{24}{ 5}=4\frac{4}{5}$

Практические задачи

1

Какой из этих шагов является первым шагом к умножению смешанных чисел?

Вычисление НОК знаменателей

Умножение числителей

Умножение знаменателей

Преобразование смешанных чисел в неправильные дроби

Правильный ответ: Преобразование смешанных чисел в неправильные дроби
Преобразование смешанных чисел в неправильные дроби Первым шагом к умножению смешанных чисел является преобразование их в неправильные дроби.

2

При умножении $10\frac{1}{6}$ на $2\frac{2}{11}$ получаем ____.

целое число

смешанное число

правильная дробь

отрицательное число

Правильный ответ: смешанное число
$10\frac{1}{6}\times\frac2{2}{11}=\frac{61} {6}\times\frac{24}{11}=\frac{244}{11}=22\frac{2}{11}$, т. е. смешанное число

3

Значение $4\frac{2}{9}\times1\frac{1}{7}$:

$1\frac{52}{63}$

$2\frac{52} {63}$

$4\frac{52}{63}$

$\frac{61}{63}$

Правильный ответ: $4\frac{52}{63}$
$4\frac{2 {9}\times1\frac{1}{7}=\frac{38}{9}\times{8}{7}=\frac{304}{63}=4\frac{52}{63} $

Часто задаваемые вопросы

Нужны ли одинаковые знаменатели при умножении двух или более смешанных чисел ?

Нет. Нам не нужны одинаковые знаменатели для умножения двух или более смешанных чисел. Мы даже можем умножать непохожие дроби.

Как еще называют смешанные числа?

Другое название смешанных чисел — смешанные дроби.

Всегда ли произведение смешанного числа на другое смешанное число является смешанным числом?

Нет. Смешанное число всегда больше 1. Таким образом, произведение 2 чисел больше 1 всегда будет больше 1, т. е. смешанное/целое число.

Умножение дробей – Этапы и примеры

Умножение дробей: Когда дробь умножается на другую дробь, результатом является дробь или целое число. Мы знаем, что дробь состоит из двух частей: числителя и знаменателя. Таким образом, когда мы умножаем любые две дроби, то соответственно умножаются числители и знаменатели. Пример умножения дробей: ⅔ x ¼ = (2 x 1)/(3 x 4) = 2/12 = ⅙. Умножение дробей не похоже на сложение или вычитание дробей, где знаменатели обеих дробей должны быть одинаковыми. Две дроби можно легко умножить, даже если знаменатели у них разные. При умножении дробей следует иметь в виду, что дроби могут быть правильной или неправильной дробью, но они не могут быть смешанной дробью.

Содержание: Фракции и типы Как умножать дроби Деление дробей Упрощение дроби Умножение дробей на дроби Умножение дробей на целые числа Умножение дробей с переменными Свойства дробного умножения Умножение смешанных дробей Практические задачи Часто задаваемые вопросы

Фракции и типы

Если дробь записывается в виде a/b, то a и b – части дроби, где a называется числителем, а b – знаменателем.

Например,

Предположим, что ⅖ — дробь, тогда 2 — числитель, а 5 — знаменатель.

Существует три основных типа дробей: правильные дроби, неправильные дроби и смешанные дроби. Ниже приводится краткое описание каждого из типов.

Правильные дроби

Когда числитель дроби меньше знаменателя.

Пример: ½, ⅗, 7/9

Неправильные дроби

Когда числитель больше знаменателя

Пример: 3/2, 5/4, 8/3

Смешанная фракция

Сочетание целого числа и дроби. Его еще называют смешанным числом.

Пример: 13/4 = 3 ¼

21/5 = 4 ⅕

Как умножать дроби?

Умножение дробей определяется как произведение дроби на дробь или на целое число или на переменные. Процедура умножения дробей:

• Умножить числитель на числитель
• Умножить знаменатель на знаменатель
• При необходимости упростите дроби

Например,

3/2 и ⅓ две дроби

Умножение двух дробей:

(3/2)× (⅓) = [3×1]/[2×3]

(3/2)× (⅓) = 3/6

Теперь упростим дробь, получим ½

Следовательно, произведение двух дробей 3/2 и ⅓ равно ½.

Просто мы можем записать формулу умножения дроби как;

Если «a/b» и «p/q — множимое и множитель, то произведение (a/b) и (p/q) равно «ap/bq»

Умножение дробей
\(\begin{array}{l}\frac{a}{b}\times \frac{p}{q}\end{array} \)	\(\begin{array}{l}\frac{a\times p}{b\times q}\end{массив} \)	\(\begin{array}{l}\frac{ap}{bq}\end{array} \)

Таким образом,

Произведение дроби = произведение числителя на произведение знаменателя

Попробуйте это: Калькулятор умножения дробей

Деление дробей

Когда мы делим дробь на другую дробь, мы превращаем последнюю в обратную, а затем умножаем на первую дробь. Научитесь делить дроби подробно на BYJU’S.

Пример: ⅔ ÷ ¾

Решение: преобразовать ¾ в обратное число, чтобы получить 4/3.

Теперь умножьте ⅔ на 4/3

⇒ ⅔ x 4/3

⇒ (2×4)/(3×3)

⇒ 8/9.

Упрощение дробей

При умножении дробей мы обычно умножаем верхние числа (числители) друг на друга, а нижние числа (знаменатели) друг на друга. Чтобы упростить дробное умножение, мы можем уменьшить дробь, сократив общие множители. Это означает, что вы можете исключить общие множители с одной стороны дроби, которые дублируются с другой стороны дробной части.

Например, (4/9) и (3/16) — две дроби.

(4/9) можно записать как (2×2)/(3×3)

(3/16) можно записать как (1×3)/(2×2×2×2)

Следовательно,

\(\begin{array}{l}\frac{4}{9}\times \frac{3}{16} = \frac{2\times 2}{3\times 3} \times \frac{1 \times 3}{2\times 2\times 2\times 2}\end{массив} \)

Теперь, сократив общие множители, мы получим

.

\(\begin{array}{l}\frac{4}{9}\times \frac{3}{16} = \frac{1}{3}\times \frac{1}{4}\end {массив} \)

Теперь мы можем умножить числитель на числитель и знаменатель на знаменатель.

(4/9) × (3/16) = 1/12

В случае, если у дроби нет общих множителей, то нужно прямо перемножить числители и знаменатели, чтобы получить произведение дробей.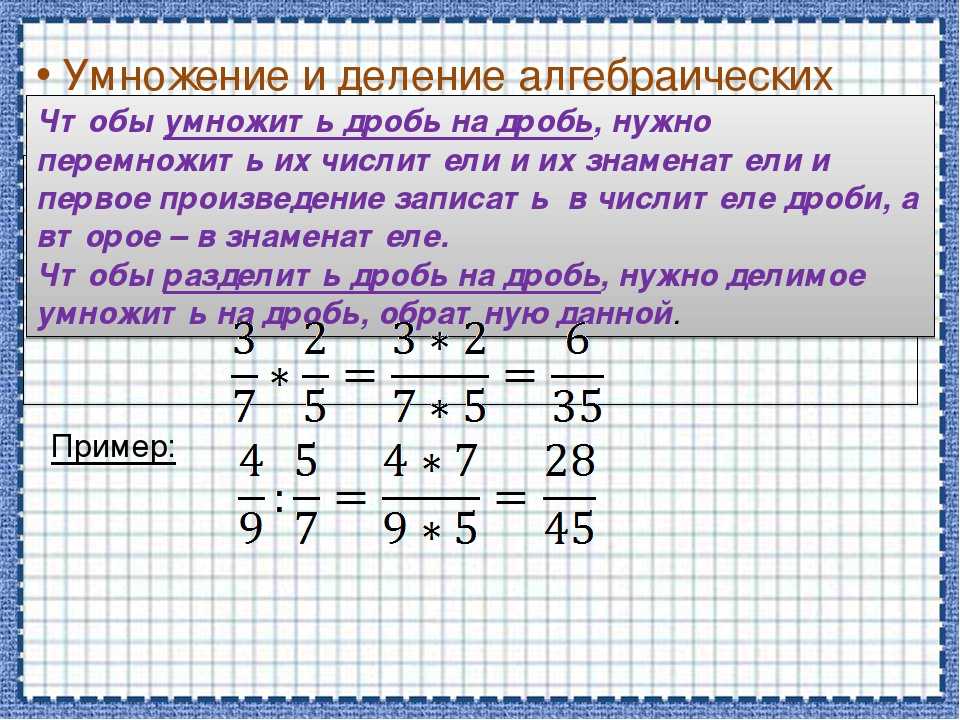

Умножение дробей на дроби

Умножение правильных дробей

Умножение правильных дробей простое, так как мы можем напрямую умножить числитель одной дроби на другую дробь и знаменатель одной дроби на другую дробь. При необходимости мы можем упростить полученные дроби до их наименьшего члена.

Например, умножение 5/9 и 2/3.

(5/9)×(2/3)= (5×2)/(9×3) = 10/27.

Умножение неправильных дробей

Мы знаем, что в неправильной дроби числитель больше знаменателя. При умножении двух неправильных дробей тоже получится неправильная дробь. Например, умножение двух неправильных дробей, таких как 9/2 и 6/5, дает:

.

(9/2)×(6/5) = (9/1)×(3/5)= 27/5.

При необходимости неправильную дробь можно преобразовать в смешанную.

Пример 1 : Решите ⅔×½

Решение: ⅔×½ = 2×1/3×2 = 2/6 = ⅓

Таким образом, из приведенного выше примера мы можем наблюдать, что путем умножения двух дробей мы получаем дробное число. Это правильная дробь.

Пример 2: Умножить ⅘×⅞

Решение: ⅘×⅞ = 4×7 / 5×8 = 28/40

Мы можем упростить это как;

28/40 = 7/10

Если нам нужно умножить три дроби, то приведенная выше формула останется прежней.

Пример 3: Умножить ¼×⅖×⅛

Решение: Умножив данную дробь ¼×⅖×⅛, получим

Произведение = 1×2×1 / 4×5×8

= 2/160

= 1/80

Умножение дробей на целые числа

Если целое число или действительное число умножается на дробь, то оно равно произведению действительного числа на дробь.

Пример 4: Умножить 5×1/2

Решение: 5×½ означает 5 раз по ½

Это означает, что если мы добавим ½ пять раз, мы получим ответ.

Следовательно,

½ + ½ + ½ + ½ +½ = (1+1+1+1+1)/2 = 5/2 = 2,5

Пример 5: Умножить 8/7×10

Решение: Дано, 8/7×10

Мы можем записать это как 8×10/7

Следовательно, ответ 80/7.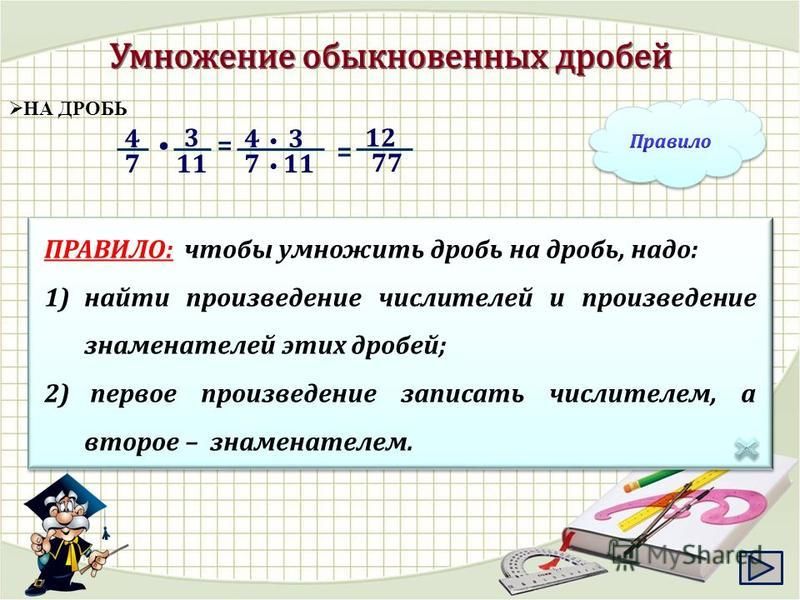 В десятичном виде это 11,42.

• Примечание: Если смешанную дробь умножить на целое или действительное число, то получится сама дробь.

Пример 6: Умножить

\(\begin{array}{l}3\frac{1}{5}\end{array} \)

×12

Решение: Упрощая значение

\(\begin{array}{l}3\frac{1}{5}\end{array} \)

получаем,

16/5×12 = 16×12 / 5 = 192 / 5 = 38,4

Умножение дробей с переменными

Теперь предположим, что дробь умножается на переменную, тогда результаты будут такими, как в приведенном ниже примере.

9{2}}{6yz}\end{массив} \)

Свойства дробного умножения

Ниже приведены свойства умножения дробей:

• Если два заданных дробных числа умножить в любом порядке, произведение дроби останется прежним.

           Например, (⅔) × (4/6) = 8/18 = 4/9

           Аналогично, (4/6)×(⅔) = 8/18 = 4/9

• Если данное дробное число умножить на (1/1), произведение останется тем же дробным числом.

           Например, (⅘) × (1/1) = (⅘)

• Если данное дробное число умножить на 0, произведение останется равным нулю.

           Например, (½)× 0 = 0

Умножение смешанных дробей

Умножать простые дроби несложно, нужно просто умножить числители и знаменатели соответственно. Но чтобы умножить смешанные числа или дроби, нам нужно добавить еще один шаг.

• Сначала преобразуйте заданную смешанную дробь в неправильные дроби
• Теперь умножьте дроби
• Упростите ответ
• Снова преобразовать в смешанные числа

Трюки с умножением дробей:

• Обычно мы упрощаем дробь после перемножения дробей. Однако, чтобы упростить вычисления, мы можем упростить дроби до их наименьшего члена перед умножением, если это возможно. Например, (6/2)×(8/10) можно упростить как (3/1)×(4/5). Теперь мы можем умножить дроби (3/1)×(4/5)= 12/5.
• Упрощение также может быть выполнено для двух дробей. Например, (10/7)×(21/5) можно упростить до (2/1)×(3/1), и мы можем умножить дроби, что даст 6/1.

Видео урок по дробям

Решенные примеры

1. Умножить 2 ¹ / ₃ и 3.

Мы можем написать,

2 ¹ / ₃ = 7/3

Теперь умножьте 7/3 на 3

7/3 х 3 = 7

2. Умножить 1 ¹ / ₂ и 2 ¹ / ₅ .

Мы можем написать,

1 ¹ / ₂  = 3/2

2 ¹ / ₅ = 11/5

Теперь умножьте обе дроби.

3/2 х 11/5

(3 х 11)/(2 х 5)

33/10

Теперь преобразуйте 33/10 в смешанную дробь

33/10 = 33/10

Проблемы и решения

Q.1: Умножьте ⅖ и 6/7.

Решение: ⅖ x 6/7

⇒ (2×6)/(5×7)

⇒

35 декабря.

Q.2: Умножьте ⅓ и 1/10.

Раствор: ⅓ x 1/10

⇒ 1/(3 х 10)

.

⇒ 1/30

.

Q.3: Найдите произведение ⅝ и 4/10.

Решение: ⅝ x 4/10

⇒ (5 х 4)/(8 х 10)

⇒ 20/80

.

⇒ 1/4

.

Практические задачи

1. Чему равно произведение (½) и 6?
2. Произведение (¾) и (12/6) равно ______.
3. Чему равно произведение 3 ½ и ⅔?
4. Найдите площадь квадратной фермы, длина стороны которой равна 10 ⅔ м.
5. В классе f 50 учеников, ⅔ из них девочки. Узнай, сколько мальчиков?

Темы, связанные с дробями

Часто задаваемые вопросы об умножении дробей

Что понимают под дробями?

Дробь определяется как отношение двух чисел. Как правило, это части целого. Дробь можно записать в виде «a/b». Где верхнее число «а» называется числителем, а нижнее число «б» называется знаменателем.

Как умножить две дроби?

Чтобы умножить дроби, сначала просто доведите дробь до ее наименьшего члена.