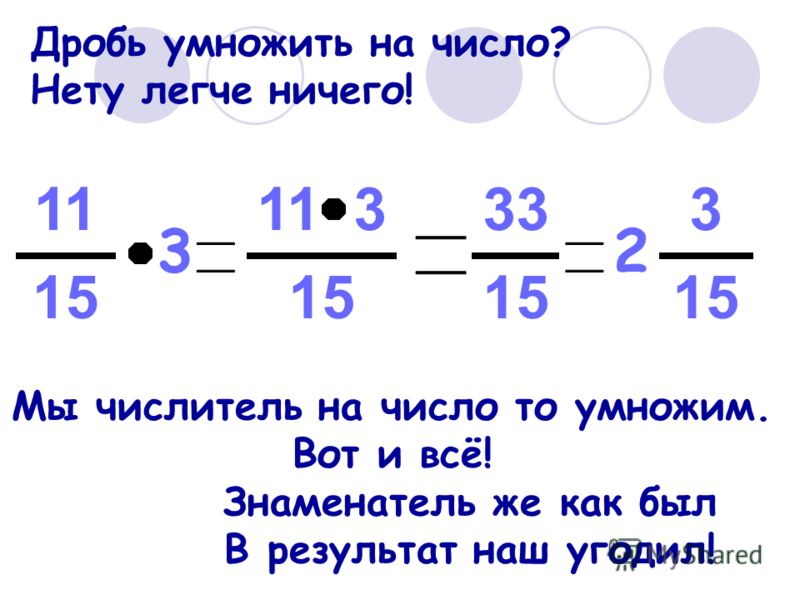
§ Умножение отрицательных чисел. Умножение рациональных чисел

Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел

Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.

Умножение чисел с одинаковыми знаками

Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.

Чтобы умножить два числа с одинаковыми знаками надо:

• перемножить модули чисел;
• перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Примеры умножения отрицательных и положительных чисел.

• (−3) · (−6) = +18 = 18
• 2 · 3 = 6

Умножение чисел с разными знаками

Второй возможный случай — это умножение чисел с разными знаками.

Чтобы умножить два числа с разными знаками, надо

:

• перемножить модули чисел;
• перед полученным произведением поставить знак «−».

Примеры умножения отрицательных и положительных чисел.

• (−0,3) · 0,5 = −0,15
• 1,2 · (−7) = −8,4

Правила знаков для умножения

Запомнить правило знаков для умножения очень просто. Данное правило совпадает с правилом раскрытия скобок.

Запомните!

Минус на минус даёт плюс,

  Плюс на минус даёт минус.

+ · (+) = +	+ · (−) = −
− · (−) = +	− · (+) = −

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.

При чётном числе отрицательных множителей результат будет положительным, а при нечётном количестве — отрицательным.

Пример.

(−6) · (−3) · (−4) · (−2) · 12 · (−1) =

В примере пять отрицательных множителей. Значит, знак результата будет «минус».

Теперь вычислим произведение модулей, не обращая внимание на знаки.

6 · 3 · 4 · 2 · 12 · 1 = 1728

Конечный результат умножения исходных чисел будет:

(−6) · (−3) · (−4) · (−2) · 12 · (−1) = −1728

Умножение на ноль и единицу

Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.

• 0 · a = 0
• a · 0 = 0
• a · 1 = a

Примеры:

• 0 · (−3) = 0
• 0,4 · 1 = 0,4

Особую роль при умножении рациональных чисел играет отрицательная единица «−1».

Запомните!

При умножении на «−1» число меняется на противоположное.

В буквенном выражении это свойство можно записать:

a · (−1) = (−1) · a = −a

При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.

Пример умножения отрицательных и положительных чисел.

Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел

правило, примеры, умножение отрицательных чисел на положительные

В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение. Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.

Умножение отрицательных чисел

Определение 1

Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, -b данное равенство считается верным.

(-а)·(-b)=a·b.

Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: (-а)·(-b)=a·b. Статья умножение чисел с разными знаками рассказывает о том, что равенств а·(-b)=-a·b справедливое, как и (-а)·b=-a·b.

Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:

(-a)·(-b)=(-a·(-b))=-(-(a·b))= a·b.

Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.

Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.

Примеры умножения отрицательных чисел

Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.

Пример 1

Произвести умножение чисел -3 и -5.

Решение.

По модулю умножаемые данные два числа равны положительным числам 3 и 5. Их произведение дает  в результате 15. Отсюда следует, что произведение заданных чисел равно 15

Запишем кратко само умножение отрицательных чисел:

(-3)·(-5)=3·5=15

Ответ: (-3)·(-5)=15.

При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.

Пример 2

Вычислить произведение (-0,125)·(-6).

Решение.

Используя правило умножения отрицательных чисел, получим, что  (−0,125)·(−6)=0,125·6. Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:

Получили, что выражение примет вид (−0,125)·(−6)=0,125·6=0,75.

Ответ:  (−0,125)·(−6)=0,75.

В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.

Пример 3

Необходимо произвести умножение отрицательного -2 на неотрицательное log5 13.

Решение

Находим модули заданных чисел:

-2=2 и log513=-log5 3=log5 3.

Следуя из правил умножения отрицательных чисел, получим результат -2·log5 13=-2·log5 3=2·log5 3. Это выражение и является ответом.

Ответ:  -2·log5 13=-2·log5 3=2·log5 3.

Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Как использовать отрицательные фракции в уравнениях

Как использовать отрицательные фракции в уравнениях

Jana Russick

29 августов дробь — это дробь со знаком минус перед ней. Давайте покажем вам, как применять отрицательные дроби к уравнениям.

Что такое отрицательная дробь?

Вычитание дробей и применение отрицательной дроби к уравнению работают одинаково:

Когда вы вычитаете число, вы отнимаете его значение от другого числа. Иногда это может привести к тому, что конечное число будет меньше 0. Это показано в числовой строке ниже:

Изображение предоставлено: Desmos

Сложение двух чисел объединяет их значения. В приведенной выше числовой строке вы складываете значение положительной 1 и отрицательной , что равносильно вычитанию 1 .

При вычитании отрицательной дроби знак минус отменяется знаком вычитания. Вот почему исходная дробь превращается в положительное число:

То же самое происходит, когда вы умножаете дроби, обе из которых являются отрицательными числами:

Если вы посмотрите на переднюю часть дробей в этих скобках, обе они имеют отрицательные знаки. Когда вы умножаете две отрицательные дроби (или любые два отрицательных числа), результатом будет положительное число.

Примеры отрицательных дробей

Давайте решим эти математические задачи с отрицательными дробями, которые включают неправильные дроби и наименьший общий знаменатель:

Приведенные выше дроби являются неправильными дробями, потому что у каждой из них верхнее число (числитель) больше нижнего числа (знаменателя). Они также имеют разные знаменатели, поэтому нам нужно найти наименьший общий знаменатель, который является наименьшим членом, на который делятся 7 и 14 :

28 , это будет наименьший общий знаменатель. Теперь давайте перемножим числители и знаменатели, чтобы получить знаменатели числа 9.0053 28 .

Теперь, когда это эквивалентные дроби (у них один и тот же знаменатель), мы можем перейти к этой отрицательной дроби:

Мы можем упростить эту отрицательную дробь, разделив оба значения на 14, так как 14 входит в оба 14 поровну. и 28:

Когда вы будете использовать отрицательные дроби?

Вычитание дроби — это то же самое, что добавление отрицательной дроби. А умножение двух отрицательных дробей всегда дает положительный ответ. Знание того, как использовать отрицательные дроби, поможет вам лучше понять, как комбинировать дробные значения, и может быть полезно в вашей повседневной деятельности, такой как приготовление пищи.

Дополнительная помощь с домашним заданием по математике

• Лучшие стратегии умножения десятичных дробей
• Как решать дроби с показателями
• Пошаговое руководство по делению дробей на целые числа

Умножение и деление рациональных чисел| Turito

Ключевые понятия

• Умножение рациональных чисел
• Деление рациональных чисел

Введение :

• Понимание умножения и деления рациональных чисел.
• Применение правил умножения целых, десятичных и дробных чисел.
• Определите эквивалентные выражения для двух или более выражений.
• Примените правила деления целых, десятичных и дробных чисел, чтобы найти частное.
• Поймите, что целые числа делятся и делитель не равен нулю.
• Поймите, что отрицательная дробь записывается как положительный числитель и отрицательный знаменатель или как отрицательный числитель и положительный знаменатель.

1.8 Умножение рациональных чисел  

Умножение:

Когда мы умножаем целые числа, мы обычно заменяем многократное сложение знаком умножения  
(×).

Пример:  

3+3+3+3 = 4×3 = 12

Как умножать рациональные числа?  

Рассмотрим a/b,c/d как рациональные числа, тогда произведение рациональных чисел будет

a / b×c / d= a×c / b×d

Правила умножения: 

Правило 1. Если знаки множителей одинаковы, произведение положительное.

Правило 2: Если знаки множителей разные, то произведение отрицательное.

Пример:     

На изображении файлов cookie ниже показан пример 

Умножение десятичных дробей: 

Мы можем умножать десятичные дроби так же, как мы умножаем целые числа с несколькими цифрами.

• Умножить в обычном режиме, игнорируя десятичные точки.
• Поставьте в ответе запятую.

В ответе будет столько знаков после запятой, сколько исходных чисел вместе взятых.

Пример:  

Умножьте 3,1 × 2,9.

Решение:

3,1 × 2,9

Умножение без десятичных точек, мы получаем

31 × 29 = 899

3,1 имеет 1 десятичные места

и 2.9 имеет 1 десятичное место

So, продукт, у продукта 2 есть 2, у продукта есть 2, у продукта есть 2, у продукта есть 2, у продукта. десятичные разряды

Если поставить десятичную точку в произведении, то получится 8,99.

Умножение рациональных чисел на числовой прямой: умножьте − 2 / 7 на 3 в числовой прямой, 

Это означает 3 скачка − 2/7 влево от нуля. Теперь мы достигаем – 2/7. Таким образом, мы находим

− 2/7 × 3 = − 6/7,

т. е. − − 2/7 × 3 = − 2/7 × 3/1 =

− 2 × 3 / 7 × 1 = − 6 /7

1.8.1 Умножение отрицательного числа на положительное рациональное число  

Умножая отрицательное число на положительное рациональное число, мы просто умножаем целое число на числитель. Знаменатель остается прежним, и результирующее рациональное число будет отрицательным рациональным числом. Пример 10106  

3,5 × (–1,2) = –4,2

1.8.2 Умножение положительного числа на отрицательное рациональное число тогда результирующее рациональное число будет отрицательным рациональным числом.

−a / b×c / d=−ac / bd

Пример:  

Найдите произведение −5/6 и 2/5.

Решение:  

−5 / 6 × 2 / 5 = −5 × 2 / 6 × 5

= −10 / 30

  = −1/3

1.8.3 Умножение отрицательного числа на отрицательное рациональное число

 Умножая отрицательное число на отрицательное рациональное число, мы просто умножаем числитель и знаменатель, тогда полученное рациональное число будет положительным рациональным числом.

−a / b×−c=ac / b

Пример:  

Найдите произведение –0,3 и –11/30.

Решение:

−0,3×(−11/30) = −0,30×(−11/30)

Преобразуйте одно из рациональных чисел так, чтобы они оба были дробями или десятичными.

⇒ — 3 /10 × (-11/30)

= -3 × (-11) / 10 × 30

⇒33 / 300 или 0,11

1.9 Разделение рациональных чисел

Введение:

Что такое деление?

Деление — операция, обратная умножению.

Как делить рациональные числа?

Ниже приведены шаги для решения задач на деление рациональных чисел.

Шаг 1: Представить заданные рациональные числа в виде дроби.

Шаг 2: Оставьте числитель без изменений и умножьте на обратную величину знаменателя в рациональном числе.

Шаг 3: Найдите произведение рациональных чисел, которое есть не что иное, как деление рациональных чисел.

Пример 1: В следующем примере показано деление рациональных чисел в виде дроби: 

Пример 2: В следующем примере показано деление рациональных чисел в десятичной форме: 

Обратное: 

Когда множитель умножается на его обратное значение для данного рационального числа, мы получаем произведение 1.  

Обратное число a / b равно b/a

b/a

Произведение обратного числа 

Если мы умножим обратное значение рационального числа на это рациональное число, то произведение всегда будет равно 1. 

Пример  

Правила деления:

Если знаки делимого и делителя совпадают, то частное положительно.

Если знаки делимого и делителя разные, то частное отрицательно.

1.9.1 Деление отрицательного числа на положительное рациональное число  

Рациональное число называется отрицательным, если одно из них является положительным рациональным числом, а другое — отрицательным рациональным числом.

Примеры:  –2/5,3/–5,–5/7,11/–13 и т. д.

Пример 1:

Divide −3 (3/5) ÷ 6

Решение:

Дано

−3 (3/5) ÷ 6

= -18/5 ÷ 6

66) Обратное число 6 равно 1/6

= −18/5×1/6

=−18×1/5×6=−18/30=−3/5.  

1.9.2 Деление положительного числа число отрицательным рациональным числом  

Рациональное число называется положительным, если его числитель и знаменатель таковы, что один из них является отрицательным целым числом, а другой — положительным целым числом.

Примеры:  

2/−3,−3 / 5,−9 / 5,7 /−3 и т. д.

Пример 1:  Упростить 3x 2/3−2/3

Дано 3(2 / 3)÷−2 / 3

=11 / 3÷−2 / 3

Поскольку мультипликативная обратная величина −2 /3 равно −3/2, тогда мы получаем

= 11/3×−3/2

=11×(−3)/3×2=−33/6=−11/2=−5(1 /2).

1.9.3 Деление рациональных чисел с одинаковым знаком  

Когда и числитель, и знаменатель рационального числа либо положительные, либо отрицательные, то такие числа называются положительными рациональными числами.

Примеры:  

5 / 7, −30 / −9,95, −7 / −3 и т. д.

Пример 1:

Divide −3 / 4 ÷ −0,06

Решение:

Указано

−3 / 4 ÷ −0,06

= ( — 0,75) ÷ (0,06)

.