Умножить смешанное число на целое. Умножение дробей

Умножение и деление дробей.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:

Например:

Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…

Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:

Например:

Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:

В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями.

Например:

Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:

Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:

В первом случае (выражение слева):

Во втором (выражение справа):

Чувствуете разницу? 4 и 1/9!

А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:

то делим-умножаем по порядочку, слева направо !

И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:

Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.

Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!

Практические советы:

1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.

2. В примерах с разными видами дробей — переходим к обыкновенным дробям.

3. Все дроби сокращаем до упора.

4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно.

С первого раза! Без калькулятора! И сделайте верные выводы…

Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.

Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.

Вычислить:

Порешали?

Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать… Вот они, ответы, через точку с запятой записаны.

0; 17/22; 3/4; 2/5; 1; 25.

А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…

Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

1. Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
2. Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби .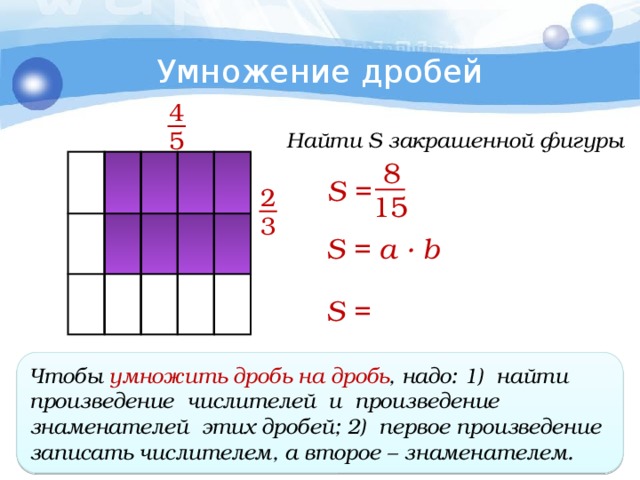

Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

• преобразовываем смешанные дроби в неправильные;
• перемножаем числители и знаменатели дробей;
• сокращаем дробь;
• если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.

Что такое дробь?

Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.

Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.

Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.

Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.

Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.

Разновидности дробей

Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.

Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.

Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.

Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями.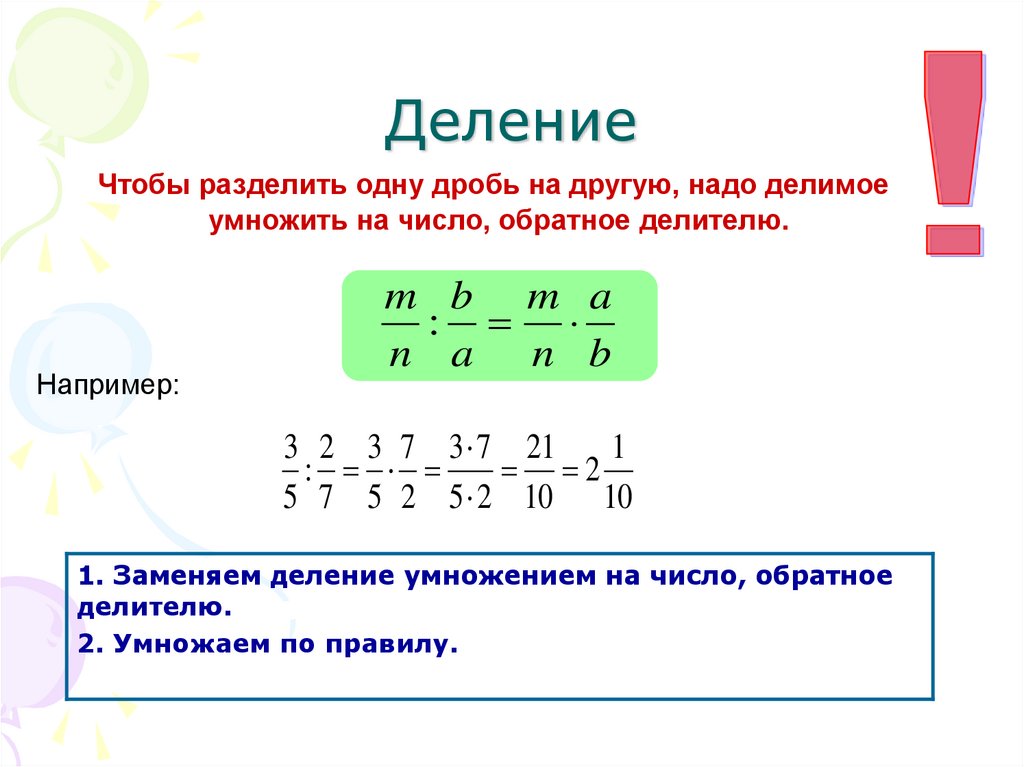 Если дробь правильная, то целая часть в десятичной записи будет равна нулю.

Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.

Пример . Представить дробь 7 21 / 1000 в десятичной записи.

Алгоритм перевода неправильной дроби в смешанное число и наоборот

Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:

• разделить числитель на имеющийся знаменатель;
• в конкретном примере неполное частное — целое;
• и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .

Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .

Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:

• целая часть умножается на знаменатель дробного выражения;
• полученное произведение прибавляется к числителю;
• результат записывается в числителе, знаменатель остается неизменным.

Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .

Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.

Ответ : 98 / 10.

Умножение дробей обыкновенных

Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.

Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.

Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .

Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .

Умножение дробей десятичных

Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:

• две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
• нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
• подсчитать количество цифр после знака запятой в каждом из чисел;
• в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
• если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.

Решение .

Умножение смешанных дробей

Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:

• перевести числа в смешанном виде в неправильные дроби;
• найти произведение числителей;
• найти произведение знаменателей;
• записать получившийся результат;
• максимально упростить выражение.

Пример . Найти произведение 4½ и 6 2 / 5.

Умножение числа на дробь (дроби на число)

Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.

Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:

• записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
• найти произведение, несмотря на запятую;
• в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.

Пример . Вычислить произведение 5 / 8 и 12.

Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

Ответ : 7 1 / 2.

Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.

Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.

Пример . Найти произведение 9 5 / 6 и 9.

Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.

Ответ : 88 1 / 2.

Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001

Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.

Пример 1 . Найти произведение 0,065 и 1000.

Решение . 0,065 х 1000 = 0065 = 65.

Ответ : 65.

Пример 2 . Найти произведение 3,9 и 1000.

Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.

Ответ : 3900.

Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.

Пример 1 . Найти произведение 56 и 0,01.

Решение . 56 х 0,01 = 0056 = 0,56.

Ответ : 0,56.

Пример 2 . Найти произведение 4 и 0,001.

Решение . 4 х 0,001 = 0004 = 0,004.

Ответ : 0,004.

Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.

Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.

Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.

Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.

Умножение дробей с разными знаменателями

Изначально стоит определить разновидности дробей :

• правильные;
• неправильные;
• смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей.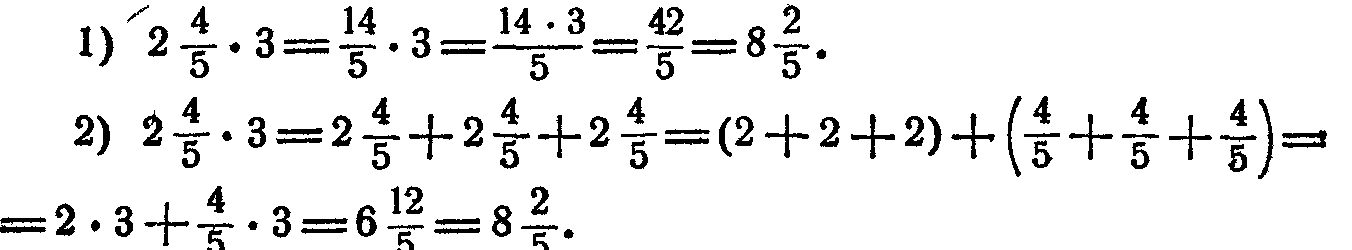 То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.

При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:

a/ b * c/ d = a*c / b*d.

Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.

Стоит рассмотреть умножение дробей с разными знаменателями на примерах:

• 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
• 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.

Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:

1 4/ 11 =1 + 4/ 11.

Как происходит перемножение

Предлагается несколько примеров для рассмотрения.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:

a * b/ c = a*b / c.

По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:

d * e/ f = e/ f: d.

Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.

Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.

В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:

a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.

Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».

Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.

В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.

Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.

В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».

Что будет, если переменную разделить и сразу умножить на одно и то же число

В одном из ИТ-пабликов мы увидели такой код на JavaScript:

> 7110 / 100 * 100 === 7110
< false
> 7120 / 100 * 100 === 7120
> true

Читается это так: сначала число 7110 делится на 100 и умножается на сто. Результат деления сравнивается с числом 7110, и JavaScript говорит, что результат не равен. Как будто если разделить на 100 и тут же умножить на 100, ты получишь не то же самое число, с которого начинал.

Во втором примере то же самое, но с числом 7120. Если его разделить на 100 и умножить на 100, получится ровно 7120. Получается, что одни и те же математические действия в двух случаях дали разные результаты. Как такое возможно? 

Если разобрать этот код, мы увидим, что ошибки нет, — но нужно понимать, как работает JavaScript.

Деление и дробные числа

Когда мы делим одно число на другое и они не делятся нацело, то получаем дробное число — целую часть и то, что идёт после запятой. Но компьютер не использует стандартное школьное деление в столбик — вместо этого он представляет число в виде последовательности нулей и единиц и использует побитовые операции для деления. 

Это значит, что он не останавливается, например, после точного вычисления 7110 / 100 = 71,1, а работает со всеми битами сразу. После такого деления у компьютера получается последовательность, например 11101011011011101, где 11010 — это целая часть, а всё остальное — дробная. Если ему понадобится в целой части хранить число побольше, то он просто возьмёт дополнительное место за счёт дробной части. 

Получается, что запятая в такой переменной как бы плавает в зависимости от знаков до запятой, отсюда и название — «число с плавающей запятой» (floating point по-английски). Но когда компьютер забирает разряды у дробной части, он иногда может этим внести небольшую погрешность, например потерять последнюю цифру в дробной части (например, одну миллиардную).

Как точность деления влияет на умножение

Когда мы после деления умножаем результат на 100, то с точки зрения компьютера это просто побитовый сдвиг точки вправо на несколько разрядов. Если у нас всё было посчитано точно, то результат будет таким же, что и до деления.

Но всё дело в том, что иногда компьютер не может что-то поделить, хотя с точки зрения математики там всё просто. В этом случае он заполняет результатами вычисления все доступные нули и единицы в переменной, а остальное отбрасывает. Это значит, что результат уже получился неточный, а приблизительный, и дальше ошибка будет только расти.

Давайте посмотрим, что получается в каждом случае после деления:

В первом случае компьютер не смог поделить 7110 на 100 без остатка, поэтому при умножении он потащил за собой девятки после запятой. Отсюда и неточность при сравнении. 

Как исправить

В JavaScript есть объект Math, который занимается всякой полезной математикой. И у этого объекта есть метод .round(), который может корректно округлить число до ближайшего целого. Зная о возможной ошибке в коде, нам стоит использовать это округление: 

>Math.round(7110/100*100)===7110
<true
>Math. round(7120/100*100)===7120
<true

Где это может пригодиться

Обратите внимание на этот эффект, если пишете программу, в которой используется деление непредсказуемых чисел — например, если пользователь вводит что-то с клавиатуры, а вы потом совершаете с этими числами свои операции. Например, вы получили рост человека, поделили его на какой-то внутренний коэффициент и сравниваете со своими референсными значениями. Сделайте поправку на то, что при делении могла сломаться точность, и либо округляйте число, либо предусматривайте запасы при сравнении. 

Кстати, ровно для этого и существуют тестировщики. Их задача, в частности, в том, чтобы прогнать сквозь программу все возможные варианты значений, которые может ввести пользователь, и отловить вот такие ошибки вычислений. Чаще всего для такого используют автоматические тесты — но чтобы понимать, что тестировать, нужно знать, где может быть ошибка. Теперь вы знаете. 

Бонус: строгое сравнение ===

В нашем коде используется строгое сравнение, которое в JavaScript обозначается тремя знаками равенства. Строгое сравнение означает, что сравниваются не только значения, но и типы сравниваемых данных. Грубо говоря, число 1 и строка с символом ‘1’ с точки зрения строгого сравнения — разные вещи, хотя для людей внешне это одно и то же. 

Есть ещё нестрогий оператор ==. Вот как он работает: 

1. Берёт оба аргумента сравнения.
2. Смотрит, к какому единому общем типу данных их можно привести. Например, сделать оба аргумента строками, числами или превратить их в логические элементы.
3. Сравнивает данные одного типа и понимает, равны они или нет.

В обычных ситуациях сравнение работает хорошо и мы даже не задумываемся о том, как оно устроено внутри. Но иногда нужно точно выяснить, одинаковые ли у нас аргументы по всем параметрам или нет — вот для этого и используется оператор строгого сравнения ===. Он работает так:

1. Берёт первый аргумент и выясняет его тип — целое число, дробное, логический тип и так далее.
2. Делает то же самое со вторым аргументом.
3. Сравнивает их типы между собой. Если они равны — переходит к дальнейшему сравнению. Если не равны — возвращает false.
4. Если типы равны, то сравнивает значения — и тоже возвращает false, если значения не совпадают между собой.

Текст:

Михаил Полянин

Редактор:

Максим Ильяхов

Художник:

Даня Берковский

Корректор:

Ирина Михеева

Вёрстка:

Кирилл Климентьев

Соцсети:

Алина Грызлова

Пошаговое руководство — Психометрический успех

Обновлено 18 мая 2022 г.

Что такое дроби?

Дроби — это числовые величины, представляющие значения меньше единицы. Также известные как дробные числа, они обычно используются для измерения частей целого, например:

• Половина (1/2)
• Одна пятая (1/5)
• Две трети (2/3)

Дроби

Дроби состоят из двух чисел, одно над и одно под разделительной чертой.

Нижнее число известно как знаменатель и относится к отдельным частям целого.

Когда мы говорим о знаменателе, мы используем порядковые числительные, то есть числа, определяющие положение, например «третье» или «четвертое».

Верхнее число дроби называется числителем и указывает на то, со сколькими частями целого мы имеем дело.

Самый простой способ определить дробь — представить себе круг, разделенный поровну на шесть частей.

Сам пирог представляет собой единое целое, а отдельные ломтики — его части. Поскольку у нас есть шесть равных частей одного целого, наш знаменатель здесь равен 6.

Если мы возьмем один кусок пирога, у нас будет одна шестая (1/6). Два среза эквивалентны двум шестым (2/6) и так далее.

Само по себе это довольно просто понять. Однако существуют разные типы дробей и разные методы для выполнения каждого типа дробного уравнения.

Ключевые факты о фракциях

Чтобы понять, как вычислять дроби, важно усвоить основы. Во-первых, давайте рассмотрим три разных типа дробей:

Определения и примеры дробей

• Правильная дробь – Правильная дробь – это дробь, в которой числитель меньше знаменателя. 1/2, 10/15 и 85/100 — все это примеры правильных дробей. Общее значение правильной дроби всегда меньше единицы.

• Неправильная дробь – В неправильной дроби значение числителя больше значения знаменателя. 6/3, 25/18 и 50/20 — все это примеры неправильных дробей. Общее значение неправильной дроби всегда больше единицы.

• Смешанные дроби – Смешанная дробь представлена ​​целым числом, за которым следует дробное число, например 2⅔, 6⅘ или 25⅝. Смешанные дроби также известны как смешанные числа.

Ключевые термины

Теперь, когда мы знаем, какие бывают дроби, давайте посмотрим на некоторые другие ключевые термины и фразы:

• Эквивалентные дроби – это дроби, которые кажутся разными, но имеют одинаковое значение. Например, 2/3 равно 4/6.

• Упрощенные дроби – это дроби, приведенные к наименьшей форме. По сути, низший эквивалент высшей дроби. Итак, в приведенном выше примере 2/3 — это упрощенная версия 4/6.

• Обратные числа — Здесь дробь переворачивается путем размещения знаменателя над числителем. Например, обратное 2/3 равно 3/2. Обратные числа используются при делении и умножении дробей (5 ÷ 1/5 равно 5 х 5/1 или 5 х 5).

Дроби также могут быть представлены в виде десятичных знаков и процентов . Мы рассмотрим, как преобразовать дроби в приведенных ниже примерах уравнений.

10 простых дробей и способы их решения

Ниже приведены десять примеров дробных уравнений и рекомендации по их решению. Если вы работаете с дробями на экзамене, обязательно покажите свой метод.

1. Как преобразовать смешанную дробь в неправильную дробь

Как уже говорилось, смешанная дробь состоит из целого числа, за которым следует дробное число. В этом примере мы будем использовать смешанную дробь семи и четырех пятых, записанную численно как 7⅘.

При запросе на преобразование смешанной дроби в неправильную:

• Сначала умножьте целое число на знаменатель дробной части.
• Возьмите полученное число и добавьте его к числителю дроби.
• Возьмите эту последнюю цифру в качестве нового числителя и поместите ее над первоначальным знаменателем. Это дает вам неправильную дробь.

Пример:

Пример вопроса

Преобразуйте 7⅘ в неправильную дробь.

2. Как преобразовать дробь в десятичную

Поскольку оба используются для определения значений меньше единицы, десятичная дробь — это просто другой способ представления дроби.

Метод, используемый для преобразования дроби в десятичную, представляет собой простое деление: вы просто делите числитель на знаменатель.

Пример:

Пример вопроса

Преобразование 3/10 в десятичную дробь.

Практика числового мышления

3. Как преобразовать дробь в проценты

Существует три простых способа преобразования дроби в проценты. Мы рассмотрим их все здесь, используя одну и ту же дробь 7/20.

Первый метод:

Разделите числитель на знаменатель, затем умножьте полученное число на 100, чтобы получить процентное преобразование:

7 ÷ 20 = 0,35

Умножить числитель на 100, затем разделить полученное число на знаменатель:

7 x 100 = 700

700 ÷ 20 = 35%

Метод третий:

3 десятичная точка вашего ответа на два знака вправо:

7 ÷ 20 = 0,35

Перемещение десятичной точки дает преобразование 35%.

При преобразовании дроби в процент всегда не забывайте включать в свой ответ знак %.

4. Как складывать дроби

Процесс сложения дробей прост при условии, что знаменатели совпадают.

В качестве базового примера возьмем 1/6 + 3/6. В этом случае у вас равные знаменатели, поэтому просто сложите числители обеих дробей, придерживаясь нижней цифры 6:9.0003

1 + 3 = 4

Итак, 1/6 + 3/6 = 4/6

При сложении дробей, в которых меньшие числа не совпадают, вам сначала нужно найти наименьший общий знаменатель . Это наименьшее число, которое полностью делится на оба существующих знаменателя.

Пример:

Пример вопроса

1/4 + 2/3

5. Как вычитать дроби

Как и в случае сложения, вычитание дробей легко, когда знаменатели одинаковы. Нужно просто вычесть второй числитель из первого, сохранив нижнее число тем же.

Пример:

Пример вопроса

4/7 – 3/7.

Теперь давайте посмотрим на вычитание дробей с различными знаменателями .

Пример:

Пример вопроса

4/5 – 2/3

6. Как делить дроби

Чтобы разделить одну дробь на другую, сначала нужно превратить делимую дробь в обратную, переключив знаменатель и числитель.

Пример:

Пример вопроса

Возьмем пример 1/2 ÷ 1/5, последняя дробь как обратная 5/1.

Теперь умножьте первую дробь на обратную:

1/2 x 5/1

Для этого умножьте числители и знаменатели:

1 x 5 = 5 (числители)

2 x 1 = 2 (знаменатели)

Итак, 1/2 x 5/1 = 5/2

7. Как умножать дроби

Процесс вычисления дробей путем умножения друг на друга прост:

• Умножьте ваши числители
• Умножьте ваши знаменатели
• Напишите новый числитель над новым знаменателем

Пример:

Пример вопроса

Используя пример уравнения 1/2 x 1/6:

1 x 1 = 1 (числители)
2 x 6 = 12 (знаменатели)

Как сделать Упростить дробь

Упростить дробь означает привести ее к самой простой форме. По сути, найти наименьшую возможную эквивалентную дробь.

Сначала найдите наибольший общий делитель . Это наибольшее целое число, на которое делятся и числитель, и знаменатель.

Для этого запишите все множители для обеих частей вашей дроби, как показано ниже на примере 32/48:

Пример вопроса

• Множители 32: 1, 2, 4, 8, 16, 32
• Коэффициенты 48: 1, 2, 3, 4, 8, 12, 16, 24, 48

Наибольший общий множитель здесь: 16

Теперь разделите числитель и знаменатель на это число, чтобы найти упрощенную дробь:

32 ÷ 16 = 2 (числители)
48 ÷ 16 = 3 (знаменатели)

Заполняя любую форму дробного уравнения, всегда упрощайте свой ответ. до минимально возможной формы.

9. Как вычислять дроби величин

Когда вам представят количество и попросят вычислить дробную часть, просто разделите данное количество на знаменатель дроби, а затем умножьте это число на числитель.

Пример:

Пример вопроса

У вас есть 55 конфет, две пятых из которых вы хотите отдать соседу, чтобы он забрал его домой. Сколько конфет она возьмет?

Разделите данную сумму на знаменатель дроби: 55 ÷ 5 = 11

Умножьте это число на числитель: 11 x 2 = 22

другой, либо умножить, либо разделить обе части одной дроби на одно и то же целое число.

Если ваши ответы также являются целыми числами, то дробь сохраняет свое значение и эквивалентна.

Пример:

Пример вопроса

Чтобы определить, равно ли 12/15 4/5, разделите 12 и 15 на целое число:

12 ÷ 2 = 6
15 ÷ 2 = 7,3 900

Поскольку у вас нет целой цифры в качестве ответа, перейдите к следующему основному числу:

12 ÷ 3 = 4
15 ÷ 3 = 5

Вы также можете сделать это в обратном порядке, умножив обе части нижняя дробь:

4 x 3 = 12
5 x 3 = 15

По сути, если одна дробь является упрощенной версией другой, то они эквивалентны.

Практика числового мышления

Резюме

Дроби — это числовые величины, которые помогают нам измерять равные части целого.

Они бывают в виде правильных, неправильных и смешанных дробей и могут быть легко преобразованы в десятичные точки и проценты.

Методы, используемые в дробных уравнениях, различаются в зависимости от решаемой задачи, и каждый из них необходимо практиковать с осторожностью, убедившись, что вы полностью понимаете вопрос, и показывая, как вы работаете.

Хотя поначалу они могут показаться пугающими, время, потраченное на понимание основных правил, должно помочь вам научиться с легкостью вычислять дроби.

Подготовка учащихся к умножению дробей

Стенограмма подготовки к умножению дробей
Карточка: TCH Teaching Channel TeachingChannel.org

Карточка: Mount Erie Elementary Anacortes, Washington

+++ 00:00:04 +++
Olivia: You разделите его пополам, вот так, а потом будет три, шесть, девять, двенадцать.
Студент: Итак, мы сделали 12 разделить на 12 равно 1.
Студент: Я совсем не понимаю.
Алисия Фармер: На самом деле мы работаем с двумя фракциями, и мы собираемся говорить об этом, это новый тип мышления.
Карточка: Иллюстративная математика: Подготовка к умножению дробей

+++ 00:00:25 +++
Алисия Фармер: Хорошо. Мы собираемся начать с половины от 16.
Алисия Фармер: Начала урок с числа, поэтому все ученики выходят на этаж, и мы следуем некоторым процедурам для нашего числа, когда дети показывают мне, что они могут сделать. ментальный—
Карточка: Алисия Фармер, учитель математики 5-го класса, начальная школа Маунт-Эри, Анакортес, Вашингтон,

Алисия Фармер: — арифметика, но с концептуальным пониманием. Так что дело не только в том, что я умножаю или прибавляю в уме, а в том, что я делаю с этими числами, что позволяет мне это делать.

+++ 00:00:51 +++
Алисия Фармер: Хорошо. У кого есть решение для половины от 16? Фредди?
Фредди: Думаю, ответ восемь.
Алисия Фармер: У тебя восемь. Дайте мне встряхнуть, если у вас тоже есть восемь?

Алисия Фармер: Хорошо. Все получили восемь. Хорошо. Давай, расскажи нам, как ты получил восемь?
Фредди: Хорошо. Итак, я получил, что восемь плюс восемь будет равно 16, а также восемь умножить на два будет равно 16, так что я это знал.
Алисия Фармер: Хорошо. Значит, половина этого числа будет одной из этих восьмерок?
Фредди: Ага.
Алисия Фармер: Хорошо. Хорошо. Итак, давайте попробуем — хотите попробовать посложнее?
Студенты: Да.

+++ 00:01:21 +++
Алисия Фармер: Итак, мы просто взяли половину из 16, затем четверть из 16, а затем восьмую из 16. А потом я перешла к трем восьмым. Я хотел посмотреть, что они могут сделать с неединичными дробями, потому что в четвертом классе это все единичные дроби с целыми числами.
Алисия Фармер: Хорошо. Вот так. Три восьмых из 16.
Ученики:
Алисия Фармер: Вы всегда понимаете, что это вызов, когда слышите потом.

+++ 00:01:47 +++
Алисия Фармер: Тоскан, что ты взял?
Тоскан: У меня шесть.
Алисия Фармер: Хорошо. Дайте мне встряхнуть, если у вас есть шесть.

Алисия Фармер: Хорошо. Почему бы тебе не начать с того, что ты сделал?
Тосканский: это вроде как 16 разделить на два равно восьми. Однако —
Карта: тосканская, ½ от 16 равно 8. 16/2 = 8
Тоскан: тогда я знаю, что при делении можно поменять местами двойку и восьмерку, и это все равно будет правильно.
Тоскана: Значит, два — это одна восьмая от 16, а затем…
Тоскана: — дважды три равно шести, потому что это три восьмых.
Алисия Фармер: равно шести?
Тоскан: Ага.

+++ 00:02:17 +++
Алисия Фармер: Значит, нам стоит нервничать, если числитель не равен единице?
Студенты: №
Алисия Фармер: Хорошо.

Алисия Фармер: Отличная работа, ребята.

+++ 00:02:24 +++
Алисия Фармер: После телефонного разговора они вернулись на свои места, и я представляю ситуацию: у нас был сбор средств, и мы продавали квадратные формы кукурузного хлеба. И обычно, когда вы покупаете кукурузный хлеб, он обычно уже нарезан для вас. Это мило. Но мы математики, так что бросим себе вызов.
Алисия Фармер: Всю неделю мы говорили о сборе средств для нашей горной школы. Вы, ребята, помните это?
Студентов:
Алисия Фармер: Хорошо. И мы решили, что у нас будет этот Chili Cook-Off для округа. Итак, мы собираемся продавать квадратные формы кукурузного хлеба на этом Chili Cook-Off, верно?

+++ 00:02:55 +++
Алисия Фармер: Когда вы начинаете, первая дробь говорит вам, сколько кукурузного хлеба еще осталось на сковороде. И тогда вы должны перейти к тому, что кукурузный хлеб теперь ваше новое целое. Вместо сковороды теперь только кукурузный хлеб, и вы берете его часть. Но тогда вопрос на самом деле заставляет вас вернуться назад и выяснить, сколько на самом деле купил этот человек.
Алисия Фармер: Итак, давайте поговорим о нашей цели обучения на сегодня.
Карточка: Учебная цель, Мы можем… решать задачи реального мира, используя дроби, Критерии успеха, Успех означает, что я могу:
Алисия Фармер: Мы можем решать задачи реального мира, используя дроби. Карта
: общие базовые стандарты, решение реальных задач, связанных с умножением дробей.
Алисия Фармер: Заметьте, я не сказала вам, что это: сложение, вычитание, умножение или деление. Карта
: общие базовые стандарты, решение реальных задач, связанных с умножением дробей.
Алисия Фармер: Это часть сегодняшнего обучения, хорошо?

+++ 00:03:26 +++
Алисия Фармер: Это действительно первый раз, когда ученики принимают участие в чем-либо. В четвертом классе рассматривают повторение с целыми числами и дробями.
Алисия Фармер: Это требует, чтобы вы изменили свой мыслительный процесс о том, о чем я на самом деле говорю.
Алисия Фармер: Хорошо. Мы собираемся начать с личного времени на размышления. Я даю тебе пять минут на таймере, и в конце ты уходишь на второй круг. Таким образом, ожидается, что у вас есть чем поделиться в конце пяти минут. Значит ли это, что у вас должен быть ответ?
Студенты: №

+++ 00:03:54 +++
Алисия Фармер: Может кто-нибудь сказать мне, что вы могли бы сказать на уход, если у вас еще нет решения? Эрик?
Эрик: Вы можете сказать, с чего вы начали или что вы понимаете и чего не понимаете.
Алисия Фармер: Да, это было бы очень хорошо. Я имею в виду, что я начал это, а затем застрял, потому что это не имело смысла, и вы хотите быть конкретными в отношении того, что это за вещи. Вы, ребята, можете идти вперед и начинать.

+++ 00:04:16 +++
Алисия Фармер: Я пыталась создать культуру, в которой все ученики понимают, что их мнения, их мысли и их рассуждения ценятся. Даже оплошности. Даже недостатки. Даже ошибки, которые вы делаете. Все они ценны, потому что все они представляют собой возможности обучения от старых стандартов до стандартов Common Core, получить правильный ответ недостаточно. Это не готовит наших учеников к тому, чтобы они были грамотными математическими гражданами мира.
Алисия Фармер: Они должны понимать концепции, лежащие в основе этих процедур. Таким образом, происходит переход к пониманию того, что вы делаете на этом пути, к способности объяснить это, сообщить об этом.

+++ 00:04:49 +++
Алисия Фармер: Сейчас мы начнем уход на второй круг. После того, как все четыре человека поделятся, я бы хотел, чтобы вы поработали за столом, чтобы прийти к окончательному решению, с которым все согласны.
Ученик: Я хотел превратить ту, что у нее осталась из одной четверти, в третью.
Алисия Фармер: Если вам нужно прийти к общему мнению, это означает, что вы должны быть в состоянии объяснить, о чем вы думаете.

+++ 00:05:12 +++
Алисия Фармер: Значит, им нужно не только показать работу, но и построить эти математические аргументы и произнести их вслух.
Оливия: Как вы думаете, ребята, сколько она выкупила из всего лотка?
Студент: 13, один и 13.
Студент: Почему ты… почему ты…
Студент: Подумай.
Оливия: Ага.
Студент: Я нашел здесь кое-что, на котором было написано половина 12 долларов. Итак, я знал, что одна треть обошлась мисс Фармер в 13 долларов, вот откуда я это знал.

+++ 00:05:36 +++
Оливия: Вы, ребята, думаете, что это может быть одна двенадцатая, потому что если вы пойдете так, вам понадобится еще одна, потому что там написано одна четвертая—
Студент: Да. Ага.
Оливия: — о кукурузном хлебе.
Ученик: И ты получил только. ..
Ученик: А потом…
Ученик: Ты должен был все это вычеркнуть.
Оливия: Да, потому что…
Студент: Вот такие вещи.
Студент: Хорошо. Хорошо.
Оливия: Теперь понятно?
Студент: Это было…
Студент: Да.
Оливия: Ага.

+++ 00:05:54 +++
Алисия Фармер: Я хожу и просто делаю заметки, как мысленные, так и часто физические, где дети. Например, где они могли войти в проблему или у них не было доступа. Я изучаю, какие из них могут читать контекст, а затем применять его и иметь стратегию для решения этой проблемы.
Алисия Фармер: А еще я ищу и выбираю работы для детей.
Алисия Фармер: Итак, я хотела бы начать с Энджи. Можешь привести туда свою схему?
Энджи: Здесь?
Алисия Фармер: Ммм.

+++ 00:06:23 +++
Энджи: Я поняла, что не могу вычесть три из четырех, так что я сделала модель столбцов и то, что я сделала, я превратила ее в четверти, затем разрезал его на три части и раскрасил одну треть, а затем обвел одну и пересчитал все маленькие квадратики, и я получил одну двенадцатую.

+++ 00:06:46 +++
Алисия Фармер: Я упомянула, а затем я добавила к ней Эрика, потому что хотела показать, что Энджи — это то, что мы уже делали в классе с эквивалентными дробями. И тогда у Эрика было немного по-другому.
Эрик: Я много раз пытался и потерпел неудачу, но в конце концов у меня получилось. Итак, что я сделал, так это разделил свою диаграмму на четыре части, а затем заштриховал эту одну четверть, чтобы напомнить себе, что там только одна четверть. а затем я разделил каждую четвертую на три, а эту заштриховал темнее, чтобы вы знали, что это одна треть, которую я использую.

+++ 00:07:25 +++
Алисия Фармер: Чем этот отличается или похож на Энджи? Оливия?
Оливия: Его модель немного по-другому устроена. Таким образом, они настроены на трети.
Алисия Фармер: Значит, у него два…
Оливия: Да.
Алисия Фармер: — ряды—
Карточка: Эрик, Энджи
Алисия Фармер: — шесть штук, а на самом деле у нее три ряда по четыре. Хорошо. Спасибо, Эрик. Присаживайся.
Алисия Фармер: Затем ученики вернулись и решили новую задачу с неединичной дробью.

+++ 00:07:49 +++
Алисия Фармер: Значит, у него был числитель, отличный от единицы. И это немного сложнее, потому что вы говорите о большем количестве кусочков кукурузного хлеба, которые на самом деле есть. и они попытались применить стратегии, которые они увидели у студентов, которые представили или уже работали в их группе, к новой ситуации.
Ученик: Я перечеркнул эту часть кукурузного хлеба прямо здесь, а потом у меня осталось пять здесь, и я знаю, что всего 12, так что у меня получилось пять двенадцатых.

+++ 00:08:21 +++
Алисия Фармер: И в этой части я действительно увидела, способны ли ученики применять то, что мы узнали, о чем я спрашивал, что они узнали. отвечал о. Так что это была практика, но также и углубление этого понимания.
Ученик: Я обвел пять, которые он купил, и вот что он оставил, и столько он взял с собой.

+++ 00:08:43 +++
Алисия Фармер: Процедуры, дети называют их как угодно, от трюков до ярлыков, эти вещи можно запомнить, а потом быстро забыть.