Преобразование дробей
В школе VIII вида учащиеся знакомятся со следующими преобразованиями дробей: выражением дроби в более крупных долях (6-й класс), выражением неправильной дроби целым или смешанным числом (6-й класс), выражением дробей в одинаковых долях (7-й класс), выражением смешанного числа неправильной дробью (7-й класс).
300
Выражение неправильной дроби целым или смешанным числом
I Изучение данного материала следует начать с задания: взять 2 шитых круга и каждый из них разделить на 4 равные доли, подсчи-ь количество четвертых долей (рис. 25). Далее предлагается Писать это количество дробью ( т ) • Затем четвертые доли при-1дываются друг к другу и ученики убеждаются, что получился
л
1ый круг. Следовательно, -т= 1 . К четырем четвертям добавляет-последовательно еще по -т, и ученики записывают: т=1, -7=1 6 2 7 3 8 9
4′
Г=1 4′
 е. выражали неправильную дробь целым
или смешанным числом.
Далее надо стремиться к тому, чтобы
учащиеся самостоятельно
определили, каким арифметическим
действием это преобразова-» пие
можно выполнить. Яркими примерами,
приводящими к ответу
е. выражали неправильную дробь целым
или смешанным числом.
Далее надо стремиться к тому, чтобы
учащиеся самостоятельно
определили, каким арифметическим
действием это преобразова-» пие
можно выполнить. Яркими примерами,
приводящими к ответу4 . 8 0 5 ,1 7 ,3 „ Л
на вопрос, являются: -2-=! и т=2, 4″=1т и т Т «ЫВ°Д: чтобы
выразить неправильную дробь целым или смешанным числом, нужно числитель дроби разделить на знаменатель, частное записать целым числом, остаток записать в числитель, а знаменатель оставить тот же. Так как правило громоздкое, совсем не обязательно, чтобы учащиеся заучивали его наизусть. Они должны уметь последовательно рассказать о действиях при выполнении данного преобразования.
Перед
тем как познакомить учащихся с выражением
неправильной
дроби целым или смешанным числом,
целесообразно повторить
с ними деление целого числа на целое с
остатком. -. В итоге формулируется правило:
чтобы смешанное число
-. В итоге формулируется правило:
чтобы смешанное число
выразить неправильной дробью, надо знаменатель умножить на целое число, прибавить к произведению числитель и сумму записать числителем, а знаменатель оставить без изменения.
Вначале нужно упражнять учащихся в выражении неправильной дробью единицы, затем любого другого целого числа с указанием знаменателя, а уже затем смешанного числа:
7′
302
Основное свойство дроби1
[онятие неизменяемости дроби при одновременном увеличении
1 уменьшении ее членов, т. е. числителя и знаменателя, усваи- 1тся учащимися школы VIII вида с большим трудом. Это поня- Ь необходимо вводить на наглядном и дидактическом материале,
,’ичем
важно, чтобы учащиеся не только наблюдали
за деятельностью учителя, но и сами
активно работали с дидактическим
материалом
и на основе наблюдений и практической
деятельности приходили
к определенным выводам, обобщению. обнаруживается,
что
обнаруживается,
что
числитель и знаменатель дроби тг увеличивается в одно и то же число раз, дробь от этого не изменяется.
После рассмотрения ряда примеров следует предложить учащимся ответить на вопрос: «Изменится ли дробь, если числитель Некоторые знания по теме «Обыкновенные дроби» исключаются из учебных программ по математике в коррекционных школах VIII вида, но они сообщаются учащимся в школах для детей с задержкой психического развития, в классах выравнивания для детей, испытывающих трудности в обучении математике. В данном учебнике параграфы, где дается методика изучения этого материала,
обозначены звездочкой (*).
303
I
л
и знаменатель дроби умножить на одно и то же число (увеличит -в одно и то же число раз)?» Кроме того, надо попросить учащихс самим привести примеры.
Аналогичные
примеры приводятся при рассмотрении
уменыш ния
числителя и знаменателя в одно и то же
число раз (числители и
знаменатель делятся на одно то же
число). Например, кр>’
Например, кр>’
( 4 \ делят на 8 равных частей, берут 4 восьмые доли круга I -о- ]
укрупнив доли, берут четвертые, их будет 2. Укрупнив доли
4 2
1 берут вторые. Их будет 1
числители и знаменатели этих дробей, отвечая на вопросы: «В<> сколько раз уменьшается числитель и знаменатель? Изменится ли дробь?».
Хорошим пособием являются полосы, разделенные на 12, 6, 3 равные части (рис. 26).
-1 =1-1
12 6 3 Рис. 26
На
основании рассмотренных примеров
учащиеся могут сделать
вывод: дробь не изменится, если
числитель и знаменатель дроби
разделить на одно и то же
число (уменьшить в одно и то
же число раз). Затем дается обобщенный
вывод — основное свойство дроби: дробь
не изменится,
если числитель и знаменатель дроби
увеличить или умень шить
в одно и то же число раз.
Конспект урока математики в 8 классе «Умножение обыкновенных дробей на целое число» | План-конспект урока по математике (8 класс) на тему:
8 класс
Тема: Умножение обыкновенных дробей на целое число
Тип урока: урок закрепления знаний и умений
Цель: закрепить алгоритм выполнения умножения обыкновенных дробей на целое число.
Задачи:
Образовательные: развивать умение учащихся выполнять умножение обыкновенных дробей на целое число. Отрабатывать умение преобразовывать обыкновенные дроби.
Коррекционно-развивающие: корригировать мышление посредством развития умения рассуждать (на примере выполнения действия умножения обыкновенных дробей и преобразования обыкновенных дробей).
Воспитательные: развивать умения и навыки работать в коллективе и самостоятельно; воспитывать у учащихся стремление к знаниям, упорство в достижении цели, уважение к другим людям, к их мнению.
Оборудование: учебник, опорные таблицы «Сокращение дробей», «Замена неправильной дроби целым числом», «Замена неправильной дроби смешанным числом», таблица №5 «Обыкновенные дроби – умножение и деление» (шкаф №13), набор «Доли и дроби» (шкаф №7, коробки №4,5), набор цифр (шкаф №10, коробка №11), карточки с числами для устного счета.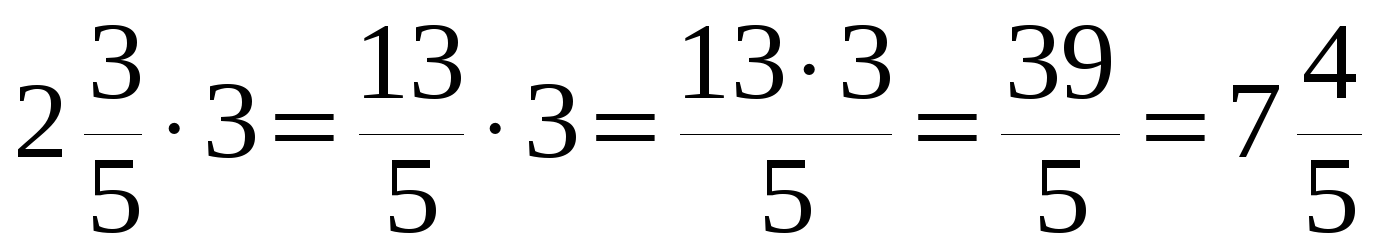
Ход урока
№ | Содержание урока | Оборудование |
1 | Организационный момент Организация рабочего места, правильная посадка, настрой на урок | |
2 | Устный счет
; ; ; ;
; ; ; ;
8000 и 5 6 и 100 3 и 90 22 и 4. | Карточки с числами (зрительная опора) |
3 | Основная часть урока
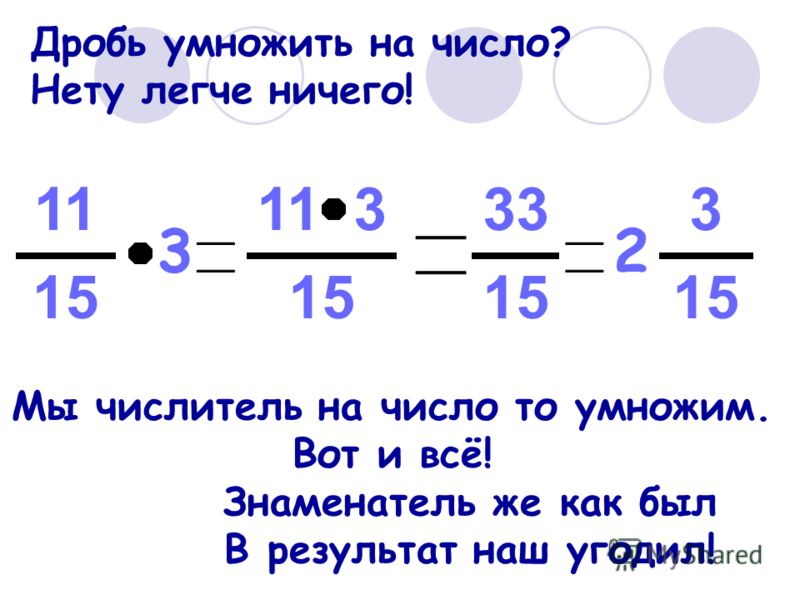
х 3 = + + = = = 1 = 1 3 х 21 = = = = = 12 1 Вывод: чтобы умножить дробь на целое число, нужно числитель дроби умножить на целое число, а знаменатель оставить без изменения (стр.109 – правило в рамочке).
Найти произведение чисел: х 3 х 20 х 20 х 2 х 7 х 4 Фронтальная проверка | Набор «Доли и дроби», таблица «Обыкновенные дроби – умножение и деление», тетради Учебник Разноуровневые карточки, тетради |
4 | Физкультминутка Упражнения на коррекцию осанки Выполнить названное учителем движение такое количество раз, которое соответствует цифре на карточке | Карточки с цифрами |
5 | Закрепление материала
Фронтальное решение
Сравнить выражения: х 15 … х 28 х 25 … х 21 Взаимопроверка | Учебник, тетради Учебник, тетради, инд. |
6 | Физкультминутка Упражнения для глаз Дыхательная гимнастика | |
7 | Итог урока
Найти значение выражения: х 7 + 5 – 14 х Индивидуальная проверка | Учебники, тетради |
8 | Домашнее задание Примеры № 309 2) 1я стр. | Учебник, дневники |
9 | Выставление оценок | Дневники |
Приложения
8000 и 5
6 и 100
- и 90
22 и 4
Карточка № 1. 1
1
Найти произведение чисел:
х 3 х 20 х 20
х 2 х 7 х 4
Карточка № 2.1
Сравнить выражения:
х 15 … х 28
х 25 … х 21
Карточка № 3.1
Найти значение выражения:
х 7 +
5 – 14 х
Карточка № 1.2
Найти произведение чисел:
х 3 х 20
х 10 х 2
Карточка № 2.2
Сравнить выражения:
х 16 … х 28
Карточка № 3.2
Найти значение выражения:
х 7 +
5 – 2 х
Обучение 4.NF.B.4 .a.b.c — Понимание дроби a/b как кратной 1/b — Умножение дроби на целое число
Составление дробей из единичных дробей. CCSS.Math.Content.4.NF.B.4
Применение и расширение предыдущего понимания умножения для умножения дроби на целое число.
CCSS.Math.Content.4.NF.B.4.a
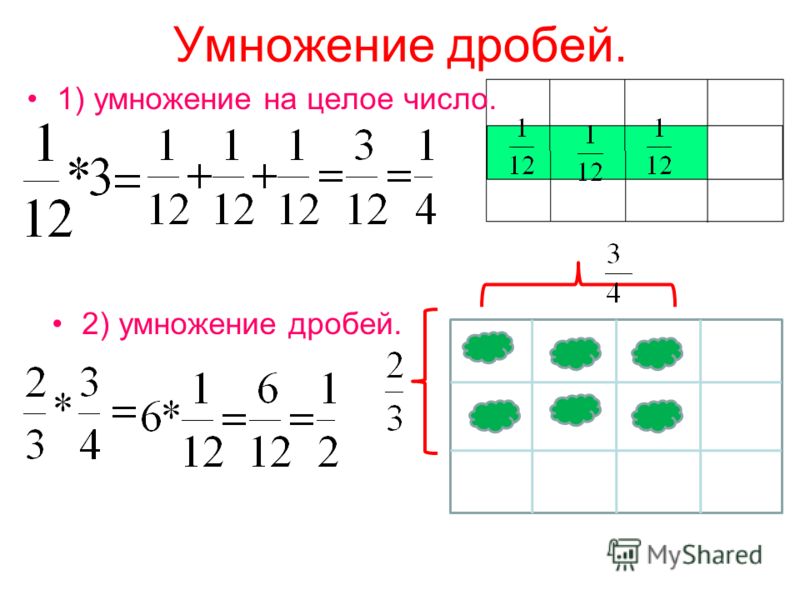
Понимать дробь a / b как кратное 1/ b . Например, используйте модель визуальной дроби, чтобы представить 5/4 как произведение 5 × (1/4), записав заключение по уравнению 5/4 = 5 × (1/4) .
Например, используйте модель визуальной дроби, чтобы представить 5/4 как произведение 5 × (1/4), записав заключение по уравнению 5/4 = 5 × (1/4) .
CCSS.Math.Content.4.NF.B.4.b
Понимание кратного a/b как кратного 1/b и использование этого понимания для умножения дроби на целое число. Например, используйте модель визуальной дроби, чтобы выразить 3 × (2/5) как 6 × (1/5), распознав это произведение как 6/5. (В общем случае n × (a/b) = (n × a)/b.)
CCSS.Math.Content.4.NF.B.4.c
Решать текстовые задачи на умножение дроби на a целое число, например, с помощью моделей визуальных дробей и уравнений для представления проблемы. Например, если каждый человек на вечеринке съест 3/8 фунта ростбифа, а на вечеринке будет 5 человек, сколько фунтов ростбифа потребуется? Между какими двумя целыми числами лежит ваш ответ?
Заметки для учителя
Как многократное сложение дробей связано с умножением дроби на целое число?
Фракции можно рассматривать как части целого или как отдельные единицы. Умножение дроби на целое число дает количество единичных дробей или отдельных единиц.
Умножение дроби на целое число дает количество единичных дробей или отдельных единиц.
После обучения тому, что умножение — это то же самое, что многократное сложение с дробями, объясните учащимся, что умножение целого числа на дробь всегда приводит к меньшему целому числу, используя пример с половиной. Пример: Половина четырех равна двум, верно? Это то же самое, что половина умножить на четыре, что равняется двум.
Цели знаний учащихся
Я знаю, что умножение — это многократное сложение.
Я знаю, что сложение единичных дробей равносильно умножению единичной дроби на целое число.
Я могу объяснить, как одна дробь кратна другой дроби, используя модели, рисунки или уравнения.
Словарь
Нет нового словаря
Уроки
Engage NY Модуль 5 G-35-представляет собой умножение N Times A / B AS ( N × / B AS ( N × / B . b с использованием ассоциативного свойства и визуальных моделей.
b с использованием ассоциативного свойства и визуальных моделей.
Engage NY Module 5 G-36 — Представьте умножение на , умноженное на 9.0054 a / b as ( n × a )/ b с использованием ассоциативного свойства и визуальных моделей.
Engage NY Модуль 5 G-37. Найдите произведение целого числа на смешанное число, используя свойство распределения.
Engage NY Module 5 G-38. Найдите произведение целого числа на смешанное число, используя свойство распределения.
Engage NY Модуль 5 G-39 – Решайте задачи на мультипликативное сравнение слов с участием дробей.
Engage NY Module 5 G-40 – Решение текстовых задач на умножение целых чисел и дробей, в том числе на линейные графики.
Умножение дробей — различные уроки
Видеоуроки для учащихся
Виртуальный ботаник — понимать, что число a/b кратно 1/b, и использовать это понимание для умножения дроби на целое число.
Онлайн-задачи и тесты
Академия Хана – Вопросы и видеоуроки
Умножение единичных дробей на целые числа с помощью числовых рядов
Умножение единичных дробей и целых чисел: сортировка
Умножение единичных дробей на целые числа
Умножение дробей на целые числа с помощью числовых рядов
Умножение дробей и целых чисел: сортировка
Умножение дробей на целые числа
Умножение единичных дробей на целые числа: текстовые задачи
Умножение дробей на целые числа: текстовые задачи
Умножение дробей и смешанных чисел на целые числа в рецептах
Онлайн-игры
Умножение дробей
Печатные формы
Умножение дробей
Оценочное задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание 8
Умножение и деление дробей на целое
Умножение дробей на целое номер | НЦЭТМ- Фракции
- Умножение дробей и деление дробей на целое число
- Мастерство PD Материалы
Умножение дробей и деление дробей на целое число
Корешок 3: Дроби – Тема 3.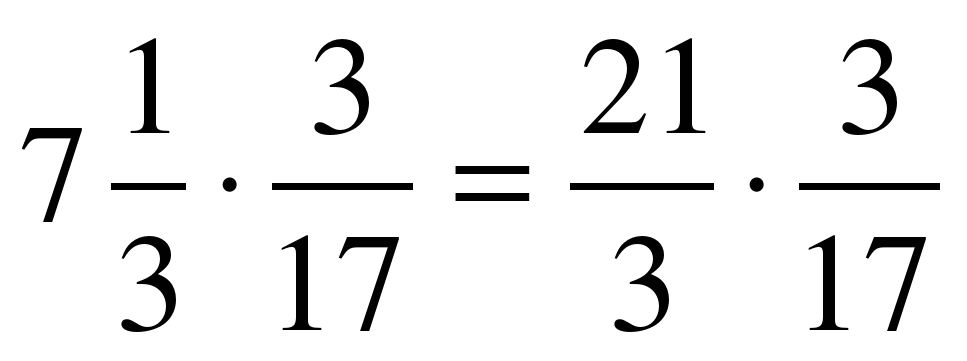
 альбомы с опорными таблицами
альбомы с опорными таблицами