Как умножить дробь на отрицательную дробь: Отрицательные дроби. Действия с отрицательными дробями

Содержание

Отрицательные дроби. Действия с отрицательными дробями

Сложение и вычитание
Умножение и деление

Отрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.

Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:

-2 : 7 и 2 : (-7),

каждое из них равно отрицательному числу

Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:

-2 : 7	=	-2	и	2 : (-7)	=	2	.
		7				-7

Следовательно, при записи отрицательных дробей знак минус можно ставить перед дробью, перед числителем или перед знаменателем:

—	2	=	-2	=	2	.
	7		7		-7

Сложение и вычитание

Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.

Пример.

—	2	+ (-	1	)	.
	5		4

Приведём дроби к общему знаменателю:

—	2	+ (-	1	) =	-8	+	-5	.
	5		4		20		20

Теперь сложим числители дробей по правилам сложения рациональных чисел:

-8	+	-5	=	-8 + (-5)	=	-13	=	—	13	.
20		20		20		20			20

Таким образом:

—	2	+ (-	1	) =	-8	+	-5	=
	5		4		20		20

=	-8 + (-5)	=	-13	=	—	13	.
	20		20			20

Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.

Пример.

—	5	— (-	11	) =	—	5	+ (+	11	) =
	12		12			12		12

=	—	5	+	11	=	-5 + 11	=	6	.
		12		12		12		12

Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.

Умножение и деление

Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.

Пример.

—	2	· (-	4	) =	-2	·	-4	=	-2 · (-4)	=	8	.
	3		5		3		5		3 · 5		15

Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:

—	2	· (-	4	) =	2	·	4	=	2 · 4	=	8	.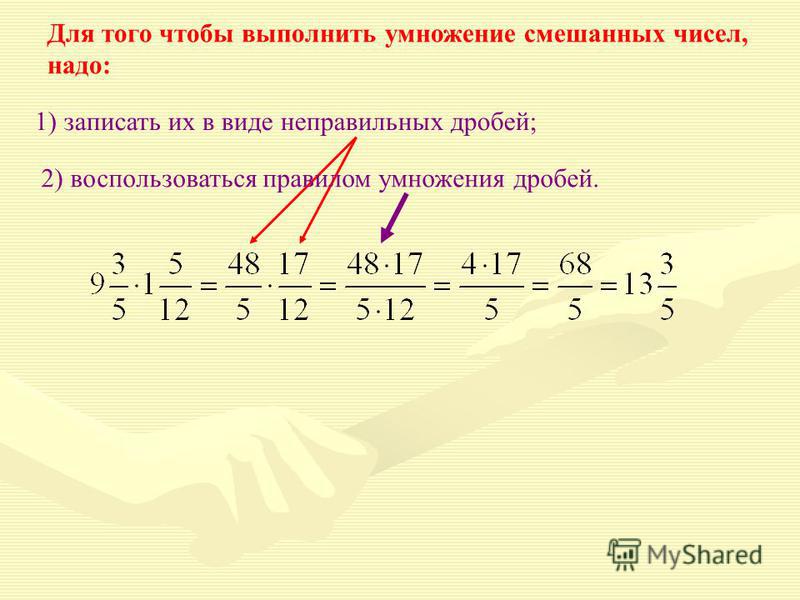
	3		5		3		5		3 · 5		15

При умножении отрицательной дроби на положительную результат будет отрицательным.

Пример.

—	2	·	4	=	—	2 · 4	=	—	8	.
	3		5			3 · 5			15

К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:

4	· (-	2	) =	—	4 · 2	=	—	8	.
5		3			5 · 3			15

То есть при умножении положительной дроби на отрицательную результат будет отрицательным.

Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.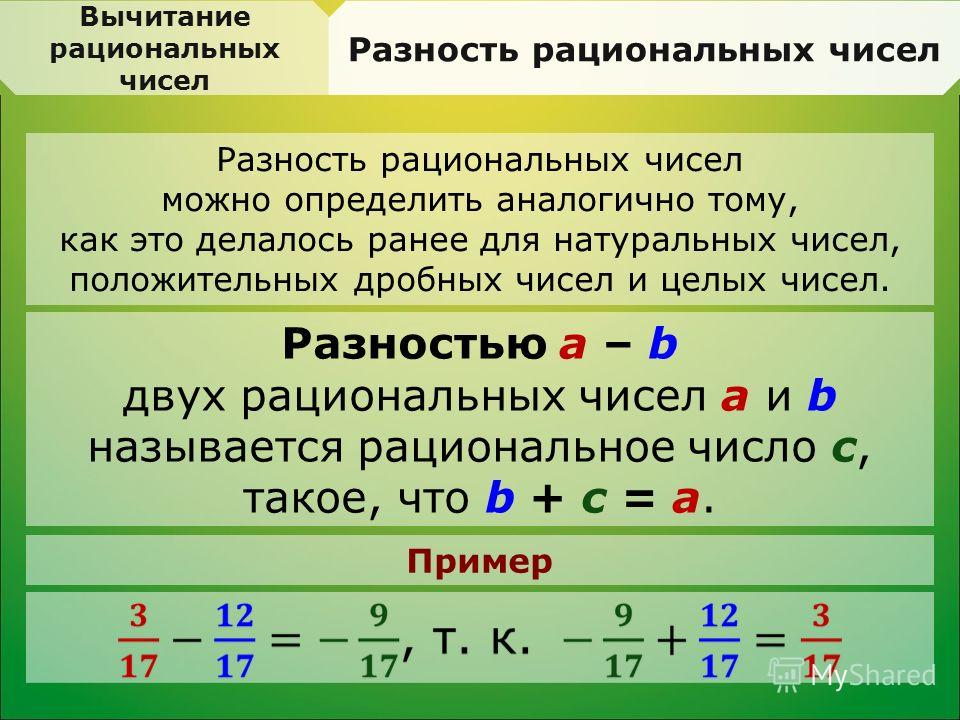

Пример.

—	2	: (-	4	) =	-2	:	-4	=
	3		5		3		5

=	-2 · 5	=	-10	=	10	.
	3 · (-4)		-12		12

Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.

Умножение положительных и отрицательных чисел — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Содержание

Отрицательные дроби, понятие и правила.

В этой теме разберем новое понятие “Отрицательные дроби”. Дроби, как и любые числа могут быть положительными и отрицательными.

Отрицательные дроби понятие и смысл. Примеры.

Ранее мы изучили тему обыкновенные дроби. Отрицательные дроби отличаются от обыкновенных дробей лишь знаком. Обыкновенные дроби имеют знак “+”. Например:

$\frac{1}{2}; \frac{3}{5}; \frac{7}{10}; \frac{8}{8}; \frac{9}{5}; \frac{3}{1}$

Все эти дроби можно записать со знаком плюс и смысл дробей не изменится.

$\frac{1}{2}= +\frac{1}{2}; \frac{3}{5}= +\frac{3}{5}; \frac{7}{10}= +\frac{7}{10}; \frac{8}{8}= +\frac{8}{8}; \frac{9}{5}= +\frac{9}{5}; \frac{3}{1}= +\frac{3}{1}$

Если перед дробью поставить знак “–”, то дробь станет отрицательной. Например перед дробью $\frac{1}{2}$ поставим знак минус, получим $-\frac{1}{2}$Дроби вида $-\frac{1}{2}; -\frac{3}{5}; -\frac{7}{10}; -\frac{8}{8}; -\frac{9}{5}; -\frac{3}{1}$ называются отрицательными дробями.

Противоположные дроби, правила.

Дроби $\frac{1}{2}$ и $-\frac{1}{2}$ называются

противоположными дробями. Дроби или числа, которые отличаются только знаком называются противоположными дробями или числами.

Вывод: если перед дробью поставить знак “+”, то дробь смысл дроби не изменится. Если поставить перед дробью знак “–”, то получим противоположную дробь данной дроби.

Не всегда знак минус пишется перед дробью, иногда минус записывают в числители или знаменателе. Рассмотрим пример:

$-\frac{7}{10}=\frac{-7}{10}=\frac{7}{-10}$

Отрицательные дроби и нуль.

Нуль является исключением, нуль – противоположен самому себе.

$0=+\frac{0}{n}=-\frac{0}{n}$

Вопросы по теме “Отрицательные дроби”:
Назовите три отрицательные дроби?
Ответ: $-\frac{1}{3}; -\frac{4}{4}; -\frac{7}{3}; $

Приведите пример противоположных чисел?
Ответ: $-\frac{8}{5}$ и $\frac{8}{5}$

Назовите какому числу противоположно число нуль?

Ответ: нуль противоположен сам себе.

Какому числу противоположно положительное число?
Ответ: положительное число противоположно данному отрицательному числу.

Отрицательная дробь противоположна какой дроби?
Ответ: отрицательная дробь противоположна данной положительной дроби.

Пример:
Является ли дробь положительной или отрицательной: $\frac{1}{5}; -\frac{3}{7}; \frac{4}{1}; \frac{5}{5}; -\frac{9}{4}; -\frac{2}{3}; -\frac{0}{6}.$

Решение:
Отрицательные дроби $-\frac{3}{7}; -\frac{9}{4}; -\frac{2}{3}$
Положительные дроби $\frac{1}{5}; \frac{4}{1}; \frac{5}{5}$
Является ни положительной, ни отрицательной дробью $-\frac{0}{6}.$

Как правильно умножать отрицательные числа?

Основные определения

Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.

Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:

Два главных определения:

Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.

Запоминаем!

Положительные числа — это те, что больше нуля, а отрицательные — меньшие.

Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».

Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!

Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).

Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:

Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.

Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.

Свойства умножения

От перестановки множителей местами произведение не меняется.
a * b = b * a
Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
a * b * c = (a * b) * c = a * (b * c)

Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.

Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:

А вот как умножить два числа с разными знаками:

перемножить модули этих чисел
перед полученным числом поставить знак минус

А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:

«—» — при умножении минус на минус ответ будет положительным
или минус на минус дает плюс
«-+» — при умножении минуса на плюс ответ будет отрицательным
или минус на плюс дает минус
«+-» — при умножении плюса на минус ответ будет отрицательным
или плюс на минус дает минус
«++» — при умножении плюса на плюс ответ будет положительным
или плюс на плюс дает плюс.

Примеры умножения отрицательных чисел

Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)

Как решаем:

Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:

(-2)∗(-2) = 4

(-3)∗(-7) = 21

Ответ: 4; 21.

Пример 2. Вычислить: (-11)∗11 и (-20)∗2

Как решаем:

Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:

-11 * 11 = -121

(-20) * 2 = -40

Ответ: -121; -40.

Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)

Как решаем:

Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:

5 ∗ (-5)= -25

12 ∗ (-8)= -96

Ответ: -25; -96.

Пример 4. Вычислить произведение: (-0,125 ) * (-6)

Как решаем:

Используем правило умножения отрицательных чисел:
(-0,125 ) * (-6) = 0,125 * 6.

Выполним умножение десятичной дроби на натуральное число столбиком:

Ответ: 0,75.

Развивайте математическое мышление детей на наших уроках математики вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее справиться со школьной математикой.

Приходите на бесплатный вводный урок вместе с ребенком: познакомимся, порешаем задачки и вдохновим на учебу!

правило, примеры, умножение отрицательных чисел на положительные

В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение. Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.

Умножение отрицательных чисел

Определение 1

Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, -b данное равенство считается верным.

(-а)·(-b)=a·b.

Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: (-а)·(-b)=a·b. Статья умножение чисел с разными знаками рассказывает о том, что равенств а·(-b)=-a·b справедливое, как и (-а)·b=-a·b. Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:

(-a)·(-b)=(-a·(-b))=-(-(a·b))= a·b.

Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.

Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.

Примеры умножения отрицательных чисел

Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.

Пример 1

Произвести умножение чисел -3 и -5.

Решение.

По модулю умножаемые данные два числа равны положительным числам 3 и 5. Их произведение дает в результате 15. Отсюда следует, что произведение заданных чисел равно 15

Запишем кратко само умножение отрицательных чисел:

(-3)·(-5)=3·5=15

Ответ: (-3)·(-5)=15.

При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 2

Вычислить произведение (-0,125)·(-6).

Решение.

Используя правило умножения отрицательных чисел, получим, что (−0,125)·(−6)=0,125·6. Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:

Получили, что выражение примет вид (−0,125)·(−6)=0,125·6=0,75.

Ответ: (−0,125)·(−6)=0,75.

В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.

Пример 3

Необходимо произвести умножение отрицательного -2 на неотрицательное log5 13.

Решение

Находим модули заданных чисел:

-2=2 и log513=-log5 3=log5 3.

Следуя из правил умножения отрицательных чисел, получим результат -2·log5 13=-2·log5 3=2·log5 3. Это выражение и является ответом.

Ответ: -2·log5 13=-2·log5 3=2·log5 3.

Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.

Умножение и деление рациональных чисел

1.	Утверждение (умножение)	1 вид — рецептивный	лёгкое	1 Б.	Необходимо выбрать верное/ложное утверждение (умножение).
2.	Утверждение (частное)	1 вид — рецептивный	лёгкое	1 Б.	Необходимо выбрать верное/ложное утверждение (частное).
3.	Умножение на единицу	1 вид — рецептивный	лёгкое	2 Б.	Умножение на единицу.
4.	Произведение целых чисел (до 10)	1 вид — рецептивный	лёгкое	1 Б.	Произведение целых чисел.
5.	Произведение рациональных чисел (десятичные дроби)	2 вид — интерпретация	среднее	1 Б.	Десятичная дробь и целое число.
6.	Умножение обыкновенной дроби на положительное или отрицательное целое число	2 вид — интерпретация	среднее	2 Б.	Один или оба множителя отрицательные.
7.	Произведение двух десятичных дробей с разными знаками	2 вид — интерпретация	среднее	1 Б.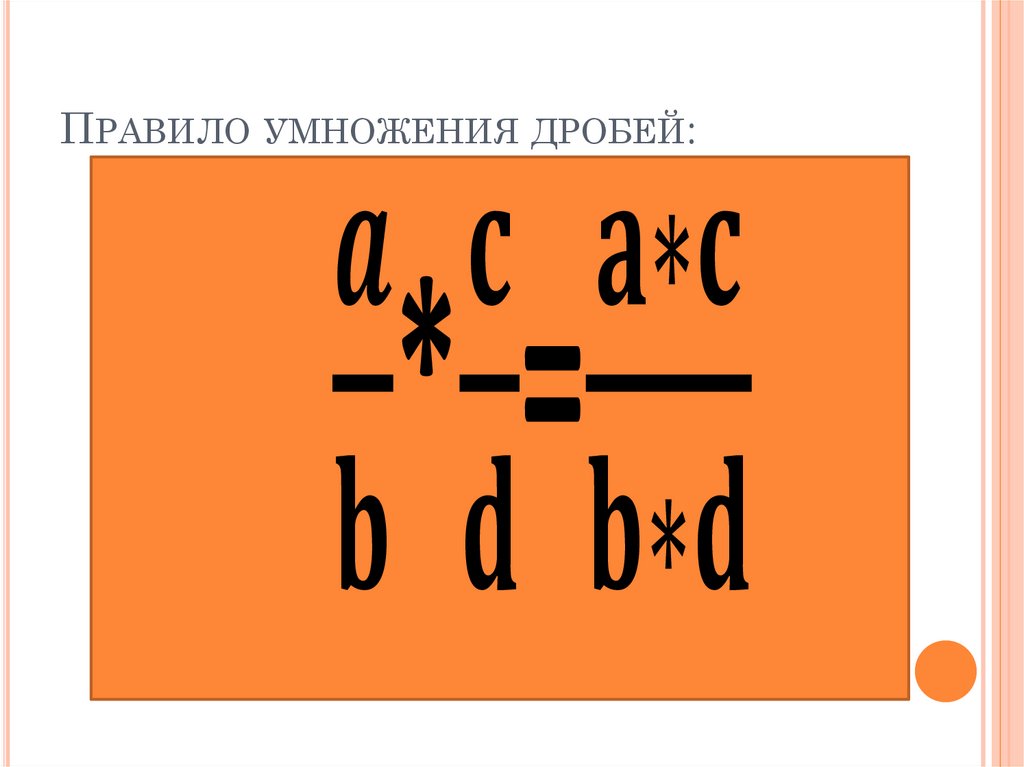	Произведение двух десятичных дробей с разными знаками.
8.	Произведение целого числа и смешанного (отрицательные числа)	2 вид — интерпретация	среднее	3 Б.	Произведение целого числа и смешанного.
9.	Произведение десятичной дроби и обыкновенной (отрицательные числа)	2 вид — интерпретация	среднее	3 Б.	Произведение десятичной дроби и обыкновенной.
10.	Произведение десятичной дроби и смешанного числа (отрицательные)	2 вид — интерпретация	среднее	3 Б.	Произведение десятичной дроби и смешанного числа.
11.	Частное чисел с разными знаками	2 вид — интерпретация	среднее	1 Б.	Целые числа.
12.	Деление обыкновенной дроби на положительное или отрицательное целое число	2 вид — интерпретация	среднее	3 Б.	Деление обыкновенной дроби на положительное или отрицательное целое число.
13.	Деление целого числа на правильную дробь	2 вид — интерпретация	среднее	2 Б.	Одно число или оба числа отрицательные. Результат — целое число.
14.	Деление смешанного числа на положительное или отрицательное целое число	2 вид — интерпретация	среднее	3 Б.	Деление целой части и дробной отдельно.
15.	Деление десятичной дроби / целого числа на обыкновенную дробь (разные знаки)	2 вид — интерпретация	среднее	3 Б.	Деление десятичной дроби / целого числа на обыкновенную дробь.
16.	Деление десятичных дробей (разные знаки)	2 вид — интерпретация	среднее	2 Б.	Деление десятичных дробей.
17.	Деление десятичной дроби на обыкновенную (разные знаки)	2 вид — интерпретация	среднее	3 Б.	Деление десятичной дроби на обыкновенную.
18.	Деление двух отрицательных десятичных дробей	2 вид — интерпретация	среднее	2 Б.	Деление двух отрицательных десятичных дробей.
19.	Частное двух отрицательных смешанных чисел	2 вид — интерпретация	среднее	3 Б.	Частное двух отрицательных смешанных чисел.
20.	Произведение	2 вид — интерпретация	среднее	1 Б.	Определение знака произведения.
21.	Произведение нескольких целых чисел с разными знаками	2 вид — интерпретация	среднее	2 Б.	Произведение нескольких целых чисел с разными знаками.
22.	Произведение трёх обыкновенных дробей, как минимум одна дробь — отрицательная	2 вид — интерпретация	среднее	3 Б.	Сокращение, приведение к правильной дроби.
23.	Деление на дробь и умножение на дробь, как минимум одна дробь — отрицательная	2 вид — интерпретация	среднее	3 Б.	Действия с тремя дробями. Деление и умножение.
24.	Уравнение (десятичные дроби и целые числа)	2 вид — интерпретация	сложное	3 Б.	Решение уравнения.
25.	Уравнение с модулем	2 вид — интерпретация	сложное	6 Б.	Решение уравнения.
26.	Неизвестный член пропорции	2 вид — интерпретация	сложное	4 Б.	Применение основного свойства пропорции.

Сложение и вычитание рациональных чисел

В данном уроке рассматривается сложение и вычитание рациональных чисел. Тема относится к категории сложных. Здесь необходимо использовать весь арсенал полученных ранее знаний.

Правила сложения и вычитания целых чисел справедливы и для рациональных чисел. Напомним, что рациональными называют числа, которые могут быть представлены в виде дроби , где a – это числитель дроби, b – знаменатель дроби. При этом, b не должно быть нулём.

В данном уроке дроби и смешанные числа мы всё чаще будем называть одним общим словосочетанием — рациональные числа.

Пример 1. Найти значение выражения:

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:

Это сложение рациональных чисел с разными знаками. Чтобы сложить рациональные числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того рационального числа, модуль которого больше. А чтобы понять какой модуль больше, а какой меньше, нужно суметь сравнить модули этих дробей до их вычисления:

Модуль рационального числа больше, чем модуль рационального числа . Поэтому мы из вычли . Получили ответ . Затем сократив эту дробь на 2, получили окончательный ответ .

Некоторые примитивные действия, такие как заключение чисел в скобки и проставление модулей, можно пропустить.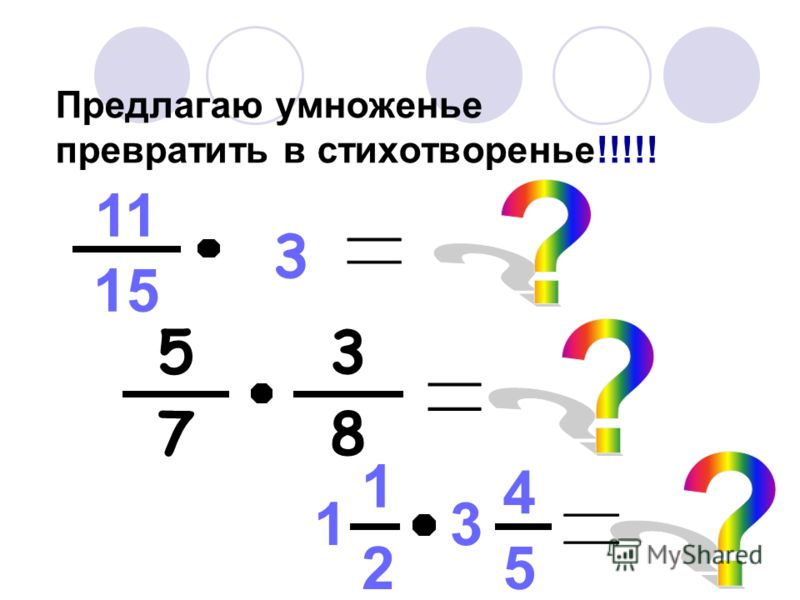 Данный пример вполне можно записать покороче:

Пример 2. Найти значение выражения:

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус, стоящий между рациональными числами и является знаком операции и не относится к дроби . У этой дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы запишем его для наглядности:

Заменим вычитание сложением. Напомним, что для этого нужно к уменьшаемому прибавить число, противоположное вычитаемому:

Получили сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус:

Запишем решение данного примера покороче:

Примечание. Заключать в скобки каждое рациональное число вовсе необязательно. Делается это для удобства, чтобы хорошо видеть какие знаки имеют рациональные числа.

Пример 3. Найти значение выражения:

В этом выражении у дробей разные знаменатели. Чтобы облегчить себе задачу, приведём эти дроби к общему знаменателю. Не будем подробно останавливаться на том как это сделать. Если испытываете с этим затруднения, обязательно повторите урок действия с дробями.

После приведения дробей к общему знаменателю выражение примет следующий вид:

Заключим каждое рациональное число в скобки вместе своими знаками:

Это сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:

Запишем решение данного примера покороче:

Пример 4. Найти значение выражения

Заключим каждое рациональное число в скобки вместе со своими знаками:

Вычислим данное выражение в следующем порядке: слóжим рациональные числа и , затем из полученного результата вычтем рациональное число .

Первое действие:

Второе действие:

Таким образом, значение выражения равно

Пример 5. Найти значение выражения:

Представим целое число −1 в виде дроби , а смешанное число переведём в неправильную дробь:

Приведём данные дроби к общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Получили сложение рациональных чисел с разными знаками. Вычитаем из большего модуля меньший модуль, и перед полученным ответом ставим знак того рационального числа, модуль которого больше:

Получили ответ .

Есть и второй способ решения. Он заключается в том, чтобы сложить отдельно целые части.

Итак, вернёмся к изначальному выражению:

Заключим каждое число в скобки. Для этого смешанное число временно развернём:

Вычислим целые части:

(−1) + (+2) = 1

В главном выражении вместо (−1) + (+2) запишем полученную единицу:

Полученное выражение свернём. Для этого запишем единицу и дробь вместе:

Запишем решение этим способом покороче:

Пример 6. Найти значение выражения

Переведём смешанное число в неправильную дробь. Остальную часть перепишем без изменения:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус:

Запишем решение данного примера покороче:

Пример 7. Найти значение выражение

Представим целое число −5 в виде дроби , а смешанное число переведём в неправильную дробь:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Таким образом, значение выражения равно .

Решим данный пример вторым способом. Вернемся к изначальному выражению:

Запишем смешанное число в развёрнутом виде. Остальное перепишем без изменений:

Заключим каждое рациональное число в скобки вместе своими знаками:

Заменим вычитание сложением там, где это можно:

Вычислим целые части:

В главном выражении вместо запишем полученное число −7

Выражение является развёрнутой формой записи смешанного числа . Запишем число −7 и дробь вместе, образуя окончательный ответ:

Запишем это решение покороче:

Пример 8. Найти значение выражения

Переведём смешанные числа в неправильные дроби:

Заключим каждое рациональное число в скобки вместе своими знаками:

Заменим вычитание сложением:

Таким образом, значение выражения равно

Данный пример можно решить и вторым способом. Он заключается в том, чтобы сложить целые и дробные части по отдельности. Вернёмся к изначальному выражению:

Заключим каждое рациональное число в скобки вместе со своими знаками:

Заменим вычитание сложением:

Получили сложение отрицательных рациональных чисел. Слóжим модули этих чисел и перед полученным ответом поставим минус. Но в этот раз слóжим по отдельности целые части (−1 и −2), и дробные и

Запишем это решение покороче:

Пример 9. Найти выражения выражения

Переведём смешанные числа в неправильные дроби:

Заключим рациональное число в скобки вместе своим знаком. Рациональное число в скобки заключать не нужно, поскольку оно уже в скобках:

Приведём данные дроби в общему знаменателю. После их приведения к общему знаменателю, они примут следующий вид:

Таким образом, значение выражения равно

Теперь попробуем решить этот же пример вторым способом, а именно сложением целых и дробных частей по отдельности.

В этот раз, в целях получения короткого решения, попробуем пропустить некоторые действия, такие как: запись смешанного числа в развёрнутом виде и замена вычитания сложением:

Обратите внимание, что дробные части были приведены к общему знаменателю.

Пример 10. Найти значение выражения

Заменим вычитание сложением:

В получившемся выражении нет отрицательных чисел, которые являются основной причиной допущения ошибок. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вычитаемым, а также убрать скобки:

Получилось простейшее выражение, которое вычисляется легко. Вычислим его любым удобным для нас способом:

Пример 11. Найти значение выражения

Это сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:

Пример 12. Найти значение выражения

Выражение состоит из нескольких рациональных чисел.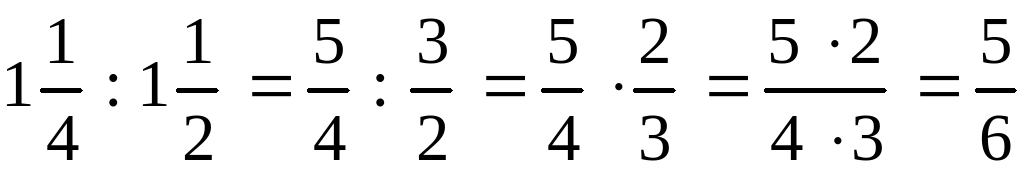 Согласно порядку действий, в первую очередь необходимо выполнить действия в скобках.

Сначала вычислим выражение , затем выражение Полученные результаты слóжим .

Первое действие:

Второе действие:

Третье действие:

Ответ: значение выражения равно

Пример 13. Найти значение выражения

Переведём смешанные числа в неправильные дроби:

Заключим рациональное число в скобки вместе со своим знаком. Рациональное число заключать в скобки не нужно, поскольку оно уже в скобках:

Заменим вычитание сложением:

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед полученными ответом поставим знак того рационального числа, модуль которого больше:

Таким образом, значение выражения равно

Рассмотрим сложение и вычитание десятичных дробей, которые тоже относятся к рациональным числам и которые могут быть как положительными, так и отрицательными.

Пример 14. Найти значение выражения −3,2 + 4,3

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что плюс который дан в выражении, является знаком операции и не относится к десятичной дроби 4,3. У этой десятичной дроби свой знак плюса, который невидим по причине того, что его не записывают. Но мы его запишем для наглядности:

(−3,2) + (+4,3)

(−3,2) + (+4,3) = |+4,3| − |−3,2| = 1,1

Модуль числа 4,3 больше, чем модуль числа −3,2 поэтому мы из 4,3 вычли 3,2. Получили ответ 1,1. Ответ положителен, поскольку перед ответом должен стоять знак того рационального числа, модуль которого больше.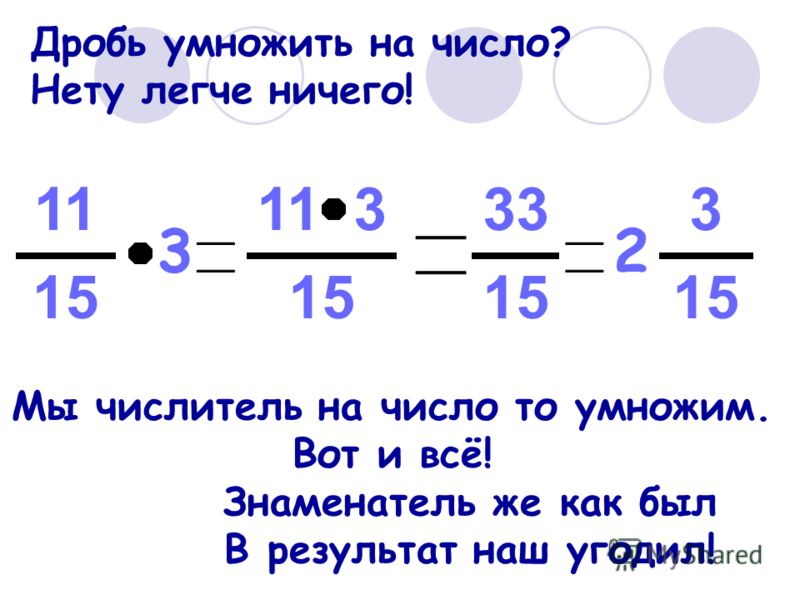 А модуль числа 4,3 больше, чем модуль числа −3,2

Таким образом, значение выражения −3,2 + (+4,3) равно 1,1

Этот пример можно записать покороче:

−3,2 + (+4,3) = 1,1

Пример 15. Найти значение выражения 3,5 + (−8,3)

Это сложение рациональных чисел с разными знаками. Как и в прошлом примере из большего модуля вычитаем меньший и перед ответом ставим знак того рационального числа, модуль которого больше:

3,5 + (−8,3) = −(|−8,3| − |3,5|) = −(8,3 − 3,5) = −(4,8) = −4,8

Таким образом, значение выражения 3,5 + (−8,3) равно −4,8

Этот пример можно записать покороче:

3,5 + (−8,3) = −4,8

Пример 16. Найти значение выражения −7,2 + (−3,11)

Это сложение отрицательных рациональных чисел. Чтобы сложить отрицательные рациональные числа, нужно сложить их модули и перед полученным ответом поставить минус.

Запись с модулями можно пропустить, чтобы не загромождать выражение:

−7,2 + (−3,11) = −7,20 + (−3,11) = −(7,20 + 3,11) = −(10,31) = −10,31

Таким образом, значение выражения −7,2 + (−3,11) равно −10,31

Этот пример можно записать покороче:

−7,2 + (−3,11) = −10,31

Пример 17. Найти значение выражения −0,48 + (−2,7)

Это сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение:

−0,48 + (−2,7) = (−0,48) + (−2,70) = −(0,48 + 2,70) = −(3,18) = −3,18

Пример 18. Найти значение выражения −4,9 − 5,9

Заключим каждое рациональное число в скобки вместе со своими знаками. Учитываем, что минус который располагается между рациональными числами −4,9 и 5,9 является знаком операции и не относится к числу 5,9. У этого рационального числа свой знак плюса, который невидим по причине того, что он не записывается. Но мы запишем его для наглядности:

(−4,9) − (+5,9)

Заменим вычитание сложением:

(−4,9) + (−5,9)

Получили сложение отрицательных рациональных чисел. Слóжим их модули и перед полученным ответом поставим минус:

(−4,9) + (−5,9) = −(4,9 + 5,9) = −(10,8) = −10,8

Таким образом, значение выражения −4,9 − 5,9 равно −10,8

Запишем решение этого примера покороче:

−4,9 − 5,9 = −10,8

Пример 19.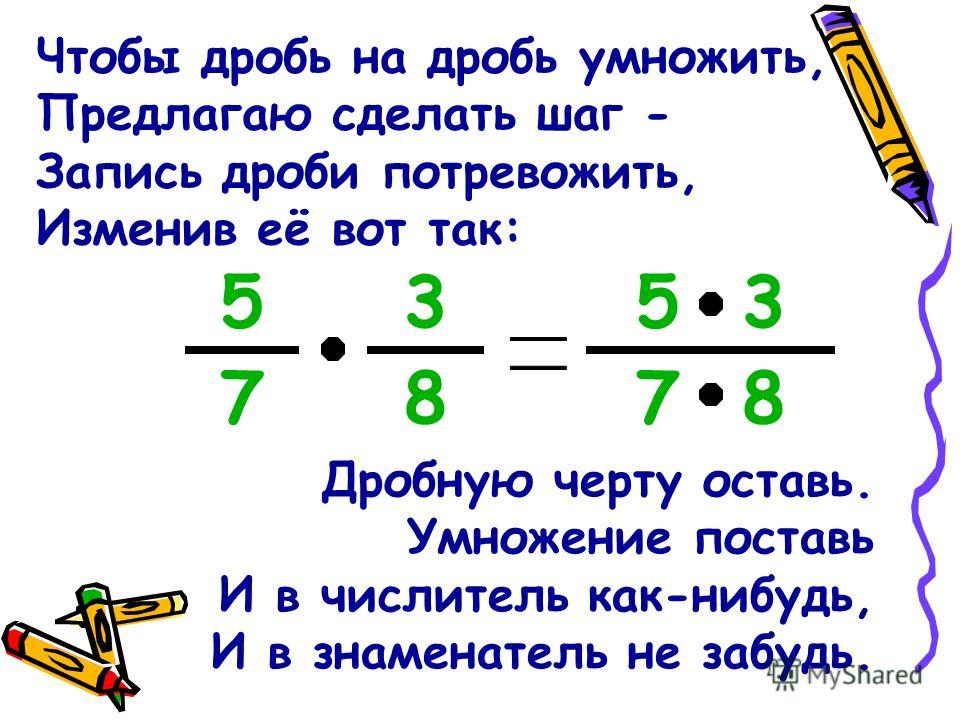 Найти значение выражения 7 − 9,3

Заключим в скобки каждое число вместе со своими знаками

(+7) − (+9,3)

Заменим вычитание сложением

(+7) + (−9,3)

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль, и перед ответом поставим знак того числа, модуль которого больше:

(+7) + (−9,3) = −(9,3 − 7) = −(2,3) = −2,3

Таким образом, значение выражения 7 − 9,3 равно −2,3

Запишем решение этого примера покороче:

7 − 9,3 = −2,3

Пример 20. Найти значение выражения −0,25 − (−1,2)

Заменим вычитание сложением:

−0,25 + (+1,2)

−0,25 + (+1,2) = 1,2 − 0,25 = 0,95

Запишем решение этого примера покороче:

−0,25 − (−1,2) = 0,95

Пример 21. Найти значение выражения −3,5 + (4,1 − 7,1)

Выполним действия в скобках, затем слóжим полученный ответ с числом −3,5

Первое действие:

4,1 − 7,1 = (+4,1) − (+7,1) = (+4,1) + (−7,1) = −(7,1 − 4,1) = −(3,0) = −3,0

Второе действие:

−3,5 + (−3,0) = −(3,5 + 3,0) = −(6,5) = −6,5

Ответ: значение выражения −3,5 + (4,1 − 7,1) равно −6,5.

Пример 22. Найти значение выражения (3,5 − 2,9) − (3,7 − 9,1)

Выполним действия в скобках. Затем из числа, которое получилось в результате выполнения первых скобок, вычтем число, которое получилось в результате выполнения вторых скобок:

Первое действие:

3,5 − 2,9 = (+3,5) − (+2,9) = (+3,5) + (−2,9) = 3,5 − 2,9 = 0,6

Второе действие:

3,7 − 9,1 = (+3,7) − (+9,1) = (+3,7) + (−9,1) = −(9,1 − 3,7) = −(5,4) = −5,4

Третье действие

0,6 − (−5,4) = (+0,6) + (+5,4) = 0,6 + 5,4 = 6,0 = 6

Ответ: значение выражения (3,5 − 2,9) − (3,7 − 9,1) равно 6.

Пример 23. Найти значение выражения −3,8 + 17,15 − 6,2 − 6,15

Заключим в скобки каждое рациональное число вместе со своими знаками

(−3,8) + (+17,15) − (+6,2) − (+6,15)

Заменим вычитание сложением там, где это можно:

(−3,8) + (+17,15) + (−6,2) + (−6,15)

Выражение состоит из нескольких слагаемых. Согласно сочетательному закону сложения, если выражение состоит из нескольких слагаемых, то сумма не будет зависеть от порядка действий. Это значит, что слагаемые можно складывать в любом порядке.

Не будем изобретать велосипед, а слóжим все слагаемые слева направо в порядке их следования:

Первое действие:

(−3,8) + (+17,15) = 17,15 − 3,80 = 13,35

Второе действие:

13,35 + (−6,2) = 13,35 − −6,20 = 7,15

Третье действие:

7,15 + (−6,15) = 7,15 − 6,15 = 1,00 = 1

Ответ: значение выражения −3,8 + 17,15 − 6,2 − 6,15 равно 1.

Пример 24. Найти значение выражения

Переведём десятичную дробь −1,8 в смешанное число. Остальное перепишем без изменения:

Далее вычисляем данное выражение, применяя ранее изученные правила:

Пример 25. Найти значение выражения

Заменим вычитание сложением. Попутно переведём десятичную дробь (−4,4) в неправильную дробь

В получившемся выражении нет отрицательных чисел. А поскольку нет отрицательных чисел, мы можем убрать плюс перед вторым числом, и убрать скобки. Тогда получим простое выражение на сложение, которое решается легко

Пример 26. Найти значение выражения

Переведём смешанное число в неправильную дробь, а десятичную дробь −0,85 в обыкновенную дробь. Получим следующее выражение:

Пример 27. Найти значение выражения

Переведём обе дроби в неправильные дроби. Чтобы перевести десятичную дробь 2,05 в неправильную дробь, можно перевести ее сначала в смешанное число, а затем в неправильную дробь:

После перевода обеих дробей в неправильные дроби, получим следующее выражение:

Получили сложение рациональных чисел с разными знаками. Вычтем из большего модуля меньший модуль и перед полученным ответом поставим знак того числа, модуль которого больше:

Пример 28.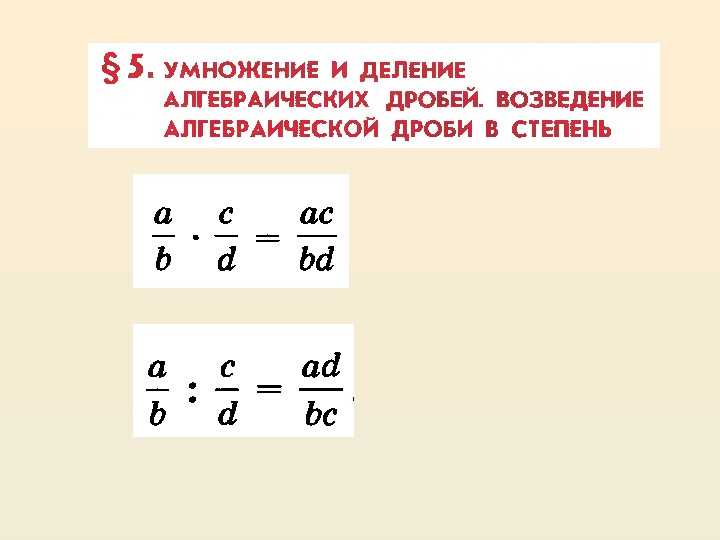 Найти значение выражения

Заменим вычитание сложением. Далее переведём десятичную дробь в обыкновенную дробь. Затем вычислим получившееся выражение, применяя ранее изученные правила:

Пример 29. Найти значение выражения

Переведём десятичные дроби −0,25 и −1,25 в обыкновенные дроби, остальное перепишем без изменения. Получим следующее выражение:

Можно сначала заменить вычитание сложением там, где это можно и сложить рациональные числа одно за другим.

Есть и второй вариант: сначала сложить рациональные числа и , а затем из полученного результата вычесть . Этим вариантом и воспользуемся.

Первое действие:

Второе действие:

Ответ: значение выражения равно −2.

Пример 30. Найти значение выражения

Переведём десятичные дроби в обыкновенные. Остальное перепишем без изменения:

Получили сумму из нескольких слагаемых. Если сумма состоит из нескольких слагаемых, то выражение можно вычислять в любом порядке. Это следует из сочетательного закона сложения.

Поэтому мы можем организовать наиболее удобный для нас вариант. В первую очередь можно сложить первое и последнее слагаемое, а именно рациональные числа и . У этих чисел одинаковые знаменатели, а значит это освободит нас от необходимости приводить их к нему.

Первое действие:

Полученное число можно сложить со вторым слагаемым, а именно с рациональным числом . У рациональных чисел и одинаковые знаменатели в дробных частях, что опять же является преимуществом для нас

Второе действие:

Ну и слóжим полученное число −7 с последним слагаемым, а именно с рациональным числом . Удобно то, что при вычислении данного выражения, семёрки исчезнут, поскольку их сумма будет равна нулю:

Третье действие:

Ответ: значение выражения равно

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

Решение:

Задание 2.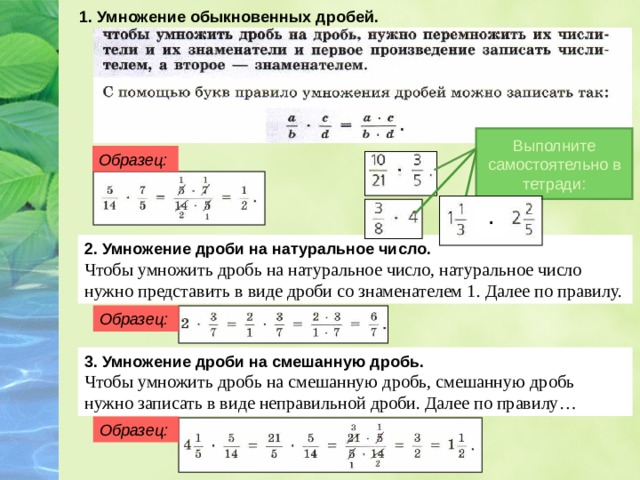 Найдите значение выражения:

Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:

Задание 5. Найдите значение выражения:

Решение:

Задание 6. Найдите значение выражения:

Решение:

Задание 7. Найдите значение выражения:

Решение:

Задание 8. Найдите значение выражения:

Решение:

Задание 9. Найдите значение выражения:

Решение:

Задание 10. Найдите значение выражения:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Как из отрицательной степени сделать положительную

Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».

Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.

Как возвести число в отрицательную степень

Чтобы возвести число в отрицательную степень нужно:

«перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
заменить отрицательную степень на положительную ;
возвести число в положительную степень.

Общая формула возведения в отрицательную степень выглядит следующим образом.

a −n =

,где a ≠ 0, n ∈ z ( n принадлежит целым числам).

Примеры возведения в отрицательную степень.

6 −2 =
=
(−3) −3 =
=
= −
0,2 −2 =
=

Любое число в нулевой степени — единица.

Примеры возведения в нулевую степень.

Как найти

10 в минус 1 степени

В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:

Теперь, зная определение отрицательной степени, давайте разберемся, почему « 10 » в минус первой степени равно « 0,1 ».

Возведем « 10 −1 » по правилам отрицательной степени. Перевернем « 10 » и запишем её в виде дроби «

» и заменим отрицательную степень « −1 » на
положительную степень « 1 ».

10 −1 =

Возведем « 10 » в « 1 » степень. Помним, что любое число в первой степени равно самому числу.

10 −1 =

Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.

10 −1 =

= 0,1

По такому же принципу можно найти « 10 » в минус второй, третьей и т.д.

Для упрощения перевода « 10 » в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один ».

Проверим правило выше для « 10 −2 ».

Т.к. у нас степень « −2 », значит, будет всего один ноль (положительное значение степени « 2 − 1 = 1 ». Сразу после запятой ставим один ноль и за ним « 1 ».

Рассмотрим « 10 −1 ».

Т.к. у нас степень « −1 », значит, нулей после запятой не будет (положительное значение степени « 1 − 1 = 0 ». Сразу после запятой ставим « 1 ».

То же самое правило работает и для « 10 −12 ». При переводе в десятичную дробь будет « 12 − 1 = 11 » нулей и « 1 » в конце.

Как возвести в отрицательную степень дробь

Чтобы возвести дробь в отрицательную степень нужно:

«перевернуть» дробь;
заменить отрицательную степень на положительную ;
возвести дробь в положительную степень.

Пример. Требуется возвести в отрицательную степень дробь.

(

) −3 =
Перевернем дробь «

» и заменим отрицательную степень « −3 » на положительную « 3 ».
(

) −3 = (

) 3

Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель « 3 », и знаменатель « 10 » в третью степень.

(

) −3 = (

) 3 =

Для более грамотного ответа запишем полученный результат в виде десятичной дроби.

(

) −3 = (

) 3 =

= 0,027

Как возвести отрицательное число в отрицательную степень

Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.

Отрицательное число, возведённое в чётную степень, — число положительное .

Отрицательное число, возведённое в нечётную степень, — число отрицательное .

Перевернем число « −5 » и заменим отрицательную степень « −2 »
на положительную « 2 ».

(−5) −2 = (−

) 2 =

Так как степень « 2 » — четная , значит, результат возведения в степень будет положительный . Поэтому убираем знак минуса при раскрытии скобок.

Далее откроем скобки и возведем во вторую степень и числитель « 1 »,
и знаменатель « 5 ».

(−5) −2 = (−

) 2 =

Как возвести отрицательную дробь в отрицательную степень

Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.

Отрицательная дробь, возведённая в чётную степень, — дробь положительная .

Отрицательная дробь, возведённая в нечётную степень, — дробь отрицательная .

Разберемся на примере.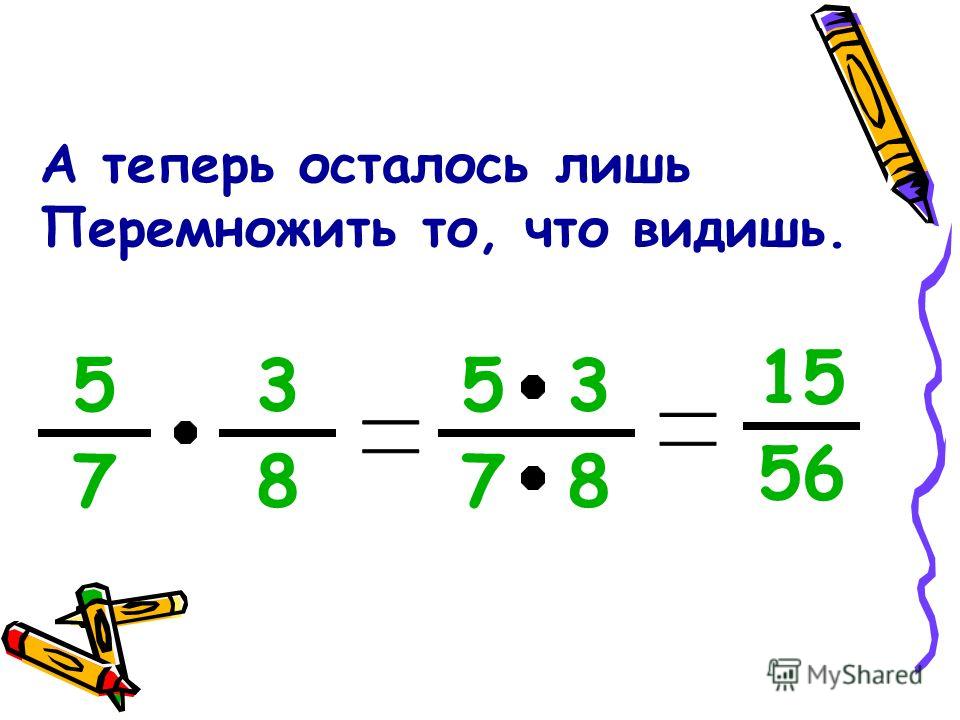 Задание: возвести отрицательную дробь « (−

) » в « −3 » степень.

По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень « −3 » на положительную « 3 ».

(−

) −3 = (−

) 3 =

Теперь определим конечный знак результата возведения в « 3 » степень.

Степень « 3 » — нечетная , значит, по правилу возведения отрицательного числа в степень дробь останется отрицательной .

Нам остается только раскрыть скобки и возвести в степень и числитель « 3 », и знаменатель « 2 » в третью степень.

(−

) −3 = (−

) 3 = −

= −

Для окончательного ответа выделим целую часть из дроби.

(−

) −3 = (−

) 3 = −

= −

= − 3

Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.

Правило возведения отрицательного числа в степень гласит: если степень четная , значит, результат возведения будет положительным .

(−

) −2 = (−

) 2 =

= 1

Свойства отрицательной степени

Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.

В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.

Запомните!

a m · a n = a m + n
= a m − n
(a n ) m = a n · m
(a · b) n = a n · b n

Примеры решений заданий с отрицательной

степенью

Колягин 9 класс. Задание № 1

Представить в виде степени.

2) a 6 · b 6 = (ab) 6

Колягин 9 класс. Задание № 5

Записать в виде степени с отрицательным числом.

Что такое степень с отрицательным показателем (отрицательная степень)? Как выполнить возведение числа в отрицательную степень? Как возвести в отрицательную степень дробь?

В частности, число в степени минус один — это число, обратное данному:

Если n — целое число, то речь идет о степени с целым отрицательным показателем и равенство верно для любого a, отличного от нуля (т.е. при a≠0).

Если n — дробное число, то речь идет о степени с рациональным показателем:

(m — целое число, n — натуральное число). Степень с дробным показателем определена только для положительных a (a>0).

Дробь в степени с отрицательным показателем равна обратному этой дроби числу в степени с показателем, противоположным данному:

Другими словами, чтобы возвести дробь в отрицательную степень, надо эту дробь «перевернуть»(числитель и знаменатель поменять местами) и изменить знак в показателе степени.

Дробь в минус первой степени — это «перевернутая» дробь.

Рассмотрим примеры возведения чисел в степень с отрицательным показателем.

Для ускорения вычислений используем таблицу степеней.

Чтобы возвести в отрицательную степень смешанное число, надо сначала перевести его в неправильную дробь:

Возведем числа в степень с дробным отрицательным показателем:

При возведении в отрицательную степень десятичной дроби можно сначала перевести ее в обыкновенную и, если возможно, сократить:

Если в показателе степени стоит десятичная дробь, нужно перевести ее в обыкновенную:

Возведение в степень с отрицательным показателем в алгебре встречается достаточно часто, поэтому важно вовремя усвоить эту тему.

13 комментариев

Спасибо! врубился) жаль, что в школе не учился(

Что ж, учиться никогда не поздно). Но всё же лучше вовремя.

Забавно, что за время работы встречал множество коллег, кому приходилось на внутренних курсах разжёвывать какие вещи начального уровня и все сокрушались: «Что же я в школе-то (институте) не учил это? Это же так просто, понятно, полезно и ИНТЕРЕСНО. »

А вся проблема в том, что ни в школе, ни в институте перед тем, как что-то начать рассказывать не проводят красочные, завлекательные, познавательные, весёлые и игровые презентации будущего курса, чтобы было понятно, а где же то, что будем скоро изучать, применяется в жизни? Каким профессиям и в каких житейских ситуациях это может быть полезно?

Учат каким-то абстрактным формулам вместо того, чтобы рассказать, что это пригодится на кухне, при разделе земли, при строительстве сарая на даче, при стрельбе из пушки, при запуске спутника и т. д.

При разбавлении спирта водой, в конце концов! :))

Ведь часто женщины встают в ступор от элементарной задачи:

В рецепте указано «1 ст. ложка 3 %-го уксуса», а у неё на кухне только 9 % или («О, БОЖЕ! Крах! Провал!») вообще уксусная эссенция! А по сути та же кислота, но в концентрации 70 %…

Возведение в отрицательную степень – один из основных элементов математики, который часто встречается при решении алгебраических задач. Ниже приведена подробная инструкция.

Как возводить в отрицательную степень – теория

Когда мы число в обычную степень, мы умножаем его значение несколько раз. Например, 3 3 = 3×3×3 = 27. С отрицательной дробью все наоборот. Общий вид по формуле будет иметь следующий вид: a -n = 1/a n . Таким образом, чтобы возвести число в отрицательную степень, нужно единицу поделить на данное число, но уже в положительной степени.

Как возводить в отрицательную степень – примеры на обычных числах

Держа вышеприведенное правило на уме, решим несколько примеров.

4 -2 = 1/4 2 = 1/16
Ответ: 4 -2 = 1/16

4 -2 = 1/-4 2 = 1/16.
Ответ -4 -2 = 1/16.

Но почему ответ в первом и втором примерах одинаковый? Дело в том, что при возведении отрицательного числа в четную степень (2, 4, 6 и т. д.), знак становится положительным. Если бы степень была четной, то минус сохранился:

Как возводить в отрицательную степень – числа от 0 до 1

Вспомним, что при возведении числа в промежутке от 0 до 1 в положительную степень, значение уменьшается с возрастанием степени. Так например, 0,5 2 = 0,25. 0,25 1/1/4 = 4

Пример 4: Вычислить 0,5 -3
Решение: 0,5 -3 = (1/2) -3 = 1/(1/2) 3 = 1/(1/8) = 8

Пример 5: Вычислить -0,5 -3
Решение: -0,5 -3 = (-1/2) -3 = 1/(-1/2) 3 = 1/(-1/8) = -8
Ответ: -0,5 -3 = -8

Исходя из 4-го и 5-ого примеров, сделаем несколько выводов:

Для положительного числа в промежутке от 0 до 1 (пример 4), возводимого в отрицательную степень, четность или нечетность степени не важна, значение выражения будет положительным. При этом, чем больше степень, тем больше значение.
Для отрицательного числа в промежутке от 0 до 1 (пример 5), возводимого в отрицательную степень, четность или нечетность степени неважна, значение выражения будет отрицательным. При этом, чем больше степень, тем меньше значение.

Как возводить в отрицательную степень – степень в виде дробного числа

Выражения данного типа имеют следующий вид: a -m/n , где a – обычное число, m – числитель степени, n – знаменатель степени.

Рассмотрим пример:
Вычислить: 8 -1/3

Решение (последовательность действий):

Вспоминаем правило возведения числа в отрицательную степень. Получим: 8 -1/3 = 1/(8) 1/3 .
Заметьте, в знаменателе число 8 в дробной степени. Общий вид вычисления дробной степени таков: a m/n = n √8 m .
Таким образом, 1/(8) 1/3 = 1/(3 √8 1). Получаем кубический корень из восьми, который равен 2. Исходя отсюда, 1/(8) 1/3 = 1/(1/2) = 2.
Ответ: 8 -1/3 = 2

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Возведение в степень – это вычисление значения степени некоторого числа.

То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени (0 , 5) 5 .

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Условие: возведите – 2 в степень 4 .

Используя определение выше, запишем: (− 2) 4 = (− 2) · (− 2) · (− 2) · (− 2) . Далее нам нужно просто выполнить указанные действия и получить 16 .

Возьмем пример посложнее.

Вычислите значение 3 2 7 2

Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Выполните возведение в квадрат числа π .

Для начала округлим его до сотых. Тогда π 2 ≈ (3 , 14) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ (3 , 14159) 2 = 9 , 8695877281 .

Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени (ln 6) 3 или преобразовать, если это возможно: 5 7 = 125 5 .

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Так, (− 9) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .

Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .

5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1

0 0 – не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.

Возведите 3 в степень – 2 .

Используя определение выше, запишем: 2 – 3 = 1 2 3

Подсчитаем знаменатель этой дроби и получим 8: 2 3 = 2 · 2 · 2 = 8 .

Тогда ответ таков: 2 – 3 = 1 2 3 = 1 8

Возведите 1 , 43 в степень – 2 .

Переформулируем: 1 , 43 – 2 = 1 (1 , 43) 2

Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:

В итоге у нас вышло (1 , 43) – 2 = 1 (1 , 43) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: (1 , 43) – 2 = 10000 20449

Отдельный случай – возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a – 1 = 1 a 1 = 1 a .

Пример: 3 − 1 = 1 / 3

9 13 – 1 = 13 9 6 4 – 1 = 1 6 4 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.

У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а, потом возводим результат в степень с целым показателем m .

Проиллюстрируем на примере.

Вычислите 8 – 2 3 .

Способ 1. Согласно основному определению, мы можем представить это в виде: 8 – 2 3 = 8 – 2 3

Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 – 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Способ 2. Преобразуем основное равенство: 8 – 2 3 = 8 – 2 3 = 8 3 – 2

После этого извлечем корень 8 3 – 2 = 2 3 3 – 2 = 2 – 2 и результат возведем в квадрат: 2 – 2 = 1 2 2 = 1 4

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Возведите 44 , 89 в степень 2 , 5 .

Преобразуем значение показателя в обыкновенную дробь – 44 , 89 2 , 5 = 49 , 89 5 2 .

А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107

Ответ: 13 501 , 25107 . s=frac$.

Справочный материал по математике (6 класс) Дроби

Справочный материал по математике (6 класс) Дроби — страница №1/1

Справочный материал по математике (6 класс)

Дроби

Основное свойство дроби

: Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь (используется при сокращении дробей).

Перевод дробей

Чтобы записать обыкновенную дробь в виде десятичной, нужно разделить числитель на знаменатель

Действия с дробями

Чтобы сложить дроби с разными знаменателями, надо: привести данные дроби к наименьшему общему знаменателю; сложить полученные дроби (сложить числители дробей, знаменатель переписать без изменений).
Чтобы умножить дробь на дробь, надо: найти произведение числителей и произведение знаменателей этих дробей; первое произведение записать числителем, а второе – знаменателем.
Чтобы разделить одну дробь на другую, надо делимое (первую дробь) умножить на число, обратное делителю («перевернутая» вторая дробь).

Пропорции

Частное двух чисел называют

отношением

этих чисел. (4:5)

Равенство двух отношений называется пропорцией. (a:b=c:d)

Свойство пропорции: в верной пропорции произведение крайних членов равно произведению средних. (ad=bc)

Положительные и отрицательные числа

Числа, лежащие на координатной прямой

левее

0, называются

отрицательными

, а

правее 0

–

положительными

Сравнение чисел

На координатной прямой точка с большей координатой лежит правее точки с меньшей координатой.

Модуль числа

Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).

Действия с отрицательными и положительными числами

Чтобы сложить два отрицательных числа, надо: сложить их модули, поставить перед полученным числом знак «-». Результат сложения двух отрицательных чисел – отрицательное число! (-4-5=-4+(-5)=-9)

Чтобы сложить два числа с разными знаками, надо из большего модуля слагаемых вычесть меньший, поставить перед полученным числом знак того слагаемого, модуль которого больше.

-2+3=3-2=1, 5-8=-(8-5)=-3

Чтобы перемножить два отрицательных числа, надо перемножить их модули. Результат умножения двух отрицательных чисел – число положительное! (-4^. (-5)=20) (аналогично выполняется деление отрицательных чисел).

Чтобы перемножить два числа с разными знаками нужно перемножить их модули и перед полученным числом поставить знак «-». Результат умножения положительного и отрицательного чисел – отрицательное число! (-4^. 5=-20)

Решение уравнений

Раскрытие скобок

Если перед скобками стоит знак «+», то можно опустить скобки и этот знак, сохранив знаки слагаемых, стоящих в скобках.

Если перед скобками стоит знак «-», надо заменить этот знак на «+», поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.

Слагаемые, имеющие одинаковую буквенную часть, называют подобными.

Чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на их общую буквенную часть.

Алгоритм решения линейного уравнения

Раскрыть скобки (если таковые имеются), используя правила (см.выше) или свойства умножения.
Перенести все слагаемые с переменной в одну часть уравнения, а известные слагаемые – в другую. При переносе слагаемого из одной части уравнения в другую его знак меняется!
Привести подобные слагаемые, используя действия с положительными и отрицательными числами.
Разделить число, стоящее справа, на коэффициент, стоящий перед переменной (слева).

Умножение отрицательных дробей — Видео и стенограмма урока

Умножение отрицательных дробей

Вот четыре шага для умножения отрицательных дробей. Давайте воспользуемся следующей задачей, чтобы проиллюстрировать шаги.

Помните, что числители — это числа над чертой в дробной части, а знаменатели — это числа под чертой в дробях.

Помните, что целое число можно превратить в дробь, просто поместив целое число над единицей.Например, целое число 7 становится 7/1.

Попрактикуемся

Давайте вместе попробуем. Давайте найдем произведение -2/7 * 3/4

Шаг 1) Когда мы умножим числители (2 * 3), ответ будет 6.

Шаг 2) Когда мы умножим знаменатели (7 * 4), ответ равно 28.

Шаг 3) Новая дробь — 6/28. Оба числа делятся на 2 и могут быть упрощены до 3/14.

Шаг 4) У дробей разные знаки, так как одна положительная, а другая отрицательная, поэтому ответ отрицательный.

Произведение -2/7 * 3/4 = -3/14.

Попробуем еще парочку. Не стесняйтесь брать лист бумаги и карандаш и самостоятельно решать следующие задачи, прежде чем искать решение.

Решить: -3/4 * 2/3

Шаг 1) Умножить числители: 3 * 2 = 6

Шаг 2) Умножить знаменатели: 4 * 3 = 12

Шаг 3) Упростить 6/12 ( оба делятся на 6) до 1/2

Шаг 4) Знаки разные, поэтому ответ отрицательный.

Ответ -1/2.

Решить: -1/2 * 3/4

Шаг 1) Умножить числители: 1 * 3 = 3

Шаг 2) Умножить знаменатели: 2 * 4 = 8

Шаг 3) 3/8 уже в простейшей форме

Шаг 4) Знаки разные, поэтому ответ отрицательный.

Итак, -1/2 * 3/4 = -3/8.

Краткое содержание урока

При умножении дробей помните, что если дроби имеют одинаковый знак, ответ будет положительным, а если дроби имеют разные знаки, ответ будет отрицательным.Также помните, что умножение отрицательных дробей состоит из четырех простых шагов, и это, безусловно, положительный момент!

Упрощение выражения с помощью дроби

Результаты обучения

Определите отрицательные дроби, которые эквивалентны, учитывая, что их отрицательный знак находится в другом месте
Упростите выражения, содержащие дробные черты, используя порядок операций

Где идет знак минус в дроби? Обычно перед дробью ставится знак минус, но иногда можно увидеть дробь с отрицательным числителем или знаменателем. Помните, что дроби представляют собой деление. Дробь [латекс] — \ frac {1} {3} [/ latex] может быть результатом деления [latex] \ frac {-1} {3} [/ latex], отрицательного на положительный или деления [latex] \ frac {1} {- 3} [/ latex], положительное за отрицательным. Когда числитель и знаменатель имеют разные знаки, частное отрицательное.

Если и числитель, и знаменатель отрицательны, тогда сама дробь положительна, потому что мы делим отрицательное на отрицательное.

[латекс] \ frac {-1} {- 3} = \ frac {1} {3} \ frac {\ text {negative}} {\ text {negative}} = \ text {positive} [/ latex]

Размещение отрицательного знака в дроби

Для любых положительных чисел [латекс] a \ text {и} b [/ latex],

[латекс] \ frac {-a} {b} = \ frac {a} {- b} = — \ frac {a} {b} [/ latex]

Пример

Какая из следующих фракций эквивалентна [latex] \ frac {7} {- 8}? [/ Latex]

[латекс] \ frac {-7} {- 8}, \ frac {-7} {8}, \ frac {7} {8}, — \ frac {7} {8} [/ latex]

Решение:
Частное положительного и отрицательного отрицательно, поэтому [latex] \ frac {7} {- 8} [/ latex] отрицательно. Из перечисленных фракций [latex] \ frac {-7} {8} \ text {и} — \ frac {7} {8} [/ latex] также отрицательны.

Упрощение выражения с помощью дроби

Полоски дроби действуют как символы группировки. Выражения над и под дробной чертой следует рассматривать так, как если бы они были заключены в круглые скобки. Например, [латекс] \ frac {4 + 8} {5 — 3} [/ latex] означает [латекс] \ left (4 + 8 \ right) \ div \ left (5 — 3 \ right) [/ latex] . Порядок операций говорит нам сначала упростить числитель и знаменатель — как если бы были круглые скобки — перед тем, как делить.
Мы добавим дробные черты к нашему набору символов группировки из раздела «Использование языка алгебры», чтобы получить здесь более полный набор.

Группировка символов

Упростите выражение с помощью дробной линейки

Упростим числитель.
Упростим знаменатель.
Упростите дробь.

Пример

Упростить: [латекс] \ frac {4 + 8} {5 — 3} [/ латекс]

Показать решение

Решение:

» data-label=»»>

	[латекс] \ frac {4 + 8} {5 — 3} [/ латекс]
Упростите выражение в числителе.	[латекс] \ frac {12} {5 — 3} [/ латекс]
Упростим выражение в знаменателе. {2} +2} [/ latex]
Используйте порядок операций.{2}} {64 — 16} [/ латекс]
Упростим числитель и знаменатель.	[латекс] \ frac {16} {48} [/ латекс]
Упростим дробь.	[латекс] \ frac {1} {3} [/ латекс]

Пример

Упростить: [латекс] \ frac {4 \ left (-3 \ right) +6 \ left (-2 \ right)} {- 3 \ left (2 \ right) -2} [/ latex]

Показать решение

Решение:

[латекс] \ frac {4 \ left (-3 \ right) +6 \ left (-2 \ right)} {- 3 \ left (2 \ right) -2} [/ латекс]
Умножить.	[латекс] \ frac {-12+ \ left (-12 \ right)} {- 6 — 2} [/ латекс]
Упростить.	[латекс] \ frac {-24} {- 8} [/ латекс]
Разделить.	[латекс] 3 [/ латекс]

Посмотрите это видео, чтобы увидеть еще один пример того, как упростить выражение с помощью дробной линейки, содержащей несколько различных операций.

Умножение положительных и отрицательных чисел: 3 простых правила

При умножении положительных и отрицательных чисел существует меньше правил, чем при сложении и вычитании положительных и отрицательных чисел.Следует запомнить всего три правила:

Правило 1. Положительное число, умноженное на положительное, равняется положительному числу.

Это умножение, которое вы делали все время: положительные числа, умноженные на положительные, равны положительным числам.

Например, 5 x 3 = 15. 5 — положительное число, 3 — положительное число, а умножение дает положительное число: 15.

Ответ: 5 x 3 = 15.

Правило 2: Отрицательное число, умноженное на положительное, равняется отрицательному числу.

Когда вы умножаете отрицательное число на положительное, ваш ответ — отрицательное число. Неважно, в каком порядке вы умножаете положительные и отрицательные числа, ответ всегда будет отрицательным.

Например: -2 x 4, что по сути то же самое, что -2 + (-2) + (-2) + (-2)

Ответ: -2 х 4 = -8.

И, как мы уже сказали, если около 4 x -2 наоборот, ответ все тот же: -8.

Ответ: 4 х -2 = -8.

Правило 3. Отрицательное число, умноженное на отрицательное число, равняется положительному числу.

Два отрицательных числа дают положительное число, поэтому умноженное на отрицательное число дает положительное число. Если вы посмотрите на него на числовой прямой, идя назад и повернувшись лицом в отрицательном направлении, вы двинетесь в положительном направлении.

Например. -2 x -4 отрицательны, поэтому мы знаем, что ответ будет положительным.

Ответ: -2 x -4 = 8.

Вот общее правило, которое следует помнить при умножении положительных и отрицательных чисел:

Два одинаковых знака дают положительный знак:

Два непохожих знака образуют отрицательный знак:

Если вы все еще не понимаете, почему отрицательное число, умноженное на отрицательное, дает положительное число, Диана Браун с факультета математики Университета Джорджии объясняет это разными способами в этой статье.

Скотт из About.com также собрал удобное видео о том, как создать шпаргалку для умножения отрицательных и положительных чисел (прокрутите страницу вниз, и вы найдете видео).

Умножение и деление отрицательных дробей и смешанных чисел

Дроби Смешанные числа и неправильные дроби. Смешанное число содержит целую часть и дробную часть. смешанное число. Он содержит как целую часть, 3, так и дробную часть, 2/5. Мы читаем дробь как «три и две пятых», и это именно то, что мы имеем в виду.= Добавление целого числа к дроби — это особый случай сложения двух … Бесплатные рабочие листы по математике для сложения, вычитания, умножения, среднего, деления, алгебры и тем меньше, чем больше, в соответствии с общими основными стандартами для 5-го и 4-го классов класс, 3 класс, 2 класс, 1 класс, средняя школа и дошкольное учреждение

Способность записывать смешанные дроби как неправильные дроби и наоборот является важной предпосылкой для сложения и вычитания смешанных дробей (CCSS. Math.4.NF.3c): складывать и вычитать смешанные числа с одинаковыми знаменателями, например, заменяя каждое смешанное число эквивалентной дробью и / или используя свойства операций и … На этой странице вы найдете наши рабочие листы с отрицательными целыми числами, отрицательными десятичными знаками. и отрицательные дроби. Наши рабочие листы с отрицательными числами подходят для 6 и 7 классов математики и являются отличным математическим ресурсом для корректирующих целей по математике или математическому обучению. У нас есть целые листы, в которых описывается сложение и вычитание целых и отрицательных чисел из числа…

Умножайте или делите смешанные числа. Преобразуйте смешанные числа в неправильные дроби. Следуйте правилам умножения или деления дробей. Если возможно, упростите. Упростите сложную дробь. Перепишите сложную дробь как задачу деления. Соблюдайте правила деления дробей. Если возможно, упростите. Размещение знака минус в дроби CCBC Math 081 Умножение дробей и смешанных чисел Раздел 3. 2 Третье издание 17 страниц 162 Пример 4a: Умножение: 29 3 14 u 2 9 2 9 18 3 14 3 14 42 uuu Умножьте числители вместе и знаменатели вместе.Проверьте, можно ли упростить ответ. Есть общие множители для 18 и 42, так что это

9 апреля 2015 г. · Идея состоит в том, что пары чисел сами по себе связаны с ассоциациями. У этого утверждения есть жесткая версия, которую я не собираюсь делать. Я не хочу сказать, что независимо от контекста, вы ожидаете, что ученик сложит вместе 5 1/2 и 2 1/4. Я думаю, что проблема деления смешанных чисел вряд ли вызовет ассоциации с … Как пользоваться калькулятором. Введите свою задачу по алгебре в текстовое поле.Например, введите 3x + 2 = 14 в текстовое поле, чтобы получить пошаговое объяснение того, как решить 3x + 2 = 14.

Вычитание целых чисел от (-15) до (+15) (отрицательные числа в круглых скобках) (106 просмотров на этой неделе) Все операции с целыми числами (диапазон от -9 до 9) со всеми целыми числами в круглых скобках (81 просмотр на этой неделе) Целочисленное сложение и вычитание с круглыми скобками вокруг всех целых чисел (диапазон от -25 до 25) (60 просмотров на этой неделе) Добавление целых чисел от (-15) до (+15) (все числа в круглых скобках) (49 просмотров на этой неделе… Практика сложения, вычитания, умножения и деления на смешанные дроби, рабочая тетрадь улучшит вашу беглость математики том 14 25 октября 2020 г.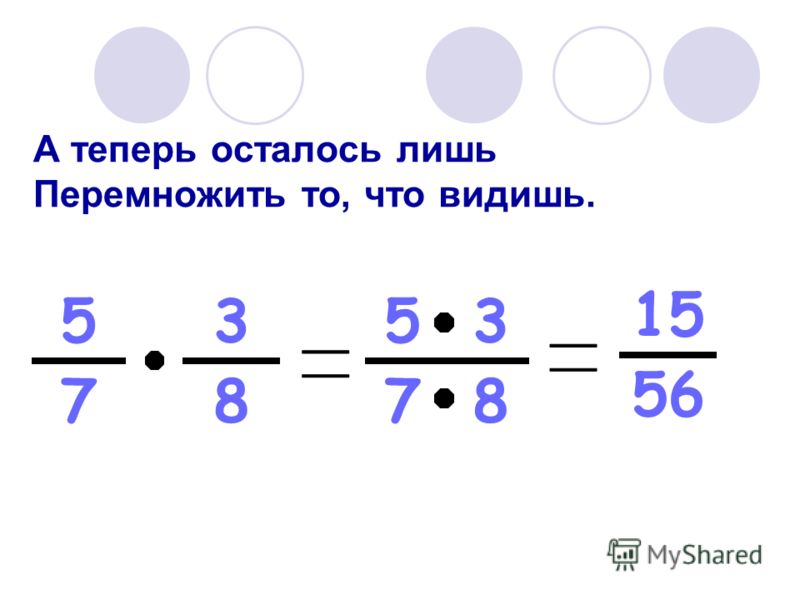 Автор: Джеки Коллинз Паблишинг …

Умножение — это математическая операция, которая масштабирует одно число на другое ( умножение — знак: x). Он заменяет сложение большого количества чисел подряд. Умножение — математическая операция, противоположная делению. Например: вы можете заменить математическое выражение 5 + 5 + 5 + 5 на 5 × 4 (число 5, умноженное на количество раз, которое оно появилось в строке).

Умножение имеет несколько свойств. Когда число умножается на число 1, произведение (результат умножения) совпадает с этим числом. Когда число умножается на ноль, произведение всегда равно нулю. Когда число умножается на отрицательное, результатом является отрицательная версия этого числа. Он также обладает свойствами коммутативности, ассоциативности и дистрибутивности.

Коммутативные и ассоциативные свойства аналогичны этим свойствам.Распределительность применяется при объединении сложения и умножения, как в этом примере:

а * (б + в) = а * б + а * в

Очень важно помнить, что порядок важности умножения всегда больше, чем порядок важности сложения или вычитания. Сначала вы умножаете числа (где это необходимо), а затем складываете или вычитаете их. Вот пример:

5 * 4 + 3 = 20 + 3 = 23

Единственным исключением из правила является то, что сложение или вычитание имеет приоритет над умножением, когда числа, которые нужно сложить, и оператор заключены в квадратные скобки, а оператор умножения — нет.

Умножение экзаменов для учителей

Название экзамена	Размер файла	Загрузки	Дата загрузки
Целые положительные числа
Умножение положительных целых чисел — очень просто	78 Кбайт	2899	3 сентября 2019 г.
Умножение положительных целых чисел — легко	143 Кбайт	2902	3 сентября 2019 г.
Умножение положительных целых чисел — среднее	166.3 кБ	3194	3 сентября 2019 г.
Умножение положительных целых чисел — средней сложности	173.1 Кбайт	2675	3 сентября 2019 г.
Умножение положительных целых чисел — жесткое	561.5 кБ	2082	3 сентября 2019 г.
Умножение положительных целых чисел — очень сложно	571.8 Кбайт	2294	3 сентября 2019 г.
Положительные десятичные знаки
Умножение положительных десятичных знаков — очень просто	554.5 кБ	1936	3 сентября 2019 г.
Умножение положительных десятичных знаков — легко	555.5 Кбайт	1927	3 сентября 2019 г.
Умножение положительных десятичных знаков — среднее	579.2 Кбайт	1752	3 сентября 2019 г.
Умножение положительных десятичных знаков — средне-жесткий	580. 2 Кбайт	1573	3 сентября 2019 г.
Умножение положительных десятичных знаков — жесткое	569.5 кБ	1736	3 сентября 2019 г.
Умножение положительных десятичных знаков — очень сложно	567.2 Кбайт	1576	3 сентября 2019 г.
Положительные дроби
Умножение положительных дробей — очень сложно	567.2 Кбайт	1576	3 сентября 2019 г.
Умножение положительных дробей — очень просто	172.7 Кбайт	2353	3 сентября 2019 г.
Умножение положительных дробей — легко	188.9 кБ	2049	3 сентября 2019 г.
Умножение положительных дробей — среднее	577.2 Кбайт	1765	3 сентября 2019 г.
Умножение положительных дробей — средней твердости	591. 9 Кбайт	1557	3 сентября 2019 г.
Умножение положительных дробей — жесткое	575.7 Кбайт	1569	3 сентября 2019 г.
Умножение положительных дробей — очень сложно	581 Кбайт	1553	3 сентября 2019 г.
Положительные смешанные числа
Умножение положительных смешанных чисел — очень просто	176.8 кБ	1749	3 сентября 2019 г.
Умножение положительных смешанных чисел — легко	209.8 Кбайт	1761	3 сентября 2019 г.
Умножение смешанных положительных чисел — среднее	585.6 Кбайт	1592	3 сентября 2019 г.
Умножение смешанных положительных чисел — средней сложности	592.9 Кбайт	1513	3 сентября 2019 г.
Умножение положительных смешанных чисел — жесткое	589. 3 кБ	1517	3 сентября 2019 г.
Умножение положительных смешанных чисел — очень сложно	596.6 Кбайт	1483	3 сентября 2019 г.
Положительные неправильные дроби
Умножение положительных неправильных дробей — очень просто	166 Кбайт	1539	3 сентября 2019 г.
Умножение положительных неправильных дробей — легко	169.9 кБ	1640	3 сентября 2019 г.
Умножение положительных неправильных дробей — среднее	571.6 Кбайт	1520	3 сентября 2019 г.
Умножение положительных неправильных дробей — средней твердости	569.5 Кбайт	1483	3 сентября 2019 г.
Умножение положительных неправильных дробей — жесткое	560.5 Кбайт	1426	3 сентября 2019 г.
Умножение положительных неправильных дробей — очень сложно	571.8 кБ	1494	3 сентября 2019 г.
Целые неположительные числа
Умножение целых чисел — очень просто	137.9 Кбайт	2107	3 сентября 2019 г.
Умножение целых чисел — легко	143.6 Кбайт	2143	3 сентября 2019 г.
Умножение целых чисел — среднее	173.3 Кбайт	2097	3 сентября 2019 г.
Умножение целых чисел — средней сложности	173.5 кБ	1957	3 сентября 2019 г.
Умножение целых чисел — жесткое	565.9 Кбайт	1746	3 сентября 2019 г.
Умножение целых чисел — очень сложно	568 Кбайт	1641	3 сентября 2019 г.
Неположительные десятичные числа
Умножение десятичных знаков — очень просто	186. 6 Кбайт	1983	3 сентября 2019 г.
Умножение десятичных знаков — просто	187 Кбайт	2103	3 сентября 2019 г.
Умножение десятичных знаков — среднее	578.8 кБ	1601	3 сентября 2019 г.
Умножение десятичных знаков — средней жесткости	577 Кбайт	1520	3 сентября 2019 г.
Умножение десятичных знаков — жесткое	564.9 Кбайт	1591	3 сентября 2019 г.
Умножение десятичных знаков — очень сложно	567.9 Кбайт	1501	3 сентября 2019 г.
Неположительные дроби
Умножение дробей — очень просто	179.6 кБ	1594	3 сентября 2019 г.
Умножение дробей — легко	186.7 Кбайт	1866	3 сентября 2019 г.
Умножение дробей — среднее	583.8 Кбайт	1596	3 сентября 2019 г.
Умножение дробей — средней твердости	589 Кбайт	1511	3 сентября 2019 г.
Умножение дробей — жесткое	588 Кбайт	1422	3 сентября 2019 г.
Умножение дробей — очень сложно	594.9 кБ	1436	3 сентября 2019 г.
Неположительные смешанные числа
Умножение смешанных чисел — очень просто	192.9 кБ	1468	3 сентября 2019 г.
Умножение смешанных чисел — просто	209 Кбайт	1635	3 сентября 2019 г.
Умножение смешанных чисел — среднее	594.7 Кбайт	1510	3 сентября 2019 г.
Умножение смешанных чисел — средней сложности	602. 2 кБ	1354	3 сентября 2019 г.
Умножение смешанных чисел — сложное	586.3 Кбайт	1380	3 сентября 2019 г.
Умножение смешанных чисел — очень сложно	591.3 Кбайт	1360	3 сентября 2019 г.
Неположительные неправильные дроби
Умножение неправильных дробей — очень просто	171.2 Кбайт	1411	3 сентября 2019 г.
Умножение неправильных дробей — легко	174 Кбайт	1454	3 сентября 2019 г.
Умножение неправильных дробей — среднее	574.7 кБ	1419	3 сентября 2019 г.
Умножение неправильных дробей — средней твердости	573.9 Кбайт	1333	3 сентября 2019 г.
Умножение неправильных дробей — жесткое	570. 7 Кбайт	1351	3 сентября 2019 г.
Умножение неправильных дробей — очень сложно	577.4 Кбайт	1348	3 сентября 2019 г.

Умножение рабочих листов для студентов

Название листа	Размер файла	Загрузки	Дата загрузки
Положительно
Умножение натуральных чисел	496.1 кБ	2432	3 сентября 2019 г.
Умножение положительных десятичных знаков	51.8 Кбайт	1768	3 сентября 2019 г.
Умножение положительных дробей	632.1 Кбайт	1571	3 сентября 2019 г.
Умножение смешанных положительных чисел	637.8 Кбайт	1784	3 сентября 2019 г.
Умножение положительных неправильных дробей	594. 6 кБ	1390	3 сентября 2019 г.
Неположительный
Умножение целых чисел	166.8 Кбайт	1810	3 сентября 2019 г.
Умножение десятичных знаков	246.3 Кбайт	1644	3 сентября 2019 г.
Умножение дробей	393.1 Кбайт	1639	3 сентября 2019 г.
Умножение смешанных чисел	412.4 кБ	1534	3 сентября 2019 г.
Умножение неправильных дробей	334.1 Кбайт	1440	3 сентября 2019 г.

Обратная дробь — ChiliMath

Помните, что дробь состоит из трех частей.

ЧАСТИ ФРАКЦИИ

Как найти величину, обратную дроби

Чтобы получить величину, обратную дроби

просто меняет местами или местами числитель и знаменатель. Вы можете сказать, что мы просто переворачиваем исходную дробь вверх дном.

Примеры нахождения обратной дроби

Пример 1: Найдите величину, обратную дроби, указанной ниже.

Давайте перевернем дробь {3 \ over 7} вверх дном, чтобы получить обратную величину. Это дает нам

Пример 2: Найдите величину, обратную дроби, указанной ниже.

Для некоторых это может быть непросто. Обратите внимание, что числитель отрицательный. Если перевернуть эту дробь вверх дном, то естественно должно получиться

Поскольку это отрицательная дробь, отрицательный символ не всегда может «следовать» за числом, к которому он изначально прикреплен.

Другими словами, отрицательный символ может оставаться в числителе. Итак, после инвертирования двух чисел отрицательный символ присоединяется к 2. Это также правильный ответ, поскольку он является обратной величиной исходной дроби.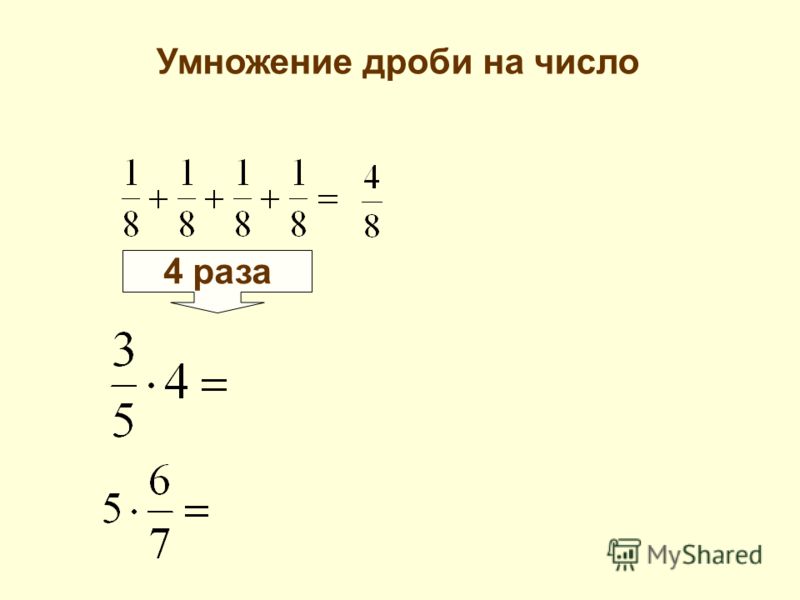

Есть еще один способ записать обратную величину этой отрицательной дроби. Отрицательный символ не может быть присоединен к числителю или знаменателю , .

Также правильно размещать отрицательный символ непосредственно слева от дроби .Вот как это выглядит!

Итак, если дробь отрицательная, ее обратная величина может быть записана тремя способами.

Отрицательный символ остается с числителем
Отрицательный символ остается со знаменателем
Отрицательный символ остается с дробной чертой

Пример 3: Запишите обратную величину отрицательной дроби ниже тремя различными способами.

Решение:

Пример 4: Найдите значение, обратное целому числу 15.

Любое ненулевое целое число может быть выражено знаменателем , равным 1.

Имея четкий знаменатель, мы можем легко перевернуть эту дробь вверх дном, чтобы получить обратную величину.

Пример 5: Найдите обратное целому числу — 11.

Сначала перепишите это целое число со знаменателем , равным 1.

Теперь, имея четкий знаменатель, мы можем найти его обратную величину. У нас есть отрицательный символ в числителе, помните, что его можно расположить в трех разных местах: числитель, знаменатель и дробь.Вот возможные ответы!

Вас также может заинтересовать:

Сложение и вычитание дробей с одним знаменателем
Сложение и вычитание дробей с разными знаменателями
Умножение дробей
Деление дробей
Упрощение дробей
Эквивалентные дроби

Рабочий лист

дробей

Добро пожаловать на страницу рабочих листов для дробей на Math-Drills.com, где чашка наполовину заполнена! Скорее всего, это одна из самых популярных наших страниц, потому что изучение дробей невероятно важно в жизни человека, и это математическая тема, к которой многие подходят с трепетом из-за плохой репутации на протяжении многих лет. Освоить дроби на самом деле не так сложно, особенно с поддержкой нашего широкого выбора рабочих листов.

Эта страница включает в себя рабочие листы дробей для понимания дробей, включая моделирование, сравнение, упорядочение, упрощение и преобразование дробей и операции с дробями. Начнем с очевидного: моделирование дробей. Это отличная идея, если студенты действительно могут понять, что такое дробь, поэтому, пожалуйста, уделите немного времени аспекту моделирования. Связь моделирования с реальной жизнью тоже очень помогает, так как гораздо легче связать половину печенья, чем половину квадрата.Спросите у большинства студентов, что вы получите, если добавите половину печенья и половину печенья, и они, вероятно, дадут вам знать, что из этого получится одна вкусная закуска.

Другие рабочие листы на этой странице посвящены тому, чтобы помочь студентам понять концепцию дробей. От сравнения и упорядочения до упрощения и преобразования … к тому времени, когда студенты усвоят материал на этой странице, операции с дробями будут похожи на прогулку по парку.

Рабочие листы с самыми популярными дробями на этой неделе

Распечатки с дробями общего назначения

Дробные круги

Черные и белые круги дробей можно использовать как манипуляторы для сравнения дробей.Сделайте фотокопию рабочего листа на слайд с проекцией сверху. Карандашом слегка закрасьте соответствующий кружок, чтобы изобразить первую дробь на бумажной копии. Используйте непостоянную ручку над головой, чтобы раскрасить соответствующий круг, чтобы обозначить вторую дробь. Положите слайд на бумагу и сравните два круга. Вы легко сможете определить, какая дробь больше или меньше или равны две дроби. Используйте оба листа повторно, стирая карандаш и смывая маркер.

Фракционные полоски

Полоски с дробями можно ламинировать для повышения прочности и вырезать для сравнения, упорядочивания, сложения и вычитания дробей.Они очень полезны для сравнения дробей.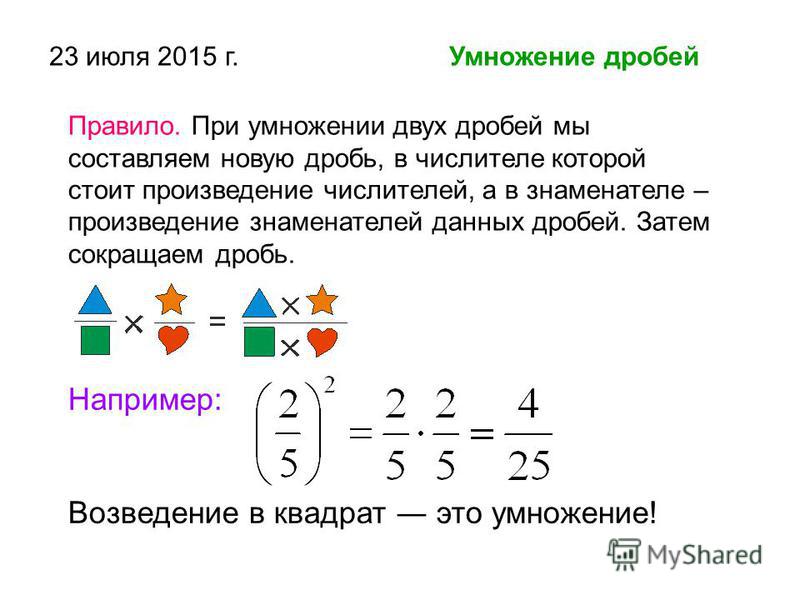 Вы также можете скопировать полоски с дробями на слайды проекции и вырезать их. Они будут не только долговечными, но и прозрачными, что полезно при использовании в сочетании с бумажными версиями (например, для сравнения дробей).

Рабочие листы моделирования дробей

Помимо использования приведенных ниже таблиц, вы также можете попробовать еще несколько интересных способов моделирования дробей. Здоровые закуски могут стать отличными моделями для дробей.Можно ли разрезать огурец пополам? Помидор на четвертинки? Можно ли сделать две трети винограда красными, а одну треть — зелеными?

Моделирование фракций с группами фигур

Дроби могут представлять части группы или части целого. В этих таблицах дроби моделируются как части группы.

Моделирование фракций прямоугольниками

Моделирование фракций с кругами

Таблицы соотношений и пропорций

Соотношение изображений

Эквивалентные дроби

Рабочие листы моделей эквивалентных фракций включают только «фракции выпечки» в версиях A. Чтобы увидеть более сложные и разнообразные дроби, выберите версии от B до J после загрузки версии A.

Эквивалентные соотношения

Таблицы сравнения и сортировки дробей

Сравнение простых дробей

Есть много разных стратегий, кроме просмотра страницы, которые помогут в сравнении дробей. Попробуйте начать с чего-нибудь наглядного, что будет изображать рассматриваемые дроби.Мы настоятельно рекомендуем наши дробные полоски (прокрутите немного вверх). Использование линейки, такой как линейка, книга или складка, поможет учащимся легко увидеть, какая дробь больше или равна ли они. Следует также отметить, что сравниваемые вещи должны быть одинаковыми. Например, каждая фракционная полоска имеет одинаковый размер, тогда как если вы возьмете треть арбуза и половину винограда, арбуз, вероятно, победит.

Сравнение простых и неправильных дробей

Еще одна стратегия, которую можно использовать при сравнении дробей, — использовать числовую линию и использовать контрольные цифры, такие как 0, 1, 1/2, чтобы выяснить, куда идет каждая дробь, а затем посмотреть, какая из них больше. Студенты на самом деле делают это все время, так как они часто могут сравнивать дроби, осознавая, что одна меньше половины, а другая больше половины. Они также могут увидеть, что одна фракция намного ближе к целому, чем другая фракция, даже если они обе могут быть больше половины.

Сравнение простых, неправильных и смешанных дробей

Другая стратегия сравнения дробей — преобразовать каждую дробь в десятичную дробь и сравнить десятичные дроби.Десятичные преобразования можно запомнить (особенно для обычных дробей), рассчитанные путем деления в столбик, с помощью калькулятора или справочной таблицы. Мы предлагаем последнее, поскольку использование справочной таблицы часто приводит к мысленному вспоминанию.

Заказ дробей в числовой строке

Многие из тех же стратегий, которые работают для сравнения дробей, также работают для упорядочивания дробей. Использование таких манипуляторов, как полоски дробей, использование числовых линий или поиск десятичных эквивалентов, заставит ваших учеников быстро расставить дроби в правильном порядке.Мы, вероятно, говорили об этом раньше, но убедитесь, что вы подчеркнули, что при сравнении или упорядочивании дробей учащиеся понимают, что целое должно быть одинаковым. Сравнение половины населения Канады с третью населения Соединенных Штатов не поможет. Попробуйте использовать визуальные эффекты, чтобы усилить эту важную концепцию. Несмотря на то, что мы включили числовые линии ниже, вы можете свободно использовать свои собственные стратегии.

Заказ дробей

Рабочие листы с упорядочением дробей в этом разделе не включают числовую строку, чтобы студенты могли использовать различные стратегии сортировки.

Рабочие листы для упрощения и преобразования дробей

Округление дробей

Округление дробей помогает учащимся немного лучше понимать дроби и может применяться для оценки ответов на вопросы о дробях. Например, если нужно было оценить 1 4/7 × 6, они, вероятно, могли бы сказать, что ответ будет примерно 9, поскольку 1 4/7 составляет примерно 1 1/2, а 1 1/2 × 6 — 9.

Упрощение дробей

Изучение того, как упрощать дроби, значительно облегчает жизнь студента в дальнейшем, когда он будет изучать операции с дробями.Это также помогает им узнать, что дроби, которые выглядят по-разному, могут быть эквивалентными. Один из способов продемонстрировать это — разделить две эквивалентные дроби. Например, 3/2 и 6/4 при делении дают частное 1,5. Будем надеяться, что практикуя упрощение дробей, студенты будут распознавать неупрощенные дроби, когда они начнут складывать, вычитать, умножать и делить на дроби.

Преобразование из неправильной дроби в смешанную

Преобразование между дробями, десятичными знаками, процентами и отношениями Преобразование дробей в завершающие десятичные дроби Преобразование дробей в завершающие и повторяющиеся десятичные дроби Преобразование завершающих десятичных знаков в дроби Преобразование завершающих и повторяющихся десятичных знаков в дроби Преобразование дробей в сотые

Преобразование дробей в десятичные, проценты и частичные в Части соотношений ( только завершающие десятичные дроби) Преобразование дробей в десятичные дроби, проценты и части-к- целые отношения ( только завершающие десятичные дроби) Преобразование десятичных дробей в дроби, проценты и частичные-к- Части отношения ( только завершающие десятичные дроби) Преобразование десятичных дробей в дроби, проценты и части-к- целые отношения ( только завершающие десятичные числа) Преобразование процентов в дроби, десятичные дроби и частичные-к- частичные отношения ( только завершающие десятичные дроби) Преобразование процентов в дроби, десятичные дроби и частичные-к- целые отношения ( только завершающие десятичные дроби) Преобразование дробных соотношений в дроби, десятичные дроби и проценты ( только завершает десятичные дроби) Преобразование отношения части к целому в дроби, десятичные дроби и проценты ( только завершает десятичные дроби) Преобразование различных дробей, десятичных знаков, процентов и дробных чисел в Части соотношений (, завершающее десятичных знаков) Преобразование различных дробей, десятичных знаков, процентов и частей в целых соотношений (, завершающее десятичных знаков) Преобразование дробей в десятичные дроби, проценты и дробные части Часть соотношений Преобразование дробей в десятичные, проценты и частичные целые отношения Преобразование десятичных дробей в дроби, проценты и частичные к Части отношения Преобразование десятичных дробей в дроби, проценты и дробные части Целые отношения Преобразование процентов в дроби, десятичные дроби и части Часть отношений Преобразование процентов в дроби, десятичные дроби и дроби в целые отношения Преобразование частичных соотношений в дроби, десятичные дроби и проценты Преобразование целого числа в дроби, десятичные дроби и проценты Преобразование различных дробей, десятичных знаков, процентов и дробей в Части соотношений Преобразование различных дробей, десятичных знаков, процентов и дробей в целых соотношений Преобразование различных дробей, десятичных знаков, процентов и частей в Части отношений с 7-ми и 11-ми Преобразование различных дробей, десятичных знаков, процентов и частей в целых соотношений с 7 и 11 (СТАРЫЙ) Преобразование дробей, десятичных знаков, процентов и соотношений

Рабочие листы операций с дробями

Умножение дробей

Умножение дробей обычно менее запутанно с операционной точки зрения, чем любая другая операция, и может быть менее запутанным в концептуальном плане при правильном подходе. Алгоритм умножения — это просто умножение числителей, а затем знаменателей. Волшебное слово в понимании умножения дробей — «из». Например, что составляет две трети ОТ шести? Что такое треть от половины? Когда вы используете слово «из», становится намного легче визуализировать умножение дробей. Пример: разрезать буханку хлеба пополам, затем половину разрезать на три части. Одна треть полбуханки хлеба такая же, как 1/3 x 1/2, и вкусная с маслом.

На дроби

По идее, деление на дроби, вероятно, самая сложная из всех операций, но мы собираемся помочь вам.Алгоритм деления дробей аналогичен умножению дробей, но вы находите обратное значение второй дроби или производите перекрестное умножение. Это даст вам правильный ответ, что чрезвычайно важно, особенно если вы строите мост. Мы рассказали вам, как концептуализировать умножение дробей, но как оно работает с делением? Легкий! Вам просто нужно выучить волшебную фразу: «Сколько ____ в ______? Например, в вопросе 6 & div; 1/2 вы спросите:« Сколько половинок в 6? »Становится немного больше.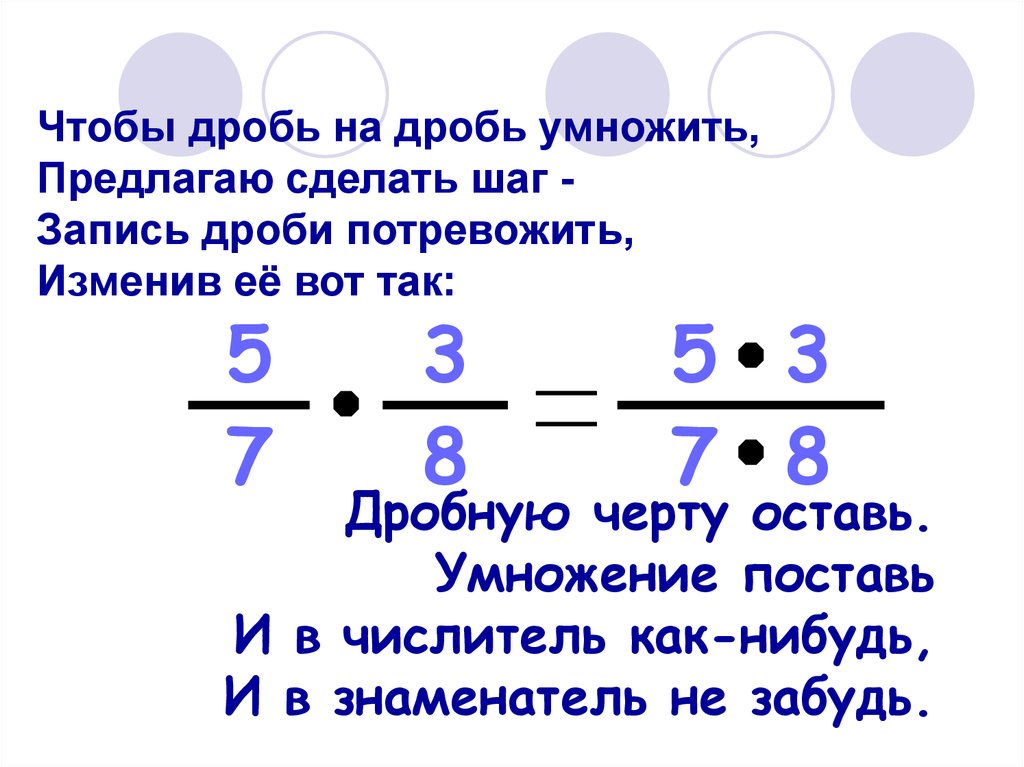 трудно, когда оба числа являются дробными, но это не гигантский скачок, чтобы понять это.1/2 & div; 1/4 — довольно простой пример, особенно если вы думаете о монетах США или Канады. Сколько четвертей в полдолларе?

Сложение дробей

Для сложения дробей нужен надоедливый общий знаменатель. Упростите жизнь своих учеников, сначала обучив их понятиям эквивалентных дробей и наименьших общих кратных. Как только учащиеся знакомы с этими двумя концепциями, идея поиска дробей с общими знаменателями для сложения становится намного проще.Время, потраченное на моделирование дробей, также поможет учащимся понять сложение дробей. Связь дробей с знакомыми примерами, безусловно, поможет. Например, если вы добавите 1/2 банана и 1/2 банана, вы получите целый банан. Что произойдет, если вы добавите 1/2 банана и 3/4 другого банана?

Добавление смешанных фракций Рабочие листы

Обычная стратегия, которую используют при добавлении смешанных фракций, состоит в том, чтобы преобразовать смешанные фракции в неправильные фракции, завершить сложение, а затем переключиться обратно. Другая стратегия, требующая немного меньших умственных способностей, — рассматривать целые числа и дроби по отдельности. Сначала сложите целые числа. Добавьте доли секунды. Если полученная дробь неправильная, ее нужно преобразовать в смешанное число. Часть целого числа может быть добавлена к исходной части целого числа.

Вычитание Дробей

Нет большой разницы между сложением и вычитанием дробей.Оба требуют общего знаменателя, что требует некоторых предварительных знаний. Единственная разница в том, что второй и последующие числители вычитаются из первого. Существует опасность того, что вы можете получить отрицательное число при вычитании дробей, поэтому учащимся, возможно, потребуется узнать, что это означает в этом случае. Когда дело доходит до любого понятия в дробях, всегда полезно связать его с знакомой или простой для понимания ситуацией. Например, 7/8 — 3/4 = 1/8 может иметь значение в контексте гонки.Первый бегун шел на 7/8 по трассе, а второй бегун на 3/4 по трассе.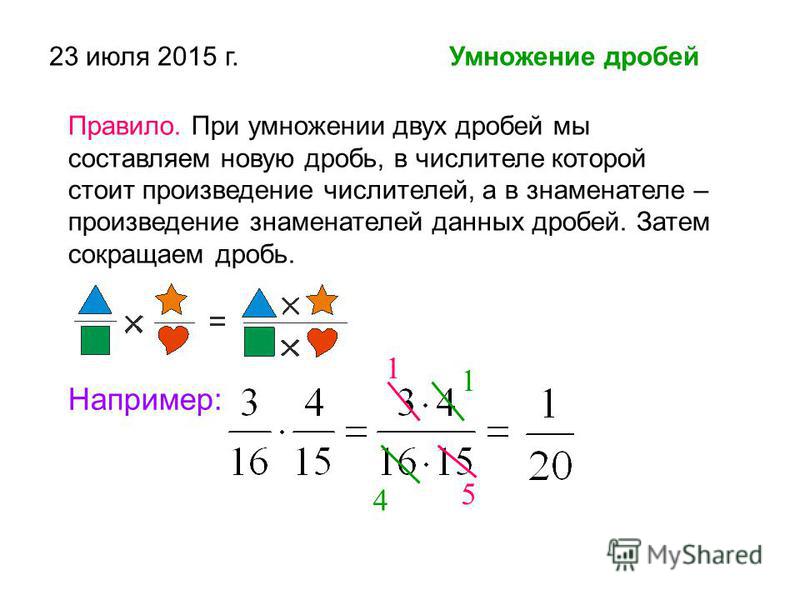 Как далеко впереди был первый бегун? (1/8 трека).

Вычитание смешанных дробей Рабочие листы

Рабочие листы с дробями различных операций

Смешивание знаков операций с рабочими листами с дробями заставляет учащихся уделять больше внимания тому, что они делают, и позволяет хорошо проверить свои навыки в более чем одной операции.

Сложение и вычитание дробей

Умножение и деление дробей

Смешанные операции с дробями

Операции с

Отрицательными дробями

Хотя некоторые из этих листов представляют собой отдельные операции, было бы полезно иметь все они в одном месте.При выполнении операций с отрицательными дробями следует учитывать некоторые особенности. Обычно очень полезно перед тем, как продолжить, заменить любые смешанные числа на неправильную дробь. Важно обращать внимание на знаки и знать правила умножения положительных и отрицательных (++ = +, + — = -, — + = — и — = +).

Порядок операций с дробями Рабочие листы

Порядок операций с листами дробей с опциями как положительных, так и отрицательных дробей различной сложности.

Порядок операций с

дробями

Как и другие рабочие листы с порядком операций, рабочие листы с порядком дроби операций требуют некоторых предварительных знаний. Если ваши ученики борются с этими вопросами, вероятно, это больше связано с их способностью работать с дробями, чем с самими вопросами. Внимательно наблюдайте и постарайтесь точно указать, каких необходимых знаний не хватает, а затем потратьте некоторое время на изучение этих концепций / навыков, прежде чем продолжить.В противном случае приведенные ниже рабочие листы должны содержать довольно простые ответы и не должны приводить к чрезмерному выпадению волос.

Порядок операций с

десятичными и смешанными дробями .

Умножение дробей с разными знаками. Умножение и деление отрицательных чисел

В данном уроке рассматривается умножение и деление рациональных чисел.

Содержание урока

Умножение рациональных чисел

Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь

Также, необходимо знать основные законы умножения, такие как: переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и умножение на ноль.

Пример 1. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.

Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками

Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.

Короткое решение выглядит следующим образом:

Пример 2. Найти значение выражения

Пример 3. Найти значение выражения

Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

Решение для данного примера можно записать покороче:

Пример 4. Найти значение выражения

Решение для данного примера можно записать покороче:

Пример 5. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус

Короткое решение будет выглядеть значительно проще:

Пример 6. Найти значение выражения

Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть

Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение

Решение для данного примера можно записать покороче

Пример 7. Найти значение выражения

Сначала в ответе получилась неправильная дробь , но мы выделили в ней целую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.

Решение для данного примера можно записать покороче:

Пример 8. Найти значение выражения

Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.

Ответ: значение выражения равно −2.

Пример 9. Найти значение выражения:

Переведём смешанные числа в неправильные дроби:

Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение

Пример 10. Найти значение выражения

Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.

Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение

Третье действие:

Четвёртое действие:

Ответ: значение выражения равно

Пример 11. Найти значение выражения

Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.

В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:

Пример 12. Найти значение выражения

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Пример 13. Найти значение выражения

Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .

Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.

Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те параметры, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:

Третье действие:

Ответ: значение выражения равно

Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:

Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.

Пример 14. Найти значение выражения −4,2 × 3,2

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось .

Пример 15. Найти значение выражения −0,15 × 4

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь .

Пример 16. Найти значение выражения −4,2 × (−7,5)

Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс

Деление рациональных чисел

Правила деления целых чисел справедливы и для рациональных чисел. Иными словами, чтобы уметь делить рациональные числа, нужно уметь

В остальном же применяются те же методы деления обыкновенных и десятичных дробей. Чтобы разделить обыкновенную дробь на другую дробь, нужно первую дробь умножить на дробь, обратную второй.

А чтобы разделить десятичную дробь на другую десятичную дробь, нужно в делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, затем выполнить деление, как на обычное число.

Пример 1. Найти значение выражения:

Это деление рациональных чисел с разными знаками. Чтобы вычислить такое выражение, нужно первую дробь умножить на дробь, обратную второй.

Итак, умножим первую дробь на дробь обратную второй.

Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули этих рациональных чисел и перед полученным ответом поставить минус.

Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение

Таким образом, значение выражения равно

Подробное решение выглядит следующим образом:

Короткое решение будет выглядеть так:

Пример 2. Найти значение выражения

Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно первую дробь умножить на дробь, обратную второй.

Обратная для второй дроби это дробь . На неё и умножим первую дробь:

Короткое решение будет выглядеть следующим образом:

Пример 3. Найти значение выражения

Это деление отрицательных рациональных чисел. Чтобы вычислить данное выражение, опять же нужно первую дробь умножить на дробь обратную второй.

Обратная для второй дроби это дробь . На неё и умножим первую дробь:

Получили умножение отрицательных рациональных чисел. Как вычисляется подобное выражение мы уже знаем. Нужно перемножить модули рациональных чисел и перед полученным ответом поставить плюс.

Дорешаем этот пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение:

Пример 4. Найти значение выражения

Чтобы вычислить данное выражение, нужно первое число −3 умножить на дробь, обратную дроби .

Обратная для дроби это дробь . На неё и умножим первое число −3

Пример 6. Найти значение выражения

Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу 4.

Обратное для числа 4 это дробь . На неё и умножим первую дробь

Пример 5. Найти значение выражения

Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу −3

Обратное для числа −3 это дробь . На неё и умножим первую дробь:

Пример 6. Найти значение выражение −14,4: 1,8

Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус

Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае, чтобы сделать это правильно, потребовалось суметь .

Если нет желания возиться с десятичными дробями (а это бывает часто), то эти , затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.

Вычислим предыдущее выражение −14,4: 1,8 этим способом. Переведём десятичные дроби в смешанные числа:

Теперь переведём полученные смешанные числа в неправильные дроби:

Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:

Пример 7. Найти значение выражения

Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:

Многоэтажные дроби

Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:

В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:

В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной .

При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.

Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.

Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.

После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:

Пример 2.

Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь

А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .

Пример 3. Запишем в понятном виде многоэтажную дробь

Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2

А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.

Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.

Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.

Реализуется этот метод следующим образом:

Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения (×)

В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!

Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:

С первого на четвёртый. Со второго на третий.

В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.

Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.

Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж

В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:

Попробуем вычислить многоэтажную дробь пользуясь новой схемой.

Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть

В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:

Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.

Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:

В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:

Использование переменных

Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.

Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.

Использование переменных оправдано, при работе с многоэтажными дробями. Например:

Найти значение выражения

Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.

Выражение, находящееся в числителе можно занести в переменную с любым названием, например:

Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A

А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B

Теперь наше изначальное выражение принимает вид . То есть, мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.

Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .

Найдём значение переменной A

Найдём значение переменной B

Теперь подставим в главное выражения вместо переменных A и B их значения:

Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:

Таким образом, значение выражения равно −1.

Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.

Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как

Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

В этой статье мы разберемся с умножением чисел с разными знаками . Здесь мы сначала сформулируем правило умножения положительного и отрицательного числа, обоснуем его, а после этого рассмотрим применение данного правила при решении примеров.

Навигация по странице.

Правило умножения чисел с разными знаками

Умножение положительного числа на отрицательное, а также отрицательного на положительное, проводится по следующему правилу умножения чисел с разными знаками : чтобы умножить числа с разными знаками, надо умножить , и перед полученным произведением поставить знак минус.

Запишем данное правило в буквенном виде. Для любого положительного действительного числа a и действительного отрицательного числа −b справедливо равенство a·(−b)=−(|a|·|b|) , а также для отрицательного числа −a и положительного числа b справедливо равенство (−a)·b=−(|a|·|b|) .

Правило умножения чисел с разными знаками полностью согласуется со свойствами действий с действительными числами . Действительно, на их основе несложно показать, что для действительных и положительных чисел a и b справедлива цепочка равенств вида a·(−b)+a·b=a·((−b)+b)=a·0=0 , которая доказывает, что a·(−b) и a·b – противоположные числа, откуда следует равенство a·(−b)=−(a·b) . А из него следует справедливость рассматриваемого правила умножения.

Следует отметить, что озвученное правило умножения чисел с разными знаками справедливо как для действительных чисел, так и для рациональных чисел и для целых чисел . Это следует из того, что действия с рациональными и целыми числами обладают теми же свойствами, которые использовались при доказательстве выше.

Понятно, что умножение чисел с разными знаками по полученному правилу сводится к умножению положительных чисел.

Осталось лишь рассмотреть примеры применения разобранного правила умножения при умножении чисел с разными знаками.

Примеры умножения чисел с разными знаками

Разберем решения нескольких примеров умножения чисел с разными знаками . Начнем с простого случая, чтобы сосредоточиться на шагах правила, а не на вычислительных сложностях.

Пример.

Выполните умножение отрицательного числа −4 на положительное число 5 .

Решение.

По правилу умножения чисел с разными знаками нам сначала нужно перемножить модули исходных множителей. Модуль −4 равен 4 , а модуль 5 равен 5 , а умножение натуральных чисел 4 и 5 дает 20 . Наконец, осталось поставить знак минус перед полученным числом, имеем −20 . На этом умножение завершено.

Кратко решение можно записать так: (−4)·5=−(4·5)=−20 .

Ответ:

(−4)·5=−20 .

При умножении дробных чисел с разными знаками нужно уметь выполнять умножение обыкновенных дробей , умножение десятичных дробей и их комбинаций с натуральными и смешанными числами.

Пример.

Проведите умножение чисел с разными знаками 0,(2) и .

Решение.

Выполнив перевод периодической десятичной дроби в обыкновенную дробь , а также выполнив переход от смешанного числа к неправильной дроби , от исходного произведения мы придем к произведению обыкновенных дробей с разными знаками вида . Это произведение по правилу умножения чисел с разными знаками равно . Осталось лишь перемножить обыкновенные дроби в скобках, имеем .

Сложение и вычитание отрицательных дробей.

Альфашкола
Статьи
Сложение и вычитание отрицательных дробей

Отрицательные дроби складываются и вычитаются также как и отрицательные числа, только по правилам сложения дробей. Мы можете добавлять только половинки к половинкам, четверти к четвертям или десятые к десятым и так далее. Вычитание отрицательных дробей следует тем же правилам. Для того чтобы сложить или вычесть две дроби нам нужно привести их к общему знаменателю. Если дробь отрицательная мы можем знак минус поставить в числитель и наоборот. Ниже расписано сложение $-\frac{7}{6}+\frac{5}{7}$:

При сложении двух отрицательных дробей результат будет отрицательным. Когда мы вычитаем две отрицательные дроби, то мы к первой отрицательной дроби прибавляем положительную вторую, так как минус на минус дает плюс.

Рассмотрим сложение и вычитание следующих отрицательных дробей.

Задача 1. Вычислите $\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2}).$.

Решение. Приводим к наименьшему общему знаменателю:

$\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2})=\frac{5-3*2+10}{20}=\frac{9}{20}$

Ответ: $\frac{9}{20}$.

Задача 2. Вычислите $\frac{1}{7}-(-\frac{5}{6})-(-\frac{1}{3})$.

Решение. Приводим к наименьшему общему знаменателю:

$\frac{6-35+14}{42}=-\frac{15}{42}=-\frac{5}{14}$

Ответ: $-\frac{5}{14}$.

Задача 3. Вычислите $\frac{1}{4}+\frac{5}{3}-(-\frac{1}{12})$.

Решение. Приводим к наименьшему общему знаменателю:

$\frac{3+20+1}{12}=\frac{24}{12}=2.$

Ответ: $2.$.

Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Анна Александровна Ваструхина

Репетитор по математике

Стаж (лет)

Образование:

Краснодарский государственный университет культуры и искусств

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Веду занятия по обществознанию с учениками 6-11 классов, готовлю к успешной сдаче ВПР/ОГЭ/ЕГЭ. В работе используются одобренные ФГОС материалы: как учебники, так и интернет ресурсы.

Виктория Александровна Симаго

Репетитор по математике

Стаж (лет)

Образование:

Гродненский государственный университет им. Янки Купалы

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор 1-6 классов. В математике есть не только истина, но и наивысшая красота! Помогу Вам познать эту красоту и простоту. Понять математику не сложно, эта наука — фактов. И как ни странно это звучит, легче понимают этот язык фактов именно дети. И чем раньше мы начинаем уделять этому время, тем больших высот мы достигаем! Мы будем развивать мозг, он также как мускулы, развивается, когда его тренируешь! В процессе учебы будет развиваться воображение и логическое мышление и самое главное — уверенность в себе. Ты точно сможешь овладеть математическими знаниями, умениями и навыками так необходимыми в жизни. Доверьтесь мне и моему опыту и все получится!

Елизавета Бимбетовна Тулемисова

Репетитор по математике

Стаж (лет)

Образование:

Астраханский государственный педагогический институт

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Сердечно всех приветствую! Меня зовут Елизавета Бимбетовна, учитель высшей категории, Почетный работник воспитания и образования РФ, 2020 г. . Имею большой опыт обучения иностранным языкам (немецкий и английский), последние 18 лет работала учителем в лингвистической гимназии. Есть богатый опыт работы с учебными пособиями иностранных издательств Hueber, Oxford, Cambridge, подготовки учеников к международным экзаменам. Владею коммуникативной методикой обучения и ориентируюсь на личность ученика, его пожелания, цели, уровень владения иностранным языком. Готовлю к ЕГЭ, ОГЭ, ВПР, результаты от 65 до 100 баллов. Выпускники успешно обучаются в ведущих вузах страны, а также за рубежом. Буду рада сотрудничеству! До встречи!

Умножение отрицательных чисел кратко Арифметика

Привет, мой друг, тебе интересно узнать все про умножение отрицательных чисел, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое умножение отрицательных чисел , настоятельно рекомендую прочитать все из категории Арифметика.

Используя понятие модуля числа, сформулируем правила умножения положительных и отрицательных чисел.

Умножение чисел с одинаковыми знаками

Первый случай, который может вам встретиться — это умножение чисел с одинаковыми знаками.

Чтобы умножить два числа с одинаковыми знаками надо:

перемножить модули чисел;
перед полученным произведением поставить знак «+» (при записи ответа знак «плюс» перед первым числом слева можно опускать).

Примеры умножения отрицательных и положительных чисел.

(- 3) • (- 6) = + 18 = 18
2 • 3 = 6

Умножение чисел с разными знаками

Второй возможный случай — это умножение чисел с разными знаками.

Чтобы умножить два числа с разными знаками, надо:

перемножить модули чисел;
перед полученным произведением поставить знак «-».

Примеры умножения отрицательных и положительных чисел.

(- 0,3) • 0,5 = — 1,5
1,2 • (- 7) = — 8,4

Правила знаков для умножения

Запомнить правило знаков для умножения очень просто . Об этом говорит сайт https://intellect.icu . Данное правило совпадает с правилом раскрытия скобок.

Минус на минус дает плюс,

Плюс на минус дает минус.

+ • (+) = +	+ • (-) = —
— • (-) = +	— • (+) = —

В «длинных» примерах, в которых есть только действие умножение, знак произведения можно определять по количеству отрицательных множителей.

При четном числе отрицательных множителей результат будет положительным, а при нечетном количестве — отрицательным.

Пример.

(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) =

В примере пять отрицательных множителей. Значит, знак результата будет «минус».

Теперь вычислим произведение модулей, не обращая внимание на знаки.

6 • 3 • 4 • 2 • 12 • 1 = 1728

Конечный результат умножения исходных чисел будет:

(- 6) • (- 3) • (- 4) • (- 2) • 12 • (- 1) = — 1728

Умножение на ноль и единицу

Если среди множителей есть число ноль или положительная единица, то умножение выполняется по известным правилам.

0 • a = 0
a • 0 = 0
a • 1 = a

Примеры:

0 • (- 3) = 0
0,4 • 1 = 0,4

Особую роль при умножении рациональных чисел играет отрицательная единица (- 1).

При умножении на (- 1) число меняется на противоположное.

В буквенном выражении это свойство можно записать:

a • (- 1) = (- 1) • a = — a

При совместном выполнении сложения, вычитания и умножения рациональных чисел сохраняется порядок действий, установленный для положительных чисел и нуля.

Пример умножения отрицательных и положительных чисел.

См. также

сложение отрицательных чисел ,
деление отрицательных чисел ,
методы декомпозиции ячеек ,
десятичные дроби ,
умножение в столбик ,
как читать десятичные дроби ,
перевод обыкновенной дроби в десятичную ,
нахождение обыкновенной дроби от числа ,
деление обыкновенных дробей ,
умножение обыкновенных дробей ,
вычитание обыкновенных дробей ,
взаимно обратные числа , взаимно обратные дроби ,
сравнение обыкновенных дробей ,
периодическая дробь ,
сложение обыкновенных дробей , общий знаменатель ,
сокращение обыкновенных дробей ,
смешанные числа , выделение целой части обыкновенной дроби ,
свойства умножения , свойства деления ,

Как ты считаеешь, будет ли теория про умножение отрицательных чисел улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое умножение отрицательных чисел и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика

Из статьи мы узнали кратко, но емко про умножение отрицательных чисел

Что будет, если дробь умножить на минус 1? – Обзоры Вики

Если обе дроби имеют одинаковые знаки, либо обе положительные, либо обе отрицательные, ответ будет положительным. Тис обе дроби имеют разные знаки, один положительный и один отрицательный, ответ будет отрицательным.

Дополнительно Что происходит, когда вы умножаете отрицательное значение на отрицательное? Ответ: Когда вы умножаете отрицательное значение на отрицательное, вы получить положительный результат, потому что два отрицательных знака сокращаются. Таким образом, минус, умноженный на минус, всегда будет плюсом.

Как умножить отрицательную дробь на смешанное число?

Как делить на отрицательное число? При делении двух отрицательных чисел ответ будет всегда положительное число. Например, -4, разделенное на -2, равно 2. Когда оба числа отрицательны, отрицательные значения компенсируются, в результате чего ответ всегда будет положительным числом.

Можно ли делить на отрицательное число? Умножение и деление с отрицательными числами практически так же, как и с положительными числами. … Вопрос только в том, положительный это знак или отрицательный. Просто помните, что когда вы умножаете или делите два числа, если числа имеют одинаковый знак, результат всегда положительный.

Что такое отрицательное 1 в виде дроби?

Также Что происходит, когда вы умножаете отрицательное на положительное? Когда вы умножаете отрицательное число на положительное число, то продукт всегда отрицательный. Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда положительно. … Теперь у нас есть два отрицательных числа, поэтому результат положительный.

Почему 2 минуса дают плюс?

С каждым числом связано «аддитивное обратное» (своего рода «противоположное» число), которое при добавлении к исходному числу дает ноль. … Тот факт, что произведение двух негативов является положительным, Следовательно, это связано с тем, что обратное к положительному числу является обратным положительным числом..

Как узнать, когда нужно сложить, вычесть, умножить или разделить?

Со временем математики пришли к соглашению о наборе правил, называемых порядок операций чтобы определить, какую операцию выполнить в первую очередь. Когда выражение включает только четыре основных операции, вот правила: Умножение и деление слева направо. Сложите и вычтите слева направо.

Как к смешанному числу добавить отрицательную дробь?

Как умножать дроби? Первый шаг при умножении дробей умножить два числителя. Второй шаг — умножить два знаменателя. Наконец, упростите новые дроби. Перед умножением дроби также можно упростить, вычленив общие множители в числителе и знаменателе.

Почему положительное делится на отрицательное отрицательное? Потому что позитив представляет только количество раз, которое делитель вписывается в разделенное. По той же причине, что отрицательное, умноженное на отрицательное, является положительным. Обратите внимание, что мультипликативная инверсия -1 равна -1.

Что такое половина отрицательного числа?

Половина отрицательного числа равна то же, что деление положительного числа пополам. Вы можете смотреть на это как на абсолютное значение. Скажем, у нас есть положительное число х, х это х от нуля. Половина этого расстояния равна половине х или х/2.

Какое число делится на минус 1?

Все целые числа делятся на -1. Когда вы делите на минус 1, вы меняете число с положительного на отрицательный или отрицательное на положительное. 50 ÷ -1 = -50. -2 ÷ -1 = 2.

Почему отрицательное, деленное на отрицательное, равно положительному? Первоначальный ответ: Почему деление отрицательного на отрицательное равно положительному? Поскольку умножение отрицательного на отрицательное дает положительное значение, он сохраняет состоящую математику.

Являются ли отрицательные дроби правильными дробями?

A отрицательная правильная дробь будет иметь отрицательный знак либо в числителе, либо в знаменателе. Положительная правильная дробь: положительная правильная дробь будет иметь положительный знак как в числителе, так и в знаменателе. … Дроби, у которых числитель (верхнее число) больше или равен знаменателю (нижнему числу).

Может ли быть отрицательный числитель? Обычно перед дробью ставится знак «минус», но иногда встречаются дроби с отрицательным числителем или знаменателем. … Если и числитель, и знаменатель отрицательны, то сама дробь положительна, потому что мы делим отрицательное на отрицательное.

Является ли отрицательная дробь действительным числом?

Действительные числа включают в себя положительные и отрицательные целые числа и дроби (или рациональные числа), а также иррациональный номера.

Как найти обратную дробь

Как найти обратную дробь — SAT Math

—>

Войти
Биографии репетитора
Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
Репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- обзоров и отзывов
- Освещение в СМИ
- О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

SAT Math Help » Арифметика » Фракции » Взаимные платежи » Как найти обратную дробь

Что является взаимным из следующей фракции: 18/27

Возможные ответы:

-18/27

27/18

9/27

Правильный ответ:

27 27 27 27 27 27 27 27 27 27 27 27 27 27 27 27 27 27 27 27

. /18
Пояснение:
Дробь, умноженная на обратную, будет равна 1. Чтобы найти обратную дробь, поменяйте местами знаменатель и числитель. Обратное число 18/27 равно 27/18.
Сообщить об ошибке
Чему равна дробь, обратная приведенной ниже?
Возможные ответы:
Правильный ответ:
Пояснение:
Обратная дробь может быть получена путем замены числителя и знаменателя.

Числитель в данном случае таков, что он станет знаменателем.
Знаменатель в этом случае равен , поэтому он станет числителем.
Следовательно, обратное значение равно .
Сообщить об ошибке
Что является обратным значением ?
Возможные ответы:
Правильный ответ:
Объяснение:
Обратная величина может быть определена путем деления всего количества на единицу.
Это просто перестановка числителя и знаменателя.
Ответ .
Сообщить об ошибке
Что является обратным значением ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти обратную, нужно взять 1 и разделить на все количество дроби. Обратное просто меняет местами числитель и знаменатель.
Сообщить об ошибке
Чему равно отрицательное обратное значение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Отрицательная обратная величина числа состоит в том, чтобы взять отрицательную единицу и разделить на значение. Просто поменяйте местами числитель и знаменатель и добавьте знак минус.
Напомним, что деление на дробь равносильно умножению на обратное.
Правильный ответ:
Сообщить об ошибке0192
Объяснение:
Обратная часть дроби на единицу больше количества дроби.
Просто поменяйте местами члены числителя и знаменателя.
Ответ .
Сообщить об ошибке
Обратная величина равна .
Что является обратным значением ?
Возможные ответы:
Правильный ответ:
Объяснение:
Обратная величина равна , поэтому – величина, обратная величине , является обратной величиной . , так является обратным этому, или .
Так как ,
Обратная величина равна .
Сообщить об ошибке.
Уведомление об авторских правах.
Посмотреть Репетиторы по математике SAT
Эрик
Сертифицированный преподаватель
Университет Иллинойса в Урбана-Шампейн, бакалавр наук, физика. Калифорнийский университет в Сан-Диего, магистр наук…
View SAT Репетиторы по математике
Райан
Сертифицированный репетитор
Университет Миссури-Колумбия, бакалавр наук, образование. Вашингтонский университет в Сент-Луисе, доктор юридических наук, юридический…
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Учитесь по концепции
Калькулятор дробей

Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражения с дробями:
Дроби — используйте косую черту для деления числителя на знаменатель, т. е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Math Symbols

Symbol Symbol name Symbol Meaning Example
+ plus sign addition 1/2 + 1/3
— знак минус вычитание 1 1/2 — 2/3
* asterisk multiplication 2/3 * 3/4 
× times sign multiplication 2 /3 × 5/6
: division sign division 1/2 : 3
/ division slash division 1/3 / 5
/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3
Калькулятор следует известным правилам для порядка операций . Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
В столовой
В классной комнате Джейкоба 18 учеников. Шесть учеников приносят обед в школу. Остальные обедают в столовой. Проще говоря, какая часть студентов обедает в столовой?
У Макса 2
У Макса 13 пар носков. Отсюда шесть пар синих, три пары коричневых, две черных и две белых. Какая часть носков Макса коричневого или черного цвета?
Значение Z
При x = -9, каково значение Z, где Z равно числителю дроби x минус 17 в знаменателе 6,5 конец дроби Дайте ответ с точностью до 2 знаков после запятой.
Корзина с фруктами
Если в корзине 7 яблок и 5 апельсинов, то какая доля апельсинов в корзине с фруктами?
Дробь и десятичная дробь
Пишите в виде дроби и десятичной дроби. Один и два плюс три и пять сотых
Дробь до десятичной
Запишите дробь 3/22 в виде десятичной дроби.
Компания
Компания имеет 860 сотрудников, из которых 500 женщин. Напишите дробь, обозначающую сотрудниц компании.
Кто-то
Кто-то съел 1/10 торта, осталось только 9/10. Если вы съедите 2/3 оставшегося торта, сколько всего торта вы съедите?
Дробями
Муравей поднимается на 2/5 шеста за первый час и на 1/4 шеста за следующий час. Какую часть шеста преодолевает муравей за два часа?
Мэтью
У Мэтью восемь карандашей. У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?
a Quarter
a Quarter от числа 72 IS:
Подробнее задачи по математике »
Десятиц
Фракции
Треугольные
НОД
ЖКИ
Комбинаторика
уравнения
статистика
… все математические калькуляторы
Умножение и деление отрицательных чисел
ВведениеСложение и вычитаниеЭкспоненты
Purplemath На самом деле, мы уже рассмотрели сложную часть: вы уже знаете правила «знака»:
плюс умножить на плюс это плюс
(добавление большого количества горячих кубиков повышает температуру)
минус умножить плюс минус
(удаление большого количества горячих кубиков снижает температуру)
плюс раз минус минус
(добавление большого количества холодных кубиков снижает температуру)
минус раз минус плюс
(удаление большого количества кубиков холода повышает температуру)
Содержание продолжается ниже
MathHelp.
com
Умножение и деление целых чисел
Правила знаков работают так же для деления; просто замените «раз» на «делится на». Вот пример правил в дивизионе:
(Помните, что дроби — это еще одна форма деления! «Дроби — это деление»!)
Некоторым людям нравится думать об отрицательных числах в терминах долгов. Так, например, если вы должны 10 долларов шести людям, ваш общий долг будет 6 × 10 долларов = 60 долларов. В этом контексте получение отрицательного ответа имеет смысл. Но в каком контексте может иметь смысл деление отрицательного на отрицательное (и получение положительного)?
Подумайте о перекусе в кафе. Когда вы идете платить, у ребенка возникают проблемы с вашей дебетовой картой. Он проводит ею шесть раз, прежде чем, наконец, вернуть карту вам. Вернувшись домой, вы проверяете свой банковский счет онлайн. Вы можете сказать по сумме, что да, он действительно взял с вас путь более одного раза. Некоторая часть этого общего дебета (отрицательная сумма на вашем счету) неверна.
Прежде чем звонить в свой банк, чтобы исправить ситуацию, вы хотите подтвердить количество перерасходов. Как вы можете понять это? Вы можете разделить всю сумму (скажем, 76,02 доллара США) на сумму, указанную в квитанции (например, 12,67 доллара США), которая является суммой одного платежа. Каждое списание — это минус на вашем счете, поэтому математика такова:
(- 76,02 доллара США) ÷ (- 12,67 доллара США) = 6
Таким образом, всего было действительно шесть списаний. Количество зарядов, 6, по подсчету количества событий, должно быть положительным . В этом реальном контексте деление минуса на минус и получение плюса имеет смысл. И теперь вы знаете, что поручить службе поддержки отменить ровно пять платежей.
Вы можете заметить, что люди «отменяют» знаки минус. Они пользуются тем фактом, что «минус умножить на минус — это плюс». Например, предположим, что у вас есть (−2)(−3)(−4). Любые два отрицательных числа, перемноженные вместе, становятся одним положительным. Итак, выберите любые два умноженных (или разделенных) отрицания и «отмените» их знаки:
Я начну с того, что уберу одну пару знаков «минус». Потом умножу как обычно.
(-2)(-3)(-4)
= (-2)(-3) (-4)
= (+6) (-4)
= -24
Если вам дано длинное умножение с отрицательными числами, просто сократите знаки «минус» попарно:
Первое, что я сделаю, это посчитаю знаки «минус». Один два три четыре пять шесть семь. Итак, есть три пары, которые я могу отменить, и одна останется. В результате мой окончательный ответ должен быть отрицательным. Если я получу положительный результат, я буду знать, что сделал что-то не так.
(-1)(-2)(-1)(-3)(-4)(-2)(-1)
= (-1)(-2) (-1)(-3 )(−4)(−2)(−1)
= (+1)(+2) (−1)(−3)(−4)(−2)(−1)
= ( 1)(2) (-1)(-3) (-4)(-2)(-1)
= (1)(2) (+1)(+3) (-4) (−2)(−1)
= (1)(2)(1)(3) (−4)(−2) (−1)
= (1)(2)(1)( 3) (+4)(+2) (-1)
= (1)(2)(1)(3)(4)(2)(-1)
= (2)(3) (4)(2)(-1)
= 48(-1)
= -48
Я получил отрицательный ответ, поэтому я знаю, что мой знак правильный.
Вот еще один пример, показывающий тот же процесс отмены в контексте деления:
Отрицательные числа через круглые скобки
Основная трудность, с которой люди сталкиваются с отрицаниями, заключается в работе со скобками; особенно при взятии отрицания через круглые скобки. Обычная ситуация примерно такая:
−3( x + 4)
Если бы у вас было «3 ( x + 4)», вы бы знали, что нужно «распределить» 3 «по» скобкам:
3( x + 4) = 3( x ) + 3(4) = 3 x + 12
Те же правила применяются при работе с отрицаниями. Если у вас возникли проблемы с отслеживанием, используйте маленькие стрелки:
← пролистните , чтобы просмотреть полное изображение →
Упростить 3 (
x − 5).
Мне нужно взять 3 через круглые скобки:
3( х — 5) = 3( х ) + 3(-5) = 3 х — 15
Упростить −2 (
x − 3).
Здесь я возьму «минус» через круглые скобки; Я буду распределять -2 на x и минус 3.
-2( х — 3) = -2( х ) — 2(-3) = -2 х + 2(+3) = -2 х + 6
Обратите внимание, как я тщательно следил за знаками в скобках. «Минус» был сохранен с 3 за счет использования другого набора скобок. Не стесняйтесь использовать группирующие символы, чтобы сделать ваше предполагаемое значение ясным как для оценщика, так и для вас самих.
Другая проблема, связанная с предыдущей, связана с вычитанием скобок. Вы можете отслеживать знак вычитания, преобразуя вычитание в умножение на минус:
Я начну с того, что напишу маленькую «1» перед скобками. Затем я нарисую стрелки от этой 1 к терминам в скобках, чтобы напомнить себе, что мне нужно сделать.
← пролистните для просмотра полного изображения →
Не бойтесь писать в этой маленькой «1» и рисовать эти маленькие стрелки. Вы должны делать все, что вам нужно, чтобы ваша работа была правильной, и вы постоянно получали правильный ответ.
Я буду работать изнутри, упрощая сначала внутри внутренние символы группировки, в соответствии с Порядком операций. Итак, первое, что я сделаю, это пронесу −4 сквозь скобки. Тогда я упрощу; Я продолжу, поставив 1 перед круглыми скобками, и, чтобы помочь мне отслеживать это -1, которое я буду распределять, я нарисую свои маленькие стрелки.
← пролистните для просмотра полного изображения →
Это сложно. Они заставляют меня вычесть дробь. Мне нужно сложить дроби, а значит сложить числители. Чтобы убедиться, что я не упустил из виду, что именно означает этот «минус» (а именно, что я минусую весь числитель второй дроби, а не только x ), я преобразую минус плюс -1:
← пролистните , чтобы просмотреть полное изображение →
Обратите внимание, что я перешел от вычитания дроби к добавлению отрицательной единицы, умноженной на дробь. Очень легко «потерять» минус, когда вы складываете такие беспорядочные полиномиальные дроби. Самая распространенная ошибка — поставить минус на x и забыть довести до −2. Будьте особенно осторожны с дробями!
Для дополнительной практики со скобками попробуйте здесь.
URL: https://www.purplemath.com/modules/negative3.htm
Страница 1Страница 2Страница 4
Перекрестное умножение дробей (видео и практические вопросы)
TranscriptFAQsTractice Привет, ребята! Добро пожаловать в это видео о том, как скрестить дроби . При умножении дробей название намекает на то, как это делается на самом деле. Вы буквально умножаете на . Допустим, у вас есть две дроби, которые равны друг другу.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Допустим, $\frac{a}{b}=\frac{c}{d}$. Чтобы их умножить, нужно умножить числитель первой дроби на знаменатель второй дроби, а затем записать это число. Затем вы умножаете числитель второй дроби на число в знаменателе первой дроби и записываете это число. Причина, по которой мы скрещиваем умножение дробей, состоит в том, чтобы сравнивать их. Перекрестное умножение дробей говорит нам, равны ли две дроби или какая из них больше. Это особенно полезно, когда вы работаете с более крупными дробями, которые вы не знаете, как уменьшить.<h3> Как скрестить-умножить </h3><h4><span class="ez-toc-section" id="%D0%A1%D0%BA%D1%80%D0%B5%D1%81%D1%82%D0%B8%D1%82%D1%8C%D1%83%D0%BC%D0%BD%D0%BE%D0%B6%D0%B8%D1%82%D1%8C_%D0%B4%D1%80%D0%BE%D0%B1%D0%B8_%E2%80%93_%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D1%80_1"> Скрестить-умножить дроби – Пример 1 </h4> Найдите, какая из двух дробей наибольшая.<blockquote> $\frac{4}{26}=\frac{7}{32}$</blockquote> Итак, когда мы умножаем это, когда мы приравниваем его, а затем перемножаем эти две дроби вместе, мы получаем 128. Итак, $4\times 32=128$. И когда мы перемножим эти два числа, мы получим $7\times 26=182$. Итак, мы знаем, что $\frac{7}{32}$ больше, чем $\frac{4}{26}$, потому что 182 больше, чем 128.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Мы всегда должны помнить, что число, которое мы умноженная на наш числитель, представляет соответствующую дробь. Таким образом, это число (128) представляет эту дробь $(\frac{4}{26})$, а это число (182) представляет эту дробь $(\frac{7}{32})$. Я упоминаю об этом, потому что может быть немного запутанно видеть, как числа, взятые из двух разных дробей, умножаются вместе, но произведение представляет только одну из дробей, а не другую. 128 идет слева, чтобы представить $\frac{4}{26}$, а $7\times 26=182$ идет справа, чтобы представить эту дробь вот здесь $(\frac{7} {32})$. Перемножение дробей помогает нам узнать, равны ли числа, а если нет, то какое из них больше, а какое меньше. Но это не единственное его использование. Перемножение дробей может помочь нам найти неизвестные переменные в дробях.<h4><span class="ez-toc-section" id="%D0%9F%D0%B5%D1%80%D0%B5%D0%BA%D1%80%D0%B5%D1%81%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B4%D1%80%D0%BE%D0%B1%D0%B5%D0%B9_%E2%80%94_%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D1%80_2"> Перекрестное умножение дробей — Пример 2 </h4> Допустим, у нас есть две дроби $\frac{9}{16}=\frac{x}{27}$. Мы можем перекрестно умножить в любое время, когда у нас есть дробь, которая установлена равной другой дроби.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Теперь, чтобы скрестить умножение, мы делаем то же самое, что и в нашем последнем примере. Мы берем числитель одной стороны и умножаем его на знаменатель другой стороны, и делаем то же самое с числителем другой стороны. В этом случае мы умножаем $9\умножить на 27$ и $16\умножить на х$. Это даст нам $243=16x$. Теперь все, что нам нужно сделать, чтобы получить x сам по себе, это разделить обе части на 16. Это сокращается, и мы получаем $x=\frac{243}{16}$, и вы можете упростить это еще больше. Теперь мы сделали бы то же самое, даже если $x$ стоит в нашем знаменателе, это не имеет значения. Я надеюсь, что это видео о перекрестном умножении дробей было полезным для вас. Увидимся в следующий раз! Сложение и вычитание дробей | Умножение и деление дробей <h3> Часто задаваемые вопросы </h3><h5> Q </h5><h4> Как скрестить дроби? </h4><h5> A </h5> Перекрестное умножение дробей путем умножения знаменателя одной дроби на числитель другой дроби и последующего сравнения двух значений.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Дробь с большим значением является большей дробью. *Примечание: Будьте осторожны, всегда переходите от знаменателя к числителю! Если привести числитель к знаменателю, получится не та дробь, как та, что больше. Пример. Какая дробь больше: $\frac{4}{5}$ или $\frac{3}{8}$? $\frac{4}{5}$ больше, чем $\frac{3}{8}$.<h5> Q </h5><h4> Когда вы скрещиваете дроби? </h4><h5> A </h5> Перемножить дроби, если вы хотите определить, больше ли одна дробь другой, или если вы ищете недостающий числитель или знаменатель в эквивалентных дробях.<h5> Q </h5><h4><span class="ez-toc-section" id="%D0%9A%D0%B0%D0%BA_%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%82%D0%B8%D1%82%D1%8C_%D0%B4%D1%80%D0%BE%D0%B1%D0%B8_%D1%81_%D1%80%D0%B0%D0%B7%D0%BD%D1%8B%D0%BC%D0%B8_%D0%B7%D0%BD%D0%B0%D0%BC%D0%B5%D0%BD%D0%B0%D1%82%D0%B5%D0%BB%D1%8F%D0%BC%D0%B8"> Как скрестить дроби с разными знаменателями? </h4><h5> A </h5> Почти все перемножаемые дроби будут иметь разные знаменатели. Это никак не влияет на процесс. Перекрестное умножение как обычно.<h5> Q </h5><h4><span class="ez-toc-section" id="%D0%9F%D0%BE%D1%87%D0%B5%D0%BC%D1%83_%D1%80%D0%B0%D0%B1%D0%BE%D1%82%D0%B0%D0%B5%D1%82_%D0%BF%D0%B5%D1%80%D0%B5%D0%BA%D1%80%D0%B5%D1%81%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B4%D1%80%D0%BE%D0%B1%D0%B5%D0%B9"> Почему работает перекрестное умножение дробей? </h4><h5> A </h5> Перемножение дробей, чтобы определить, больше ли одна, работает, потому что это быстрый способ приведения дробей к общему знаменателю и сравнения дробей.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> пр. Что больше: $\frac{7}{9}$ или $\frac{8}{12}$? Перекрестное умножение: 84>72, поэтому $\frac{7}{9}$>$\frac{8}{12}$ Преобразовать и сравнить: $\frac{7}{9 }×\frac{12}{12}=\frac{84}{108}$ $\frac{8}{12}×\frac{9}{9}=\frac{72}{108} $ 84>72, поэтому $\frac{7}{9}>\frac{8}{12}$ Перемножение дробей для нахождения отсутствующего числителя или знаменателя для эквивалентных дробей работает, потому что это сокращение для перестановка, чтобы изолировать переменную. пр. Найдите x: $\frac{3}{7}=\frac{2}{x}$ Крест-умножение: $\frac{3}{7}=\frac{2}{x}$ 3x=14 $x=\frac{14}{3}$ Перестановка: \ (\frac{3}{7}=\frac{2}{x}\) $\frac{3}{7}$ x=2 $x=2×\frac{7}{3) }$ $x=\frac{14}{3}$<h5> Q </h5><h4><span class="ez-toc-section" id="%D0%9C%D0%BE%D0%B6%D0%B5%D1%82%D0%B5_%D0%BB%D0%B8_%D0%B2%D1%8B_%D0%BF%D0%B5%D1%80%D0%B5%D0%BA%D1%80%D0%B5%D1%81%D1%82%D0%B8%D1%82%D1%8C_%D1%83%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%BF%D1%80%D0%B8_%D1%81%D0%BB%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B8_%D0%B4%D1%80%D0%BE%D0%B1%D0%B5%D0%B9"> Можете ли вы перекрестить умножение при сложении дробей? </h4><h5> A </h5> Нет, при сложении дробей нельзя умножать. Перекрестное умножение только тогда, когда вам нужно определить, больше ли одна дробь другой, или если вы пытаетесь найти недостающий числитель или знаменатель в эквивалентных дробях.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript><h5> Q </h5><h4><span class="ez-toc-section" id="%D0%9A%D0%B0%D0%BA_%D1%81%D0%BA%D1%80%D0%B5%D1%81%D1%82%D0%B8%D1%82%D1%8C_%D0%B4%D1%80%D0%BE%D0%B1%D0%B8_%D1%81_%D0%BF%D0%B5%D1%80%D0%B5%D0%BC%D0%B5%D0%BD%D0%BD%D1%8B%D0%BC%D0%B8"> Как скрестить дроби с переменными? </h4><h5> A </h5> Перемножить дроби с переменными, умножая противоположные числители и знаменатели эквивалентных дробей, устанавливая значения равными друг другу и находя переменную. пр. $\frac{4}{5}=\frac{x}{20}$ 4×20=5x 80=5x 16=x<h3> Практические вопросы </h3> Вопрос №1: Какая дробь больше: $\frac{17}{29{30}}{17}\rightarrow\frac{3}{5}>\frac{6}{17}\text{, потому что }51$>$30$ Следовательно, $\frac{3 }{8}$ Скрыть ответ Вопрос № 3: Найдите отсутствующую переменную. $\frac{18}{21}=\frac{x}{63}$ $x=6$ $x=27$ $x=54$ $x=85$ Показать ответ Ответ: Правильный ответ: $x=54$.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Чтобы решить эту проблему, начните с перекрестного умножения. $18\times63=21x$ $1,134=21x$ Затем разделите на 21 с обеих сторон. $54=x$ Скрыть ответ Вопрос №4: Найдите отсутствующую переменную. $\frac{7}{y}=\frac{42}{72}$ $y=9$ $y=12$ $y=229$ $y=432$ Показать ответ Ответ: Правильный ответ: $y=12$. Чтобы решить эту проблему, начните с перекрестного умножения. $7\times72=42y$ $504=42y$ Затем разделите на 42 с обеих сторон. $12=y$ Скрыть ответ Вопрос № 5: У человека есть сад шириной 6 футов и длиной 9 футов. Он планирует увеличить ширину до 9 футов.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Если он хочет пропорционально увеличить длину, какой будет новая длина? 6 футов 13,5 футов 18 футов 81,5 футов Показать ответ Ответ: Чтобы решить эту проблему, сначала настройте пропорциональные дроби. $\frac{\text{длина}}{\text{ширина}}=\frac{6}{9}=\frac{9}{l}$ Затем умножьте крест-накрест, чтобы найти l . $9\times9=6l$ $81=6l$ $13,5=l$ Новый сад будет 13,5 футов в длину. Скрыть ответ Вернуться к видео по основам арифметики 893904<h2> Дроби: умножение и деление дробей </h2> Умножение дробей.0069 /ru/фракции/сложение и вычитание дробей/содержание/<h4> Умножение дробей </h4> Дробь — это часть целого . На прошлом уроке вы научились складывать и вычитать дроби.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Но это не единственный вид математики, который вы можете делать с дробями. Бывают случаи, когда полезно будет умножать и дроби. Щелкните слайд-шоу, чтобы узнать, как написать задачу на умножение с дробями.<ul><li> Приведем пример умножения дробей. Предположим, вы выпиваете 2/4 чашки кофе каждое утро.</li><li> Но ваш врач только что сказал вам, что вам нужно сократить потребление кофе на вдвое .</li><li> Теперь вам нужно выяснить, сколько стоит 1/2 от 2/4 кофейника.</li><li> Это может не выглядеть как задача на умножение. Но когда вы видите слово из с дробями, значит нужно умножать.</li><li> Чтобы настроить пример, мы просто заменим слово из знаком умножения.</li><li> Теперь наш пример готов к решению.</li><li> В отличие от обычного умножения, которое дает большее число…</li><li> В отличие от обычного умножения, которое дает большее число.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> .. умножение дробей обычно дает меньшее число.</li><li> Итак, когда мы умножаем 1/2 на 2/4…</li><li> Итак, когда мы умножаем 1/2 на 2/4… наш ответ будет меньше, чем 2/4.</li><li> Вот еще один пример. Допустим, у вас есть 3/5 чашки шоколадной начинки.</li><li> Вы хотите положить одинаковое количество начинки в каждый из этих 4 кексов.</li><li> Можно сказать, что вы хотите положить 1/4 от 3/5 стакана начинки в каждый кекс.</li><li> Как и раньше, мы изменим слово из на знак умножения.</li><li> Теперь наши дроби готовы к умножению.</li><li></li></ul><h5> Попробуйте! </h5> Попробуйте решить приведенную ниже задачу на умножение. Пока не беспокойтесь о ее решении! Рецепт требует 2/3 стакана молока. Вы хотите сократить рецепт вдвое. Примечание : Хотя в нашем примере правильный ответ 2/3 x 1/2, помните, что порядок умножения не имеет значения.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> 1/2 х 2/3 тоже будет правильно.<h4><span class="ez-toc-section" id="%D0%A0%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87_%D0%BD%D0%B0_%D1%83%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81_%D0%B4%D1%80%D0%BE%D0%B1%D1%8F%D0%BC%D0%B8"> Решение задач на умножение с дробями </h4> Теперь, когда мы знаем, как решать задачи на умножение с дробями, давайте попрактикуемся в решении некоторых из них. Если вам удобно умножать целые числа, вы готовы к умножению дробей. Щелкните слайд-шоу, чтобы научиться умножать две дроби.<ul><li> Давайте умножим, чтобы найти 1/2 от 7/10.</li><li> Как и раньше, мы заменим слово из знаком умножения. Теперь мы готовы к умножению.</li><li> Сначала мы умножим числители: 1 и 7.</li><li> 1 умножить на 7 равно 7, поэтому мы напишем 7 справа от числителей.</li><li> Когда мы добавили дроби, знаменатели остались прежними. Но когда мы умножаем, знаменатели тоже умножаются.</li><li> 2 умножить на 10 равно 20, поэтому мы напишем 20 справа от знаменателя.</li><li> Теперь мы знаем, что 1/2 умножить на 7/10 равно 7/20.</li><li> Можно также сказать, что 1/2 от 7/10 равно 7/20.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript></li><li> Попробуем другой пример: 3/5 умножить на 2/3.</li><li> Сначала умножим наши числители. 3 умножить на 2 равно 6.</li><li> Далее мы умножим наши знаменатели. 5 умножить на 3 равно 15.</li><li> Итак, 3/5 умножить на 2/3 равно 6/15.</li><li></li></ul><h5> Попробуйте! </h5> Попробуйте решить приведенные ниже задачи на умножение. <h5> Умножение дроби на целое число </h5> Умножение дроби на целое число аналогично умножению двух дробей. Есть только один дополнительный шаг: прежде чем вы сможете умножать, вам нужно превратить целое число в дробь. Это слайд-шоу покажет вам, как это сделать. Щелкните слайд-шоу, чтобы узнать, как умножать дробь и целое число.<ul><li> Умножим 2 раза на 1/3. Помните, это всего лишь еще один способ спросить: «Сколько будет 1/3 от 2?»</li><li> Прежде чем мы начнем, нам нужно убедиться, что эти числа готовы к умножению.</li><li> Мы не можем умножить целое число на дробь, поэтому нам придется записать 2 в виде дроби.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript></li><li> Как вы узнали из раздела «Введение в дроби», мы также можем записать 2 как 2/1. Это потому, что 2 можно дважды разделить на 1.</li><li> Теперь мы готовы к умножению!</li><li> Сначала мы умножим числители : 2 и 1.</li><li> 2 умножить на 1 равно 2. Выровняем 2 с числителями.</li><li> Далее мы умножим знаменатели: 1 и 3.</li><li> 1 умножить на 3 равно 3. Мы выстроим 3 в ряд со знаменателями.</li><li> Итак, 2/1 умножить на 1/3 равно 2/3. Мы могли бы также сказать, что 1/3 от 2 равно 2/3.</li><li> Попробуем другой пример: 4 раза по 1/5.</li><li> Прежде чем мы начнем, нам придется записать 4 в виде дроби.</li><li> Мы перепишем 4 как 4/1. Теперь мы готовы к умножению.</li><li> Сначала умножим числители: 4 и 1.</li><li> 4 умножить на 1 равно 4, поэтому числитель нашего ответа равен 4.</li><li> Далее умножим знаменатели: 1 и 5.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript></li><li> 1 умножить на 5 равно 5, поэтому 5 — знаменатель нашего ответа.</li><li> Итак, 4/1 умножить на 1/5 равно 4/5.</li><li></li></ul><h5> Попробуйте! </h5> Попробуйте решить приведенные ниже задачи на умножение. <h4> Деление дробей </h4> За последние несколько страниц вы узнали, как умножать дроби. Вы, наверное, уже догадались, что 90 191 можно разделить и на 90 192 дроби. Вы делите дроби, чтобы увидеть, сколько частей чего-то содержится в чем-то еще. Например, если вы хотите узнать, сколько четвертей дюйма составляет четыре дюйма, вы можете разделить 4 на 1/4. Попробуем другой пример. Представьте, что рецепт требует 3 стакана муки, но ваш мерный стакан вмещает только 1/3, или 90 191 одну треть 90 192 , стакана. Сколько третей чашки нужно добавить? Нам нужно выяснить, сколько третей чашки содержится в трех чашках. Другими словами, нам нужно разделить три на одну треть.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Мы запишем задачу так: 3 ÷ 1/3<h5> Попробуйте! </h5> Попробуйте решить эти задачи на деление дробями. Не беспокойтесь об их решении! Рецепт требует 3/4 стакана воды. У вас есть только мерный стакан 1/8.<h4><span class="ez-toc-section" id="%D0%A0%D0%B5%D1%88%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87_%D0%BD%D0%B0_%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81_%D0%B4%D1%80%D0%BE%D0%B1%D1%8F%D0%BC%D0%B8"> Решение задач на деление с дробями </h4> Теперь, когда мы знаем, как писать задачи на деление, давайте потренируемся, решив несколько задач. Деление дробей очень похоже на умножение. Просто требуется один дополнительный шаг. Если вы можете умножать дроби, вы можете их и делить! Просмотрите слайд-шоу, чтобы узнать, как разделить целое число на дробь.<ul><li> Разделим 3 на 1/3. Помните, это всего лишь еще один способ спросить: «Сколько трети составляют 3?»</li><li> В нашем уроке по делению вы научились писать знак деления следующим образом (/).</li><li> При делении дробей полезно использовать другой знак деления (÷) чтобы не ошибиться с дробью</li><li> Так же, как и с умножением, мы начнем с поиска любых целых чисел в нашей задаче.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> то же самое, что и 3/1.</li><li> Прежде чем мы сможем разделить, нам нужно сделать еще одно изменение.</li><li> Мы поменяем местами числитель и знаменатель дроби, на которую мы делим: 1/3 в этом примере.</li><li> Итак, 1/3 становится 3/1.</li><li> Это называется нахождением обратной или мультипликативной обратной , дроби.</li><li> Поскольку мы меняем исходную дробь, мы также меняем знак деления (÷) на умножение на знак (х).</li><li> Это потому, что умножение является обратным делению.</li><li> Теперь мы можем рассматривать это как обычную задачу на умножение.</li><li> Сначала мы умножим числители: 3 и 3.</li><li> 3 умножить на 3 равно 9, поэтому мы напишем это рядом с числителями.</li><li> Далее перемножим знаменатели: 1 и 1.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript></li><li> 1 умножить на 1 равно 1, поэтому мы напишем 1 рядом со знаменателем. </li><li> Как видите, 3/1 х 1/3 = 9/1.</li><li> Помните, что любая дробь больше 1 также может быть выражена как целое число . Итак, 9/1 = 9.</li><li> 3 ÷ 1/3 = 9. Другими словами, в 3 содержится 9 третей .</li><li> Давайте попробуем другой пример: 5 разделить на 4/7.</li><li> Как обычно, мы перепишем любые целые числа, чтобы 5 стало 5/1.</li><li> Далее мы найдем обратное числа 4/7. Это дробь, на которую мы делим.</li><li> Для этого мы поменяем местами числитель и знаменатель, так что 4/7 станет 7/4.</li><li> Затем мы изменим знак деления (÷) на знак умножения (x).</li><li> Теперь мы можем умножать, как обычно. Сначала умножим числители: 5 и 7.</li><li> 5 умножить на 7 равно 35, поэтому мы напишем это рядом с числителями.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript></li><li> Далее мы умножим знаменатели: 1 и 4.</li><li> 1 умножить на 4 равно 4, поэтому мы напишем это рядом со знаменателями. </li><li> Итак, 5/1 х 4/7 = 35/4. </li><li> Как вы узнали ранее, мы можем преобразовать нашу неправильную дробь в смешанное число , чтобы наш ответ было легче читать.</li><li> 35/4 = 8 3/4. Итак, 5 ÷ 4/7 = 8 3/4. </li><li></li></ul><h5> Попробуйте! </h5> Попробуйте решить эти задачи на деление. Пока не беспокойтесь о сокращении ответа.<h5> Деление двух дробей </h5> Мы только что научились делить целое число на дробь . Вы можете использовать тот же метод, чтобы разделить на две дроби . Щелкните слайд-шоу, чтобы узнать, как делить на две дроби.<ul><li> Давайте попробуем решить задачу с двумя дробями: 2/3 ÷ 3/4. Здесь мы хотим знать, сколько 3/4 в 2/3.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> </li><li> Сначала мы найдем обратное число дроби, на которую мы делим: 3/4.</li><li> Для этого мы поменяем местами числитель и знаменатель. Таким образом, 3/4 становится 4/3.</li><li> Далее мы изменим знак деления (÷) на знак умножения (x).</li><li> Теперь умножим числители. 2 x 4 = 8, поэтому мы напишем 8 рядом с верхними числами.</li><li> Далее мы умножим знаменатели. 3 x 3 = 9, поэтому мы напишем 9 рядом с нижними числами. </li><li> Итак, 2/3 х 4/3 = 8/9. </li><li> Мы могли бы также записать это как 2/3 ÷ 3/4 = 8/9. </li><li> Попробуем другой пример: 4/7 разделить на 2/9.</li><li> Целых чисел нет, поэтому найдем обратное дроби, на которую мы делим. Это 2/9.</li><li> Для этого мы поменяем местами числитель и знаменатель. Таким образом, 2/9 становится 9/2.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript></li><li> Теперь мы изменим знак деления (÷) на знак умножения (x) и умножим как обычно.</li><li> Сначала умножим числители. 4 x 9 = 36.</li><li> Далее мы умножим знаменатели. 7 х 2 = 14,</li><li> Итак, 4/7 х 9/2 = 36/14. Как и раньше, вы можете преобразовать эту неправильную дробь в смешанное число.</li><li> Итак, 4/7 ÷ 2/9 = 2 8/14.</li><li></li></ul><h5> Попробуйте! </h5> Попробуйте решить эти задачи на деление. Пока не беспокойтесь о сокращении ответа.<h5><span class="ez-toc-section" id="%D0%A3%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5_%D0%B8_%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%B8%D0%B5_%D1%81%D0%BC%D0%B5%D1%88%D0%B0%D0%BD%D0%BD%D1%8B%D1%85_%D1%87%D0%B8%D1%81%D0%B5%D0%BB"> Умножение и деление смешанных чисел </h5> Как бы вы решили подобную задачу? Как вы узнали из предыдущего урока, всякий раз, когда вы решаете задачу с помощью смешанный число вам нужно сначала преобразовать его в неправильную дробь . Затем вы можете умножать или делить, как обычно.<h4><span class="ez-toc-section" id="%D0%98%D1%81%D0%BF%D0%BE%D0%BB%D1%8C%D0%B7%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5_%D1%81%D0%BE%D0%BA%D1%80%D0%B0%D1%89%D0%B5%D0%BD%D0%B8%D1%8F_%D0%B4%D0%BB%D1%8F_%D1%83%D0%BF%D1%80%D0%BE%D1%89%D0%B5%D0%BD%D0%B8%D1%8F_%D0%B7%D0%B0%D0%B4%D0%B0%D1%87"> Использование сокращения для упрощения задач </h4> Иногда вам может понадобиться решить такие задачи: Обе эти дроби включают большие числа .<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Вы можете умножать эти дроби так же, как и любые другие дроби. Однако такие большие числа трудно понять. Можете ли вы представить 21/50 или двадцать одна пятидесятая , в голове? 21/50 x 25/14 = 525/700 Даже ответ кажется сложным. Это 525/700, или пятьсот двадцать пять семисотых . Какой глоток! Если вам не нравится работать с большими числами, вы можете упростить подобную задачу, используя метод, называемый отменой . Когда вы отменяете дроби в задаче, вы уменьшаете их обе одновременно. Сначала отмена может показаться сложной, но мы покажем вам, как это сделать шаг за шагом. Давайте еще раз взглянем на пример, который мы только что видели.<h5> Шаг 1 </h5> Во-первых, посмотрите на числитель первой дроби и знаменатель второй. Мы хотим посмотреть, можно ли разделить на на одно и то же число.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> В нашем примере похоже, что и 21, и 14 можно разделить на 7.<h5> Шаг 2 </h5> Далее мы разделим 21 и 14 на 7. Сначала мы разделим наше верхнее число слева: 21. 21 ÷ 7 = 3 Затем разделим нижнее число справа: 14. 14 ÷ 7 = 2 Ответы на каждую задачу запишем рядом с числами, которые мы разделили. Поскольку 21 ÷ 7 равно 3, мы напишем 3 там, где было 21. 14 ÷ 7 равно 2, поэтому мы напишем 2 там, где было 14. Мы можем вычеркнуть или отменить , числа, с которых мы начали. Теперь наша задача выглядит намного проще, не так ли?<h5> Шаг 3 </h5> Давайте посмотрим на другие числа дроби. На этот раз мы рассмотрим знаменатель первой дроби и числитель второй. Можно ли разделить на одно и то же число? Обратите внимание, что их можно разделить на 25! Вы могли также заметить, что они оба могут делиться на 5. Мы могли бы также использовать 5 , но обычно, когда вы отменяете, вы хотите найти наибольшее число , на которое можно разделить оба числа.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Таким образом, вам не придется снова сокращать дробь в конце.<h5> Шаг 4 </h5> Затем мы отменим так же, как мы делали это в шаге 2. Мы разделим наше нижнее число слева: 50. 50 ÷ 25 = 2 Затем мы разделим верхнее число на справа: 25. 25 ÷ 25 = 1 Ответы на каждую задачу запишем рядом с числами, которые мы разделили.<h5> Шаг 5 </h5> Теперь, когда мы отменили исходные дроби, мы можем умножить наши новые дроби, как обычно. Как всегда, сначала умножьте числители: 3 x 1 = 3 Затем умножьте знаменатели: 2 x 2 = 4 Итак, 3/2 x 1/2 = 3/4, или три четверти .<h5> Шаг 6 </h5> Наконец, давайте еще раз проверим нашу работу. 525/700 был бы нашим ответом, если бы мы решили проблему без отмены. Если мы разделим и 525, и 700 на 175, то увидим, что 525/700 равно 3/4. Можно также сказать, что мы уменьшаем 525/700 до 3/4.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Помните, отмена — это еще один способ сократить дроби перед решением задачи. Вы получите один и тот же ответ, независимо от того, когда вы их уменьшите. Продолжать Предыдущий: Сложение и вычитание дробей Next:Преобразование процентов, десятичных дробей и дробей /en/fractions/converting-percentages-decimals-and-fractions/content/<h2><span class="ez-toc-section" id="%D0%9E%D1%82%D1%80%D0%B8%D1%86%D0%B0%D1%82%D0%B5%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BF%D0%BE%D0%BA%D0%B0%D0%B7%D0%B0%D1%82%D0%B5%D0%BB%D0%B8_%D1%81%D1%82%D0%B5%D0%BF%D0%B5%D0%BD%D0%B8_%D0%BA%D0%B0%D0%BA_%D0%BD%D0%B0%D1%83%D1%87%D0%B8%D1%82%D1%8C_%D1%83%D1%87%D0%B0%D1%89%D0%B8%D1%85%D1%81%D1%8F_%D1%80%D0%B5%D1%88%D0%B0%D1%82%D1%8C_%D0%B8%D1%85_%D0%B1%D1%8B%D1%81%D1%82%D1%80%D0%BE_%D0%B8_%D0%BB%D0%B5%D0%B3%D0%BA%D0%BE"> Отрицательные показатели степени: как научить учащихся решать их быстро и легко </h2> Многие ученики уже с трудом понимают отрицательные числа, правила возведения в степень и дроби. Итак, что происходит, когда вы добавляете отрицательных показателей в уравнении? Полный хаос. Ну, не совсем так. Но понимание отрицательных показателей — это , важный строительный блок для курсов математики на уровне средней школы, и это также концепция, которую многие ученики считают сложной.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Когда вы постепенно наращиваете знания своих учеников, вы гарантируете, что они готовы решать сложные задачи в классе и вне его. Если вы не знаете, с чего начать, эта запись в блоге поможет вам превратить ваш модуль по отрицательным показателям в положительный опыт для вас и ваших учеников!<h3></h3> Правила для отрицательных показателей </h3> Как и все остальное на уроках математики, отрицательные показатели должны подчиняться правилам. Если вам нужно напоминание, вот краткий обзор семи правил возведения в степень:<ol><li> Произведение степеней : Сложение степеней при умножении одинаковых оснований</li><li> Правило отношения степеней : Вычитание степеней при делении одинаковых оснований</li><li> Сила степеней правило : Умножайте степени вместе при возведении степени в другую степень</li><li> Степень правила произведения : Распределить мощность по каждому основанию при возведении нескольких переменных в степень</li><li> Степень правила частного : Распределить мощность по каждому основанию при возведении нескольких переменных в степень</li><li> Правило нулевой мощности : Любое основание, возведенное в нулевую степень, становится единицей.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript></li><li> Правило отрицательного показателя степени : Чтобы изменить отрицательный показатель степени на положительный, превратите его в обратный.</li></ol> Напомните учащимся, что правила остаются теми же с отрицательными показателями — просто может потребоваться выполнить несколько дополнительных шагов.<h3></h3> Краткий обзор отрицательных чисел </h3> Отрицательные числа требуют определенного абстрактного мышления, которое не всегда приходит естественным образом. Но без четкого понимания отрицательных чисел учащиеся не будут готовы решать отрицательные показатели. Вот краткий обзор: Отрицательное число — это любое число меньше нуля. Отрицательные числа выражаются знаком минус. Например, -4 на четыре меньше нуля. Полезно думать, что отрицательные числа существуют на числовой прямой: Когда вы складываете и вычитаете отрицательные числа, вы перемещаетесь либо вправо, либо влево от числовой строки.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Когда вы вычитаете отрицательное число, вы перемещаетесь влево от числовой строки, потому что это то же самое, что складывать положительное число. Если вы добавляете отрицательное число, вы перемещаетесь вправо, потому что это то же самое, что вычитание положительного числа. При умножении отрицательного числа на положительное (или наоборот) произведение будет отрицательным. Если вы умножите два отрицательных числа или два положительных числа, результат будет положительным. Умножение разных знаков всегда дает отрицательное произведение, а умножение одинаковых знаков дает положительное произведение. Всегда предполагайте, что число положительное, если перед ним нет знака.<h3></h3> Что означают отрицательные показатели? </h3> Мы уже знаем, что положительные показатели степени — это способ выражения многократного умножения. Например: Есть несколько разных способов думать об отрицательных показателях, но в целом отрицательные показатели противоположны положительным.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Все отрицательные показатели могут быть выражены как их положительные обратные . Обратная дробь — это дробь, в которой числитель и знаменатель меняются местами. Как можно что-то превратить в обратное, если в начале не было дроби? Мы знаем, что числа могут быть выражены более чем одним способом. Например, восемь также можно записать как: Таким образом, отрицательные показатели степени можно выразить как положительную обратную величину основания, умноженного на себя x раз. Чем больше отрицательный показатель, тем меньше число, которое он представляет. В то время как положительные показатели степени указывают на повторяющееся умножение, отрицательные степени представляют повторяющееся деление. Вот почему 2-3 больше, чем 2-6.<h3></h3> Как решать отрицательные показатели </h3> В большинстве вопросов вам будет предложено решить отрицательные показатели, представив их в виде положительных уравнений .<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Вот как: Превратите основание и показатель степени в обратную величину, затем найдите знаменатель. Разделите числитель на знаменатель, чтобы найти последнее десятичное число.<h3></h3> Умножение и деление отрицательных степеней </h3> Мы уже рассмотрели умножение степеней, но вот краткий обзор того, как умножать и делить отрицательные степени.<h4></h4> Умножение отрицательных показателей </h4> Хорошие новости! Правила умножения показателей одинаковы, даже если показатель степени отрицательный. Если основания совпадают, добавьте показатели степени. Помните о правилах сложения и вычитания отрицательных чисел. Если основания разные, а степени одинаковые, умножьте основания и оставьте степени такими, какие они есть. Если ничего общего нет, сразу переходим к решению уравнения. Переверните показатели в их обратные числа, затем умножьте. Если вам нужно напоминание, прочтите нашу статью о том, как умножать дроби.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript><h4></h4> Деление отрицательных степеней </h4> Деление отрицательных степеней почти то же самое, что и их умножение, за исключением того, что вы делаете обратное: вычитаете там, где вы должны были бы сложить, и делите там, где вы должны были бы умножать. Если основания одинаковые, вычесть степени. Не забудьте перевернуть экспоненту и сделать ее положительной, если это необходимо. Если степени одинаковы, но основания разные, сначала разделите основания. Если ничего общего нет, сразу переходим к решению уравнения. Чтобы освежить в памяти информацию о делении дробей, ознакомьтесь с нашей записью в блоге «Как разделить дроби».<h3></h3> Отрицательные числа с показателями степени </h3> Что произойдет, если вместо показателей степени будет отрицательное основание? Если показатель степени положительный, работайте с ним так же, как и с обычным показателем степени, но помните о двух вещах:<ul><li> Если основание отрицательное, а показатель степени — четное число, конечным произведением всегда будет положительное число.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> </li><li> Если основание отрицательное, а показатель степени — нечетное число, конечным произведением всегда будет отрицательное число. </li></ul> Если отрицательное основание заключено в круглые скобки, степень применяется ко всему уравнению, включая отрицательный знак. Если скобок нет, степень относится только к основанию, а не к отрицательному знаку. Поскольку первый пример возводится в четную степень, два отрицательных знака сокращаются, и у вас остается положительное произведение. Если бы показатель степени был нечетной степенью, произведение было бы отрицательным, потому что было бы одно число, которое не могло бы сократиться. Во втором примере положительная степень относится только к четырем, а не к отрицательному знаку. В этом случае отрицательный знак говорит вам, что произведение будет отрицательным независимо от того, четная или нечетная степень.<h3></h3> Упрощение отрицательных показателей </h3> Умножение, деление и понимание отрицательных показателей — это первый шаг к упрощению выражений с отрицательными показателями.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Помните: все описанные выше шаги остаются в силе, независимо от сложности выражения. Начнем с умножения отрицательных показателей на переменные. В этом примере мощность применяется только к основанию x, а не к 4. Чтобы сделать это выражение положительным, переверните x на обратную величину и оставьте 4 сверху. Попробуем что-нибудь посложнее. Переменные здесь одинаковые, поэтому в соответствии с правилом первой степени мы можем умножать числа, сохраняя основание и складывая степени. Умножьте 6 и 4, чтобы получить произведение 24. Затем сложите показатели степени, чтобы умножить переменные x. Как насчет деления отрицательных показателей на переменные? Начнем с простого примера: Чтобы отрицательный показатель степени стал положительным, переместите ???? в начало уравнения и умножить. Вот пример отрицательного показателя степени с несколькими переменными: Поскольку отрицательный показатель степени применяется только к переменной, переместите 𝑥-4 в конец уравнения, чтобы сделать его положительным, и оставьте 6 на месте.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Вот и ваше упрощенное уравнение! Попробуем еще. Сначала перераспределите мощность внутри скобок, следуя правилу третьего порядка. Затем измените переменные 𝑥 с отрицательными показателями на их обратные значения. Наконец, умножьте переменные 𝑥, сложив степени вместе. Давайте еще раз. Для начала либо возведите уравнение в квадрат, либо сначала переместите скобки. Мы начнем с возведения верхней скобки в квадрат и перераспределения мощности. Затем переместите отрицательные показатели вниз или вверх, в зависимости от их положения. Отрицательная экспонента сверху может быть приведена к низу, так что это будет обратная величина, и наоборот. Закончите упрощением. Часто существует несколько способов упростить выражения с отрицательным показателем степени. Поскольку показатели степени представляют собой многократное умножение, и вы можете умножать числа в любом порядке, разные шаги могут привести к одному и тому же результату.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript><h3></h3> Дроби с отрицательными показателями </h3> Мы знаем, что делать с целыми числами с отрицательными показателями, но как насчет дробей с отрицательными показателями? Чтобы упростить дроби с отрицательными показателями, преобразуйте их в обратные, умножьте и уменьшите .<h3></h3> Как учить отрицательные степени с помощью Prodigy </h3> Учащимся понравится практиковаться в отрицательных показателях с Prodigy: бесплатной математической платформой, ориентированной на учебную программу, с экзотическими домашними животными, веселыми заданиями и образовательными приключениями. Отрицательные показатели являются важной концепцией, которую учащиеся должны усвоить перед поступлением в среднюю школу, но многие учащиеся испытывают трудности с ключевыми концепциями. Используя мощные инструменты отчетности на панели инструментов учителя , вы увидите, какие темы освоили ваши ученики и где им нужно больше практики.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript> Функции Prodigy Assignments, Plans и Test Prep позволяют назначать целевую математическую практику учащимся, которые борются с или превосходно. Вы будете получать данные в режиме реального времени, пока ученики играют, и сможете давать дифференцированные задания, соответствующие тому, что вы преподаете в классе. Вы можете использовать Prodigy, чтобы: <ul><li> проводить спиральные оценки</li><li> готовиться к стандартным тестам</li><li> усиливать уроки в классе (например, отрицательные показатели!)</li></ul> Лучший из всех? Эти инструменты совершенно бесплатны для преподавателей и студентов. Чтобы узнать больше о согласовании Prodigy с вашим классом, узнайте, как вы можете использовать индивидуальные планы для улучшения содержания вашего урока. Зарегистрируйтесь сейчас<h3></h3> Заключительные мысли об отрицательных показателях степени </h3> Если вы хотите больше попрактиковаться в показателях степени в целом, наш рабочий лист правил показателей степени дает учащимся возможность лучше ознакомиться с тем, как работают показатели степени.<img class="lazy lazy-hidden" loading='lazy' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='' /><noscript><img loading='lazy' src='' /></noscript></div><footer class="entry-footer"><div id="author_box" class="row no-gutters"><div class="author_avatar col-2"> <img alt='' src="//xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif" data-lazy-type="image" data-src='https://secure.gravatar.com/avatar/b142b184aa8663e4da31fb1a71be88cc?s=96&d=mm&r=g' srcset="" data-srcset='https://secure.gravatar.com/avatar/b142b184aa8663e4da31fb1a71be88cc?s=192&d=mm&r=g 2x' class='lazy lazy-hidden avatar avatar-96 photo' height='96' width='96' decoding='async'/><noscript><img alt='' src='https://secure.gravatar.com/avatar/b142b184aa8663e4da31fb1a71be88cc?s=96&d=mm&r=g' srcset='https://secure.gravatar.com/avatar/b142b184aa8663e4da31fb1a71be88cc?s=192&d=mm&r=g 2x' class='avatar avatar-96 photo' height='96' width='96' decoding='async'/></noscript></div><div class="author_info col-10"><h4 class="author_name title-font"> admin</h4><div class="author_bio"></div></div></div></footer></article><nav class="navigation post-navigation" aria-label="Записи"><h2 class="screen-reader-text">Навигация по записям</h2><div class="nav-links"><div class="nav-previous"><a href="https://xn--7-dtbea5camjj.xn--p1ai/raznoe/slovo-provoda-razobrat-po-sostavu-provod-koren-slova-i-razbor-po-sostavu.html" rel="prev">Слово провода разобрать по составу: «Провод» корень слова и разбор по составу</a></div><div class="nav-next"><a href="https://xn--7-dtbea5camjj.xn--p1ai/raznoe/golovolomki-svoimi-rukami-iz-bumagi-shemy-obemnye-golovolomki-iz-bumagi-kak-iz-bumagi-sdelat-golovolomku-podelki-svoimi-rukami.html" rel="next">Головоломки своими руками из бумаги схемы: Объемные головоломки из бумаги. Как из бумаги сделать головоломку? Поделки своими руками</a></div></div></nav><div id="comments" class="comments-area"><div id="respond" class="comment-respond"><h3 id="reply-title" class="comment-reply-title">Добавить комментарий <a rel="nofollow" id="cancel-comment-reply-link" href="/raznoe/kak-umnozhit-drob-na-otriczatelnuyu-drob-otriczatelnye-drobi-dejstviya-s-otriczatelnymi-drobyami.html#respond" style="display:none;">Отменить ответ</a></h3><form action="https://xn--7-dtbea5camjj.xn--p1ai/wp-comments-post.php" method="post" id="commentform" class="comment-form" novalidate>Ваш адрес email не будет опубликован. Обязательные поля помечены *<label for="comment">Комментарий *</label><textarea id="comment" name="comment" cols="45" rows="8" maxlength="65525" required></textarea><label for="author">Имя *</label> <input id="author" name="author" type="text" value="" size="30" maxlength="245" autocomplete="name" required /><label for="email">Email *</label> <input id="email" name="email" type="email" value="" size="30" maxlength="100" aria-describedby="email-notes" autocomplete="email" required /><label for="url">Сайт</label> <input id="url" name="url" type="url" value="" size="30" maxlength="200" autocomplete="url" /><input name="submit" type="submit" id="submit" class="submit" value="Отправить комментарий" /> <input type='hidden' name='comment_post_ID' value='30462' id='comment_post_ID' /> <input type='hidden' name='comment_parent' id='comment_parent' value='0' /></form></div></div></main><aside id="secondary" class="widget-area order-2"><section id="categories-47" class="widget widget_categories"><h3 class="widget-title title-font">Рубрики</h3><ul><li class="cat-item cat-item-10"><a href="https://xn--7-dtbea5camjj.xn--p1ai/category/vospityvat">Воспитывать</a></li><li class="cat-item cat-item-11"><a href="https://xn--7-dtbea5camjj.xn--p1ai/category/deti">Дети</a></li><li class="cat-item cat-item-13"><a href="https://xn--7-dtbea5camjj.xn--p1ai/category/podrostok">Подросток</a></li><li class="cat-item cat-item-9"><a href="https://xn--7-dtbea5camjj.xn--p1ai/category/pravilno">Правильно</a></li><li class="cat-item cat-item-8"><a href="https://xn--7-dtbea5camjj.xn--p1ai/category/raznoe">Разное</a></li><li class="cat-item cat-item-12"><a href="https://xn--7-dtbea5camjj.xn--p1ai/category/rekomendaczii">Рекомендации</a></li><li class="cat-item cat-item-1"><a href="https://xn--7-dtbea5camjj.xn--p1ai/category/sovety">Советы</a></li></ul></section></aside></div></div><div id="footer-sidebar" class="widget-area"><div class="container"><div class="row"></div></div></div><footer id="colophon" class="site-footer"><div class="site-info"> 2025 © Все права защищены.</div></footer></div><nav id="menu" class="panel" role="navigation"> <button class="go-to-bottom"></button> <button id="close-menu" class="menu-link"></button> <button class="go-to-top"></button></nav> <noscript><style>.lazyload{display:none}</style></noscript><script data-noptimize="1">window.lazySizesConfig=window.lazySizesConfig||{};window.lazySizesConfig.loadMode=1;</script><script async data-noptimize="1" src='https://xn--7-dtbea5camjj.xn--p1ai/wp-content/plugins/autoptimize/classes/external/js/lazysizes.min.js'></script>  <style>iframe,object{width:100%;height:480px}img{max-width:100%}</style><script>new Image().src="//counter.yadro.ru/hit?r"+escape(document.referrer)+((typeof(screen)=="undefined")?"":";s"+screen.width+"*"+screen.height+"*"+(screen.colorDepth?screen.colorDepth:screen.pixelDepth))+";u"+escape(document.URL)+";h"+escape(document.title.substring(0,150))+";"+Math.random();</script>  <script defer src="https://xn--7-dtbea5camjj.xn--p1ai/wp-content/cache/autoptimize/js/autoptimize_1ef490c9359ea65f37b76aed46105dbe.js"></script></body></html><script src="/cdn-cgi/scripts/7d0fa10a/cloudflare-static/rocket-loader.min.js" data-cf-settings="a7ae73eff440cea8957d76aa-|49" defer></script>