Смешанная дробь. Действия со смешанными дробями

Смешанной называют дробь, имеющую целую и дробную части.

Записываются они как \(a\)\(\frac{m}{n}\), где – \(a\) целое число,\(\frac{m}{n}\) — правильная дробь. 

Например:   \(2\)\(\frac{3}{5}\) здесь \(2\) – целая часть, \(\frac{3}{5}\) – дробная часть (правильная дробь).

                     \(17\)\(\frac{17}{18}\) здесь \(17\) – целая часть, \(\frac{17}{18}\) – дробная часть (правильная дробь).

Фактически такие дроби представляют собой сумму целого числа и дроби, то есть между целой и дробной частью стоит знак «плюс» (а не «умножить»).

Например:  \(2\frac{3}{5}=2+\frac{3}{5}\)

Это не нужно заучивать, просто поймите суть. Вдумайтесь, что на практике означает, например, запись: «на складе осталось \(2\)\(\frac{3}{5}\) мешка муки»? Что на складе лежит два полных мешка и еще один заполненный на \(\frac{3}{5}\). Где здесь место умножению? Очевидно ведь, что это два плюс еще \(\frac{3}{5}\) мешка муки! Понимать этот момент очень важно, потому что здесь допускается огромное количество ошибок при вычислениях со смешанными дробями (см. ниже).

Превращение смешанной дроби в неправильную

Чтобы преобразовать смешанную дробь в неправильную нужно целую часть умножить на знаменатель дробной и прибавить к результату числитель — получиться числитель неправильной дроби. Знаменатель при этом не меняется. То есть,

\(a\)\(\frac{m}{n}\)\(=\)\(\frac{a·n + m}{n}\).

Например, при преобразовании \(2\)\(\frac{3}{5}\) получим \(\frac{2·5 + 3}{5}=\frac{13}{5}\).

Почему вычисление производиться именно так? Все дело в плюсе, стоящем между целой и дробной частью (см. выше). На самом деле, полное преобразование выглядит вот так:

Но расписывать все так подробно слишком долго, да и незачем, проще сразу получать ответ, пользуясь формулой выше.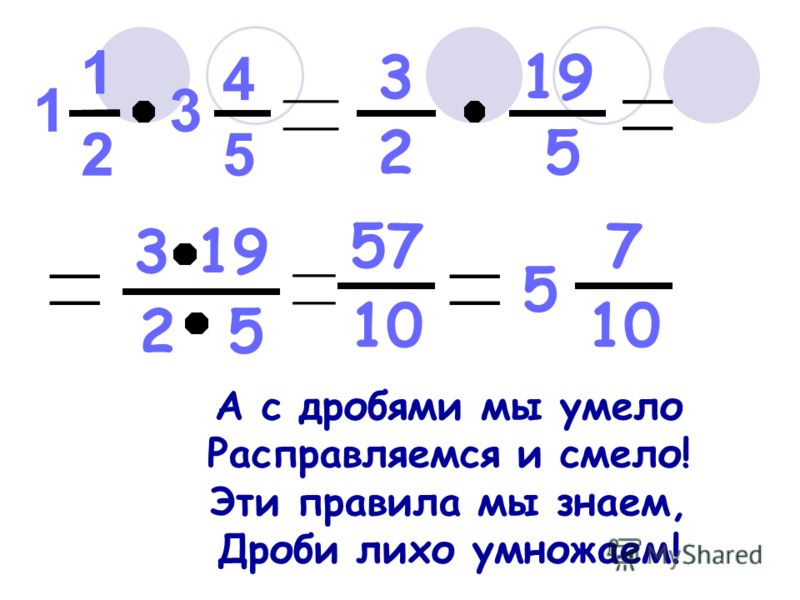

Превращение неправильной дроби в смешанную

Чтобы преобразовать неправильную дробь в смешанную, в ней нужно выделить целую часть.

Чтобы этого добиться, мы задаем себе вопрос – сколько раз знаменатель целиком «помещается» в числителе?

Например, пусть нам нужно представить как смешанную дробь \(\frac{13}{5}\). Сколько раз пятерка «помещается» в тринадцати? Два раза. Третий раз уже «не влезет». Значит, целая часть будет равна двойке, а дробная – остатку, то есть \(\frac{3}{5}\). Оформляем: \(\frac{13}{5}\)\(=\)\(\frac{10 + 3}{5}\)\(=\)\(\frac{10}{5}\)\(+\)\(\frac{3}{5}\)\(=2+\)\(\frac{3}{5}\)\(=2\)\(\frac{3}{5}\). Вот еще примеры с верным преобразованием:

\(\frac{37}{11}\)\(=\)\(\frac{33 + 4}{11}\)\(=\)\(\frac{33}{11}\)\(+\)\(\frac{4}{11}\)\(=3+\)\(\frac{4}{11}\)\(=3\)\(\frac{4}{11}\)
\(\frac{26}{3}\)\(=\)\(\frac{24 + 2}{3}\)\(=\)\(\frac{24}{3}\)\(+\)\(\frac{2}{3}\)\(=8+\)\(\frac{2}{3}\)\(=8\)\(\frac{2}{3}\)

А вот пример неправильного выделения целой части:

\(\frac{7}{2}\)\(=\)\(\frac{4 + 3}{2}\)\(=\)\(\frac{4}{2}\)\(+\)\(\frac{3}{2}\)\(=2+\)\(\frac{3}{2}\)\(=2\)\(\frac{3}{2}\)

В чем ошибка? В том, что дробная часть должна быть правильной дробью. А здесь не так — значит целая часть выделена не полностью. Действительно, ведь двойка в семерке нацело помещается три раза, а не два. Поэтому верным будет вот такое выделение:

\(\frac{7}{2}\)\(=\)\(\frac{6 + 1}{2}\)\(=\)\(\frac{6}{2}\)\(+\)\(\frac{1}{2}\)\(=3+\)\(\frac{1}{2}\)\(=3\)\(\frac{1}{2}\)

Превращение смешанной дроби в десятичную

Чтобы преобразовать смешанную дробь в десятичную, нужно в дробной части поделить числитель на знаменатель, после чего сложить результат с целой частью.

Например: \(2\)\(\frac{3}{5}\)\(=2+\)\(\frac{3}{5}\)\(=2+0,6=2,6\)
                      \(7\)\(\frac{11}{25}\)\(=7+\)\(\frac{11}{25}\)\(=7+0,44=7,44\)

Отсюда вывод:

Смешанная дробь – обычное число, причем целая часть представляет собой то, что будет стоять до запятой, а дробная – после.

Наиболее частые ошибки при работе со смешанной дробью

Главной причиной большинства ошибок является забывание описанного выше момента – между целой и дробной частью стоит «плюс», а не «умножить»

.

Пример: Вычислить \(2\)\(\frac{3}{5}\)\(:\)\(\frac{1}{5}\)
Ошибочное решение: \(2\)\(\frac{3}{5}\)\(:\)\(\frac{1}{5}\)\(=2\)\(\frac{3}{5}\)\(·\)\(\frac{5}{1}\)\(=2\)\(\frac{3 · 5}{5 · 1}\)\(=2·3=6\)
Правильное решение: \(2\)\(\frac{3}{5}\)\(:\)\(\frac{1}{5}\)\(=(2+\)\(\frac{3}{5}\)\():\)\(\frac{1}{5}\)\(=\)\(\frac{2·5+3}{5}\)\(:\)\(\frac{1}{5}\)\(=\)\(\frac{13}{5}\)\(·\)\(\frac{5}{1}\)\(=\)\(\frac{13 · 5}{5 · 1}\)\(=13\)

Пример: Вычислить \(3\)\(\frac{1}{5}\)\(·1\)\(\frac{1}{4}\)
Ошибочное решение: \(3\)\(\frac{1}{5}\)\(·1\)\(\frac{1}{4}\)\(=3·\)\(\frac{1}{5}\)\(·1·\)\(\frac{1}{4}\)\(=\)\(\frac{3}{5}\)\(·\)\(\frac{1}{4}\)\(=\)\(\frac{3 · 1}{5 · 4}\)\(=\)\(\frac{3}{20}\)
Правильное решение: \(3\)\(\frac{1}{5}\)\(·1\)\(\frac{1}{4}\)\(=(3+\)\(\frac{1}{5}\)\()·(1+\)\(\frac{1}{4}\)\()=\)\(\frac{3·5 + 1}{5}\)\(·\)\(\frac{1·4 + 1}{4}\)\(=\)\(\frac{16}{5}\)\(·\)\(\frac{5}{4}\)\(=\)\(\frac{16 · 5}{5 · 4}\)\(=4\)

Из того, что целая и дробная части соединены знаком плюс следует еще один вывод:

Если перед смешанной дробью стоит знак минус, то он стоит и перед целой частью, и перед дробной.

Например: \(-7\) \(\frac{5}{9}\)\(=-(7+\) \(\frac{5}{9}\)\()=-7-\) \(\frac{5}{9}\).
Это важно помнить при вычитании смешанных дробей.

Пример. Вычислить \(4\)\(\frac{3}{5}\)\(-2\)\(\frac{1}{5}\).
Решение: \(4\)\(\frac{3}{5}\)\(-2\)\(\frac{1}{5}\)\(=(4+\)\(\frac{3}{5}\)\()-(2+\)\(\frac{1}{5}\)\()=4+\)\(\frac{3}{5}\)\(-2-\)\(\frac{1}{5}\)\(=4-2+\)\(\frac{3}{5}\)\(-\)\(\frac{1}{5}\)\(=2+\)\(\frac{3-1}{5}\)\(=2+\)\(\frac{2}{5}\)\(=2\)\(\frac{2}{5}\).

Вообще вычитание (сложение) смешанных дробей удобно проводить в два этапа: сначала отдельно вычесть (сложить) целые части, а затем – дробные.

Смотрите также:
Дроби (шпаргалка)

примеры перевода для обыкновенных дробей и целых чисел

Содержание:

• Общие сведения о дробях
• Формы дробной записи
• Понятие смешанного числа
• Как соотносятся между собой неправильные дроби и смешанные числа
• Необходимость и алгоритм преобразования
  • Как перевести смешанное число в неправильную дробь
  • Как выделить из неправильной дроби целую часть

Содержание

• Общие сведения о дробях
• Формы дробной записи
• Понятие смешанного числа
• Как соотносятся между собой неправильные дроби и смешанные числа
• Необходимость и алгоритм преобразования
  • Как перевести смешанное число в неправильную дробь
  • Как выделить из неправильной дроби целую часть

Общие сведения о дробях

Определение

Дробь — форма записи рационального числа в виде доли целого.

В стандартном виде дроби записываются так: \( \frac mn.\)

Число над чертой называется числителем, под ней — знаменателем. Такую запись можно передать словами, как m частей из n, причем \(\frac nn\) равняется единице.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Например, \(\frac67\) — это 6 частей из 7.

В такой форме можно записать любое рациональное число, в том числе целое. При этом в качестве знаменателя может выступать любое натуральное число.

Так, единицу можно представить как \(\frac88,\;\frac{13}{13},\;\frac{857}{857}\) и так далее.

Для записи чисел больше одного в дробной форме необходимо это число умножить на числитель:

\(2=2\cdot1=2\cdot\frac55=\frac{10}5.\)

Существует понятие правильных и неправильных дробей.

Определение

Правильной называют дробь, у которой модуль числителя меньше модуля знаменателя.

Соответственно, у неправильной дроби числитель больше или равен знаменателю. Из приведенных выше примеров\( \frac67\) — правильная дробь, а \(\frac88,\;\frac{13}{13},\;\frac{857}{857}\) и \(\frac{10}5\) — неправильные.

Формы дробной записи

Как уже описывалось выше, стандартный способ записи обыкновенных дробей — через горизонтальную черту. Числитель помещается сверху, знаменатель — под чертой: \(\frac mn.\)

Также распространена строчная форма записи через наклонную черту: . Так, числитель оказывается слева, знаменатель — справа.

Один из самых распространенных и часто используемых на практике методов записи дробей — десятичная дробь. В этом случае число записывается как результат деления числителя на знаменатель. При этом, целая часть отделяется от остаточной при помощи запятой (в стандарте стран СНГ) или точкой.

Десятичные дроби могут быть конечными и бесконечными. У конечных ограниченное количество знаков после запятой: 0,15; 7,1; 871,986 и т. д. Пример бесконечной десятичной дроби — число \( \mathrm\pi\). В обычной форме оно выглядит, как \(\frac{22}7\), в десятичной: 3,1415926535897…

По своей сути, все десятичные дроби являются смешанными числами.

Понятие смешанного числа

Определение

Смешанное число — комбинация целочисленной и дробной форм записи рациональных чисел.

По сути, смешанное число — это упрощенный вид записи суммы целого числа и правильной дроби. Например, \(2\frac57\) можно обозначить, как \(2+\frac57\). Читаться такая запись будет так: «две целых, пять седьмых».

Как соотносятся между собой неправильные дроби и смешанные числа

Неправильные дроби отличаются от правильных тем, что в них числитель больше знаменателя. То есть, если представлять их буквально как операцию деления, то делимое больше делителя. Это значит, что в них содержится целая часть, выделив которую можно получить смешанное число.

Необходимость и алгоритм преобразования

В первую очередь, выделение целой части повышает удобство чтения записанных нецелых чисел и позволяет лучше понимать их значение. Это можно оценить на простом примере: \(\frac{12}5=2\frac25\). Можно пойти дальше и перевести смешанное число в десятичную дробь: \(2\frac25=2,4\). 

При решении задач зачастую необходимо преобразовать смешанные числа в дробные, так как с ними проще проводить вычисления.

Как перевести смешанное число в неправильную дробь

Чтобы записать смешанное число в форме неправильной дроби необходимо выполнить два действия: умножить целую часть на знаменатель и прибавить полученный результат к числителю.

Пример:

\(4\frac78=\frac{4\cdot8+7}8=\frac{32+7}8=\frac{39}8\)

Этот упрощенный способ преобразования работает на том принципе, что любое целое число можно представить в виде произведения этого числа на единицу. Единицу же в свою очередь можно представить в виде дроби, где числитель равен знаменателю. Разберем предыдущий пример более подробно:

\(4\frac78=4+\frac78=4\cdot1+\frac78=4\cdot\frac88+\frac78=\frac{32}8+\frac78=\frac{39}8\)

Как выделить из неправильной дроби целую часть

Обратное преобразование работает на принципе, согласно которому, при делении двух некратных друг другу чисел, делимое можно представить в виде суммы кратного делителю числа и некоего остатка. В качестве примера возьмем число из предыдущего пункта:

\(\frac{39}8=\frac{32}8+\frac78=4+\frac78=4\frac78\)

В этом преобразовании можно пойти дальше и представить смешанное число в виде десятичной дроби. Для этого целая часть отделяется запятой, а операция деления продолжается с остатком, умноженным на 10. Само деление продолжается до тех пор, пока остаток не окажется равен нулю.

\(4\frac78=4,0+\frac{7\cdot10}8=4,0+\left(\frac{64}8+\frac68\right)=4,8+\frac{6\cdot10}8=4,8+\left(\frac{56}8+\frac48\right)=4,87+\frac{40}8=4,875\)

В случае с бесконечными десятичными дробями, деление продолжается до тех пор, пока число знаков после запятой не удовлетворит условие задачи. В таком случае, последняя цифра округляется согласно установленным правилам.

Насколько полезной была для вас статья?

Рейтинг: 1.33 (Голосов: 3)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Как умножать смешанные числа

Что такое смешанные числа

Смешанное число — это целое число и правильная дробь, представленные вместе. Обычно представляет собой число между любыми двумя целыми числами.

Посмотрите на данное изображение, оно представляет собой дробь, которая больше 1, но меньше 2. Таким образом, это смешанное число.

Некоторые другие примеры смешанных чисел: 

Части смешанного числа

Смешанное число образуется путем объединения трех частей: целого числа, числителя и знаменателя. Числитель и знаменатель являются частью правильной дроби, составляющей смешанное число.

Преобразование смешанных чисел в неправильные дроби

• Умножить целое число на знаменатель дроби.
• Прибавьте ответ, полученный на шаге 1, к числителю дроби.
• Запишите ответ, полученный на шаге 2, над знаменателем.

Предположим, нам нужно преобразовать $2\frac{2}{3}$ в неправильную дробь.

Шаг 1 : Умножаем 3 на 2, получаем 3$\умножить на 2 = 6$.

Шаг 2 : Складываем 6 и 2, получаем 6$ + 2 = 8$

Шаг 3: Полученная дробь равна $\frac{8}{3}$.

Умножение смешанного числа на целое число

Шаг 1: Преобразуйте смешанное число в неправильную дробь.

Шаг 2: Перепишите целое число в виде дроби со знаменателем 1.

Шаг 3: Умножьте две дроби, умножая числители и знаменатели отдельно.

Шаг 4: При необходимости преобразуйте его в упрощенную форму.

Предположим, нам нужно перемножить 3 и $2\frac{1}{2}$.

$2\frac{1}{2}=\frac{2\times2+1}{2}=\frac{5}{2}$

$3\times\frac{5}{2}=\frac {3}{1}\times\frac{5}{2}=\frac{15}{2}=7\frac{1}{2}$

Умножение смешанного числа на дробь

Шаг 1 : Преобразуйте смешанное число в неправильную дробь.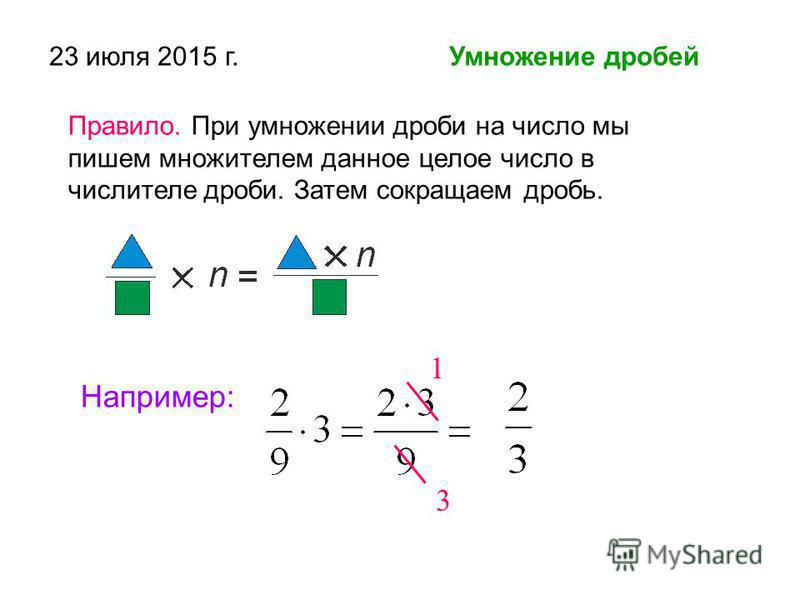

Шаг 2: Умножьте числители дроби и умножьте знаменатели дроби.

Шаг 3: При необходимости преобразовать в упрощенную форму.

Предположим, нам нужно перемножить $\frac{2}{5}$ и $3\frac{1}{2}$.

$3\frac{1}{2}=\frac{3\times2+1}{2}=\frac{7}{2}$

$\frac{2}{5}\times\frac{ 7}{2}=\frac{14}{10}=\frac{7}{5}=1\frac{2}{5}$

Умножение двух смешанных чисел

Шаг 1: Преобразование смешанных чисел числа в неправильные дроби.

Шаг 2: Умножьте две дроби, раздельно умножив числители и знаменатели.

Шаг 3: При необходимости преобразуйте его в упрощенную форму.

Например: умножьте $4\frac{1}{2}$ и $3\frac{1}{3}$.

$4\frac{1}{2}=\frac{4\times2+1}{2}=\frac{9}{2}$

$3\frac{1}{3}=\frac{3 \times3+1}{3}=\frac{10}{3}$

$4\frac{1}{2}\times3\frac{1}{3}=\frac{9}{2}\times \frac{10}{3}=\frac{90}{6}=15$ 

Заключение

В этой статье мы узнали об умножении смешанных чисел. Смешанные числа также известны как смешанные дроби. Чтобы прочитать больше таких информативных статей о других концепциях, посетите наш веб-сайт. Мы в SplashLearn стремимся сделать обучение интересным и интерактивным для всех учащихся.

Решенные примеры

1. Умножьте $5\frac{3}{7}$ на мультипликативное значение, обратное $7\frac{3}{5}$ .

Решение: $5\frac{3}{7}=\frac{5\times7+3}{7}=\frac{38}{7}$

$7\frac{3}{5} =\frac{7\times5+3}{5}=\frac{38}{5}$

Мультипликативное значение, обратное $\frac{38}{5}$ равно $\frac{5}{38} $.

Продукт $= \frac{38}{7}\times\frac{5}{38}=\frac{5}{7}$

2. Эмма идет 5 2 3 миль в день. Какое расстояние она преодолеет за 9 дней?

Решение: Расстояние, пройденное Эммой за 1 дней $= 5\frac{2}{3}$ миль $=\frac{17}{3}$ миль.

Расстояние, пройденное Эммой за 9 дней $= 9\times\frac{17}{3}= 51$ миль 

3. Умножьте $6\frac{2}{5}\times\frac{3} {4}$ .

Решение: $6\frac{2}{5}=\frac{6\times5+2}{5}=\frac{32}{5}$

$\frac{32}{5}\times \frac{3}{4}=\frac{32\times3}{5\times4}=\frac{96}{20}=\frac{24}{ 5}=4\frac{4}{5}$

Практические задачи

1

Какой из этих шагов является первым шагом к умножению смешанных чисел?

Вычисление НОК знаменателей

Умножение числителей

Умножение знаменателей

Преобразование смешанных чисел в неправильные дроби

Правильный ответ: Преобразование смешанных чисел в неправильные дроби
Преобразование смешанных чисел в неправильные дроби Первым шагом к умножению смешанных чисел является преобразование их в неправильные дроби.

2

При умножении $10\frac{1}{6}$ на $2\frac{2}{11}$ получаем ____.

целое число

смешанное число

правильная дробь

отрицательное число

Правильный ответ: смешанное число
$10\frac{1}{6}\times\frac2{2}{11}=\frac{61} {6}\times\frac{24}{11}=\frac{244}{11}=22\frac{2}{11}$, т. е. смешанное число

3

Значение $4\frac{2}{9}\times1\frac{1}{7}$:

$1\frac{52}{63}$

$2\frac{52} {63}$

$4\frac{52}{63}$

$\frac{61}{63}$

Правильный ответ: $4\frac{52}{63}$
$4\frac{2 {9}\times1\frac{1}{7}=\frac{38}{9}\times{8}{7}=\frac{304}{63}=4\frac{52}{63} $

Часто задаваемые вопросы

Требуются ли одинаковые знаменатели при умножении двух или более смешанных чисел ?

Нет. Нам не нужны одинаковые знаменатели для умножения двух или более смешанных чисел. Мы даже можем умножать непохожие дроби.

Как еще называют смешанные числа?

Другое название смешанных чисел — смешанные дроби.

Всегда ли произведение смешанного числа на другое смешанное число является смешанным числом?

Нет. Смешанное число всегда больше 1. Таким образом, произведение 2 чисел больше 1 всегда будет больше 1, т. е. смешанное/целое число.

Умножение дробей и целых чисел: два типа задач

Признание: Мне пришлось заново изучать математику в 4-м и 5-м классах, чтобы лучше обучать и поддерживать своих учеников.

Я узнал, что когда я преподавал алгоритмы и трюки без фундамента концептуального понимания, это действительно повлияло на понимание математики моими учениками и на то, как они решали текстовые задачи. Когда у моих учеников не было концептуального понимания математической операции, им не удавалось решать текстовые задачи, требующие этих операций.

Учитывая все сказанное, мне пришлось учиться этому самому (трудным путем), и я хочу сэкономить ваше время, поделившись с вами тем, что мне пришлось заново выучить. В этом посте я расскажу о двух типах задач на умножение дробей и целых чисел, которым я обучаю своих студентов, и почему я подчеркиваю концептуальное понимание этих задач.

Два типа задач на умножение дробей и целых чисел

Первый тип: целое число, умноженное на дробь (равные группы дробной суммы)

4 x 1/2 =

Пекарь хочет продать четыре плитки шоколадной помадки. Каждая плита весит ½ фунта. Определить общий вес четырех плит.

В этой задаче участвуют одинаковых групп .

У пекаря четыре равные группы по ½. Группы — это кусочки выдумки. Каждая плита весит ½ фунта, поэтому ½ — это количество или размер каждой группы.

Проблема заключается в том, чтобы указать общий вес, поэтому вы умножаете количество плит (4) на вес каждой плиты (½).

Четыре группы по ½ = 4 x ½

Второй тип: Дробь, умноженная на целое число (взятие дробной части целого числа)

1/2 x 4 =

У пекаря четыре фунта шоколадной помадки. Он продает ½ помадки покупателю. Сколько фунтов он продал покупателю?

Эта задача требует части целого числа .

Целое число — это количество помадки, которое есть у пекаря, а часть, которую берут, — это ½ помадки, которую купил покупатель.

Проблема заключается в том, чтобы указать дробную часть суммы, поэтому вы умножаете полученную часть (½) на начальную сумму (4).

½ от 4 = ½ x 4

Щелкните здесь, чтобы получить распечатку, показанную для иллюстрации различий между двумя типами задач. Я использую эту печатную форму после того, как представил оба типа по отдельности.

Но коммутативность…

Я знаю, что коммутативность делает ответ правильным независимо от того, где числа расположены в задаче. Но обучение студентов этим двум типам и различиям между ними действительно меняет их концептуальное понимание и их способность правильно решать текстовые задачи.

Вот как я учу своих учеников читать различные типы умножения дробей и задачи на целые числа:

4 x ½ = 2: четыре группы по половине равно двум

½ x 4 = 2: один -половина четырех равна двум

Когда они могут прочитать подобное уравнение и связать его с проблемой, они лучше понимают проблему и способы ее решения.

Знакомство с умножением дробей на целые числа

Чтобы помочь моим учащимся понять эти два типа и помочь им использовать модели для точного представления задач, я всегда использую словесные задачи или ситуации в качестве введения.

Мы читаем задачу, используем визуальные или манипулятивные средства для определения ответа, а затем пишем уравнение, представляющее проделанную нами работу.

Это действительно помогает моим ученикам сделать шаг назад и подумать о проблеме, прежде чем спешить писать на операцию.

Сначала я ввожу первый тип (равные группы), потому что могу связать это с их прежним пониманием умножения. Затем, после того как они это освоили, я ввожу второй тип (беря дробную часть целого числа).

После того, как мои ученики познакомили меня с отдельными типами и позволили им как можно лучше освоить их, я использую печатную форму, показанную выше, чтобы сравнить и сопоставить два типа.

Нужны материалы по математике для 4-го класса?

Если вам нужны математические ресурсы для 4-го класса, нажмите на ссылки ниже, чтобы просмотреть мои самые рекомендуемые ресурсы.