Умножение и деление дробей (онлайн калькулятор)
Онлайн калькулятор умножения и деления дробей. Можно вводить как простые, так и смешанные дроби с выделенной целой частью, а также преобразовывать простые дроби в смешанные и наоборот. Приводится решение с подробным объяснением. Калькулятор использует длинную арифметику, и работает с большими числами.
Онлайн калькулятор
Краткое решение задачи
938 • 847 = 9 • 8 + 38 • 8 • 7 + 47 = 758 • 607 = 75 • 608 • 7 = 450056 = 4500 / 456 / 4 = 112514 = 80 • 14 + 514 = 80514 .
Ответ
938 • 847 = 80514 .
Подробное решение
- Переводим смешанные дроби в простые.
938 = 9 + 38 = 9 • 88 + 38 = 9 • 8 + 38 = 72 + 38 = 758 .
847 = 8 + 47 = 8 • 77 + 47 = 8 • 7 + 47 = 56 + 47 = 607 .
- Умножаем дроби, перемножая их числители и знаменатели.
938 • 847 = 758 • 607 = 75 • 608 • 7 = 450056 .
- Проверим, нельзя ли сократить дробь. Для этого найдем наибольший общий делитель (НОД) числителя и знаменателя.

НОД( 4500, 56 ) = 4
См. Вычисление НОД этих чисел двумя способами с подробными объяснениями.
Дроби можно сократить. Делим числитель и знаменатель на НОД.450056 = 4500 / 456 / 4 = 112514 .
- Переводим простую дробь в смешанную.
112514 = 80 • 14 + 514 = 80 • 1414 + 514 = 80 + 514 = 80514 .
Ответ
938 • 847 = 80514 .
Описание калькулятора
- В поля ввода введите целую часть, числитель и знаменатель первой дроби.
- Далее, из выпадающего списка выберите операцию умножения или деления.
- После этого введите данные второй дроби.
- Если нужно изменить знак введенного числа, нажмите кнопку «+/–».
- Если заданы только простые дроби (без целой части), и результат вычислений нужно представить только в виде простой дроби, то нажмите переключатель «Простые дроби».
- Нажмите кнопку «Умножить дроби» (или «Разделить дроби»).
- В результате появится краткое и подробное решение.
Калькулятор использует длинную арифметику и позволяет работать с большими числами. То есть вводимые числа могут быть сколь угодно большими.
То есть вводимые числа могут быть сколь угодно большими.
Справочные данные
- Обыкновенная дробь
- – это форма записи числа в виде дроби , состоящая из числителя и знаменателя , которые являются натуральными числами. Как правило, обыкновенную дробь называют просто дробью, опуская слово “обыкновенная”. Число, представленное дробью является результатом деления числителя на знаменатель . Натуральное число также можно записать в виде обыкновенной дроби, знаменатель которой равен единице: .
Дробь может быть положительной: , и отрицательной: . Здесь – натуральные числа: . - Правильная дробь
- – это дробь, у которой числитель меньше знаменателя.
- Неправильная дробь
- – это дробь, у которой числитель больше или равен знаменателю.
- Смешанная дробь
- – это форма записи неправильной дроби, состоящая из целого числа и правильной дроби. Смешанное число равно сумме целого числа и правильной дроби.
- Сокращение дроби
- – это деление числителя и знаменателя дроби на их общий делитель, отличный от единицы.

- Несократимая дробь
- – это дробь, числитель и знаменатель которой не имеют общего делителя, кроме единицы.
- Наибольший общий делитель числителя и знаменателя дроби
- – это наибольшее число, на которое можно сократить дробь.
Представление целого числа дробью
Целое числоможно представить в виде простой дроби, знаменатель которой равен единице:
.
Умножение дробей
Чтобы умножить простую дробь на дробь ,нужно перемножить их числители и знаменатели:
.
Деление дробей
Чтобы разделить простую дробь на дробь ,нужно умножить на :
.
Перевод смешанной дроби в простую
Чтобы перевести смешанную дробь в простую,нужно к целой части прибавить дробную:
.
Перевод простой дроби в смешанную
Чтобы перевести простую дробь в смешанную ,нужно разделить с остатком натуральное число на натуральное число . В результате мы получим неполное частное и остаток . Тогда число можно представить так:
.

Неполное частное будет целой частью смешанного числа; остаток от деления – числителем дробной части:
.
Автор: Олег Одинцов. Опубликовано:
Обыкновенные дроби и действия с ними — что это, определение и ответ
Доля – это часть от целого.
Например, пирог разделили на 8 частей, значит каждый кусочек пирога равен одной восьмой доле пирога или просто одной восьмой пирога. Записать такую долю можно в виде дроби\(\ = \frac{1}{8}\).
Если из полученных кусочков забрать три и оставить пять, получится, что забрали три восьмые\(\ –\ \frac{3}{8}\ \)пирога и оставили пять восьмых \(–\ \frac{5}{8}.\)
Число выше черты дроби называется числителем, число ниже черты – знаменателем, а запись вида \(\frac{5}{8}\) – обыкновенной дробью.
Дробь \(\frac{1}{2}\) называется половиной, \(\frac{1}{3}\) – третью, а \(\frac{1}{4}\) – четвертью.
ОСНОВНОЕ СВОЙСТВО ДРОБЕЙ:
Если мы представим пирог, который разделили на четыре части и забрали две из них (\(\frac{2}{4}\)), мы увидим, что забрали ровно половину пирога, то есть \(\frac{1}{2}\).
Значит \(\frac{2}{4} = \frac{1}{2}\). Так получается, потому что дроби можно сокращать (делить) и расширять (умножать). Если числитель и знаменатель дроби умножить или разделить на одно число, то дробь останется такой же.
Например:
\(\frac{1}{2} = \frac{1 \bullet 2}{2 \bullet 2} = \frac{2}{4}\)
\(\frac{28}{77} = \frac{28 : 7}{77 : 7} = \frac{4}{11}\)
\(\frac{5}{12} = \frac{5 \bullet 4}{12 \bullet 4} = \frac{20}{48}\)
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ:
Можно складывать и вычитать только те дроби, у которых одинаковый знаменатель. Тогда знаменатель суммы или разности будет такой же, как и у слагаемых, а числители складываются или вычитаются.
\(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)
Например:
\(\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}\)
\(\frac{8}{9}\ –\ \frac{3}{9} = \frac{8\ –\ 3}{9} = \frac{5}{9}\)
Если у дробей разные знаменатели, то нужно привести их к общему знаменателю.

Приведем дробь \(\frac{5}{6}\ \)к знаменателю 42. Чтобы это сделать, нужно знаменатель 6 умножить на \(42 : 6 = 7\), значит и числительно тоже нужно умножить на 7:
\(\frac{5}{7} = \frac{5 \bullet 7}{6 \bullet 7} = \frac{35}{42}\)
Таким образом, мы пришли к новому знаменателю 42 с помощью дополнительного множителя 7.
Общим знаменателем является общее кратное исходных знаменателей. Обычно дроби приводят к наименьшему общему знаменателю. А уже дроби с общим знаменателем можно складывать и вычитать.
АЛГОРИТМ СЛОЖЕНИЯ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ:
Найти наименьшее общее кратное знаменателей дробей. Оно и будет новым знаменателем суммы.
Разделить найденный наименьший общий знаменатель на знаменатели слагаемых. Это будут дополнительные множители для дробей.
Умножить и числитель, и знаменатель каждой дроби на её дополнительный множитель. Получим сумму дробей с одинаковым знаменателем.

Складывать или вычитать дроби как обыкновенные дроби с одинаковыми знаменателями.
Например:
\(\frac{3}{4} + \frac{5}{6} = \frac{3 \bullet 3}{4 \bullet 3} + \frac{5 \bullet 2}{6 \bullet 2} = \frac{9}{12} + \frac{10}{12} = \frac{9 + 10}{12} = \frac{19}{12}\)
УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ:
Обратные числа:
Любая дробь – это действие деления. Один пирог разделили на восемь частей – получили одну восьмую пирога. Если мы видим дробь с единицей в знаменателе, то эту дробь можно представить числом:
\(\frac{a}{1} = a : 1 = a\)
Например: \(\frac{4}{1} = 4\), \(\frac{27}{1} = 27\).
Если дробь «перевернуть», то есть поменять местами числитель и знаменатель, тогда получится число обратное исходному. Например, числа \(\frac{4}{11}\) и \(\frac{11}{4}\) или \(19\) и \(\frac{1}{19}\) – обратные друг другу.
Умножение дробей:
Представим умножение дроби на число как сумму дробей:
\(\frac{3}{5} \bullet 3 = \frac{3}{5} + \frac{3}{5} + \frac{3}{5} = \frac{3 + 3 + 3}{5} = \frac{3 \bullet 3}{5} = \frac{9}{5}\)
Видим, что таким образом при умножении дроби на число перемножается число и числитель без изменения знаменателя:
\(\frac{a}{c} \bullet b = \frac{a}{c} \bullet \frac{b}{1} = \frac{a \bullet b}{c \bullet 1}\)
Деление дробей:
Чтобы разделить дробь на число, представим это число как дробь с единицей в знаменателе. Тогда мы делим дробь на дробь.
Тогда мы делим дробь на дробь.
Чтобы разделить дробь на дробь, нужно вторую дробь перевернуть и перемножить соответственно числители и знаменатели получившихся дробей:
\(\frac{a}{c} : b = \frac{a}{c} : \frac{b}{1} = \frac{a}{c} \bullet \frac{1}{b} = \frac{a}{c \bullet b}\)
Таким же образом делят дроби на дроби:
\(\frac{a}{c} : \frac{b}{d} = \frac{a}{c} \bullet \frac{d}{b} = \frac{a \bullet d}{c \bullet b} = \frac{\text{ad}}{\text{cb}}\)
Как умножать простые дроби « Математика :: WonderHowTo
- Автор Шон Конати
Посмотрите это видео, чтобы узнать, как умножать дроби на дроби. Сначала умножьте верхние числа вместе. Например, если у вас есть 3/5 * 4/7, умножьте 3 * 4 и положите свой продукт сверху дроби, которую вы получите как продукт. Затем перемножьте нижние числа вместе и поместите их в нижнюю часть полученной дроби. Затем посмотрите, можете ли вы уменьшить свой продукт, чтобы упростить его. Вы также можете сначала выполнить шаг сокращения, отменив любые общие множители в числителях и знаменателях умножаемых дробей. Посмотрите это видео, чтобы получить представление о том, как умножать простые дроби, и научиться использовать эту технику в математике, а также в повседневной жизни.
Хотите освоить Microsoft Excel и поднять перспективы работы на дому на новый уровень? Начните свою карьеру с нашего учебного комплекта Microsoft Excel Premium от А до Я в новом магазине Gadget Hacks Shop и получите пожизненный доступ к более чем 40 часам базовых и продвинутых инструкций по функциям, формулам, инструментам и многому другому.
Купить сейчас (скидка 97%) >
Другие выгодные предложения:
- Скидка 97 % на The Ultimate White Hat Hacker Certification Bundle 2021
- Скидка 98 % на комплект Accounting Mastery Bootcamp 2021
- Скидка 99 % на Mega Bundle All-in-One Data Scientist 2021
- 5 Скидка 9% на XSplit VCam: Lifetime Подписка (Windows)
- Скидка 98 % на пакет сертификации Premium Learn To Code 2021
- Скидка 62 % Программное обеспечение MindMaster Mind Mapping: бессрочная лицензия
- Скидка 41 % NetSpot Home Wi-Fi Analyzer: пожизненные обновления
- Горячий
- Последние
2.
 2.1: Умножение дробей и смешанных чисел
2.1: Умножение дробей и смешанных чисел- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 61459
- Проект NROC
Цели обучения
- Умножение двух или более дробей.
- Умножить дробь на целое число.
- Умножить два или более смешанных числа.
- Решение прикладных задач, требующих умножения дробей или смешанных чисел.
Введение
Так же, как сложение, вычитание, умножение и деление при работе с целыми числами, вы также используете эти операции при работе с дробями. Есть много случаев, когда необходимо умножить дроби и смешанные числа . Например, по этому рецепту получится 4 коржа для пирога:
Например, по этому рецепту получится 4 коржа для пирога:
5 чашек крекеров
8 столовых ложек сахара
\(\ 1 \frac{1}{2}\) чашек растопленного сливочного масла
\(\ \frac{1 }{4}\) чайная ложка ванили
Предположим, вы хотите испечь только 2 коржа для пирога. Вы можете умножить все ингредиенты на \(\ \frac{1}{2}\), так как требуется только половина количества коржей. Научившись умножать дробь на другую дробь, целое число или смешанное число, вы сможете рассчитать ингредиенты, необходимые для 2 коржей для пирога.
Умножение дробей
Когда вы умножаете дробь на дробь, вы получаете «долю дроби». Предположим, у вас есть \(\ \frac{3}{4}\) шоколадного батончика, и вы хотите найти \(\ \frac{1}{2}\) из \(\ \frac{3}{4} }\):
Разделив каждую четверть пополам, вы можете разделить моноблок на восьмые части.
Затем выберите половину из них, чтобы получить \(\ \frac{3}{8}\).
В обоих приведенных выше случаях, чтобы найти ответ, вы можете перемножить числители вместе и знаменатели вместе.
Умножение двух дробей
\(\ \frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d}=\frac{\text { произведение числителей }}{\text { произведение знаменателей }}\)
Пример:
\(\ \frac{3}{4} \cdot \frac{1}{2}=\frac{3 \cdot 1}{4 \cdot 2}=\frac{3}{8}\)
Умножение более двух дробей
\(\ \frac{a}{b} \cdot \frac{c}{d } \cdot \frac{e}{f}=\frac{a \cdot c \cdot e}{b \cdot d \cdot f}\)
Пример:
\(\ \frac{1}{3 } \cdot \frac{2}{4} \cdot \frac{3}{5}=\frac{1 \cdot 2 \cdot 3}{3 \cdot 4 \cdot 5}=\frac{6}{60 }\)
Пример
| \(\ \frac{2}{3} \cdot \frac{4}{5}\) | Умножить. |
Решение
| \(\ \frac{2 \cdot 4}{3 \cdot 5}\) | Умножьте числители и умножьте знаменатели. |
| \(\ \frac{8}{15}\) | Упростите, если возможно. Эта фракция уже находится в наименьших условиях. Эта фракция уже находится в наименьших условиях. |
\(\ \frac{8}{15}\)
Если полученное произведение необходимо упростить до наименьших членов, разделите числитель и знаменатель на общие множители.
Пример
| \(\ \frac{2}{3} \cdot \frac{1}{4}\) | Умножить. Упростите ответ. |
Решение
| \(\ \frac{2 \cdot 1}{3 \cdot 4}\) | Умножьте числители и умножьте знаменатели. |
| \(\ \frac{2}{12}\) | Упростите, если возможно. |
| \(\ \frac{2 \div 2}{12 \div 2}\) | Упростите, разделив числитель и знаменатель на общий делитель 2. |
\(\ \frac{2}{3} \cdot \frac{1}{4}=\frac{1}{6}\)
Вы также можете упростить задачу перед умножением, разделив общие факторы.
Пример
| \(\ \frac{2}{3} \cdot \frac{1}{4}\) | Умножить. Упростите ответ. |
Решение
| \(\ \frac{2 \cdot 1}{3 \cdot 4}=\frac{1 \cdot 2}{3 \cdot 4}\) | Переставьте числители так, чтобы вы увидели дробь с общим множителем. |
| \(\ \frac{1 \cdot 1}{3 \cdot 2}\) | Упростить. \(\ \frac{2}{4}=\frac{2 \div 2}{4 \div 2}=\frac{1}{2}\) |
\(\ \frac{2}{3} \cdot \frac{1}{4}=\frac{1}{6}\)
Вам не нужно использовать ярлык «сначала упростить» , но это может облегчить вашу работу, потому что числа в числителе и знаменателе будут меньше, пока вы работаете с ними.
Упражнение
\(\ \frac{3}{4} \cdot \frac{1}{3}\) Умножить.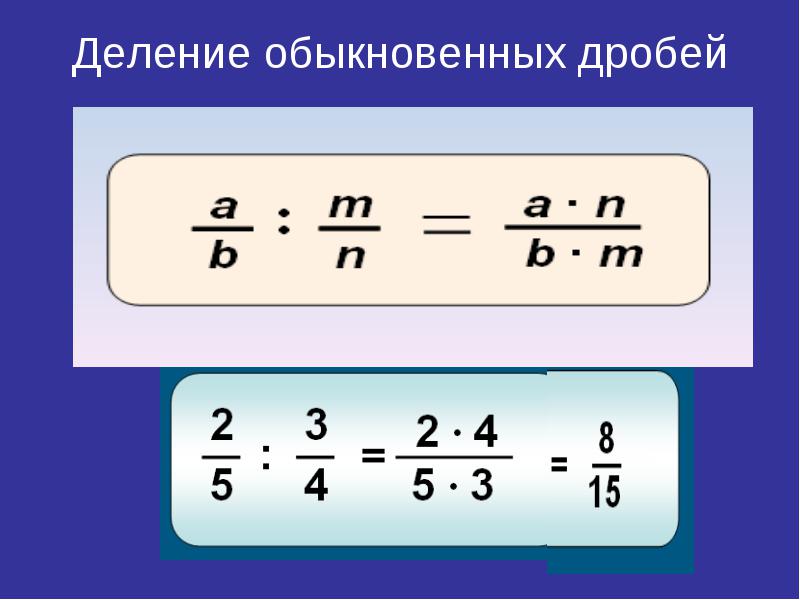 Упростите ответ.
Упростите ответ.
- \(\ \frac{3}{12}\)
- \(\ \frac{4}{7}\)
- \(\ \фракция{1}{4}\)
- \(\ \frac{36}{144}\)
- Ответить
- Неверно. \(\ \frac{3}{12}\) – это дробь, эквивалентная правильному ответу \(\ \frac{1}{4}\), но не в самом низком выражении. Вы должны разделить числитель и знаменатель на общий множитель 3. Правильный ответ: \(\ \frac{1}{4}\).
- Неверно. Возможно, вы добавили числители (3+1) и добавили знаменатели (4+3) вместо умножения. Правильный ответ: \(\ \frac{1}{4}\).
- Правильно. Один из способов найти этот ответ — перемножить числители и знаменатели, \(\ \frac{3 \cdot 1}{4 \cdot 3}=\frac{3}{12}\), а затем упростить: \(\ \frac {3 \div 3}{12 \div 3}=\frac{1}{4}\).
- Неверно. Вы наверное нашли общий знаменатель, правильно перемножили, но потом забыли упростить. Поиск общего знаменателя не обязателен и усложняет умножение, потому что вы работаете с большими, чем необходимо, числами.
 Правильный ответ: \(\ \frac{1}{4}\).
Правильный ответ: \(\ \frac{1}{4}\).
Умножение дроби на целое число
При работе как с дробями, так и с целыми числами полезно записывать целое число в виде неправильной дроби (дроби, в которой числитель больше или равен знаменателю). Все целые числа можно записать с «1» в знаменателе. Например: \(\ 2=\frac{2}{1}\), \(\ 5=\frac{5}{1}\) и \(\ 100=\frac{100}{1}\ ). Помните, что знаменатель говорит, сколько частей в одном целом, а числитель говорит, сколько частей у вас есть.
Умножение дроби на целое число
\(\ a \cdot \frac{b}{c}=\frac{a}{1} \cdot \frac{b}{c}\)
Пример:
\(\ 4 \cdot \frac{2}{3}=\frac{4}{1} \cdot \frac{2}{3}=\frac{8}{3}\)
Часто, когда умножив целое число на дробь, получится неправильная дробь. Часто желательно записать неправильные дроби в виде смешанного числа для окончательного ответа. Вы можете упростить дробь до или после переписывания ее в виде смешанного числа.
Пример
| \(\ 7 \cdot \frac{3}{5}\) | Умножить. Упростите ответ и запишите в виде смешанного числа. |
Раствор
| \(\ \frac{7}{1} \cdot \frac{3}{5}\) | Перепишите число 7 в виде неправильной дроби \(\ \frac{7}{1}\). |
| \(\ \frac{7 \cdot 3}{1 \cdot 5}=\frac{21}{5}\) | Умножьте числители и умножьте знаменатели. |
| \(\ 4 \frac{1}{5}\) | Перепишите как смешанное число. \(\ 21 \div 5=4\) с остатком 1. |
\(\ 7 \cdot \frac{3}{5}=4 \frac{1}{5}\)
Пример
| \(\ 4 \cdot \frac{3} {4}\) | Умножить. Упростите ответ и запишите в виде смешанного числа. |
Решение
| \(\ \frac{4}{1} \cdot \frac{3}{4}\) | Перепишите число 4 в виде неправильной дроби \(\ \frac{4}{1}\). |
| \(\ \frac{4 \cdot 3}{1 \cdot 4}\) | Умножьте числители и умножьте знаменатели. |
| \(\ \frac{12}{4}=3\) | Упростить. |
\(\ 4 \cdot \frac{3}{4}=3\)
Упражнение
\(\ 3 \cdot \frac{5}{6}\) Умножить. Упростите ответ и запишите его в виде смешанного числа.
- \(\ 1 \frac{1}{7}\)
- \(\ 2 \frac{1}{2}\)
- \(\ \фракция{8}{6}\)
- Ответить
- Неверно. Возможно, вы добавили числители и добавили знаменатели, чтобы получить \(\ \frac{8}{7}\), которое является смешанным числом \(\ 1 \frac{1}{7}\).
 Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac {3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac {3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\). - Правильно. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac{ 3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\).
- Неверно. Умножение числителей и умножение знаменателей приводит к неправильной дроби \(\ \frac{5}{2}\), но вам нужно выразить это как смешанное число. Правильный ответ: \(\ 2 \frac{1}{2}\).
- Неверно. Возможно, вы добавили числители и поместили их над знаменателем числа 6. Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac{ 3}{6}\).
 Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
- Неверно. Возможно, вы добавили числители и добавили знаменатели, чтобы получить \(\ \frac{8}{7}\), которое является смешанным числом \(\ 1 \frac{1}{7}\).
Умножение смешанных чисел
Если вы хотите умножить два смешанных числа или дробь и смешанное число, вы можете снова записать любое смешанное число как неправильную дробь.
Итак, чтобы умножить два смешанных числа, запишите каждое из них как неправильную дробь, а затем умножьте, как обычно. Умножьте числители и умножьте знаменатели и упростите. И, как и раньше, при упрощении, если ответ выходит неправильной дробью, то переводить ответ в смешанное число.
Пример
| \(\ 2 \frac{1}{5} \cdot 4 \frac{1}{2}\) | Умножить. Упростите ответ и запишите в виде смешанного числа. |
Раствор
| \(\ 2 \frac{1}{5}=\frac{11}{5}\) | Замените 2 \(\ \frac{1}{5}\) на неправильную дробь. \(\ 5 \cdot 2+1=11\), а знаменатель равен 5. \(\ 5 \cdot 2+1=11\), а знаменатель равен 5. |
| \(\ 4 \frac{1}{2}=\frac{9{2}\) | Замените \(\ 4 \frac{1}{2}\) на неправильную дробь. \(\ 2 \cdot 4+1=9\), а знаменатель равен 2. |
| \(\ \frac{11}{5} \cdot \frac{9}{2}\) | Перепишите задачу на умножение, используя неправильные дроби. |
| \(\ \frac{11 \cdot 9}{5 \cdot 2}=\frac{99}{10}\) | Умножение числителей и умножение знаменателей. |
| \(\ \frac{99}{10}=9 \фракция{9}{10}\) | Запишите как смешанное число. \(\ 99 \div 10=9\) с остатком 9. |
\(\ 2 \frac{1}{5} \cdot 4 \frac{1}{2}=9 \frac{9}{10}\)
Пример
| \( \ \frac{1}{2} \cdot 3 \frac{1}{3}\) | Умножить. Упростите ответ и запишите в виде смешанного числа. |
Раствор
| \(\ 3 \frac{1}{3}=\frac{10}{3}\) | Замените \(\ 3 \frac{1}{3}\) на неправильную дробь. \(\ 3 \cdot 3+1=10\), а знаменатель равен 3. \(\ 3 \cdot 3+1=10\), а знаменатель равен 3. |
| \(\ \frac{1}{2} \cdot \frac{10}{3}\) | Перепишите задачу на умножение, используя неправильную дробь вместо смешанного числа. |
| \(\ \frac{1 \cdot 10}{2 \cdot 3}=\frac{10}{6}\) | Умножение числителей и умножение знаменателей. |
| \(\ \frac{10}{6}=1 \frac{4}{6}\) | Перепишите как смешанное число. \(\ 10 \div 6=1\) с остатком 4. |
| \(\ 1 \frac{2}{3}\) | Упростите дробную часть до меньших членов, разделив числитель и знаменатель на общий множитель 2. |
\(\ \frac{1}{2} \cdot 3 \frac{1}{3}=1 \frac{2}{3}\)
Как вы видели ранее, иногда полезно посмотреть для общих делителей в числителе и знаменателе, прежде чем упростить продукты.
Пример
| \(\ 1 \frac{3}{5} \cdot 2 \frac{1}{4}\) | Умножить. Упростите ответ и запишите в виде смешанного числа. Упростите ответ и запишите в виде смешанного числа. |
Раствор
| \(\ 1 \frac{3}{5}=\frac{8}{5}\) | Замените \(\ 1 \frac{3}{5}\) на неправильную дробь. \(\ 5 \cdot 1+3=8\), а знаменатель равен 5. |
| \(\ 2 \frac{1}{4}=\frac{9{4}\) | Замените \(\ 2 \frac{1}{4}\) на неправильную дробь. \(\ 4 \cdot 2+1=9\), а знаменатель равен 4. |
| \(\ \frac{8}{5} \cdot \frac{9}{4}\) | Перепишите задачу на умножение, используя неправильные дроби. |
| \(\ \frac{8 \cdot 9}{5 \cdot 4}=\frac{9 \cdot 8}{5 \cdot 4}\) | Переставьте числители так, чтобы вы увидели дробь с общим множителем. |
| \(\ \frac{9 \cdot 8}{5 \cdot 4}=\frac{9 \cdot 2}{5 \cdot 1}\) | Упростить. \(\ \frac{8}{4}=\frac{8 \div 4}{4 \div 4}=\frac{2}{1}\) |
| \(\ \frac{18}{5}\) | Умножить. |
| \(\ \frac{18}{5}=3 \frac{3}{5}\) | Запишите в виде смешанной дроби. |
\(\ 1 \frac{3}{5} \cdot 2 \frac{1}{4}=3 \frac{3}{5}\)
В последнем примере тот же ответ будет можно найти, если перемножить числители и знаменатели, не удаляя общий множитель. Однако вы получите \(\ \frac{72}{20}\), а затем вам нужно будет еще упростить, чтобы получить окончательный ответ.
Упражнение
\(\ 1 \frac{3}{5} \cdot 3 \frac{1}{3}\)
- \(\ \frac{80}{15}\)
- \(\ 5 \фрак{5}{15}\)
- \(\ 4 \frac{14}{15}\)
- \(\ 5 \frac{1}{3}\)
- Ответить
- Неверно. Вероятно, вы правильно записали оба смешанных числа в виде неправильных дробей. Вы, вероятно, также правильно перемножили числители и знаменатели. Однако эту неправильную дробь еще нужно переписать как смешанное число и упростить.
 Деление \(\ 80 \div 15=5\) с остатком 5 или \(\ 5 \frac{5}{15}\), затем упрощение дробной части, правильный ответ \(\ 5 \frac{ 1}{3}\).
Деление \(\ 80 \div 15=5\) с остатком 5 или \(\ 5 \frac{5}{15}\), затем упрощение дробной части, правильный ответ \(\ 5 \frac{ 1}{3}\). - Неверно. Вероятно, вы правильно записали оба смешанных числа в виде неправильных дробей. Вы наверное тоже правильно перемножили числители и знаменатели, а ответ записали как смешанное число. Однако смешанное число не является самым низким. \(\ \frac{5}{15}\) можно упростить до \(\ \frac{1}{3}\) путем деления числителя и знаменателя на общий делитель 5. Правильный ответ: \(\ 5 \ дробь{1}{3}\).
- Неверно. Это результат сложения двух чисел. Чтобы умножить, запишите каждое смешанное число как неправильную дробь: \(\ 1 \frac{3}{5}=\frac{8}{5}\) и \(\ 3 \frac{1}{3}=\ гидроразрыв{10}{3}\). Затем умножьте числители и умножьте знаменатели: \(\ \frac{8}{5} \cdot \frac{10}{3}=\frac{80}{15}\). Затем запишите полученную неправильную дробь в виде смешанного числа: \(\ \frac{80}{15}=5 \frac{5}{15}\). Наконец, упростите дробную часть, разделив числитель и знаменатель на общий множитель 5.
 Правильный ответ: \(\ 5 \frac{1}{3}\).
Правильный ответ: \(\ 5 \frac{1}{3}\). - Правильно. Сначала перепишем каждое смешанное число в виде неправильной дроби: \(\ 1 \frac{3}{5}=\frac{8}{5}\) и \(\ 3 \frac{1}{3}=\frac {10}{3}\). Затем умножьте числители и умножьте знаменатели: \(\ \frac{8}{5} \cdot \frac{10}{3}=\frac{80}{15}\). Затем запишите в виде смешанной дроби \(\ \frac{80}{15}=5 \frac{5}{15}\). Наконец, упростите дробную часть, разделив и числитель, и знаменатель на общий множитель 5.
- Неверно. Вероятно, вы правильно записали оба смешанных числа в виде неправильных дробей. Вы, вероятно, также правильно перемножили числители и знаменатели. Однако эту неправильную дробь еще нужно переписать как смешанное число и упростить.
Решение задач на умножение дробей и смешанных чисел
Теперь, когда вы знаете, как умножать дробь на другую дробь, на целое число или на смешанное число, вы можете использовать эти знания для решения задач, связанных с умножением и дробными числами. Например, теперь вы можете рассчитать ингредиенты, необходимые для 2 крошек для пирога.
Пример
| 5 чашек крекеров 8 столовых ложек сахара \(\ 1 \frac{1}{2}\) чашек растопленного масла \(\ \frac{1}{4}\) чайная ложка ванили | Рецепт слева рассчитан на 4 коржа. Найдите ингредиенты, необходимые для приготовления только 2 коржей для пирога. Найдите ингредиенты, необходимые для приготовления только 2 коржей для пирога. |
Раствор
| Поскольку рецепт рассчитан на 4 коржа, вы можете умножить каждый из ингредиентов на \(\ \frac{1}{2}\), чтобы найти размеры только для 2 коржей. | |
\(\ 5 \cdot \frac{1}{2}=\frac{5}{1} \cdot \frac{1}{2}=\frac{5}{2}\) Требуется\(\ 2 \frac{1}{2}\) стаканов крекеров. | 5 чашек крекеров Грэма: так как результатом является неправильная дробь, перепишите \(\ \frac{5}{2}\) как неправильную дробь \(\ 2 \frac{1}{2}\). |
\(\ 8 \cdot \frac{1}{2}=\frac{8}{1} \cdot \frac{1}{2}=\frac{8}{2}=4\) Необходимо 4 столовые ложки сахара. | 8 столовых ложек сахара: Это еще один пример умножения целого числа на дробь. |
\(\ \frac{3}{2} \cdot \frac{1}{2}=\frac{3}{4}\) Требуется\(\ \frac{3}{4}\) стакана растопленного сливочного масла. | \(\ 1 \frac{1}{2}\) стаканов топленого масла: нужно умножить смешанное число на дробь. Итак, сначала перепишем \(\ 1 \frac{1}{2}\) как неправильную дробь \(\ \frac{3}{2}\): \(\ 2 \cdot 1+1\), а знаменатель равен 2. Затем перепишите задачу на умножение, используя неправильную дробь вместо смешанного числа. Умножить. |
\(\ \frac{1}{4} \cdot \frac{1}{2}=\frac{1}{8}\) Требуется\(\ \frac{1}{8}\) чайной ложки ванили. | \(\ \frac{1}{4}\) чайная ложка ванили: Здесь вы умножаете дробь на дробь. |
Ингредиенты, необходимые для 2 корок для пирога:
\(\ 2 \frac{1}{2}\) стаканов крекеров
4 столовые ложки сахара
\(\ \frac{3}{4} \) стакан топленого масла
\(\ \frac{1}{8}\) чайная ложка ванили
Часто задача указывает на необходимость умножения на дробь с использованием таких фраз, как «половина», «треть» или «\( \ \frac{3}{4}\) of. »
»
Пример
Стоимость отпуска составляет \(\ \$ 4500\), и вы должны заплатить \(\ \frac{1}{5}\) этой суммы при бронировании поездки. Сколько вам придется заплатить при бронировании поездки?
Раствор
| \(\ 4500 \cdot \frac{1}{5}\) | Вам нужно найти \(\ \frac{1}{5}\) из 4500. «Из» говорит вам умножать. |
| \(\ \frac{4,500}{1} \cdot \frac{1}{5}\) | Замените 4500 неправильной дробью, переписав ее с 1 в знаменателе. |
| \(\ \frac{4,500}{5}\) | Разделить. |
| \(\ 900\) | Упростить. |
Вам нужно будет заплатить \(\ \$ 900\) при бронировании поездки.
Пример
Круговая диаграмма слева представляет дробную часть ежедневной деятельности. Учитывая 24-часовой день, сколько часов тратится на сон? Посещение школы? Принимать пищу? Используйте круговую диаграмму, чтобы определить свои ответы. |
Решение
| \(\ \frac{1}{3} \cdot 24\) = количество часов сна | Сон — это \(\ \frac{1}{3}\) части пирога, поэтому количество часов, потраченных на сон, равно \(\ \frac{1}{3}\) из 24. |
| \(\ \frac{1}{3} \cdot \frac{24}{1}=8\) | Перепишите 24 в виде неправильной дроби со знаменателем 1. |
\(\ \frac{24}{3}=8\) 8 часов сна | Умножение числителей и умножение знаменателей. Упростить \(\ \frac{24}{3}\) до 8. |
| \(\ \frac{1}{6} \cdot 24\) = количество часов, проведенных в школе | Посещение школы составляет \(\ \frac{1}{6}\) круга, поэтому количество часов, проведенных в школе, равно \(\ \frac{1}{6}\) из 24. |
| \(\ \frac{1}{6} \cdot \frac{24}{1}\) | Перепишите 24 в виде неправильной дроби со знаменателем 1. |
\(\ \frac{24}{6}=4\) 4 часов посещения школы | Умножение числителей и умножение знаменателей. Упростите \(\ \frac{24}{6}\) до 4. |
| \(\ \frac{1}{12} \cdot 24\) = количество часов, потраченных на еду | Еда равна \(\ \frac{1}{12}\) пирога, поэтому количество часов, проведенных за едой, равно \(\ \frac{1}{12}\) из 24. |
| \(\ \frac{1}{12} \cdot \frac{24}{1}\) | Перепишите 24 в виде неправильной дроби со знаменателем 1. |
\(\ \frac{24}{12}=2\) 2 часов, потраченных на еду | Умножение числителей и умножение знаменателей.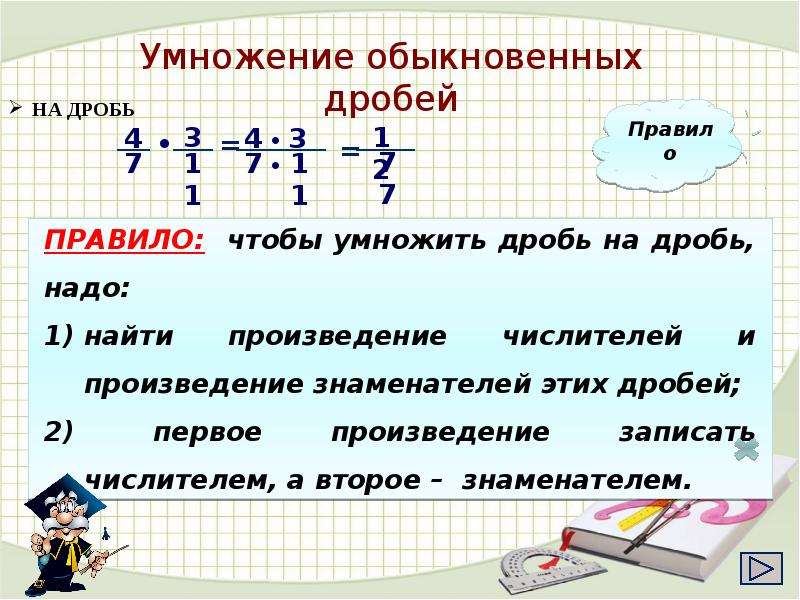 Упростите \(\ \frac{24}{12}\) до 2. Упростите \(\ \frac{24}{12}\) до 2. |
Количество часов:
Сон: 8 часов
посещение школы: 4 часа
прием пищи: 2 часа
упражнения
Нейл купил дюжину (12) яиц. Он использовал \(\ \frac{1}{3}\) яиц на завтрак. Сколько яиц осталось?
- 8
- 4
- 9
- 3
- Ответить
- Правильно. \(\ \frac{1}{3}\) из 12 равно \(\ 4\left(\frac{1}{3} \cdot \frac{12}{1}=\frac{12}{3} =4\справа)\), поэтому он использовал 4 яйца. Поскольку \(\ 12-4=8\), осталось 8 яиц.
- Неверно. \(\ \frac{1}{3}\) от 12 равно 4, но это показывает, сколько яиц использовал Нейл, а не сколько у него осталось. Вам нужно вычесть 4 из 12, чтобы найти количество оставшихся яиц. Правильный ответ 8.
- Неверно. Возможно, вы ошибочно обнаружили, что \(\ \frac{1}{3}\) от 12 равно \(\ \text { 3.





 Правильный ответ: \(\ \frac{1}{4}\).
Правильный ответ: \(\ \frac{1}{4}\). Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac {3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
Убедитесь, что вы умножаете числители и умножаете знаменатели. Умножение двух чисел дает \(\ \frac{15}{6}\), а поскольку \(\ 15 \div 6=2 \mathrm{R} 3\), смешанное число равно \(\ 2 \frac {3}{6}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\). Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).
Дробная часть упрощается до \(\ \frac{1}{2}\). Правильный ответ: \(\ 2 \frac{1}{2}\).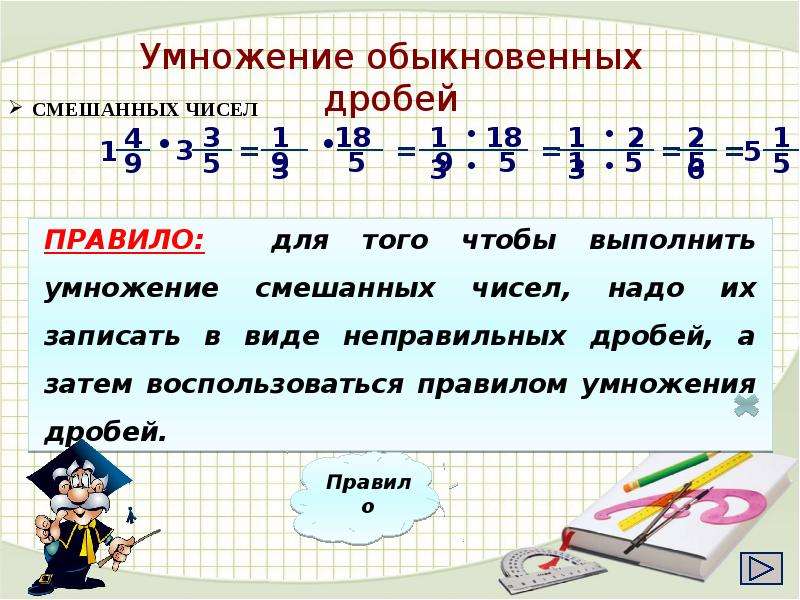 Деление \(\ 80 \div 15=5\) с остатком 5 или \(\ 5 \frac{5}{15}\), затем упрощение дробной части, правильный ответ \(\ 5 \frac{ 1}{3}\).
Деление \(\ 80 \div 15=5\) с остатком 5 или \(\ 5 \frac{5}{15}\), затем упрощение дробной части, правильный ответ \(\ 5 \frac{ 1}{3}\). Правильный ответ: \(\ 5 \frac{1}{3}\).
Правильный ответ: \(\ 5 \frac{1}{3}\).
