Как считать на древних счетах: тренируем мозги
Счёты это вещь, которую уже мало кто помнит. Теперь мир заполонили калькуляторы, ноутбуки и мобильные телефоны. Однако такой давно забытый предмет как счёты очень удобны и нужны людям, о чем сейчас мало кто знает.
История древних счёт
Давным-давно, около 5000 лет назад, в Месопотамии и Древней Греции появилась счетная доска для арифметических вычислении. Она состояла из:
- Рамки
- Поперечной перекладины (планки)
- Спиц, проходящих сквозь перекладину
- Косточек, нанизанных на спицы
На каждой спице было нанизано по пять косточек. Одна косточка находилась над перекладиной(планкой), а четыре под ней.
Такие счеты назывались Абак. Со временем они были усовершенствованы в Китае и Японии и стали назваться Суаньпань и Соробан. Спустя какое-то время Абак стали называть Абакусом. Вместе с Ментальной арифметикой, для которой Абакус является основным инструментом, Абакус пришел в Россию.
Учимся считать на счётах
Ментальная арифметика это уникальный курс для развития умственных способностей и творческого потенциала за счёт вычисления на абакусе. Во время обучения у детей гармонично развиваются оба полушария головного мозга, благодаря чему все школьные предметы даются ребёнку с лёгкостью. Она учит ребенка, как считать на счетах.
Научится считать на счётах абакус не очень сложно. Главное ; это тренироваться каждый день, выполнять домашнее задание и верить в себя. Несмотря на доказанные результаты, некоторые родители сомневаются, стоит ли отдавать ребёнка на ментальную арифметику. Ведь у него большая нагрузка в школе, репетиторы, плюс он ходит на легкую атлетику. Будет ли малыш всё успевать? Прелесть этой методики в том, что она поможет ребёнку быстрее делать домашнее задание, правильно распределять время, сформировать уверенность в себе.
Смысл данной программы ; тренировка головного мозга для максимальной скорости восприятия и обработки информации. На занятиях по ментальной арифметике дети сначала учатся, как считать на счётах абакус, механически перебирая косточки. Потом ученики представляют счёты в уме и пытаются считать на ментальных счётах.
На занятиях по ментальной арифметике дети сначала учатся, как считать на счётах абакус, механически перебирая косточки. Потом ученики представляют счёты в уме и пытаются считать на ментальных счётах.
Учим ребёнка считать на счётах абакус
В школе у ребят развивают в большинстве своём левое полушарие мозга, которое отвечает за логику, речь, мелкую моторику и аналитические операции. Занимаясь же ментальной арифметикой, у ребёнка вместе с левым полушарием одновременно развивается и правое. Последнее ответственно за воображение, образное мышление, фантазию.
Оптимальный возраст для обучения от 5 лет. Существуют курсы и для подростков 13-16 лет. Но лучше начать ходить на занятия, когда ребёнок находится ещё в дошкольном возрасте. Потому что тогда у него мозг очень пластичный и занятия проходят более успешно.
На занятиях по ментальной арифметике мы учим ребенка считать на счётах. Благодаря этой методике у ребёнка развивается воображение. От этого появляется любовь к чтению. Научившись быстро считать, малыш завоюет авторитет в детском саду и школе, что поднимет его в глазах одноклассников и сформирует лидерские качества.
Научившись быстро считать, малыш завоюет авторитет в детском саду и школе, что поднимет его в глазах одноклассников и сформирует лидерские качества.
Преимущества ментальной арифметики для детей
- Формирование мелкой моторики рук за счёт перебирания косточек на абакусе.
- Гармоничное развитие левого и правого полушарий головного мозга за счёт работы на абакусе обоих рук.
- Тренировка зрительной памяти, потому что ребенок проводит в уме сложные арифметические операции.
- Получение такого навыка как быстрый устный счёт. Ребенок сможет решать примеры с многозначными числами быстрее калькулятора.
- Подход к решению любых задач двумя способами: аналитическим и творческим.
- Развитие сосредоточенности, концентрации внимания, образного мышления, воображения, наблюдательности.
- Умение быстро принимать решения и повышение уровня ответственности.
Положительное влияние ментальной арифметики
С помощью абакуса малыш через год-два сможет умножить и делить многозначные числа в уме. Некоторые родители волнуются, а не будет ли мозг их ребенка излишне загружен? Будет ли в нём место для другой полезной информации?
Некоторые родители волнуются, а не будет ли мозг их ребенка излишне загружен? Будет ли в нём место для другой полезной информации?
Бояться не стоит. Ментальная арифметика входит в официальную школьную программу почти во всех учебных заведениях Азии. И как отмечает история, у детей складывается только положительная динамика:
- Усиление зрительной и слуховой памяти;
- Увеличение концентрации внимания;
- Активизация смекалки и интуиции;
- Возникновение самостоятельности и уверенности;
- Формирование нестандартного мышления;
- Получение хорошего высшего образования и престижной работы;
- Изучение иностранных языков;
- Развитие творческих способностей.
Глядя на этот список, становится не совсем ясно, как математика влияет на всё выше перечисленное. Но в этом и есть особенность этой уникальной методики. Вычисления на абакусе помогают сформировать связь между двумя полушариями мозга.
Правое отвечает за:
- интуицию
- образное мышление
- воображение
- способность к творчеству
- понимание подтекста
- ориентацию в пространстве
- музыкальный слух
- обработку материала из нескольких источников сразу
Левое отвечает за:
- речь
- чтение
- письмо
- память
- логику
- рациональное мышление
- числа и символы
- последовательность событий
А совместная деятельность обоих полушария и даёт такой впечатляющий эффект.
Как самостоятельно научить ребёнка считать на абакусе
Для чего нужно домашнее задание? Тренировка мозга поможет детям стать умнее и с каждым уроком считать быстрее.
Начальные три уровня ментальный счет формируется и нет конкретных стандартов. После того, как ученики изучили все формулы и выработали скорость на двух-трехзначных ментальный счет становится необходимым во время контрольных работ и экзаменов, а скорость ментального счета должна быть быстрее чем скорость на соробане или абакусе.
Перед занятием
Необходимо конкретно пояснить детям и родителям, что домашнее задание нужно выполнять ежедневно. Благодаря этому так у них улучшится скорость решения примеров, будет тренироваться мозг, а значит будет результат от ментальной арифметики (память, внимательность, быстрота реакции, концентрация внимания, слуховая память, фотографическая память, творчество, логика, мелкая моторика рук и т.д.).
В отчетах преподаватель обязан отображать сколько примеров выполнил дома за неделю каждый ребенок.
Cчет «Просто»
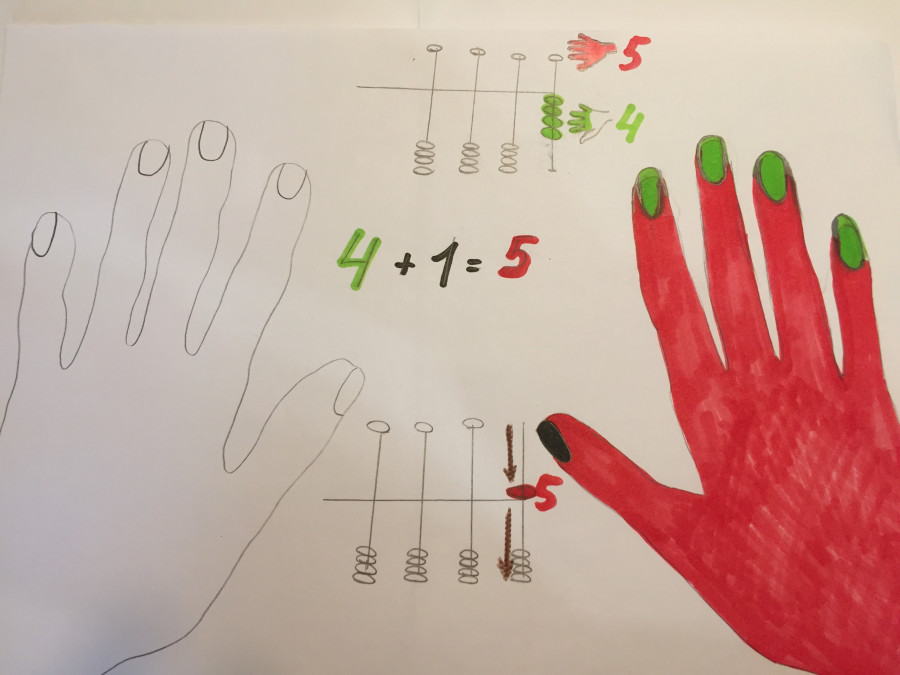
Рисуем на доске «дом числа 5». Просим детей перерисовать этот дом в тетради и написать: «Младшие товарищи. Состав числа 5».
Объяснение: «Дети, это дом, в котором живет число „5“. На каждом этаже живут младшие товарищи. Как вы думаете почему именно эти циферки? Ну давайте я вам объясню, это не простые циферки. Это младшие товарищи. Они будут помогать друг другу в сложных ситуациях как товарищи. Например, у числа „1“ младший товарищ число „4“, у цифры „2“ младший товарищ „3“, и т. д. Сумма младших товарищей равна пяти. Смотрите сами: 1+4=5, 2+3=5 и т.д.».
д. Сумма младших товарищей равна пяти. Смотрите сами: 1+4=5, 2+3=5 и т.д.».
Нужно чтобы каждый ребенок запомнил младших товарищей. Спросите каждого: «кто младший товарищ числа „3“, кто младший товарищ числа „4“ и т.д.».
При объяснении формул младших товарищей напишите, как можно больше примеров на доске и проговаривая показывайте решение на большом абакусе. Обязательно побольше времени уделите на фундаментальные упражнения и решение примеров на большом абакусе. Можно диктовать чуть медленнее, но на следующее занятие скорость диктовки по пройденной теме должна быть быстрой.
Двузначные числа, как решать на абакусе
Двузначные числа необходимо решать на абакусе двумя руками. Объясните ученикам, что так они будут решать примеры быстрее. Рабочие пальцы правой руки большой и указательный, левой руки — средний и указательный, так как ассиметричное решение развивает межполушарные связи.
Концепция старших товарищей и составных формул (микс формулы)
Старшие товарищи
Рисуем на доске «дом числа 10» и просим детей перерисовать дом с надписью: «Старшие товарищи. Состав числа 10».
Состав числа 10».
Объяснение: «Дети, это дом, в котором живет число „10“. На каждом этаже живут старшие товарищи. Как вы думаете почему именно эти циферки? Ну давайте я вам объясню, это не простые циферки. Это старшие товарищи. Они будут помогать друг другу в сложных ситуациях как товарищи. Например, у числа „9“ старший товарищ число „1“, у цифры „8“ младший товарищ „2“, и т. д. Сумма старших товарищей равна десяти. Смотрите сами: 9+1=10, 8+2=10 и т.д.».
Нужно чтобы каждый ребенок запомнил старших товарищей. Спросите каждого: «кто младший товарищ числа „7“, кто младший товарищ числа „6“ и т.д.».
Составные формулы (микс формулы)
В начале объяснения этой темы напишите формулу на доске: «+6 = +10 −5 +1». Дальше говорим: «Ребята, число 6 на абакусе выглядит так: 5 и 1, верно? Шесть — это пять и одна косточка снизу. Мы это все знаем. А чтобы на абакусе 5 прибавить 6, мы используем микс формулу, которая написана на доске (также на доске напишите пример: 5 +6 = _____). Смотрите: „+6 = +10 −5 +1“. Давайте я покажу как решить такой пример на большом абакусе, а вы повторяйте за мной в воздухе. Чтобы к 5 прибавить 6, мы левой рукой прибавляем 10, а правой делаем одновременно −5 +1. Сколько получилось? 11! Правильно! (дописываем на доске ответ 5 +6=11, и решаем на большом абакусе примеры: 6+6, 7+6, 8+6, 15+6, 16+6, 17+6, 18+6, 25+6 и т. д. Дети повторяют в воздухе за учителем. Сначала пример пишем на доске потом только показываем решение на большом абакусе. Затем все дети делают ФУ на микс формулы под диктовку учителя:5+6, 15+6, 26+6, 17+6, 8+6 и так далее. После ФУ по два-три ученика выходят решать на большом абакусе).
Смотрите: „+6 = +10 −5 +1“. Давайте я покажу как решить такой пример на большом абакусе, а вы повторяйте за мной в воздухе. Чтобы к 5 прибавить 6, мы левой рукой прибавляем 10, а правой делаем одновременно −5 +1. Сколько получилось? 11! Правильно! (дописываем на доске ответ 5 +6=11, и решаем на большом абакусе примеры: 6+6, 7+6, 8+6, 15+6, 16+6, 17+6, 18+6, 25+6 и т. д. Дети повторяют в воздухе за учителем. Сначала пример пишем на доске потом только показываем решение на большом абакусе. Затем все дети делают ФУ на микс формулы под диктовку учителя:5+6, 15+6, 26+6, 17+6, 8+6 и так далее. После ФУ по два-три ученика выходят решать на большом абакусе).
Теперь посмотрите какую формулу я написала на доске: +7 = +10 −5 +2. Знаете почему +2? Потому что число 7 на счётах — это 5 плюс 2. Все поняли? Молодцы! Давайте решим пример: 5+7=_____. Чтобы решить такой пример нам поможет микс формула. Давайте я покажу как решить такой пример на большом абакусе, а вы повторяйте за мной в воздухе. Чтобы к 5 прибавить 7, мы левой рукой прибавляем 10, а правой делаем одновременно −5 +2.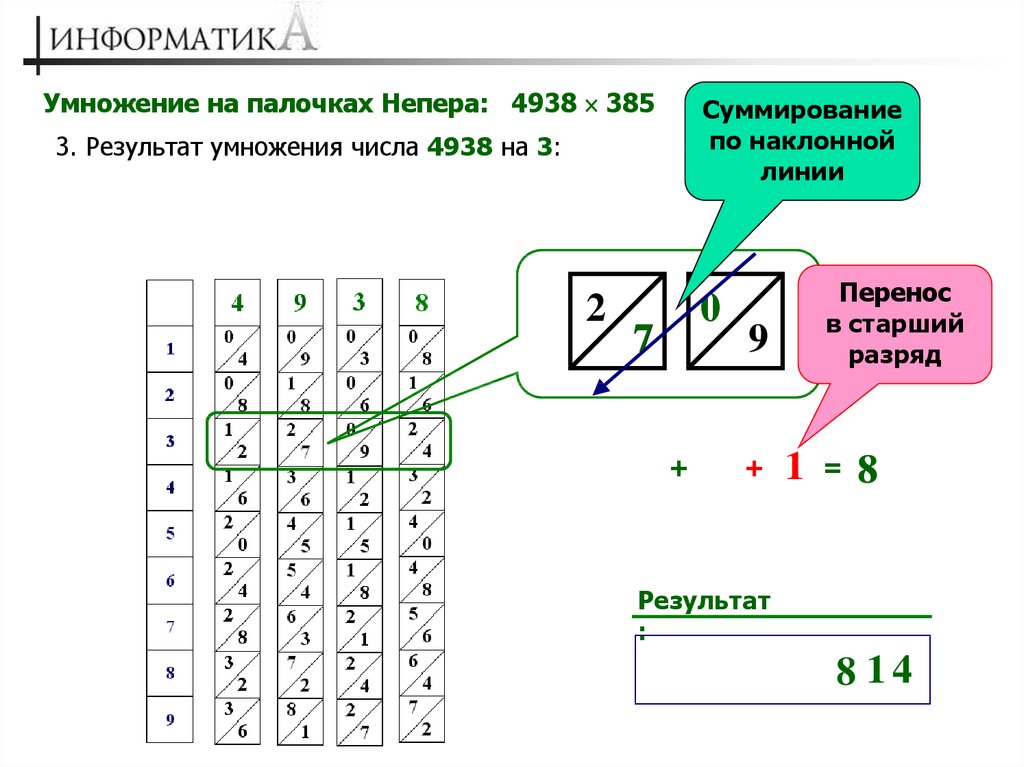 Сколько получилось? 12! Правильно! Теперь я покажу как решить такой пример: 6+7, повторяем за мной в воздухе (показываем несколько примеров на доске и большом абакусе. Следим, чтобы дети повторяли в воздухе. Затем под диктовку учителя ФУ: 5+7, 6+7, 7+7, 15+7, 16+7, 17+7 и т. д. После этого по два-три ученика на большом абакусе решаем примеры)».
Сколько получилось? 12! Правильно! Теперь я покажу как решить такой пример: 6+7, повторяем за мной в воздухе (показываем несколько примеров на доске и большом абакусе. Следим, чтобы дети повторяли в воздухе. Затем под диктовку учителя ФУ: 5+7, 6+7, 7+7, 15+7, 16+7, 17+7 и т. д. После этого по два-три ученика на большом абакусе решаем примеры)».
Аналогично обучаем формуле +8 = +10 −5 +3. Почему +3? Потому что 8 на счётах — это 5 плюс 3. Также и формула +9 = +10 −5 +4, так как 9 на счётах — это 5 плюс 4.
На минус микс формулы нужно обратить особое внимание, так как формулы на минус иногда воспринимается сложнее:
— 6 = −10 +5 −1
— 7 = −10 +5 −2
— 8 = −10 +5 −3
— 9 = −10 +5 −4
1.11 Экзамен ученика после каждого уровня
После завершения каждого уровня ученики сдают экзамен.
Преподаватель фиксирует время и записывает результаты.
План проведения экзамена:
1) За 30 минут до конца урока раздаем экзаменационные листочки детям. Ученики пишут имена, фамилии и дату на экзаменационных листочках.
2) Затем ученики записывают состав чисел 5 и 10.
3) Повторяем правила диктанта и правило одинаковых знаков. Засекаем время и начинаем диктант. Диктовать нужно чуть медленнее чем на занятиях. Примеры должны быть на все пройденные темы.
4) Ученики одновременно под команду учителя (засекаем время на секундомере) начинают решать примеры. Заранее нужно сообщить детям, что экзамен проверяется на ошибки и на скорость.
Сдавшим экзамен считается тот ученик, который решил примеры за нужное время и с количеством ошибок менее 20%. Время, за которое ученик должен решить примеры экзамена, зависит от возраста ученика. Нормативы устанавливаются каждым центром индивидуально.
Пересдача экзамена допустима один раз. При провале экзамена если причиной провала было отсутствие скорости, то ученик может продолжить обучение следующего уровня ментальной арифметики вместе со своей группой.
При провале экзамена если причиной провала было большое количество ошибок, отсутствие скорости, незнание формул, пропуски и так далее, то ученику предлагают заново пройти первый уровень с другой группой или присоединится к другой группе, которая проходит ту, тему с которой этот ученик стал отставать.
Связь с родителями при обучении
Преподаватель должен после каждого урока высылает бланк урока или результаты урока с доски с показателями успеваемости учеников и домашнее задание родителям учеников.
Универсальный поурочный план
Дополнительные развивающие игры на занятиях используются на усмотрение преподавателя.
С учениками 4–6 лет желательно использовать раскраски, прописи и другие игры на развитие мелкой моторики, памяти, логики и т. д. Ученикам 4–6 лет следует делать переменку 5 минут каждые 30 минут.
Если группа быстро усваивает программный материал, необходимо давать материал быстрее, при этом отработка всех ФУ и решение примеров сохраняются.
2. Материал для обучения преподавателей счету на абакусе. Сложение и вычитание. Умножение и деление
Сложение и вычитание
В youtube большое количество видеоуроков по ментальной арифметике. Перед решением примеров на отработку формул, рекомендую изучить теорию. Также обучиться формулам бесплатно и набрать скорость в счете на абакусе можно при помощи приложения для Android Simple Soroban (в отличие от других аналогичных приложений в Simple Soroban можно одновременно перемещать несколько косточек, что очень важно в технике пальцев).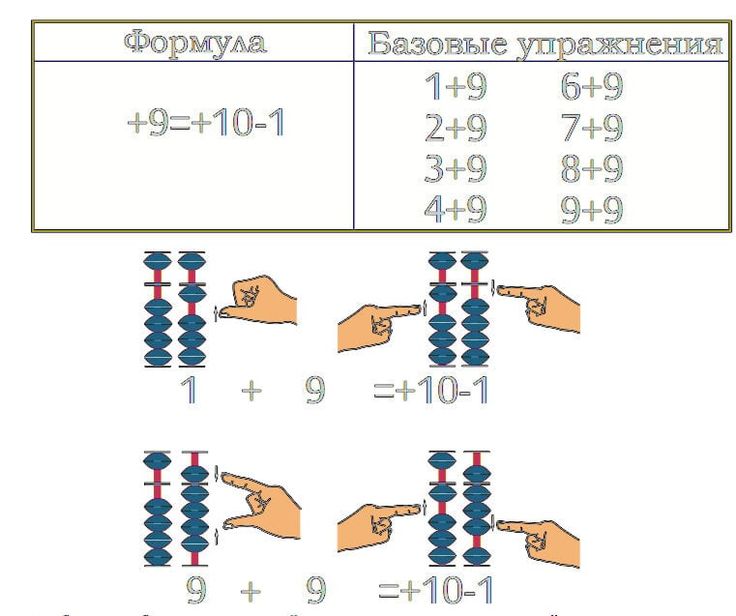 Формулы для решения примеров на абакусе до 5 называют младшими товарищами, до 10 старшими товарищами, составные формулы микс формулами. Некоторые центры называют их друзьями, семьей и т. д. Суть не в названии. За 2000 лет формулы не изменились. Главное их понять и набрать скорость как при решении на счётах, так и в ментальном счете.
Формулы для решения примеров на абакусе до 5 называют младшими товарищами, до 10 старшими товарищами, составные формулы микс формулами. Некоторые центры называют их друзьями, семьей и т. д. Суть не в названии. За 2000 лет формулы не изменились. Главное их понять и набрать скорость как при решении на счётах, так и в ментальном счете.
План обучения преподавателей:
— прямой счет на однозначных числах
— младшие товарищи
— старшие товарищи
— двузначные числа
— составные формулы
— переход на 50, 100
— трехзначные
— подготовка к умножению и делению, умножение и деление на абакусе.
Фундаментальные упражнения на отработку составных формул.
+6=-5+1+10
5+6, 6+6, 7+6, 8+6, 15+6, 16+6, 17+6, 18+6, 25+6, 26+6, 27+6, 28+6, 35+6, 36+6, 36+6, 37+6, 38+6
+7=-5+2+10
5+7, 6+7, 7+7, 15+7, 16+7, 17+7, 25+7, 26+7, 27+7, 35+7, 36+7, 37+7
+8=-5+3+10
5+8, 6+8, 15+8, 16+8, 25+8, 26+8, 35+8, 36+8
+9=-5+4+10
5+9, 15+9, 25+9, 35+9, 55+9, 65+9, 75+9, 85+9
— 6=-10+5—1
11–6, 12–6, 13–6, 14–6, 21–6, 22–6, 23–6, 24–6, 31–6, 32–6, 33–6, 34–6, 41–6, 42–6, 43–6, 44–6
— 7=-10+5—2
12–7, 13–7, 14–7, 22–7, 23–7, 24–7, 32–7, 33–7, 34–7, 42–7, 43–7, 44–7
— 8=-10+5—3
13–8, 14–8, 23–8, 24–8, 33–8, 34–8, 43–8, 44–8, 63–8, 64–8, 73–8, 74–8, 83–8, 84–8, 93–8, 94–8
— 9=-10+5—4
14–9, 24–9, 34–9, 44–9, 64–9, 74–9, 84–9, 94–9
Фундаментальные упражнения на отработку формул старших товарищей (минус) −9=-10+1
10–9, 11–9, 12–9, 13–9, 15–9, 16–9, 17–9, 18–9, 20–9, 21–9, 22–9, 23–9, 25–9, 26–9, 27–9, 28–9
— 8=-10+2
10–8, 11–8, 12–8, 20–8, 21–8, 22–8, 30–8, 31–8, 32–8, 40–8, 41–8, 42–8
— 7=-10+3
10–7, 11–7, 20–7, 21–7, 30–7, 31–7, 40–7, 41–7, 60–7, 61–7, 70–7, 71–7, 80–7, 81–7, 90–7, 91–7
— 6=-10+4
10–6, 15–6, 20–6, 25–6, 30–6, 35–6, 40–6, 45–6, 60–6, 65–6, 70–6, 75–6, 80–6, 85–6, 90–6, 95–6
— 5=-10+5
10–5, 11–5, 12–5, 13–5, 14–5, 20–5, 21–5, 22–5, 23–5, 24–5, 30–5, 31–5, 32–5, 33–5, 34–5, 41–5, 42–5,
43–5, 44–5
— 4=-10+6
10–4, 11–4, 12–4, 13–4, 20–4, 21–4, 22–4, 23–4, 30–4, 31–4, 32–4, 33–4, 40–4, 41–4, 42–4, 43–4
— 3=-10+7
10–3, 11–3, 12–3, 20–3, 21–3, 22–3, 30–3, 31–3, 32–3, 40–3, 41–3, 42–3
— 2=-10+8
10–2, 11–2, 20–2, 21–2, 30–2, 31–2, 40–2, 41–2, 60–2, 61–2
— 1=-10+9
10–1, 20–1, 30–1, 40–1, 60–1, 70–1, 80–1, 90–1
Переход через 50
+50
41+9
42+9 42+8
43+9 43+8 43+7
44+9 44+8 44+7 44+6
45+9 45+8 45+7 45+6 45+5
46+9 46+8 46+7 46+6 46+5 46+4
47+9 47+8 47+7 47+6 47+5 47+4 47+3
48+9 48+8 48+7 48+6 48+5 48+4 48+3 48+2
49+9 49+8 49+7 49+6 49+5 49+4 49+3 49+2 49+1
— 50
50–9 50–8 50–7 50–6 50–5 50–4 50–3 50–2 50–1
51–9 51–8 51–7 51–6 51–5 51–4 51–3 51–2
52–9 52–8 52–7 52–6 52–5 52–4 52–3
53–9 53–8 53–7 53–6 53–5 53–4
54–9 54–8 54–7 54–6 54–5
55–9 55–8 55–7 55–6
56–9 56–8 56–7
57–9 57–8
58–9
Переход через 100
+100
91+9
92+9 92+8
93+9 93+8 93+7
94+9 94+8 94+7 94+6
95+9 95+8 95+7 95+6 95+5
96+9 96+8 96+7 96+6 96+5 96+4
97+9 97+8 97+7 97+6 97+5 97+4 97+3
98+9 98+8 98+7 98+6 98+5 98+4 98+3 98+2
99+9 99+8 99+7 99+6 99+5 99+4 99+3 99+2 99+1
— 100
100–9 100–8 100–7 100–6 100–5 100–4 100–3 100–2 100–1
101–9 101–8 101–7 101–6 101–5 101–4 101–3 101–2
102–9 102–8 102–7 102–6 102–5 102–4 102–3
103–9 103–8 103–7 103–6 103–5 103–4
104–9 104–8 104–7 104–6 104–5
105–9 105–8 105–7 105–6
106–9 106–8 106–7
107–9 107–8
108–9
Умножение и деление на счётах
В ютубе имеется большое количество обучающих видео роликов по умножению и делению на счётах. Рекомендуется просмотреть их перед тем, как обучаться по книге.
Рекомендуется просмотреть их перед тем, как обучаться по книге.
Ментальный счет можно тренировать параллельно обучаясь умножению и делению, либо после того как обучились этому. На усмотрение преподавателя в зависимости от успеваемости группы. Нормативы тоже зависят от успеваемости учеников. В некоторых учебниках уже указаны нормативы.
Умножение на счётах основано на обычном умножении 7чисел. Ученики должны знать таблицу умножения наизусть перед тем, как начнут решать примеры на умножение на счётах.
Умножение однозначных (1дх1д) — это обычная таблица Пифагора. 2дх1д
1 пример
23×4. Точка отсчета находится примерно в середине абакуса. Имеем три цифры: 2,3,4, значит ответ откладываем на трех спицах. Откладываем слева направо.
1 действие — десяток первого множителя умножаем на другой множитель (на единицу):
2×4=08.
Правило: ЕСЛИ ОТВЕТ ОДНОЗНАЧНЫЙ, ТО ВОСПРИНИМАЕМ ЕГО КАК ДВУЗНАЧНОЕ, МЕНТАЛЬНО ПРЕДСТАВЛЯЯ ПЕРЕД НИМ 0.
На спицах слева направо откладываем 08.
Если результат откладываем на 3 спицах, в умножении откладывать нужно слева направо, значит 08 откладываем на первой и второй спицах слева, то есть на сотнях и десятках.
2 действие — единицу первого множителя умножаем на другой множитель (на единицу).
3×4=12
Откладываем 12, на второй и третьей спицах слева (на десятках и единицах).
Ответ: 92.
2 пример
65×7
— 6×7=42, откладываем на сотнях и десятках.
— 5×7=35, откладываем на десятках и сотнях.
Ответ: 455.
2дх2д
73×45
В примере 4 цифры, значит откладываем решение на 4 спицах.
— 7×4= 28 умножаем десяток одного множителя на десяток другого множителя и откладываем на 1 и 2 спицах слева направо, то есть на тысячах и сотнях.
— 7×5=35 умножаем десяток первого множителя на единицу второго множителя и откладываем на 2 и 3 спицах, то есть на сотнях и десятках.
— 3×4=12 умножаем единицу первого множителя на десяток второго множителя и откладываем на 2 и 3 спицах, то есть на сотнях и десятках.
— 3×5=15 умножаем единицу первого множителя на единицу другого множителя и откладываем на 3 и 4 спицах, то есть на десятках и единицах..
Ответ: 3285.
3дх2д
926×52
В примере 5 цифр, значит откладываем результат на 5 спицах слева направо.
— 9×5=45 умножаем сотню первого множителя на десяток второго множителя и откладываем на 1 и 2 спицах слева направо, то есть на десятках тысячах и на тысячах.
— 9×2=18 умножаем сотню первого множителя на единицу второго множителя и откладываем на 2 и 3 спицах слева направо, то есть на тысячах и на сотнях.
— 2×5=10 умножаем десяток первого множителя на десяток второго множителя и откладываем на 2 и 3 спицах слева направо, то есть на тысячах и сотнях.
— 2×2=4 умножаем десяток первого множителя на единицу второго множителя и откладываем на 3 и 4 спицах слева направо, то есть на сотнях и десятках.
— 6×5=30 умножаем единицу первого множителя на десяток второго множителя и откладываем на 3 и 4 спицах слева направо, то есть на сотнях и десятках.
— 6×2=12 умножаем единицу первого множителя на единицу второго множителя и откладываем на 4 и 5 спицах слева направо, то есть на десятках и единицах.
Решение более сложных примеров на умножение на счётах является аналогичным. Чтобы запомнить алгоритм откладывания ответа на абакусе, нужна практика и скорость.
Деление на абакусе
Само решение примера выполняется справа от точки отсчета (область решения). Результат откладывается слева от точки отсчета (область ответа).
Решение примеров без остатка
1 пример.
8816:8
Откладываем справа от точки отсчета 8816
1 действие — делим тысячи (8) из делимого делим на делитель, то есть на 8.
8:8=1. В области решения нужно отразить результат. 8×1=8, убираем цифру 8 из области решения. Остается 816. В область ответа откладываем 1 (на тысячах).
2 действие. Осталось 816.. Делим сотни (8) из делимого на делитель, то есть 8 на 8.
8:8=1. В области решения нужно отразить результат. 8×1=8, убираем цифру 8 из области решения. Остается 16. В область ответа откладываем 1 (на сотнях).
Остается 16. В область ответа откладываем 1 (на сотнях).
3 действие. Осталось 16. Пробуем десяток из делимого разделить на делитель, 1:8, не делится (значит на десятках в области ответа будет 0), значит пробуем весь оставшийся ответ разделить на делитель.
16:8=2. В области решения нужно отразить результат. 8×2=16, значит, убираем цифру 16 из области решения. В область ответа откладываем 2 (на единицах).
Ответ: 1102
2 пример.
8145:9
Откладываем в области решения 8145. Так как 8 не делится на 9, то берем 81.
— 81:9 =9
В области решения чистим 81, так как 9×9=81. В области ответа откладываем 9 на сотнях.
— так как 4 на 9 не делится, то берем 45, а на десятках в области ответа представляем 0.
45:9=5
В области решения чистим 45, так как 9×5=45. В области ответа откладываем 5 на единицах.
Ответ: 905
Решение примеров с остатком
1 пример.
9:4
Откладываем в области решения 9
Берем по 2, 4×2=8. 9—8=1. В области решения от 9 отнимаем 8. Остаток 1. В области ответа откладываем 2.
9—8=1. В области решения от 9 отнимаем 8. Остаток 1. В области ответа откладываем 2.
Остаток 1 не делится на 4. Ментально представляем 10 вместо 1, и ставим ментально запятую в области ответа после 2.
В области ответов есть 10, пробуем 10 делить на 4. Берем по 2. 2×4=8. Там же от 10 отнимаем 8, остается 2. Также в области ответа откладываем 2.
Остаток 2 не делится на 4, представляем 2 как 20 и пробуем делить на 4. Берем по 5. 4×5=20. В области решения отнимаем 20. В области ответа откладываем 5. Ответ 2.25.
Попробуйте сами решить аналогичные примеры:
6:5
4:3
5:2
5:4
7:4
3:2
7:3
8:3
2 пример.
255:55
— 255:55 берем по 4. 55×4=220. 255—220=35
— 35 на 55 не делится, ментально ставим запятую после 4 и после 35 представляем 0. 350:55 берем по 6. 55×6=330. 350—330=20.
— 20 на 55 не делится, 200 делим на 55. берем по 3. 55×3=165. 200—165=35 остаток.
Ответ: 4.63
3 пример.
314:49
— Берем по 6. 49×6=294. 314—294=20
49×6=294. 314—294=20
— 20 не делится на 49, ментально ставим запятую после 6 и 0 после 20.
49×4=196. 200—196=4
Ответ округляем до десятых: 6.4
Решение более сложных примеров на деление на абакусе является аналогичным. Чтобы запомнить алгоритм откладывания ответа на абакусе, нужна практика и скорость
Удачи Вам!
Как использовать счеты для основных математических операций
Знаете ли вы, что использование счетов может улучшить интеллект вашего ребенка?
Согласно исследованиям, использование счетов может улучшить навыки решения проблем у детей, воздействуя на их интеллект.
Помимо навыков решения задач, использование счетов в раннем возрасте дает больше когнитивных преимуществ.
Но, полагаю, для вас это не новая информация. Это?
На самом деле, большинство из нас знают, что счеты обладают невероятными преимуществами, но лишь немногие из нас знают, как научить детей играть на счетах.
Уважаемые родители, я понимаю вашу озабоченность. Поэтому здесь я собираюсь объяснить, как использовать счеты для решения основных математических операций.
Как использовать абакус?
1. Подсчет
2. Преподавание значения места
3. Представьте большее число
4. Дополнение
5. Вычитание
6. Умножение
7. Дивизион
О чем нужно помнить, обучая детей абакусу
Викторина: проверьте, что вы узнали
Заключение
Как пользоваться счетами?
Счеты можно использовать по-разному в зависимости от того, что вы пытаетесь выполнить. Эта замечательная счетная рамка имеет множество применений: от представления чисел ребенку до извлечения кубических корней.
Эта замечательная счетная рамка имеет множество применений: от представления чисел ребенку до извлечения кубических корней.
Здесь я расскажу о счетах, обычно используемых в школах. Я расскажу вам, как пользоваться счетами шаг за шагом.
Во-первых, я расскажу вам, как научить вас считать и расставлять значения с помощью счетов. Затем я объясню, как выполнять основные математические операции, такие как сложение, вычитание, умножение, деление.
1. Счет
Согласно нескольким исследованиям, использование счетов показало значительные результаты в когнитивных функциях и нервной системе. Поэтому в настоящее время счеты широко используются в различных школах – дошкольных учреждениях, детских садах, начальных школах, школах для слабовидящих детей.
И какое самое популярное использование счетов в этих школах? Это , считая .
Итак, разберемся как научиться считать на счетах .
Счет от 1 до 10 на AbacusПошаговый процесс
- Сначала расположите бусины с левой стороны счетов.

- Теперь отделите по одной бисерине в каждом ряду и продвиньте ее в правый угол.
- Далее считайте бусины одну за другой. Так как в каждом ряду по одной бисерине, общее количество будет десять.
Дорогой читатель, это один из методов, который вы можете использовать, чтобы познакомить вашего маленького ребенка со счетом на счетах.
Хотите знать, каковы преимущества Abacus?
Узнайте, как счеты влияют на рост и обучение, улучшая когнитивное развитие.
Прочитать
На обычных счетах, которые используются в школах и дома, 100 бусин. Вы можете научить ребенка считать, перебирая бусины одну за другой.
Счет от 1 до 100 на счетахПошаговый процесс
- Перед началом счета сдвиньте все бусины влево.
- Теперь начните сдвигать по 1 бусине в первом ряду слева направо.
- Продолжайте считать, пока не закончатся бусины и счет не будет 10.
- Затем повторите тот же процесс, чтобы сосчитать от 11 до 20 во второй строке, от 20 до 30 в третьей строке и так далее.

- Продолжайте считать ряд за рядом, пока не дойдете до последнего и не получите 100.
Это самый традиционный и распространенный метод обучения счету на счетах. Кроме того, это самый эффективный способ запомнить числа.
Если вашему малышу все еще трудно считать, посмотрите это видео, чтобы помочь ему понять подсчет чисел в шаблонах.
Узнайте о различных частях счетов и их использованииПрочтите Что такое Абакус , чтобы узнать.
Узнать сейчас
2. Обучение разрядным значениям
Я понимаю, что обучение разрядным значениям может быть одним из самых сложных уровней в математике для начинающих. Но, не беспокойтесь больше! Если вы умеете пользоваться счетами, ваша проблема решена.
Но, не беспокойтесь больше! Если вы умеете пользоваться счетами, ваша проблема решена.
Счеты – самый эффективный инструмент для обучения расстановке знаков . Поэтому предлагаю вам попробовать счетную рамку.
Метод 1
В первую очередь необходимо объяснить ребенку, что 10 бусинок в единичном ряду = 1 бусина в десяточном ряду (на счетах).
Понимание значений мест на счетахПошаговый процесс
- Начните с перемещения 10 бусин вправо в последнем ряду (как показано на первых счетах на рисунке). Теперь попросите ребенка сосчитать.
- Далее, оставьте все бисерины слева, но только одну бисеринку справа в предпоследнем ряду, т.е. в десятом ряду.
- Теперь объясните, почему 10 бисерин в единичном ряду равны 1 бисеринке в десятом ряду. Обращайтесь к картинке при объяснении.
- Далее расположите 10 бисерин в 10 рядов и покажите, как 10 десятков становятся 1 сотней.

Воспользуйтесь счетной рамкой и следуйте описанным выше методам. Уверена, ваш ребенок очень скоро поймет, как 10 бисерин в сотом ряду = 1 бисерина в тысячном ряду.
Метод 2
Пошаговый процесс
- Начните с последней строки. Объясните ребенку, что последний ряд обозначает единицы – 1, 2, 3… и так далее.
- Второй ряд обозначает 10, 20, 30 и т. д.
- Третий ряд соответствует 100, 200, 300, 400 и т. д.
- Таким образом, по мере продвижения вверх значение позиции продолжает увеличиваться, пока мы не достигнем 5-й строки снизу, которая является десятичной строкой.
- Как показано на рисунке, верхние ряды также соответствуют одинаковым разрядным значениям. Верхний ряд — это ряд единиц, следующий — ряд десятков, третий ряд — ряд сотых, а четвертый ряд — ряд десятитысячных.
Уважаемые читатели, помните, вы можете изменить разрядность строк по своему усмотрению.
Например, , если вы представляете 1 миллион на счетах, вам нужно отказаться от десятичной строки и продолжать увеличивать разрядные значения строк, пока не достигнете 7-й строки снизу.
Тем не менее, вы должны следовать приведенной выше системе разрядов на счетах для решения основных математических операций. Почему? Потому что это удобно и просто для детей.
Идеальный возраст для изучения счетов — 3 года.Хотите знать почему? Прочтите Какой возраст подходит для Abacus , чтобы узнать.
Прочитать
3. Представлять большее число
Как только вы решите, что ваш ребенок понимает разрядные значения, следующим шагом будет научить его представлять большие числа на счетах.
Пример: представить 58 на счетах .
Пошаговый процесс
- W вторая цифра стоит в разряде десятков. 5, верно? Итак, на десятый ряд (предпоследний ряд) набираем 5 бисеринок влево.

- Затем спросите их о цифре на месте единиц. Затем натяните 8 бисерин первого ряда (нижний ряд) влево. Вот вам и 58 на счетах.
Когда ваш ребенок разберется со значениями разрядов, попросите его представлять тысячи и миллионы дальше.
Попробуйте представить 50043024 на Abacus .
Сначала преобразуйте число в слова; 50043024 — это пятьдесят миллионов сорок три тысячи двадцать четыре. Если вам это трудно, просто постарайтесь помнить о разрядности строк.
Корни Abacus восходят к 27 веку до н.э.
Хотите узнать больше? Прочтите «Историю абака», чтобы узнать.
Прочитать
4. Дополнение
Знаете ли вы, что абаки используются в различных программах развития ума?
Да, вы правильно прочитали. Использование абаки показало значительные результаты для программ обучения умственной арифметике.
Дорогой читатель, хотя сложение кажется простой математической операцией, на самом деле это ступенька к обучению сложным математическим вычислениям в уме.
Итак, давайте продолжим и научимся пользоваться счетами для сложения.
Метод 1
Начнем с самых простых задач на сложение. Допустим, мы добавляем 2+2.
2+2=4 на счетахПошаговый процесс
- Начните с перемещения всех бусин влево.
- Теперь возьмите две бусины первого ряда и продвиньте их вправо.
- Затем попросите ребенка повторить тот же шаг во втором ряду. Что у нас есть?
- У нас есть 4 бусины.
- Это традиционный, но самый простой метод сложения на счетах.
- Вы можете попробовать это, если ваш ребенок дошкольник или в детском саду.
«Метод 10» — это стратегия сложения , выполняемая на счетах. Это очень важно, потому что это один из первых шагов к изучению ментальной арифметики.
Давайте рассмотрим пример. Допустим, вы хотите к добавить 9 + 4 .
Пошаговый процесс
- Итак, сначала расположите 4 и 9 бисерин (справа) в первых двух рядах счетной рамки.

- Затем возьмите одну бисеринку из 4-х бисеринового ряда и продвиньте ее влево, добавляя еще одну бисеринку в 9-й ряд.бисерный ряд. Что происходит?
- 9 бусин становятся полными 10, а 4 становятся 3.
- Вот как вы можете научить своего ребенка 9 + 4 = 10 + 3 = 13.
После того, как ваш ребенок несколько раз попрактикуется в этом методе, предложите ему мысленно представить бусинки. Вы также можете дать им задачу для решения, не используя бусины.
Я привел пример для детей от 3 до 6 лет. Вы можете повысить уровень в соответствии со стандартом вашего ребенка.
Чтобы понять этот метод, попробуйте добавить 7+8 .
Метод двух пятерок: 7+8Пошаговый процесс
- Начните с расположения 7 и 8 бисерин в первых двух рядах.
- Как только вы это сделаете, разделите первые 5 бисерин каждого ряда, чтобы получилось две 5 и получилось 10.
- Теперь оставшиеся бусины складываются в 5, что дает 15.

Попробуем к добавить 56+27.
Пошаговый процесс
- Начните с 56 на счетах, что означает 5 бусин в десятом ряду и 6 бусин в единичном ряду.
- Далее нам нужно прибавить 27. Итак, спросите у изучающего счеты , что стоит на десятом месте? Это 2, поэтому в десятом ряду добавляем 2 бисерины.
- Теперь начинаем прибавлять по 7 бисеринок в одном ряду. Итак, продолжайте нажимать бусины слева направо в единичном ряду.
- После добавления 4 бисерин, когда в первом ряду закончились бисерины, сдвиньте все бисерины влево.
- Взамен вы можете добавить 1 бисерину в ряд десятков. (Потому что 10 бисерин в единичном ряду = 1 бисерина в десятом ряду.)
- Теперь сдвинем оставшиеся 3 бисерины влево в единичном ряду.
- С 8 бисеринами в десятом ряду и 3 бисеринами в единичном ряду, ответ 83
Попробуем к добавить 789+105.
Пошаговый процесс
- Начните с представления 789 на счетах, что означает 7 бусин в сотых рядах, 8 бусин в десятых рядах и 9бисер в одноряд.
- Далее нам нужно прибавить 105. Итак, спросите ученика, изучающего счеты, о цифрах и их разрядах.
- Теперь прибавляем 1 бисеринку в сотом ряду, потому что в 105-м ряду 1 на сотом месте.
- Мы не добавляем ни одной бусины слева направо в десятом ряду, потому что это 0 на десятом месте в числе 105.
- Теперь, так как 5 на месте единиц, нам нужно добавить 5 бисерин в единичном ряду.
- После добавления 1 бисерины, когда у вас закончились бисерины в первом ряду, сдвиньте все бисеринки влево.
- Взамен добавьте 1 бисеринку в десятый ряд. (Потому что 10 бисерин в единичном ряду = 1 бисерина в десятом ряду.)
- Теперь сдвинем оставшиеся 4 бисерины влево в единичном ряду.
- С 8 бисеринами в сотом ряду, 9 бисеринами в десятом ряду и 4 бисеринами в первом ряду, ответ 894.

5. Вычитание
Всегда начинайте с обучения детей вычитанию однозначных чисел на счетах. Попробуем 8-5.
Вычитание одной цифрыПошаговый процесс
- Сначала сдвиньте все бусины первого ряда влево.
- Затем попросите ребенка сосчитать 8 бусин и сдвиньте их вправо.
- Пока мы вычитаем 5, попросите ребенка отсчитать 5 бусинок из 8 и отодвинуть их влево.
- У нас осталось 3 бисерины; следовательно, ответ равен 3.
Допустим, мы пытаемся решить 67-32.
Вычитание двузначных чисел на счетахПошаговый процесс
- Сначала начните с изображения 67 на счетах: 6 бусин в ряду десятков и 7 бусин в ряду единиц.
- Далее нужно минус 32. Так как 3 стоит на разряде десятков, то отодвиньте 3 бисерины из ряда десятков.
- На месте единиц у нас 2. Итак, наденьте 2 бусинки справа налево на единичный ряд .

- Теперь посчитайте остальные бусины, и вы получите ответ.
Маленьким детям часто трудно научиться вычитанию. Если ваш малыш тоже борется с этим, вы можете попробовать метод, описанный выше, чтобы научить его вычитать двузначные числа.
Попробуйте решить 653-159 на Abacus .
Трехзначное вычитание на счетахПошаговый процесс
- Сначала начните с представления 653 на счетах: 6 бусин в сотом ряду, 5 бусин в десятом ряду и 3 бусины в однорядные.
- Далее нужно вычесть 159. Так как 1 стоит на разряде десятков сотого ряда, то отодвиньте 1 бисеринку справа налево в сотом ряду.
- В разряде десятков у нас 5. Итак, наденьте все 5 бусинок справа налево на десятый ряд .
- Аналогично нужно набрать 9 бисеринок справа налево в единичном ряду.
- Однако после того, как вы переместите 3 бусины, когда у вас закончатся бусины, вам нужно обменять 1 бусину в десятом ряду на 10 бусинок справа в единичном ряду.

- Но, как видите, в десятом ряду бусинок нет. Итак, переходим к сотому ряду и сдвигаем 1 бисеринку влево, чтобы поменять 10 бисерин в десятом ряду.
- Теперь можно сдвинуть 1 бисеринку справа налево в десятом ряду и набрать 10 бисерин в единичном ряду.
- Нам нужно вычесть всего 9 бисерин. Так как мы уже убавили 3 бисерины, теперь пришло время убавить еще 6 бисерин, оставив только 4 бисеринки в первом ряду.
- Наконец, у вас есть ответ: 494
Закажите бесплатный демонстрационный урок с одним из наших лучших преподавателей и начните изучать счеты
Запишитесь на бесплатный урок
6. Умножение
Понимание умножения с использованием счетов
После того, как новые учащиеся привыкнут пользоваться счетами и толкать бусы из одного угла в другой, я думаю, они готовы научиться использовать счеты для умножения.
Но один предостерегающий совет: не пытайтесь учить умножению, пока они не научатся складывать и вычитать.
Для этой математической операции давайте попробуем понять, как 3×4=12
Объясните умножение на счетахПопросите ребенка расположить 3 бусины в 4 разных рядах , а затем попросите их посчитать. Благодаря этому процессу у них будет мысленная картина того, как 4 умножить на 3 дает 12.
Помните, что этот процесс нужен только , чтобы понять, как работает умножение.
Метод 1: Умножение однозначных чисел на счетах
Чтобы увидеть как выполнять умножение на счетах , давайте рассмотрим пример: 6×5
Умножение однозначных чисел на счетахДля этого учащийся должен знать как представлять разрядные значения. Итак, начнем с того, что последнюю строку и первую строку будем считать единицами. Зачем нам две строки?
Потому что вы умножаете.
Пошаговый процесс
- Начните с 5 в первом ряду с 5 бисеринами справа.
- Переместите 1 бисерину (из 5 бисерин) верхнего ряда влево, затем 6 бисерин нижнего ряда переместите вправо.

- Снова переместите еще одну бисеринку влево. На этот раз вам нужно добавить еще 6 бисерин в нижний ряд.
- Итак, вы продолжаете сдвигать… 1…2…3…4 бусины, пока не закончатся бусины.
- Теперь поменяйте все бусины единичного ряда (сдвиньте влево) на 1 бисеринку десятого ряда вправо.
- После этого продолжайте прибавлять бисеринки в первом ряду вправо и считать…5…6.
- Продолжайте, сдвинув 3-ю бисеринку из верхнего ряда влево и добавьте еще 6 бисерин в нижний ряд.
- Продолжайте повторять шаги, пока у вас не будет 0 бисерин в верхнем и нижнем рядах и 3 бусины в ряду десятков.
- Теперь вы уже можете угадать ответ: 3 десятка равно 30 .
Если вы хотите умножить двузначные числа , например 21×5, вам нужно взять две строки сверху как единицы и десятки, как вы сделали для нижних строк в последнем примере.
Всегда изображайте большее число внизу. Почему? Это удобно.
Пошаговый процесс
- Расположите 5 бисеринок в верхнем ряду (считайте его единичным рядом).
- Далее набираем 2 бисеринки с правой стороны нижнего ряда десятков и 1 бисеринку ряда единиц, чтобы получилось 21.
- Теперь каждый раз, когда вы сдвигаете 1 бисеринку из верхнего «единичного ряда» влево, вам нужно будет прибавлять еще 21. Продолжайте повторять это, пока не закончатся десятки бисерин.
- Когда закончились бусины в десяточном ряду, у вас есть 1 сотня, поэтому добавьте 1 бусину в «сотый ряд» и сдвиньте все бусины с десятками влево, чтобы продолжить счет заново.
- Продолжайте в том же духе, пока у вас не будет 1 бусина в сотенном ряду, 0 бусинок в десяточном ряду и 5 бусинок в единичном ряду.
- Ответ: 105.
Хотите знать почему? Прочтите Danish Abacus Vs. Рекенрек , чтобы узнать.
Рекенрек , чтобы узнать.
Прочитать
Попробуем умножить на 143×4.
143×4=572 на счетахПошаговый процесс
- Расположите 4 бусины в верхнем ряду.
- Теперь наденьте все 4 бусины справа налево одну за другой.
- Каждый раз, когда вы сдвигаете 1 бисеринку влево, вам нужно прибавлять 143 в нижних рядах.
- Как прибавить 143 на счетах? Наденьте 1 бисеринку в сотом ряду (снизу), 4 бисерины в ряду десятков и 3 бисерины в ряду единиц, чтобы получилось 143.
- Теперь каждый раз, когда вы сдвигаете 1 бисерину из верхнего «единичного ряда» влево, добавляйте еще 143. Продолжайте повторять это, пока не закончатся десятки бисерин.
- Когда закончились бисерины в десяточном ряду, у вас есть 1 сотня, поэтому добавьте 1 бисеринку в «сотом ряду» и отодвиньте все бисеринки влево, чтобы продолжить счет заново.
- Продолжайте в том же духе, пока не получите 5 бисерин в сотом ряду, 7 бисерин в десятом ряду и 2 бисеринки в единичном ряду.

- Ответ: 572 .
7. Деление
Понимание деления на счетах
Деление является одним из четырех основных математических действий, и его рекомендуется преподавать после того, как учащиеся освоят первые.
Поэтому, прежде чем обучать делению на счетах, , пожалуйста, убедитесь, что ваш ребенок умеет складывать, вычитать и умножать на счетах.
Пройдёмся по понятиям делимое и делитель.
Всегда представляйте делимое в верхних строках и делитель в нижних строках.
Для операций деления объясните, какие строки являются единицами, десятками, сотнями и т. д.
Первые ряды сверху и снизу: однорядные
Вторые ряды сверху и снизу: десятирядные
Третьи ряды сверху и снизу: сотые ряды
901 15 Метод 1: Деление однозначного числа на счетах Всегда начинайте с простого примера для детей. Возьмем 9÷3. Для деления представьте делимое в верхней строке.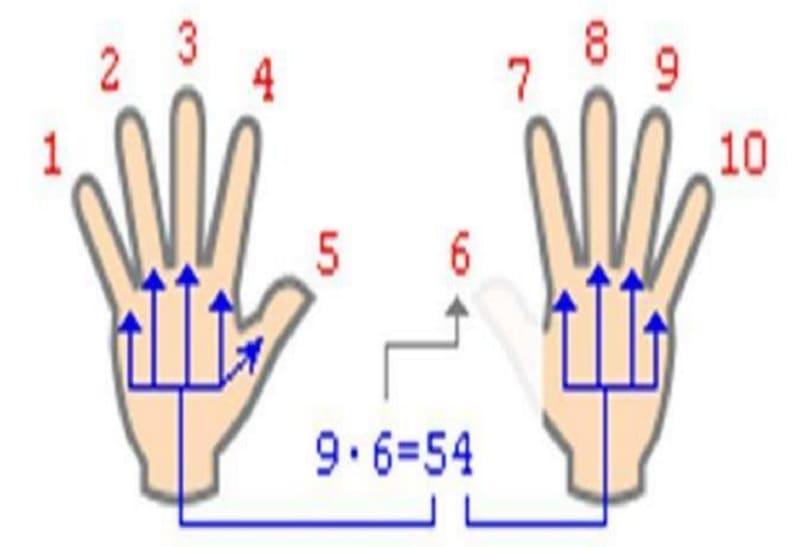
Пошаговый процесс
- Сдвиньте 9 бисеринок вправо в верхнем ряду, как показано на рисунке выше.
- Далее, как вы знаете, делитель равен 3, поэтому продолжайте сдвигать по 3 бусины за раз влево в верхнем ряду.
- На каждый набор из 3 бисеринок сдвиньте 1 бисеринку вправо в нижнем ряду.
- В конце операции (как показано на картинке) у вас в нижнем ряду будет 3 бисеринки.
Следовательно, частное равно 3 и 0 бисеринок справа от верхнего ряда, поэтому 0 это остаток.
Метод 2: Как разделить двузначное число на счетах
Пример 1Попробуем разделить 10÷4
9000 2 Пошаговый процесс- Представляют делим, сдвинув 10 бисеринок вправо сверху.
- Делитель равен 4.
- Итак, продолжайте перемещать по 4 бисерины справа налево в первом ряду.
- Для каждого набора из 4-х бусин сдвиньте 1 бисеринку вправо в нижнем ряду.
 ‘
‘ - В итоге у вас будет по 2 бусины, как с правой стороны нижнего ряда, так и с верхнего ряда.
Следовательно, частное равно 2 , а остаток тоже 2 .
Пример 2Разделим 25÷5
25÷5 на счетахКак и в примерах умножения, вам нужно взять две строки сверху, чтобы представить двузначное число, отличное от 10.
Как известно, в числе 25 2 десятка и 5 единиц.
Пошаговый процесс
- Наденьте 2 бисеринки и 5 бисеринок вправо во втором и первом рядах сверху соответственно. Вот вам 25.
- Теперь, так как делитель равен 5, продолжайте сдвигать 5 бисерин в верхнем ряду, и для каждого набора из 5 бисеринок вы сдвигайте 1 бисеринку вправо в нижнем ряду.
- Когда у вас будет 1 бусина внизу, у вас закончатся бусины в верхнем ряду.
- Итак, что делать?
- Далее вы сдвигаете бусину из десятого ряда влево и в обмен на это приносите 10 бусинок из единичного ряда.

- Теперь у вас хватило еще на 2 бисеринки нижнего ряда. Продолжайте в том же духе, пока в нижнем ряду не будет 5 бисерин.
Частное равно 5, а остаток равен 0.
Способ 3. Как разделить трехзначное число на счетах
Попробуем разделить 225÷25
Пошаговый процесс
- Чтобы изобразить делимое 225, наденьте 2 бисерины на ряд сотен, 2 бисерины на ряд десятков и 5 бисерин на ряд единиц- ряд сверху.
- Теперь, как и в предыдущем примере, продолжайте убавлять 25 (2 бисерины десятиряда и 5 бисеринок одноряда) слева направо сверху.
- В каждом наборе из 25 нанижите 1 бисеринку влево в нижнем ряду.
- После ввода первого набора из 25 верхний ряд десятков пуст.
- Итак, вы сдвигаете 1 бисеринку в сотенном ряду слева направо и взамен получаете 10 бисеринок в десятом ряду.
- Теперь продолжайте натягивать 2 бисерины десятого ряда и 5 бисерин первого ряда, пока не получите 9 бисерин нижнего ряда.

Частное равно 9, а остаток равен 0.
Вот как вы делите на счетах. Если у вас все еще есть путаница в отношении сумм на счетах, посмотрите это видео.
О чем следует помнить при обучении детей счету
1. Познакомьте детей со счетами
Дети, которые используют счеты после поступления в школу, находят счеты очень сложными.
Если вы хотите, чтобы ваш малыш не паниковал и чувствовал себя комфортно со счетной рамкой, то вводите прибор правильно.
Во-первых, научите их, как заставить четки читать 5, 6 или другие числа. Научите их, как считать и как работать с бусинами.
2. Научите детей представлять большие числа для выполнения математических операций на счетах
Вы должны хотя бы научить детей представлять трехзначные числа на датских счетах, прежде чем погрузиться в основные операции.
3. Всегда начинайте с однозначных операций
Поначалу древний калькулятор всем кажется странным. Поэтому я предлагаю каждому родителю научить складывать/вычитать/умножать/делить однозначные числа, прежде чем иметь дело с большими числами.
4. Будьте терпеливы
Пройдет много времени, прежде чем ваш ребенок начнет решать математические задачи на счетах. Итак, приготовьтесь к терпению.
Держись с ребенком. Дай мне уверенность. Поощряйте их.
Помните, если вы расстроитесь, они сдадутся гораздо раньше, чем вы ожидаете.
5. Превратите математические задачи в игру
Будучи родителем, вы, возможно, уже заметили, как дети реагируют, когда какая-либо рутинная работа доставляет им удовольствие.
Если вы изо всех сил пытаетесь привлечь внимание ребенка, попробуйте превратить задачи, связанные со счетами, в игру.
Дайте им очки после каждой успешной операции. Чтобы сделать его еще более интересным, вы также можете добавить награды.
6. Купить Абачи с разноцветными бусинами
Броские цвета. Дети предпочитают абаки с разноцветными бусинами тусклым.
Итак, всегда старайтесь выбирать устройство, которое понравится вашим детям. Вы также можете узнать их мнение перед покупкой.
Теперь пришло время для быстрой викторины по счету.
Тест: проверьте, что вы узнали
Дорогие читатели, возьмите свои счеты и попробуйте найти ответ на следующие суммы.
Дружеское предупреждение: не пользуйтесь современным калькулятором. Пусть ваши пальцы найдут ответ на бусах.
Часто задаваемые вопросы
Какие операции можно выполнять на счетах?
Вы можете выполнять сложение, вычитание, умножение и деление на счетах. В дополнение к этому, вы также можете представлять большие числа на счетах. Кроме того, на счетной рамке можно извлекать квадратные и кубические корни.
Полезны ли счеты для обучения математике?
Да, счеты полезны для обучения математике, особенно для дошкольников, детсадовцев и слабовидящих учащихся.
Что такое число бабочки на счетах?
Десятичные числа называются числом бабочки на счетах, потому что они содержат нить бусинок во время счета.
Как пользоваться счетами и быстро считать на них в уме?
Во-первых, на счетах нельзя считать в уме. Вы изучаете счеты, тренируетесь быстро считать, а затем мысленно представляете счеты в своем уме. Процесс умственного счета включает в себя представление счетов в уме и перемещение бусинок для расчета без использования каких-либо физических устройств.
Запишитесь на бесплатный демонстрационный урок с одним из наших лучших преподавателей и начните изучать счеты
Запишитесь на бесплатный урок
Заключение
Несомненно, счеты являются наиболее эффективным инструментом для выполнения основных математических операций. Вы можете быть учителем или родителем; это не имеет значения. Если вам сложно объяснить детям основы математики, я предлагаю вам попробовать счеты.
Я надеюсь, что эта статья поможет вам понять, как пользоваться простыми счетами. Пожалуйста, дайте мне знать, как складываются ваши приключенческие счеты в комментариях.
Как умножить два числа на счетах?
Содержание| 1. | Введение |
| 2. | Краткое путешествие Абака во времени |
| 3. | Как считать числа на счетах? |
| 4. | Как выполнить умножение на счетах? |
| 5. | Резюме |
| 6. | Часто задаваемые вопросы |
| 7. | Внешние ссылки |
13 ноября 2020 г.
Время чтения: 5 минут Можете ли вы представить наш мир, если не существует чисел? Насколько сложно было бы считать без чисел? Было время, когда не существовало письменных чисел. Для больших или больших чисел люди зависели бы от доступных им природных ресурсов, таких как галька, ракушки и т. д. Так что на протяжении всей истории подсчет больших чисел был трудным, особенно для типичного необразованного торговца. В этом сценарии родилась идея абака. Счеты — это вневременной вычислительный инструмент, который до сих пор применим в современных классах. Решение задач на счетах — это быстрый механический процесс по сравнению с современными многофункциональными калькуляторами. После изучения необходимых процедур счета и запоминания нескольких простых правил учащиеся могут использовать счеты для решения различных задач. Согласно письменному тексту, таблицы для счета использовались более 2000 лет, начиная с греков и римлян. Обычный метод расчета в Древней Греции и Риме заключался в перемещении жетонов на гладкой доске или столе, соответствующим образом отмеченных линиями или символами, показывающими места. Происхождение портативных счетов с рамкой для бус неизвестно. Считалось, что он возник из-за необходимости странствующих торговцев. Некоторые историки отдают должное китайцам как изобретателям счетов, в то время как другие считают, что римляне представили счеты китайцам через торговлю. Сегодня счеты живут в сельских районах Азии и Африки и зарекомендовали себя как удобный вычислительный инструмент. Счеты, широко используемые в Китае и других частях Азии, известны как Suanpan. Он имеет пять единичных бусин на каждом нижнем стержне и две «пятерки» на каждом верхнем стержне. Современные японские счеты, известные как Soroban , были разработаны на основе китайских Suan-pan. Русские счеты, Schoty , имеют десять бусин на стержне и не имеют разделительной планки. Счеты Soroban считаются идеальными для десятичной системы счисления, в которой каждый стержень действует как заполнитель и может представлять значения от 0 до 9. Счеты — это окно в прошлое, позволяющее пользователям выполнять все операции так же, как это делается тысячи лет . Кроме того, устройство предоставляет учащимся в современных классах альтернативу процедурам с бумагой и карандашом, которые позволяют им изучать вычисления более практическим образом, что также способствует общему развитию учащихся. Для получения более подробной информации об истории Abacus см. Abacus History На каждом стержне счеты Соробан имеют одну бусину на верхней палубе, известную как небесная бусина, и четыре бусины на нижней палубе, известные как бусины земли. Каждая небесная бусина на верхней палубе имеет значение 5; каждая бусина земли в нижней колоде имеет значение 1. Как только вы поймете, как считать с помощью счетов, пользователю будет несложно найти любое целое число. Есть два основных правила решения любой задачи на сложение и вычитание на счетах Соробан. Значение, добавленное к исходному числу, чтобы получить 10, является дополнением числа. Например, дополнение 7 по отношению к 10 равно 3, а дополнение 6 по отношению к 10 равно 4. Другой пример, рассмотрим сложение 8 и 4. Процесс начинается с регистрации 4 единичный стержень H, Поскольку сумма двух чисел больше 9, необходимо использовать вычитание. Вычитаем дополнение 8, а именно 2, из 4 на стержне H и прибавляем 1 бисеринку к десятому стержню G. Это оставляет нам 1 бусину, зарегистрированную на стержне G (стержень десятков) и 2 бусины на стержне H (стержень единиц) Это правило остается неизменным независимо от используемых чисел. Как известно, вычитание — это операция, обратная сложению. Таким образом, при вычитании на счетах Соробана мы прибавляем дополнение и вычитаем 1 бисеринку из следующего по величине разряда. Задачи на умножение сложнее, чем на сложение и вычитание, но их легко решить с помощью счетов Соробана. Прежде чем учащиеся смогут решать задачи на умножение, они должны сначала ознакомиться с таблицами умножения от 1 до 9. Регистрация множимого и множителя является наиболее важным шагом в этом процессе. Это гарантирует, что стоимость продукта точно попадает на единичный стержень. В качестве примера рассмотрим задачу на умножение 36 × 4 с множимым 36 и множителем 4. Начнем с того, что поместим палец на единичный стержень H и посчитаем слева один стержень для каждой цифры в множителе (1 позиция до стержня G) и по одному стержню на каждую цифру множимого (2 позиции до стержня E). Затем запишите 36 на стержнях E и F. Затем поместите 4 на стержне B. Это оставит достаточно места, чтобы помочь учащимся отличить множимое от множителя. Умножение на счетах включает только сложение частичных произведений. Наш первый шаг — умножение 6 на 4 и добавление частичного произведения двух стержней, GH, справа от множимого. Поскольку мы учли 6, мы обнуляем стержень F. Аналогичный процесс используется для умножения 30 на 4. Его произведение, 120, прибавляется к стержням EFG. Поскольку в наших расчетах мы учли 30, мы обнуляем стержень D. Это оставляет конечный продукт 144 на стержнях FGH. После освоения сложения читателю предлагается попробовать задачи на умножение, связанные с переносом, например, 36 × 9. Итак, подведем итоги Выполнение основных операций, таких как умножение на счетах , задействует и развивает ум ребенка. Вот несколько дополнительных моментов, которые говорят о том, как умножить два числа с помощью Abacus. Для их просмотра нажмите на кнопку Скачать. Как умножить два числа на счетах? Скачать Cuemath, удобная для учащихся платформа математики и кодирования, проводит регулярные онлайн-занятия в режиме реального времени для обучения и развития навыков, а их приложение Mental Math для iOS и Android является универсальным решение для детей, чтобы развить несколько навыков. Ознакомьтесь со структурой оплаты для всех классов и запишитесь на пробное занятие уже сегодня! Счеты — это ручное средство для счета, состоящее из бусин, которые можно перемещать вверх и вниз на ряде палочек или веревок внутри обычно деревянной рамы. Самым ранним счетным устройством были человеческие пальцы рук или ног.
Самым ранним счетным устройством были человеческие пальцы рук или ног.
Краткое путешествие абака во времени 

Как считать числа на Abacus? 
Как выполнить умножение на счетах? 
Резюме 
Загружаемый PDF 📥
О Cuemath
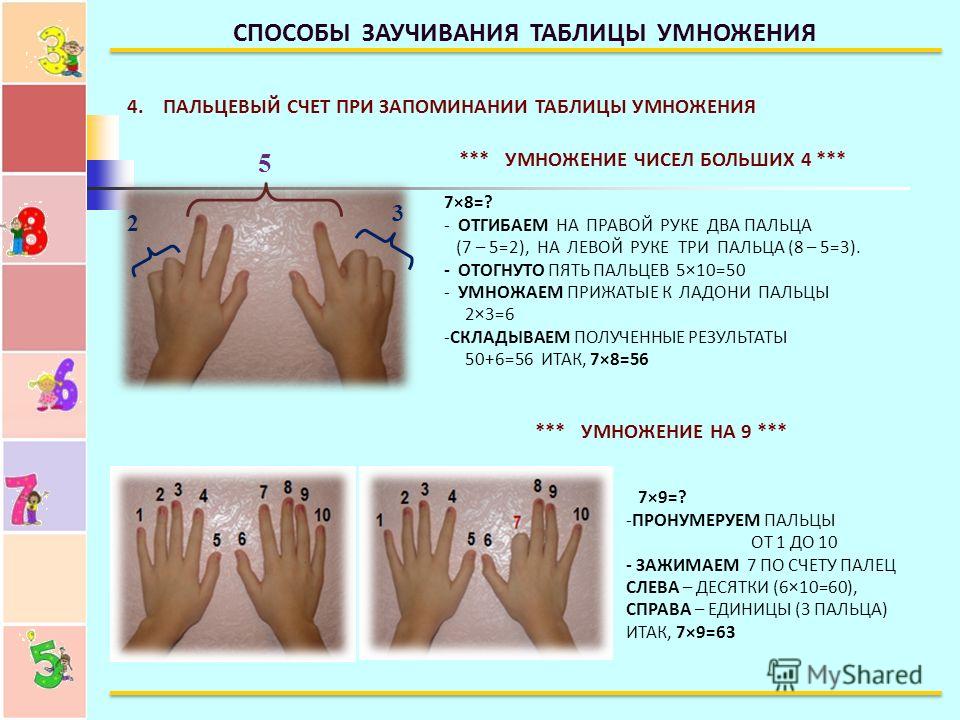
Часто задаваемые вопросы (FAQ) Что такое счеты?











 ‘
‘