Наконец то разобрался как считать на счетах!!!!
Описание
Сложение
Вычитание
Умножение
Деление
Описание
Знаменитые деревянные счеты, изображенные на рисунке ниже, повсеместно использовались в СССР первые две трети двадцатого века в основном для операций сложения и вычитания. Как же кассиры и бухгалтера пользовались этими русскими счетами? Давайте разберемся. Если же вы умеете пользоваться счетами, то можете перейти сразу к описанию более сложных операций.
В исходном положении в «обнуленных» счетах все костяшки выровнены по правому краю (как показано на рисунке). Каждый ряд костяшек представляет собой разряд числа, единицы находятся над четырьмя костяшками. Выше единиц – десятки, сотни и т.д., ниже – четверти, десятые и сотые. С таким раскладом удобно считать деньги, где в ходу есть четвертаки (например, 25 копеек). Черным цветом выделены центральные костяшки (для удобства).
Набор числа. Если мы хотим установить какое-нибудь число на счетах (для совершения с ним в дальнейшем арифметических действий), то необходимо просто передвинуть нужные костяшки налево.
Например, для набора числа «3 251,5» передвигаем 2 четвертака (или 5 десятых), 1 единицу, 5 десяток, 2 сотни и 3 тысячи.
Но набор числа, это только начало. По-настоящему пользоваться деревянными счетами, значит совершать арифметические операции.
Сложение:
Чтобы сложить на счетах два числа, нужно просто набрать костяшками одно число, а затем перенести налево каждый разряд второго числа, начиная с нижних рядов (именно с нижних!). Если вдруг выясняется, что костяшек в каком-то ряду не хватает, то в этом ряду нужно оставить столько костяшек, сколько не хватает, а на уровне выше перекинуть влево еще 1 костяшку. Чтобы лучше разобраться, как правильно складывать числа на счетах, смотрите пример ниже (987 + 134 = 1 121):
Вычитание:
Вычитание на счетах производится точно таким же образом как сложение, сверху вниз. Только если костяшек в ряду не хватает, в этом ряду нужно оставить (10-x) костяшек, где x-число нехвативших костяшек, а в ряду выше нужно убрать одну костяшку (сдвинуть ее вправо).
Ниже смотрите пример, как правильно считать разность на русских счетах (121 – 98 = 23):
Умножение:
Умножение на счетах является не самым быстрым и простым. В некоторых случаях, гораздо проще воспользоваться навыкамибыстрого умножения в уме. Однако в рамках данной статьи приведены некоторые методики умножения на деревянных счетах. Для того, чтобы умножить число на 2 или на 3, нужно просто сложить данное число с собой (при умножении на 2), и повторить эту процедуру при умножении на 3. Умножение на 4 производится как умножение на 2 с последующим умножением на 2 полученного результата. Что касается умножения на 5, как вы можете убедиться из этого урока, оно равносильно делению на 2 и последующему умножению на 10. В этом случае, после деления на 2 вы просто переносите разряды (костяшки) на уровень выше. Умножение на большие числа осуществляется при помощи комбинации описанных методов.
Деление:
Деление на русских счетах является достаточно сложной процедурой.
Использовать для этого счеты иногда просто иррационально. Если пример удобный, допустим, необходимо разделить 280 на 2, тогда действительно, нужно просто из каждого ряда отодвинуть направо половину костяшек и тогда получится 140. Но иные примеры в большинстве своем требуют сложных алгоритмов и хорошего развития внимания и краткосрочной памяти.
Как считать на счетах
Книга Загадки и диковинки в мире чисел
Вот несколько приемов, пользуясь которыми, всякий, умеющий быстро складывать на счетах, сможет проворно выполнять встречающиеся на практике примеры умножения.
Умножение на 2 и на 3 заменяется простым сложением.
При умножении на 4 умножают сначала на 2 и складывают этот результат с самим собою.
Умножение числа на 5 выполняется на счетах так: переносят все число одной проволокой выше, – т. е. умножают его на 10, а затем делят это 10-кратное число пополам (как делить на 2 с помощью счетов – мы уже объяснили выше, на стр.
37).
Вместо умножения на 6 умножают на 5 и прибавляют умножаемое.
Вместо умножения на 7 множат на 10 и отнимают умножаемое три раза.
Умножение на 8 заменяют умножением на 10 без двух.
Точно так же множат на 9: заменяют умножением на 10 без 1.
При умножении на 10 – переносят, как мы уже сказали, все число одной проволокой выше.
Читатель теперь, вероятно, уже и сам сообразит, как надо поступать при умножении на числа больше 10 и какого рода замены тут окажутся наиболее удобными. Множитель 11 надо, конечно, заменить 10+1; множитель 12 заменяют 10 + 2, или практически 2 + 10, т. е. сначала откладывают удвоенное число, а затем прибавляют удесятеренное. Множитель 13 заменяется 10 + 3 и т. д.
Вот несколько особых случаев для множителей первой сотни:
20 = 10 ? 2
22 = 11 ? 2
25 = (100: 2): 2
26 = 25 + 1
27 = 30 – 3
32 = 22 + 10
42 = 22 + 20
43 = 33 + 10
45 = 50 – 5
63 = 33 + 30 и т. д.
Легко видеть, между прочим, что с помощью счетов очень удобно умножать на такие числа, как на 22, 33, 44, 55 и т.
п., а потому следует стремиться при разбивке множителей пользоваться подобными числами с одинаковыми цифрами.
К сходным приемам прибегают и при умножении на числа, большие 100. Если искусственные приемы утомительны, мы всегда можем умножить с помощью счетов по общему правилу, умножая каждую цифру множителя и записывая частные произведения – это все же дает некоторое сокращение времени.
Деление на счетах
Выполнять деление с помощью конторских счетов гораздо труднее, чем умножать; для этого нужно запомнить целый ряд особых приемов, подчас довольно сложных. Интересующимся ими придется обратиться к специальным руководствам. Здесь же укажу лишь, для примера, удобные приемы деления с помощью счетов на числа первого десятка (кроме числа 7, способ деления на которое чересчур сложен).
Как делить на 2, мы уже знаем – способ этот очень прост.
Гораздо сложнее прием деления на 3: он состоит в замене деления умножением на бесконечную периодическую дробь 3,3333… (известно, что 0,333… = 1/3).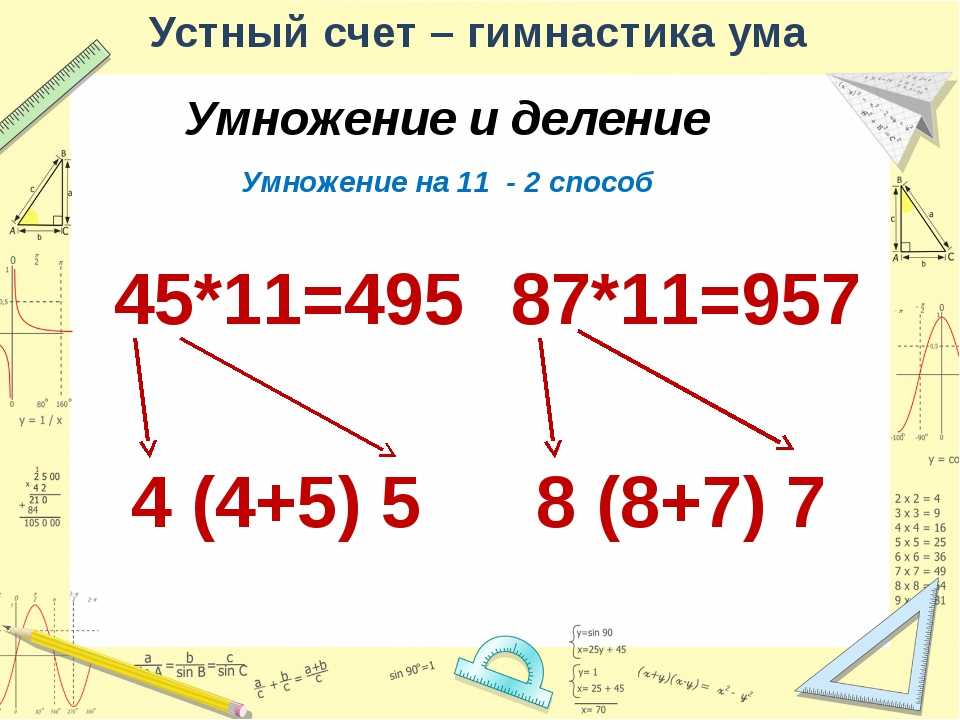
Деление на 4, конечно, заменяется двукратным делением на 2.
Еще проще деление на 5: его заменяют делением на 10 и удвоением результата.
На 6 делят с помощью счетов в два приема: сначала делят на 2, потом полученное делят на 3.
Деление на 7, как мы уже сказали, выполняется помощью счетов чересчур сложно, и потому мы излагать его не будем.
На 8 делят в три приема: сначала делят на 2, потом полученное вновь на 2, и затем еще раз на 2.
Очень интересен прием деления на 9. Он основан на том, что 1/9 = 0,1111… Отсюда ясно, что, вместо деления на 9, можно последовательно складывать 0,1 делимого + 0,1 его + 0,001 его и т. д.[10 — Этот прием полезен и для устного деления на 9.].
Всего проще, как видно, делить на 2,10 и 5 – и, конечно, на такие кратные им числа, как 4, 8, 16, 20, 25, 40, 50, 75, 80,100.
Эти случаи деления не представляют трудности и для малоопытного счетчика.
Отголоски старины
С отдаленными предками наших русских счетов связаны некоторые пережитки старины в языке и обычаях. Мало кто подозревает, например, что, завязывая «для памяти» узелок на носовом платке, мы повторяем то, что некогда с большим смыслом делали наши предки, «записывая» таким образом итог счета на шнурках. Веревка с узлами представляла собой счетный прибор, в принципе аналогичный нашим счетам и, без сомнения, связанный с ними общностью происхождения: это – «веревочный абак».
С абаком же связаны и такие распространенные теперь слова, как «банк» и «чек». «Банк» по-немецки означает скамья. Что же общего между финансовым учреждением, «банком» в современном смысле слова, и скамьей? Оказывается, что здесь далеко не простое совпадение. Абак в форме скамьи был широко распространен в деловых кругах Германии в XV–XVI веках; каждая меняльная лавка или банкирская контора характеризовалась присутствием «счетной скамьи» – и естественно, что скамья стала синонимом банка.
Более косвенное отношение к абаку имеет слово «чек». Оно английского происхождения и производится от глагола «чекер» (chequer, или checker) – графить; «чекеред» (графленый) называли разграфленную в форме абака кожаную салфетку, которую в XVI–XVII веках английские коммерсанты носили с собою в свернутом виде и, в случае надобности произвести подсчет, развертывали на столе. Бланки для расчетов графились по образцу этих свертывающихся абаков, и неудивительно, что на них перенесено было, в сокращенном виде, и название этих счетных приборов: от слова «чекеред» произошло слово «чек».
Любопытно, откуда произошло выражение «остаться на бобах», которое мы применяем теперь к человеку, проигравшему все свои деньги. Оно очень древнего происхождения и относится к тому времени, когда все денежные расчеты – в том числе и расчеты между игроками – производились на абаке, на счетном столе или скамье, с помощью бобов, игравших роль косточек наших счетов[11 — Один считает на камешках, другой – на бобах, читаем у Кампанеллы в «Государстве Солнца» (1602).
]. Человек проигравший свои деньги, оставался с одними бобами, выражавшими сумму его проигрыша – отсюда и соответствующий оборот речи, надолго переживший породившие его обстоятельства.
Глава IV Немного истории
«Трудное дело – деление»
Привычным движением зажигая спичку, мы иной раз еще задумываемся о том, каких трудов стоило добывание огня нашим предкам, не очень даже отдаленным. Но мало кто подозревает, что и употребительные ныне способы выполнения четырех арифметических действий тоже не всегда были так просты и удобны, так прямо и быстро приводили к искомому результату. Предки наши пользовались приемами, гораздо более громоздкими и медленными. И если бы школьник XX века мог перенестись за четыре, даже всего за три века назад, он поразил бы наших предков быстротой и безошибочностью своих арифметических выкладок. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи. Со всех концов Европы приезжали бы учиться у нового великого мастера счетного дела… Особенно сложны и трудны были для наших предков действия умножения и деления – последнее всего больше.
Дивизия счетов | Введение в Abacus
ВведениеВы когда-нибудь задумывались, как люди обходились без такого важного устройства, как Калькуляторы, столетия назад?
Что, если я скажу вам, что у них всегда был калькулятор!
Да, именно счеты широко использовались для сложных вычислений до изобретения электронных калькуляторов.
Счеты – это полезное учебное оборудование для слабовидящих, а также для всех, кто хочет узнать об истоках современного калькулятора.
Просто передвигая бусины слева направо, вы можете добавить до миллиарда и более.
Счеты — это инструмент, который можно использовать для вычислений — сложения, вычитания, умножения и деления, помимо других арифметических функций и активации мозга.
В этой статье вы узнаете, как использовать счеты для простого деления. Загрузите PDF-файл ниже, чтобы узнать историю счетов и деления с помощью счетов.
Краткое путешествие Абака во времени
Согласно письменному тексту, таблицы для счета использовались более 2000 лет, начиная с греков и римлян.
«Обычный метод подсчета в Древней Греции и Риме осуществлялся путем перемещения счетчиков на гладкой доске или столе, соответствующим образом отмеченных линиями или символами, чтобы показать «места». -известен. Считалось, что он возник из-за необходимости странствующих торговцев.
Некоторые историки отдают должное китайцам как изобретателям счетов, в то время как другие считают, что римляне представили счеты китайцам через торговлю.
Сегодня счеты живут в сельских районах Азии и Африки и зарекомендовали себя как удобный вычислительный инструмент.
Широко используемые счеты в Китае и других частях Азии известны как Suanpan . На каждом нижнем стержне по пять единичных бусинок, а на каждом верхнем стержне по две пятигранника.
Современные японские счеты, известные как Soroban , были разработаны на основе китайских Suan-pan.
Русские счеты, Schoty , имеют десять бусин на стержне и не имеют разделительной планки.
Счеты Soroban считаются идеальными для системы счисления с основанием десять, в которой каждый стержень выступает в качестве заполнителя и может представлять значения от 0 до 9. сегодня.
Счеты портативны для использования торговцами и позволяют использовать их во всех частях мира.
Он также гибок для использования в разных культурах.
Как считать числа на счетах?
На каждом стержне счеты Соробан имеют одну бусину на верхней палубе, известную как небесная бусина, и четыре бусинки на нижней палубе, известные как бусины земли.
Каждая небесная бусина на верхней палубе имеет значение 5; каждая бусина земли в нижней колоде имеет значение 1.
Как только вы поймете, как считать с помощью счетов, пользователю будет несложно найти любое целое число.
Есть два основных правила решения любой задачи на сложение и вычитание на счетах Соробан.
- Оператор всегда должен решать задачи слева направо.
- Оператор должен уметь находить дополнительные числа, в частности, всегда относительно 10
Значение, добавленное к исходному числу, чтобы получить 10, является дополнением числа.
Например, дополнение 7 по отношению к 10 равно 3, а дополнение 6 по отношению к 10 равно 4.
Рассмотрим сложение 8 и 4. Процесс начинается с регистрации 4 на единичном стержне H ,
Поскольку сумма двух чисел больше 9, необходимо использовать вычитание.
Это правило остается неизменным независимо от используемых чисел. Как известно, вычитание — это операция, обратная сложению.
Таким образом, при вычитании на счетах Соробана мы прибавляем дополнение и вычитаем 1 бисер из следующего по величине разряда.
Как выполнить деление на счетах?
Решение задач на деление на счетах Соробана напоминает знакомые вычисления на бумаге и карандаше. Кроме того, в процессе используются сложение, вычитание и умножение.
Деление производится путем деления одного числа в делителе на одно или, возможно, два числа делимого одновременно.
Оператор умножает после каждого шага деления и вычитает произведение.
Затем к остатку прибавляется следующая часть дивиденда, и процесс продолжается. Это больше похоже на работу с карандашом и бумагой.
Ниже приведена методика работы с задачами на деление с четырьмя и более цифрами в уравнении на счетах.
При постановке задач на деление на счетах делимое ставится справа, а делитель слева.
Обычной практикой является оставление 4 неиспользованных стержней между двумя номерами. Именно на этих неиспользованных стержнях формируется частный ответ.
Итак, начнем с рассмотрения стандартного бумажного метода.
- Найдите начальный столбец для частного. Это будет *первая* позиция *n*, где число, сформированное в столбцах с 1 по *n* делимого, больше или равно делителю.
- Столбцы с *1* по *n* называются *рабочими цифрами*; столбец *n* называется *текущим частным столбцом*.
- Используя аппроксимацию, найдите *наибольшее* число *i* такое, что *i* делитель меньше или равен числу, образованному рабочими цифрами.
- Напишите *i* в текущем столбце частных и вычтите *i*, умноженное на делитель, из рабочих цифр. Результат *должен быть* числом *меньше*, чем делитель. Это *рабочий остаток*.
- Копируйте цифры справа от рабочих цифр и добавляйте их к рабочему остатку из шага 3, пока не получите число *больше или равное* делителю.
- Рабочий остаток + скопированные цифры становятся новыми рабочими цифрами. Последний столбец, который вы скопировали, является новым *текущим частным столбцом*.
- Если между старым и новым текущими столбцами частных есть пробелы, заполните их нулями.
- Возвращайтесь к шагу 2, используя новые рабочие цифры и текущий столбец частных, пока рабочий остаток не станет равным нулю.
То, как мы делаем это на счетах, очень похоже на то, как мы это делаем на бумаге. Единственное отличие состоит в том, что на бумаге мы выполняли умножение и вычитание в два этапа; на счетах, мы собираемся объединить.
Рассмотрим несколько примеров:
| Пример 1 |
951 ÷ 3 = 317
В этом примере делимое состоит из трех целых чисел.
- Выберите стержень F в качестве единицы измерения и отсчитайте три стержня слева.
- Делитель имеет одно целое число, поэтому считайте один плюс два назад вправо. Установите первое число делимого на стержне F.
Шаг 1: Установите делимое 951 на стержни FGH и делитель 3 на A.
Шаг 2: Делитель (3 на A) меньше делимого (9 на F). Поэтому примените «Правило I» и поставьте первое число в частном на два стержня слева от D. Разделите 3 на A на 9 на F и подложите 3 в частном на стержне D.
Умножьте частное 3 на 3 на A и вычтите произведение 9 из стержня F. При этом останется частичное частное 3 на D и остаток от делимого 51 на стержнях GH.
Шаг 3: Разделите 3 на A на 5 на G. Делитель снова меньше делимого, поэтому следуйте «Правилу 1». Установите частное 1 на стержне E.
Умножьте частное 1 на 3 на стержне A и вычтите произведение 3 из 5 на стержне G. Таким образом, частичное частное 31 останется на стержне DE, а остаток делимого 21 на стержне GH.
Шаг 4: Разделите 3 на A на 21 на GH и установите частное 7 на стержне F.
Умножьте частное 7 на 3 на A и вычтите произведение 21 из стержней GH, оставив ответ 317 на стержнях DEF.
| Таким образом, после деления на счеты мы получили 951 ÷ 3 = 317. |
В задачах на деление правильный ответ иногда требует проб и ошибок. Проблема деления, показанная ниже, является примером.
В задачах такого типа может быть сложно определить точное частное.
Оценка часто является лучшим способом действий. Легкость, с которой оператор может исправить неправильный ответ, делает соробан таким превосходным инструментом для решения задач на деление.
| Пример 2 |
0,14 ÷ 1,6 = 0,0875
- В качестве единичного стержня выберите D.
- В этом примере, поскольку в делимом нет целых чисел, нет необходимости считать влево. Делитель имеет одно целое число.
- Начиная со стержня D, считайте один плюс два вправо. Установите первое число делимого на стержне G.
Шаг 1: Установите делитель 14 на стержни GH и делитель 16 на стержни AB.
Шаг 2: В этой задаче первые две цифры делителя больше, чем у делимого.
Применить «Правило II». Установите первое число в частном на один стержень слева от делимого, в данном случае на стержне F. Думайте о задаче как о делении 16 на AB на 140 на GHI. Теперь оцените частное.
Кажется разумным оценить частное равным 7. Поставьте 7 рядом с делимым на стержне F.
Умножьте частное 7 на 1 на стержне A и вычтите произведение 7 из 14 на стержне GH.
Умножьте частное 7 на 6 на B и вычтите произведение 42 из стержней HI.
Пересмотреть частное и делимое. Добавьте 1 к частному стержня F, чтобы получилось 8. Вычтите еще 16 из стержней HI.
Это оставляет неполное частное 0,08 на CDEF и остаток 12 на HI.
Шаг 3: Заимствуйте ноль из стержня J и думайте о задаче как о делении 16 на AB на 120 на HIJ. Оцените частное 8. Установите 8 на стержне G.
Умножьте частное 8 на 1 на стержне A и вычтите произведение 8 из 12 на стержне HI.
Умножьте частное 8 на 6 на B и вычтите произведение 48 из стержней IJ.
Пересмотреть частное и делимое. Вычтите 1 из 8 на G. Добавьте 1 к 4 на стержне I.
Продолжайте решать задачу, но на этот раз используйте измененное частное 7. Умножьте 7 на G на 6 на B и вычтите 42 из стержней IJ. Таким образом, на стержнях CDEFG остается частичное частное 0,087, а на стержне J — остаток 8. Оцените частное 5. Установите 5 на стержне H 9.0007
Умножьте частное 5 на 1 на A и вычтите произведение 5 из 8 на стержне J.
Умножьте частное 5 на 6 на B и вычтите произведение 30 на стержнях JK, оставив 875 на стержнях FGH. С стержнем D, выступающим в качестве единицы, ответ будет равен 0,0875 на стержнях CDEFGH.
| Таким образом, после деления на счеты получается: 0,14 ÷ 1,6 = 0,0875 |
Сводка
Деление на счетах будет действительно интересно. Впечатляет, как быстро вы можете выполнять деление на таком тривиальном устройстве, основанном на сложении.
Всего лишь послеобеденная тренировка, и вы, вероятно, сможете выполнить большинство делений на счетах намного быстрее, чем на бумаге.
Настоящая хитрость в выполнении сложных вещей — это именно то, что мы видели в делении: разделение счетов на области.
Выполнение основных операций, таких как деление на счетах , задействует и развивает ум ребенка.
Итак, подведем итоги
- Счеты долговечны
- Счеты можно использовать для обучения маленьких детей числовым понятиям.
- Помогает развить навыки правильного обращения с бусинами на счетном инструменте.
- Развивает понимание математических процессов, таких как деление, умножение, вычитание и сложение.
Ниже приведены некоторые блоги, связанные с Abacus, которые помогут вам лучше понять Abacus. Приложение Math для iOS и Android — это универсальное решение для детей, позволяющее развивать различные навыки.
Ознакомьтесь со структурой оплаты для всех классов и запишитесь на пробное занятие уже сегодня!
Часто задаваемые вопросы (FAQ) Что такое счеты?
Счеты — это ручное вспомогательное средство для счета, состоящее из бусин, которые можно перемещать вверх и вниз на ряде палочек или веревок внутри обычно деревянной рамы. Сами по себе счеты не считают; это просто средство, помогающее человеку считать, запоминая то, что было подсчитано.
Где впервые использовали абакус? Счеты (множественное число abaci или abacuses), также называемые счетной рамкой, представляют собой вычислительный инструмент, использовавшийся на древнем Ближнем Востоке, в Европе, Китае и России за столетия до принятия письменной арабской системы счисления.
Точное происхождение абака до сих пор неизвестно.
Математические навыки закладывают прочную основу для поступления в высшие классы.
Обучение счету улучшает навыки
- Визуализация (фотографическая память)
- Концентрация
- Навыки слушания
- Память, Скорость
- Точность
- Творчество
- Уверенность в себе
- Уверенность в себе, приводящая к развитию всего мозга
Это простое устройство, используемое для счета, очень полезное для слабовидящих, когда вы
знаете основы счета на счетах, легко можете выполнять на нем различные операции.
Ниже приведены основные шаги, которые необходимо выполнить:
- Присвойте каждому столбцу разрядное значение.
- Начинайте считать с бусинок нижнего ряда.
- Завершить обмен 4/5.
- Повторите шаблон для более высоких чисел.
Мы можем легко освоить счеты. Как только мы научимся считать на счетах с помощью бусинок и их размещения, мы сможем выполнять основные операции на счетах.
Как делить на счетах? – Блог SumoMath
Перейти к содержимому
Опубликовано от terry
Мы начинаем учиться выполнять деление на счетах с одноразрядным делителем. Как и в стандартном алгоритме, мы преобразуем проблемы деления в серию фактов вычитания, когда мы перемещаем делитель через делимое. В следующем примере мы поймем, что решили задачу на деление, когда процесс вычитания уменьшит делимое до нуля. По мере продвижения к более высоким уровням мы будем выполнять длинный процесс деления, в котором нам нужно будет округлить наш ответ до определенного количества значащих цифр.
А пока давайте разработаем базовый пример деления счетов.
Примечание: в следующих примерах делитель будет помещен на счеты для справки, но это не обязательно и является вопросом предпочтения. Более продвинутые пользователи счетов обычно не помещают делитель на счеты, чтобы сэкономить время.
Пример №1 280/8 = 35
Чтобы выполнить деление на счетах, сначала нужно решить задачу на счетах. Мы будем следовать обычным соглашениям для постановки нашей задачи деления, которые оказались наиболее эффективными для вычисления частного. Сначала мы размещаем делимое, в данном случае 280, на счетах по соглашению справа от счетов, что дает нам место для размещения частного слева от делимого. Затем рекомендуется зарезервировать 3 или 4 стержня слева от делимого, где мы поместим частное. Наконец, необязательно размещать делитель на счетах. Если это так, поместите делитель слева от частных стержней.
Теперь мы готовы приступить к нашей задаче на деление. Как и при умножении, мы будем работать с делимым по одной цифре за раз, используя по одной цифре делителя за раз.
Мы снова будем в полной мере использовать наши факты умножения 9 × 9, чтобы определить каждое вычитание из делимого. Итак, мы начнем нашу задачу с того, что заметим, что наш делитель 8 больше, чем первая цифра делимого 2. Таким образом, мы не можем разделить 8 на 2. Поэтому мы переместим еще 1 цифру прямо на делимое и рассмотрим первые две цифры делимого 28. Теперь мы знаем из наших фактов умножения, что 8×3 = 24 и 8×4 = 32. Таким образом, наибольшее количество раз, которое мы можем взять 8 из 28, равно 3. Поэтому мы поместим нашу первую цифру частного, 3 , на втором стержне слева от частного стержня.
Здесь мы должны прояснить, как мы поддерживаем правильное значение места для частного, когда мы работаем с делимым. Наше делимое имеет 3 цифры, поэтому наибольшее наше частное может быть 3-значным. Однако в этой задаче, поскольку мы не могли разделить 8 на 2, первую цифру делимого, мы переместили еще 1 цифру вправо на делимом. Поэтому мы также должны переместить 1 цифру вправо в частном.