Урок математики по теме: «Умножение дробей». 6-й класс
Цели урока:
- Обучающие:
- сформулировать правило умножения обыкновенной дроби на натуральное число, правило умножения обыкновенных дробей;
- вырабатывать у учащихся навыки применения правил при выполнении действий.
- Развивающиея:
- развитие аналитического мышления учащихся;
- формирование умения выделять главное и обобщать.
- Воспитывающие:
- формирование умения организовать свою деятельность.
Тип урока: изучение нового материала.
Задачи урока:
- настроить детей на рабочий лад;
- повторить правила сложения, вычитания дробей; сложения и вычитания смешанных чисел;
- проверить умение детей выполнять сложение и вычитание дробей;
- сформулировать правило умножения обыкновенной дроби на натуральное число; правило умножения обыкновенных дробей;
- отрабатывать навыки умножения дроби на натуральное число, дроби на дробь;
- проверить уровень усвоения материала.

По завершении урока учащийся должен:
- Знать: правило умножения дроби на натуральное число; дроби на дробь.
- Уметь: умножать дробь на натуральное число, дробь на дробь.
Методы организации учебной деятельности: проблемный, объяснительно-иллюстративный, использование ИКТ.
Оборудование:
учебник математики 6-й класс, автор Н. Л. Виленкин; сборник математических диктантов; мультимедийный проектор.ХОД УРОКА
1. Организационный момент (2 мин.) (Приложение. Слайд 2)
Учитель. Эпиграф нашего урока “О,
сколько нам открытий чудных готовит просвещенья
дух…”. А были ли открытия в вашей жизни? Что
значат слова “Я сделал открытие”? Если человек
своим трудолюбием, упорством достигает истины в
чем-либо, то это и есть его открытие. По этому
поводу Борис Пастернак сказал:
По этому
поводу Борис Пастернак сказал:
Во всем мне хочется дойти
До самой сути.
В работе, в поисках пути,
В сердечной смуте.
До сущности истекших дней
До их причины,
До оснований, до корней,До сердцевины
Всё время схватывая нить
Судеб, событий,
Жить, думать, чувствовать, любить
Свершать открытья.
– На сегодняшнем уроке мы тоже попытаемся совершить маленькое, но самостоятельное открытие. Для этого надо быть настойчивым и внимательным.
2. Вводный контроль (3 мин.)
Учитель. Начнём урок с повторения. (Приложение. Слайд 3)
1 вариант 2 вариант
1) =
п 1)
= л
2) =
л 2)
= о
3) = а 3)
= м
4) =
н
4) = а
5) =
у
5) = т
ПЛАНУД ЛОМАТЬ
Сначала на слайде видны примеры и таблицы
ответов, затем ответы и слова.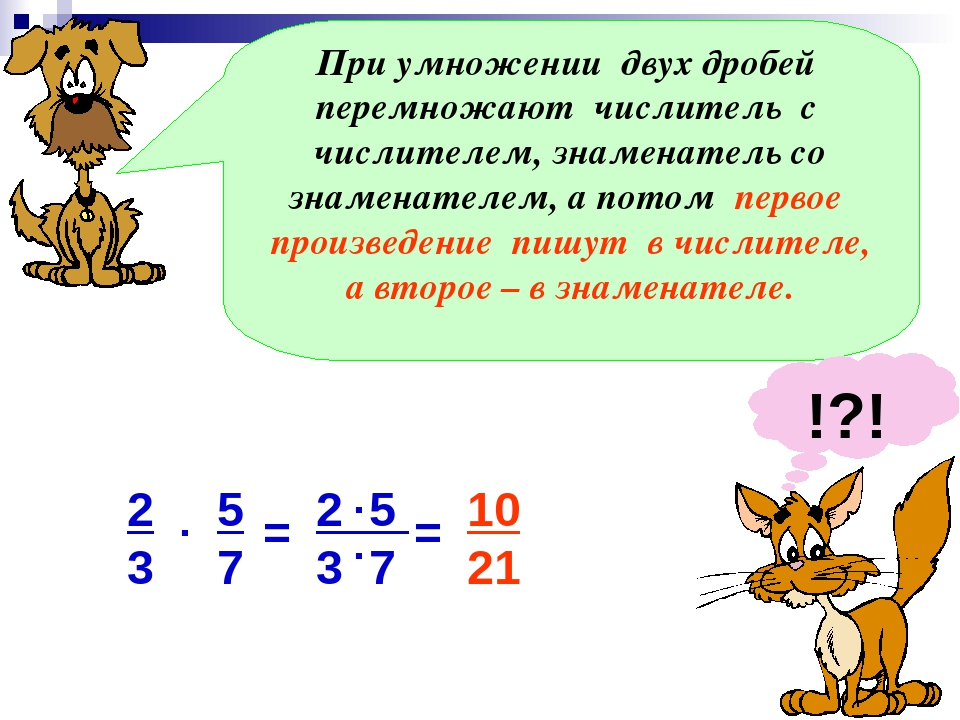
Рассказывает учащийся, подготовленный дома.
Первое понятие дроби появилось в древнем
Египте много веков назад. У многих народов дроби
называли ломаными числами. Этим названием
пользуется и автор первого русского учебника по
математике Л.Ф.Магницкий. В русском языке слово
«дробь» появилось лишь в VIII веке.
Происходит слово “дробь” от слова “дробить,
разбивать, ломать на части”. Современное
обозначение дробей берет своё начало в древней
Индии; дробная черта появилась в записи дробей
лишь около 300 лет назад. Название “числитель” и
“знаменатель” ввёл в употребление греческий
монах учёный-математик Максим Плануд. Для
запоминания: “Человек стоит на земле”. Долгое
время дроби считались самым трудным разделом
математики. У немцев даже сложилась поговорка
“попасть в дроби”, что означает попасть в
трудное положение.

- Какие правила вы применяли?
- Как читается правило сложения, сравнения, вычитания дробей с разными знаменателями?
- Как выполнить сложение смешанных чисел?
- Как выполнить вычитание смешанных чисел?
Повторяем правила сложения, сравнения, вычитания дробей с разными знаменателями. Учащиеся формулируют правила.
3. Сообщение темы урока (4 мин.)
Учитель. Какие действия вы умеете
выполнять и знаете правило, как это сделать?
Какие действия с обыкновенными дробями нам
предстоит научиться выполнять?
Дети. Действия с дробями. Мы умеем
сравнивать, складывать, вычитать дроби с разными
знаменателями и эти же действия со смешанными
числами.
Учитель. Сегодня на уроке будем
работать над темой:
«Умножение дробей». Сформулируем правило
умножения дробей, научимся его применять.
Подготовительная работа (Приложение. Слайд 4)
Замените сумму произведением:
5 + 5 + 5 = 5 • 3
2 + 2 + 2 + 2 + 2 + 2 + 2 = 2 • 7
а + а + а + а + а + а = а•6
Замените произведение суммой (
3 • 5 = 3 + 3 + 3 + 3 + 3
8 • 2 = 8 + 8
b • 3 = b + b + b
4. Изучение нового материала (10 мин.)
Задача. (Приложение.
Слайд 6)
Скорость улитки см
/мин. Какое расстояние проползёт улитка за 4
минуты?
– Что неизвестно в задаче?
– Как найти расстояние, зная скорость и время? (Скорость
умножить на время)
– Мы умножать не умеем, а только складывать и
вычитать.
– Как быть?
– Как быстрее получить? (Заменить произведение
суммой одинаковых слагаемых).
• 4 = + + + =
= 2см.
Что значит умножить на 4? (Найти сумму четырёх слагаемых
каждое из которых равно
Сравните • 4 и , что интересного заметили? (Числитель дроби равен произведению числителя дроби и числа 4, а знаменатель остался без изменения.)
Попробуем сформулировать правило умножения дроби на натуральное число.
Дети выдвигают версии правила умножения дроби на натуральное число. (Приложение. Слайд 7)
– Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменений.
Записывают в буклет правило умножения дроби на число (начало правила уже вписано, нужно только закончить).
5. Закрепление новых знаний (10 мин.)
Задача: отработать навыки умножения
дроби на натуральное число и дроби на дробь.
№ 413 б, в – на доске, г – с комментированием на месте, ж, з – самостоятельно.
б)
,
.
Физкультминутка (3 мин.)
Сокращение дробей. Если верно – поднимаем руки вверх, неверно – делаем круговые движения головой. (Приложение. Слайд 9)
6/8 = 1/3; 21/49 = 3/8; 15/20 = 3/4; 16/32 = 1/3.
6. Работа с учебником (5 мин.)
Цель: научиться умножать дробь на дробь.
– Самостоятельно рассмотрите по учебнику задачу 2 на стр 71. Попробуйте сформулировать правило умножения дроби на дробь.
Дети формулируют правило, оно появляется на слайде. (Приложение. Слайд 10)
Чтобы умножить дробь на дробь, надо:
1) найти произведение числителей и произведение
знаменателей этих дробей;
2) первое произведение записать числителем, а
второе – знаменателем.
– Выполните умножение дробей (учащиеся проговаривают правило): № 419 (в; е – на доске; з; и – с комментированием с места; к; л – сам-но, 2 человека за доской).
– Нужно ли в данном случае находить отдельно
произведение числителей и произведение
знаменателей? (Нет, нужно сначала сократить
дробь, а затем умножить оставшиеся множители.)
– Прочитайте текст в учебнике на стр74 под
рубрикой «Говори правильно».
– Выполните умножение дробей (на доске):
а)
б)
– Составьте алгоритм умножения трёх и более
дробей (Приложение.
Слайд 11)
При умножении и трёх и более дробей:
- Удобнее сначала в числителе записать произведение всех числителей, в знаменателе – произведение всех знаменателей.
- Сократить получившуюся дробь.

- Выполнить умножение оставшихся множителей.
- Если надо, выделить целую часть.
7. Рефлексия (1 мин.) (Приложение. Слайд 12)
Я хорошо понял, как умножать дроби (приклеить
на круг зелёную полоску).
Я не всё понял, у меня были ошибки (приклеить на
круг жёлтую полоску).
Я не понял, как умножать дроби (приклеить на
круг красную полоску).
Приклеивают полоски на круг и показывают.
8. Домашнее задание (1 мин.) (Приложение. Слайд 13)
п.13 (1, 2), № 457 (а, б, ж, з), № 463 (а, б), дополнительное задание в буклете.
9. Итог урока (2 мин.)
Учитель. Какое открытие вы сделали для себя сегодня на уроке? Как умножить дробь на натуральное число? Как умножить дробь на дробь?
Дети. Научились умножать дробь на
натуральное число, дробь на дробь. Учащиеся
отвечают правило.
Научились умножать дробь на
натуральное число, дробь на дробь. Учащиеся
отвечают правило.
Умножение дробей. — tutomath репетитор по математике
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
Дробь \( \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.
Умножение дроби на число.

Для начала вспомним правило, любое число можно представить в виде дроби \( \bf n = \frac{n}{1}\) .
Воспользуемся этим правилом при умножении.
\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)Умножение смешанных дробей.
Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)
Умножение взаимно обратных дробей и чисел.
Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)
Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.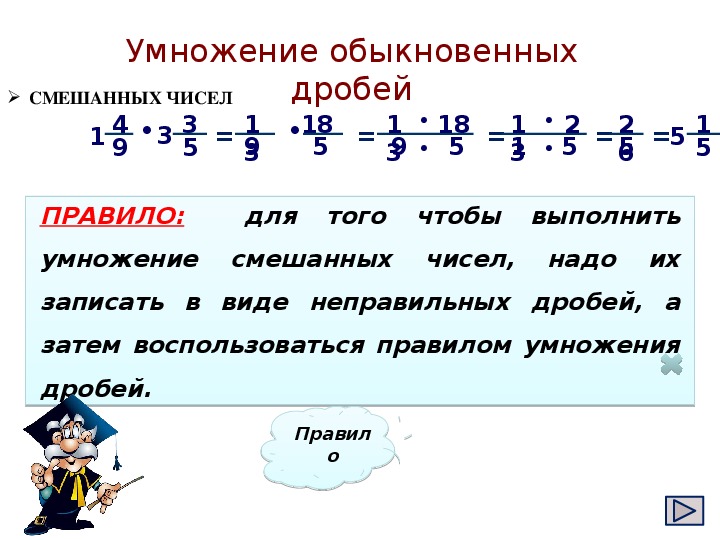
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)
Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)
Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)
Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)
Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)
Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Урок 17. Умножение дробей | Уроки математики и физики для школьников и родителей
ВИДЕО УРОК
Здесь многое придётся делать по–новому, потому что действие умножение дробей во многом отличается от умножения над натуральными числами.
Умножение обыкновенной дроби на обыкновенную дробь.
Произведением дробей называют такую дробь, числитель которой равен произведению числителей данных дробей, а знаменатель – произведению их знаменателей.

Чтобы умножить дробь на дробь, нужно умножить числитель на числитель, а знаменатель на знаменатель и первое произведение сделать числителем, а второе – знаменателем произведения.
При умножении следует делать (если возможно) сокращение.
ПРИМЕР:
Приведём пример, иллюстрирующий правило умножения обыкновенных дробей.
Рассмотрим квадрат со стороной 1 ед., при этом его площадь равна 1 ед2.
Разделим этот квадрат на равные прямоугольники со сторонами 1/4 ед. и 1/8 ед., при этом исходный квадрат будет состоять из
прямоугольников. Следовательно, площадь каждого прямоугольника составляет 1/32 долю площади исходного квадрата, то есть она равна 1/32 ед2.
 Теперь закрасим часть исходного квадрата.
Теперь закрасим часть исходного квадрата.Стороны закрашенного прямоугольника равны 5/8 ед. и 3/4 ед., значит, его площадь равна произведению дробей 5/8 и 3/4, то есть,
Но закрашенный прямоугольник состоит из 15 маленьких прямоугольников, значит его площадь равна 15/32 ед2. Следовательно,
Так как
то последнее равенство можно переписать как
что подтверждает формулу умножения обыкновенных дробей.
С помощь этого правила умножения можно умножать и правильные и неправильные дроби, и дроби с одинаковыми знаменателями, и дроби с разными знаменателями.
Выполните умножение обыкновенной дроби 7/11 на обыкновенную дробь 9/8.

Произведение числителей умножаемых дробей 7 и 9 равно 63, а произведение знаменателей 11 и 8 равно 88. Таким образом, умножение обыкновенных дробей 7/11 и 9/8 даёт дробь 63/88. Краткая запись решения:
ОТВЕТ: 63/88
Помните про сокращение полученной дроби, если в результате умножения получается сократимая дробь, и при выделении целой части из неправильной дроби.
Выполните умножение обыкновенной дроби 4/15 на обыкновенную дробь 55/6.
Применим правило умножения обыкновенных дробей:
Очевидно, что полученная дробь сократима. Выполним сокращение дроби.
НОД (220; 90) = 10.
Осталось выделить целую часть из полученной неправильной дроби:
Краткая запись решения:
ОТВЕТ: 24/9
Сокращение дроби можно проводить до вычисления произведений числителей и произведений знаменателей умножаемых дробей, то есть когда дробь имеет вид
Для этого числа
заменяют их разложениями на простые множители, после чего сокращаются одинаковые множители числителя и знаменателя.
 Решим предыдущий пример другим способом. Выполните умножение обыкновенной дроби 4/15 на обыкновенную дробь 55/6.
Решим предыдущий пример другим способом. Выполните умножение обыкновенной дроби 4/15 на обыкновенную дробь 55/6. Применим правило умножения обыкновенных дробей:
Так как
6 = 2 ∙ 3, то
Теперь сокращаем общие простые множители:
Вычислим произведения в числителе и знаменателе дроби, после чего выделим целую часть из неправильной дроби.
Краткая запись решения:
ОТВЕТ: 24/9
Для умножения дробей характерно переместительное свойство, то есть умножаемые дроби можно менять местами:
Умножение обыкновенной дроби на натуральное число.
Смысл умножения обыкновенной дроби на натуральное число выясняется из следующего определения: умножить обыкновенную дробь (множимое) на натуральное число (множитель) – значит найти эту дробь множимого.
 Чтобы умножить натуральное число на дробь, надо умножить натуральное число на числитель дроби и это произведение сделать числителем, а знаменателем подписать знаменатель данной дроби.
Чтобы умножить натуральное число на дробь, надо умножить натуральное число на числитель дроби и это произведение сделать числителем, а знаменателем подписать знаменатель данной дроби. С помощью букв правило умножение дроби a/b на натуральное число n имеет вид:
Эта формула следует из формулы умножения двух обыкновенных дробей:
Представив натуральное число как дробь со знаменателем 1, получим:
Если учесть, что целое число представляет собой дробь со знаменателем 1, то умножение дроби на целое число и целого числа на дробь можно выполнить по этому же правилу.
ПРИМЕР:
ПРИМЕР:
ПРИМЕР:
Выполните умножение дроби 2/27 на 5.
Умножение числителя 2 на число 5 даёт 10, поэтому в силу правила умножения дроби на натуральное число, произведение 2/27 на 5 равно дроби 10/27.

ОТВЕТ: 10/27
При умножении дроби на натуральное число полученную дробь часто приходится сокращать, а если она ещё и неправильная, то представить её в виде смешанной дроби. Выполните умножение дроби 5/12 на 8.
По формуле умножения дроби на натуральное число имеем:
Полученная дробь сократима. Выполним сокращение дроби. Так как
НОК (40: 12) = 4, то
Осталось выделить целую часть:
Краткое решение примера:
Сокращение можно было провести, заменив числа в числителе и знаменателе их разложением на простые множители. В этом случае решение выглядело бы так:
ОТВЕТ: 31/3
Умножение дроби на натуральное число обладает переместительным свойством, то есть произведение дроби на натуральное число, равно произведению этого натурального числа на дробь.

Умножение смешанных чисел.
Чтобы перемножить смешанные числа, нужно предварительно обратить их в неправильные дроби и потом перемножить по правилу умножения дроби на дробь.
ПРИМЕР:
Если же перемножают смешанное число на целое, то проще множить отдельно целую и дробную части. ПРИМЕР:
Законы и правила умножения натуральных чисел справедливы и для дробей. Их использование упрощает устные и письменные вычисления.
Произведение дробных чисел подчиняется переместительному, сочетательному и распределительному закону. Если один из сомножителей – целое число, то умножение может быть выполнено на основании распределительного закона. 42/5 ∙ 3 = (4 + 2/5) ∙ 3 = 4 ∙ 3 + 2/5 ∙ 3 = 12 + 6/5 = 131/5.
 97/8 ∙ 8 = 9 ∙ 8 + 7/8 ∙ 8 Если один из двух сомножителей увеличим в несколько раз, а другой оставим без изменения, то произведение увеличится во столько же раз. Если один из сомножителей уменьшим в несколько раз, а другой оставим без изменения, то произведение уменьшится во столько же раз. Умножение трёх и большего количества дробей. Свойства умножения натуральных чисел распространяются и на умножение дробей. Переместительное и сочетательное свойства умножения позволяют однозначно определить умножение трёх и большего количества дробей. При этом всё происходит по аналогии с умножением трёх и большего количества натуральных чисел. В частности, дроби и натуральные числа в произведении можно для удобства вычисления переставлять местами, а при отсутствии скобок, указывающих порядок выполнения действий, можно самим расставить скобки любым из доступных способов. 3/4 ∙ (79/31 ∙ 11/3) = (3/4 ∙ 4/3) ∙ 79/31 = (122/5 ∙ 435/17) ∙ 5/31 = (122/5 ∙ 5/31) ∙ 435/17 = 2 ∙ 435/17 = 8610/17.
97/8 ∙ 8 = 9 ∙ 8 + 7/8 ∙ 8 Если один из двух сомножителей увеличим в несколько раз, а другой оставим без изменения, то произведение увеличится во столько же раз. Если один из сомножителей уменьшим в несколько раз, а другой оставим без изменения, то произведение уменьшится во столько же раз. Умножение трёх и большего количества дробей. Свойства умножения натуральных чисел распространяются и на умножение дробей. Переместительное и сочетательное свойства умножения позволяют однозначно определить умножение трёх и большего количества дробей. При этом всё происходит по аналогии с умножением трёх и большего количества натуральных чисел. В частности, дроби и натуральные числа в произведении можно для удобства вычисления переставлять местами, а при отсутствии скобок, указывающих порядок выполнения действий, можно самим расставить скобки любым из доступных способов. 3/4 ∙ (79/31 ∙ 11/3) = (3/4 ∙ 4/3) ∙ 79/31 = (122/5 ∙ 435/17) ∙ 5/31 = (122/5 ∙ 5/31) ∙ 435/17 = 2 ∙ 435/17 = 8610/17. Выполните умножение четырёх обыкновенных дробей:
Выполните умножение четырёх обыкновенных дробей: Запишем произведение, которое нам нужно вычислить:
В силу правила умножения дробей записанное произведение равно дроби, числитель которой равен произведению числителей всех дробей, а знаменатель – произведению знаменателей.
Прежде чем вычислить произведения в числителе и знаменателе, целесообразно заменить все множители их разложениями на простые множители и провести сокращение:
ОТВЕТ: 9/280
Выполните умножение пяти чисел:
РЕШЕНИЕ: В этом произведении удобно сгруппировать дробь 7/8 с числом 8, а число 12 с дробью 5/36, это позволит упростить вычисления, так как при такой группировке очевидно сокращение. Имеем
ОТВЕТ: 116 2/3
Задания к уроку 17
Конспект урока по математике «Умножение дробей» 6 класс
Урок математики по теме: «Умножение дробей». 6-й класс
6-й класс
Цели урока:
Обучающие: 1)сформулировать правило умножения обыкновенной дроби на натуральное число, правило умножения обыкновенных дробей;
2)вырабатывать у учащихся навыки применения правил при выполнении действий.
Развивающие:
1)развитие аналитического мышления учащихся;
2)формирование умения выделять главное и обобщать.
Воспитывающие:
формирование умения организовать свою деятельность.
Тип урока: изучение нового материала.
Задачи урока:
настроить детей на рабочий лад;
повторить правила сложения, вычитания дробей; сложения и вычитания смешанных чисел;
проверить умение детей выполнять сложение и вычитание дробей;
сформулировать правило умножения обыкновенной дроби на натуральное число; правило умножения обыкновенных дробей;
отрабатывать навыки умножения дроби на натуральное число, дроби на дробь;
проверить уровень усвоения материала.
По завершении урока учащийся должен:
Знать: правило умножения дроби на натуральное число; дроби на дробь.
Уметь: умножать дробь на натуральное число, дробь на дробь.
Методы организации учебной деятельности: проблемный, объяснительно-иллюстративный, использование ИКТ.
Оборудование: учебник математики 6-й класс, автор Н. Л. Виленкин; сборник математических диктантов; мультимедийный проектор.
ХОД УРОКА
1. Организационный момент (2 мин.) (Приложение. Слайд 2)
Учитель. Эпиграф нашего урока “О, сколько нам открытий чудных готовит просвещенья дух…”. А были ли открытия в вашей жизни? Что значат слова “Я сделал открытие”? Если человек своим трудолюбием, упорством достигает истины в чем-либо, то это и есть его открытие. По этому поводу Борис Пастернак сказал:
Во всем мне хочется дойти
До самой сути.
В работе, в поисках пути,
В сердечной смуте.
До сущности истекших дней
До их причины,
До оснований, до корней,
До сердцевины
Всё время схватывая нить
Судеб, событий,
Жить, думать, чувствовать, любить
Свершать открытья.
– На сегодняшнем уроке мы тоже попытаемся совершить маленькое, но самостоятельное открытие. Для этого надо быть настойчивым и внимательным.
2. Вводный контроль (3 мин.)
Учитель. Начнём урок с повторения. (Приложение. Слайд 3)
1 вариант 2 вариант
1) 2-2/3 =1 1/3 п 1)5-7/12 =4 5/12 л
2) 2 ½-1/3 =2 1/6 л 2) 3 1/5-1/7=3 2/35 о
3) 3 1/4+4 1/5 =7 9/20 а 3) 2 1/8+3 1/3=5 11/24 м
4) 2/5-1/3 =1/15 н 4) 2/3+1/9 =7/9 а
5) 1/6+5/12=7/12 у 5) 5-3 5/6=1 1/6 т
6) 2-1 11/12 =1/12 д 6) 3/5+6/25 =21/25 ь
ПЛАНУД ЛОМАТЬ
Сначала на слайде видны примеры и таблицы ответов, затем ответы и слова.
Рассказывает учащийся, подготовленный дома.
Первое понятие дроби появилось в древнем Египте много веков назад. У многих народов дроби называли ломаными числами. Этим названием пользуется и автор первого русского учебника по математике Л.Ф.Магницкий. В русском языке слово «дробь» появилось лишь в VIII веке.
Происходит слово “дробь” от слова “дробить, разбивать, ломать на части”. Современное обозначение дробей берет своё начало в древней Индии; дробная черта появилась в записи дробей лишь около 300 лет назад. Название “числитель” и “знаменатель” ввёл в употребление греческий монах учёный-математик Максим Плануд. Для запоминания: “Человек стоит на земле”. Долгое время дроби считались самым трудным разделом математики. У немцев даже сложилась поговорка “попасть в дроби”, что означает попасть в трудное положение.
Учитель: задача сегодняшнего урока – доказать, что дроби не смогут поставить вас в трудное положение.
Какие правила вы применяли?
Как читается правило сложения, сравнения, вычитания дробей с разными знаменателями?
Как выполнить сложение смешанных чисел?
Как выполнить вычитание смешанных чисел?
Повторяем правила сложения, сравнения, вычитания дробей с разными знаменателями. Учащиеся формулируют правила.
3. Сообщение темы урока (4 мин. )
)
Учитель. Какие действия вы умеете выполнять и знаете правило, как это сделать? Какие действия с обыкновенными дробями нам предстоит научиться выполнять?
Дети. Действия с дробями. Мы умеем сравнивать, складывать, вычитать дроби с разными знаменателями и эти же действия со смешанными числами.
Учитель. Сегодня на уроке будем работать над темой:
«Умножение дробей». Сформулируем правило умножения дробей, научимся его применять.
Подготовительная работа (Приложение. Слайд 4)
Замените сумму произведением:
5 + 5 + 5 = 5 • 3
2 + 2 + 2 + 2 + 2 + 2 + 2 = 2 • 7
а + а + а + а + а + а = а•6
Замените произведение суммой (Приложение. Слайд 5):
3 • 5 = 3 + 3 + 3 + 3 + 3
8 • 2 = 8 + 8
b • 3 = b + b + b
4. Изучение нового материала (10 мин.)
Задача. (Приложение. Слайд 6)
Скорость улитки 2/3 см /мин. Какое расстояние проползёт улитка за 4 минуты?
– Что неизвестно в задаче?
– Как найти расстояние, зная скорость и время? (Скорость умножить на время)
– Мы умножать не умеем, а только складывать и вычитать.
– Как быть?
– Как быстрее получить? (Заменить произведение суммой одинаковых слагаемых).
2/3• 4 =2/3 +2/3+2/3+2/3 =8/3 = 2 2/3 см.
Что значит умножить 2/3 на 4? (Найти сумму четырёх слагаемых каждое из которых равно 2/3).
Сравните 2/3 • 4 и 8/3 , что интересного заметили? (Числитель дроби 8/3 равен произведению числителя дроби 2/3 и числа 4, а знаменатель остался без изменения.)
Попробуем сформулировать правило умножения дроби на натуральное число.
Дети выдвигают версии правила умножения дроби на натуральное число. (Приложение. Слайд 7)
– Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменений.
Записывают в буклет правило умножения дроби на число (начало правила уже вписано, нужно только закончить).
5. Закрепление новых знаний (10 мин.)
Задача: отработать навыки умножения дроби на натуральное число и дроби на дробь. (Приложение. Слайд 8)
№ 427 б, в – на доске, г – с комментированием на месте, ж, з – самостоятельно.
б) 5/18*12=5*12/18=10/3=3 1/3
в) 7/15*40=7*40/15=56/3=18 2/3
г) 7/8*24=7*24/8=21
ж) 2/3*1=2/3
з)19/20*0=0 .
Физкультминутка (3 мин.)
Сокращение дробей. Если верно – поднимаем руки вверх, неверно – делаем круговые движения головой. (Приложение. Слайд 9)
6/8 = 1/3; 21/49 = 3/8; 15/20 = 3/4; 16/32 = 1/3.
6. Работа с учебником (5 мин.)
Цель: научиться умножать дробь на дробь.
– Самостоятельно рассмотрите по учебнику задачу 2 на стр 71. Попробуйте сформулировать правило умножения дроби на дробь.
Дети формулируют правило, оно появляется на слайде. (Приложение. Слайд 10)
Чтобы умножить дробь на дробь, надо:
1) найти произведение числителей и произведение знаменателей этих дробей;
2) первое произведение записать числителем, а второе – знаменателем.
– Выполните умножение дробей (учащиеся проговаривают правило): № 433 (в; е – на доске; з; и – с комментированием с места; к; л – сам-но, 2 человека за доской).
в)4/7*5/6=10/21
е)11/12*8/9=11/27
з)11/15*3/5=11/25
и)15/16*5/9=25/48
к)12/25*9/16=27/100
л)14/17*34/63=4/9
– Нужно ли в данном случае находить отдельно произведение числителей и произведение знаменателей? (Нет, нужно сначала сократить дробь, а затем умножить оставшиеся множители.)
– Прочитайте текст в учебнике на стр71 под рубрикой «Говори правильно».
– Выполните умножение дробей (на доске):
а) 4/7*14/25*5/16=4*14*5 /7*25*16=3/10
б) 24/7*21/15*35/36=24*21*35 /7*15*36=14/9=1 5/9
– Составьте алгоритм умножения трёх и более дробей (Приложение. Слайд 11)
При умножении и трёх и более дробей:
Удобнее сначала в числителе записать произведение всех числителей, в знаменателе – произведение всех знаменателей.
Сократить получившуюся дробь.
Выполнить умножение оставшихся множителей.
Если надо, выделить целую часть.
7. Рефлексия (1 мин.) (Приложение. Слайд 12)
Я хорошо понял, как умножать дроби (приклеить на круг зелёную полоску).
Я не всё понял, у меня были ошибки (приклеить на круг жёлтую полоску).
Я не понял, как умножать дроби (приклеить на круг красную полоску).
Приклеивают полоски на круг и показывают.
8. Домашнее задание (1 мин.) (Приложение. Слайд 13)
п.13 (1, 2), № 472 (а, б, ж, з), № 478 (а, б), дополнительное задание в буклете.
9. Итог урока (2 мин.)
Учитель. Какое открытие вы сделали для себя сегодня на уроке? Как умножить дробь на натуральное число? Как умножить дробь на дробь?
Дети. Научились умножать дробь на натуральное число, дробь на дробь. Учащиеся отвечают правило.
Урок разработали
учителя математики
Гарайшина Г.Р.
Закирова Н.И.
Нуриахметов А.Р.
Так как дробь равна частному 2 : 3, то и частное от деления одного выражения на другое можно записать с помощью черты. Например, выражние (41,3 — 4,4) : (15,3 + 33,9) можно записать так: . Выполнив указанные действия, найдем значение этого выражения: 0,75 или .
Выполнив указанные действия, найдем значение этого выражения: 0,75 или .
Частное двух чисел или выражений, в котором знак деления обозначен чертой, называют дробным выражением.
Например, − дробные выражения.
Выражение, стоящее над чертой, называют числителем, а выражение, стоящее под чертой, — знаменателем дробного выражения. Числителем и знаменателем дробного выражения могут быть любые числа, а также числовые или буквенные выражения.
С дробными выражениями можно выполнять действия по тем же правилам, что и с обыкновенными дробями.
Пример 1. Найдем значение выражения .
Решение. Умножив числитель и знаменатель этого дробного выражения на 6, получим:
Пример 2. Найдем произведение и .
Решение.
Пример 3. Найдем сумму .
Решение. .
При сложении дробных выражений удобнее сначала представить их в виде обыкновенных дробей, а потом уже выполнять сложение:
.
| Табличка на двери |
«Умножение дробей» 5 класс
Муниципальное бюджетное общеобразовательное учреждение «Основная общеобразовательная школа с. Репьевка Базарно-Карабулакского муниципального района Саратовской области»
План открытого урока по математике
Абушаева Р.М.
учитель математики
2020 г.
- Педагогические цели урока
1.Создать условия для формирования и усвоения новой учебной информации.
2. Создание условий для развития мышления логики, познавательного интереса, способности к конструктивному творчеству
3. Создать условия для формирования способности учащихся к новому способу действия.
Задачи урока
Образовательные (формирование познавательных УУД):
Ознакомление уч-ся с правилом умножения обыкновенных дробей
Выработка умений умножения обыкновенных дробей и их применение к решению практических задач.
Развивающие (формирование регулятивных УУД):
Выработка умений обрабатывать информацию и ранжировать ее по компонентам; представлять информацию в виде алгоритма; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Воспитательные (формирование коммуникативных и личностных УУД):
Выработка умений слушать и вступать в диалог, участвовать в обсуждении проблемы, интегрироваться в пару, в группу со сверстником/ами и строить продуктивное взаимодействие; формирование коммуникативной компетенцию учащихся; воспитание ответственности и аккуратности.
Тип урока
Урок открытия нового знания
Планируемые образовательные результаты
Предметные
Метапредметные
Личностные
формулировать и записывать с помощью букв правило умножения обыкновенных дробей;
вычислять произведение обыкновенных дробей.
познавательные: строить логическую цепочку рассуждений;
регулятивные: осуществлять целеполагание; адекватно самостоятельно оценивать правильность выполнения действий и вносить необходимые коррективы в исполнение, как в конце действия, так и по ходу его реализации;
коммуникативные: владеть устной и письменной речью; отображать в речи содержание совершаемых действий.
Формировать готовность к самообразованию на основе мотивации учебной деятельности и личностного смысла изучения математики, заинтересованность в приобретении математических знаний и способов действий
Условия реализации урока
Информационные ресурсы (в том числе ЦОР и Интернет)
Учебная литература
Методические ресурсы (методическая литература, стратегическая технология и тактические технологии
Оборудование
Электронное приложение, презентация
дидактический материал
Методическое пособие. Групповая (парная) работа, эвристическая беседа, работа с текстом учебника.
проектор
Опорные понятия, термины
Обыкновенная дробь, произведение, числитель, знаменатель, сокращение дроби.
Форма проведения урока
Урок – исследование
Формы контроля
Блиц-опрос, фронтальная проверка, анализ результатов исследования, самостоятельная работа
ХОД УРОКА
Мотивация к учебной деятельности. Организационный момент (1-2 мин). (Включение учащихся в учебную деятельность на личностно значимом уровне).Деятельность
учителя
Название используемых ЭОР
(презентация)
Деятельность
учеников
Формируемые УУД
Здравствуйте, дорогие ребята!
(приветствие)
Я рада приветствовать Вас на уроке математики и прошу обратить внимание на доску. Прочитайте, что там написано.
Как Вы понимаете это высказывание?
Абсолютно точно! Это высказывание будет девизом нашего сегодняшнего урока! Мы будем мыслить, рассуждать, исследовать и только так получать знания по математике!
А какую тему мы изучаем, какую область математики мы «осиливаем» сейчас?
Что из этого раздела мы уже знаем и умеем?
Чтобы продуктивно работать на уроке нам нужно достать из наших сундучков знания, которые мы уже имеем. Предлагаю Вам игру «Лото».
Слайд
«Дорогу осилит — идущий, математику – мыслящий!»
присаживаются)
Дорогу осилит идущий, а математику мыслящий!
(пример ответа ученика) Я понимаю это так: если человек знает куда идти, то он осилит дорогу, также и в математике, если ты мыслишь, то встречаясь с проблемой, всегда сможешь найти способ её решения!
Мы изучаем тему «Обыкновенные дроби».
Мы умеем складывать дроби с одинаковыми, разными знаменателями, складывать и вычитать смешанные дроби.
Личностные:
Уважение личности и её достоинства, доброжелательное отношение к окружающим.
Регулятивные:
Формирование способности к организации своей деятельности.
Этап урока (название, время, цель)
Актуализация знаний (5-6мин). Выявление места и причины затруднения. (Готовность мышления и осознание потребности к построению нового способа действия учащихся).
(Проводится инструктаж игры «Лото»)
Необходимо выполнить задания на листе, полученный результат найти на соответствующей карточке и приложить её обратной стороной к заданию. В результате получится шифр. Если какое-то задание Вы выполнить не можете, положите на него знак «?».
(Контролирует выполнение заданий)
(Фронтальная работа, вместе с учащимися заполняют табло на доске, анализируют шифр)
Какой у Вас получился шифр?
(Подводит учащихся к формулировке проблемного вопроса – как умножить обыкновенную дробь на дробь).
Слайд «Игра «ЛОТО»
Выполните сложениеВыполните вычитание
Сократите дробь
Выделите целую часть из дроби
Выполните сложение
Выполните умножение
Внимательно слушают, задают вопросы, если они есть).
(Выполняют задания, пара, заполнившая карточку «Лото» поднимает руку, после того как большинство выполнили задание – фронтальная проверка)
КАК УМНОЖИТЬ ОБЫКНОВЕННУЮ ДРОБЬ НА ?
(В результате работы приходят к проблемному вопросу – как умножить обыкновенную дробь на дробь, так как решить последний пример им не удалось, в силу того, что задание новой не изученной темы)
Личностные: умение ясно, точно, грамотно излагать свои мысли в устной речи и приводить примеры
Регулятивные: Умение слушать, дополнять и уточнять, умение ориентироваться в ситуации
Познавательные: выделение существенной информации, обоснование и актуализация личного жизненного опыта
Коммуникативные: Выражать с достаточной полнотой и точностью свои мысли в соответствии с задачами и условиями коммуникации
Этап урока (название, время, цель)
Постановка учебной задачи. Целеполагание. (2 мин.)
Что ж, сегодня наши мыслительные операции будут направлены на то, чтобы найти ответ на этот проблемный вопрос, этому и посвятим наш урок. Итак, тема нашего урока… ?
Курс задан, какова цель урока?
Тема урока:
Умножение обыкновенных дробей
(формулируют с учителем тему урока, записывают её в тетрадь)
Умножение обыкновенных дробей!
Научиться умножать обыкновенные дроби, вывести правило умножения обыкновенных дробей и закрепить.
Личностные:
Ответственное отношение к учению; готовность и способность учащихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; умение ясно, точно, грамотно излагать свои мысли в устной речи, понимать смысл поставленной задачи, выстраивать аргументацию.
Коммуникативные:
Адекватно используют речевые средства и аргументируют свою позицию; представляют конкретное содержание и сообщают его в письменной и устной форме; учитывают разные мнения, владеют монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.
Познавательные:
Анализируют и осмысливают текст задачи.
Этап урока (название, время)
Проблемное объяснение нового знания. Построение проекта выхода из затруднения. Реализация построенного проекта. (Построение и фиксация нового знания) (5-6 мин).
Для достижения цели и получения ответа на проблемный вопрос предлагаю Вам выполнить небольшое исследование.
Обратите внимание на доску. Охарактеризуйте условие и данные.
Как найти площадь данного прямоугольника?
Что произойдет с площадью прямоугольника, если длину и ширину одновременно уменьшить в 10 раз?
Как это можно записать в виде равенства с обыкновенными дробями?
Но ребята, посмотрите внимательно, что у нас получилось – сами того не предполагая мы выполнили умножение обыкновенных дробей!
Проанализируйте равенство, выделите закономерности- как же выполнить умножение обыкновенных дробей.
(по схеме: УЧЕНИК-УЧИТЕЛЬ-УЧЕНИК формулируется правило)
Молодцы!!! А теперь давайте проверим верно ли вы сформулировали правило. Для этого к чему обращаемся?
Молодцы!!! Вот и наше открытие!
Запишем правило в тетради в буквенной форме.
Рассмотрим произведение дробей:
Что бы Вы здесь предприняли?
Действительно, чтобы вычисления не были слишком громоздкими, Вы можете для начала в процессе умножения сократить дроби.
Выполним это действие.
Слайд «Юный исследователь»
Чему равна площадь данного прямоугольника?
4*5=20 см2
Слайд «Результат исследования»
Дан прямоугольник со сторонами 4см и 5 см. Нужно найти площадь прямоугольника.
Нужно длину умножить на ширину и получится 20 квадратных сантиметров.
(Выслушиваются ответы)
Площадь уменьшится в 100 раз.
(внимательно изучают, предлагают свои варианты ответов)
Нужно числители перемножить и знаменатели перемножить!
(по схеме: УЧЕНИК-УЧИТЕЛЬ-УЧЕНИК формулируется правило)
Чтобы умножить обыкновенные дроби нужно числители перемножить и результат записать в числитель, знаменатели перемножить и результат записать в знаменатель.
Открывают учебник и читают правило.
записывают)
Сократили дроби.
Выполняют вместе с учителем.
Личностные:
готовность и способность учащихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию; умение контролировать процесс и результат учебной математической деятельности; коммуникативная компетентность в общении и сотрудничестве со сверстниками в образовательной, учебно-исследовательской, творческой и других видах деятельности;
Регулятивные:
Критически оценивают полученный ответ; осуществляют самоконтроль, проверяя ответ на соответствие условию; вносят изменения в результат своей деятельности, исходя из оценки этого результата самим обучающимся, учителем, товарищами.
Коммуникативные:
Адекватно используют речевые средства и аргументируют свою позицию; представляют конкретное содержание и сообщают его в письменной и устной форме; учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве, договариваются о совместной деятельности, приходят к общему решению; контролируют действия партнера; владеют монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.
Познавательные:
Моделируют в графической форме понятия, связанные с понятием обыкновенной дроби; выполняют вычисления с обыкновенными дробями; анализируют и осмысливают текст задачи, переформулируют условие, извлекают необходимую информацию, моделируют условие с помощью рисунков; строят логическую цепочку рассуждений; проводят несложные исследования, связанные со свойствами дробных чисел, опираясь на числовые эксперименты.
Этап урока (название, время, цель
Первичная проверка знаний (3 мин)
Цель: Устное закрепление материала.
А теперь, ребята, я предлагаю Вам стать настоящими экспертами! Наш любимый стеснительный друг Петя Васечкин уже решил задания и доверил Вам проверку! Найдите ошибку в данных заданиях.
(направляет деятельность учащихся на нахождение ошибок, выявление их характер)
Оцените работу этапа «Работа экспертов»
(После определения ошибки, она выделяется анимацией в примере на доске)
Слайд «Работа экспертов»
1)
2)
3)
(анализируют, находят ошибки и их характер)
Арифметическая ошибка.
Не сокращена дробь.
Неправильную дробь нужно переводить в число.
Личностные:
Умение контролировать процесс и результат учебной математической деятельности;
Регулятивные:
Критически оценивают полученный ответ; осуществляют самоконтроль, проверяя ответ на соответствие условию.
Коммуникативные:
Адекватно используют речевые средства и аргументируют свою позицию; представляют конкретное содержание и сообщают его в письменной и устной форме; контролируют действия партнера; владеют монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка.
Познавательные:
Выполняют вычисления с обыкновенными дробями.
Этап урока (название, время, цель
Релаксирующая деятельности. Физкультминутка
Цель: смена видов деятельности для релаксации
Этап урока (название, время)
Первичное закрепление с комментированием во внешней речи(5 мин)
Цель: Применение нового знания в типовых заданиях
Для закрепления правила, нужно…
(2 ученика вызываются к доске, выполняют задания)
Задания на закрепление
Вычислить:
1) 1)
2) 2)
3) 3)
Ответы:
решить примеры!
(все решают самостоятельно, затем проводят проверку решений на доске)
Этап урока (название, время, цель)
Самостоятельная работа с самопроверкой по эталону (5 мин)
Цель: Самопроверка умения применять новое знание в типовых условиях
Эмоциональный настрой обучающихся.
(Раздаются карточки с заданиями, время работы 5 минут, затем взаимопроверка).
1 вариант. 2 вариант
1.
2.
3. 3.
4.
5. 5.
Кто выполнил все 5 заданий правильно?
Кто выполнил 4 задания правильно?
(Проводится анализ: количество выполнивших заданий, количество допустивших ошибки, характер ошибок, выявляется степень усвоения материала)
1 вариант
1.
2.
3.
4.
5.
2 вариант
(Решают задания на карточке, подписывают их, затем обмениваются с соседом по парте и выполняют с помощью доски взаимопроверку).
(Проводится анализ: количество выполнивших заданий, количество допустивших ошибки, характер ошибок, выявляется степень усвоения материала )
(поднимают руки)
Личностные:
Умение контролировать процесс и результат учебной математической деятельности;
Регулятивные:
Осуществляют самоконтроль, проверяя ответ на соответствие условию; вносят необходимые дополнения и коррективы в план и способ действия в случае расхождения реального действия и его результата; вносят изменения в результат своей деятельности, исходя из оценки этого результата.
Познавательные:
Выполняют вычисления с обыкновенными дробями.
Этап урока (название, время, цель)
Включение нового знания в систему знаний и повторение (5-8 мин) Цель: Включение нового знания в систему знаний, повторение и закрепление ранее изученного
Регулятивные: Критически оценивать полученный ответ, осуществлять самоконтроль, проверять ответ на соответствие условию
Познавательные: Владеть общими приёмами решения задач
Коммуникативные:
Организовывать и планировать учебное сотрудничество с учителем и одноклассниками
Этап урока (название, время, цель)
Рефлексия учебной деятельности на уроке (итог урока) (2-3 мин)
Цель: Соотнесение цели урока и его результатов, самооценка работы на уроке, осознание метода построения нового знания
Игра «Микрофон»
Предлагаю обучающимся закончить предложения на выбор
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
(заканчивают предложения , анализируя собственную деятельность на уроке)
Регулятивные: Осознавать уровень и качество усвоения знаний и умений
Познавательные: Осуществлять анализ результатов деятельности с выделением существенных признаков
Этап урока (название, время, цель)
Домашнее задание – 3 мин
Записываем домашнее задание.
есть ли вопросы?
(контролирует запись домашнего задания в дневник или тетрадь)
Умножение дробей. Дроби. Умножение и деление дробей
Умножение целого числа на дробь – несложная задача. Но есть тонкости, в которых вы, наверняка, разбирались в школе, но с тех пор забыли.
Как умножить целое число на дробь – немного терминов
Если вы помните, что такое числитель, знаменатель и чем отличается правильная дробь от неправильной – пропустите этот абзац. Он для тех, кто совсем забыл теорию.
Числитель – это верхняя часть дроби – то, что делим. Знаменатель – нижняя. Это то, на что делим.
Правильная дробь та, у которой числитель меньше знаменателя. Неправильной называется дробь, у которой числитель больше или равен знаменателю.
Как умножить целое число на дробь
Правило умножения целого числа на дробь очень простое – умножаем числитель на целое, а знаменатель не трогаем. Например: два умножить на одну пятую – получаем две пятых. Четыре умножить на три шестнадцатых – получится двенадцать шестнадцатых.
Сокращение
Во втором примере полученную дробь можно сократить.
Что это значит? Обратите внимание – и числитель, и знаменатель этой дроби делятся на четыре. Разделить оба числа на общий делитель и называется – сократить дробь. Получим три четвертых.
Неправильные дроби
Но, предположим, мы умножили четыре на две пятых. Получилось восемь пятых. Это неправильная дробь.
Её обязательно нужно привести к правильному виду. Для это нужно выделить из нее целую часть.
Здесь нужно использовать деление с остатком. Получаем единицу и три в остатке.
Одна целая и три пятых и есть наша правильная дробь.
Привести к правильному виду тридцать пять восьмых – задача чуть посложнее.Самое близкое к тридцати семи число, которое делится на восемь – это тридцать два. При делении получим четыре. Отнимем от тридцати пяти тридцать два – получим три. Итог: четыре целых и три восьмых.
Равенство числителя и знаменателя. А тут все очень просто и красиво. При равенстве числителя и знаменателя получается просто единица.
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.
Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.
Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.
Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.
Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)
Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.
Умножение дроби на число.
Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .
Воспользуемся этим правилом при умножении.
\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)
Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)
Умножение смешанных дробей.
Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)
Умножение взаимно обратных дробей и чисел.
Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)
Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)
Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)
Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)
Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)
Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)
Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Умножение дробей — как умножить дроби?
Умножение дробей начинается с умножения заданных числителей, за которым следует умножение знаменателей. Затем результирующая дробь дополнительно упрощается и при необходимости сокращается до самых низких значений.
Есть интересный стишок для запоминания приведенных выше шагов. «Умножение дробей — не большая проблема; верхнее умножение на верхнее нижнее умножение на низ. И не забывайте упрощать, пока не пришло время прощаться.»Теперь давайте заглянем в будущее, чтобы узнать больше об умножении дробей.
Введение в умножение дробей
Умножение дробей не похоже на сложение или вычитание дробей, где знаменатель должен быть одинаковым. Здесь любые две дроби с разными знаменателями легко перемножаются. Единственное, что следует иметь в виду, это то, что дроби не должны быть в смешанной форме, они должны быть либо правильными, либо неправильными дробями.Давайте узнаем, как умножать дроби, выполнив следующие шаги:
- Умножьте числители.
- Умножить знаменатели.
- Уменьшите полученную фракцию до наименьшего значения.
Например, умножим следующие дроби: 2/3 × 4/5. Начнем с умножения числителей: 2 × 4 = 8, затем знаменатели: 3 × 5 = 15. Это можно записать как (2 × 4) / (3 × 5) = 8/15. Теперь продукт уже находится на самом низком уровне, поэтому нам не нужно его сокращать, и мы даем это в качестве ответа.
Визуальное представление умножения дробей
Теперь давайте посмотрим на визуальное представление умножения дробей. Визуализация умножения дробей с использованием дробных квадратов — очень интересный метод для понимания концепции. Вы знаете, что такое дробные квадраты? Дробные квадраты — это представление данной дроби в форме квадратов, где числитель обозначен заштрихованной частью. Давайте посмотрим, как умножить дробь с помощью дробных квадратов.Умножим эти две дроби: 2/3 × 1/2.
На приведенном выше рисунке дробный квадрат слева состоит из 2 частей, заштрихованных оранжевым, из 3 равных частей. Эта оранжевая область представляет две трети дробного квадрата. Точно так же вторая заштрихованная область представляет половину квадрата дроби. Умножив эти две дробные квадраты, мы получим 2/6. Его можно свести к простейшему виду и представить в виде одной части из трех квадратов. Таким образом, 2/3 × 1/2 = 2/6 = 1/3. Теперь, когда у вас есть представление об умножении дробей, давайте продолжим изучение этой темы.
Умножение дробей
Умножение дробей на целые числа: Умножение дробей на целые числа — простая идея. Давайте рассмотрим этот пример: 4 × 2/3. Сначала мы представим этот пример с помощью дробных квадратов. Четыре раза две трети представлены как:
Теперь заменим полученную неправильную дробь на смешанную. 8/3 = \ (2 \ frac {2} {3} \). Две целых и две трети, что равно 8/3.В итоге получаем следующее представление.
Умножение правильных дробей: Умножение правильных дробей — самый простой из всех. Например, возьмем 2/3 × 4/6. Здесь 2/3 и 4/6 — правильные дроби. Чтобы их умножить, сделаем следующие шаги:
- Умножим числители вместе: 2 × 4 = 8.
- Затем умножьте знаменатели вместе: 3 × 6 = 18. Это также можно записать как: (2 × 4) / (3 × 6) = 8/18.
- Затем уменьшите полученную дробь до наименьшего значения, равного 4/9.
Умножение неправильных дробей: Теперь давайте разберемся с умножением неправильных дробей. Мы уже знаем, что неправильная дробь — это такая дробь, у которой числитель больше знаменателя. Умножая две неправильные дроби, мы часто получаем неправильную дробь. Например, чтобы умножить 3/2 × 7/5, которые являются двумя неправильными дробями, нам нужно предпринять следующие шаги:
- Умножьте числители и знаменатели.(3 × 7) / (2 × 5) = 21/10.
- Дробь 21/10 не может быть далее уменьшена до наименьшего значения.
- Следовательно, ответ: 21/10, что можно записать как \ (2 \ frac {1} {10} \).
Умножение смешанных дробей: Смешанные дроби — это дроби, состоящие из целого числа и дроби, например \ (2 \ frac {1} {2} \). При умножении смешанных дробей нам нужно преобразовать смешанные дроби в неправильную дробь перед умножением. Например, если это число \ (2 \ frac {2} {3} \), вы должны изменить его на (3 × 2 + 2) / 3 = 8/3.Рассмотрим пример. Чтобы умножить \ (2 \ frac {2} {3} \) и \ (3 \ frac {1} {4} \), можно использовать следующие шаги:
- Заменить указанные смешанные фракции на неправильные. (8/3) × (13/4)
- Умножьте числители неправильных дробей, а затем умножьте знаменатели. Это даст 104/12.
- Теперь уменьшите полученную дробь до наименьшего значения, что составит 26/3.
- Далее, преобразует ответ обратно в смешанную дробь, которая будет: \ (8 \ frac {2} {3} \)
Обратите внимание, что в приведенном выше примере показано, как смешанные дроби могут быть представлены дробными квадратами.Первые два блока показывают целое число 2, а третий представляет дробь 2/3. Теперь, когда мы увидели умножение дробей в различных формах, давайте пересмотрим шаги, которые объясняют, как умножаются две данные дроби. На следующем рисунке показаны шаги умножения двух смешанных дробей.
Важные примечания:
Вот несколько важных примечаний, которые помогут при умножении дробей.
- Обычно учащиеся упрощают дробь после умножения.Однако, чтобы упростить вычисления, проверьте, находятся ли уже две умножаемые дроби в их низших формах. Если нет, сначала упростите их, а затем умножьте. Например, \ (\ begin {align} \ frac {4} {12} \ times \ frac {5} {13} \ end {align} \) будет сложно умножить напрямую.
- Теперь, если мы сначала упростим дробь, мы получим: \ (\ begin {align} \ frac {1} {3} \ times \ frac {5} {13} = \ frac {5} {39} \ end { выровнять}\).
- Упрощение также может быть выполнено для двух дробей. Если есть общий множитель между числителем одной дроби и знаменателем другой дроби, вы можете упростить их и продолжить.Например, \ (\ begin {align} \ frac {5} {28} \ times \ frac {7} {9} \ end {align} \) можно упростить до \ (\ begin {align} \ frac {5 } {4} \ times \ frac {1} {9} \ end {align} \) перед умножением.
Часто задаваемые вопросы об умножении дробей
Как умножить дроби?
Чтобы умножить любые две дроби, мы можем выполнить следующие шаги:
- Умножьте числители.
- Умножить знаменатели.
- Упростите полученную дробь до наименьших значений.
Как умножить смешанные дроби?
Для умножения смешанных дробей можно использовать следующие шаги:
- Заменить смешанную дробь на неправильную.
- Упростите, если возможно.
- Умножьте числители, а затем знаменатели.
- Убедитесь, что ответ дан в кратчайшие сроки
Как умножить дробь на целое число?
Чтобы понять умножение дроби на целое число, мы можем взять простой числовой пример умножения.2/7 × 3. Начните с переписывания целого числа (3 в этом примере) в виде дроби, 3/1. Теперь мы можем применить шаги, которые мы используем для умножения дробей.
2/7 × 3/1 = (2 × 3) / (7 × 1) = 6/7.
Как умножить дробь на дробь?
Умножение двух дробей — это простейшая форма арифметических операций между двумя дробями. Сначала нужно умножить числители обеих дробей, а затем — знаменатели. Затем, при необходимости, результирующая дробь упрощается до самых низких значений.
Как решать дроби?
Решение дробей состоит из двух простых шагов. Во-первых, фракции, если они даны в форме смешанных фракций, должны быть преобразованы в неправильные фракции. Затем мы можем выполнить необходимые арифметические операции между дробью и упростить ответ до самых младших членов.
Как складывать или умножать дроби?
Сложение дробей отличается от умножения дробей. При умножении сначала умножаются числители двух дробей, затем знаменатели умножаются, чтобы получить результирующую дробь.Но в процессе сложения дробей нам сначала нужно уравнять знаменатели обеих дробей, а затем мы складываем числители, чтобы получить результирующую дробь.
Какое правило умножается на дроби?
Есть два простых правила умножения дробей. Сначала умножьте числители, а затем знаменатели обеих дробей, чтобы получить результирующую дробь. Во-вторых, нам нужно упростить полученную дробь, чтобы получить окончательный ответ. Это можно понять на простом примере.2/6 × 4/7 = (2 × 4) / (6 × 7) = 8/42 = 4/21
Как научить умножению дробей?
Умножению дробей можно научить так же, как и умножению целых чисел. Важным аспектом перед умножением дробей является преобразование смешанной дроби в неправильную дробь. После этого шага мы умножаем числители обеих дробей, а затем знаменатели обеих дробей, чтобы получить результирующую дробь.
Умножение дробей на дроби — бесплатный урок с видео
На этом уроке 5-го класса ученики сначала замечают сокращение для умножения дробей типа 1 / n (например, 1/3 x 1/4).Отсюда мы приходим к общему ярлыку или правилу умножения дробей. Урок также содержит много словесных задач.
В видео ниже я сначала объясняю, как это (1/2) x (1/3) означает 1/2 от 1/3, и мы находим это визуально. Далее мы находим, что составляет 2/3 от 1/4. Во-первых, мы находим 1/3 от 1/4 как 1/12. Следовательно, 2/3 должно быть вдвое больше, или 2/12. После введения быстрого способа умножения дробей (умножение числителей, умножение знаменателей) я решаю несколько простых задач и задачу со словами.Наконец, в видео я обосновываю общее правило дробного деления.
Мы изучили, как найти дробную часть целого числа с помощью умножения.
Обратите внимание слово из переводит здесь в УМНОЖЕНИЕ . | |||||||||||||||||||||||
| Мы можем использовать ту же идею, чтобы найти дробную часть из дробь ! | |||||||||||||||||||||||
|
| ||||||||||||||||||||||
1.Найдите дробную часть данного
доля. Вы можете представить себе оставшийся кусок пиццы, который вы должны
разделить поровну с одним, двумя или тремя другими людьми. Напишите предложение умножения.
|
|
| |||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||
| |||||||||||||||||||||||||||
| Сокращение: умножение дробей типа 1/ n Для умножения дробей вида 1/ n , где
|
2.Умножить.
|
|
|
Теперь мы изучили, как найти 1/2, 1/3 или 1/5
некоторых фракций. А как насчет того, чтобы найти
Мы можем использовать ту же идею при нахождении дробной части из другая дробь. | ||||||||||||||||||||
| ||||||||||||||||||||
| ||||||||||||||||||||
| Умножение дроби на дробь означает получение дроби
часть из дроби. Это все равно, что взять определенную часть остатки, когда то, что осталось, — это дробь. |
3. На фотографиях видно, сколько пиццы осталось, и вы получаете
определенная часть остатков. Сколько
вы получите? Раскрасьте картинку, чтобы показать ответ.
4. Решите произведение умножения, используя две подсказки. умножения. Наконец, по возможности упростите.
Первая находка 1/3 от 1/8, затем умножьте результат на 2.
|
Первая находка 1/4 от 1/10, затем умножьте результат на 3.
| ||||||||||||||||||||||||||||||||||
Первая находка 1/5 от 1/6, затем умножьте результат на 3.
|
Первая находка 1/6 из 1/9, затем умножьте результат на 5.
| ||||||||||||||||||||||||||||||||||
|
|
| Ярлык для умножения дробей Умножьте числители, чтобы получить
числитель для ответа. | |||||||||||
| Изучите примеры справа. Не забывайте всегда отдавать
окончательный |
| ||||||||||
| |||||||||||
5.Умножить. Дайте свои ответы в кратчайшие сроки (упрощенно) и, если возможно, в виде смешанных чисел.
|
| ||||||||
|
| ||||||||
|
|
| СРАВНИТЬ | ||||||||||||||||||||||||||||||||||
| Объездной путь | Ярлык | |||||||||||||||||||||||||||||||||
Первая находка 1/6 от 1/2, затем умножьте результат на 5.
|
| |||||||||||||||||||||||||||||||||
Найти
1/8 из 3/5, затем умножьте этот результат на 2.И чтобы найти
|
| |||||||||||||||||||||||||||||||||
| «Окольными путями» мы производим каждое умножение отдельно. В ярлык, мы можем просто сделай их все сразу. | ||||||||||||||||||||||||||||||||||
6. Умножить. Дайте свои ответы в краткой форме (упрощенно) и как смешанные числа, если возможно.
|
| ||||||||||
|
| ||||||||||
|
| ||||||||||
|
|
7. Осталась 1/4 пиццы. Мари съела 2/3 из этого.
а. Какую часть пиццы оригинальной она ела?
г. Какая часть пиццы оригинала осталась сейчас?
8. Тереза покрасила 5/8 комнаты.
а. Какая часть еще осталась покрасить?
г. Итак, Тереза нарисовала половину того, что
все еще оставалось.
Нарисуйте столбиковую модель ситуации.
Какая часть комнаты еще осталась
рисовать?
9. Тед выполнил 2/3 работы, порученной ему боссом.
а. Что еще осталось сделать?
г. Теперь Тед выполнил треть того, что еще оставалось
делать.
Нарисуйте столбиковую модель ситуации.
Какая (дробная) часть
исходная работа все еще не выполнена?
Какая часть завершена?
| 10. Салли хочет приготовить 1/3 рецепта справа. Сколько она потребность каждого ингредиента? |
|
| 11.Для предстоящей тусовки Элисон нужно приумножить
рецепт кофе . Предположим, что половина гостей пьет на одну порцию, половину другой порции и две порции. Находить сколько ей понадобится кофе , если есть: a. 30 гостей г. 50 гостей г. 80 гости. |
Здесь вы можете найти бесплатные распечатанные рабочие листы для умножения дробей на дроби. Этот урок взят из книги Марии Миллер Math Mammoth Fractions 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер. Пошаговый калькулятор для умножения и деления дробейКак умножить дроби с разными знаменателями?Так же, как вы их умножаете, если бы у них был одинаковый знаменатель! Ознакомьтесь с нашим руководством ниже для получения более подробной информации. Общие вопросы
Умножение и деление дробей может показаться запутанным, но на самом деле это намного проще, чем сложение и вычитание дробей. Главное помнить, что если у нас есть одно и то же число в числителе и знаменателе, они сокращаются: 5 × 35 × 2 = 5 × 35 × 2 = 32Посмотрите наш пример ниже. или попробуйте наш калькулятор . 352 ÷ 620
Калькулятор умножения и деления дробейПопробуйте сами — введите две дроби, чтобы умножить или разделить. Вычислить 👏🏿👏🏾👏🏼
ДалееУмножение дробей — обучение с видом на горыМы закончили сложение и вычитание дробей прямо перед перерывом, и теперь мы ударяем по умножению и делению дробей. Мы начали с умножения дробей и составили мега-якорную диаграмму. Я обучаю студентов TAG 4-го класса, поэтому технически я преподаю им стандарты 5-го класса, но им часто требуется пересмотр стандартов 4-го класса, поэтому мы объединили все это в один. Вот наша диаграмма привязки больших умножающихся дробей! Мы рассмотрели умножение целых чисел на дроби, умножение дробей на дроби и умножение смешанных чисел. Ух! Поскольку часть общего ядра требует, чтобы они использовали визуальные модели областей для умножения дробей, мы немного повеселились с калькой! Каждый ребенок получил по два одинаковых листа кальки и разбил их на части. Затем, когда вы кладете их друг на друга, вы можете увидеть, где они образуют модель области, которая совпадает с умноженными знаменателями, а перекрывающиеся цветные секции являются вашим числителем.Им это понравилось! Мы повесили их на окно, потому что, когда мы делали это таким образом, вы действительно могли видеть перекрытие на кальке. Дети также скопировали заметки в свой математический журнал, а затем показали пошаговые модели площадей. Они также использовали кальку для этого, но они показали шаги, чтобы добраться до окончательной модели области. Нам было так весело практиковаться в умножении дробей! (Мой вид на горы сегодня был покрыт облаками и туманом! Я был так огорчен.) Наконец, мы поработали над карточками задач на умножение дробей.Я пишу о них в Уголке карточек задач, потому что они являются отличным примером того, как я формирую карточки задач, чтобы различать и удовлетворять потребности студентов. Но вот вам возможность взглянуть на них! Если вам нужны карточки с заданиями на умножение дробей, вы можете купить их всего за 2,25 доллара в моем магазине TpT.Если вы ищете еще больше ресурсов для обучения операциям с дробями, зайдите в мой магазин и посмотрите пакет ресурсов Ultimate Fraction Operations! Просмотры сообщений: 1 201 Рабочие листы по умножению дробейУмножение пар дробей.По возможности упрощайте ответы. Включает две задачи со словами. 4-6 классы Зарегистрированные участники могут использовать шкаф для документов Суперучитель, чтобы сохранять свои любимые рабочие листы. Быстрый доступ к наиболее часто используемым файлам И настраиваемым рабочим листам! Пожалуйста, войдите в свою учетную запись или станьте участником и присоединитесь к нашему сообществу сегодня, чтобы воспользоваться этой полезной функцией. В этом рабочем листе есть поле с пояснениями, чтобы показать студентам, как умножать дроби, а также 11 практических задач. 5-е и 6-е классы Умножайте дроби для решения каждой задачи со словами. Обязательно упростите, если возможно, и покажите свою работу. С 4-го по 6-й классы Разрежьте и используйте эти 30 карточек с заданиями для дополнительной практики, обучения в небольших группах, охоты за мусором в классе или занятий со сверстниками. 5 и 6 классы Фигуры с дробями отображаются вверху страницы. Ученики умножаются на фракции одинаковой формы. Пример: Умножьте дроби на шестиугольники. С 4-го по 6-й классы Умножение дробей на целые числаНа этом рабочем листе есть визуальные представления задач умножения дробей. 5-й класс Решите эти задачи на умножение дробей о поездке в ремесленный магазин. 4-6 классы Каждая из этих задач со словами требует, чтобы учащиеся умножили целое число на дробь или другое целое число. 5-е и 6-е классы Эти задачи со словами требуют от учащихся умножать дроби на целые числа. 4-й и 5-й классы Вот 30 карточек с заданиями, которые вы можете использовать на своей документ-камере, для обучения в небольших группах или для классных игр. 5-е и 6-е классы Смешанные навыки: умножение дробей, целых чисел и смешанных чиселИспользуйте математические вычисления для сравнения произведений дробей и целых чисел на дроби. 5 класс Определите, что произойдет, если вы умножите неправильную дробь на целое число.Будет ли произведение больше или меньше 1? Что произойдет, если умножить обычную дробь на целое число? Будет произведение больше или меньше 1? 5 класс Умножение дробей | NZ MathsНазначение Цель этой серии уроков — развить понимание умножения дробей. Конкретные результаты обучения
Описание математики Эта серия уроков основана на понимании учащимися и использовании эквивалентных дробей при решении задач на сложение и вычитание дробей. Как и в предыдущих разделах работы, упор делается на то, чтобы учащиеся моделировали операции с дробями, используя ряд материалов и записывали, используя слова и символы. Хорошие знания об основах умножения и деления имеют основополагающее значение для успешной работы учащихся с эквивалентными дробями и их понимания, а в этом разделе — умножения дробей. Есть три ключевых понятия, лежащих в основе умножения дробей. Во-первых, умножение двух дробей предполагает нахождение дроби от другой дроби. Например, 1/2 x 1/4 интерпретируется как 1/2 от 1/4. Во-вторых, когда умножаются две дроби меньше единицы, произведение всегда меньше любого из множителей. Умножая целые числа, учащиеся ожидают, что произведение окажется больше любого из этих множителей. Умножение дробей требует концептуального сдвига для студентов, которые должны четко понимать, что они находят часть части.В-третьих, понимая свойство коммутативности, студенты могут упростить задачи, изменив порядок факторов. При умножении дробей учащиеся начинают понимать, что слова «времена» и «из» взаимозаменяемы. Использование модели массива для визуализации и решения проблем, связанных с нахождением дробной части, путем разбиения области на части, по горизонтали и вертикали, способствует переходу от понимания целого числа к дробному. Начиная с задач, связанных с работой с частями агрегата без подразделения (например,1/3 из 3/8), устанавливает концептуальное понимание операции умножения с дробями. Как только это будет ясно понято, работа с частями единицы, которые включают подразделение (например, 3/4 из 2/3), сосредотачивает внимание студентов на записи и вычислениях, поскольку они исследуют отношения между числами. Использование реалистичного контекста для нахождения дробных частей очень важно. Если учащиеся ответят на эти вопросы и создадут собственный контекст, это поможет им осознать практическое применение умножения дробей. Эти идеи представлены в пяти занятиях, однако, поскольку они включают сложные концепции, которые имеют фундаментальное значение для успеха ученика с дробями, эти занятия можно продлить на более длительный период времени. Хотя игры вводятся и используются на занятиях для обобщения идей, их также можно добавить к занятиям в классе или группе, или отправить домой для семейных задач и развлечения. Необходимые ресурсные материалы Деятельность Сессия 1 SLO:
Деятельность 1
Деятельность 2
Деятельность 3
Сессия 2 SLO:
Деятельность 1 См. Проблему 1 из сеанса 1. Деятельность 2 Напишите в таблице классов Деятельность 3 Изучите дроби дробей: 1/2 от 4/9 = 2/9 Имейте они обсуждают свои аналитические доски с партнером. Деятельность 4 Попросите учащихся найти свою копию Приложения 1 (Сессия 1, Задание 2, Шаг 3). Попросите учащихся записать уравнения для каждого из примеров. Деятельность 5
Сессия 3 SLO:
Деятельность 1
Деятельность 2 Учащиеся играют в игру Умножение (Приложение 3)
Деятельность 3
Деятельность 4
Сессия 4 SLO:
Деятельность 1
Деятельность 2
Деятельность 3
Деятельность 4
Деятельность 5 Завершите занятие, предложив учащимся предложить сводные утверждения для сегодняшнего обучения и записать их в таблице класса. Сессия 5 SLO:
Деятельность 1
Деятельность 2 Попросите учащихся сформировать пары. Раздайте карты из Приложения 4 каждой паре. Пусть пары рассортируют карты по стопкам «Истина» и «Ложь». Затем пары должны делиться парами, по очереди читать карточку и обсуждать, и обосновывают свое решение , используют примеры . Деятельность 3
Домашняя ссылка Уважаемые родители и ванау, Мы изучали умножение дробей и были бы признательны, если бы вы поиграли со своим ребенком в игру « Умножение ».Карты включены в колоду. Вашему ребенку будет приятно объяснить инструкции к игре, как в нее играли в классе. Мы надеемся, что вам тоже понравится. Рабочий лист умножения дробейДобро пожаловать на нашу страницу рабочих листов по умножению дробей. Здесь вы найдете ряд бесплатных листов для печати и поддержку, чтобы помочь Ваш ребенок научится умножать дроби на целые или другие дроби. У нас есть калькулятор, который поможет вам умножить две дроби. Вы можете умножать смешанные числа или дробь на целое число. Все тренировки показаны поэтапно, поэтому вы можете увидеть, как они работают. Эта страница поддержки поможет вам узнать все о том, как умножать дроби вместе. Есть несколько рабочих примеров и вспомогательный лист для печати. Здесь вы найдете подборку разработанных рабочих листов дроби. чтобы помочь ребенку понять, как умножить дробь на другая дробь или умножение дроби на целое число. Листы тщательно сортируются так, чтобы самые легкие листы идет первым, а самый сложный лист — последний. Прежде чем ваш ребенок займется умножением дробей, его следует умеет переводить неправильные дроби в смешанные числа, а также используя простейшую форму. Использование этих листов поможет вашему ребенку:
Для умножения смешанных дробей воспользуйтесь ссылкой ниже! Взгляните на некоторые из наших других страниц поддержки умножения и деления дробей, если вам нужна дополнительная помощь. с умножением или делением дробей. У нас есть другие рабочие листы, которые помогут вашему ребенку научиться и практиковаться в умножении и делении дробей. Все листы тщательно сортируются с разными уровнями поддержки. Взгляните на наш полный ассортимент ниже. На этой странице поддержки показано, как преобразовать неправильные дроби. в смешанные числа и как преобразовать смешанные числа в неправильные дроби. Вы также найдете вспомогательные листы для печати и несколько Практикуйте рабочие листы по математике для этого навыка изучения дробей. Это также иногда называют сокращением дробей до их простейшей формы. Это предполагает деление числителя и знаменателя на общий коэффициент, чтобы уменьшить дробь до эквивалентной дроби с наименьший возможный числитель и знаменатель. На приведенной ниже странице дроби для печати содержится дополнительная информация, примеры и практика по упрощению дробей. Саламандры по математике надеются, что вам понравятся эти бесплатные распечатываемые рабочие листы по математике. | |||||||||||||||||||||||||||||||||||

