| Табличка на двери |
Умножить на 0,25. Умножение дроби на число. Умножение дробей на целое число.
- Альфашкола
- Статьи
- Как легко умножить на 0,25
В этой статье ты узнаешь как легко умножить любое число на \(0,25\), для этого тебе даже не понадобится калькулятор. \(0,25-\) это десятичная дробь приведём её к виду обыкновенной дроби:
При умножении на \(0,25\) можно заменить умножением на \(\frac{1}{4}\). Обратная дробь одной четвертой \(-4\) То есть для того чтобы умножить на \(0,25\) надо разделить на \(4.\) Легко не так ли?
Пример 1. Умножьте \(12\) на \(0,25\).
Решение: \(12*0,25=12*\frac{1}{4}=12:4=3\)
Ответ: \(3\).
Пример 2. Умножьте \(36\) на \(0,25\).
Решение: \(36*0,25=36*\frac{1}{4}=36:4=9\)
Ответ: \(9\).
Пример 2. Умножьте \(100\) на \(0,25\).
Решение: \(100*0,25=100*\frac{1}{4}=100:4=25\)
Ответ: \(25\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Алесандр Викторович Рудаков
Репетитор по математике
Стаж (лет)
Образование:
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике для 5 классов и по информатике для 7-9 классов, подготовка к ОГЭ. Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку.
Самые сложные темы по математике на моих занятиях станут для вас очень простыми. Подготовлю вас к ВПР по математике, к ОГЭ по информатике. Пропагандирую сотрудничество на равных, дружественная атмосфера на занятиях. Индивидуальный подход к каждому ребенку.
Денис Александрович Косвинцев
Репетитор по математике
Стаж (лет)
Образование:
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Курс информатики с 7 по 11 класс. Подготовка к ОГЭ и ЕГЭ (на не Microsoft-ПО). Практические занятия по программированию на Python, Pascal, C или Java и в офисном пакете LibreOffice. Индивидуальные программы обучения по выборочным темам.
Подготовка к ОГЭ и ЕГЭ (на не Microsoft-ПО). Практические занятия по программированию на Python, Pascal, C или Java и в офисном пакете LibreOffice. Индивидуальные программы обучения по выборочным темам.
Олеся Гвидоновна Сиротенко
Репетитор по математике
Стаж (лет)
Образование:
Могилевский государственный университет им А.А. Кулешова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 8-11 классов. Занимаюсь подготовкой к сдаче ОГЭ, ЕГЭ. В преподавании считаю самым главным комфортную атмосферу и доверие. Помогаю ученикам не бояться ошибок. Считаю, что умение помочь ученику поверить в свои силы, увидеть свой потенциал — это миссия каждого учителя!
В преподавании считаю самым главным комфортную атмосферу и доверие. Помогаю ученикам не бояться ошибок. Считаю, что умение помочь ученику поверить в свои силы, увидеть свой потенциал — это миссия каждого учителя!
Похожие статьи
- Формула площади эллипса
- Cреднее арифметическое: примеры решения
- Как легко разделить на 0,1; 0,01; 0,001
- Как построить график гиперболы?
- Как написать каноническое и параметрическое уравнение прямой, образованной пересечением плоскостей
- Интеграл с переменным верхним пределом
- Задачи с показательными уравнениями и неравенствами
- Задачи с прикладным содержанием (вариант 4)
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Умножение дробей.
 — tutomath.ru репетитор по математике
— tutomath.ru репетитор по математикеЧтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
\( \frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)
Дробь \( \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.
Умножение дроби на число.
Для начала вспомним правило, любое число можно представить в виде дроби \( \bf n = \frac{n}{1}\) .
Воспользуемся этим правилом при умножении.
\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)
Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)
Умножение смешанных дробей.
Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)
Умножение взаимно обратных дробей и чисел.

Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)
Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)
Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)
Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)
Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)
Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)
Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Умножение дробей — интернет энциклопедия для студентов
УМНОЖЕНИЕ ДРОБИ НА ЧИСЛА
Умножение дроби \(\ \frac{a}{b} \) на число \(\ n \) эквивалентно добавлению тех же терминов:
Таким образом, мы можем сделать вывод, что для умножения дроби на число необходимо умножить числитель этой дроби на это число и оставить знаменатель без изменений.
ПРИМЕР
Аналогично умножение чисел на дробь.
ПРИМЕР:
УМНОЖЕНИЕ ДРОБЕЙ
Определение
Произведение дробей называется такой дробью, числитель которой равен произведению числителей исходных дробей, а знаменатель — произведением их знаменателей:
\(\ \frac{a}{b} \cdot \frac{c}{d}=\frac{a \cdot c}{b \cdot d} \)
Таким образом, чтобы умножить дробь на дробь, необходимо умножить числитель первой дроби на числитель второй и записать результат в числитель; и умножьте знаменатели и запишите результат в знаменатель.
Комментарий. При выполнении умножения, по возможности, следует уменьшить. Вы можете уменьшить только числа в числителе с числами в знаменателе. Числитель с числителем и знаменатель со знаменателем не могут быть уменьшены.
ПРИМЕР
 \(\
\frac{1}{3} \cdot \frac{4}{5}=\frac{1 \cdot 4}{3 \cdot 5}=\frac{4}{15}
\)
\(\
\frac{1}{3} \cdot \frac{4}{5}=\frac{1 \cdot 4}{3 \cdot 5}=\frac{4}{15}
\)ПРИМЕР
УМНОЖЕНИЕ СМЕШАННЫХ ДРОБЕЙ
Чтобы умножить смешанные дроби, вам нужно представить их в виде неправильных дробей, а затем умножить на обычные дроби.
ПРИМЕР
\(\ 3 \frac{1}{3} \cdot 4 \frac{2}{5}=\frac{3 \cdot 3+1}{3} \cdot \frac{4 \cdot 5+2}{5}=\frac{10}{3} \cdot \frac{22}{5}= \)
Чтобы умножить смешанную дробь на целое число, сделайте то же самое или умножьте дробь на число, или умножьте целую часть на целое число, а дробную часть смешанного числа отдельно.
ПРИМЕР
Или же
\(\ =(6+1)+\frac{1}{2}=7+\frac{1}{2}=7 \frac{1}{2} \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Сложение дробей Приведение дробей к общему знаменателю Сокращение дроби Правильные и неправильные дроби. Смешанные дроби.
Смешанные дроби.
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Умножение дробей, деление дробей
Умножение обыкновенных дробей
Определение 1
Умножение дробей рассматривается как действие нахождения дроби от дроби.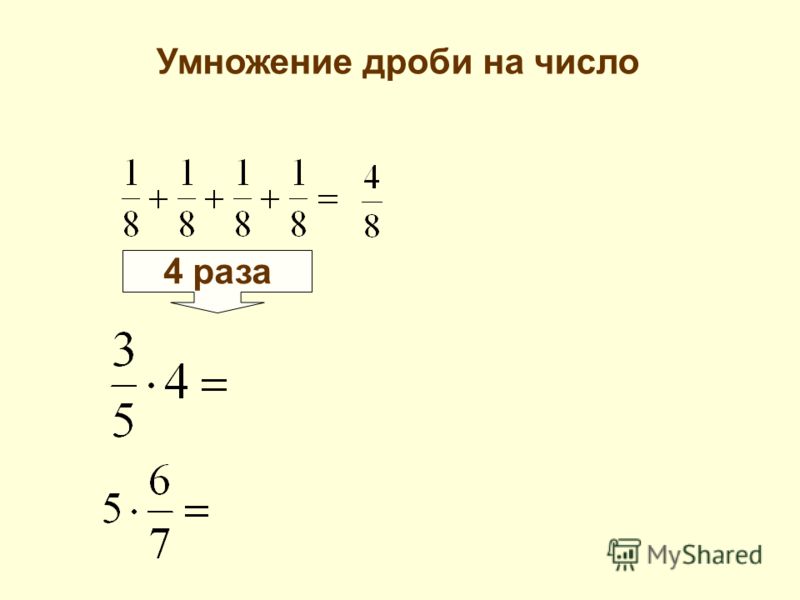
Рассмотрим пример.
Пусть на тарелке лежит $\frac{1}{3}$ часть яблока. Нужно найти $\frac{1}{2}$ часть от нее. Необходимая часть является результатом умножения дробей $\frac{1}{3}$ и $\frac{1}{2}$. Результат умножения двух обыкновенных дробей — это обыкновенная дробь.
Умножение двух обыкновенных дробей
Правило умножения обыкновенных дробей:
Результатом умножения дроби на дробь является дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей:
Пример 1
Выполнить умножение обыкновенных дробей $\frac{3}{7}$ и $\frac{5}{11}$.
Решение.
Воспользуемся правилом умножения обыкновенных дробей:
\[\frac{3}{7}\cdot \frac{5}{11}=\frac{3\cdot 5}{7\cdot 11}=\frac{15}{77}\]
Ответ: $\frac{15}{77}$
Если в результате умножения дробей получается сократимая или неправильная дробь, то нужно ее упростить.
Пример 2
Выполнить умножение дробей $\frac{3}{8}$ и $\frac{1}{9}$.
Решение.
Используем правило умножения обыкновенных дробей:
\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}\]
В результате получили сократимую дробь (по признаку деления на $3$. Числитель и знаменатель дроби разделим на $3$, получим:
\[\frac{3}{72}=\frac{3:3}{72:3}=\frac{1}{24}\]
Краткое решение:
\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}=\frac{1}{24}\]
Ответ: $\frac{1}{24}.$
При умножении дробей сокращать числители и знаменатели можно до нахождения их произведения. При этом числитель и знаменатель дроби раскладывается на простые множители, после чего сокращаются повторяющиеся множители и находится результат.
Пример 3
Вычислить произведение дробей $\frac{6}{75}$ и $\frac{15}{24}$.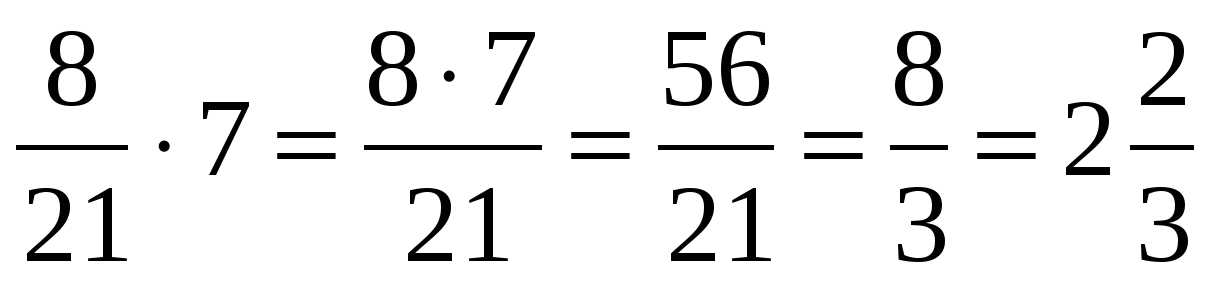
Решение.
Воспользуемся формулой умножения обыкновенных дробей:
\[\frac{6}{75}\cdot \frac{15}{24}=\frac{6\cdot 15}{75\cdot 24}\]
Очевидно, что в числителе и знаменателе есть числа, которые попарно можно сократить на числа $2$, $3$ и $5$. Разложим числитель и знаменатель на простые множители и произведем сокращение:
\[\frac{6\cdot 15}{75\cdot 24}=\frac{2\cdot 3\cdot 3\cdot 5}{3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3}=\frac{1}{5\cdot 2\cdot 2}=\frac{1}{20}\]
Ответ: $\frac{1}{20}.$
При умножении дробей можно применять переместительный закон:
Умножение обыкновенной дроби на натуральное число
Правило умножения обыкновенной дроби на натуральное число:
Результатом умножения дроби на натуральное число является дробь, у которой числитель равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби:
где $\frac{a}{b}$ — обыкновенная дробь, $n$ — натуральное число.
Пример 4
Выполнить умножение дроби $\frac{3}{17}$ на $4$.
Решение.
Воспользуемся правилом умножения обыкновенной дроби на натуральное число:
\[\frac{3}{17}\cdot 4=\frac{3\cdot 4}{17}=\frac{12}{17}\]
Ответ: $\frac{12}{17}.$
Не стоит забывать о проверке результата умножения на сократимость дроби или на неправильную дробь.
Пример 5
Умножить дробь $\frac{7}{15}$ на число $3$.
Решение.
Воспользуемся формулой умножения дроби на натуральное число:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}\]
По признаку деления на число $3$} можно определить, что полученную дробь можно сократить:
\[\frac{21}{15}=\frac{21:3}{15:3}=\frac{7}{5}\]
В результате получили неправильную дробь. Выделим целую часть:
\[\frac{7}{5}=1\frac{2}{5}\]
Краткое решение:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}=\frac{7}{5}=1\frac{2}{5}\]
Сократить дроби также можно было заменой чисел в числителе и знаменателе на их разложения на простые множители.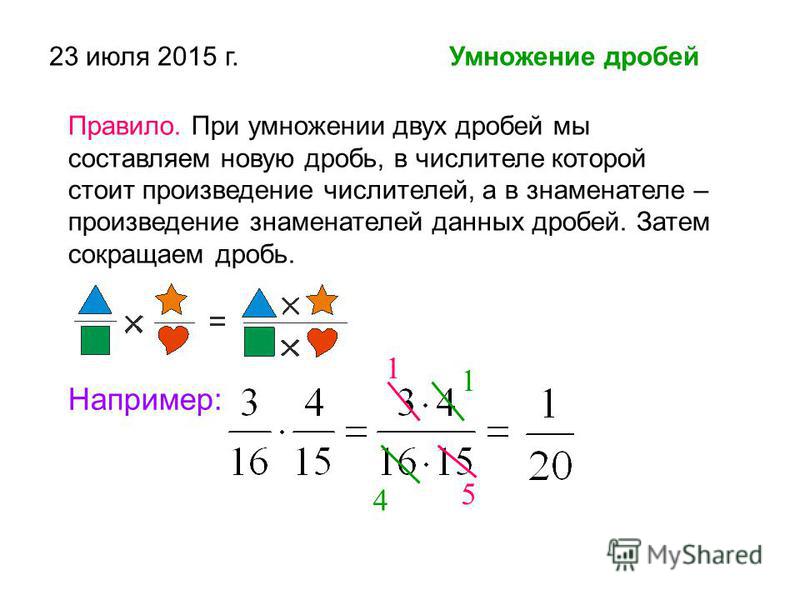 В таком случае решение можно было записать так:
В таком случае решение можно было записать так:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{7\cdot 3}{3\cdot 5}=\frac{7}{5}=1\frac{2}{5}\]
Ответ: $1\frac{2}{5}.$
При умножении дроби на натуральное число можно использовать переместительный закон:
Деление обыкновенных дробей
Операция деления является обратной к умножению и результатом ее является дробь, на которую нужно умножить известную дробь чтобы получить известное произведение двух дробей.
Деление двух обыкновенных дробей
Правило деления обыкновенных дробей:
При делении обыкновенной дроби $\frac{a}{b}$ на дробь $\frac{c}{d}$ необходимо делимое умножить на число, которое является обратным делителю:
Пример 6
Выполнить деление дробей $\frac{7}{4}$ и $\frac{3}{5}$.
Решение.
Числом, обратным делителю $\frac{3}{5}$, является дробь $\frac{5}{3}$. Воспользуемся правилом деления обыкновенных дробей:
\[\frac{7}{4}:\frac{3}{5}=\frac{7}{4}\cdot \frac{5}{3}=\frac{7\cdot 5}{4\cdot 3}=\frac{35}{12}\]
Ответ: $\frac{35}{12}. $
$
Результат деления дробей необходимо проверять на сократимость дроби и на возможность выделения целой части из неправильной дроби.
Пример 7
Выполнить деление дробей $\frac{8}{15}:\frac{12}{35}$.
Решение.
Применим правило деления дробей:
\[\frac{8}{15}:\frac{12}{35}=\frac{8}{15}\cdot \frac{35}{12}=\frac{8\cdot 35}{15\cdot 12}\]
Очевидно, что числитель и знаменатель полученной дроби можно разложить на простые множители и произвести сокращение:
\[\frac{8\cdot 35}{15\cdot 12}=\frac{2\cdot 2\cdot 2\cdot 5\cdot 7}{3\cdot 5\cdot 2\cdot 2\cdot 3}=\frac{2\cdot 7}{3\cdot 3}=\frac{14}{9}\]
В результате получили неправильную дробь, из которой выделим целую часть:
\[\frac{14}{9}=1\frac{5}{9}\]
Ответ: $1\frac{5}{9}.$
Урок «Умножение дробей», посвященный 300-летию рождения М.В. Ломоносова. 6-й класс
«Дроби всякие нужны, дроби разные важны.

Дробь учи, тогда сверкнет тебе удача.
Станет легкой даже трудная задача».
Цели:
- закрепить умение умножать обыкновенные дроби на натуральное число, на обыкновенную дробь, умножать смешанные числа;
- продолжить развивать мыслительную деятельность учащихся, развивать гибкость ума, внимание;
- повышать интерес к предмету, расширить кругозор учащихся, способствовать формированию чувства патриотизма.
Оборудование: компьютер, проектор, раздаточный материал (Приложение № 2), презентация, текст к слайдам (Приложение № 1)
1. Вступительное слово: Сегодня мы с вами
продолжаем работать над умножением дробей (слайд
№ 1). Наше занятие посвящено величайшему
человеку, гениальному русскому учёному,
просветителю, своими идеями, опередившего науку
18 века. Его вклад в развитие российской науки
бесценен. 19 ноября исполнилось 300 лет со дня его
рождения (слайд № 2). Кто же это?… А фамилию
этого учёного вы узнаете, проверив решение
домашней работы.
Его вклад в развитие российской науки
бесценен. 19 ноября исполнилось 300 лет со дня его
рождения (слайд № 2). Кто же это?… А фамилию
этого учёного вы узнаете, проверив решение
домашней работы.
2. Проверка домашнего задания. Проверьте по буквам в том порядке, как они записаны. №472(а, б, в, г, ж, з, к, л, н, п, о) (слайд №3)
Таблица № 1
Учитель: Вы получили имя: М.В. ЛОМОНОСОВ. (далее биография на слайдах №4, 5, 6)
3. Устная работа.
Учитель: «Скажите: Сколько лет должно исполниться ребёнку, чтобы его приняли в школу?»
А сколько лет было Ломоносову, когда он пришёл учиться? Расшифруйте запись (слайд №7). Перепишите её в тетрадь.
05 06 03 33 20 15 01 05 24 01 20 30
Учитель: Как вы думаете, что вам надо для расшифровки? (Алфавит) А что с ним надо сделать? (Надо пронумеровать буквы) (слайд №8)
А-01 З-09 П-17 Ч-25 Я-33 Б-02 И-10 Р-18 Ш-26 В-03 Й-11 С-19 Щ-27 Г-04 К-12 Т-20 Ъ-28 Д-05 Л-13 У-21 Ы-29 Е-06 М-14 Ф-22 Ь-30 Ё-07 Н-15 Х-23 Э-31 Ж-08 О-16 Ц-24 Ю-32
(слайд №9)
Учитель: что же получилось? (девятнадцать).
(продолжение биографии слайды №10,11,12)
4. Повторение.
Учитель: Давайте, узнаем с вами некоторые из интересов Михаила Васильевича. А для этого вспомним таблицу умножения.
(слайд № 13) Каждому варианту даны ряды чисел. Надо числа заменить буквами из таблицы, вспомнив как получаются эти числа.
1 вариант
45 30 15 35 30 24 63 24 54 49 72 27 32 20 21
2 вариант
56 27 42 24 28 16 42 40 28 16 48 27 36 18 25 16
Таблица №2 (Приложение 2)
x 3 4 5 9 8 7 4 о а и з м р 5 р и к г у н 6 и е о л ф т 7 я р н д л о 8 е т у х я л 9 и з г е х д
Учитель: Какие же слова вы получили?
- 1 вариант: горное дело, химия.

- 2 вариант: литература, физика.
Учитель: Интересы Михаила Васильевича были обширными. Чтобы их узнать, для начала вспомним правила умножения дробей.
Вопросы: Как умножить обыкновенную дробь на натуральное число? Как умножить обыкновенную дробь на обыкновенную дробь? Как умножить смешанные числа?
5. Решение заданий. (слайд № 14) А теперь выполним задание на доске. (2 чел. Решают, рассказывают правила)
Таблица №3
Р В А Н Е С М Л Т Ь О Ё 13 2 4 26 5 1 1 4
По полученным ответам найдём слово. (Венера)
(слайды №15,16)
(Венера)
(слайды №15,16)
Ломоносов был любознательным человеком. И мы не будем от него отставать и решим с вами задачу № 452.
Вопросы: О чём задача? С помощью чего его получают? Что известно о 1 кране? Можно найти, сколько он израсходовал воды? Как? Что известно о 2 кране? Что надо найти, чтобы узнать, сколько он израсходовал воды?
Решение:
6. Самостоятельная работа. Пользуясь предыдущей таблицей, самостоятельно определите, чем ещё занимался Ломоносов (слайд № 17,18).
В результате получается ВЕРТОЛЁТ (слайд № 19) и СМАЛЬТА (слайд № 20, 21,22)
Мы с вами познакомились с малой толикой
огромнейшего творчества, изобретений М.В.
Ломоносова (слайд №23). Вот как его
характеризует А.С. Пушкин: «Ломоносов был
великий человек, он обнял все отрасли
просвещения. Жажда науки была сильнейшею
страстью, сей души.: Он создал первый
университет, вернее сказать, сам был первым
русским университетом».
Жажда науки была сильнейшею
страстью, сей души.: Он создал первый
университет, вернее сказать, сам был первым
русским университетом».
Учитель: Сегодня, ребята, вы закрепили правила умножения обыкновенных дробей. Узнали много интересного о выдающемся учёном, талантливом человеке М.В. Ломоносове. Стремитесь к лучшему, чтобы приумножать богатства и славу России.
7. Домашнее задание: п.13, №472 (д, е, и, м), №474, № 473.
8. Подведение итогов урока.
Литература.
1. Математика — 6класс.Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Изд. Мнемозина, М. 2010г.
2. Карпеев Э. П. М. В. Ломоносов : крат. биогр. / Э. П. Карпеев; Межрегион. Ломоносов. фонд, Музей М. В. Ломоносова (С.-Петербург). — Архангельск, 2000г.
3. М.В. Ломоносов, сайт Академик.
Объяснение урока: Умножение дробей | Nagwa
В этом объяснителе мы научимся находить произведение двух правильных дробей путем умножения числителей и знаменателей и записывать ответ в простейшей форме.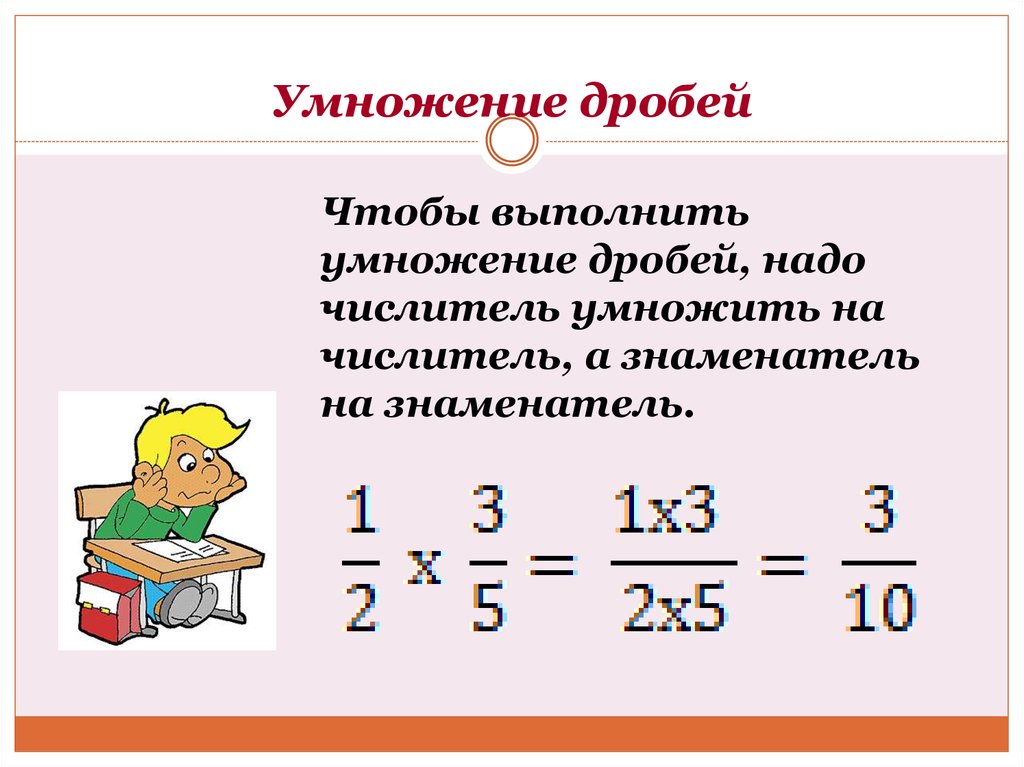
Давайте быстро вспомним, что такое дробь. Дробь сравнивает часть с целым и описывает то, что мы называем пропорцией. Знаменатель дроби — это количество равных долей (или «частей»), на которые делится целое, а числитель — это количество этих акций, составляющих рассматриваемую нами часть.
Теперь мы, конечно, можем выполнять операции над дробями. Мы можем добавить четверть 14 к половина 12, что дает нам три четверти 34, или решить, что одна десятая часть торта — это недостаточно большой кусок, и взять вместо этого два среза (т. Е. 2 × 110 = 15). В последнем примере мы умножили дробь на целое число. Здесь нас интересует умножение дроби на другую дробь. Это можно понимать как долю доли данного целого.
Рассмотрим следующую ситуацию: Каждый из двух человек съедает на обед по одной трети 13 остатков пиццы, приготовленной накануне. Остаток составляет две пятых 25 всей пиццы. Какую часть пиццы они собираются съесть вместе? Эта часть пиццы показана на диаграмме.
Чтобы узнать, какая это часть пиццы, нам нужно разделить остаток (25 штук) на 3 равные части и взять две из них. Как видно из следующей диаграммы, деление 25 на 3 дает 215.
Обратите внимание, что деление дроби (здесь 25) на 3 эквивалентно умножению ее знаменателя на 3. А часть двух 215 — это просто 415.
Подобно тому, как дробь данного числа получается путем умножения дроби на число, дробь дроби эквивалентна умножению дробей. Итак, 23 из 25 от всего дается 23×25=415.
Мы также можем представить произведение дробей как площадь, учитывая, что обе дроби описывают длины (как доли единицы длины). Предыдущий пример 23×25 можно представить как заштрихованную область внутри единичного квадрата. (т. е. стороны 1 и области 1) на показанной диаграмме.
Размеры серого прямоугольника равны 23 и 25, поэтому дана его площадь
на 23×25. Мы видим, что единичный квадрат разделен на 15 равных частей, каждая из которых имеет площадь
115.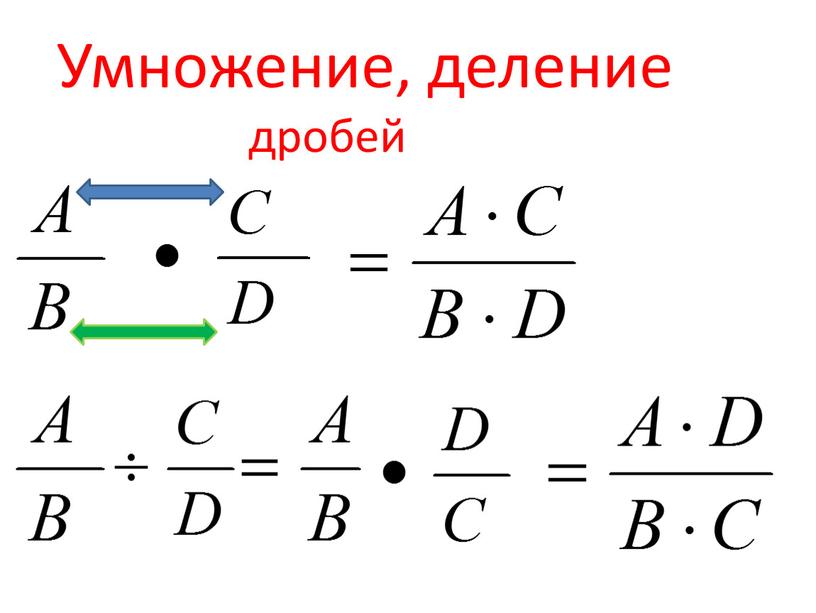 Серый прямоугольник состоит из 4-х штук. Следовательно, его площадь равна 415. Мы снова проиллюстрировали тот факт, что
23×25=415.
Серый прямоугольник состоит из 4-х штук. Следовательно, его площадь равна 415. Мы снова проиллюстрировали тот факт, что
23×25=415.
Обратите внимание, что если бы квадрат был нашей пиццей, которую мы сначала разрезали на 5 равных частей (розовые линии), часть двух третей двух пятых действительно будет представлена заштрихованной областью.
Мы видели, что результат умножения дробей получается простым перемножением числителей и знаменателей: 23×25=2×23×5=415.
Это квадратное изображение ясно показывает, почему: произведение знаменателей дает количество равных долей, на которые был разделен квадрат, а произведение числителей действительно дает количество долей, составляющих заштрихованную площадь.
Зная это, умножать дроби довольно просто. Тем не менее, мы часто хотим выразить
дробь в простейшем виде. А чтобы не делать двойную работу, эффективнее при умножении дробей,
искать общие множители между числителем и знаменателем, а не умножать числители вместе
и знаменатели вместе и только потом уменьшать дробь.
Давайте посмотрим на первый пример, как это работает.
Пример 1. Умножение простых дробей
Вычислите 25×34, дав ответ в простейшей форме.
Ответ
Когда мы перемножаем дроби, получается дробь, числитель которой равен произведению всех числителей исходных дробей, а знаменатель равен произведению всех знаменателей исходных дробей. Итак, здесь у нас есть 25×34=2×35×4.
Теперь нам нужно проверить, есть ли какие-то общие множители между числителем (2×3) и знаменатель (5×4). Мы видим, что 2 является общим делителем 2 в числителе и 4 в знаменателе. Мы можем переписать нашу дробь как 2×35×4=2×35×2×2, и мы видим, что его можно упростить на 2: 2×35×2×2=35×2.
Теперь мы можем произвести умножение в знаменателе, что приводит к 25×34=310.
Давайте рассмотрим еще один пример с тремя дробями.
Пример 2.
 Умножение трех дробей
Умножение трех дробейВычислить 2144×67×1112, давая ответ в виде дроби в простейшей форме.
Ответ
Когда мы умножаем дроби, получается дробь, в которой числитель равен произведение всех числителей исходных дробей, а знаменатель — произведение всех знаменатели исходных дробей. Итак, здесь у нас есть 2144×37×1112=21×3×1144×7×12.
Теперь нам нужно проверить, есть ли общие множители между числителем (21×3×11) и знаменатель (44×7×12).
Мы видим, что 21 и 7 имеют общий множитель (21=7×3); 3 и 12 имеют общий делитель (12=3×4); а 11 и 44 имеют общий множитель (44=11×4). Следовательно, мы можем переписать наша фракция как 21×3×1144×7×12=7×3×3×1111×4×7×3×4, который можно упростить на 3, 7 и 11: 7×3×3×1111×4×7×3×4=34×4.
Числа были записаны здесь как сумма факторов, чтобы точно показать, что происходит. если ты
знакомы с методом, можно просто зачеркнуть, например, 21 и 7 и написать 3 в
числитель как результат упрощения на 7.
Теперь мы можем произвести умножение в знаменателе, что приводит к 2144×37×1112=316.
Рассмотрим пример со смешанными числами.
Пример 3: Умножение смешанных чисел
Вычислить 323×123.
Ответ
Здесь нас просят умножить смешанные числа. Самый простой способ здесь — преобразовать смешанный числа в дроби, умножить дроби и преобразовать результат обратно в смешанное число.
Оба смешанных числа, представленные здесь, имеют дробные части как трети, поэтому мы собираемся преобразовать их на трети.
Мы находим, что 323=3+23=93+23=113 а также 123=33+23=53.
Теперь нам нужно перемножить эти две дроби вместе: 113×53=559.
И, наконец, преобразуем эту дробь обратно в смешанное число. 6 умножить на 9 в 55, с остаток от 1, поэтому мы получаем 559=6×9+19=619. Ответ: 619.
В следующем примере используются три смешанных числа.
Пример 4. Умножение трех смешанных чисел
Вычислить 112×334×179.
Ответ
Здесь нас просят умножать смешанные числа. Самый простой способ здесь — преобразовать смешанный числа в дроби, умножить дроби и преобразовать результат обратно в смешанное число.
Мы находим, что 112=22+12=32 334=124+34=154 179=99+79=169.
Теперь нам нужно перемножить эти три дроби вместе: 32×154×169.
Прежде чем перемножать числители вместе и знаменатели вместе, мы проверяем на общие множители между числителями и знаменателями. Мы находим, что 3 и 15 будут упростить с 9, а также 16 с 2 и 4: 3×15×1682×4×93=5×21=10.
Ответ: 10.
Последний пример — задача со словами.
Пример 5. Умножение смешанных чисел в словесной задаче
Найдите объем деревянного ящика размером 235×318×312 футов.
Ответ
Нам даны три измерения деревянного ящика. Мы знаем, что форма коробки
кубовидный. Следовательно, чтобы найти его объем, нам нужно умножить его три измерения вместе. Поскольку
размеры в футах даны как смешанные числа, мы собираемся, во-первых, преобразовать смешанные
числа в неправильные дроби.
Мы знаем, что форма коробки
кубовидный. Следовательно, чтобы найти его объем, нам нужно умножить его три измерения вместе. Поскольку
размеры в футах даны как смешанные числа, мы собираемся, во-первых, преобразовать смешанные
числа в неправильные дроби.
Мы находим, что 235=105+35=135 318=248+18=258 312=62+12=72.
Теперь нам нужно перемножить эти три дроби вместе: 135×258×72.
Прежде чем перемножать числители вместе и знаменатели вместе, мы проверяем на общие множители между числителями и знаменателями. Мы находим, что 25 упростит с 5: 13×25×75×8×2=13×5×78×2.
Выполняя умножение, мы находим 45516. Наконец, нам нужно преобразовать его обратно в смешанное количество. 28 умножить на 16 в 455, а в остатке 7; следовательно, 45516=28716.
Ответ: объем деревянного ящика 28716 футов 3 .
Ключевые моменты
- Дробь сравнивает часть с целым.
 Знаменатель дроби — это количество
равные доли (или «части»), на которые делится целое, а числитель — это число
из этих акций, которые составляют часть, которую мы рассматриваем.
Знаменатель дроби — это количество
равные доли (или «части»), на которые делится целое, а числитель — это число
из этих акций, которые составляют часть, которую мы рассматриваем. - Доля другой дроби данного целого находится путем умножения дроби на другая фракция.
- Произведение дробей также можно интерпретировать как площадь, учитывая, что обе дроби описывают длины (как доли единицы длины). Например, 23×25 может быть представлен как заштрихованная площадь внутри единичного квадрата (т. е. стороны 1 и площади 1) в показана схема.
Умножение дробей — математика GCSE
Введение
Что такое умножение дробей?
Как умножить две дроби
Рабочий лист «Умножение дробей»
Как умножить дроби на целое число
Как умножать смешанные дроби
Распространенные заблуждения
Похожие уроки
Вопросы на умножение дробей
Умножение дробей Вопросы GCSE
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Теперь доступны еженедельные онлайн-уроки повторения математики GCSE
Узнать больше
Введение
Что такое умножение дробей?
Как умножить две дроби
Рабочий лист «Умножение дробей»
Как умножать дроби на целое число
Как умножать смешанные дроби
Распространенные заблуждения
Похожие уроки
Вопросы на умножение дробей
Умножение дробей Вопросы GCSE
Следующие уроки
Все еще застряли?
Здесь мы узнаем о умножении дробей в том числе о том, как умножать дроби вместе, умножать дроби на целые числа и умножать смешанные дроби.
Существуют также рабочие листы для умножения дробей на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое умножение дробей?
Умножение дробей — это где мы умножаем числители вместе и умножаем знаменатели вместе. Если есть смешанные числа, мы должны сначала преобразовать их в неправильные дроби.
Произведения дробей
Чтобы перемножить две правильные дроби:
Напр. Умножьте две правильные дроби
\frac{1}{2} x \frac{1}{3}
- Умножьте числители вместе: \pmb{1} x \pmb{1=1}
- Умножьте знаменатели вместе: \pmb{2} x \pmb{3=6}
- Если возможно, упростите: \pmb{\frac{1}{6}}.
Чтобы умножить дробь на целое число:
Напр. Умножить дробь на целое число
4 x \frac{1}{3}
- Положите целое число на 1: \pmb{\frac{4}{1} \times \frac{1}{3}}
- Умножьте числители вместе: \pmb{4} x \pmb{1=4}
- Умножьте знаменатели вместе: \pmb{1} x \pmb{3=3}
- Если возможно, упростите: \pmb{\frac {4}{3}}
Чтобы умножить две смешанные числовые дроби:
Напр. Умножить две смешанные числовые дроби
Умножить две смешанные числовые дроби
1 \frac{1}{2} x 2 \frac{1}{4}
- Замените смешанные дроби на неправильные: \pmb{\frac{3}{2} \times \frac{9}{4}}
- Умножьте числители вместе: \pmb{3} x \pmb {9=27}
- Умножьте знаменатели вместе: \pmb{2}x\pmb{4=8}
- Упростите, если возможно: \pmb{\frac{27}{8}}
Что такое умножение дроби?
Как умножить две дроби
Чтобы умножить две дроби:
- Перемножьте числители.
- Перемножьте знаменатели.
- Если возможно, упростите.
Объясните, как умножать дроби в 3 шага
Рабочий лист по умножению дробей
Получите бесплатный рабочий лист с более чем 20 вопросами и ответами. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист по умножению дробей
Получите бесплатный рабочий лист по умножению дробей, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры умножения дробей
Пример 1: умножение двух правильных дробей
Умножение приведенных ниже дробей вместе:
\[\frac{6}{7} \times \frac{4}{9}\]
- Умножьте числители вместе .
\[6×4=24\]
2 Умножьте знаменатели .
\[7×9=63\]
3 Упростите, если возможно .
Когда мы сложим числитель и знаменатель вместе, у нас останется:
\[\frac{24}{63} \]
Если мы разделим и числитель, и знаменатель на 3, мы получим упрощенную дробь:
\[\frac{24 \div 3}{63 \div 3}=\frac{8}{21}\]
Пример 2: умножение двух неправильных дробей (формулированный вопрос)
Найдите площадь фигуры ниже:
Чтобы найти площадь прямоугольника, мы должны использовать формулу:
\[\begin{aligned} A &=l \times w \\ &=\frac{15}{2} \times \frac{5}{4} \end{aligned}\]
Умножьте числители на .
\[15×5=75\]
Умножьте знаменатели вместе .
\[4×2=8\]
Упростите, если возможно .
Когда мы сложим числитель и знаменатель вместе, у нас останется: 9{2} \]
Примечание: всегда помните, что при вычислении площади необходимо возводить единицы в квадрат. }{7} \times \frac{4}{5} \times \frac{1}{2}\]
Умножьте числители на .
\[3×4×1=12\]
Умножьте знаменатели вместе .
\[7×5×2=70\]
Упростите, если возможно .
Когда мы сложим числитель и знаменатель вместе, у нас останется:
\[\frac{12}{70}\]
Если мы разделим и числитель, и знаменатель на 2, мы получим упрощенную дробь:
\[\frac{12 \div 2}{70 \div 2}=\frac{6}{35}\]
Как умножать дроби на целое число
Чтобы умножить две дроби вместе:
- Преобразуйте целое число в дробь, поставив число над знаменателем 1.

- Перемножьте числители.
- Перемножьте знаменатели.
- Если возможно, упростите.
Примеры умножения дробей на целое число
Пример 4: умножение одной правильной дроби на целое число
Умножение: Преобразуйте целое число в дробь, поставив число над знаменателем 1 .
Перепишите вопрос как
\[\frac{2}{3} \times \frac{4}{1}\]
Перемножьте числители вместе .
\[2×4=8\]
Умножьте знаменатели вместе .
\[3×1=3\]
Упростите, если возможно .
Когда мы сложим числитель и знаменатель вместе, у нас останется:
\[\frac{8}{3} \]
Пример 5: нахождение дробей сумм
Что равно
\[\frac{2}{9} \text { of } 45\]
Преобразуйте целое число в дробь, поставив число над знаменателем 1 .
В этом вопросе слово « из » можно заменить знаком умножения.
Перепишите вопрос как
\[ \frac{2}{9} \times \frac{45}{1}\]
Умножьте числители на .
\[2×45=90\]
Умножьте знаменатели вместе .
\[9×1=9\]
Упростите, если возможно .
Когда мы сложим числитель и знаменатель вместе, у нас останется:
\[\frac{90}{9}\]
Это можно еще упростить до 10 (потому что 90 ÷ 9 = 10) .
Примечание: кратчайший путь для проверки вашего ответа при работе с дробями сумм — «разделить на знаменатель и умножить на числитель». :
- Преобразуйте смешанные числа в неправильные дроби. Упростите, если возможно.
- Умножение числителей вместе
- Умножением знаментов вместе
- Упрощайте, если возможны
, умноженные. Пример
.
\[2 \frac{1}{4} \times 2 \frac{1}{2}\]
Преобразуйте смешанные числа в неправильные дроби.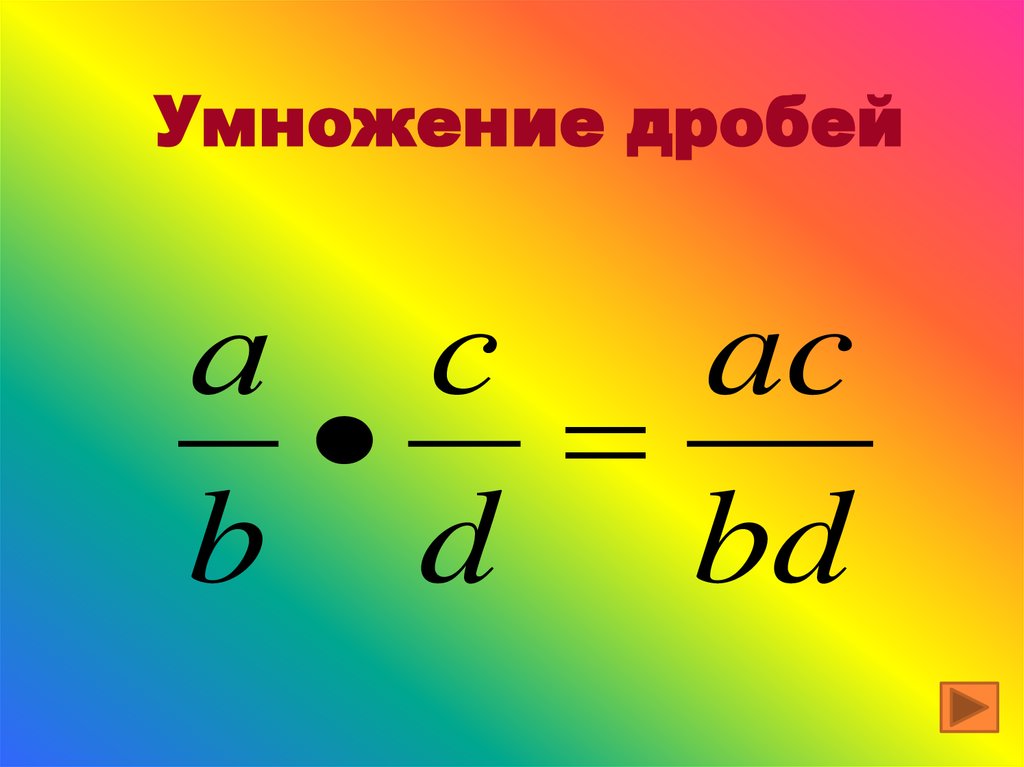 Упростите, если возможно.
Упростите, если возможно.
Чтобы преобразовать смешанное число в неправильную дробь, умножьте знаменатель на целое число и прибавьте его к числителю.
\[2 \frac{+1}{\times4}=\frac{9}{4}\]
\[2 \frac{+1}{\times2}=\frac{5}{2} \]
Итак, теперь у нас осталось:
\[\frac{9}{4} \times \frac{5}{2}\]
Умножьте числители вместе .
\[9×5=45\]
Умножьте знаменатели .
\[4×2=8\]
Упростите, если возможно .
Эту дробь нельзя упростить, поэтому мы остаемся с нашим окончательным ответом в виде
\[\frac{45}{8}\]
Распространенные заблуждения
- Запутанные правила умножения и деления
Распространенный Ошибка состоит в том, что вы перепутали правила умножения и деления и случайно перевернули вторую дробь во время умножения.
- Перекрестное умножение вместо умножения числителей и знаменателей вместе
Напр.
\[\frac{2}{3} \times \frac{1}{4} \neq \frac{8}{3}\]
- Нахождение общего знаменателя
Распространенная ошибка путать правила сложения и вычитания дробей с умножением и делением. При умножении дробей не обязательно находить общий знаменатель.
Умножение дробей является частью нашей серии уроков, посвященных повторению дробей. Возможно, вам будет полезно начать с урока по основным дробям, чтобы получить общее представление о том, чего ожидать, или использовать пошаговые руководства ниже для получения дополнительной информации по отдельным темам. Другие уроки в этой серии включают в себя:
- Fractions
- Subtracting fractions
- Adding fractions
- Dividing fractions
- Equivalent fractions
- Improper fractions and mixed numbers
- Ordering fractions
- Fractions of amounts
Practice multiplying fractions questions
\frac{4} {9}
\frac{36}{11}
\frac{47}{99}
\frac{4}{99}
Умножьте числители: 4\times1=4
Умножьте знаменатели: 11\times9=99
Следовательно, ответ равен \frac{4}{99}
\frac{6}{35}
\frac{3}{35}
\frac{31 }{35}
\frac{10}{21}
Умножьте числители: 2\times6=12
Умножьте знаменатели: 7\times10=70
Упростите дробь: \frac{12}{70} =\frac{6}{35}
\frac{2}{55}
\frac{10}{45}
\frac{10}{11}
5\frac{57}{9}
Сначала напишите 5 как \frac{5}{1} . Теперь мы можем вычислить \frac{2}{11} \times \frac{5}{1}
Теперь мы можем вычислить \frac{2}{11} \times \frac{5}{1}
Умножьте числители: 2\times5=10
Умножьте знаменатели: 11\times1=11
Следовательно, ответ равен \frac{10}{11}
\frac{160}{200}
\frac {204}{5}
\frac{4}{5} of 40 равно \frac{4}{5} \times 40 . Затем мы можем переписать это как \frac{4}{5} \times \frac{40}{1} .
Умножьте числители: 4\times40=160
Умножьте знаменатели: 5\times1=5
Упростите дробь: \frac{160}{5} = 32
4 \frac{2}{5}
3 \frac{2}{15}
2 \frac{17}{18}
2 \frac{13}{15}
числа, нам нужно заменить их неправильными дробями.
3 \ гидроразрыва {2} {3} = \ гидроразрыва {11} {3} \\
1 \frac{1}{5} = \frac{6}{5}
Теперь нам нужно вычислить \frac{11}{3} \times \frac{6}{5}
Умножьте числители: 11 \times6=66
Умножьте знаменатели: 3\times5=15
Упростите дробь: \frac{66}{15} = \frac{22}{5} = 4 \frac{2}{5}
Площадь прямоугольника равна его основанию, умноженному на высоту, поэтому для определения площади стены нам нужно вычислить 4 \frac{2}{5} \times 2 \frac{1}{4} .
Для этого нам нужно преобразовать смешанные числа в неправильные дроби.
4 \ гидроразрыва {2} {5} = \ гидроразрыва {22} {5} \\
2 \frac{1}{4} = \frac{9}{4}
Теперь нам нужно вычислить \frac{22}{5} \times \frac{9}{4} .
Умножить числители: 22\times9=198
Умножить знаменатели: 5\times4=20
9{2} .Итак, 9,9\дел 3 = 3,3
Следовательно, чтобы покрасить стену, нужно 4 банки краски.
Умножение дробей Вопросы GCSE
1.
(a) Решите \frac{3}{5} \times \frac{2}{7}.
(b) Вычислите 1\frac{1}{4} \times 4 \frac{2}{9} . Изложите ответ в простейшей форме.
(3 балла)
Показать ответ
a)
\frac{6}{35}
Правильно умножает числители и знаменатели.
(1)
b)
\frac{5}{4} или \frac{38}{9} видно (преобразует в неправильную дробь)
(3 51 151)
\frac{95}{18}
(1)
2.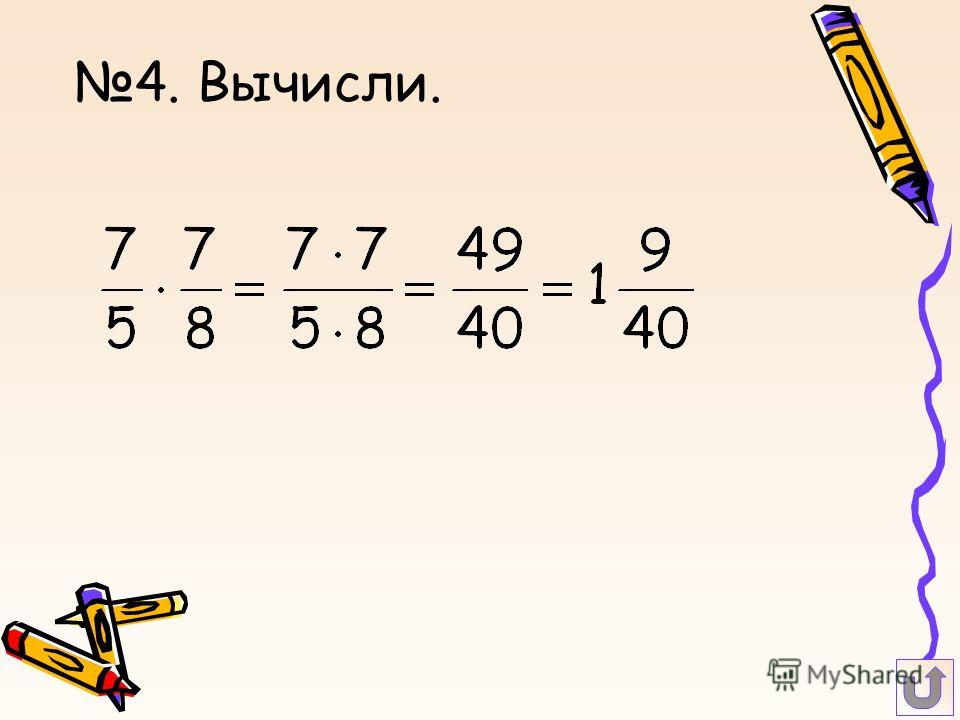 Вот рецепт 12 кексов:
Вот рецепт 12 кексов:
Лили хочет испечь 30 кексов, поэтому ей нужно сделать 1 2\frac{ в {2} раза больше рецепта.
Сколько чашек сахара должна использовать Лили?
Дайте ответ в виде смешанного числа.
(3 балла)
Показать ответ
1\frac{1}{4} = \frac{5}{4} или 2 \frac{1}{2} = \frac{5} {2}
(1)
\frac{5}{4} \times \frac{5}{2}
(1)
\фракция{25}{8}
(1)
3.
(a) Фермер-животновод владеет прямоугольным полем размером \frac{3}{5} \mathrm{km} by \frac{1}{2} \mathrm {км}.
Какова площадь поля? 9{2}
(1)
б)
\frac{3}{10}\div \frac{1}{250}
(1)
\frac{3}{10} \times\frac{250}{1}
(1)
\frac{750}{10} видно.
(1)
75 коров
(1)
Учебный контрольный список
Теперь вы научились: и смешанные числа
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Умножение дробей — EnchantedLearning.com
Умножение дробей — EnchantedLearning.com EnchantedLearning.com — это сайт, поддерживаемый пользователями.
В качестве бонуса участники сайта получают доступ к версии сайта без баннерной рекламы и страницам, удобным для печати.
Щелкните здесь, чтобы узнать больше.
 )
) | You might also like: | Multiplying Fractions Worksheet Printout #1 | Multiplying Fractions Worksheet Printout #3 | Multiplying Fractions Worksheet Printout #2 | Dividing Fractions Worksheet Printout #3 | Subtracting Fractions с одинаковыми знаменателями Распечатка рабочего листа №2 | Сегодняшняя избранная страница: Вопросы по правописанию гласных звуков |
| Оценочный уровень наших подписчиков для этой страницы: 5-й |
| Дополнительная математика Действия | EnchantedLearning.com Дроби | ЧИСЛИТЕЛЬ Знаменатель |
| Определение дробей | Приведение к Простейшая форма, Эквивалентные дроби | Неправильные Дроби | Дроби до Десятичные числа, проценты | Сравнение Дробей | Добавление дробей | Умножение Дроби | Рабочие листы и книги для печати |
| Вычитание Дроби | Деление Дроби |
| Дроби | Умножение дробей | ЧИСЛИТЕЛЬ Знаменатель |
Умножение дробей:
Чтобы умножить две или более дробей, умножьте числители и умножьте знаменатели.
 Затем упростите ответ (уменьшите дробь).
Затем упростите ответ (уменьшите дробь).Один из способов думать об умножении дробей — думать об этом как о нахождении части чего-то. Например, половина числа равна половине этого числа. Половина, умноженная на одну треть, равна одной шестой (или 1/2 х 1/3 = (1 х 1)/(2 х 3) = 1/6).
Умножение дробей Рабочие листы:
| Умножение дробей Умножение дробей. Рабочий лист № 1 — Перейти к ответам. Рабочий лист № 2 — Перейти к ответам. Рабочий лист №3 — Перейти к ответам. |
| + , — | Математика | х , ÷ |
| А | Б | С | Д | Е | Ф | Г | Н | Я | Дж | К | Л | М | Н | О | П | Q | Р | С | Т | У | В | Ш | Х | Д | З |
| Подсчет | Дополнение | Вычитание | Умножение | Подразделение |
| Номер линии | Дроби | Десятичные числа | Измерение | Округление | Графики |
Зачарованное обучение ®
Более 35 000 веб-страниц
Примеры страниц для потенциальных подписчиков или нажмите ниже
| Обзор Зоны Что нового Enchanted Learning Home Ежемесячный календарь активности Книги для печати Указатель сайта K-3 Ремесла K-3 Темы Маленькие исследователи Словарь с картинками Занятия PreK/K Rebus Rhymes Рассказы Письмо Клоузные занятия Темы для эссе Газета Письмо Части речи Художественная литература Испытание временем | Биология Распечатки животных Распечатки этикеток биологии Биомы Птицы Бабочки Динозавры Пищевая цепь Анатомия человека Млекопитающие Растения Тропические леса Акулы Киты Физические науки: K-12 Астрономия Земля Геология Ураганы Формы рельефа Океаны Цунами Вулкан | Языки Голландский Французский Немецкий Итальянский Японский (ромадзи) Португальский Испанский Шведский География/История Исследователи Флаги География Изобретатели История США Другие темы Искусство и художники Календари Поиск колледжей Ремесла Графические органайзеры Label Me! Распечатки Математика Музыка Word Wheels |
Нажмите, чтобы прочитать нашу Политику конфиденциальности
| Электронная почта |
| Найдите на веб-сайте Enchanted Learning: |

Copyright © 2005-2018 EnchantedLearning.com —— Как цитировать веб-страницу
Умножение дробей и десятичных знаков – The Math Doctors
(Новый вопрос недели)
Давайте рассмотрим быстрый вопрос из середины сентября, на который было несколько разных ответов. В некотором смысле это простой вопрос; но мы пойдем немного дальше, так что продолжайте читать до конца.
Можно ли умножить обыкновенную и десятичную дробь?
Азраф спросил:
Можно ли умножить дробь на десятичное число?
Нас регулярно учат, как умножать две дроби и как умножать два десятичных числа; но что происходит, когда вы объединяете их? Пример был бы полезен, чтобы убедиться, что мы имеем дело с той проблемой, с которой имеет дело Азраф, но вопрос достаточно ясен, если не считать того факта, что его, вероятно, не следует воспринимать буквально как вопрос «да/нет»! Большой вопрос, как ? И, может быть, есть какой-то конкретный способ сделать такое умножение напрямую на ?
Три способа
Я ответил, выбрав для начала простой пример:
Привет, Азраф.
Быстрый ответ: да . Дроби и десятичные дроби являются числами, поэтому их можно умножать.
Длинный ответ: Я хочу посмотреть, что вы думаете, когда задаете вопрос. Возможно, на самом деле вы спрашиваете что-то вроде этого: Могу ли я умножить дробь и десятичное число без предварительного преобразования одной формы в другую ?
Например, мы можем умножить 1/3 × 0,75, преобразовав 1/3 в (приблизительное) десятичное число 0,3333 и умножив, чтобы получить 0,249975, что округляется до 0,25.
Или мы можем сделать это, преобразовав 0,75 в дробь 3/4, а затем умножив 1/3 × 3/4 = 1/4. Этот ответ точен.
Но нам не нужно явно преобразовывать. Вместо этого мы можем просто разделить 0,75 на 3, чтобы получить 0,25 (опять же точно). Здесь мы ничего не конвертировали, а использовали правила работы с дробями. Мы можем думать об этом как о переписывании 1/3 × 0,75 как дроби 0,75/3 и упрощении путем деления.
Есть несколько других способов сделать это.
Я хотел бы услышать, что конкретно вы имели в виду, чтобы мы могли обсудить ваши мысли.
Мой первый предложенный метод выполняет умножение в десятичной форме : $$\frac{1}{3}\times 0,75 = 0,333…\times 0,75 = 0,249975…\примерно 0,25$$ Это создает впечатление, что ответ не обязательно точен; и это требует долгой и утомительной работы, если вы хотите умножить вручную. (Если вы используете этот метод на калькуляторе, вы просто будете рассматривать дробь как деление, которое будет автоматически выполнено как десятичное число: \(1\div 3\times 0,75 = 0,25\). Делая это таким образом, калькулятор не округляем, и получим ответ точнее, чем вручную.)
Мой второй метод выполняет умножение в дробной форме : $$\frac{1}{3}\times 0,75 = \frac{1}{3}\times \frac{3}{4} = \frac{ 1\times 3}{3\times 4} = \frac{1}{4}$$ Отсюда ясно, что наш ответ на самом деле точен. Если мы сделаем это вручную, трудная часть будет заключаться в преобразовании десятичной дроби в дробь путем деления в большую сторону (хотя в этом случае вы вполне можете просто распознать ее). Тогда мы должны упростить ответ. Но это достаточно просто. (Используя калькулятор, вы должны иметь возможность конвертировать десятичную дробь в дробь; мой TI-30X IIS делает это для 0,75 с помощью кнопки «F◄►D», но он не работает для более уродливых десятичных дробей, таких как 0,7557. .)
Тогда мы должны упростить ответ. Но это достаточно просто. (Используя калькулятор, вы должны иметь возможность конвертировать десятичную дробь в дробь; мой TI-30X IIS делает это для 0,75 с помощью кнопки «F◄►D», но он не работает для более уродливых десятичных дробей, таких как 0,7557. .)
Мое третье предложение использует методы дроби с десятичным числом точно так же, как мы умножаем дробь \(\frac{1}{3}\) на целое число 75: $$\frac{1}{3}\times 0,75 = \frac{1}{3}\times \frac{0,75}{1} = \frac{1\times 0,75}{3\times 1} = \frac{0,75}{3} = 0,25$$
конкретная проблема
Теперь, как и предполагалось, Азраф привел конкретный пример; как я и ожидал, он оказался немного сложнее моего намеренно простого, но ненамного:
Я хочу сделать такой расчет: 110/100×694.44. Я изо всех сил пытаюсь это сделать.
Пока я был занят этим утром, доктор Рик заинтересовался и ответил:
Привет, Азраф. Доктор Петерсон, вероятно, поделится с вами своими мыслями, но пока позвольте мне указать, что все три метода, которые он упомянул, могут быть применены к вашему выражению:
110/100 × 694,44
Во-первых, мы можем преобразовать дробь 110/100 в десятичную; это особенно легко из-за его знаменателя.
Можете ли вы сделать это, а затем завершить умножение?
Во-вторых, мы можем преобразовать десятичное число 694,44 в дробь. Это обратный процесс, который вы использовали бы для преобразования 110/100 в десятичное; на самом деле мы получим тот же знаменатель, 100.
В-третьих, мы можем использовать правила работы с дробями. Как бы вы умножили 110/100 на целое число 694? Вы сможете сделать то же самое с 694,44 вместо 694; если вы не можете понять, как это сделать, покажите нам шаги, которые вы бы использовали, и мы сможем помочь.
На самом деле, будет полезно, если вы сможете попробовать все три метода и показать нам свою работу. Это даст нам больше тем для разговора и лучшее представление о том, где вы боретесь.
Применим три метода, как я сделал выше:
В виде десятичных дробей: $$\frac{110}{100}\times 694,44 = 1,10\times 694,44 = 763,884$$ Поскольку десятичная дробь заканчивается (деление на 100 всегда будет), это точный ответ, несмотря на то, что он работает с десятичными знаками.
В виде дробей: $$\frac{110}{100}\times 694,44 = \frac{110}{100}\times \frac{69444}{100} = \frac{110\times 69444}{100\times 100} = \frac{7638840}{10000} = \frac{1
Суммарно: $$\frac{110}{100}\times 694,44 = \frac{110}{100}\times \frac{694,44}{1} = \frac{110\times 694,44}{100\times 1 } = \frac{76388.4}{100} = 763.884$$
Я видел ответ и немного подумал, но когда у меня было время ответить, я обнаружил, что мне нечего добавить:
Доктор Рик сказал именно то, что я собирался сказать, так что это должен быть хороший совет!
Я с нетерпением жду возможности увидеть вашу работу, независимо от того, сможете ли вы сделать ее успешно или нет, так как, возможно, есть что обсудить.
Азраф ответил с некоторой работой:
Это правильно? Перепробовав много, я пришел к этому этапу.
Если не так, пожалуйста, опишите это.
Ясно, что это правильно; Азраф использовал мой третий метод, с некоторым упрощением, перед тем, как умножить, сначала отменив 10, а затем разделив, чтобы получить десятичную дробь.
Я ответил с одобрением плюс демонстрация других методов:
Да, верно. Хорошая работа!
Если бы вы преобразовали дробь в десятичную, работа была бы очень похожей. Поскольку 110/100 = 1,1, вам нужно умножить 1,1 × 694,44; делая это вручную, вы должны умножить 11 × 69444, чтобы получить 763884, а затем разделить на 1000 (передвинуть запятую на три знака), чтобы получить 763,884.
А если вы преобразуете 694,44 в дробь, то умножаете 110/100 × 69444/100, поэтому числитель будет 110 × 69444 = 7638840, а знаменатель будет 10000. Все выглядит очень похоже.
Азраф закрыт:
Спасибо за помощь. В ближайшем будущем снова обсудим математические проблемы.
Берегите себя.
Азраф
Старый пример
Но не будем останавливаться на достигнутом. Задача Азрафа решалась всеми тремя способами особенно легко, потому что знаменатель был таков, что дробь была почти десятичной. Давайте сделаем еще пару примеров?
При написании этого поста я нашел только один подобный вопрос в Ask Dr. Math 9Архив 0377, с 1996 г.:
Умножение дроби на десятичную. Как упростить и умножить: 40 ----- х 78,5 360
Доктор Майк ответил:
Привет, Гленн!
Есть несколько способов сделать это. Если у вас есть калькулятор, вы можете сначала вычислить 40/360, а затем умножить на 78,5.
Если вы делаете это вручную, то проще всего сначала сократить дробь до меньших членов. Числитель 40 и знаменатель 360 кратны 10, поэтому вы можете разделить и числитель, и знаменатель на 10, чтобы получить эквивалент дроби 4/36. Так как 4 раза 9равно 36, эта дробь эквивалентна 1/9.
Ваша первоначальная проблема теперь
1
--- х 78,5
9
Это то же самое, что 78,5/9, что вы можете сделать на бумаге с делением в длину. В любом случае ответом является бесконечно повторяющееся десятичное число 8,722222222... . Хорошее приблизительное значение — 8,722.
В любом случае ответом является бесконечно повторяющееся десятичное число 8,722222222... . Хорошее приблизительное значение — 8,722. Итак, он сначала дал то, что составляет десятичный подход , просто выполнив деление и получив десятичный результат: $$\frac{40}{360}\times 78,5 = 0,111…\times 78,5 = 8,7222…$$ сделал это на моем калькуляторе, не записывая и не перепечатывая промежуточный результат, так что не было никакого округления (кроме дальнего конца памяти калькулятора). Вероятно, именно так это обычно и делается в реальном мире.
Затем он сделал то, что составляет мой смешанный метод , сначала упростив дробь (что я бы сделал, только если бы это было легко, как это), а затем обработав полученную дробь как деление: $$\frac{40 }{360}\times 78,5 = \frac{1}{9}\times 78,5 = 78,5\div 9 = 8,7222…$$
Если бы у нас была какая-то причина, чтобы получить дробный результат, мы могли бы использовать мой метод чистой дроби . , умножив \(\frac{1}{9}\times 78\frac{1}{2}\). Напомним, что мы делаем такое умножение, записывая смешанное число в виде неправильной дроби: $$\frac{40}{360}\times 78,5 = \frac{1}{9}\times 78\frac{1}{2} = \frac{1}{9}\times \frac{157}{2} = \frac{157}{18} = 8\frac{13}{18} $$ Конечно, \(\frac{13}{18} = 0,7222…\).
, умножив \(\frac{1}{9}\times 78\frac{1}{2}\). Напомним, что мы делаем такое умножение, записывая смешанное число в виде неправильной дроби: $$\frac{40}{360}\times 78,5 = \frac{1}{9}\times 78\frac{1}{2} = \frac{1}{9}\times \frac{157}{2} = \frac{157}{18} = 8\frac{13}{18} $$ Конечно, \(\frac{13}{18} = 0,7222…\).
На шаг сложнее!
Давайте займемся еще одним делом, которое связано с последним, что мы делали. В поисках вопросов такого типа, которые кажутся очень редкими, я нашел этот незаархивированный вопрос от 2009 года, который делает еще один шаг вперед:
У меня есть домашнее задание, с которым у меня проблемы, и я не понимаю, как это сделать. это в классе, но я боюсь спросить своего учителя, потому что я не хочу говорить перед всем классом.
Мне нужно умножить неправильную дробь на десятичную, но я не знаю, как это сделать. Мне было интересно, не могли бы вы объяснить, как получить ответ.
3,2 лк 10 1/3
Спасибо, что нашли время, чтобы помочь мне! Разобравшись со вторым вопросом, который я здесь пропустил, я сказал:
Теперь вернемся к другому вопросу об умножении смешанного числа на десятичное.Не знаю, чему вас об этом учили! Обычно, когда вам нужно умножить два разных вида числительных, вы переписываете одно в той же форме, что и другое, так что вы можете умножать как обычно. В вашем примере 3,2 л х 10 1/3 мы можем либо изменить десятичное число на смешанное, 3 21/100 х 10 1/3 а затем умножить их, преобразовав обе в неправильные дроби, или изменить смешанное число на десятичное, 3,21 х 10,333... что немного более неудобно.
Это, конечно же, те самые методы, которые мы обсуждали. Используя дроби, мы получаем $$3\frac{21}{100}\times 10\frac{1}{3} = \frac{321}{100}\times\frac{31}{3} = \frac{321 \times 31}{100\times 3} = \frac{9951}{300} = \frac{3317}{100} = 33\frac{17}{100}$$
Используя десятичные дроби, мы имеем не- завершающая десятичная дробь, что дает $3,21\times 10\frac{1}{3} \приблизительно 3,21\times 10,333 = 33,16893\приблизительно 33,17$$ Опять же, если я выполняю умножение в своем калькуляторе без округления, он показывает ответ как точно 33.17.
Не зная, была ли конкретная причина проблемы, связанной со смешанным числом, я предложил другой метод, который, вероятно, никогда бы не сделал иначе:
Вас учили чему-то другому? Единственный другой метод, который я могу придумать (и тот, который имеет какое-то отношение к вашему другому вопросу), - это «распространить», если вы знакомы с этим термином. Умножение на 10 + 1/3 равносильно умножению на 10 и 1/3 и сложению результатов: 3,21 х (10 + 1/3) = 3,21 х 10 + 3,21 х 1/3 Умножьте на 10, переместив запятую, и умножьте на 1/3, разделив на 3. Сомневаюсь, что вас этому учили.
Мы находим, что \(3,21\times 10 = 32,1\) и \(3,21\times\frac{1}{3} = 3,21\div 3 = 1,07\), поэтому результат равен \(32,1 + 1,07 = 33,17 \) еще раз.
Итак, покажите мне, как, по вашему мнению, вы должны это сделать, и покажите мне вашу работу. Я помогу вам, если вы ошибетесь, так что не бойтесь показать мне, что вы пытаетесь сделать. Кстати, я учу взрослых, у которых есть проблемы с некоторыми из этих вещей, и я всегда рад, когда есть кто-то, кто задает вопросы, которые есть у всех остальных! Возможно, вы обнаружите, что ваш класс ждет, пока кто-нибудь осмелится спросить об этом, и за это вы полюбите его больше.

 ..
.. )
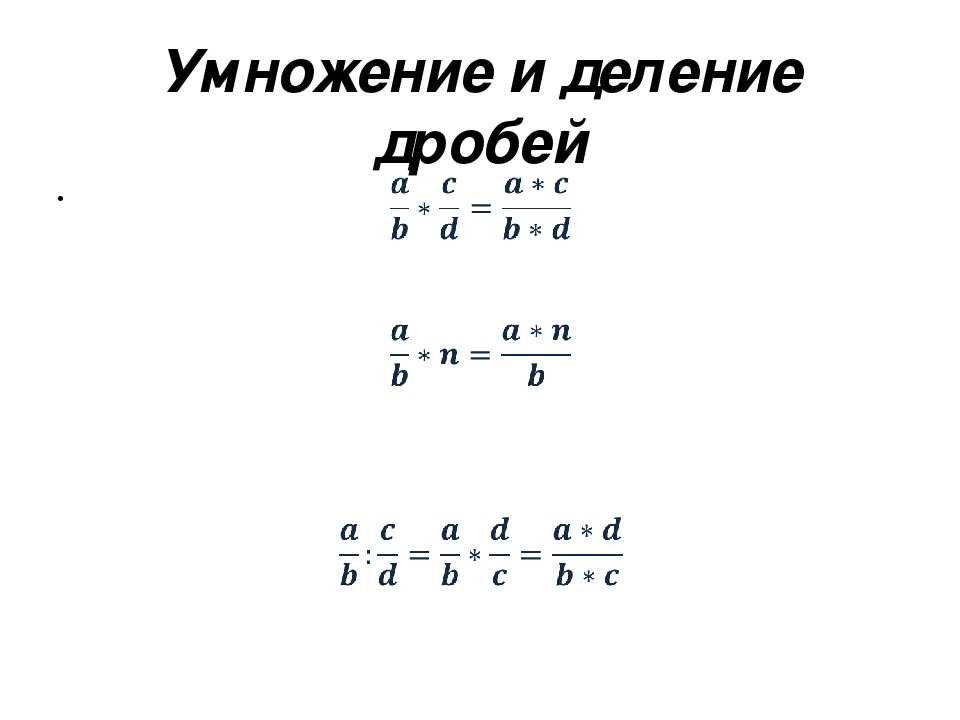
)  Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов: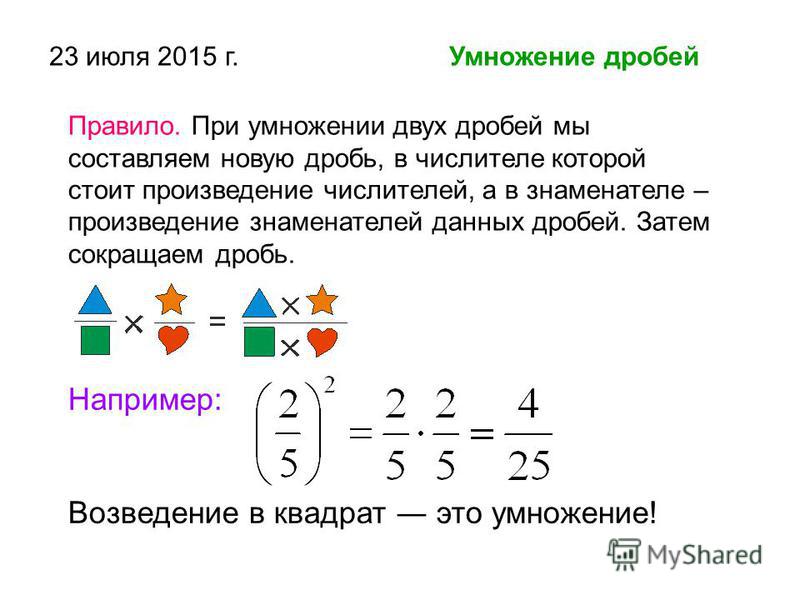




 .. к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
.. к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху».
Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху». Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения. На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
 Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально…
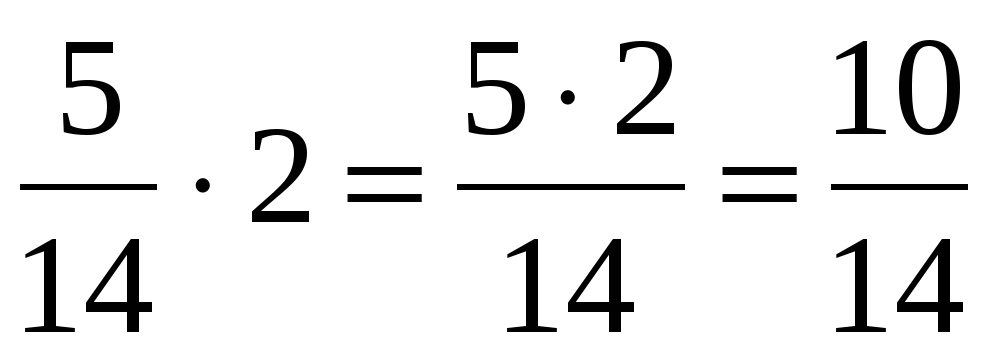 Математики эту задачу решить не могут, а вот шаманы — элементарно.
Математики эту задачу решить не могут, а вот шаманы — элементарно. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.
 И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.
И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример.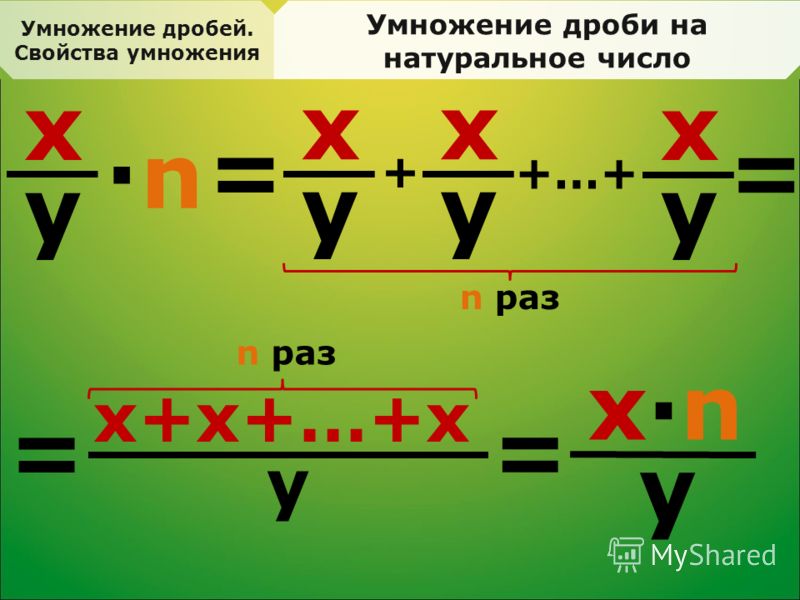


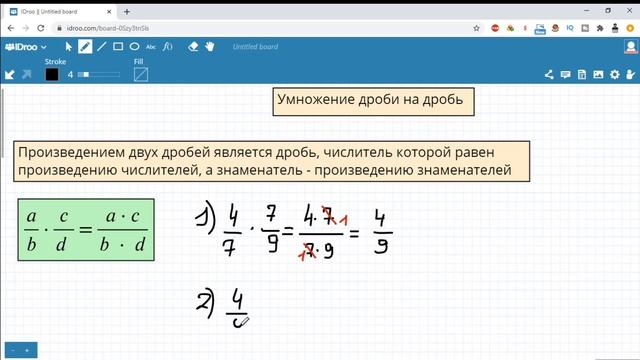 В таком случае решение можно было записать так:
В таком случае решение можно было записать так: $
$

 Знаменатель дроби — это количество
равные доли (или «части»), на которые делится целое, а числитель — это число
из этих акций, которые составляют часть, которую мы рассматриваем.
Знаменатель дроби — это количество
равные доли (или «части»), на которые делится целое, а числитель — это число
из этих акций, которые составляют часть, которую мы рассматриваем.


 Можете ли вы сделать это, а затем завершить умножение?
Можете ли вы сделать это, а затем завершить умножение? Если не так, пожалуйста, опишите это.
Если не так, пожалуйста, опишите это.
 В любом случае ответом является бесконечно повторяющееся десятичное число 8,722222222... . Хорошее приблизительное значение — 8,722.
В любом случае ответом является бесконечно повторяющееся десятичное число 8,722222222... . Хорошее приблизительное значение — 8,722.  Не знаю, чему вас об этом учили! Обычно, когда вам нужно умножить два разных вида числительных, вы переписываете одно в той же форме, что и другое, так что вы можете умножать как обычно. В вашем примере
3,2 л х 10 1/3
мы можем либо изменить десятичное число на смешанное,
3 21/100 х 10 1/3
а затем умножить их, преобразовав обе в неправильные дроби, или изменить смешанное число на десятичное,
3,21 х 10,333...
что немного более неудобно.
Не знаю, чему вас об этом учили! Обычно, когда вам нужно умножить два разных вида числительных, вы переписываете одно в той же форме, что и другое, так что вы можете умножать как обычно. В вашем примере
3,2 л х 10 1/3
мы можем либо изменить десятичное число на смешанное,
3 21/100 х 10 1/3
а затем умножить их, преобразовав обе в неправильные дроби, или изменить смешанное число на десятичное,
3,21 х 10,333...
что немного более неудобно. 