| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Как доступно объяснить ребёнку суть деления числ в столбик.

Содержание
- Подготовка в обучению
- Как объяснить деление в столбик
- Обучение делению в столбик в форме игры
- Обучение делению в столбик при помощи таблицы умножения
- Обучение делению в столбик в тетради
- Многозначные числа
- Обучение делению с остатком
- Как делать проверку
- Видео: как научиться делить в столбик
- Обучение делению столбиком десятичных дробей с запятой
- Советы по наиболее быстрому и продуктивному обучению ребенка подсчета «столбиком»
- Как научить ребенка делению – закрепляем навык
- Видео: тренажёр быстрого деления в уме для школьников
Подготовка в обучению
Для того, чтобы начать объяснять ребенку принцип счета столбиком, Вы должны понять: готов ли он к этому. Обучение должно начинаться только в том случае, если малыш свободно и правильно производит простые арифметические действия с числами от 0 до 10.
Сюда входят сложение, вычитание, деление и умножение (если ребенок не знает одно из приведенных действий, то лучше научите его заранее, ведь «столбик» желательно учить комплексом, т. е. все вариации разбирать вместе). Важно повторить все перед «стартом», ведь это — самая основа, которую закладывают во 2 — 3 классе.
е. все вариации разбирать вместе). Важно повторить все перед «стартом», ведь это — самая основа, которую закладывают во 2 — 3 классе.
Не забудьте «разобрать по полочкам» понятие единиц, десятков, сотен и тысяч! Без этого ребенок не сможет наиболее точно понять принцип подсчета и дальше двузначных чисел вы не уйдете.
Здесь отлично подойдет методика, где ученик записывает разные цифры числа под строкой своего разряда. Например: 2312 и 534 — тут получится, что 5 будет под 3, 3 под 1, а 4 под 2, двойка в разряде тысяч будет стоять одна, ведь тысячных частей больше нет.
Как объяснить деление в столбик
Поскольку деление может быть без остатка, а может быть с остатком, рассмотрим два варианта объяснение такого арифметического действия.
Обучение делению в столбик в форме игры
Дети устают в школе, они устают от учебников. Поэтому родителям нужно отказаться от учебников. Подавайте информацию в форме увлекательной игры.
Можно поставить задачи таким образом:
Посадите его игрушки в круг, а ребенку дайте груши или конфеты. Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10.
Предложите ученику разделить 4 конфеты между 2 или 3 куклами. Чтобы добиться понимания со стороны ребенка, постепенно прибавляйте количество конфет до 8 и 10.
Даже если малыш будет долго действовать, не давите и не кричите на него. Вам потребуется терпение. Если ребенок делает что-то неправильно, исправляйте его спокойно.
Затем, как он завершит первое действие деления конфет между участниками игры, попросит его вычислить, сколько конфет досталось каждой игрушке. Теперь вывод. Если было 8 конфет и 4 игрушки, то каждой досталось по 2 конфеты.
Дайте ребенку понять, что разделить – это значит распределить равное количество конфет всем игрушкам.
Обучать математическому действию можно с помощью цифр.
Дайте ученику понять, что цифры можно квалифицировать, как груши или конфеты. Скажите, что количество груш, которое требуется разделить – это делимое. А количество игрушек, на которых приходятся конфеты – это делитель.
Дайте ребенку 6 груш.
Поставьте перед ним задачу: разделить количество груш между дедушкой, собакой и папой. Затем попросите его поделить 6 груш между дедушкой и папой. Объясните ребенку причину, по которой получился неодинаковый результат при делении.
Расскажите ученику о делении с остатком.
Дайте ребенку 5 конфет и попросите его раздать их поровну между котом и папой. У ребенка останется 1 конфета. Расскажите ребенку, почему получилось именно так. Данное математическое действие стоит рассмотреть отдельно, так как это может вызвать сложности.
Деление чисел
Обучение в игровой форме может помочь ребенку быстрее понять весь процесс деления чисел. Он сможет усвоить, что наибольшее число делится на наименьшее или наоборот. То есть, наибольшее число – это конфеты, а наименьшее – участники. В столбике 1 числом будет количество конфет, а 2 – количество участников.
Не перегружайте ребенка новыми знаниями. Обучать нужно постепенно. Переходить к новому материалу нужно тогда, когда предыдущий материал закреплен.
Обучение делению в столбик при помощи таблицы умножения
Ученики смогут разобраться в делении быстрее, при условии того, что они хорошо знают умножение.
Родителям необходимо разъяснить, что деление имеет сходство с таблицей умножения. Только действия противоположны. Для наглядности нужно привести пример:
- Скажите ученику, чтобы он произвол умножение значений 6 и 5. Ответ – 30.
- Подскажите школьнику, что число 30 является результатом математического действия с двумя числами: 6 и 5. А именно, результатом умножения.
- Разделите 30 на 6. В результате математического действия получится 5. Школьник сможет убедиться в том, что деление – это то же, что и умножение, но наоборот.
Можно воспользоваться таблицей умножения для наглядности деления, если ребенок хорошо ее усвоил.
Также нужно научить юного ученика, тому, как называются категории, описывающие операцию деления – «делимое», «делитель» и «частное». На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
На примере покажите, какие цифры являются делимым, делителем и частным. Закрепите эти знания, они необходимы для дальнейшего обучения!
Двигайтесь дальше, разбирая другие примеры из таблицы умножения.
По сути, вам нужно научить ребёнка таблице умножения «наоборот», и запомнить её необходимо так же хорошо, как и саму таблицу умножения, ведь это будет необходимым, когда вы начнёте обучение делению в столбик.
Обучение делению в столбик в тетради
Начинать обучение нужно тогда, когда ученик понял материал о делении на практике, с помощью игры и таблицы умножения.
Пример деления
Нужно начинать делить таким образом, применяя простые примеры. Так, деление 105 на 5.
Объяснять математическое действие нужно подробно:
- Напишите в тетради пример: 105 разделить на 5.
- Запишите это, как при делении в столбик.
- Расскажите, что 105 – делимое, а 5 – делитель.
- С учеником определите 1 цифру, которая допускает деление.
 Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10. - В столбике деления, под числом 5, напишите цифру 2.
- Попросите ребенка число 5 умножить на 2. По итогу умножения получится 10. Это значение нужно записать под числом 10. Далее нужно написать в столбике знак вычитания. От 10 нужно отнять 10. Получится 0.
- Запишите в столбике число, получившееся в результате вычитания – 0. У 105 осталось число, которое не участвовало в делении – 5. Это число нужно записать.
- В итоге получится 5. Это значение нужно разделить на 5. Результат – цифра 1. Это число нужно записать под 5. Результат деления – 21.
Родителям нужно объяснить, что это деление не имеет остатка.
Начать деление можно с цифр 6,8,9, затем переходить к 22, 44, 66, а после к 232, 342, 345, и так далее.
Еще один пример деления
Многозначные числа
Сложнее всего детям даются задачи на трехзначные и четырехзначные числа. Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:
Четверокласснику тяжело оперировать тысячами и сотнями тысяч. У школьника возникают следующие проблемы:
- Не может определить неполное число делимого для первого действия. Вернитесь к изучению разрядов натуральных чисел, поработайте над развитием внимания малыша.
- Пропускает 0 в записи частного. Это самая распространенная проблема. В результате у ребенка получается число на несколько разрядов меньше правильного. Чтобы избежать этой ошибки, нужно распечатывать памятку с последовательностью действий в примерах, где в середине частного есть нули. Предложите ребенку тренажер с такими заданиями для отработки навыка.
При обучении решению задач с крупными числами действуйте поэтапно:
- Объясните, что такое неполное делимое и зачем его выделять.
- Потренируйтесь в поиске делимого устно без последующего решения задач. Например, дайте детям такие задания:
Найдите неполное частное в примерах: 369:28; 897:12; 698:36.
- Теперь приступайте к решению на бумаге.
 Запишите столбиком: 1068:89.
Запишите столбиком: 1068:89. - Сначала нужно отделить неполное делимое. Можно использовать запятую сверху над числами.
106’8:89
- Подбирайте частное на отдельном листочке или посчитайте в уме.
- Распишите результат.
- Внимательно отнимайте цифры от делимого. Следите за тем, чтобы результат после вычитания был меньше делителя.
- Продолжайте деление до конца, пока не получится 0.
- Придумайте еще несколько похожих примеров без остатка. Степень сложности увеличивайте постепенно.
На заметку! Примеры с семизначными цифрами с третьеклассниками решать не нужно. Это лишнее. Достаточно остановиться на заданиях с пятизначными числами (до 10 000). Деление миллионов дети проходят в старших классах.
Обучение делению с остатком
Когда ребенок усвоит материал о делении, можно усложнять задачу. Деление с остатком – это следующая ступень обучения. Объяснять нужно на доступных примерах:
- Предложите ребенку разделить 35 на 8.
 Запишите в столбик задачу.
Запишите в столбик задачу. - Чтобы ребенку было максимально понятно, можно показать ему таблицу умножения. В таблице наглядно видно, что в число 35 входит 4 раза число 8.
- Запишите под числом 35 число 32.
- Ребенку нужно от 35 вычесть 32. Получится 3. Число 3 является остатком.
Деление с остатком
Как делать проверку
Проверка деления производится с помощью умножения: делитель умножается на делитель. Делать это можно столбиком:
Теперь проверим:
Для проверки деления с остатком нужно:
- Умножить полное частное на делитель.
- Прибавить к результату остаток.
17х2=34
34+1 (остаток) =35
Алгоритм проверки правильности решения примера деления не изменяется от разрядности цифр.
Важно! Первое время просите ребенка расписывать проверку умножением подробно, чтобы проверить и закрепить знание таблицы.
Видео: как научиться делить в столбик
youtube.com/embed/e136C1dGMmE?feature=oembed» frameborder=»0″ allowfullscreen=»allowfullscreen»/>Обучение делению столбиком десятичных дробей с запятой
Деление десятичных дробей может запутать ребенка из-за постановки запятой.
Деление десятичных дробей
Чтобы ребенок сориентировался в этом математическом действие, ему необходимо разложить информацию «по полочкам»:
Десятичная дробь допускает деление не только на десятичную дробь, но и на целое значение. В таких задачах необходимо действовать, как с обычными примерами. Только когда у делимого закончатся значения до запятой, ее нужно поставить в частное. Далее деление тоже протекает привычным способом.
Десятичные дроби так же делятся на десятичные дроби. В этом математическом действии нужно убрать запятые у второго числа. Для этого требуется перенести ее вправо в обоих значениях на то количество цифр, которое отделено у делителя.
Советы по наиболее быстрому и продуктивному обучению ребенка подсчета «столбиком»
- Не торопитесь! Дайте ребенку разобраться с правилами подсчета столбиком.
 Только если он все поймет, то обучение можно назвать успешным;
Только если он все поймет, то обучение можно назвать успешным; - Давайте ребенку отдыхать. Только при сочетании продуктивной работы и отдыха его мозг сможет наиболее точно обработать массивный поток новой информации;
- Поощряйте правильные ответы. Больше хвалите или угощайте ребенка. Так у него появится стимул заниматься, а значит и интерес, что Вам и нужно, ведь так он сможет выполнять данные действия. Все у вас получится, главное — заниматься!
Главное из-за чего у многих школьников возникает проблема с математикой — это неумение быстро делать простые арифметические расчеты. А на этой основе построена вся математика в начальной школе. Особенно часто проблема именно в умножении и делении.
Чтобы ребенок научился быстро и качественно проводить расчеты деления в уме — необходима правильная методика обучения и закрепление навыка. Для этого мы советуем воспользоваться популярными на сегодня пособиями в усвоение навыка деления. Одни предназначены для занятий детей с родителями, другие для самостоятельной работы.
- «Деление. Уровень 3. Рабочая тетрадь» от крупнейшего международного центра дополнительного образования Kumon
- «Деление. Уровень 4. Рабочая тетрадь» от Kumon
- «Не Ментальная арифметика. Система обучения ребенка быстрому умножению и делению. За 21 день. Блокнот-тренажёр.» от Ш. Ахмадулина – автора обучающих книг-бестселлеров
Самым главным, когда вы учите ребёнка делению в столбик, является усвоение алгоритма, который, в общем-то, достаточно прост.
Если ребёнок хорошо оперирует таблицей умножения и «обратным» делением, у него не возникнет трудностей. Тем не менее очень важно постоянно тренировать полученный навык. Не останавливайтесь на достигнутом, как только вы поймёте, что ребёнок уловил суть метода.
Для того чтобы легко научить ребёнка операции деления нужно:
- Чтобы в возрасте двух–трех лет он освоил отношения «целое – часть». У него должно сложиться понимание целого, как неразделимой категории и восприятие отдельной части целого как самостоятельного объекта.
 Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. - Чтобы в младшем школьном возрасте ребенок свободно оперировал действиями по сложению и вычитанию чисел, понимал суть процессов умножения и деления.
Для того чтобы занятия математикой доставляли ребёнку удовольствие, необходимо возбуждать его интерес к математике и математическим действиям, не только во время обучения, но и в бытовых ситуациях.
Поэтому поощряйте и развивайте наблюдательность у ребёнка, проводите аналогии с математическими действиями (операции на счёт и деление, анализ отношений «часть-целое» и т.д.) во время конструирования, игр и наблюдений за природой.
Видео: тренажёр быстрого деления в уме для школьников
Источники
- https://zen.yandex.ru/media/id/5b73c8c1f43a0900a9f1263b/5c6361690cfdc500ac23e4ce
- https://babyzzz.
 ru/parents/kids/31507.html
ru/parents/kids/31507.html - https://slovami.net/delenie-chisel-stolbikom/
- http://MaryPop.ru/shkola/obuchenie-matematike/obyasnit-rebenku-delenie-v-stolbik.html
- https://razvitie-vospitanie.ru/kak_nauchit/rebenka_delit_v_stolbik.html
Как делить в Excel и Google Таблицах
Деление — одна из самых основных операций, которую мы выучили в детстве. Для большинства людей деление довольно сложно. Благодаря Excel деление теперь можно выполнять легко и точно.
Как разделить? Делениев Excel легко выполняется с помощью косой черты «/», , которая является символом деления.
Предположим, мы хотим разделить любое число ( a) на другое число ( б) . Формула деления:
. =а/б
, где a — делимое, а b — делитель.
Рисунок 1. формула деления
Как разделить два числа? Деление очень простое. Мы вводим знак равенства «=», чтобы активировать функцию формулы, затем числитель, за которым следует косая черта «/», за которой следует знаменатель.
Мы вводим знак равенства «=», чтобы активировать функцию формулы, затем числитель, за которым следует косая черта «/», за которой следует знаменатель.
Если мы хотим разделить 8 на 2, используем следующую формулу:
. =8/2
, где 8 — числитель или делимое, а 2 — знаменатель или делитель.
Рисунок 2. Разделить числа
Как разделить две клетки в?Формула для деления ячеек использует ссылки на ячейки, содержащие значения, в качестве числителя и знаменателя.
Когда мы хотим разделить ячейку B3 на ячейку C3, мы вводим формулу:
=B3/C3
Рисунок 3. Формула для деления двух ячеек
Как разделить столбец на число?Мы также можем разделить столбец на число. Когда мы хотим разделить столбец B на число 2, мы вводим формулу
=B3/2
Где числитель — это ссылка на ячейку, а знаменатель — число.
Рис. 4. Разделение столбца на число в Excel
Как разделить столбцы и листы Google? Разделить столбцыМожно выполнить деление на несколько столбцов за минимально возможное время. Чтобы разделить столбцы, мы выполняем следующие шаги:
- Введите формулу в ячейку E3:
=B3/C3 - Нажмите ВВОД
- Скопируйте формулу в ячейку E3, нажав Ctrl + C , затем выберите ячейки E4 и E5 и нажмите Ctrl + V , чтобы вставить формулу
Рис. 5. Разделить столбцы
В результате значения в столбце B делятся на соответствующие значения в столбце C.
Разделить столбцы в листах GoogleФормула разделения столбцов в листах Google аналогична формуле Excel. Мы просто используем ссылки на ячейки в качестве числителя и знаменателя в нашей формуле деления.
Рис. 6. Разделение столбцов в таблицах Google
Есть ли функция деления? Проще говоря, нет функции для операции деления. Чтобы разделить, мы должны использовать символ деления в формуле.
Чтобы разделить, мы должны использовать символ деления в формуле.
Однако существует функция ЧАСТНОЕ, которая возвращает только целую часть любого деления, исключая остаток.
Синтаксис:
= ЧАСТНОЕ ( числитель , знаменатель )
- Числитель – делимое
- Знаменатель – делитель
Пример:
Мы хотим разделить 10 на 3. С помощью функции ЧАСТНОЕ вводим формулу
= ЧАСТНОЕ ( 10 , 3 )
Рис. 7. Функция ЧАСТНОЕ
Функция ЧАСТНОЕ не учитывает остаток от деления. Деление 10 на 3 приводит к 3 с остатком 1. Однако функция ЧАСТНОЕ возвращает только целую часть результата, то есть «3».
В большинстве случаев проблема, которую вам нужно будет решить, будет более сложной, чем простое применение формулы или функции. Если вы хотите сэкономить часы исследований и разочарований, попробуйте наш онлайн-сервис Excelchat! Наши эксперты по Excel доступны круглосуточно и без выходных, чтобы ответить на любой вопрос, который у вас может возникнуть. Мы гарантируем подключение в течение 30 секунд и индивидуальное решение в течение 20 минут.
Мы гарантируем подключение в течение 30 секунд и индивидуальное решение в течение 20 минут.
Умножение и деление на столбики: примеры
Математика сродни головоломкам. Особенно это касается деления и умножения в столбик. В школе эти действия изучаются от простого к сложному. Поэтому непременно нужно хорошо понимать алгоритм выполнения этих операций на простых примерах. Чтобы потом не было сложностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.
Советы для тех, кто хочет хорошо знать математику
Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Этот принцип должен усвоить каждый ученик первого класса. Поэтому, если вы пропускаете несколько уроков подряд, материал придется осваивать самостоятельно. В противном случае впоследствии возникнут проблемы не только с математикой, но и с другими предметами, с ней связанными.
Второе обязательное условие успешного изучения математики — переходить к примерам делением в столбик только после того, как будут освоены сложение, вычитание и умножение.
Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, лучше учиться по таблице Пифагора. Здесь нет ничего лишнего, и умножение усваивается в этом случае проще.
Как умножаются натуральные числа в столбик?
Если при решении примеров в столбце на деление и умножение возникает затруднение, то начинать решать задачу с опоры на умножение. Поскольку деление является обратной операцией умножения:
- Прежде чем перемножать два числа, нужно внимательно на них посмотреть. Выберите тот, у которого больше цифр (длиннее), напишите его первым. Поместите второй ниже него. И цифры соответствующей цифры должны быть под одним и тем же рангом. То есть самая правая цифра первого числа должна быть выше самой правой второй.
- Умножьте крайнюю правую цифру нижнего числа на каждую старшую цифру, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той, которую вы умножили.
- Проделайте то же самое с другой нижней цифрой.
 Но результат умножения нужно сдвинуть на один разряд влево. При этом его последняя цифра будет под той, на которую умножали.
Но результат умножения нужно сдвинуть на один разряд влево. При этом его последняя цифра будет под той, на которую умножали.
Продолжайте это умножение в столбце, пока числа во втором множителе не будут исчерпаны. Теперь их нужно сложить. Это будет желаемый ответ.
Алгоритм умножения в столбик десятичных знаков
Во-первых, предполагается, что даны не десятичные дроби, а натуральные дроби. То есть уберите из них запятые и далее действуйте, как описано в предыдущем случае.
Разница начинается, когда записывается ответ. На этом этапе вам нужно посчитать все числа, которые стоят после запятых в обеих дробях. Вот сколько их надо отсчитать от конца ответа и там поставить запятую.
Этот алгоритм удобно проиллюстрировать на примере: 0,25 х 0,33:
- Для записи этих дробей необходимо, чтобы число 33 было меньше 25.
- Теперь правую тройку надо умножить на 25. Это получается 75. Записывать полагается так, чтобы пятерка находилась под тройкой, на которую производилось умножение.

- Затем умножьте 25 на первые 3. Опять будет 75, но будет написано так, чтобы под предыдущим числом 7 оказалось 5.
- Сложив эти два числа, мы получим 825. В десятичных дробях 4 цифры разделяются запятыми. Поэтому в ответе нужно отделять запятую тоже 4 цифрами. Но их всего три. Для этого перед 8 надо написать 0, поставить запятую, перед ней еще один 0.
- Ответом в примере является число 0,0825.
Как начать обучение в отделении?
Прежде чем определиться с примерами деления на столбик, предполагается запомнить названия цифр, стоящих в примере деления. Первый из них (тот, который делит) — делимое. Второй (разделенный на него) является делителем. Ответ частный.
После этого на простом бытовом примере поясним суть этой математической операции. Например, если вы возьмете 10 шоколадок, то сможете разделить их поровну между мамой и папой. Но что, если вам нужно подарить их своим родителям и брату?
После этого можно ознакомиться с правилами деления и освоить их на конкретных примерах. Сначала простое, а потом переходим ко все более сложному.
Сначала простое, а потом переходим ко все более сложному.
Алгоритм деления чисел на столбцы
Сначала представим порядок действий для натуральных чисел, которые делятся на однозначное число. Они будут основой для многозначных делителей или десятичных дробей. Только потом надо вносить небольшие изменения, но об этом позже:
- Прежде чем делить на столбик, нужно узнать, где делимое и делитель.
- Напишите дивиденды. Справа от него разделитель.
- Нарисуйте слева и снизу возле последнего угла.
- Определите неполное делимое, то есть число, которое будет минимальным для деления. Обычно он состоит из одного номера, максимум из двух.
- Найдите число, которое будет написано первым в ответе. Это должно быть количество раз, когда делитель помещается в делимое.
- Запишите результат умножения этого числа на делитель.
- Запишите его при неполной делимости. Выполните вычитание.
- Запишите первую цифру до остатка после уже разделенной части.

- Снова выберите число для ответа.
- Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример выполнен. В противном случае повторить действие: снести фигуру, подобрать число, умножить, вычесть.
Как решить деление в столбик, если делитель больше одной цифры?
Сам алгоритм идентичен описанному выше. Разница состоит в количестве цифр в неполной делимости. Их теперь должно быть как минимум два, но если они меньше делителя, то работает с первыми тремя цифрами.
В этом делении есть еще один нюанс. Дело в том, что баланс и снесенная фигура иногда не делятся на делитель. Затем необходимо присвоить еще одну цифру по порядку. Но в этом случае в ответ необходимо поставить нолик. Если вы делите трехзначные числа в столбик, вам может понадобиться снести более двух цифр. Затем вводится правило: нулей в ответе должно быть на один меньше, чем количество сносимых чисел.
Рассмотрим это деление, например — 12082:863.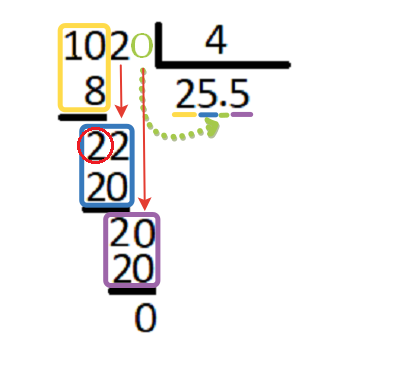
- Неполным делителем в нем является число 1208. Число 863 ставится только один раз. Поэтому в ответе полагается ставить 1, а под 1208 записывать 863.
- После вычитания в остатке 345.
- К нему нужно записать цифру 2.
- В числе 3452 четыре раза 863 подходит.
- Четверка должна быть записана в ответ. И при умножении на 4 получается это число.
- Остаток после вычитания равен нулю. То есть разделение закончилось.
Ответ в примере — число 14.
Что, если делимое оканчивается на ноль?
Или какие-то нули? В этом случае получается нулевой остаток, но в разделителе остаются нули. Отчаиваться не стоит, это проще, чем может показаться. Достаточно просто приписать к ответу все неразделенные нули.
Например, нужно разделить 400 на 5. Неполное делимое 40. Это 8 раз ставится пятерка. Итак, в ответ нам полагается написать 8. При вычитании остатка не остается. То есть деление полное, но в разделителе стоял ноль. Придется отнести к ответу. Таким образом, при делении 400 на 5 получается 80.
Придется отнести к ответу. Таким образом, при делении 400 на 5 получается 80.
Что делать, если вам нужно разделить десятичную дробь?
Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это говорит о том, что деление десятичных дробей в столбик аналогично описанному выше.
Единственным отличием является точка с запятой. Его полагается ставить в ответ сразу, как только из дробной части будет удалена первая цифра. По-другому можно сказать так: закончилось деление целой части — ставь запятую и продолжай решение дальше.
При решении примеров на деление в столбик десятичными дробями следует помнить, что в части после запятой можно приписать любое количество нулей. Иногда это необходимо для того, чтобы разделить числа до конца.
Деление двух знаков после запятой
Это может показаться сложным. Но только в начале. Ведь как сделать деление в столбик дроби на натуральное число и так понятно. Следовательно, нам нужно привести этот пример к уже знакомому виду.
Полегче. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, и на миллион, если этого требует задача. Множитель предполагается выбирать исходя из того, сколько нулей в десятичной части делителя. То есть в итоге получается, что нужно будет разделить дробь на натуральное число.
И это будет в худшем случае. Ведь может случиться так, что дивиденд от этой операции будет целым числом. Тогда решение примера с делением на столбец дробей сведется к простейшему варианту: операции с натуральными числами.
Например: 28,4 разделить на 3,2:
- Сначала их надо умножить на 10, потому что во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
- Их надо разделить. И сразу все число 284 на 32.
- Первое выбранное число для ответа 8. Из его умножения получается 256. Остаток 28.
- Деление целой части закончилось, и в ответе полагается ставить запятую.
- Снести на остаток 0.
- Снова взять 8.

- Остаток: 24. Ему присвоить еще один 0.
- Теперь нужно взять 7.
- Результат умножения 224, остаток 16
- Снять еще 0. Снять 5 и получить всего 160. Остаток — 0.
Деление окончено. Результат примера 28.4: 3.2 равен 8,875.
Что делать, если делитель равен 10, 100, 0,1 или 0,01?
Так же, как и при умножении, деление в столбик здесь не нужно. Достаточно просто перенести запятую в нужном направлении на определенное количество цифр. И по этому принципу можно решать примеры как с целыми, так и с десятичными дробями.
Итак, если вам нужно разделить на 10, 100 или 1000, то запятая переносится влево на столько цифр, сколько нулей в делителе. То есть при делении числа на 100 запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то предполагается, что запятая стоит в его конце.
Это действие дает тот же результат, что и при умножении числа на 0,1, 0,01 или 0,001. В этих примерах запятая также переносится влево на количество цифр, равное длине дробной части.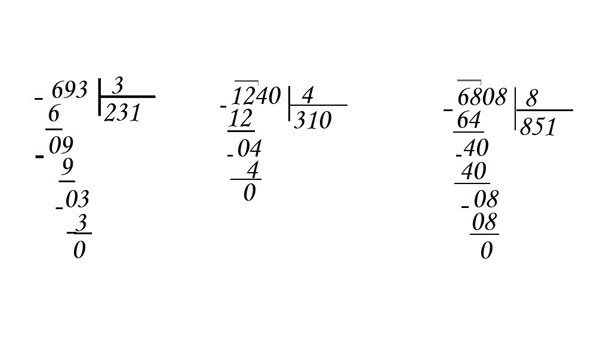
При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна смещаться вправо на одну цифру (или на две, три, в зависимости от количества нулей или длины дробной части).
Стоит отметить, что количество цифр в данных может быть недостаточным. Затем вы можете поставить недостающие нули слева (во всей части) или справа (после запятой).
Деление периодических дробей
В этом случае получить точный ответ при делении в столбик не удастся. Как решить пример, если встретилась дробь с периодом? Здесь предполагается перейти к обыкновенным дробям. А затем провести их деление по заранее изученным правилам.
Например, нужно разделить 0, (3) на 0,6. Первая дробь периодическая. Он преобразуется в дробь 3/9, что после сокращения даст 1/3. Вторая дробь является конечной десятичной дробью. Обычный написать еще проще: 6/10, то есть 3/5. Правило деления обыкновенных дробей предписывает замену деления умножением и делителя обратным числом. То есть пример сводится к умножению 1/3 на 5/3.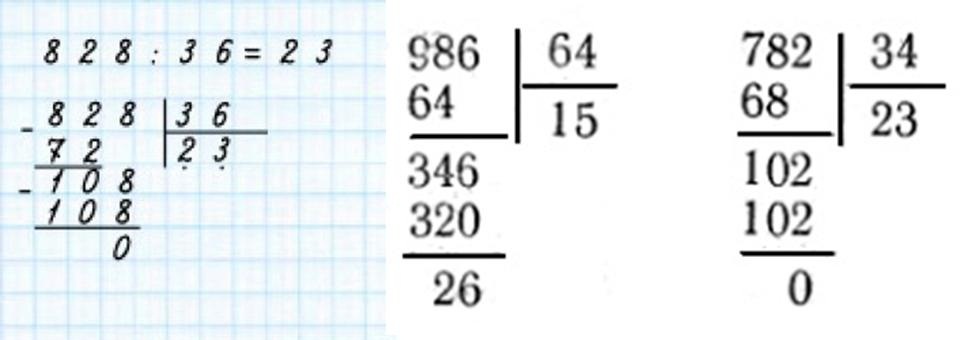
 Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10.
Значение делимого – 1, эта цифра не делится на 5. А вот второе число – 0. В итоге получится 10, это значение допускается разделить данный пример. Число 5 два раза входит в число 10. Запишите столбиком: 1068:89.
Запишите столбиком: 1068:89. Запишите в столбик задачу.
Запишите в столбик задачу. Только если он все поймет, то обучение можно назвать успешным;
Только если он все поймет, то обучение можно назвать успешным; Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого.
Например – игрушечный грузовик – целое, а его кузов, колеса, дверцы – части этого целого. ru/parents/kids/31507.html
ru/parents/kids/31507.html Но результат умножения нужно сдвинуть на один разряд влево. При этом его последняя цифра будет под той, на которую умножали.
Но результат умножения нужно сдвинуть на один разряд влево. При этом его последняя цифра будет под той, на которую умножали.

