Алгоритм сложения дробей с разными знаменателями. Как научиться вычитать дроби с разными знаменателями

Действия с дробями.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.

Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.

Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.

Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.

А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями — это основа для всей алгебры.

Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.

Сложение и вычитание дробей.

Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:

Короче, в общем виде:

А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:

Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.

Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения

.

Ещё пример:

Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:

Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:

Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!

Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:

И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем.

1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.

Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…

Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.

Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.

А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…

Итак, нам надо сложить два дробных выражения:

Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:

И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:

Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем

весь числитель и весь знаменатель! А не их отдельные кусочки…

В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:

Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!

И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.

Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)

Вычислить:

Ответы (в беспорядке):

71/20; 3/5; 17/12; -5/4; 11/6

Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Правила сложения дробей с разными знаменателями очень простые.

Рассмотрим правила сложения дробей с разными знаменателями по шагам:

1. Найти НОК (наименьшее общее кратное) знаменателей. Полученный НОК будет общим знаменателем дробей;

2. Привести дроби к общему знаменателю;

3. Сложить дроби, приведенные к общему знаменателю.

На простом примере научимся применять правила сложения дробей с разными знаменателями.

Пример

Пример сложения дробей с разными знаменателями.

Сложить дроби с разными знаменателями:

1	+	5
6		12

Будем решать по шагам.

1. Найти НОК (наименьшее общее кратное) знаменателей.

Число 12 делится на 6.

Отсюда делаем вывод, что 12 есть наименьшее общее кратное чисел 6 и 12.

Ответ: нок чисел 6 и 12 равен 12:

НОК(6, 12) = 12

Полученный НОК и будет общим знаменателем двух дробей 1/6 и 5/12.

2. Привести дроби к общему знаменателю.

В нашем примере привести к общему знаменателю 12 нужно только первую дробь, ведь у второй дроби знаменатель уже равен 12.

Разделим общий знаменатель 12 на знаменатель первой дроби:

2 есть дополнительный множитель.

Умножим числитель и знаменатель первой дроби (1/6) на дополнительный множитель 2.

На данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с разными знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с разными знаменателями. Для этого дроби необходимо привести к общему знаменателю. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. При этом мы уже умеем приводить алгебраические дроби к общему знаменателю. Сложение и вычитание дробей с разными знаменателями — одна из наиболее важных и сложных тем в курсе 8 класса. При этом данная тема будет встречаться во многих темах курса алгебры, которые вы будете изучать в дальнейшем. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с разными знаменателями, а также разберём целый ряд типовых примеров.

Рассмотрим простейший пример для обыкновенных дробей.

Пример 1. Сложить дроби: .

Решение:

Вспомним правило сложения дробей. Для начала дроби необходимо привести к общему знаменателю. В роли общего знаменателя для обыкновенных дробей выступает наименьшее общее кратное (НОК) исходных знаменателей.

Определение

Наименьшее натуральное число, которое делится одновременно на числа и .

Для нахождения НОК необходимо разложить знаменатели на простые множители, а затем выбрать все простые множители, которые входят в разложение обоих знаменателей.

; . Тогда в НОК чисел должны входить две двойки и две тройки: .

После нахождения общего знаменателя, необходимо для каждой из дробей найти дополнительный множитель (фактически, поделить общий знаменатель на знаменатель соответствующей дроби).

Затем каждая дробь умножается на полученный дополнительный множитель. Получаются дроби с одинаковыми знаменателями, складывать и вычитать которые мы научились на прошлых уроках.

Получаем: .

Ответ: .

Рассмотрим теперь сложение алгебраических дробей с разными знаменателями. Сначала рассмотрим дроби, знаменатели которых являются числами.

Пример 2. Сложить дроби: .

Решение:

Алгоритм решения абсолютно аналогичен предыдущему примеру. Легко подобрать общий знаменатель данных дробей: и дополнительные множители для каждой из них.

.

Ответ:

.

Итак, сформулируем алгоритм сложения и вычитания алгебраических дробей с разными знаменателями :

1. Найти наименьший общий знаменатель дробей.

2. Найти дополнительные множители для каждой из дробей (поделив общий знаменатель на знаменатель данной дроби).

3. Домножить числители на соответствующие дополнительные множители.

4. Сложить или вычесть дроби, пользуясь правилами сложения и вычитания дробей с одинаковыми знаменателями.

Рассмотрим теперь пример с дробями, в знаменателе которых присутствуют буквенные выражения.

Пример 3. Сложить дроби: .

Решение:

Поскольку буквенные выражения в обоих знаменателях одинаковы, то следует найти общий знаменатель для чисел . Итоговый общий знаменатель будет иметь вид: . Таким образом, решение данного примера имеет вид:.

Ответ: .

Пример 4. Вычесть дроби: .

Решение:

Если «схитрить» при подборе общего знаменателя не удаётся (нельзя разложить на множители или воспользоваться формулами сокращённого умножения), то в качестве общего знаменателя приходится брать произведение знаменателей обеих дробей.

Ответ: .

Вообще, при решении подобных примеров, наиболее сложным заданием является нахождение общего знаменателя.

Рассмотрим более сложный пример.

Пример 5. Упростить: .

Решение:

При нахождении общего знаменателя необходимо прежде всего попытаться разложить знаменатели исходных дробей на множители (чтобы упростить общий знаменатель).

В данном конкретном случае:

Тогда легко определить общий знаменатель: .

Определяем дополнительные множители и решаем данный пример:

Ответ: .

Теперь закрепим правила сложения и вычитания дробей с разными знаменателями.

Пример 6. Упростить: .

Решение:

Ответ: .

Пример 7. Упростить: .

Решение:

.

Ответ: .

Рассмотрим теперь пример, в котором складываются не две, а три дроби (ведь правила сложения и вычитания для большего количества дробей остаются такими же).

Пример 8. Упростить: .

Ваш ребенок принес домашнее задание из школы, и вы не знаете как его решить? Тогда этот мини урок для вас!

Как складывать десятичные дроби

Десятичные дроби удобнее складывать в столбик. Чтобы выполнить сложение десятичных дробей, надо придерживаться одного простого правила:

• Разряд должен находиться под разрядом, запятая под запятой.

Как вы видите на примере, целые единицы находятся друг под другом, разряд десятых и сотых находится друг под другом. Теперь складываем числа, не обращая внимания на запятую. Что же делать с запятой? Запятая переносится на то место, где стояла в разряде целых.

Сложение дробей с равными знаменателями

Чтобы выполнить сложение с общим знаменателем, надо сохранить знаменатель без изменения, найти сумму числителей и получим дробь, которая будет являться общей суммой.

Сложение дробей с разными знаменателями методом нахождения общего кратного

Первое, на что надо обратить внимание – это на знаменатели. Знаменатели разные, не делятся ли одно на другое, являются ли простыми числами. Для начала надо привести к одному общему знаменателю, для этого существует несколько способов:

• 1/3 + 3/4 = 13/12, для решения этого примера нам надо найти наименьшее общее кратное число (НОК), которое будет делиться на 2 знаменателя. Для обозначения наименьшего кратного чисел a и b – НОК (а;b). В данном примере НОК (3;4)=12. Проверяем: 12:3=4; 12:4=3.
• Перемножаем множители и выполняем сложение полученных чисел, получаем 13/12 – неправильную дробь.

• Для того чтобы перевести неправильную дробь в правильную, разделим числитель на знаменатель, получим целое число 1, остаток 1 – числитель и 12 – знаменатель.

Сложение дробей методом умножения крест на крест

Для складывания дробей с разными знаменателями существует еще один способ по формуле “крест на крест”. Это гарантированный способ уровнять знаменатели, для этого вам надо числители перемножить со знаменателем одной дроби и обратно. Если вы только на начальном этапе изучения дробей, то этот способ самый простой и точный, как получить верный результат при сложении дробей с разными знаменателями.

Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.

Вычитание дробей с одинаковыми знаменателями, примеры:

,

,

Вычитание правильной дроби из единицы.

Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.

Пример вычитания правильной дроби из единицы:

Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа.

Правила вычитания дробей — правильной из целого числа (натурального числа) :

• Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
• Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
• Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.

Пример вычитания дробей:

В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.

Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей .

Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.

Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.

Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!

Порядок действий при вычитании дробей с разными знаменателями.

• найти НОК для всех знаменателей;
• поставить для всех дробей дополнительные множители;
• умножить все числители на дополнительный множитель;
• полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
• произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.

Вычитание дробей, примеры:

Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.

Первый вариант вычитания смешанных дробей.

Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).

Например:

Второй вариант вычитания смешанных дробей.

Когда у дробных частей разные знаменатели.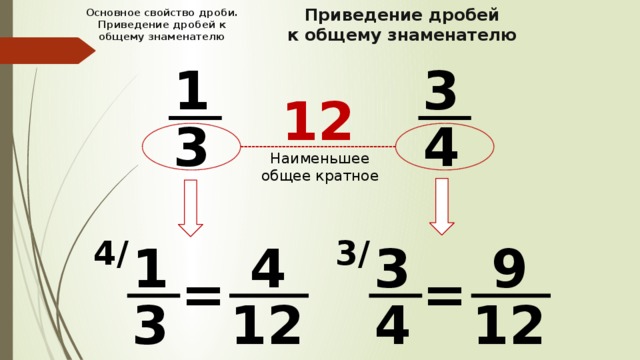 Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.

Например:

Третий вариант вычитания смешанных дробей.

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Пример:

Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.

В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:

Дети и учеба — Информационный портал

• Сложение и вычитание дробей с одинаковыми знаменателями
• Сложение и вычитание дробей с разными знаменателями
• Понятие о НОК
• Приведение дробей к одному знаменателю
• Как сложить целое число и дробь

1 Сложение и вычитание дробей с одинаковыми знаменателями

Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:

Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:

Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,

Пример 1:

Пример 2:

Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:

2 Сложение и вычитание дробей с разными знаменателями.

Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.

3 Наименьшее общее кратное (НОК)

Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:

Для того, чтобы найти НОК нескольких чисел, нужно:

1. Разложить эти числа на простые множители
2. Взять самое большое разложение, и записать эти числа в виде произведения
3. Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
4. Перемножить все числа в произведении, это и будет НОК.

Например, найдем НОК чисел 28 и 21:

4 Приведение дробей к одному знаменателю

Вернемся к сложению дробей с разными знаменателями.

Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:

Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.

5 Как сложить целое число и дробь

Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:

Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:

Тренажер 1

Сложение и вычитание дробей с одинаковыми знаменателями.

Лимит времени: 0

Навигация (только номера заданий)

0 из 20 заданий окончено

Информация

В этом тесте проверяется умение складывать дроби с одинаковыми знаменателями. При этом нужно соблюдать два правила:

• Если в результате получается неправильная дробь, нужно перевести ее в смешанное число.
• Если дробь можно сократить, обязательно сократите ее, иначе будет засчитан неправильный ответ.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Результаты

Правильных ответов: 0 из 20

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0 )

1. С ответом
2. С отметкой о просмотре

Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.

Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:

Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.

Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется приведением к общему знаменателю. А искомые числа, «выравнивающие» знаменатели, называются дополнительными множителями.

Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:

1. Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
2. Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
3. Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.

Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.

Умножение «крест-накрест»

Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:

В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:

Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.

Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.

Метод общих делителей

Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:

1. Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
2. Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
3. При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.

Задача. Найдите значения выражений:

Заметим, что 84: 21 = 4; 72: 12 = 6 . Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:

Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!

Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.

В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.

Метод наименьшего общего кратного

Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.

Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».

Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24: 8 = 3; 24: 12 = 2 . Это число намного меньше произведения 8 · 12 = 96 .

Наименьшее число, которое делится на каждый из знаменателей, называется их наименьшим общим кратным (НОК).

Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a ; b ) . Например, НОК(16; 24) = 48 ; НОК(8; 12) = 24 .

Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:

Задача. Найдите значения выражений:

Заметим, что 234 = 117 · 2; 351 = 117 · 3 . Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.

Аналогично, 15 = 5 · 3; 20 = 5 · 4 . Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.

Теперь приведем дроби к общим знаменателям:

Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:

1. Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
2. Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702 , следовательно, для первой дроби дополнительный множитель равен 3.

Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.

Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!

Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.

У дробей бывают различные или одинаковые знаменатели. Одинаковый знаменатель или по-другому называют общий знаменатель у дроби. Пример общего знаменателя:

\(\frac{17}{5}, \frac{1}{5}\)

Пример разных знаменателей у дробей:

\(\frac{8}{3}, \frac{2}{13}\)

Как привести к общему знаменателю дроби?

У первой дроби знаменатель равен 3, у второй равен 13. Нужно найти такое число, чтобы делилось и на 3 и на 13. Это число 39.

Первую дробь нужно умножить на дополнительный множитель 13. Чтобы дробь не изменилась умножаем обязательно и числитель на 13 и знаменатель.

\(\frac{8}{3} = \frac{8 \times \color{red} {13}}{3 \times \color{red} {13}} = \frac{104}{39}\)

Вторую дробь умножаем на дополнительный множитель 3.

\(\frac{2}{13} = \frac{2 \times \color{red} {3}}{13 \times \color{red} {3}} = \frac{6}{39}\)

Мы привели к общему знаменателю дроби:

\(\frac{8}{3} = \frac{104}{39}, \frac{2}{13} = \frac{6}{39}\)

Наименьший общий знаменатель.

Рассмотрим еще пример:

Приведем дроби \(\frac{5}{8}\) и \(\frac{7}{12}\) к общему знаменателю.

Общий знаменатель для чисел 8 и 12 могут быть числа 24, 48, 96, 120, …, принято выбирать наименьший общий знаменатель в нашем случае это число 24.

Наименьший общий знаменатель – это наименьшее число, на которое делиться знаменатель первой и второй дроби.

Как найти наименьший общий знаменатель?
Методом перебора чисел, на которое делиться знаменатель первой и второй дроби и выбрать из них самое наименьшее.

Нам нужно дробь со знаменателем 8 умножить на 3, а дробь со знаменателем 12 умножить на 2.

\(\begin{align}&\frac{5}{8} = \frac{5 \times \color{red} {3}}{8 \times \color{red} {3}} = \frac{15}{24}\\\\&\frac{7}{12} = \frac{7 \times \color{red} {2}}{12 \times \color{red} {2}} = \frac{14}{24}\\\\ \end{align}\)

Если у вас сразу не получиться привести дроби к наименьшему общему знаменателю в этом ничего страшного нет, в дальнейшем решая пример вам может быть придется полученный ответ

Общей знаменатель можно найти для любых двух дробей это может быть произведение знаменателей этих дробей.

Например:
Приведите дроби \(\frac{1}{4}\) и \(\frac{9}{16}\) к наименьшему общему знаменателю.

Самый простой способ найти общий знаменатель – это произведение знаменателей 4⋅16=64. Число 64 это не наименьший общий знаменатель. По заданию нужно найти именно наименьший общий знаменатель. Поэтому ищем дальше. Нам нужно число, которое делиться и на 4, и на 16, это число 16. Приведем к общему знаменателю дроби, умножим дробь со знаменателем 4 на 4, а дробь со знаменателем 16 на единицу. Получим:

\(\begin{align}&\frac{1}{4} = \frac{1 \times \color{red} {4}}{4 \times \color{red} {4}} = \frac{4}{16}\\\\&\frac{9}{16} = \frac{9 \times \color{red} {1}}{16 \times \color{red} {1}} = \frac{9}{16}\\\\ \end{align}\)

Зачастую выясняется, что действия с дробями не вызывают сложностей у учеников. Основной проблемой становится нахождение общего знаменателя. Чтобы разобраться с этим вопросом, нужно запомнить правило приведения дробей к общему знаменателю и понимать, зачем вообще этот общий знаменатель нужен.

Что такое дробь?

В 5 классе ученикам объясняют, что дробь это разделенное на кусочки целое. Причем знаменатель обозначает количество частей, на которое разделили какой-то предмет, а числитель количество этих частей, которое взяли для расчета.

Но в математике существует другое определение: дробью зовут незавершенную операцию деления. Это значит, что как любую дробь можно превратить в деление, так и любое деление можно превратить в дробь. Например:

$${5\over{7}}=5:7$$

$$7:13={7\over{13}}$$

$$12:9={12\over{9}}$$

Можно бесконечно приводить примеры, но смысл от этого не изменится: черта дроби заменяет знак деления.

Зачем нужно находить общий знаменатель?

Для того, чтобы сложить или вычесть две дроби, нужно превратить две операции деления в одну. Это возможно только при условии одинакового делителя. В виде формул это выглядит так:

а:в-с:е=(а*е):(в*е)-(с*в):(в*е)=((а*е)-(с*в)):(в*е)

То есть для того, чтобы сложить или вычесть дроби, потребуется привести их к общему знаменателю. Иначе просто не получится правильно решить пример.

Для умножения и деления дробей, приводить дроби к общему знаменателю не требуется. Для этих операций существует другое теоретическое обоснование, которое предполагает другой порядок действий.

Как найти общий знаменатель дробей

Для того, чтобы найти общий знаменатель дробей, нужно найти наибольшее общее кратное знаменателей. Приведем пример, решим небольшое выражение:

$${3\over{5}}+{7\over{15}}$$

Найдем НОК знаменателей. Число 15 делится на число 5, значит

$${3\over{5}}+{7\over{15}}={{3*3}\over{15}}+{7\over{15}}={9\over{15}}+{7\over{15}}={16\over{15}}=1 {1\over{15}}$$- обратите внимание, что при увеличении числителя, так же увеличился и знаменатель. В конце решения примера с дробями при возможности следует выделять целую часть выражения.

Привести дроби к общему знаменателю можно только пользуясь основным свойством дроби. Формулировка этого свойства звучит так: если числитель и знаменатель дроби умножить на одно и то же число, то значение дроби не изменится. Это значит, что при приведении дроби к общему знаменателю, требуется учитывать и увеличение числителя.

НОК можно найти аналитически, как мы это сделали в примере. Но чаще всего приходится прибегать к разложению на простые множители. Для того, чтобы найти НОК двух чисел следует:

• Разложить эти числа на простые множители
• Проверить, каких простых множителей не хватает в разложении.
• Берется число с наименьшим количеством множителей и к его разложению добавляют числа, которое есть в других разложениях, но отсутствуют в основном. При этом учитывается и количество чисел. Это значит, что если в основном разложении одно число 3, а в других разложениях два числа 3, то нужно домножить основное разложение на две тройки.

Что мы узнали?

Мы поговорили о приведении дробей к общему знаменателю. Рассказали, зачем это нужно, и какие операции с дробями можно выполнять без приведения к общему знаменателю. Привели пример и рассказали, как меняется числитель при приведении дробей к общему знаменателю.

Тест по теме

Оценка статьи

Средняя оценка: 4.7 . Всего получено оценок: 115.

Приведение дробей к общему знаменателю

Дроби И имеют одинаковые знаменатели. Говорят, что они имеют общий знаменатель 25. Дроби и имеют разные знаменатели, но их можно привести к общему знаменателю с помощью основного свойства дробей. Для этого найдем число, которое делится на 8 и на 3, например, 24. Приведем дроби к знаменателю 24, для этого умножим числитель и знаменатель дроби на дополнительный множитель 3. Дополнительный множитель обычно пишут слева над числителем:

Умножим числитель и знаменатель дроби на дополнительный множитель 8:

Приведем дроби и к общему знаменателю. Чаще всего дроби приводят к наименьшему общему знаменателю, который является наименьшим общим кратным знаменателей данных дробей. Так как НОК (8, 12) = 24, то дроби можно привести к знаменателю 24. Найдем дополнительные множители дробей: 24:8 = 3, 24:12 = 2. Тогда

К общему знаменателю можно приводить несколько дробей.

Пример. Приведем дроби к общему знаменателю. Так как 25 = 5 2 , 10 = 2 5, 6 = 2 3, то НОК (25, 10, 6) = 2 3 5 2 = 150.

Найдем дополнительные множители дробей и приведем их к знаменателю 150:

Сравнение дробей

На рис. 4.7 изображен отрезок АВ длины 1. Он разделен на 7 равных частей. Отрезок АС имеет длину , а отрезок AD имеет длину .

Длина отрезка AD больше длины отрезка AС т. е. дробь больше дроби

Из двух дробей с общим знаменателем больше та, у которой числитель больше, т. е.

Например, или

Чтобы сравнить любые две дроби, их приводят к общему знаменателю, а затем применяют правило сравнения дробей с общим знаменателем.

Пример. Сравнить дроби

Решение. НОК (8, 14) = 56. Тогда Так как 21 > 20, то

Если первая дробь меньше второй, а вторая меньше третьей, то первая меньше третьей.

Доказательство. Пусть даны три дроби. Приведем их к общему знаменателю. Пусть после этого они будут иметь вид Так как первая дробь меньше

второй, то r натуральных чисел следует, что r

Дробь называется правильной , если ее числитель меньше знаменателя.

Дробь называется неправильной , если ее числитель больше знаменателя или равен ему.

Например, дроби-правильные, а дроби -неправильные.

Правильная дробь меньше 1, а неправильная дробь больше или равна 1.

Действия с дробями: правила, приёмы, примеры

• Основное свойство дроби
• Сокращение дробей
• Приведение дробей к общему знаменателю
• Сложение и вычитание дробей
• Умножение и деление дробей
• Свойства пропорции
• Представление рациональной дроби в виде суммы простейших дробей

Условимся считать, что под «действиями с дробями» на нашем уроке будут пониматься действия с обыкновенными дробями. Обыкновенная дробь — это дробь, обладающая такими атрибутами, как числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается из обыкновенной путём приведения знаменателя к числу, кратному 10.

Десятичная дробь записывается с запятой, отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби особых затруднений не вызывают. Итак, вперёд!

Две дроби и называются равными, если .

Например, , так как

Равными также являются дроби и (так как ), и (так как ).

Очевидно, равными являются и дроби и . Это означает, что если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной: .

Это свойство называется основным свойством дроби.

Основное свойство дроби можно использовать для перемены знаков у числителя и знаменателя дроби. Если числитель и знаменатель дроби умножить на -1, то получим . Это означает, что значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:

;

.

Пользуясь основным свойством дроби, можно заменить данную дробь другой дробью, равной данной, но с меньшим числителем и знаменателем. Такую замену называют сокращением дроби.

Пусть, например, дана дробь . Числа 36 и 48 имеют наибольший общий делитель 12. Тогда

.

В общем случае сокращение дроби возможно всегда, если числитель и знаменатель не являются взаимно простыми числами. Если числитель и знаменатель — взаимно простые числа, то дробь называется несократимой.

Забыли, что такое простые и составные числа и чем они различаются? Сейчас узнаем заново.

Простым называется число, которое делится (нацело) на само себя и на единицу. Составным числом называется число, которое делится на само себя, единицу и минимум ещё на одно натуральное число.

Вот первые 25 простых чисел в порядке их возрастания:

2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 43; 47; 53; 59; 61; 67; 71; 73; 79; 83; 89; 97.

А вот все составные числа, не превышающие 50, также в порядке их возрастания:

4; 6; 8; 9; 10; 12; 14; 15; 16; 18; 20; 21; 22; 24; 25; 26; 27; 28; 30; 32; 33; 34; 35; 36; 38; 39; 40; 42; 44; 45; 46; 48; 49; 50.

На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.

Итак, сократить дробь — это значит разделить числитель и знаменатель дроби на общий множитель. Всё вышесказанное применимо и к дробным выражениям, содержащим переменные.

Пример 1. Сократить дробь

.

Решение. Для разложения числителя на множители, представив предварительно одночлен — 5xy в виде суммы — 2xy — 3xy, получим

Для разложения знаменателя на множители используем формулу разности квадратов:

.

В результате

.

Далее, изменяя знаки в числителе и знаменателе дроби, получим

Пусть даны две дроби и . Они имеют разные знаменатели: 5 и 7. Пользуясь основным свойством дроби, можно заменить эти дроби другими, равными им, причём такими, что у полученных дробей будут одинаковые знаменатели. Умножив числитель и знаменатель дроби на 7, получим

.

Умножив числитель и знаменатель дроби на 5, получим

.

Итак, дроби приведены к общему знаменателю:

.

Но это не единственное решение поставленной задачи: например, данные дроби можно привести также к общему знаменателю 70:

,

и вообще к любому знаменателю, делящемуся одновременно на 5 и 7.

Рассмотрим ещё один пример: приведём к общему знаменателю дроби и . Рассуждая, как в предыдущем примере, получим

,

.

Но в данном случае можно привести дроби к общему знаменателю, меньшему, чем произведение знаменателей этих дробей. Найдём наименьшее общее кратное чисел 24 и 30: НОК(24, 30) = 120.

Так как 120:4=5, то чтобы записать дробь со знаменателем 120, надо и числитель, и знаменатель умножить на 5, это число называется дополнительным множителем. Значит .

Далее, получаем 120:30=4. Умножив числитель и знаменатель дроби на дополнительный множитель 4, получим .

Итак, данные дроби приведены к общему знаменателю.

Наименьшее общее кратное знаменателей этих дробей является наименьшим возможным общим знаменателем.

На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.

Для дробных выражений, в которые входят переменные, общим знаменателем является многочлен, который делится на знаменатель каждой дроби.

Пример 2. Найти общий знаменатель дробей и .

Решение. Общим знаменателем данных дробей является многочлен , так как он делится и на , и на . Однако этот многочлен не единственный, который может быть общим знаменателем данных дробей. Им может быть также многочлен , и многочлен , и многочлен и т.д. Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без остатка. Такой знаменатель называется наименьшим общим знаменателем.

В нашем примере наименьший общий знаменатель равен . Получили:

;

.

Нам удалось привести дроби к наименьшему общему знаменателю. Это произошло путём умножения числителя и знаменателя первой дроби на , а числителя и знаменателя второй дроби — на . Многочлены и называются дополнительными множителями, соответственно для первой и для второй дроби.

Сложение дробей определяется следующим образом:

.

Например,

.

Если b = d, то

.

Это значит, что для сложения дробей с одинаковым знаменателем достаточно сложить числители, а знаменатель оставить прежним. Например,

.

Если же складываются дроби с разными знаменателями, то обычно приводят дроби к наименьшему общему знаменателю, а потом складывают числители. Например,

.

На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.

Теперь рассмотрим пример сложения дробных выражений с переменными.

Пример 3. Преобразовать в одну дробь выражение

.

Решение. Найдём наименьший общий знаменатель. Для этого сначала разложим знаменатели на множители:

1) ;

2) ;

3) .

Наименьший общий знаменатель:

Дополнительные множители, на которые умножаются числители дробей:

1) 6;

2) ;

3) .

Результат этого умножения:

.

Далее, раскрывая скобки и выполняя тождественные преобразования, получаем

.

Произведение двух дробей и равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей, т. е. .

Например,

.

При делении дроби на дробь числитель делимого умножается на знаменатель делителя, а знаменатель делимого — на числитель делителя, т. е. .

Например,

.

1. Произведение крайних членов пропорции равно произведению её средних членов, т. е. если , то .

2. Из пропорции вытекают следующие пропорции: , , , то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.

3. Чтобы найти неизвестный средний (крайний) член пропорции, нужно произведение крайних (средних) членов пропорции разделить на известный средний (крайний) член пропорции: и .

В высшей математике это действие с дробями чаще всего применяется при интегрировании рациональных функций. Поэтому оно подробно разобрано в уроке Интегрирование рациональных функций и метод неопределённых коэффициентов.

Назад

Листать

Вперёд>>>

Нет времени вникать в решение? Можно заказать работу!

К началу страницы

Другие темы в блоке «Школьная математика»

Действия со степенями и корнями

Решение квадратных уравнений

Решение дробных уравнений с преобразованием в квадратное уравнение

Как найти общий знаменатель

Быстро, сколько будет 1/4 + 3/4? Если вы помните свою математику из школы, вы, вероятно, знаете, что ответ равен 1. Как насчет 1/5 + 3/4? На этот раз не так просто, правда? Прибавление 1/4 к 3/4 довольно просто, потому что знаменатели обеих дробей одинаковы. Но прибавить 1/5 к 3/4 не так просто, и все потому, что знаменатели разные. Итак, как мы решаем такие проблемы? Начнем с того, что найдем то, что называется общим знаменателем. Что именно мы и научимся делать сегодня.

Числители и знаменатели

Прежде чем мы научимся складывать и вычитать дроби, нам нужно научиться находить общий знаменатель. И прежде чем мы это сделаем, нам нужно убедиться, что мы в курсе некоторых основных принципов дроби. В частности, когда мы впервые заговорили о числителях и знаменателях, мы узнали, что знаменатель дроби говорит вам, сколько равных частей в целом — и это может быть целый пирог, целый год, целый iPhone или что-то еще. — разбивается на части, и числитель дроби говорит вам, сколько таких равных частей содержит дробь.

Таким образом, 4 в дроби, такой как 3/4, означает, что мы разбиваем целое число на 4 равные части. Таким образом, 3 из 3/4 говорит нам, что эта дробь представляет собой сумму, которую мы получим, если возьмем 3 из этих 4 равных частей чего-либо. Хорошо, достаточно легко. Теперь давайте посмотрим, что все это означает при простом сложении и вычитании дробей.

Сложение и вычитание дробей

Для начала, что произойдет, если мы захотим взять эти 3/4 чего-то из предыдущего и добавить к 1/4 этого чего-то? Что ж, здравый смысл — и, как мы, к счастью, увидим, математика — подсказывает нам, что в итоге мы получим что-то целое. Как насчет того, чтобы начать с 1 целого чего-то и вычесть из него 1/4 этого чего-то? Конечно, в итоге мы получаем 3/4 того, с чего начали.

Эти основные факты, по сути, стали для нас здравым смыслом после многих часов, которые мы провели, разбираясь и думая о таких вещах, как пицца, пироги и все остальное в мире, которое можно разбить на части. Как многие из нас узнали в свое время, если мы начнем с целого пирога и удалим 1/4 его (предположительно, ртом), у нас останется 3/4 пирога. Если вместо этого мы начнем с 3/4 пирога, а затем каким-то образом (я не уверен, что хочу знать, как) добавим к нему 1/4 пирога, то неудивительно, что мы получим обратно весь наш пирог.

Что такое общие знаменатели?

Что делает подобные задачи довольно интуитивными и даже легкими для размышления, так это тот факт, что все дроби записываются в терминах так называемого общего знаменателя. Другими словами, они написаны в терминах одного и того же типа «чего-то» — будь то равные порции яблок, пирогов или чего-то еще. В подобных ситуациях все, что вам нужно сделать, чтобы сложить или вычесть дроби, — это добавить или вычесть их числители (поскольку это говорит нам об общем количестве вещей, которые у вас есть), а затем записать это поверх исходного знаменателя (чтобы вернуть ответ в термины тех самых).

Например, поскольку обе дроби в 3/4 + 1/4 имеют общий знаменатель 4, мы находим ответ, складывая числители 3 + 1 = 4, а затем записывая это поверх исходного знаменателя 4, чтобы найти, что 3/4 + 1/4 = 4/4. Как мы узнали, говоря об упрощении дробей, эта дробь 4/4 равна 1. Для задачи 2/3 – 1/3, поскольку обе дроби записаны в терминах одного и того же общего знаменателя, мы можем вычесть числители чтобы получить 2 — 1 = 1, и, следовательно, найти, что 2/3 — 1/3 = 1/3.

Ключевым моментом здесь (поэтому я повторяю это!) является то, что дроби легко складывать, если они записаны в терминах одного и того же общего знаменателя. Естественно возникает вопрос: как привести дроби к общему знаменателю?

Как найти общий знаменатель

Самый простой способ найти общий знаменатель пары дробей — умножить числитель и знаменатель каждой дроби на знаменатель другой. Итак, если вы пытаетесь переписать 1/3 и 1/6 с точки зрения одного и того же общего знаменателя, все, что вам нужно сделать, это умножить верхнюю и нижнюю часть 1/3 на 6 (что является знаменателем 1/6). ) и верхнюю и нижнюю части 1/6 на 3 (что является знаменателем 1/3), чтобы найти, что 1/3 = (1 x 6) / (3 x 6) = 6/18 и 1/6 = ( 1 х 3) / (6 х 3) = 3/18.

Почему это работает? Потому что, как мы знаем из нашего опыта с упрощением дробей, 1/3 и 6/18 эквивалентны, как и 1/6 и 3/18. Таким образом, изученный нами прием — не более чем метод быстрого нахождения эквивалентных форм дробей, записанных в терминах одного и того же общего знаменателя. Как обычно, обратите внимание, что после того, как мы переписали эти дроби в терминах общего знаменателя, мы можем легко складывать или вычитать их. Таким образом, 1/3 + 1/6 = 6/18 + 3/18 = 9/18 (что можно упростить до 1/2), 1/3 – 1/6 = 6/18 – 3/18 = 3/18. (которое можно упростить до 1/6) и так далее.

Хотя этот метод нахождения общего знаменателя всегда будет работать, это не обязательно лучший метод для решения каждой задачи. Почему? Ну, краткий ответ заключается в том, что это часто оставляет вас с большим количеством упрощений. И, как мы узнаем в следующий раз, большей части этого упрощения можно полностью избежать, если быть немного умнее в выборе общего знаменателя.

Подведение итогов

Итак, это все расчеты, на которые у нас есть время на сегодня. Не забудьте стать поклонником Math Dude на Facebook, где вы найдете множество отличных материалов по математике, публикуемых в течение недели. Если вы есть в Твиттере, подпишитесь на меня и там. Наконец, пожалуйста, присылайте мне свои вопросы по математике через Facebook, Twitter или по электронной почте [email protected].

До свидания, это Джейсон Маршалл с краткими и грязными советами по упрощению математики от чувака-математика. Спасибо за внимание, любители математики!

Сложение алгебраических дробей. Полный курс алгебры

Навыки
в
A L G E B R A

Содержание | Дом

23

Различные знаменатели — LCM

2-й уровень

ЕСТЬ ОДНО ПРАВИЛО для сложения или вычитания дробей: Знаменатели должны быть одинаковыми — как и в арифметике.

 

+

б в

=

а + б     с

Сложите числители и поместите их сумму
над общим знаменателем.

Пример 1.

6 x + 3     5

+

4 x − 1     5

=

10 х + 2      5

Знаменатели совпадают. Сложите числители как одинаковые члены.

Пример 2.

6 x + 3      5

−

4 x − 1     5

Чтобы вычесть, измените знаки вычитаемого и сложите.

6 x + 3      5

−

4 x − 1     5

=

6 x + 3 − 4 x + 1           5

=

2 x + 4     5

Задача 1.

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!

а)

х 3

+

г 3

=

х + у    3

б)

5 х

−

2 х

=

3 х

в)

x     x − 1

+

х + 1 х — 1

=

2 x + 1   x − 1

г)

3 x − 4   x − 4

+

х − 5 х − 4

=

4 x − 9   x − 4

д)

6 x + 1   x − 3

−

4 x + 5   x − 3

=

6 x + 1 − 4 x − 5         x − 3

=

2 x − 4   x − 3

е)

2 x − 3   x − 2

−

х − 4 х − 2

=

2 x − 3 − x + 4         x − 2

=

х + 1 х — 2

Различные знаменатели — LCM

Чтобы складывать дроби с разными знаменателями, мы должны научиться строить наименьшее общее кратное ряда членов.

Наименьшее общее кратное (НОК) ряда терминов
— это наименьшее произведение, содержащее все множители каждого термина.

Например, рассмотрим эту серию из трех терминов:

pq     pr     пс

Теперь мы построим их LCM — фактор за фактором.

Для начала у него будут множители первого члена:

LCM = pq

Переходя ко второму члену, LCM должен иметь факторы pr . Но у него уже есть множитель p — поэтому нам нужно добавить только множитель r :

LCM = пкв

Наконец, переходя к последнему члену, LCM должен содержать множители ps . Но снова у него есть множитель p , поэтому нам нужно добавить только множитель s :

ОКМ = номер .

Этот продукт является наименьшим общим кратным pq , pr , ps . Это наименьшее произведение из числа , которое содержит каждый из них в качестве множителей.

Пример 3.   Создайте НОК из этих трех терминов:   x ,   x ² ,   x ³ .

Решение . LCM должен иметь коэффициент x .

НОК = х

. Следовательно, мы должны добавить еще один коэффициент x :

.

НОК = х ²

Наконец, LCM должен иметь коэффициенты x ³ , которые равны x · x · x . Следовательно,

НОК = х ³ .

x ³ — это наименьший продукт, который содержит x , x ² и x ³ в качестве множителей.

Мы видим, что когда члены являются степенями переменной — x , x ² , x ³ — тогда их НОК является наивысшей степенью.

Задача 2.   Построить НОК каждой серии термов.

а)	аб , до н.э. , кд . абс		б)	qrs , qrs , rst . номер
в)	, 2 , 3 , и 4 . а 4		г)	а 2 б , а б 2 . а 2 б 2

 д)    аб ,   кд . абс

Теперь посмотрим, как это связано со сложением дробей.

Пример 4.   Добавить:	3 аб	+	4  до н.э.	+	5  компакт-диск

Решение . Чтобы складывать дроби, знаменатели должны быть одинаковыми. Поэтому в качестве общего знаменателя выбираем НОК исходных знаменателей. Выберите абвд . Затем преобразуйте каждую дробь в эквивалентную дробь со знаменателем abcd .

Общий знаменатель нужно написать только один раз:

3  аб

+

4  до н.э.

+

5  компакт-диск

=

3 cd + 4 ad + 5 ab         abcd

Чтобы преобразовать в эквивалентную дробь со знаменателем abcd , просто умножьте abcd на отсутствующие множители, а именно cd . Следовательно, мы должны также умножить 3 на cd . Это составляет первый член в числителе.

Чтобы преобразовать в эквивалентную дробь со знаменателем abcd , умножьте bc на отсутствующие множители, а именно и . Следовательно, мы должны также умножить 4 на и . Это составляет второй член в числителе.

Чтобы преобразовать в эквивалентную дробь со знаменателем abcd , умножьте cd на недостающие множители, а именно ab . Следовательно, мы должны также умножить 5 на аб . Это объясняет последний член в числителе.

Вот как складывать дроби с разными знаменателями.

Каждый множитель исходных знаменателей должен быть множителем
общего знаменателя.

Проблема 3.   Добавить.

а)

5  аб

+

6   ак

=

5 в + 6 б     абв

б)

2  шт.

+

3  кв.

+

4  руб.

=

2 шт. + 3 шт. + 4 шт.         шт.

в)

7  аб

+

8  до н.э.

+

9   абв

=

7 в + 8 а + 9        abc

г)

1 а

+

2  а 2

+

3 а 3

=

a 2 + 2 a + 3        a 3

д)

3 а 2 б

+

4  а б 2

=

3 б + 4 а     а 2 б 2

е)

5  аб

+

6  компакт-диск

=

5 cd + 6 ab     abcd

г)	_2_    x ( x + 2)	+	__3__       ( x + 2)( x − 3)	=	2( x — 3) + 3 x   x ( x + 2)( x — 3)
				=	_ 2 x − 6 + 3 x _ x ( x + 2)( x − 3)
				=	_5 x − 6_     x ( x + 2)( x − 3)

На 2-м уровне мы увидим аналогичную задачу, но знаменатели не будут факторизованы.

Задача 4.   Добавить:    1 −

1 а

+

в + 1   аб

. Но запишите ответ как

1 – дробь.

1 −

1 а

+

в + 1   аб

=

1 − (

1 и

−

в + 1   аб

)

=

1 −

b − ( c + 1) ab

=

1 −

б − в − 1 аб

Пример 5. Знаменатели без общих множителей.

а м

+

б н

Когда знаменатели не имеют общих делителей, их НОК является просто их произведением, мн .

а м

+

б н

=

ан + бм     мин

Числитель появляется в результате «перекрестного умножения»:

и + бм

Однако этот метод будет работать только при сложении двух дробей, а знаменатели не имеют общих множителей.

Пример 6.

2    x − 1

−

1 х

Решение . У этих знаменателей нет общих делителей — x не является делителем x − 1. Это термин. Следовательно, НОК знаменателей является их произведением.

2    x − 1

−

1 х

=

2 х — ( x − 1)    ( x − 1) x

=

2 x − x + 1    ( x − 1) x

=

_ x + 1_ ( x − 1) x

Примечание:   Вычитается все   x − 1 . Поэтому мы пишем это в скобках — и это знаки смена.

Задача 5.

а)

х а

+

у б

=

xb + ya      ab

б)

х 5

+

3 x  2

=

2 x + 15 x     10

=

17 x  10

в)	6    x − 1	+	3    x + 1	=	6( x + 1) + 3( x — 1)     ( x + 1)( x — 1)
				=	6 х + 6 + 3 x — 3   ( x + 1)( x — 1)
				=	_9 x + 3_    ( x + 1)( x − 1)

г)	6    x − 1	−	3    x + 1	=	6( x + 1) − 3( x − 1)     ( x + 1)( x − 1)
				=	6 x + 6 − 3 x + 3   ( x + 1)( x − 1)
				=	_3 x + 9_    ( x + 1)( x − 1)

д)	3    x − 3	−	2 х	=	3 x − 2( x − 3)    ( x − 3) x
				=	3 x − 2 x + 6    ( x − 3) x
				=	x + 6   ( x − 3) x

е)	3    x − 3	−	1 х	=	3 x − ( x − 3)    ( x − 3) x
				=	3 x − x + 3    ( x − 3) x
				=	2 x + 3  ( x − 3) x

г)

1 х

+

2 г

+

3 я

=

yz + 2 xz + 3 xy         xyz

Пример 7.    Добавить:    и +

б в

.

Раствор.    Мы должны выразить через со знаменателем c.

а

=

ак   с

(Урок 20)

Следовательно,

и +

б в

=

ак + б     в

.

Задача 6.

а)

р д

+   р

=

р + кв     кв

б)

1 х

−  1

=

1 − x     x

в)    x −

1 х

=

x 2 − 1     x

г)   1 −

1  х 2

=

x 2 − 1     x 2

e)    1 −

1    x + 1

=

x + 1 − 1     x + 1

=

x     x + 1

е)   3 +

2    x + 1

=

3 x + 3 + 2     x + 1

=

3 x + 5   x + 1

.

Задача 7.    Напишите обратное число

1 2

+

1 3

.

[ Подсказка :  Только одна дробь

а б

имеет обратную связь; это

б а

.]

1 2

+

1 3

=

3 + 2    6

=

5 6

Следовательно, обратное число равно

6 5

.

2-й уровень

Следующий урок:  Уравнения с дробями

Содержание | Дом

---

Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.

---

Copyright © 2021 Лоуренс Спектор

Вопросы или комментарии?

Электронная почта: [email protected]

4 способа научить учащихся составлять общий знаменатель

Обучение учащихся сложению и вычитанию дробей может быстро стать очень утомительным. Все небольшие возможности для ошибок с составлением эквивалентных дробей, сложением/вычитанием, и только когда они думают, что сделали… бум… им, возможно, придется преобразовать или упростить ответ. Это определенно может быстро надоесть. Одна область, в которой я почти довела себя до совершенства (потому что в преподавании нет ничего идеального), это научить моего ученика приводить к общему знаменателю. В этом посте я поделюсь четырьмя способами, которыми я учу студентов приводить к общему знаменателю, порядком, которым я учу каждый способ, и моим обоснованием этого.

Используйте манипуляции для поиска эквивалентных дробей

Это примерно то, на что похоже. Учащиеся используют манипуляции, либо полоски дробей, либо таблицу эквивалентных дробей (аналогичную тому, что показано на приведенной ниже диаграмме), чтобы преобразовать дроби в эквивалентные дроби с тем же знаменателем.

Эту стратегию они не могут воспроизвести без реальных манипуляций или подобных ресурсов, но она формирует концептуальное понимание того, что учащиеся находят эквивалентные дроби.

Найдите наименьшее общее кратное

Это надежная стратегия, которую мы все знаем и любим. Для этой стратегии учащиеся перечисляют кратные для каждого знаменателя и выбирают наименьшее общее кратное в качестве знаменателя. Мои ученики перечисляют первые пять, потому что обычно это все, что им нужно сделать. Когда я обучаю этой стратегии, я явно связываю ее с работой, которую мы проделали с манипуляторами.

Точно так же, когда мы говорим о следующих двух стратегиях, мы связываем их со стратегией нахождения наименьшего общего кратного, потому что, по сути, следующие две стратегии являются «кратчайшим путем» к нахождению кратного и преобразованию дробей в эквивалентные дроби.

Преобразование только одной из дробей

Как упоминалось выше, я обучаю этой стратегии и следующей только после того, как научу наименьшему общему кратному, потому что она основана на ней. Тем не менее, это одна из стратегий, которую я пытаюсь заставить своих учеников использовать, если они в состоянии это сделать. Это экономит так много времени и оставляет меньше места для ошибок, если они конвертируют только одну дробь. Это также избавляет их от необходимости перечислять кратные, если они могут использовать свое чувство числа, чтобы увидеть, является ли больший знаменатель кратным меньшему.

Для этой стратегии учащиеся изучают знаменатели и используют свои знания о множителях, чтобы определить, могут ли они преобразовать дробь с меньшим знаменателем в эквивалентную дробь с тем же знаменателем, что и у другой дроби. Я использую этот язык, чтобы подсказывать своим ученикам при работе с этой стратегией:  Является ли больший знаменатель кратным меньшему знаменателю?

Умножение знаменателей

На самом деле это моя наименее любимая стратегия, но ученикам она очень нравится. Обычно я не учу этому и обращаюсь к этому только в том случае, если это приходит от студентов. Причина, по которой мне это не нравится, заключается в том, что это может рассматриваться как трюк, и студенты могут просто делать это вслепую, не понимая, что они делают. Тем не менее, это действительно полезно для некоторых студентов.

Для этой стратегии учащиеся умножают знаменатели друг на друга, чтобы получить эквивалентные дроби с одинаковым знаменателем. Я говорю им делать это только в том случае, если это дает им знаменатель меньше 30. Все, что выше 30, становится слишком большим и сложным, когда они пытаются упростить свои ответы.

Якорная диаграмма и бесплатная версия для печати

После обучения четырем стратегиям преобразования дробей в одинаковые знаменатели я представлю якорную диаграмму, которая послужит обзором, а также способом обсуждения «стратегии», которую следует использовать.

У меня заранее подготовлена ​​примерно половина графика (работает все, кроме примера). Мы работаем над одной и той же якорной диаграммой несколько дней (темп зависит от учеников). Мы практикуем стратегии несколько раз в качестве обзора на маркерных досках, прежде чем записать пример задачи вместе на графике и на их печатных формах. Распечатки остаются в их математических тетрадях, чтобы они могли обращаться к ним по мере необходимости.

Щелкните или на изображении ниже, чтобы получить бесплатную распечатку, соответствующую якорной диаграмме.

Общие вопросы

Вы обучаете всем четырем способам?

Не всегда. Это зависит от потребностей моих учеников, но в большинстве случаев я учу всем четырем способам или обращаюсь к ним в какой-то момент. Я обнаружил, что многих моих учеников старшие братья и сестры учат трюку умножения знаменателя. Это единственная стратегия, которой я не всегда учу, но обращаюсь, если она возникает.

Как вы последовательно представляете и обучаете различным способам?

Я следую этой последовательности при вводе и обучении различным стратегиям. Я считаю, что эта последовательность создает прочную концептуальную основу, и каждый способ опирается на другой для более глубокого понимания, сохраняя при этом необходимую основу.

1. Использование манипуляций для преобразования в эквивалентные дроби
2. Нахождение наименьшего общего кратного
3. Преобразование только одной из дробей (путем обсуждения того, что больший знаменатель кратен меньшему знаменателю)
4. Умножение знаменателей

Однако на диаграмме и в печатных формах я перечисляю стратегии в том порядке, в котором они обычно используются моими учениками (пропускаю №3, если я решу не использовать его с этой группой учеников).

Вам нужно больше ресурсов фракции для вашего класса?

Нажмите на ссылки ниже, чтобы ознакомиться с несколькими рекомендуемыми ресурсами или статьями для дробей.

Мини-буклет с обзором фракций для 4-го класса: я использую этот ресурс из своего магазина TeachersPayTeachers, прежде чем преподавать навыки фракций для 5-го класса.