Как научиться перемножать большие числа и зачем вам это нужно
В школе было важно правильно писать слова «задача» и «решение» и красиво рисовать скобки. В итоге для многих алгебра и геометрия остались набором непонятных формул, которые нужно заучивать наизусть. Профессор математики Нелли Литвак и продюсер Алла Кечеджан написали об этом книгу «Математика для безнадежных гуманитариев. Для тех, кто учил языки, литературу и прочую лирику». Публикуем отрывок о разных способах умножения и о том, почему раскрытие скобок — это естественный закон о разрывании вещей.
Математика для безнадежных гуманитариев. Для тех, кто учил языки, литературу и прочую лирику
Нелли Литвак, Алла Кечеджан
АСТ. 2019
18 × 5
Начнем с задания из книги Джо Боулер «Математическое мышление». Это одно из ее любимых заданий. Оно очень простое, пожалуйста, выполните его полностью.
Задание: Умножьте в уме 18 на 5. Напишите подробно, как именно вы это сделали. То есть что на что умножили сначала, что потом, что складывали. Или, может, вы помнили ответ наизусть? Удачи!
То есть что на что умножили сначала, что потом, что складывали. Или, может, вы помнили ответ наизусть? Удачи!
Это простенькое задание Джо Боулер задавала многим, в том числе ребятам из технологического стартапа, у которых с умножением все в порядке. Тем не менее, они бурно обсуждали задание, горячились, выбегали к доске, а потом даже предложили выпустить футболку с надписью 18 × 5.
Что их так потрясло? То, что все они решили эту простую задачку разными способами! Наверное, многие из вас посчитали вот так:
18 × 5 = 10 × 5 + 8 × 5 = 50 + 40 = 90.
Кто-то посчитал по-другому:
18 × 5 = 20 × 5 — 2 × 5 = 100 — 10 = 90.
А можно еще вот так:
9 × 2 × 5 = 9 × 10 = 90.
Еще один удобный способ умножить на 5 — это сначала умножить на 10, а потом поделить пополам. Вот так:
18 × 5 = (18 × 10) / 2 = 180 / 2 = 90.
Знаете ли вы, что во французском языке считают не десятками, а двадцатками? Число 90 по-французски звучит так: quatre vingt dix, что в буквальном переводе означает «четырежды двадцать десять». И мы могли бы посчитать на французский манер:
И мы могли бы посчитать на французский манер:
18 × 5 = 4(4 × 5) + 2 × 5 = 4 × 20 + 10 = 90.
Надеемся, мы вас убедили, что даже при элементарном умножении нет единственно правильного подхода. Прийти к ответу можно самыми разными способами, и все они правильные.
Путь к решению — это и есть самое интересное в математике. А вовсе не правильный ответ!
Решение важнее ответа
«Одна из самых первых и самых сложных задач, с которой я сталкиваюсь как университетский преподаватель, — это заставить студентов (да, именно заставить!) правильно записывать математику. Их первые домашние задания — это обычно нечитабельная коллекция цифр и символов… „Зачем писать полные предложения? — удивляется первокурсник. — Я же нашел правильный ответ, вот, смотрите, внизу страницы!“»
Автор этих строк — профессор математики Кевин Хьюстон из Лидского университета в Англии и автор книги «Думать как математик» (How to Think Like a Mathematician). Под его словами подпишется подавляющее большинство университетских преподавателей.
В школе на уроках математики мы привыкли, что самое главное — это правильный ответ и что учитель из обрывков формул поймет, как мы до него добрались. Но на самом деле в математике, по словам того же Хьюстона, главное — «получить ответ с помощью обоснованных аргументов и убедить других, что ваши аргументы обоснованы».
В этом еще один колоссальный разрыв между школьной математикой и математикой на самом деле. Главное не ответ, главное — решение. Математические статьи в основном состоят из слов, а не из формул. И даже формулы, если приглядеться внимательно, это просто часть предложения! Мы могли бы это все записать словами, но формулы просто короче. Как пишет Джейсон Уилкс в книге «Математика в огне», формулы — это всего-навсего сокращения.
Работа по математике — это связное рассуждение. В этом смысле она ничем не отличается от работы, скажем, по истории.
Муж Нелли тоже университетский преподаватель математики. И, конечно, он тоже тратит много сил и времени, чтобы убедить студентов записывать решения подробно, с помощью полных предложений.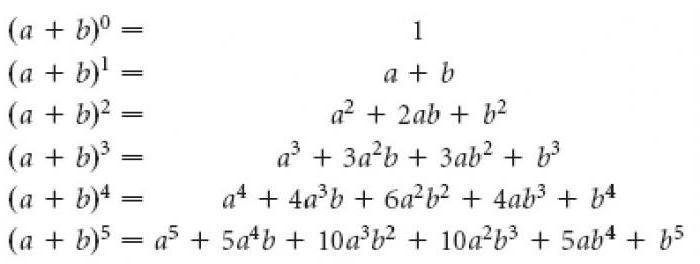 Убедить бывших школьников, что решение важнее ответа, очень непросто! На рисунке его любимый пример, который он приводит на своих занятиях.
Убедить бывших школьников, что решение важнее ответа, очень непросто! На рисунке его любимый пример, который он приводит на своих занятиях.
Ответ совершенно правильный, можете сами проверить. Но если рассуждать так, то можно получить и много всякой ерунды, например, что ¹²/₂₄ тоже равно ¼, или что ¹³/₃₉ равно ⅑.
На всякий случай приведем правильное решение. Можете в нем не разбираться, мы просто хотим показать, что оно выглядит совершенно по-другому.
Как видите, правильный ответ мало что значит. Получилась одна четвертая — ну и что. Это может посчитать любой калькулятор. Для математиков самое важное — это подход. Если нам нужно упростить дробь, то нельзя взять и зачеркнуть шестерку, а нужно искать общие множители!
Главное не ответ, а решение. И мы уже видели, что даже такую простую задачку, как 18 × 5, можно решить самыми разными способами. Поэтому математика — это не набор стандартных приемов, а творческий процесс.
В математике есть понятие вкуса: кому-то больше нравится одно решение, кому-то другое. У математиков могут быть свои любимые способы доказательств, теоремы, алгоритмы. И уж конечно, в математике есть мода и даже устаревшие задачи и устаревшие методы решения!
У математиков могут быть свои любимые способы доказательств, теоремы, алгоритмы. И уж конечно, в математике есть мода и даже устаревшие задачи и устаревшие методы решения!
Устаревшая математика?
В блестящем TED-выступлении в октябре 2014 года Эдуардо Саенц де Кабесон сказал: «Если вы хотите сделать подарок навечно, не дарите бриллианты, подарите теорему!»
Если математический результат доказан, то он верен всегда. Любая теорема — на века. В других науках это не так. Например, сначала люди считали, что земля плоская; потом стали полагать, что круглая. Сначала думали, что брожение вина — это химический процесс, потом Луи Пастер доказал, что брожение происходит из-за бактерий (кстати, именно в честь Пастера мы называем молоко пастеризованным). Математика в этом плане занимает особенное место.
Если математический результат доказан, то он — как ни крути — всегда останется верным.
Тем не менее, в математике, как в искусстве, что-то становится классикой, а что-то устаревает. Например, теорема Пифагора — это золотая классика, которая не устареет никогда! Не случайно профессор математики и популяризатор Алексей Савватеев сказал, что именно эту теорему он передал бы в капсуле инопланетянам как одно из основных достижений человеческого разума.
Например, теорема Пифагора — это золотая классика, которая не устареет никогда! Не случайно профессор математики и популяризатор Алексей Савватеев сказал, что именно эту теорему он передал бы в капсуле инопланетянам как одно из основных достижений человеческого разума.
Что же такое устаревшая теорема? Нелли запомнилась история, которую ей рассказал коллега из университета Твенте, профессор по вычислительным методам.
Вычислительные методы — это область математики, которая разрабатывает алгоритмы, чтобы решать задачи приблизительно, с помощью вычислений, а не с помощью формул. Коллега Нелли рассказал ей, как лет двадцать назад уходил на пенсию старый профессор и оставил ему журналы по вычислительным методам 60-х годов. Это были отличные журналы, в них публиковались известные авторы. Но только тогда еще не было общедоступных быстрых компьютеров. Ученые пользовались так называемыми специальными функциями и таблицами, которые занимали целые тома.
С появлением компьютеров все изменилось, потому что машины считают очень быстро. Обычный ноутбук выполняет 2 миллиарда операций в секунду! Многие результаты и подходы докомпьютерной эпохи безнадежно устарели. Коллега Нелли глубоко вздохнул и отнес все эти журналы в макулатуру.
Обычный ноутбук выполняет 2 миллиарда операций в секунду! Многие результаты и подходы докомпьютерной эпохи безнадежно устарели. Коллега Нелли глубоко вздохнул и отнес все эти журналы в макулатуру.
Вы уже раскрыли скобки!
Посмотрим снова на пример 18 × 5. Допустим, вы подсчитали так:
18 × 5 = 10 × 5 + 8 × 5 = 50 + 40 = 90.
Когда мы умножаем в уме, мы очень легко и естественно разбиваем числа на части и умножаем по отдельности. Это и есть раскрытие скобок. Скобки нам нужны, просто чтобы записать то, что мы делаем в уме:
(10 + 8) × 5 = 10 × 5 + 8 × 5 = 50 + 40 = 90.
Математики называют раскрытие скобок великими и ужасными словами «распределительный закон».
Звучит умно, но терминология не так важна. В книге «Математика в огне» Уилкс называет раскрытие скобок «естественным законом о разрывании вещей». Мы «разрываем» 18 на две части — 10 и 8, умножаем каждую из них на 5, а потом складываем.
Две скобки
Скобок может быть и больше. Принцип остается тот же самый.
Задание: Умножьте 12 на 13. Объясните, как это можно сделать с помощью раскрытия скобок. Считать в столбик, на калькуляторе или пользоваться Интернетом можно, только чтобы проверить ответ. Удачи!
Начать можно, как и раньше:
12 × 13 = (10+ 2) × 13 = 10 × 13 + 2 × 13.
В принципе теперь можно сразу посчитать ответ:
130 + 26 = 156.
Но, если подумать: как мы умножаем на 13? Может, кто-то делает это на автомате. Но обычно (может, даже незаметно для себя) мы все-таки разрываем 13 на 10 и 3. Тогда получается:
10 × 13 + 2 × 13 = 10 × (10 + 3) + 2 × (10 + 3) = 10 × 10 + 10 × 3 + 2 × 10 + 2 × 3 = 100 + 30 + 20 + 6 = 156.
Конечно, скобок может быть и больше:
12 × 13 × 14 = (10 + 2) × (10 + 3) × (10 + 4).
И чисел в скобках тоже может быть больше:
112 × 113 = (100 + 10 + 2) × (100 + 10 + 3).
Принцип тот же, просто вычисления длиннее. Сколько бы ни было скобок.
Скобки и площади
Со школы мы привыкли считать, что есть две математики — алгебра и геометрия, и каждая тема сама по себе. На самом деле в математике все взаимосвязано и наука движется вперед, как раз когда идеи из одного раздела проникают в другой.
На самом деле в математике все взаимосвязано и наука движется вперед, как раз когда идеи из одного раздела проникают в другой.
Площадь прямоугольника — скорее геометрия. Раскрытие скобок — типичная алгебра. Но площадь прямоугольника — это одна сторона, умноженная на другую. И скобки мы раскрываем тоже, когда умножаем числа. Значит, связь есть!
Алла долго воевала со скобками, пока не решила их нарисовать. Когда она увидела связь между скобками, умножением и площадью прямоугольника, все встало на свои места.
Нелли долго удивлялась: неужели на числах было непонятно? Но многим детям и взрослым — в точности как Алле — гораздо проще работать с рисунками, фигурами и площадями, чем с абстрактными числами и скобками. Классическая школьная программа обычно не рассчитана на визуалов. Мы постараемся немножко восполнить этот пробел и нарисовать тему скобок.
Нарисуйте прямоугольник 12 на 13 см. Ничего страшного, если у вас под рукой нет бумаги с карандашом — на своем любимом пляже в Варне Алла начертила прямоугольник, конечно же, пером чайки на песке.
Теперь сделайте десять «насечек» для десятков по вертикали и горизонтали, а потом две и три для единиц соответственно. Теперь проведем линию раздела между десятками и единицами. Получилось 4 прямоугольника.
Теперь перемножаем длину и ширину в каждом из прямоугольников между собой:
10 × 10 = 100
2 × 10 = 20
2 × 3 = 6
3 × 10 = 30
Потом складываем все результаты и получаем 156.
Это работает всегда! Фактически Алла предложила геометрическую трактовку раскрытия скобок. Когда мы раскрывали скобки без рисунка, мы разбивали 12 × 13 на те же самые числа:
12 × 13 = (10 + 2) × (10 + 3) = 10 × (10 + 3) + 2 × (10 + 3) = 100 + 30 + 20 + 6 = 156.
Задание: С помощью площадей прямоугольников умножьте 21 на 33. Удачи!
a плюс b в квадрате
Может быть, вы помните (а может, и нет) знаменитую формулу для вычисления (a + b) в квадрате:
a-квадрат-плюс-два-ab-плюс-b-квадрат
Мы написали эту формулу на рисунке. У кого-то она вызовет легкую ностальгию, у кого-то — давно забытое, но знакомое смятение.
Задание: Получите сами формулу для вычисления (a + b)². У нас для этого уже все есть! Вспомните, что (a + b) — это всего лишь число. А квадрат — это число, умноженное на само себя! То есть (a + b)² = (a + b)(a + b). Получив формулу, проверьте ее на числах. Удачи!
Надеемся, вы увидели связь этой формулы с предыдущей. Это в точности то же самое, что (a + b)(a + b), но только скобки одинаковые. Заметим, что когда мы перемножаем букву саму на себя, например, a × a, то знак умножения упускать не принято. На письме aa смотрится как-то некрасиво и неуместно, как крик о помощи или заикание. Принято писать a × a или a². Давайте попробуем применить эту формулу. Вот что получилось:
(a + b)² = (a + b)(a + b) = a × a + ab + ba + b × b.
Что тут можно заметить? Во-первых, a × a — это a², а b × b — это b². Кроме того, ab и ba — это одно и то же, потому что буквы просто обозначают числа, и перемножать их можно в любом порядке. Тогда ab + ba = ab + ab = 2ab. В результате выходит:
(a + b)² = (a + b)(a + b) = a × a + ab + ba + b × b = a² + 2ab + b².
То, что слева, равно тому, что справа, то есть:
(a + b)² = a² + 2ab + b².
Что и требовалось доказать.
Естественно, геометрическая интерпретация через площади по-прежнему в силе. Мы приводим рисунок ниже, но сначала попробуйте выполнить задание сами!
Задание: Объясните формулу (a + b)² = a² + 2ab + b² с помощью площадей. Удачи!
Если у вас получилось выполнить это задание, то можете снять видео и выложить его на «Ютьюбе». Как вы думаете, сколько просмотров оно наберет? Не стоит недооценивать интерес людей к раскрытию скобок. В 2012 году тридцатисекундное видео учителя математики из Индии Кхуршеда Батливалы про (a + b)² взорвало Интернет, собрав более миллиона просмотров! И это всего лишь визуализация того, как раскрыть скобки с помощью площадей.
Давайте попробуем повторить успех Батливалы. Нарисуем горизонтальную линию, состоящую из двух отрезков — a и b.
Нарисуем горизонтальную линию, состоящую из двух отрезков — a и b.
Так как в формуле мы возводим a и b в квадрат, то и рисуем квадрат — проводим вертикальную линию, также состоящую из отрезков — a и b (помните, что у квадрата все стороны равны?), и достраиваем чертеж до нужной нам фигуры. Площадь такого квадрата равна (a + b)(a + b), или (a + b)².
А теперь разделим квадрат изнутри на 4 части, соединив между собой противоположные стороны.
Из чего состоит эта площадь? a² и b² — это площади внутренних заштрихованных квадратов. Осталось два одинаковых внутренних прямоугольника, у каждого из которых площадь равна ab. Сложим четыре площади вместе и получим a × a + ab + ab + b × b. Узнаете? Это же та же формула, a² + 2ab + b²!
Если вам, как и Алле, непросто раскрывать скобки, то по картинке всегда можно вспомнить формулу или даже вывести ее заново! К этому волшебному квадрату мы еще не раз вернемся. Именно он позволит нам добраться до самых глубоких корней квадратного уравнения и доказать теорему Пифагора.
Ну и наконец, подставим числа. Давайте a примем за 4, а b — за 3. Тогда (4 + 3)² = 7² = 7 × 7 = 49. А по формуле (4 + 3)² = 42 + 2 × 4 × 3 + 32 = 16 + 24 + 9 = 49. Красота!
Игры с умножением
В Интернете можно найти много интересных игр и примеров с умножением чисел. Вот один забавный.
Задание: Возьмите калькулятор, умножьте 481 на 21 и на ваш возраст. Понимаете, как получился результат? Для самых любознательных вопрос посложнее: всегда ли это работает? Удачи!
Конечно, числа 481 и 21 выбраны не случайно. Если их перемножить, то получится 10101. Допустим вам 34 года. Тогда 10101 × 34 = 343434. Это работает, если вам от 10 до 99. Кстати, этот трюк напрямую связан с раскрытием скобок.
Смотрите, мы можем разорвать 10101 на части:
10101 = 10000 + 100 + 1. Перемножим по частям:
10000 × 34 = 340000
100 × 34 = 3400
1 × 34 = 34.
Сложим и получим 343434.
Стихия скобок
Тему раскрытия скобок можно продолжать бесконечно. Если бы мы не ограничились (a + b)², а добавили побольше скобок, например, (a + b)³ = (a + b) (a + b) (a + b), то очень быстро столкнулись бы с комбинаторикой, биномом Ньютона, треугольником Паскаля и теорией вероятностей. И предела этому нет…
Если бы мы не ограничились (a + b)², а добавили побольше скобок, например, (a + b)³ = (a + b) (a + b) (a + b), то очень быстро столкнулись бы с комбинаторикой, биномом Ньютона, треугольником Паскаля и теорией вероятностей. И предела этому нет…
Наш гуманитарий Алла, находясь под впечатлением от скобок в математике, стояла на черноморском берегу и смотрела на отплывающие от берега судна. Она заметила, что паруса издалека выглядят как скобки, и можно представить, что это числа ходят под парусами: те, что побольше, отплывают на шхунах, поменьше — на утлых лодочках. С берегом расставаться всегда немного грустно. Вот на какие стихи Аллу вдохновила математика:
Мне жалко цифры разрывать,
Они, как лодки от причала,
Не отрываются сначала,
На помощь нужно ветер звать.
И гнутся скобки — столько ветра,
А на борту одно весло.
От круглых чисел словно ветка
Откалывается колесо.
В рубрике «Открытое чтение» мы публикуем отрывки из книг в том виде, в котором их предоставляют издатели. Незначительные сокращения обозначены многоточием в квадратных скобках. Мнение автора может не совпадать с мнением редакции.
Незначительные сокращения обозначены многоточием в квадратных скобках. Мнение автора может не совпадать с мнением редакции.
Читайте нас в Facebook, VK, Twitter, Instagram, Telegram (@tandp_ru) и Яндекс.Дзен.
как перемножить две, три, примеры — «Семья и Школа»
Одинаковые множители выносим за скобку и перемножаем, а каждый компонент в скобках делим на это произведение:\( \boldsymbol a\times\boldsymbol b\times c+\boldsymbol a\times\boldsymbol b=\boldsymbol a\boldsymbol b(\frac{\boldsymbol a\times\boldsymbol b\times c}{\boldsymbol a\boldsymbol b}+\frac{\boldsymbol a\times\boldsymbol b}{\boldsymbol a\boldsymbol b}).Пример 7
Решите уравнение: \(3(x-4x)=0\).
Чтобы решить уравнение, нужно найти все его корни или доказать, что корней нет.
Корень уравнения — значение переменной, при которой получается верное равенство.
Объяснение решения.
- Раскрываем скобки: умножаем 3 на каждый компонент в скобках.

\(\begin{array}{l}3(x-4x)=0\\3\ast x-3\ast4x=0\\\end{array}.\)
- Перемножаем:\( \begin{array}{l}3\ast x-3\ast4x=0\\3x-12x=0\\\end{array}.\)
- В выражении есть подобные слагаемые\( ‒ 3x и (-12x)\).
- Упрощаем:\( \begin{array}{l}3x-12x=0\\-9x=0\\\end{array}.\)
- Осталось найти икс:
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель:
\(\begin{array}{l}x=0\div(-9)\\x=0\end{array}.\)
- Выполняем проверку. Для этого найденное значение подставляем в исходное выражение и сравниваем правую и левую части: \(\begin{array}{l}3(0-4\ast0)=0\\0=0\end{array}. \)
- Получаем верное равенство, значит, \(x=0\) — корень уравнения.
- Записываем ответ: 0.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Поиск по содержимому
Раскрытие скобок: правила, примеры, решения
Раскрытие скобок является одним из видов преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.
В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.
Что называется раскрытием скобок?
Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, заменить выражение 2·(3+4) на выражение вида
Под раскрытием скобок подразумевают приемы избавления от скобок и рассматривают его обычно в отношении выражений, которые могут содержать:
- знаки «+» или «-» перед скобками, в которые заключены суммы или разности;
- произведение числа, буквы или нескольких букв и суммы или разности, которая помещена в скобки.
Так мы привыкли рассматривать процесс раскрытия скобок в курсе школьной программы. Однако никто не мешает нам посмотреть на это действие шире. Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5+(−3)−(−7) к 5−3+7. Фактически, это тоже раскрытие скобок.
Мы можем назвать раскрытием скобок переход от выражения, которое содержит отрицательные числа в скобках, к выражению, не имеющему скобок. К примеру, мы можем перейти от 5+(−3)−(−7) к 5−3+7. Фактически, это тоже раскрытие скобок.
Точно также мы можем заменить произведение выражений в скобках вида (a+b)·(c+d) на сумму a·c+a·d+b·c+b·d. Такой прием также не противоречит смыслу раскрытия скобок.
Вот еще один пример. Мы можем допустить, что в выражениях вместо чисел и переменных могут быть использованы любые выражения. Например, выражению x2·1a-x+sin(b) будет соответствовать выражение без скобок вида x2·1a-x2·x+x2·sin(b) .
Отдельного внимания заслуживать еще один момент, который касается особенностей записи решений при раскрытии скобок. Мы можем записать начальное выражение со скобками и полученный после раскрытия скобок результат как равенство. Например, после раскрытия скобок вместо выражения 3−(5−7) мы получаем выражение 3−5+7. Оба этих выражения мы можем записать в виде равенства 3−(5−7)=3−5+7.
Проведение действий с громоздкими выражениями может потребовать записи промежуточных результатов. Тогда решение будет иметь вид цепочки равенств. Например,
Правила раскрытия скобок, примеры
Приступим к рассмотрению правил раскрытия скобок.
У одиночных чисел в скобках
Отрицательные числа в скобках часто встречаются в выражениях. Например, (−4) и 3+(−4). Положительные числа в скобках тоже имеют место быть.
Сформулируем правило раскрытия скобок, в которых заключены одиночные положительные числа. Предположим, что а – это любое положительное число. Тогда (а) мы можем заменить на а, +(а) на +а, -(а) на –а. Если вместо а взять конкретное число, то согласно правилу: число (5) запишется как 5, выражение 3+(5) без скобок примет вид 3+5, так как +(5) заменяется на +5, а выражение 3+(−5) эквивалентно выражению 3−5, так как +(−5) заменяется на −5.
Положительные числа обычно записываются без использования скобок, так как скобки в этом случае излишни.
Теперь рассмотрим правило раскрытия скобок, внутри которых содержится одиночное отрицательное число. +(−a) мы заменяем на −a, −(−a) заменяется на +a. Если выражение начинается с отрицательного числа (−a), которое записано в скобках, то скобки опускаются и вместо (−a) остается −a.
Приведем примеры: (−5) можно записать как −5, (−3)+0,5 принимает вид −3+0,5, 4+(−3) превращается в 4−3, а −(−4)−(−3) после раскрытия скобок принимает вид 4+3, так как −(−4) и −(−3) заменяется на +4 и +3.
Следует понимать, что записать выражение 3·(−5) как 3·−5 нельзя. Об этом речь пойдет в следующих пунктах.
Давайте посмотрим, на чем основываются правила раскрытия скобок.
Согласно правилу разность a−b равна a+(−b). На основе свойств действий с числами мы можем составить цепочку равенств (a+(−b))+b=a+((−b)+b)=a+0=a, которая будет справедлива. Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a+(−b) — это разность a−b.
Эта цепочка равенств в силу смысла вычитания доказывает, что выражение a+(−b) — это разность a−b.
Основываясь на свойствах противоположных чисел и правил вычитания отрицательных чисел мы можем утверждать, что −(−a)=a, a−(−b)=a+b.
Встречаются выражения, которые составляются из числа, знаков минуса и нескольких пар скобок. Использование приведенных выше правил позволяет последовательно избавляться от скобок, продвигаясь от внутренних скобок к наружным или в обратном направлении. Примером такого выражения может быть −(−((−(5)))). Раскроем скобки, продвигаясь изнутри наружу: −(−((−(5))))=−(−((−5)))=−(−(−5))=−(5)=−5. Также этот пример можно разобрать и в обратном направлении: −(−((−(5))))=((−(5)))=(−(5))=−(5)=−5.
Под a и b можно понимать не только числа, но также произвольные числовые или буквенные выражения со знаком «+» впереди, которые не являются суммами или разностями. Во всех этих случаях можно применять правила точно также, как мы делали это в отношении одиночных чисел в скобках.
К примеру, после раскрытия скобок выражение −(−2·x)−(x2)+(−1x)−(2·x·y2:z) примет вид 2·x−x2−1x−2·x·y2:z. Как мы это сделали? Мы знаем, что −(−2·x) есть +2·x, а так как это выражение стоит вначале, то +2·x можно записать как 2·x, −(x2)=−x2, +(−1x)=−1x и −(2·x·y2:z)=−2·x·y2:z.
В произведениях двух чисел
Начнем с правила раскрытия скобок в произведении двух чисел.
Предположим, что a и b – это два положительных числа. В этом случае произведение двух отрицательных чисел −a и −b вида (−a)·(−b) мы можем заменить на (a·b), а произведения двух чисел с противоположными знаками вида (−a)·b и a·(−b) заменить на (−a·b). Умножение минуса на минус дает плюс, а умножение минуса на плюс, как и умножение плюса на минус дает минус.
Верность первой части записанного правила подтверждается правилом умножения отрицательных чисел. Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.
Рассмотрим несколько примеров.
Рассмотрим алгоритм раскрытия скобок в произведении двух отрицательных чисел -435 и -2, вида(-2)·-435 . Для этого заменим исходное выражение на 2·435 . Раскроем скобки и получим 2·435 .
А если мы возьмем частное отрицательных чисел (−4):(−2), то запись после раскрытия скобок будет иметь вид 4:2
На месте отрицательных чисел −a и −b могут быть любые выражения со знаком минус впереди, которые не являются суммами или разностями. К примеру, это могут быть произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п.
Раскроем скобки в выражении -3·xx2+1·x·(ln5). Согласно правилу, мы можем произвести следующие преобразования: -3·xx2+1·x·(ln5)=-3·xx2+1·x·ln5=3·xx2+1·x·ln5.
Выражение (−3)·2 можно преобразовать в выражение (−3·2). После этого можно раскрыть скобки: −3·2.
23·-45=-23·45=-23·45
Деление чисел с разными знаками также может потребовать предварительного раскрытия скобок: (−5):2=(−5:2)=−5:2 и 234:(-3,5)=-234:3,5=-234:3,5.
Правило может быть использовано для выполнения умножения и деления выражений с разными знаками. Приведем два примера.
-1x+1:x-3=-1x+1:x-3=-1x+1:x-3
и
sin(x)·(-x2)=(-sin(x)·x2)=-sin(x)·x2
В произведениях трех и большего количества чисел
Перейдем к произведенимя и частным, которые содержат большее количество чисел. Для раскрытия скобок здесь будет действовать следующее правило. При четном количестве отрицательных чисел можно опустить скобки, заменив числа противоположными. После этого необходимо заключить полученное выражение в новые скобки. При нечетном количестве отрицательных чисел, опустив скобки, заменить числа на противоположные. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.
Пример 2Для примера, возьмем выражение 5·(−3)·(−2), которое представляет собой произведение трех чисел. Отрицательных чисел два, следовательно, мы можем записать выражение как 
В произведении (−2,5)·(−3):(−2)·4:(−1,25):(−1) пять чисел являются отрицательными. поэтому (−2,5)·(−3):(−2)·4:(−1,25):(−1)=(−2,5·3:2·4:1,25:1). Окончательно раскрыв скобки, получаем −2,5·3:2·4:1,25:1.
Обосновать приведенное выше правило можно следующим образом. Во-первых, такие выражения мы можем переписать как произведение, заменив умножением на обратное число деление. Представляем каждое отрицательное число как произведение множительного числа и -1 или -1 заменяем на (−1)·a.
Используя переместительное свойство умножения меняем местами множители и переносим все множители, равные −1, в начало выражения. Произведение четного числа минус единиц равно 1, а нечетного – равно −1
, что позволяет нам использовать знак минус.Если бы мы не использовали правило, то цепочка действий по раскрытию скобок в выражении -23:(-2)·4:-67 выглядела бы следующим образом:
-23:(-2)·4:-67=-23·-12·4·-76==(-1)·23·(-1)·12·4·(-1)·76==(-1)·(-1)·(-1)·23·12·4·76=(-1)·23·12·4·76==-23·12·4·76
Приведенное выше правило может быть использовано при раскрытии скобок в выражениях, которые представляют собой произведения и частные со знаком минус, не являющихся суммами или разностями. Возьмем для примера выражение
Возьмем для примера выражение
x2·(-x):(-1x)·x-3:2.
Его можно привести к выражению без скобок x2·x:1x·x-3:2 .
Раскрытие скобок, перед которыми стоит знак «+»
Рассмотрим правило, которое можно применить для раскрытия скобок, перед которыми стоит знак плюс, а «содержимое» этих скобок не умножается и не делится на какое-либо число или выражение.
Согласно правилу скобки вместе со стоящим перед ними знаком опускаются, при этом знаки всех слагаемых в скобках сохраняются. Если перед первым слагаемым в скобках не стоит никакого знака, то нужно поставить знак плюс.
Для примера приведем выражение (12−3,5)−7. Опустив скобки, мы сохраняем знаки слагаемых в скобках и ставим перед первым слагаемым знак плюс. Запись будет иметь вид (12−3,5)−7=+12−3,5−7. В приведенном примере знак перед первым слагаемым ставить не обязательно, так как +12−3,5−7=12−3,5−7.
Пример 4Рассмотрим еще один пример. Возьмем выражение x+2a-3×2+1-x2-4+1x и проведем с ним действия x+2a-3×2+1-x2-4+1x==x+2a-3×2+1-x2-4+1x
Вот еще один пример раскрытия скобок:
Пример 52+x2+1x-x·y·z+2·x-1+(-1+x-x2)==2+x2+1x-x·y·z+2·x-1-1+x+x2
Как раскрываются скобки, перед которыми стоит знак минус
Рассмотрим случаи, когда перед скобками стоит знак минус, и которые не не умножаются (или делятся) на какое-либо число или выражение.
К примеру:
—12=12,-1x+1=-1x+1,-(-x2)=x2
Выражения с переменными могут быть преобразованы с использованием того же правила:
—x+x3-3—2·x2+3·x3·x+1x-1-x+2,
получаем x-x3-3+2·x2-3·x3·x+1x-1-x+2.
Раскрытие скобок при умножении числа на скобку, выражения на скобку
Здесь мы рассмотрим случаи, когда нужно раскрыть скобки, которые умножаются или делятся на какое-либо число или выражение. Тут применимы формулы вида (a1±a2±…±an)·b=(a1·b±a2·b±…±an·b) или b·( a1±a2±…±an)=(b·a1±b·a2±…±b·an), где a1, a2, …, an и b – некоторые числа или выражения.
Пример 7Например, проведем раскрытие скобок в выражении (3−7)·2. Согласно правилу, мы можем провести следующие преобразования: (3−7)·2=(3·2−7·2). Получаем 3·2−7·2.
Раскрыв скобки в выражении 3·x2·1-x+1x+2, получаем 3×2·1-3·x2·x+3·x2·1x+2.
Умножение скобки на скобку
Рассмотрим произведение двух скобок вида (a1+a2)·(b1+b2). Это поможет нам получить правило для раскрытия скобок при проведении умножения скобки на скобку.
Для того, чтобы решить приведенный пример, обозначим выражение (b1+b2) как b. Это позволит нам использовать правило умножения скобки на выражение. Получим (a1+a2)·(b1+b2)=(a1+a2)·b=(a1·b+a2·b)=a1·b+a2·b. Выполнив обратную замену b на (b1+b2), снова применим правило умножения выражения на скобку: a1·b+a2·b==a1·(b1+b2)+a2·(b1+b2)==(a1·b1+a1·b2)+(a2·b1+a2·b2)==a1·b1+a1·b2+a2·b1+a2·b2
Благодаря ряду несложных приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки на каждое из слагаемых из второй скобки. Правило можно распространить на любое количество слагаемых внутри скобок.
Сформулируем правила умножения скобки на скобку: чтобы перемножить между собой две суммы, необходимо каждое из слагаемых первой суммы перемножить на каждое из слагаемых второй суммы и сложить полученные результаты.
Формула будет иметь вид:
(a1+a2+…+am)·(b1+b2+…+bn)==a1b1+a1b2+…+a1bn++a2b1+a2b2+…+a2bn++…++amb1+amb1+…ambn
Проведем раскрытие скобок в выражении (1+x)·(x2+x+6) Оно представляет собой произведение двух сумм. Запишем решение: (1+x)·(x2+x+6)==(1·x2+1·x+1·6+x·x2+x·x+x·6)==1·x2+1·x+1·6+x·x2+x·x+x·6
Отдельно стоит остановиться на тех случаях, когда в скобках присутствует знак минус наряду со знаками плюс. Для примера возьмем выражение (1−x)·(3·x·y−2·x·y3).
Сначала представим выражения в скобках в виде сумм: (1+(−x))·(3·x·y+(−2·x·y3)). Теперь мы можем применить правило: (1+(−x))·(3·x·y+(−2·x·y3))==(1·3·x·y+1·(−2·x·y3)+(−x)·3·x·y+(−x)·(−2·x·y3))
Раскроем скобки: 1·3·x·y−1·2·x·y3−x·3·x·y+x·2·x·y3.
Раскрытие скобок в произведениях нескольких скобок и выражений
При наличии в выражении трех и более выражений в скобках, раскрывать скобки необходимо последовательно. Начать преобразование необходимо с того, что два первых множителя берут в скобки. Внутри этих скобок мы можем проводить преобразования согласно правилам, рассмотренным выше. Например, скобки в выражении (2+4)·3·(5+7·8).
Внутри этих скобок мы можем проводить преобразования согласно правилам, рассмотренным выше. Например, скобки в выражении (2+4)·3·(5+7·8).
В выражении содержится сразу три множителя (2+4), 3 и (5+7·8). Будем раскрывать скобки последовательно. Заключим первые два множителя еще в одни скобки, которые для наглядности сделаем красными: (2+4)·3·(5+7·8)=((2+4)·3)·(5+7·8).
В соответствии с правилом умножения скобки на число мы можем провести следующие действия: ((2+4)·3)·(5+7·8)=(2·3+4·3)·(5+7·8).
Умножаем скобку на скобку: (2·3+4·3)·(5+7·8)=2·3·5+2·3·7·8+4·3·5+4·3·7·8.
Скобка в натуральной степени
Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок.
Рассмотрим процесс преобразования выражения (a+b+c)2. Его можно записать в виде произведения двух скобок (a+b+c)·(a+b+c). Произведем умножение скобки на скобку и получим a·a+a·b+a·c+b·a+b·b+b·c+c·a+c·b+c·c.
Произведем умножение скобки на скобку и получим a·a+a·b+a·c+b·a+b·b+b·c+c·a+c·b+c·c.
Разберем еще один пример:
Пример 81x+23=1x+2·1x+2·1x+2==1x·1x+1x·2+2·1x+2·2·1x+2==1x·1x·1x+1x·2·1x+2·1x·1x+2·2·1x+1x·1x·2++1×2·2+2·1x·2+2·2·2
Деление скобки на число и скобки на скобку
Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые. Например, (x2-x):4=x2:4-x:4 .
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Например, нам необходимо раскрыть скобки в выражении (x+2):23 . Для этого сначала заменим деление умножением на обратное число (x+2):23=(x+2)·23. Умножим скобку на число (x+2)·23=x·23+2·23.
Вот еще один пример деления на скобку:
Пример 91x+x+1:(x+2) .
Заменим деление умножением: 1x+x+1·1x+2.
Выполним умножение: 1x+x+1·1x+2=1x·1x+2+x·1x+2+1·1x+2.
Порядок раскрытия скобок
Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида, т.е. в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.
Порядок выполнения действий:
- первым делом необходимо выполнить возведение скобок в натуральную степень;
- на втором этапе производится раскрытие скобок в произведениях и частных;
- заключительным шагом будет раскрытие скобок в суммах и разностях.
Рассмотрим порядок выполнения действий на примере выражения (−5)+3·(−2):(−4)−6·(−7). Намнем преобразование с выражений 3·(−2):(−4) и 6·(−7), которые должны принять вид (3·2:4) и (−6·7). При подстановке полученных результатов в исходное выражение получаем: (−5)+3·(−2):(−4)−6·(−7)=(−5)+(3·2:4)−(−6·7). Раскрываем скобки:−5+3·2:4+6·7.
Имея дело с выражениями, которые содержат скобки в скобках, удобно проводить преобразования, продвигаясь изнутри наружу.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
MadMath: Умножение в скобках?
Являются ли скобки умножением? Мои студенты, изучающие коррекционную алгебру, почти всегда ответят «да» на этот вопрос; Я думаю, их нужно учить этому явно на других курсах. Я чертовски уверен, что ответ «нет», и я пытаюсь выбить из них это в первый день занятий.
Даже профессиональные исследователи, изучающие распространенные ошибки в алгебраическом образовании, склонны отвечать «да» на этот вопрос, например:
Неправильные представления: использование скобок. Изучающие алгебру, начинающие изучать алгебру, как правило, не знают, что скобки могут использоваться для обозначения группировки двух терминов (в аддитивной ситуации) и в качестве мультипликативного оператора Подготовка к алгебре», слайд 7; ссылки Линчевский, 1995; ссылка]
Но являются ли скобки мультипликативным оператором? Кажется очевидным, что ответ «нет». Теперь ясно, что все следующее является умножением 9, между и и b будет что-то другое; но учитывая, что умножение, вероятно, является наиболее распространенной операцией, мы читаем отсутствие письменного оператора, указывающего на умножение. 2»: «Да или нет, есть ли какая-то работа внутри скобок?» В первый день занятий по алгебре почти весь класс ответит на это «да» (и захочет умножить), после чего я объясняю, что ответ на самом деле «нет». Если нет упрощения внутри круглых скобок , то первой частью фактической работы будет применение операции экспоненты. И это все, что означают скобки. (Здесь, конечно, есть умножение — не из-за круглых скобок, а из-за поставленных рядом 3, и оно должно происходить после оператора возведения в степень.) Большинство учеников поймут это позже, но не все — — некоторая часть класса будет продолжать говорить «да» и будет сбита с толку этим конкретным вопросом в течение всего семестра. (Еще один пример: по этой и другим причинам некоторые учащиеся склонны оценивать что-то вроде «(5)-2 = -10».
Теперь ясно, что все следующее является умножением 9, между и и b будет что-то другое; но учитывая, что умножение, вероятно, является наиболее распространенной операцией, мы читаем отсутствие письменного оператора, указывающего на умножение. 2»: «Да или нет, есть ли какая-то работа внутри скобок?» В первый день занятий по алгебре почти весь класс ответит на это «да» (и захочет умножить), после чего я объясняю, что ответ на самом деле «нет». Если нет упрощения внутри круглых скобок , то первой частью фактической работы будет применение операции экспоненты. И это все, что означают скобки. (Здесь, конечно, есть умножение — не из-за круглых скобок, а из-за поставленных рядом 3, и оно должно происходить после оператора возведения в степень.) Большинство учеников поймут это позже, но не все — — некоторая часть класса будет продолжать говорить «да» и будет сбита с толку этим конкретным вопросом в течение всего семестра. (Еще один пример: по этой и другим причинам некоторые учащиеся склонны оценивать что-то вроде «(5)-2 = -10». )
)
Находится ли множитель рядом с чем-то в круглых скобках или нет, не имеет значения для умножения; круглые скобки — это отдельная и отдельная проблема. Что скажешь? Вы когда-нибудь говорили, что скобки на самом деле означают умножение?
Что такое скобки? Определение, правила, примеры
Что такое скобки?
Скобки или «круглые скобки» — это знакомые ( ) символы, которые используются парами для группировки элементов или указания порядка операций в уравнении.
В математике вам часто придется использовать скобки при составлении или решении уравнений. Они помогают группировать числа и определять порядок операций. В таких случаях используются три типа скобок:
- круглые скобки или ( )
- квадратные скобки или квадратные скобки или [ ]
- фигурные скобки или угловые скобки или { }
скобки всегда идут парами, и если есть открывающая скобка, должна быть закрывающая скобка. Открывающие скобки: (, [ и {. Соответствующие им закрывающие скобки: ), ] и }.
В этой статье мы изучим правила использования скобок в математике.
Как использовать скобки в математике?В математике вы можете использовать скобки для разделения чисел. Например, вы можете использовать их для упоминания отрицательных чисел при написании уравнения сложения.
Вот пример, чтобы лучше понять это:
3 + (-5) = -2
Второй способ использования скобок в математике — умножение чисел. Если в уравнении нет арифметической операции, наличие скобок означает, что вы должны применить умножение.
Разберем это на примере:
6 (4 + 2)
можно записать как 6 х (4 + 2)
Следовательно, ответ 6 х 6 = 36.
Третий и последний скобки в математике используются для группировки чисел и определения порядка операций.
Порядок операцийСкобки изменяют порядок операций.
Вот порядок, которому вы можете следовать, когда в уравнении присутствует несколько символов:
Если вы столкнетесь со скобками в уравнении, вы сначала посмотрите на термины, присутствующие в них.
Давайте лучше разберемся на примере.
Возьмем задачу: 9 – 10 ÷ 5 – 3 x 2 + 7
Давайте решим ее, используя изученный вами порядок операций.
= 9 – 10 ÷ 5 – 3 x 2 + 7
= 9 – 2 – 3 x 2 + 7 (сначала делим)
= 9 – 2 – 6 + 7 (затем умножаем)
= 7 – 6 + 7 (Затем вычесть)
= 1 + 7 (Затем вычесть)
= 8 (И, наконец, добавить)
Теперь давайте рассмотрим ту же задачу со скобками:
9 – 10 ÷ (5 – 3) x 2 + 7
Сначала нужно вычислить числа в скобках.
= 9 – 10 ÷ 2 x 2 + 7 (Решите выражение в скобках)
= 9 – 5 x 2 + 7 (Деление)
= 9 – 10 + 7 (Умножение)
= –1 + 7 (Добавить)
= 6
Вы заметили? Ответ на то же уравнение изменился, потому что в уравнении присутствовали круглые скобки!
Обратите внимание: если внутри других скобок есть скобки, сначала нужно решить внутреннее выражение.
Давайте разберем это на примере:
Упростим выражение (2 + (3 x 4))
Здесь мы сначала решим внутреннюю скобку.
Таким образом, выражение примет вид (2 + 12) = 14
Решенные примеры
Пример 1: Упростим выражение: (2 + 4 x 6) – 4 + (2 x 3)
Решение . Начните с решения выражений в скобках.
= (2 + 24) – 4 + 6 (умножить в скобках)
= 26 – 4 + 6 (Решите члены в скобках)
= 22 + 6 (Добавить)
= 28
Пример 2: Упростите выражение: ( 2 x (7 – 5)) – ((6 ÷ 3) + 4)
Начните с решения самых внутренних скобок
= (2 x 2) – (2 + 4)
= 4 – 6
= –2
8 Пример
Раскрывающиеся тройные скобки Рабочие листы | Вопросы и редакция
Уровень 6-7GCSE
Расширение тройных скобок При раскрытии тройных скобок мы просто умножаем первые две скобки вместе на , а затем умножаем результат на последнюю скобку . 2}\textcolor{темно-бордовый}{+92-17х-30
2}\textcolor{темно-бордовый}{+92-17х-30
Связанные темы
MME
Сбор похожих терминов – пересмотр и рабочие листы
Уровень 1-3GCSEKS3Пересмотреть
MME
Расширяющие скобки Рабочий лист, вопросы и пересмотрРасширяющие скобки Рабочий лист, вопросы и пересмотр
Уровень 1-3GCSEKS3Пересмотреть
Рабочий лист и примеры вопросов
(НОВИНКА) Раскрывающиеся скобки — вопросы в стиле экзамена с тройными скобками — MME
Уровень 4-5 Уровень 6-7 GCSENewOfficial MMEЭкзаменационные вопросы Отметить схему
Учебные вопросы
Расширяющие скобки — GCSE Maths
Здесь мы разберем все, что вам нужно знать о раскрывающихся скобках. Вы узнаете, как раскрывать одинарные и двойные скобки, чтобы получить упрощенное алгебраическое выражение.
В конце вы найдете рабочие листы с расширяющимися скобками, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что означают раскрывающиеся скобки?
Раскрытие скобок означает умножение каждого члена в скобках на выражение вне скобок.
Раскрытие скобок является обратным процессом факторизации и иногда называется умножением. По сути, раскрывая скобки, вы удаляете скобки.
Чтобы раскрыть скобки, умножаем все, что вне скобки, на все, что внутри скобки. Например, если мы расширим
\[(2x + 1)(x − 3)\] 9{2} − 5x − 3 \]
Что означают раскрывающиеся скобки?
Рабочий лист по раскрывающимся скобкам
Загрузите бесплатный рабочий лист по раскрывающимся скобкам с более чем 20 рассуждениями и прикладными вопросами, ответами и схемой выставления оценок, чтобы помочь вашим учащимся подготовиться к GCSE. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксРабочий лист по раскрывающимся скобкам
Загрузите бесплатный рабочий лист по раскрывающимся скобкам с более чем 20 аргументирующими и прикладными вопросами, ответами и схемой выставления оценок, чтобы помочь вашим учащимся подготовиться к GCSE. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Умножение скобок
«Умножение скобок» или «умножение вне» — еще один термин для раскрытия скобок. Это означает ровно то же самое. «Раскрыть скобки» — это то же самое, что «умножить скобки», это просто дает дополнительную подсказку, что когда мы раскрываем скобки, мы умножаем все, что находится за скобками, на все, что внутри скобок.
Использование квадратных скобок
Одно из применений квадратных скобок в математике — группировка элементов, другое — предоставление информации о порядке операций.
Например,
Вот прямоугольник.
Его периметр:
(х+8)+(х-3)+(х+8)+(х-3)
Здесь скобки используются для группировки терминов, чтобы выражения для сторон были понятны.
Периметр также может быть записан как:
2(х+8)+2(х-3)
Здесь скобки нужны для сохранения того, что все выражения для сторон удваиваются для нахождения периметра прямоугольника.
Как раскрыть скобки
Чтобы раскрыть скобки, нужно умножить слагаемое вне скобок (или круглых скобок) на слагаемое внутри скобок. Есть три основных способа сделать это, каждый из которых описан ниже.
- Расширяющие одинарные кронштейны
- Расширяющие двойные скобы
- Расширяющиеся тройные кронштейны
Как расширить кронштейны
- Расширяющие одинарные кронштейны
3(2x + 1) = 6x + 3
Выражения с двумя членами, такими как 6x + 3, известны как биномы .
2. Раскрывающие двойные скобки
(х + 5)(х – 1) = х 2 + 4x – 5
Выражения с тремя членами , например x 2 + 4x − 5 , известны как трехчленов .
Члены, возведенные в степень 2 , такие как x 2 , известны как квадратичные члены .
3. Раскрывающиеся тройные скобки
(x + 1)(x + 2)(x + 3) = x 3 + 6x + 11x + 6 алгебраические термины .
Расширяющие скобки с помощью surds
Существует четвертая, более сложная ситуация, в которой вам может понадобиться использовать свои знания о расширяющихся скобках, но это обычно встречается только в контрольных работах по математике более высокого уровня GCSE, поэтому не является частью этого урока.
Таким образом, чтобы расширить скобки, включающие сурды, мы умножаем каждый член вне скобок на каждый член в скобках и следуем правилам сурдов.
Например, если мы расширим
\[\sqrt{5}(\sqrt{3} – 2\sqrt{5})\]
Получим
\[\sqrt{5}(\sqrt{3} – 2\sqrt{5}) = \sqrt{15} – 10\]
Пошаговая инструкция: Surds
Чтобы раскрыть одну скобку, мы умножаем член вне скобки на все, что внутри скобки.
Чтобы раскрыть одинарные скобки:
- Умножьте член вне скобок на первый член внутри скобок.

- Умножьте член вне скобок на второй член в скобках.
Как расширить отдельные кронштейны
Example 1: two terms in the bracket
Expand:
2(x + 3)
| ✕ | x | + 3 |
| 2 | 2x |
- Умножьте член вне скобок (2) на первый член в скобках (x).
2 ✕ x = 2x
2Умножьте значение за скобками (2) на второе слагаемое внутри скобок (3).
| ✕ | x | + 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 2x | + 6 | + 6 | + 6 |
| ✕ | y | − 4 |
| − 3 | − 3y |
− 3 ✕ y = − 3y
− ✕ + = − so the answer is отрицательный .
Умножьте член вне скобок (- 3) на второй член в скобках (- 4).
| ✕ | г | − 4 |
| − 3 | − 3 года | + 9 |
− 3 x − 4 = + 12
− ✕ − = +, поэтому ответ положительный. Нам нужно написать + 12.
− 3(y − 4) = − 3y + 12
Пример 3: два слагаемых в скобках и переменные с коэффициентами больше 1
Развернуть:
3x(4x − 2y )
Умножьте член вне скобок (3x) на первый член внутри скобок (4x).
| ✕ | 4x | − 2 года |
| 3x | 12x 2 |
3x ✕ 4x = 12x 2
− 2xумножить на член, находящийся вне скобок (вторая скобка).
| ✕ | 4x | − 2y |
| 3x | 12x 2 | − 6xy |
3x ✕ − 2y = − 6xy
− ✕ + = − so the ответ отрицательный. {2}). 9{2}+20x
{2}). 9{2}+20x
При раскрытии одной скобки мы должны обязательно умножать каждый член внутри скобки на число перед скобкой. Убедитесь, что вы указали правильные порядковые номера. Следует соблюдать осторожность, когда умножение включает отрицательные числа.
32-12x-8y
32+12x+8y
32-12x+8y
32-3x+2y
При разложении в одну скобку мы должны обязательно умножить каждый член внутри скобки на число перед кронштейном.
9{2}-12xyПри раскрытии одной скобки мы должны обязательно умножать каждый член внутри скобки на число перед скобкой. Убедитесь, что вы указали правильные порядковые номера.
2) Раскрытие двойных скобок
Чтобы раскрыть двойные скобки, мы умножаем каждое слагаемое в первой скобке на каждое слагаемое во второй скобке.
Как расширить двойные скобки
Чтобы раскрыть двойные скобки, выполните следующие действия:
- Нарисуйте сетку и вставьте члены первой и второй скобок.
- Заполните сетку, перемножив каждое из условий вместе.

- Выпишите каждое из слагаемых и упростите выражение, собрав одинаковые слагаемые.
Как расширить двойные скобки
Примеры раскрывающихся скобок (двойные скобки)
Пример 1: переменные имеют коэффициент 1 и + в обеих скобках
Расширить и упростить:
(x+2)(x+3)
- Нарисуйте сетку и вставьте члены первой и второй скобок.
| ✕ | x | + 3 |
| x | ||
| + 2 |
2Fill in the grid by multiplying each of the terms together.
| ✕ | x | + 3 |
| x | x 2 | + 3x |
| + 2 | + 2x | + 6 |
x ✕ x = х 2 х ✕ 3 = 3x х ✕ 2 = 2х 2 ✕ 3 = 6
3Выпишите каждое из слагаемых и упростите выражение, собрав одинаковые слагаемые.
х 2 + 3х + 2х + 6 = x 2 + 5x + 6
Пример 2: переменные имеют коэффициент 1 и в одной скобке стоит +, а в другой –
Развернуть и упростить:
(x + 5)(x − 1)
Нарисуйте сетку и вставьте члены первой и второй скобок.
| ✕ | x | — 1 | |||||||||||
| x | |||||||||||||
| + 5 | . |
| ✕ | x | − 1 |
| x | x 2 | − x |
| + 5 | + 5x | − 5 |
x ✕ x = х 2 х ✕ - 1 = - х
+ ✕ — = — поэтому ответ отрицательный.
х ✕ 5 = 5х 5 ✕ - 1 = - 5
+ ✕ — = — поэтому ответ отрицательный.
Выпишите каждое из слагаемых и упростите выражение, собрав одинаковые слагаемые.
х 2 - х + 5х - 5 x 2 + 4x − 5
Пример 3: переменные имеют коэффициент больше 1 и в одной скобке стоит +, а в другой –
Развернуть и упростить:
(2x − 3)(x + 4)
Нарисуйте сетку и вставьте члены первой и второй скобок.
| ✕ | x | + 4 |
| 2x | ||
| − 3 |
Fill in the grid by multiplying each of the terms together.
| ✕ | x | + 4 |
| 2x | 2x 2 7 8×4879 | |
| − 3 | − 3x | − 12 |
2x ✕ x = 2x 2 2x ✕ 4 = 8x x ✕ - 3 = - 3x
+ ✕ — = — поэтому ответ отрицательный.
4 ✕ - 3 = - 12
+ ✕ — = — поэтому ответ отрицательный.
Выпишите каждое из слагаемых и упростите выражение, собрав одинаковые слагаемые.
2x 2 + 8x - 3x - 12 2x 2 + 5x − 12
Пример 4: квадратные скобки
Расширьте и упростите:
(3x − 4) 2
Нарисуйте сетку и вставьте члены первой и второй скобок.
(3x - 4) 2 = (3x - 4)(3x - 4)
Помните: когда мы что-то возводим в квадрат (возводим в степень 2), мы умножаем это само на себя.
| ✕ | 3x | − 4 |
| 3x | ||
| − 4 |
Заполните таблицу, перемножив каждое из условий вместе.
| ✕ | 3x | − 4 |
| 3x | 9x 2 | − 12x |
| − 4 | − 12x | + 16 |
3x ✕ 3x = 9x 2 3x ✕ - 4 = - 12x 3x ✕ - 4 = - 12x
+ ✕ — = — поэтому ответ отрицательный.
- 4 ✕ - 4 = + 16
— ✕ — = +, поэтому ответ положительный. 9{2}+20x+25
3) Раскрытие тройных скобок
Для раскрытия тройных скобок сначала умножаем первые две скобки. Затем мы умножаем каждый член этого нового выражения на каждый член в третьей скобке.
Как раскрыть тройные скобки
Чтобы раскрыть тройные скобки:
- Нарисуйте сетку, вставьте члены первой и второй скобки, затем заполните ее, перемножив каждое из членов вместе.
- Выпишите каждое из слагаемых и упростите выражение, собрав одинаковые слагаемые.
- Нарисуйте сетку, вставьте термины из этого нового выражения и третьей скобки, затем заполните ее, перемножив каждый из терминов вместе.
- Выпишите каждое из слагаемых и упростите выражение, собрав одинаковые слагаемые.
Как расширить тройные скобки
Примеры расширяющих скобок (тройные скобки)
Пример 1: умножьте три скобки
Расширьте и упростите:
(x + 1)(x + 2)(x + 3)
- Нарисуйте сетку, вставьте члены первой и второй скобок, затем заполните это в путем умножения каждого из терминов вместе.

| ✕ | x | + 2 |
| x | x 2 | + 2x |
| + 1 | + x | + 2 |
х ✕ х = х 2 х ✕ 2 = 2х х ✕ 1 = х 1 ✕ 2 = 2
2Выпишите каждое из слагаемых и упростите выражение, собрав одинаковые слагаемые.
х 2 + 2х + х + 2 x 2 + 3x + 2
3 Начертите сетку, вставьте члены из этого нового выражения и третью скобку, затем заполните ее, перемножив каждый из членов вместе.
| ✕ | x 2 | + 3x | + 2 |
| x | x 3 | + 3x 2 | + 2x |
| + 3 | + 3x 2 | + 9x | + 6 |
x ✕ x 2 = х 3 х ✕ 3х = 3х 2 х ✕ 6 = 6х 3 ✕ х 2 = 3 х 2 3 ✕ 3x = 9x 3 ✕ 6 = 18
4Выпишите каждое из слагаемых и упростите выражение, собрав одинаковые слагаемые.
x 3 + 3x 2 + 3х 2 + 9х + 2х + 6 x 3 + 6x 2 + 11x + 6
Пример 2: квадратные скобки умножить на третью скобку
Расширить и упростить:
(x + 3) 2 (x − 4) Начертить aсетки, вставьте члены первой и второй скобок, а затем заполните ее, перемножив каждый из членов вместе.
| ✕ | x | + 3x | |||||||||||
| x | x 2 | (х + 3) х ✕ х = х 2 х ✕ 3 = 3x х ✕ 3 = 3x 3 ✕ 3 = 9
| ✕ | x 2 | + 6x | + 9 |
| x | x 3 | + 6x 2 | + 9x |
| − 1 | − x 2 | − 6x | − 9 |
x ✕ x 2 = x 3 х ✕ 6х = 6х 2 х ✕ 9 = 9х − 1 ✕ х 2 = − х 2 − 1 ✕ 6x = − 6x − 1 ✕ 9= − 99{2}+6x+1
Распространенные заблуждения
- Мы должны умножить значение вне скобок на каждый член внутри скобок.

2(6x 2 - 3x) = 12x 2 - 3x ✖
Здесь мы умножили значение за скобками на первый член внутри скобок, но не на второй член.
Правильный ответ: 2(6x 2 — 3x) = 12x 2 — 6x ✔
Нам нужно перемножить все члены в скобках.
- Чтобы два числа умножались на +, их знаки должны быть одинаковыми.
+ ✕ + = +
— ✕ — = +
напр. 2 ✕ 3 = 6
например. − 2 ✕ − 3 = 6
4 ✕ 5 = 20
− 4 ✕ − 5 = 20
- Чтобы два числа умножались на a, их знаки должны быть разными.
+ ✕ — = —
— ✕ + = —
напр. 2 ✕ — 3 = — 6
напр. − 2 ✕ 3 = − 6
4 ✕ − 5 = − 20
− 4 ✕ 5 = − 20
− 4(3y − 5) = − 12y − 20 ✖
Здесь мы не использовали − ✕ − 7 − = + 3 90 ✕ − 5 = + 20
Правильный ответ: − 4(3y − 5) = − 12y + 20 ✔
- Когда мы что-то возводим в квадрат, мы умножаем это само на себя.






