правила, примеры, решения, умножение дробей с разными знаменателями

Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.

Как умножить одну обыкновенную дробь на другую

Запишем сначала основное правило:

Определение 1

Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a/b и c/d это можно выразить как ab·cd=a·cb·d.

Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 14 и 18 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8·4=32). Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.

Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:

У нас получился закрашенный фрагмент со сторонами, равными 58 числовой единицы и 34 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 58·34 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15, значит, общая площадь составляет 1532 квадратных единиц.

Поскольку 5·3=15 и 8·4=32, мы можем записать следующее равенство:

58·34=5·38·4=1532

Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как ab·cd=a·cb·d. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.

Разберем решения нескольких задач на умножение обыкновенных дробей.

Пример 1

Умножьте 711 на 98.

Решение

Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9. У нас получилось 63. Затем вычислим произведение знаменателей и получим: 11·8=88. Составим их двух чисел ответ: 6388.

Все решение можно записать так:

711·98=7·911·8=6388

Ответ: 711·98=6388. 

Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.

Пример 2

  Вычислите произведение дробей 415 и 556.

Решение

Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:

415·556=4·5515·6=22090

Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10.

Выполним сокращение дроби: 22090 НОД (220, 90)=10, 22090=220:1090:10=229.

В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 229=249.

Ответ: 415·556=249.

  

Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a·cb·d. Разложим значения переменных на простые множители и одинаковые из них сократим.

Поясним, как это выглядит, используя данные конкретной задачи.

Пример 3

Вычислите произведение 415·556.

Решение

Запишем вычисления, исходя из правила умножения. У нас получится:

415·556=4·5515·6

Поскольку как 4=2·2, 55=5·11, 15=3·5 и 6=2·3, значит,4·5515·6=2·2·5·113·5·2·3.

Далее мы можем просто сократить некоторые множители и получить следующее: .

Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:

2·113·3=229=249

Ответ: 415·556=249.  

Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:

ab·cd=cd·ab=a·cb·d

Как перемножить обыкновенную дробь с натуральным числом

Запишем сразу основное правило, а потом попробуем объяснить его на практике.

Определение 2

Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби ab на натуральное число n  можно записать в виде формулы ab·n=a·nb.

Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:

ab·n=ab·n1=a·nb·1=a·nb

Поясним нашу мысль конкретными примерами.

Пример 4

Вычислите произведение 227 на 5.

Решение 

В результате умножения числителя исходной дроби на второй множитель получим 10. В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:

227·5=2·527=1027

Ответ: 227·5=1027 

Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.

Пример 5

Условие: вычислите произведение 8 на 512.

Решение

По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:

НОК(40, 12)=4, значит, 4012=40:412:4=103

Теперь нам осталось только выделить целую часть и записать готовый ответ: 103=313.

В этой записи можно видеть все решение целиком: 512·8=5·812=4012=103=313.

Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.

Ответ: 512·8=313.

Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:

ab·n=n·ab=a·nb

Как выполнить умножение трех и более обыкновенных дробей

Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.

Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.

Покажем на примере, как это делается.

Пример 6

Умножьте четыре обыкновенные дроби 120, 125, 37 и 58.

Решение: для начала сделаем запись произведения. У нас получится 120·125·37·58. Нам надо перемножить между собой все числители и все знаменатели: 120·125·37·58=1·12·3·520·5·7·8.

Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.

1·12·3·520·5·7·8=1·(2·2·3)·3·52·2·5·5·7(2·2·2)=3·35·7·2·2·2=9280

Ответ: 1·12·3·520·5·7·8=9280.

Пример 7

Перемножьте 5 чисел 78·12·8·536·10.

Решение

Для удобства мы можем сгруппировать дробь 78 с числом 8, а число 12 с дробью 536, поскольку при этом нам будут очевидны будущие сокращения.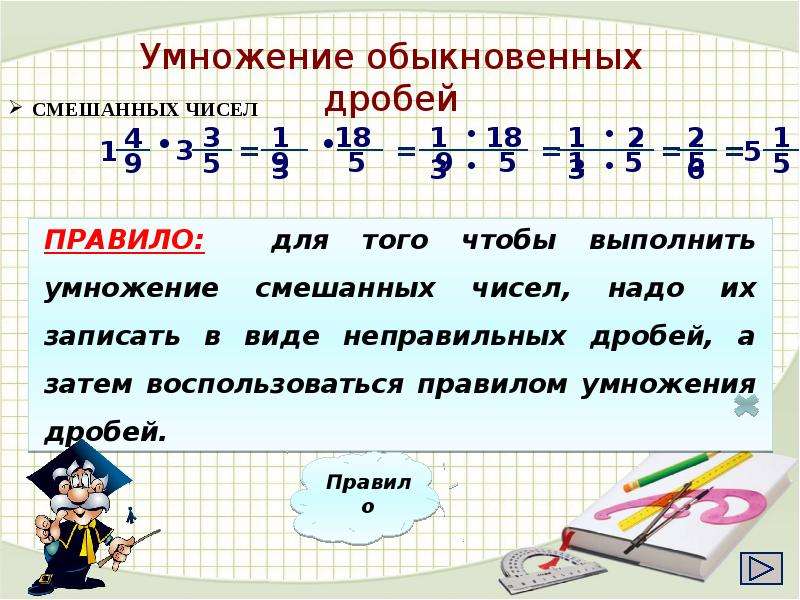

В итоге у нас получится:
78·12·8·536·10=78·8·12·536·10=7·88·12·536·10=71·2·2·3·52·2·3·3·10==7·53·10=7·5·103=3503=11623

Ответ: 78·12·8·536·10=11623.

Умножение дробей | Cubens

Умножение дробей

Умножение дроби на натуральное число

Чтобы умножить дробь на число, нужно числитель умножить на число, а знаменатель оставить без изменений.

Пример умножения дроби на натуральное число

Пример 1: Найти произведение дроби на натуральное число (умножить дробь на натуральное число): на

Ответ:

Умножение дробей с разными знаменателями

Чтобы добавить две обыкновенные дроби с разными знаменателями, нужно:

• перемножить числители и знаменатели дробей;
• сократить полученную дробь;

Пример умножения дробей с разными знаменателями

Пример 2: Перемножить две обыкновенные дроби с разными знаменателями: и

 

Ответ:

Умножение смешанных чисел

Чтобы умножить два смешанных числа, нужно:

• преобразовать смешанные дроби в неправильные;
• перемножить числители и знаменатели дробей;
• сократить полученную дробь;
• Если был получен неправильный дробь нужно преобразовать неправильный дробь в смешанный.

Примеры сложения смешанных чисел

Пример 3: Умножить обыкновенную дробь на смешанное число: и

Ответ:

Пример 4 Умножить смешанное число на натуральное число: и

Ответ:

Пример 5: Умножить смешанные числа: и

Ответ:

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, следует:

• выполнить умножение, не обращая внимания на запятые;
• отделить запятой столько цифр справа, сколько их после запятой в обоих множителях вместе.

Примеры умножения десятичных дробей

Пример 1: Перемножить дроби: 13,2 и 0,2.

Выполнив умножение, не обращая внимания на запятые, получим: .

Отделим запятой справа столько цифр, сколько стоит после запятой в обоих множителях вместе, то есть две цифры .

Рассмотрим другие примеры умножения десятичных чисел:

Пример 2:

Пример 3:

Умножение десятичной дроби и натурального числа

Произведением десятичной дроби и натурального числа называют сумму слагаемых, каждый из которых равен данному десятичной дроби, а количество слагаемых равно этому натуральному числу.

Чтобыумножить десятичную дробь на натуральное число, нужно:

• умножить его на это число, не обращая внимания на запятую;
• в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.

Умножение десятичной дроби на 10, 100, 1000 и т.д.

Чтобыумножить десятичную дробь на 10,100,1000 и т.д., следует:

• надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.

Пример 4:

Если в результате получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.

Как умножать дроби | Как работает

«» Научиться умножать дроби легко, если вы выполните три простых шага. Как это работает

Возможно, вы были в пятом классе, когда в последний раз думали о о том, как умножать дроби .

Но если вы пытаетесь сократить рецепт пополам или рассчитать новую цену на свитер со скидкой, используя дроби, вам, возможно, придется покопаться в глубине своей памяти, чтобы узнать, как умножать дроби, и получить правильный ответ.

Реклама

Содержание

1. Умножать дроби легко
2. Шаг 1: умножьте числители
3. Шаг 2: умножьте знаменатели
4. Шаг 3: Преобразуйте дробь в простейшую форму

Умножать дроби легко

В каждой дроби есть верхнее и нижнее число, разделенные короткой горизонтальной чертой.

В правильной дроби меньшее число — числитель — всегда будет сверху, а большее число — знаменатель — снизу.

Реклама

Таким образом, 2/3, 3/4 и 6/8 являются примерами правильных дробей.

Числитель говорит нам, сколько у нас единиц целого, а знаменатель говорит нам, сколько единиц составляет целое. Итак, в дроби 1/2, 1 — числитель, а 2 — знаменатель — всего две единицы, но эта дробь говорит нам, что у нас есть только одна из этих единиц.

В отличие от сложения или вычитания дробей, вы можете умножать дроби с разными знаменателями. Например, не проблема умножить 3/4 на 2/5.

Реклама

Шаг 1: умножьте числители

Первым шагом в умножении двух дробей является умножение числителей. Итак, в нашем примере:

3 x 2 = 6

Реклама

Шаг 2: умножьте знаменатели

Вторым шагом в умножении дробей является использование того же метода и умножение знаменателей. Итак, в нашем примере:

4 x 5 = 20

Реклама

Достаточно просто! Итак, наша дробь теперь выглядит так:

3/4 x 2/5 = 6/20

Реклама

htm»> Шаг 3: Преобразуйте дробь в простейшую форму

Третий шаг — упростить или уменьшить дробь до наименьшей формы, потому что есть лучший способ прочесть дробь и получить окончательный ответ.

Для этого находим наибольшее число, на которое можно разделить и числитель, и знаменатель.

Реклама

В этом примере наибольшее число, которое делится без остатка на оба числа, равно 2, поэтому сокращенный ответ на эту задачу на умножение — 3/10.

​

Процитируйте это!

Пожалуйста, скопируйте/вставьте следующий текст, чтобы правильно цитировать эту статью HowStuffWorks.com:

Джеслин Шилдс «Как умножать дроби» 5 августа 2021 г.
HowStuffWorks.com. 16 июня 2023 г.

Цитата

Умножение дробей — математика GCSE

Введение

Что такое умножение дробей?

Как умножить две дроби

Рабочий лист «Умножение дробей»

Как умножить дроби на целое число

Как умножать смешанные дроби

Распространенные заблуждения

Похожие уроки

Вопросы на умножение дробей

Умножение дробей Вопросы GCSE

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое умножение дробей?

Как умножить две дроби

Рабочий лист «Умножение дробей»

Как умножать дроби на целое число

Как умножать смешанные дроби

Распространенные заблуждения

Похожие уроки

Вопросы на умножение дробей

Умножение дробей Вопросы GCSE

Следующие уроки

Все еще застряли?

Здесь мы узнаем о умножении дробей в том числе о том, как умножать дроби вместе, умножать дроби на целые числа и умножать смешанные дроби.

Существуют также рабочие листы для умножения дробей на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое умножение дробей?

Умножение дробей — это где мы умножаем числители вместе и умножаем знаменатели вместе. Если есть смешанные числа, мы должны сначала преобразовать их в неправильные дроби.

Произведения дробей

Чтобы умножить две правильные дроби вместе:

Напр. Умножить две правильные дроби

\frac{1}{2} x \frac{1}{3}

1. Умножить числители вместе: \pmb{1} x \pmb{1=1}
2. Умножьте знаменатели вместе: \pmb{2} x \pmb{3=6}
3. Если возможно, упростите: \pmb{\frac{1}{6}}.

Чтобы умножить дробь на целое число: 

Напр. Умножить дробь на целое число

4 x \frac{1}{3}

1. Положите целое число на 1: \pmb{\frac{4}{1} \times \frac{1}{3}}
2. Умножьте числители вместе: \pmb{4} x \pmb{1=4}
3. Умножьте знаменатели вместе: \pmb{1} x \pmb{3=3}
4. Если возможно, упростите: \pmb{\frac{4}{3}}

Чтобы умножить две смешанные числовые дроби: 

Напр. Умножить две смешанные дроби

1 \frac{1}{2} x 2 \frac{1}{4}

1. Замените смешанные дроби на неправильные: \pmb{\frac{3}{2} \times \frac{9}{4}}
2. Умножьте числители вместе: \pmb{3} x \pmb{9=27}
3. Умножьте знаменатели вместе: \pmb{2}x\pmb{4=8}
4. Если возможно, упростите: \pmb{\frac{27}{8}}

Что такое умножение дробей?

Как умножить две дроби

Чтобы умножить две дроби:

1. Перемножьте числители.
2. Перемножьте знаменатели.
3. Упростите, если возможно.

Объясните, как умножать дроби в 3 шага

Рабочий лист по умножению дробей

Получите бесплатный рабочий лист с более чем 20 вопросами и ответами. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Рабочий лист по умножению дробей

Получите бесплатный рабочий лист по умножению дробей, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Примеры умножения дробей

Пример 1: умножение двух правильных дробей

Умножение приведенных ниже дробей вместе:

\[\frac{6}{7} \times \frac{4}{9}\]

1. Умножьте числители на .

\[6×4=24\]

2 Умножьте знаменатели вместе .

\[7×9=63\]

3 Упростите, если возможно .

Когда мы сложим числитель и знаменатель вместе, у нас останется:

\[\frac{24}{63} \]

Если мы разделим и числитель, и знаменатель на 3, мы получим упрощенную дробь:

\[\frac{24 \div 3}{63 \div 3}=\frac{8}{21}\]

Пример 2: умножение двух неправильных дробей (формулированный вопрос)

Найдите площадь фигуры ниже:

Чтобы найти площадь прямоугольника, мы должны использовать формулу:

\[\begin{aligned} A &=l \times w \\ &=\frac{15}{2} \times \frac{5}{4} \end{aligned}\]

Умножьте числители на .

\[15×5=75\]

Умножьте знаменатели вместе .

\[4×2=8\]

Упростите, если возможно .

Когда мы сложим числитель и знаменатель вместе, у нас останется: 9{2} \]

Примечание: всегда помните, что при расчете площади необходимо возводить единицы в квадрат

Пример 3: умножение трех дробей

Умножьте приведенные ниже дроби вместе:

\[ \фракция{3 }{7} \times \frac{4}{5} \times \frac{1}{2}\]

Умножьте числители на .

\[3×4×1=12\]

Умножьте знаменатели вместе .

\[7×5×2=70\]

Упростите, если возможно .

Когда мы сложим числитель и знаменатель вместе, у нас останется:

\[\frac{12}{70}\]

Если мы разделим и числитель, и знаменатель на 2, мы получим упрощенную дробь:

\[\frac{12 \div 2}{70 \div 2}=\frac{6}{35}\]

Как умножать дроби на целое число

Чтобы умножить две дроби вместе:

1. Преобразуйте целое число в дробь, поставив число над знаменателем 1.
2. Перемножьте числители.
3. Перемножьте знаменатели.
4. Упростите, если возможно.
Пример 4: умножение одной правильной дроби на целое число 1 Преобразовать целое число в дробь, поставив число над знаменателем 1 .

Перепишите вопрос как

\[\frac{2}{3} \times \frac{4}{1}\]

Перемножьте числители вместе .

\[2×4=8\]

Умножьте знаменатели вместе .

\[3×1=3\]

Упростите, если возможно .

Когда мы сложим числитель и знаменатель вместе, у нас останется:

\[\frac{8}{3} \]

Пример 5: нахождение дробей сумм

Что равно

\[\frac{2}{9} \text { of } 45\]

Преобразуйте целое число в дробь, поставив число над знаменателем 1 .

В этом вопросе слово « из » можно заменить знаком умножения.

Перепишите вопрос как

\[ \frac{2}{9} \times \frac{45}{1}\]

Перемножьте числители вместе .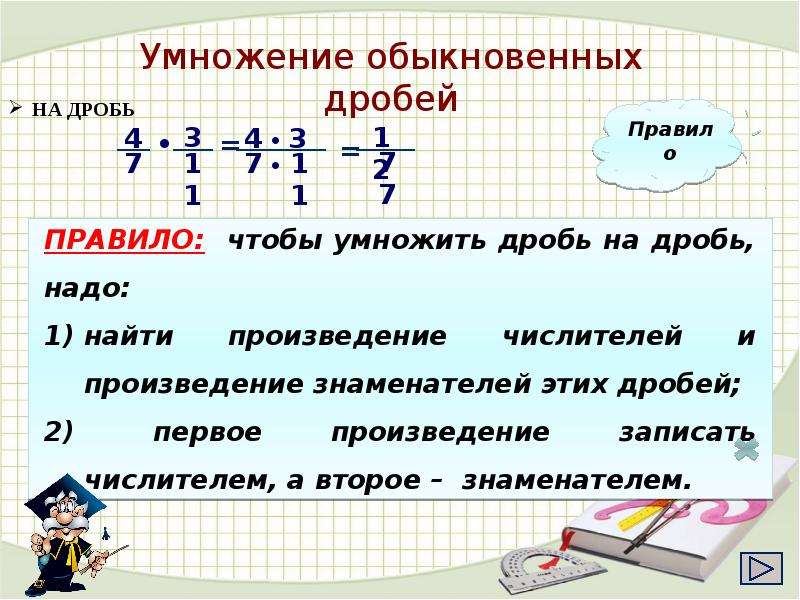

\[2×45=90\]

Умножьте знаменатели вместе .

\[9×1=9\]

Упростите, если возможно .

Когда мы сложим числитель и знаменатель вместе, у нас останется:

\[\frac{90}{9}\]

Это можно упростить до 10 (потому что 90 ÷ 9 = 10) .

Примечание: кратчайший путь для проверки вашего ответа при работе с дробями сумм — «разделить на знаменатель и умножить на числитель». :

1. Преобразуйте смешанные числа в неправильные дроби. Упростите, если возможно.
2. Умножить числители вместе
3. Умножить знаменатели вместе
4. Упростите, если возможно

Примеры умножения смешанных дробей

Пример 6: умножение двух смешанных чисел

Умножьте приведенные ниже дроби вместе:

\[2 \frac{1}{4} \times 2 \frac{1}{2}\ ]

Преобразуйте смешанные числа в неправильные дроби. Упростите, если возможно.

Чтобы преобразовать смешанное число в неправильную дробь, умножьте знаменатель на целое число и прибавьте его к числителю.

\[2 \frac{+1}{\times4}=\frac{9}{4}\]

\[2 \frac{+1}{\times2}=\frac{5}{2} \]

Итак, теперь у нас осталось: 

\[\frac{9}{4} \times \frac{5}{2}\]

Умножьте числители на .

\[9×5=45\]

Умножьте знаменатели .

\[4×2=8\]

Упростите, если возможно .

Эту дробь нельзя упростить, поэтому у нас остается окончательный ответ:

\[\frac{45}{8}\]

Распространенные заблуждения

• Запутанные правила умножения и деления

Распространенной ошибкой является перепутывание правил умножения и деления и случайное переворачивание второй дроби во время умножения.

• Перемножение вместо перемножения числителей и знаменателей

\[\frac{2}{3} \times \frac{1}{4} \neq \frac{8}{3}\]

• Нахождение общего знаменателя

Распространенная ошибка — путать правила сложения и вычитания дробей с умножением и делением. При умножении дробей не обязательно находить общий знаменатель.

Практикуйтесь в вопросах умножения дробей

\frac{4}{9}

\frac{36}{11}

\frac{47}{99}

\frac{4}{99}

Умножьте числители : 4\times1=4

Умножьте знаменатели: 11\times9=99

Следовательно, ответ равен \frac{4}{99}

\frac{6}{35}

\frac{3}{35 }

\frac{31}{35}

\frac{10}{21}

Умножить числители: 2\times6=12

Умножить знаменатели: 7\times10=70

Упростите дробь: \frac{12}{70}=\frac{6}{35}

\frac{2}{55}

\frac{10}{45}

\frac{10} {11}

5\frac{57}{9}

Сначала напишите 5 как \frac{5}{1} . Теперь мы можем вычислить \frac{2}{11} \times \frac{5}{1}

Умножить числители: 2\times5=10

Умножить знаменатели: 11\times1=11

Следовательно, ответ равно \frac{10}{11}

\frac{160}{200}

\frac{204}{5}

\frac{4}{5} of 40 равно \frac{4} {5} \раз 40 . Затем мы можем переписать это как \frac{4}{5} \times \frac{40}{1} .

Умножьте числители: 4\times40=160

Умножьте знаменатели: 5\times1=5

Упростите дробь: \frac{160}{5} = 32

4 \frac{2}{5}

3 \frac{2}{15}

2 \frac{17}{18}

2 \frac{13}{15}

Прежде чем мы умножим эти числа, нам нужно преобразовать их в неправильные дроби.
3 \ гидроразрыва {2} {3} = \ гидроразрыва {11} {3} \\ 1 \frac{1}{5} = \frac{6}{5}

Теперь нам нужно вычислить \frac{11}{3} \times \frac{6}{5}

Умножьте числители: 11\times6=66

Умножьте знаменатели: 3\times5=15

Упростите дробь: \frac{66}{15} = \frac{22}{5} = 4 \frac{ 2}{5}

Площадь прямоугольника равна его основанию, умноженному на высоту, поэтому для определения площади стены нам нужно вычислить 4 \frac{2}{5} \times 2 \frac{1}{4} .

Для этого нам нужно преобразовать смешанные числа в неправильные дроби.
4 \ гидроразрыва {2} {5} = \ гидроразрыва {22} {5} \\ 2 \ гидроразрыва {1} {4} = \ гидроразрыва {9} {4} 9{2} .
Итак, 9,9 \дел 3 = 3,3

Следовательно, чтобы покрасить стену, нужно 4 банки краски.

Умножение дробей Вопросы GCSE

1.

(a) Решите \frac{3}{5} \times \frac{2}{7}.

(b) Вычислите 1\frac{1}{4} \times 4 \frac{2}{9} . Изложите ответ в простейшей форме.

 

(3 балла)

Показать ответ

а)

\frac{6}{35}

Правильно умножает числители и знаменатели вместе.

(1)

b)

 

\frac{5}{4} или \frac{38}{9} видно  (преобразует в неправильную дробь)

(1)

 

\frac{95}{18}

(1)

2. Вот рецепт 12 кексов:

Лили хочет испечь 30 кексов, поэтому ей нужно сделать 2 \ гидроразрыва {1 в {2} раза больше рецепта.

Сколько чашек сахара должна использовать Лили?

Дайте ответ в виде смешанного числа.

 

(3 балла)

Показать ответ

1\frac{1}{4} = \frac{5}{4} или 2 \frac{1}{2} = \frac{5} {2}

(1)

\frac{5}{4} \times  \frac{5}{2}

(1)

\фракция{25}{8}

(1)

3.