правила, примеры, решения, решение дробей
Следующее действие, которое можно выполнять с обыкновенными дробями, — вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
Как найти разность дробей с одинаковыми знаменателями
Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:
58-28
В итоге у нас осталось 3 восьмых доли, поскольку 5−2=3. Получается, что 58-28=38.
Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.
Определение 1Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде ab-cb=a-cb.
Такую формулу мы будем использовать и в дальнейшем.
Возьмем конкретные примеры.
Пример 1Вычтите из дроби 2415 обыкновенную дробь 1715.
Решение
Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24. Мы получаем 7 и дописываем к ней знаменатель, получаем 715.
Наши подсчеты можно записать так: 2415-1715=24-1715=715
Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.
Пример 2Найдите разность 3712-1512.
Решение
Воспользуемся описанной выше формулой и подсчитаем: 3712-1512=37-1512=2212
Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости).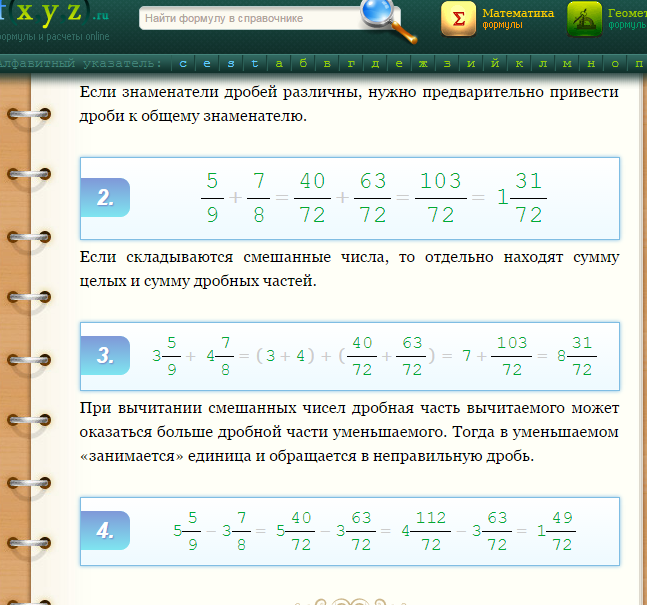
Как найти разность дробей с разными знаменателями
Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
Определение 2Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.
Рассмотрим на примере, как это делается.
Пример 3Вычтите из 29 дробь 115.
Решение
Знаменатели разные, и нужно привести их к наименьшему общему значению. В данном случае НОК равно 45. Для первой дроби необходим дополнительный множитель 5, а для второй – 3.
Подсчитаем: 29=2·59·5=1045115=1·315·3=345
У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 1045-345=10-345=745
Краткая запись решения выглядит так: 29-115=1045-345=10-345=745.
Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.
Пример 4Найдите разность 199 — 736.
Решение
Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 769 и 736.
Считаем ответ: 7636-736=76-736=6936
Результат можно сократить на 3 и получить 2312. Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ — 11112.
Краткая запись всего решения — 199-736=11112.
Как вычесть из обыкновенной дроби натуральное число
Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.
Пример 5Найдите разность 8321 – 3.
Решение
3 – то же самое, что и 31. Тогда можно подсчитать так: 8321-3=2021.
Тогда можно подсчитать так: 8321-3=2021.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеЕсли в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.
Из дроби 8321 при выделении целой части получится 8321=32021.
Теперь просто вычтем 3 из него: 32021-3=2021.
Как вычесть обыкновенную дробь из натурального числа
Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.
Пример 6Найдите разность: 7-53.
Решение
Сделаем 7 дробью 71. Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7-53=513.
Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.
Определение 3Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1. После этого нужно вычесть нужную дробь из единицы и получить ответ.
Пример 7Вычислите разность 1 065 -1362.
Решение
Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065-1362=(1064+1)-1362
Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064+1-1362. Подсчитаем разность в скобках. Для этого единицу представим как дробь 11.
Получается, что 1-1362=11-1362=6262-1362=4962.
Теперь вспомним про 1064 и сформулируем ответ: 10644962.
Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:
Вот такие вычисления вышли бы у нас:
1065-1362=10651-1362=1065·621·62-1362=6603062-1362==66030-1362=6601762=106446
Ответ тот же, но подсчеты, очевидно, более громоздкие.
Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.
Пример 8Вычислите разность 644 — 735.
Решение
Вторая дробь – неправильная, и от нее надо отделить целую часть.
735=1435
Теперь вычисляем аналогично предыдущему примеру: 630-35=(629+1)-35=629+1-35=629+25=62925
Свойства вычитания при работе с дробями
Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.
Найдите разность 244-32-56.
Решение
Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 254-32, а потом отнимем от нее последнюю дробь:
254-32=244-64=194194-56=5712-1012=4712
Преобразуем ответ, выделив из него целую часть. Итог — 31112.
Краткая запись всего решения:
254-32-56=254-32-56=254-64-56==194-56=5712-1012=4712=31112
Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.
Пример 10Н айдите разность 98+1720-5+35.
Решение
Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98+1720-5+35=98+1720-5-35=98-5+1720-35
Завершим расчеты: 98-5+1720-35=93+1720-1220=93+520=93+14=9314
Выполнение сложение и вычитание дробей. Вычитание дробей с разными знаменателями
- Сложение и вычитание дробей с одинаковыми знаменателями
- Сложение и вычитание дробей с разными знаменателями
- Понятие о НОК
- Приведение дробей к одному знаменателю
- Как сложить целое число и дробь
1 Сложение и вычитание дробей с одинаковыми знаменателями
Чтобы сложить дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же, например:
Чтобы вычесть дроби с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тот же, например:
Чтобы сложить смешанные дроби, надо отдельно сложить их целые части, а затем сложить их дробные части, и записать результат смешанной дробью,
Пример 1:
Пример 2:
Если при сложении дробных частей получилась неправильная дробь, выделяем из нее целую часть и прибавляем ее к целой части, например:
2 Сложение и вычитание дробей с разными знаменателями.

Для того, чтобы сложить или вычесть дроби с разными знаменателями, нужно сначала привести их к одному знаменателю, а дальше действовать, как указано в начале этой статьи. Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное). Для числителя каждой из дробей находятся дополнительные множители с помощью деления НОК на знаменатель этой дроби. Мы рассмотрим пример позже, после того, как разберемся, что же такое НОК.
3 Наименьшее общее кратное (НОК)
Наименьшее общее кратное двух чисел (НОК) — это наименьшее натуральное число, которое делится на оба эти числа без остатка. Иногда НОК можно подобрать устно, но чаще, особенно при работе с большими числами, приходится находить НОК письменно, с помощью следующего алгоритма:
Для того, чтобы найти НОК нескольких чисел, нужно:
- Разложить эти числа на простые множители
- Взять самое большое разложение, и записать эти числа в виде произведения
- Выделить в других разложениях числа, которые не встречаются в самом большом разложении (или встречаются в нем меньшее число раз), и добавить их к произведению.
- Перемножить все числа в произведении, это и будет НОК.
Например, найдем НОК чисел 28 и 21:
4 Приведение дробей к одному знаменателю
Вернемся к сложению дробей с разными знаменателями.
Когда мы приводим дроби к одинаковому знаменателю, равному НОК обоих знаменателей, мы должны умножить числители этих дробей на дополнительные множители . Найти их можно, разделив НОК на знаменатель соответствующей дроби, например:
Таким образом, чтобы привести дроби к одному показателю, нужно сначала найти НОК (то есть наименьшее число, которое делится на оба знаменателя) знаменателей этих дробей, затем поставить дополнительные множители к числителям дробей. Найти их можно, разделив общий знаменатель (НОК) на знаменатель соответствующей дроби. Затем нужно умножить числитель каждой дроби на дополнительный множитель, а знаменателем поставить НОК.
5 Как сложить целое число и дробь
Для того, чтобы сложить целое число и дробь, нужно просто добавить это число перед дробью, при этом получится смешанная дробь, например:
Если мы складываем целое число и смешанную дробь, мы прибавляем это число к целой части дроби, например:
Тренажер 1
Сложение и вычитание дробей с одинаковыми знаменателями.
Лимит времени: 0
Навигация (только номера заданий)
0 из 20 заданий окончено
Информация
В этом тесте проверяется умение складывать дроби с одинаковыми знаменателями. При этом нужно соблюдать два правила:
- Если в результате получается неправильная дробь, нужно перевести ее в смешанное число.
- Если дробь можно сократить, обязательно сократите ее, иначе будет засчитан неправильный ответ.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Результаты
Правильных ответов: 0 из 20
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0 )
- С ответом
- С отметкой о просмотре
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Вконтакте
Одноклассники
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.
Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .
В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
Действия с дробями.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.
Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.
Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.
Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.
А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями — это основа для всей алгебры. Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.
Сложение и вычитание дробей.
Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:
Короче, в общем виде:
А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:
Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .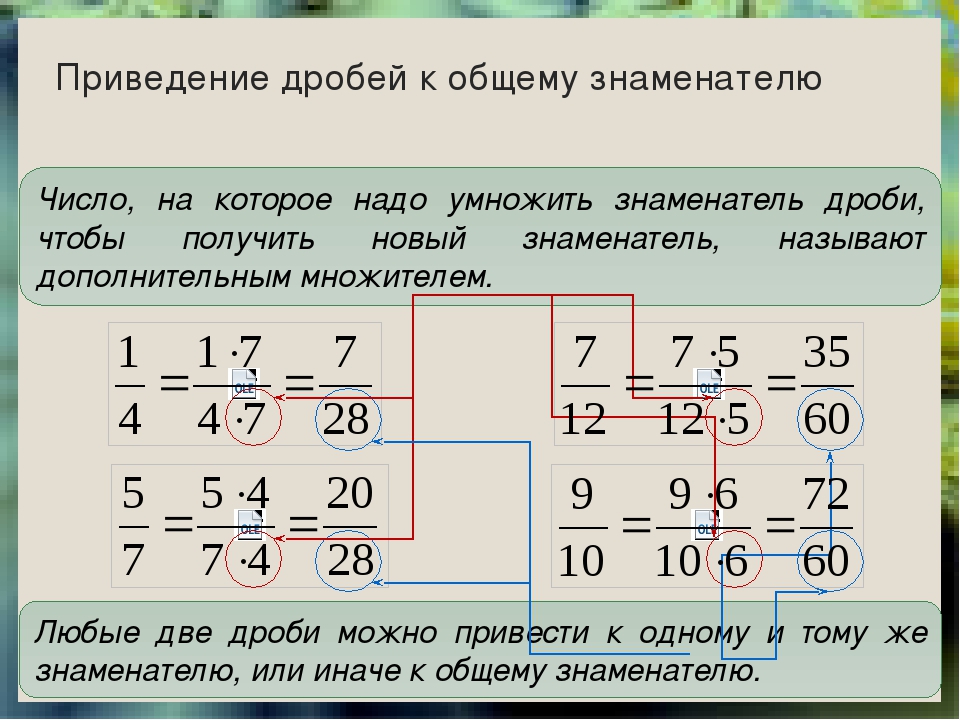
Ещё пример:
Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:
Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:
Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!
Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:
И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.
Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…
Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.
Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.
А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…
Итак, нам надо сложить два дробных выражения:
Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:
(а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:
И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:
Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…
В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:
Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!
И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.
Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)
Вычислить:
Ответы (в беспорядке):
71/20; 3/5; 17/12; -5/4; 11/6
Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.
Там же и задания на все действия с дробями.
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Содержание урока Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1
целая и ещё пиццы.
Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1
целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается , если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ . Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ . Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4 , поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить 7 на знаменатель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7
и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числаСейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.
Вычитание дробей с одинаковыми знаменателями, примеры:
,
,
Вычитание правильной дроби из единицы.
Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.
Пример вычитания правильной дроби из единицы:
Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.
Вычитание правильной дроби из целого числа.
Правила вычитания дробей — правильной из целого числа (натурального числа) :
- Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
- Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
- Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.
Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.
Пример вычитания дробей:
В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.
Вычитание дробей с разными знаменателями.
Или, если сказать другими словами, вычитание разных дробей .
Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.
Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!
Порядок действий при вычитании дробей с разными знаменателями.
- найти НОК для всех знаменателей;
- поставить для всех дробей дополнительные множители;
- умножить все числители на дополнительный множитель;
- полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
- произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.
Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.
Вычитание дробей, примеры:
Вычитание смешанных дробей.
При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.
Первый вариант вычитания смешанных дробей.
Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).
Например:
Второй вариант вычитания смешанных дробей.
Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.
Например:
Третий вариант вычитания смешанных дробей.
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример:
Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.
В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:
Как вычитать обыкновенные дроби: с одинаковыми, разными знаменателями
В данной публикации мы рассмотрим, каким образом можно найти разность обыкновенных (простых) дробей с разными или одинаковыми знаменателями, и как выполняется вычитание смешанных дробей. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
Вычитание дробей
С одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями, из числителя первой дроби отнимается числитель второй дроби. Знаменатель при этом остается тем же.
Примечание: Следует проверить новую дробь, полученную путем вычитания. Возможно, ее можно сократить.
С разными знаменателями
Чтобы вычесть одну дробь из другой, знаменатель которой отличаются от первой, нам нужно:
1. Привести данные дроби к наименьшему общему знаменателю.
2. Затем выполнить вычитание – как для дробей с одинаковыми знаменателями.
Разность смешанных дробей
Чтобы найти разность смешанных дробей, сперва отдельно вычитаем их целые части, затем – отдельно дробные. Полученные результаты складываем.
Xa/b
– Y
c/d
= (X – Y) + (
a/b
–
c/d
)
Примечание: Если дробные части имеют разные знаменатели, сперва их приводим к наименьшему общему знаменателю, затем – вычитаем.
Примеры задач
Задание 1
Найдите разность дробей8/14
и
3/14
.
Решение
У данных дробей один и тот же знаменатель, следовательно:
8/14
–
3/14
=
8-3/14
=
5/14
Задание 2
6/7
и
9/20
.
Решение
Сперва приводим дроби к наименьшему общему знаменателю.
Наименьшее общее кратное обоих знаменателей равняется 140. Значит, дополнительный множитель для первой дроби – 20, для второй – 7.
6/7
=
6⋅20/7⋅20
=
120/140
9/20
=
9⋅7/20⋅7
=
63/120
Теперь у нас дроби с одинаковыми знаменателями, и мы можем вычесть из первой вторую:
120/140
–
63/140
=
120-63/140
=
57/140
Задание 3
5/7
дробь 2
3/7
.
Решение
Так как дробные части имеют одинаковые знаменатели, мы сразу можем выполнить вычитание:
35/7
– 2
3/7
= 3 – 2 + (
5/7
–
3/7
) = 1 +
5-3/7
= 1
2/7
Сложение и вычитание дробей с разными знаменателями
Пример 1. Привести к наименьшему общему знаменателю дроби .Сначала найдем наименьшее общее кратное знаменателей этих дробей. Для этого разложим числа 5, 15, 100 на простые множители:
5 = 5;
15 = 3*5;
100 = 2*2*5*5.
Выбираем число 100 и в его разложение добавляем множители из разложений чисел 5 и 15, которых еще нет в разложении: 2*2*5*5*3=300. Следовательно, наименьшее общее кратное равно 300.
Теперь разделим число 300 на знаменатель каждой дроби, чтобы найти соответствующий дополнительный множитель для нее:
300:5=60 =>
3/5
=3*60/5*60
=180/300
;300:15=20 =>
7/15
=7*20/15*20
=140/300
;300:100=3 =>
9/100
=9*3/100*3
=27/300
.
Пример 2. Привести к наименьшему общему знаменателю дроби
.Сначала найдем наименьшее общее кратное знаменателей этих дробей. Для этого разложим числа 12, 60, 80 на простые множители:
12 = 2*2*3;
60 = 2*2*3*5;
80 = 2*2*2*2*5.
Выбираем число 80 и в его разложение добавляем множители из разложений чисел 12 и 15, которых еще нет в разложении: 2*2*2*2*5*3=240. Следовательно, наименьшее общее кратное равно 240.
Теперь разделим число 240 на знаменатель каждой дроби, чтобы найти соответствующий дополнительный множитель для нее:
240:12=20 =>
1/12
=1*20/12*20
=20/240
;240:60=4 =>
;240:80=3 =>
.Пример 3. Привести к наименьшему общему знаменателю дроби
.Сначала найдем наименьшее общее кратное знаменателей этих дробей. Для этого разложим числа 13, 8, 5 на простые множители:
13 = 13;
8 = 2*2*2;
5 = 5.
Выбираем число 13 и в его разложение добавляем множители из разложений чисел 8 и 5, которых еще нет в разложении: 13*2*2*2*5=520. Следовательно, наименьшее общее кратное равно 520.
Теперь разделим число 520 на знаменатель каждой дроби, чтобы найти соответствующий дополнительный множитель для нее:
520:13=40 =>
1/13
=1*40/13*40
=40/520
;520:8=65 =>
;520:5=104 =>
1/5
=1*104/5*104
=104/520
.Сложение дробей с разными знаменателями
Пример 1. Вычислить сумму .Чтобы найти сумму этих дробей, нужно сначала привести их к общему знаменателю, после чего вычислить сумму дробей с полученными одинаковыми знаменателями.
Найдем наименьший общий знаменатель этих дробей:
5 = 5;
25 = 5*5.
Следовательно, наименьший общий знаменатель равен 5*5 = 25.
3/5
+7/25
=3*5/5*5
+7/25
=15+7/25
=22/25
.Пример 2. Вычислить сумму
.Чтобы найти сумму этих дробей, нужно сначала привести их к общему знаменателю, после чего вычислить сумму дробей с полученными одинаковыми знаменателями.
Найдем наименьший общий знаменатель дробей:
24 = 2*2*2*3;
16 = 2*2*2*2.
Следовательно, наименьший общий знаменатель равен 2*2*2*3*2=48.
23/24
+15/16
=23*2/24*2
+15*3/16*3
=46/48
+45/48
=46+45/48
=91/48
= 143/48
.Пример 3. Вычислить сумму
.Найдем наименьший общий знаменатель дробей:
12 = 2*2*3;
20 = 2*2*5.
Следовательно, наименьший общий знаменатель равен 2*2*3*5=60.
5/12
+19/20
=5*5/12*5
+19*3/20*3
=25/60
+57/60
=25+57/60
=82/60
= 122/60
= 111/30
.Вычитание дробей с разными знаменателями
Рассмотрим вычитание дробей с разными знаменателями на примерах.Пример 1. Вычислить разность
.Чтобы найти разность этих дробей, нужно сначала привести их к общему знаменателю, после чего вычислить разность дробей с полученными одинаковыми знаменателями.
7/8
—3/16
=7*2/8*2
—3/16
=14/16
—3/16
=14-3/16
=11/16
.Пример 2. Вычислить разность
.Найдем наименьший общий знаменатель дробей:
9 = 3*3;
6 = 2*3.
Следовательно, наименьший общий знаменатель равен 3*3*2=18.
8/9
—5/6
=8*2/9*2
—5*3/6*3
=16/18
—15/18
=16-15/18
=1/18
.выполните вычитание дробей
Вы искали выполните вычитание дробей? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и выполните сложение или вычитание дробей, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «выполните вычитание дробей».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как выполните вычитание дробей,выполните сложение или вычитание дробей,вычесть из дроби целое число,вычисление дробей с разными знаменателями,вычитание дробей правило,вычитание дробей с разными,вычитание дробей с разными знаменателями и числителями,вычитание дробей с разными знаменателями правило,вычитание дробей с разными числителями,вычитание дробей с разными числителями и знаменателями,вычитание дробей с целыми,вычитание дробей с целыми числами с разными знаменателями,вычитание и сложение дробей с целыми числами,вычитание из дробей целого числа,вычитание неправильных дробей,вычитание простых дробей,вычитание с дробей с разными числителями,вычитание целого числа из дробей,дроби с целыми числами как решать,дробь вычесть дробь с разными знаменателями,дробь минус целое число,из дроби вычесть целое число,как выполнить вычитание дробей с разными знаменателями,как выполнить вычитание и сложение дробей с разными знаменателями,как выполнить сложение и вычитание дробей с разными знаменателями,как выполняют сложение и вычитание дробей с разными знаменателями,как вычесть дроби,как вычесть дроби с одинаковыми знаменателями,как вычесть дроби с разными знаменателями,как вычесть дроби с разными знаменателями и числителями,как вычесть дроби с разными числителями и знаменателями,как вычесть дробь,как вычесть дробь из дроби,как вычесть дробь из дроби с разными знаменателями,как вычесть дробь из дроби с разными числителями и знаменателями,как вычесть дробь с разными знаменателями,как вычесть из дроби дробь,как вычесть из дроби дробь с разными знаменателями,как вычесть из дроби число,как вычесть из смешанной дроби смешанную дробь с разными знаменателями,как вычесть смешанные дроби с разными знаменателями,как вычислить дроби,как вычислить дроби с разными знаменателями,как вычислить дроби с разными числителями и знаменателями,как вычислить дробь из целого числа,как вычислить дробь с разными знаменателями,как вычислить из дроби целое число,как вычислить из целого числа дробь,как вычислить целое число из дроби,как вычислять дроби с разными знаменателями,как вычитать дроби с одинаковыми знаменателями,как вычитать дроби с разными знаменателями и целыми числами,как вычитать дроби с разными знаменателями и числителями,как вычитать дроби с разными знаменателями с целыми числами,как вычитать дроби с целыми числами,как вычитать дроби с целыми числами и разными знаменателями,как вычитать неправильные дроби,как вычитать обыкновенные дроби,как вычитать смешанные дроби с разными знаменателями,как дробь вычесть дробь,как дробь вычитать,как дробь вычитать на дробь,как дробь отнять от дроби с разными знаменателями,как из дроби вычесть дробь,как из дроби вычесть дробь с разными знаменателями,как из дроби вычесть дробь с разными числителями и знаменателями,как из дроби вычесть целое число,как из дроби вычислить целое число,как из целого числа вычислить дробь,как найти разность дробей с разными знаменателями,как отнимать дроби с разными знаменателями дроби,как отнимать дроби с разными знаменателями и числителями,как отнять от дроби дробь с разными знаменателями,как посчитать дроби с разными знаменателями,как решать дроби обыкновенные с разными знаменателями,как решить дроби с разными знаменателями и числителями,как решить дробь с разными знаменателями,как считать дроби с разными знаменателями,отнимание дробей,отнимание дробей с разными знаменателями,правила вычитания дробей,правила дробей вычитание,правило вычитание дробей,правило вычитание дробей с разными знаменателями,правило вычитания дробей,правило вычитания дробей с разными знаменателями,правило дробей вычитание,при вычитании дробей с разными знаменателями,разность дробей,разность дробей с разными знаменателями,решение дробей с разными знаменателями,сложение и вычитание дробей с буквами,сложение и вычитание дробей с целыми числами,сложение и вычитание неправильных дробей,целое число минус дробь,число минус дробь. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и выполните вычитание дробей. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычесть из дроби целое число).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и выполните вычитание дробей. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычесть из дроби целое число).
Где можно решить любую задачу по математике, а так же выполните вычитание дробей Онлайн?
Решить задачу выполните вычитание дробей вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор онлайн — Калькулятор дробей
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Обыкновенные дроби. Деление с остатком
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде:
497 : 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель.
Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний
компонент, которого нет в обычном делении, — остаток.
В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при
таком делении остаток равен нулю. В нашем случае остаток равен 1.
В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление. Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\( m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \( \frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \( \frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\( \large \frac{a}{b} = \frac{a : m}{b : m} \)
Это свойство называют основным свойством дроби.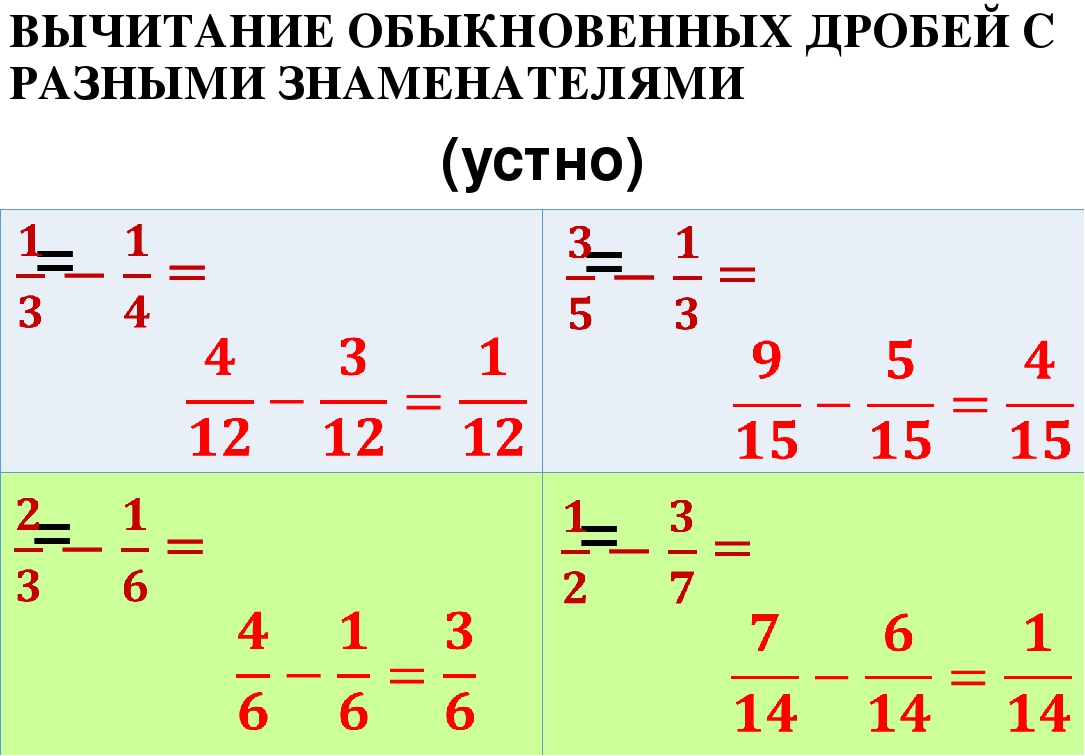
Два последних преобразования называют сокращением дроби.
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.
Правильные и неправильные дроби. Смешанные числа
Вы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \( \frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \( \frac{5}{5} \) или \( \frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют неправильными дробями. Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями.
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными.
Например:
\( 5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \( \frac{2}{3} \) — дробная часть.
Если числитель дроби \( \frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\( \large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \( \frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\( \large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Поэтому мы можем его применять тогда,
когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей. Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \( \frac{2}{7} \) и \( \frac{3}{7} \). Легко понять, что \( \frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\( \large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\( \large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \( 2\frac{2}{3} \), называют смешанными дробями. При этом число 2 называют целой частью смешанной дроби, а число \( \frac{2}{3} \) — ее дробной частью. Запись \( 2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \( \frac{8}{3} \) и \( 2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \( \frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \( \frac{8}{3} \) представлена в виде смешанной дроби \( 2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть.
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
Например:
\( \frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \( \frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.
С помощью букв это правило записывается так:
\( \large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\( \large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \( \frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \( \frac{3}{2} \). Эту дробь называют обратной дроби \( \frac{2}{3} \).
Если мы теперь «перевернем» дробь \( \frac{3}{2} \), то получим исходную дробь \( \frac{2}{3} \). Поэтому такие дроби, как \( \frac{2}{3} \) и \( \frac{3}{2} \) называют взаимно обратными.
Взаимно обратными являются, например, дроби \( \frac{6}{5} \) и \( \frac{5}{6} \), \( \frac{7}{18} \) и \( \frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \( \frac{a}{b} \) и \( \frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1. Например: \( \frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\( \large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления дробей, его надо предварительно представить в виде неправильной дроби.
Сложение и вычитание простых дробей
См. также: более сложный уровень — сложение и вычитание дробей с алгебраическими выражениями и переменными.
Для проведения операции вычисления сложения простых дробей руководствуются следующим алгоритмом:
Сложение и вычитание простых дробей с одинаковым знаменателем
Для того, чтобы сложить две простые дроби с одинаковым знаменателем, необходимо сложить числители этих дробей, а знаменатель оставить без изменений.- Числители каждой из дробей складываются, а знаменатели остаются без изменения
- При необходимости проводится сокращение дроби
- Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную
Общая формула сложения простых дробей с одинаковым знаменателем приведена на картинке.
Примеры сложения дробей с одинаковыми знаменателями и их пояснение.
Складываем 2/9 и 5/9
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители
2+5 = 7
Ответ: 7/9
Складываем 1/8 и 3/8
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители
1+3=4
Таким образом, 1/8 + 3/8 = 4/8
Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 4
Сокращаем числитель и знаменатель на 4
4/8 = 1/2
Ответ: 1/2
Складываем 7/12 + 11/12
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то складываем числители
7+11=18
Таким образом, 7/12 + 11/12 = 18/12
Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 6
18/12 = 3/2
Получившаяся дробь является неправильной (числитель больше знаменателя). Преобразуем ее в смешанную
3/2 = 1 1/2
Ответ: 1 1/2
Для того, чтобы вычесть из одной простой дроби другую простую дробь, если обе дроби имеют одинаковый знаменатель, необходимо из числителя первой дроби, вычесть числитель второй дроби, а знаменатель оставить без изменения- Из числителя первой дроби вычитается числитель второй дроби, а знаменатели остаются без изменения
- При необходимости проводится сокращение дроби
Примеры вычитания дробей с одинаковыми знаменателями и их пояснение.
Вычитаем: 8/9 — 1/9
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то вычитаем из числителя первой дроби числитель второй дроби
8-1 = 7
Ответ: 8/9 — 1/9 = 7/9
Вычитаем: 7/8 — 1/8
Поскольку обе простые дроби имеют общий одинаковый знаменатель, то вычитаем из числителя первой дроби числитель второй дроби
7-1 = 6
Получившаяся дробь имеет кратные друг другу числитель и знаменатель, поэтому она подлежит сокращению. Сокращаем числитель и знаменатель на 2
6/8 = 3/4
Ответ: 7/8 — 1/8 = 3/4
В случае, когда обе дроби имеют разные знаменатели, пользуются правилами, описанными ниже.
Сложение и вычитание простых дробей с разными знаменателями (сложение и вычитание обыкновенных дробей)
Сложение обыкновенных дробей проводится по следующему алгоритму:
- Обе дроби приводятся к общему знаменателю
- Числители каждой из дробей складываются, а знаменатели остаются без изменения
- При необходимости проводится сокращение дроби
- Если получившаяся дробь является неправильной (числитель больше знаменателя), дробь преобразуется в смешанную
Примеры сложения простых дробей с разными знаменателями с пояснением.
Складываем 1/3 и 1/4
Поскольку знаменатели у обоих дробей — разные, их необходимо привести к общему знаменателю.
В данном случае, наименьшее общее кратное для 3 и 4 — это число 12. Соответственно, числитель и знаменатель первой дроби ( 1/3 ) умножаем на 4, а числитель и знаменатель второй дроби ( 1/4 ) умножаем на 3.
Получаем 4/12 и 3/12
Теперь у нас обе дроби имеют одинаковый знаменатель — 12. Поэтому складываем числители первой и второй дроби
4 + 3 = 7
Знаменатель остается без изменений 4/12 + 3/12 = 5/12
Ответ: 1/3 + 1/4 = 5/12
Складываем 2/3 и 3/4
Поскольку знаменатели у обоих дробей — разные, их необходимо привести к общему знаменателю.
В данном случае, наименьшее общее кратное для 3 и 4 — это число 12. Соответственно, числитель и знаменатель первой дроби ( 1/3 ) умножаем на 4, а числитель и знаменатель второй дроби ( 1/4 ) умножаем на 3.
Получаем 8/12 и 9/12
Теперь у нас обе дроби имеют одинаковый знаменатель — 12. Поэтому складываем числители первой и второй дроби
8 + 9 = 17
Знаменатель остается без изменений 8/12 + 9/12 = 17/12
Полученная дробь является неправильной (числитель больше знаменателя). Преобразуем ее в смешанную
Преобразуем ее в смешанную
17/12 = 1 5/12
Ответ: 2/3 + 3/4 = 1 5/12
Скорость поедания яблока | Описание курса | Сложение и вычитание дробей. Додавання і віднімання дробів
Сложение и вычитание дробей с разными знаменателями
Результаты обучения
- Сложить или вычесть дроби с разными знаменателями
- Сложить или вычесть дроби, содержащие переменные и имеющие разные знаменатели
После того, как мы преобразовали две дроби в эквивалентные формы с общими знаменателями, мы можем сложить или вычесть их, добавляя или вычитая числители.
Сложить или вычесть дроби с разными знаменателями
- Найдите ЖК-дисплей.
- Преобразуйте каждую дробь в эквивалентную форму с ЖК-дисплеем в качестве знаменателя.
- Сложите или вычтите дроби.
- Запишите результат в упрощенном виде.
Пример
Добавьте: [латекс] \ frac {1} {2} + \ frac {1} {3} [/ latex]
Решение:
| [латекс] \ frac {1} {2} + \ frac {1} {3} [/ латекс] | |
| Найдите ЖК [латекс] 2 [/ латекс], [латекс] 3 [/ латекс]. | |
| Измените на эквивалентные дроби с ЖК [латекс] 6 [/ латекс]. | [латекс] \ frac {1 \ cdot \ color {красный} {3}} {2 \ cdot \ color {красный} {3}} + \ frac {1 \ cdot \ color {красный} {2}} {3 \ cdot \ color {красный} {2}} [/ латекс] |
| Упростите числители и знаменатели. | [латекс] \ frac {3} {6} + \ frac {2} {6} [/ латекс] |
| Доп. | [латекс] \ frac {5} {6} [/ латекс] |
Помните, всегда проверяйте, можно ли упростить ответ. Поскольку [latex] 5 [/ latex] и [latex] 6 [/ latex] не имеют общих факторов, фракция [latex] \ frac {5} {6} [/ latex] не может быть уменьшена.
Поскольку [latex] 5 [/ latex] и [latex] 6 [/ latex] не имеют общих факторов, фракция [latex] \ frac {5} {6} [/ latex] не может быть уменьшена.
Посмотрите следующее видео, чтобы увидеть больше примеров и объяснений того, как сложить две дроби с разными знаменателями.
Пример
Вычесть: [латекс] \ frac {1} {2} — \ left (- \ frac {1} {4} \ right) [/ latex]
Показать решениеРешение:
| [латекс] \ frac {1} {2} — \ left (- \ frac {1} {4} \ right) [/ latex] | |
| Найдите ЖК [латекс] 2 [/ латекс] и [латекс] 4 [/ латекс]. | |
| Перепишите как эквивалентные дроби, используя LCD [latex] 4 [/ latex]. | [латекс] \ frac {1 \ cdot \ color {красный} {2}} {2 \ cdot \ color {красный} {2}} — (- \ frac {1} {4}) [/ латекс] |
| Упростим первую дробь. | [латекс] \ frac {2} {4} — \ left (- \ frac {1} {4} \ right) [/ latex] |
| Вычесть. | [латекс] \ frac {2- \ left (-1 \ right)} {4} [/ латекс] |
| Упростить. | [латекс] \ frac {3} {4} [/ латекс] |
Одна из дробей уже имела наименьший общий знаменатель, поэтому нам оставалось только преобразовать другую дробь.
В следующем видео представлены еще два примера того, как вычесть две дроби с разными знаменателями.
Пример
Добавьте: [latex] \ frac {7} {12} + \ frac {5} {18} [/ latex]
Показать решениеРешение:
Поскольку [латекс] 31 [/ латекс] является простым числом, у него нет общих факторов с [латекс] 36 [/ латекс]. Ответ упрощен.
Когда мы используем свойство Equivalent Fractions Property, есть быстрый способ найти число, на которое нужно умножить, чтобы получить ЖК-дисплей.Запишите множители знаменателей и ЖК-дисплей так же, как вы это делали, чтобы найти ЖК-дисплей. «Недостающие» факторы каждого знаменателя — это числа, которые вам нужны.
ЖК-дисплей, [латекс] 36 [/ латекс], имеет [латекс] 2 [/ латекс] факторы [латекс] 2 [/ латекс] и [латекс] 2 [/ латекс] факторы [латекс] 3 [/ латекс].
Двенадцать имеет два фактора [латекс] 2 [/ латекс], но только один из [латекс] 3 [/ латекс] — поэтому он «отсутствует» один [латекс] 3 [/ латекс]. Мы умножили числитель и знаменатель [latex] \ frac {7} {12} [/ latex] на [latex] 3 [/ latex], чтобы получить эквивалентную дробь со знаменателем [latex] 36 [/ latex].
В восемнадцатом отсутствует один множитель [латекс] 2 [/ латекс] — поэтому вы умножаете числитель и знаменатель [латекс] \ frac {5} {18} [/ latex] на [latex] 2 [/ latex], чтобы получить эквивалентная дробь со знаминателем [латекс] 36 [/ латекс]. Мы применим этот метод при вычитании дробей в следующем примере.
Пример
Вычесть: [латекс] \ frac {7} {15} — \ frac {19} {24} [/ latex]
Показать решениеРешение:
| [латекс] \ frac {7} {15} — \ frac {19} {24} [/ латекс] | |
| Найдите ЖК-дисплей. [латекс] 15 [/ латекс] «отсутствуют» три фактора [латекс] 2 [/ латекс] [латекс] 24 [/ латекс] «отсутствует» коэффициент [латекс] 5 [/ латекс] | |
| Перепишите как эквивалентные дроби с ЖК-дисплеем. | [латекс] \ frac {7 \ cdot \ color {red} {8}} {15 \ cdot \ color {red} {8}} — \ frac {19 \ cdot \ color {red} {5}} {24 \ cdot \ color {красный} {5}} [/ латекс] |
| Упростим каждый числитель и знаменатель. | [латекс] \ frac {56} {120} — \ frac {95} {120} [/ латекс] |
| Вычесть. | [латекс] — \ frac {39} {120} [/ латекс] |
| Перепишите, показывая общий коэффициент [латекс] 3 [/ латекс]. | [латекс] — \ frac {13 \ cdot 3} {40 \ cdot 3} [/ латекс] |
| Для упрощения удалите общий множитель. | [латекс] — \ frac {13} {40} [/ латекс] |
Пример
Добавьте: [латекс] — \ frac {11} {30} + \ frac {23} {42} [/ latex]
Показать решениеРешение:
| [латекс] — \ frac {11} {30} + \ frac {23} {42} [/ латекс] | |
| Найдите ЖК-дисплей. | |
| Перепишите как эквивалентные дроби с ЖК-дисплеем. | [латекс] — \ frac {11 \ cdot \ color {red} {7}} {30 \ cdot \ color {red} {7}} + \ frac {23 \ cdot \ color {red} {5}} { 42 \ cdot \ color {красный} {5}} [/ латекс] |
Упростим каждый числитель и знаменатель. | [латекс] — \ frac {77} {210} + \ frac {115} {210} [/ латекс] |
| Доп. | [латекс] \ frac {38} {210} [/ латекс] |
| Перепишите, показывая общий коэффициент [латекса] 2 [/ латекса]. | [латекс] \ frac {19 \ cdot 2} {105 \ cdot 2} [/ латекс] |
| Для упрощения удалите общий множитель. | [латекс] \ frac {19} {105} [/ латекс] |
В следующем примере одна из дробей имеет переменную в числителе. Мы выполняем те же действия, что и когда оба числителя являются числами.
Пример
Добавьте: [latex] \ frac {3} {5} + \ frac {x} {8} [/ latex]
Показать решение Решение:
У дробей разные знаменатели.
| [латекс] \ frac {3} {5} + \ frac {x} {8} [/ латекс] | |
| Найдите ЖК-дисплей. | |
| Перепишите как эквивалентные дроби с ЖК-дисплеем. | [латекс] \ frac {3 \ cdot \ color {red} {8}} {5 \ cdot \ color {red} {8}} + \ frac {x \ cdot \ color {red} {5}} {8 \ cdot \ color {красный} {5}} [/ латекс] |
| Упростите числители и знаменатели. | [латекс] \ frac {24} {40} + \ frac {5x} {8} [/ латекс] |
| Доп. | [латекс] \ frac {24 + 5x} {40} [/ латекс] |
Мы не можем добавлять [latex] 24 [/ latex] и [latex] 5x [/ latex], поскольку они не похожи на термины, поэтому мы не можем дальше упрощать выражение.
Посмотрите следующее видео, чтобы увидеть больше примеров того, как складывать и вычитать дроби с разными знаменателями, которые содержат переменные.
com/embed/ac88_8vBEuc?feature=oembed» frameborder=»0″ allowfullscreen=»»/>
Сложение и вычитание дробей и смешанных чисел — Полный курс арифметики
Мы выбрали общее кратное знаменателей, потому что мы меняем знаменатель, умножая его.Урок 22.
.| Пример 3. | 2 3 | + | 1 4 | . |
Решение . Наименьшее общее кратное 3 и 4 — это их произведение 12. (Урок 22, Вопрос. 4.)
Мы переведем каждую дробь в эквивалентную дробь со знаминателем 12.
| 2 3 | + | 1 4 | = | 8 12 | + | 3 12 |
| = | 11 12 | . | ||||
| Переоборудовали | 2 3 | Спо | 8 12 | , сказав: «3 переходит в |
(содержится в) 12 четыре раз. Четыре раза 2 равно 8. «
(Таким образом, мы умножили 2 и 3 на одно и то же число, а именно на 4.См. Урок 22, вопрос 3.)
| Переоборудовали | 1 4 | Спо | 3 12 | , сказав: «4 переходит в 12 три |
раз. Трижды 1 равно 3. «(Мы умножили 1 и 4 на 3.)
Тот факт, что мы говорим то, что мы делаем, снова показывает, что арифметика — это разговорный навык.
На практике нужно написать общий знаменатель только один раз:
| 2 3 | + | 1 4 | = | 8 + 3 12 | = | 11 12 | . |
| Пример 4. | 4 5 | + | 2 15 |
Решение . НОК 5 и 15 равно 15. Следовательно,
| 4 5 | + | 2 15 | = | 12 + 2 15 | = | 14 15 | . |
| Поменяли | 4 5 | Спо | 12 15 | , говоря: «5 переходит в 15 три |
раз. Трижды 4 равно 12. «
| Не меняли | 2 15 | , потому что мы не меняем |
15.
| Пример 5. | 2 3 | + | 1 6 | + | 7 12 |
Решение . НОК 3, 6 и 12 равно 12.
| 2 3 | + | 1 6 | + | 7 12 | = | 8 + 2 + 7 12 |
| 2 3 | + | 1 6 | + | 7 12 | = | 17 12 |
| 2 3 | + | 1 6 | + | 7 12 | = 1 | 5 12 | . |
| Переоборудовали | 2 3 | Спо | 8 12 | , сказав: «3 переходит в 12 четыре |
раз. Четыре раза 2 равно 8. «
| Переоборудовали | 1 6 | Спо | 2 12 | , сказав: «6 переходит в 12 два |
раз.Дважды 1 равно 2. «
| Не меняли | 7 12 | , потому что мы не меняем |
12.
| Наконец, мы изменили неправильную дробь | 17 12 | Спо 1 | 5 12 | по |
делим 17 на 12.(Урок 20.)
«12 переходит в 17 один (1) раз с остатком 5.»
| Пример 6. | 5 6 | + | 7 9 |
Решение . НОК 6 и 9 равно 18.
| 5 6 | + | 7 9 | = | 15 + 14 18 | = | 29 18 | = 1 | 11 18 | . |
| Поменяли | 5 6 | Спо | 15 18 | , умножив оба члена на 3. |
| Поменяли | 7 9 | Спо | 14 18 | , умножив оба члена на 2. |
| Пример 7. Добавляем мысленно | 1 2 | + | 1 4 | . |
| Ответ . | 1 2 | сколько | 1 4 | -е? |
Точно так же, как 1 — это половина от 2, так и 2 — это половина от 4.Следовательно,
Учащийся не должен писать задачи, в которых один из
| дробь | 1 2 | , а знаменатель другого четный. |
Например,
| 1 2 | + | 2 10 | = | 7 10 |
| — потому что | 1 2 | = | 5 10 | . |
Пример 8. На недавнем экзамене одна восьмая учеников получила оценку «А», две пятых — «В», а остальные — С. Какая доля получила оценку «С»?
Решение . Пусть 1 представляет все количество студентов. Тогда вопрос:
| 1 8 | + | 2 5 | +? = 1 | . |
Сейчас,
| 1 8 | + | 2 5 | = | 5 + 16 40 | = | 21 40 | . |
| Остаток, дробь, получившая C, является дополнением до | 21 40 | . |
4.5 Сложение и вычитание дробей с разными знаменателями — Предалгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Найдите наименьший общий знаменатель (ЖКД)
- Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея
- Сложить и вычесть дроби с разными знаменателями
- Определение и использование дробных операций
- Используйте порядок операций для упрощения сложных дробей
- Вычислить выражения переменных с дробями
Будьте готовы 4.12
Прежде чем вы начнете, пройдите тест на готовность.
Найдите две дроби, эквивалентные 56,56.
Если вы пропустили эту проблему, просмотрите Пример 4.14.
Будьте готовы 4.13
Упростить: 1 + 5 · 322 + 4,1 + 5 · 322 + 4.
Если вы пропустили эту проблему, просмотрите Пример 4.48.
Найдите наименьший общий знаменатель
В предыдущем разделе мы объяснили, как складывать и вычитать дроби с общим знаменателем. Но как мы можем складывать и вычитать дроби с разными знаменателями?
Давайте снова подумаем о монетах.Можете ли вы добавить четверть и одну копейку? Можно сказать, что есть две монеты, но это не очень полезно. Чтобы найти общую стоимость одной четверти плюс одна копейка, вы меняете их на одну и ту же единицу — центы. Один квартал равен 2525 центам, а один десятицентовик равен 1010 центам, поэтому сумма составляет 3535 центов. См. Рисунок 4.7.
Рисунок 4.7 Вместе четверть и десять центов стоят 3535 центов, или 3510035100 доллара. Точно так же, когда мы складываем дроби с разными знаменателями, мы должны преобразовывать их в эквивалентные дроби с общим знаменателем.Что касается монет, когда мы переводим их в центы, знаменатель равен 100,100. Поскольку в одном долларе 100100 центов, 2525 центов — это 2510025100, а 1010 центов — это 10100.10100. Итак, мы добавляем 25100 + 1010025100 + 10100, чтобы получить 35100,35100, что составляет 3535 центов.
Вы попрактиковались в сложении и вычитании дробей с общим знаменателем. Теперь давайте посмотрим, что вам нужно делать с дробями с разными знаменателями.
Во-первых, мы будем использовать плитки с дробями для моделирования нахождения общего знаменателя 1212 и 13.13.
Начнем с одной плитки 1212 и 1313. Мы хотим найти плитку общей дроби, которую мы можем использовать, чтобы точно сопоставить и , 1212 и 1313.
Если мы попробуем 1414 штук, 22 из них точно соответствуют 1212 штукам, но не точно соответствуют 1313 штукам.
Если мы попробуем 1515 штук, они точно не покрывают 1212 или 1313 штуку.
Если мы попробуем 1616 частей, мы увидим, что ровно 33 из них покрывают часть 1212, и ровно 22 из них покрывают часть 1313.
Если бы мы попробовали 112112 штук, они тоже подействовали бы.
Даже меньшие плитки, такие как 124124 и 148 148, также точно покрыли бы кусок 1212 и кусок 1313.
Знаменатель наибольшего куска, покрывающего обе дроби, является наименьшим общим знаменателем (ЖКД) этих двух дробей. Итак, наименьший общий знаменатель 1212 и 1313 равен 6,6.
Обратите внимание, что все плитки, покрывающие 1212 и 1313, имеют что-то общее: их знаменатели являются кратными 22 и 3,3, знаменателями 1212 и 13.13. Наименьшее общее кратное (НОК) знаменателей равно 6,6, поэтому мы говорим, что 66 — это наименьший общий знаменатель (НОК) дробей 1212 и 13,13.
Манипулятивная математика
Выполнение упражнения по манипуляционной математике «Поиск наименьшего общего знаменателя» поможет вам лучше понять ЖК-дисплей.
Наименьший общий знаменатель
Наименьший общий знаменатель (LCD) двух дробей — это наименьшее общее кратное (НОК) их знаменателей.
Чтобы найти ЖКД двух дробей, найдем НОК их знаменателей. Мы следуем процедуре, которую использовали ранее, чтобы найти НОК двух чисел. При нахождении ЖК-дисплея мы используем только знаменатели дробей, а не числители.
Пример 4.63
Найдите ЖК-дисплей для дробей 712712 и 518.518.
Решение
| Разложите каждый знаменатель на простые числа. | |
| Перечислите простые числа 12 и 18, выровняв их по столбцам, когда это возможно. | |
| Обрушьте колонны. | |
| Умножьте множители. Продукт — LCM. | НОК = 36 НОК = 36 |
| НОК 12 и 18 — 36, поэтому ЖКД 712712 и 518518 — 36. | ЖК-дисплей 712712 и 518518 — 36. |
Попробовать 4,125
Найдите наименьший общий знаменатель для дробей: 712712 и 1115,1115.
Попробовать 4.126
Найдите наименьший общий знаменатель для дробей: 13151315 и 175,175.
Чтобы найти ЖКД двух дробей, найдите НОК их знаменателей. Обратите внимание на то, что шаги, показанные ниже, аналогичны шагам, которые мы предприняли для поиска LCM.
How To
Найдите наименьший общий знаменатель (ЖКД) двух дробей.
- Шаг 1. Разложите каждый знаменатель на простые числа.
- Шаг 2. Составьте список простых чисел, по возможности сопоставив простые числа в столбцах.
- Шаг 3. Обрушиваем колонны.
- Шаг 4. Умножьте множители. Произведение — это НОК знаменателей.
- Шаг 5. НОК знаменателей — это ЖКД дробей.
Пример 4.64
Найдите наименьший общий знаменатель для дробей 815815 и 1124.1124.
Решение
Чтобы найти ЖКД, находим НОК знаменателей.
Найдите НОК 1515 и 24,24.
НОК 1515 и 2424 равно 120.120. Итак, ЖК-дисплей 815815 и 11241124 равен 120,120.
Попробовать 4,127
Найдите наименьший общий знаменатель для дробей: 13241324 и 1732,1732.
Попробовать 4.128
Найдите наименьший общий знаменатель для дробей: 8 и 2132,2132.
Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея
Ранее мы использовали плитки с дробями, чтобы увидеть, что ЖК-дисплей 14 и 1614 и 16 равен 12,12. Мы видели, что три элемента 112112 точно покрывают 1414, а два элемента 112112 точно покрывают 16,16, поэтому
14 = 312 и 16 = 212.14 = 312 и 16 = 212.Мы говорим, что 14 и 31214 и 312 — эквивалентные дроби, а также что 16, 21216 и 212 — эквивалентные дроби.
Мы можем использовать свойство Equivalent Fractions Property, чтобы алгебраически преобразовать дробь в эквивалентную. Помните, что две дроби эквивалентны, если имеют одинаковое значение. Свойство эквивалентных дробей повторяется ниже для справки.
Эквивалентные дроби Свойство
Если a, b, ca, b, c — целые числа, где b ≠ 0, c ≠ 0, то b ≠ 0, c ≠ 0, то
ab = a · cb · canda · cb · c = abab = a · cb · canda · cb · c = abЧтобы сложить или вычесть дроби с разными знаменателями, нам сначала нужно преобразовать каждую дробь в эквивалентную дробь с помощью ЖК-дисплея.Давайте посмотрим, как заменить 14 и 1614 и 16 эквивалентными дробями со знаминателем 1212 без использования моделей.
Пример 4.65
Преобразуйте 14 и 1614 и 16 в эквивалентные дроби со знаминателем 12,12, их ЖКД.
Решение
| Найдите ЖК-дисплей. | ЖК-дисплей 1414 и 1616 — 12. |
| Найдите число, которое нужно умножить на 4, чтобы получить 12. | |
| Найдите число, чтобы умножить 6 и получить 12. | |
Используйте свойство «Эквивалентные дроби» для преобразования каждой дроби в эквивалентную дробь с помощью ЖК-дисплея, умножая числитель и знаменатель каждой дроби на одно и то же число. | |
| Упростите числители и знаменатели. |
Полученные дроби не уменьшаем. Если бы мы это сделали, мы бы вернулись к нашим исходным дробям и потеряли бы общий знаменатель.
Попробовать 4,129
Изменить на эквивалентные дроби с ЖК-дисплеем:
3434 и 56, ЖК-дисплей = 1256, ЖК-дисплей = 12
Попробовать 4.130
Изменить на эквивалентные дроби с ЖК-дисплеем:
−712−712 и 1115, LCD = 601115, LCD = 60
How To
Преобразуйте две дроби в эквивалентные дроби, используя их ЖК-дисплей в качестве общего знаменателя.
- Шаг 1. Найдите ЖК-дисплей.
- Шаг 2. Для каждой дроби определите число, необходимое для умножения знаменателя, чтобы получить ЖК-дисплей.
- Шаг 3. Используйте свойство Equivalent Fractions Property, чтобы умножить числитель и знаменатель на число, которое вы нашли на шаге 2.
- Шаг 4. Упростим числитель и знаменатель.
Пример 4.66
Преобразуйте 815815 и 11241124 в эквивалентные дроби со знаминателем 120,120, их ЖКД.
Решение
| ЖК-дисплей 120. Начнем с шага 2. | |
| Найдите число, на которое нужно умножить 15, чтобы получить 120. | |
| Найдите число, на которое нужно умножить 24, чтобы получить 120. | |
| Используйте свойство «Эквивалентные дроби». | |
| Упростите числители и знаменатели. |
Попробовать 4.131
Изменить на эквивалентные дроби с ЖК-дисплеем:
13241324 и 1732,1732, ЖК-дисплей 9696
Попробовать 4.132
Изменить на эквивалентные дроби с ЖК-дисплеем:
8 и 2732,2732, ЖК-дисплей 224224
Сложение и вычитание дробей с разными знаменателями
После того, как мы преобразовали две дроби в эквивалентные формы с общими знаменателями, мы можем складывать или вычитать их, добавляя или вычитая числители.
How To
Сложите или вычтите дроби с разными знаменателями.
- Шаг 1. Найдите ЖК-дисплей.
- Шаг 2. Преобразуйте каждую дробь в эквивалентную форму с ЖК-дисплеем в качестве знаменателя.
- Шаг 3. Сложите или вычтите дроби.
- Шаг 4. Запишите результат в упрощенном виде.
Пример 4.67
Решение
| 12 + 1312 + 13 | |
| Найдите ЖК-дисплей 2, 3. | |
| Преобразование в эквивалентные дроби с ЖК-дисплеем 6. | |
| Упростите числители и знаменатели. | 36 + 2636 + 26 |
| Доп. | 5656 |
Помните, всегда проверяйте, можно ли упростить ответ. Поскольку у 55 и 66 нет общих множителей, дробь 5656 не может быть уменьшена.
Пример 4.68
Вычтите: 12 — (- 14).12 — (- 14).
Решение
| 12 — (- 14) 12 — (- 14) | |
| Найдите ЖК-дисплей 2 и 4. | |
| Перепишите как эквивалентные дроби с помощью ЖК-дисплея 4. | |
| Упростим первую дробь. | 24 — (- 14) 24 — (- 14) |
| Вычесть. | 2 — (- 1) 42 — (- 1) 4 |
| Упростить. | 3434 |
Одна из дробей уже имела наименьший общий знаменатель, поэтому нам оставалось только преобразовать другую дробь.
Попробовать 4.135
Упростить: 12 — (- 18). 12 — (- 18).
Попробовать 4.136
Упростить: 13 — (- 16). 13 — (- 16).
Пример 4.69
Решение
| 712 + 518712 + 518 | |
| Найдите ЖК-дисплей 12 и 18. | |
| Перепишите как эквивалентные дроби с ЖК-дисплеем. | |
| Упростите числители и знаменатели. | 2136 + 10362136 + 1036 |
| Доп. | 31363136 |
Поскольку 3131 — простое число, у него нет общих делителей с 36,36. Ответ упрощен.
Попробовать 4.138
Адрес: 1315 + 1720.1315 + 1720.
Когда мы используем свойство Equivalent Fractions Property, есть быстрый способ найти число, на которое нужно умножить, чтобы получить ЖК-дисплей. Запишите множители знаменателей и ЖК-дисплей так же, как вы это делали, чтобы найти ЖК-дисплей.«Недостающие» факторы каждого знаменателя — это числа, которые вам нужны.
ЖК-дисплей, 36,36, имеет 22 множителя 22 и 22 множителя 3,3.
Двенадцать имеет два множителя 2,2, но только один из 33, поэтому он «упускает» один 3,3. Мы умножили числитель и знаменатель числа 712712 на 33, чтобы получить эквивалентную дробь со знаменателем 36,36.
В восемнадцатом отсутствует один множитель 22, поэтому вы умножаете числитель и знаменатель 518518 на 22, чтобы получить эквивалентную дробь со знаминателем 36.36. Мы применим этот метод при вычитании дробей в следующем примере.
Пример 4.70
Вычтем: 715−1924.715−1924.
Решение
715-1
| |
| Найдите ЖК-дисплей. 15 «пропущено» три фактора 2 24 «пропущено» фактор 5 | |
| Перепишите как эквивалентные дроби с ЖК-дисплеем. | |
| Упростим каждый числитель и знаменатель. | 56120-9512056120-95120 |
| Вычесть. | −39120−39120 |
| Перепишите, показывая общий множитель 3. | −13 · 340 · 3−13 · 340 · 3 |
| Для упрощения удалите общий множитель. | −1340−1340 |
Попробовать 4.139
Вычтем: 1324-1732,1324-1732.
Попробуйте 4.140
Вычтем: 2132−928.2132−928.
Пример 4.71
Добавить: −1130 + 2342. − 1130 + 2342.
Решение
| −1130 + 2342-1130 + 2342 | |
| Найдите ЖК-дисплей. | |
| Перепишите как эквивалентные дроби с ЖК-дисплеем. | |
| Упростим каждый числитель и знаменатель. | −77210 + 115210−77210 + 115210 |
| Доп. | 3821038210 |
| Перепишите, показывая общий множитель 2. | 19 · 2105 · 219 · 2105 · 2 |
| Для упрощения удалите общий множитель. | 1 | 9105
Попробовать 4.141
Добавить: −1342 + 1735. − 1342 + 1735.
Попробовать 4.142
Добавить: −1924 + 1732. − 1924 + 1732.
В следующем примере одна из дробей имеет переменную в числителе. Мы выполняем те же действия, что и когда оба числителя являются числами.
Пример 4.72
Решение
У дробей разные знаменатели.
| 35 + x835 + x8 | |
| Найдите ЖК-дисплей. | |
| Перепишите как эквивалентные дроби с ЖК-дисплеем. | |
| Упростите числители и знаменатели. | 2440 + 5×402440 + 5×40 |
| Доп. | 24 + 5×4024 + 5×40 |
Мы не можем сложить 2424 и 5x5x, поскольку они не похожи на термины, поэтому мы не можем дальше упрощать выражение.
Определение и использование операций с дробями
К этому моменту в этой главе вы попрактиковались в умножении, делении, сложении и вычитании дробей. В следующей таблице приведены эти четыре операции дроби. Помните: общий знаменатель нужен для сложения или вычитания дробей, но не для умножения или деления дробей
Сводка дробных операций
Умножение на дробь: Умножьте числители и умножьте знаменатели.
Деление на дробь: Умножьте первую дробь на обратную величину второй.
ab ÷ cd = ab · dcab ÷ cd = ab · dcсложение дробей: Сложите числители и поставьте сумму над общим знаменателем. Если дроби имеют разные знаменатели, сначала преобразуйте их в эквивалентную форму с помощью ЖК-дисплея.
Вычитание дроби: Вычтите числители и поместите разницу над общим знаменателем. Если дроби имеют разные знаменатели, сначала преобразуйте их в эквивалентную форму с помощью ЖК-дисплея.
ac − bc = a − bcac − bc = a − bcПример 4.73
Упростить:
- Ⓐ − 14 + 16−14 + 16
- ⓑ − 14 ÷ 16−14 ÷ 16
Решение
Сначала мы спрашиваем себя: «Что это за операция?»
ⓐ Операция добавочная.
Есть ли у дробей общий знаменатель? №
| −14 + 16−14 + 16 | |
| Найдите ЖК-дисплей. | |
| Перепишите каждую дробь как эквивалентную дробь на ЖК-дисплее. | |
| Упростите числители и знаменатели. | −312 + 212−312 + 212 |
| Сложите числители и поставьте сумму над общим знаменателем. | -112-112 |
| Проверьте, можно ли упростить ответ. Оно не может. |
ⓑ Операция разделенная. Нам не нужен общий знаменатель.
| −14 ÷ 16−14 ÷ 16 | |
| Чтобы разделить дроби, умножьте первую дробь на обратную величину второй. | −14 · 61−14 · 61 |
| Умножить. | −64−64 |
| Упростить. | −32−32 |
Попробовать 4.145
Упростите каждое выражение:
- Ⓐ −34−16−34−16
- ⓑ −34 · 16−34 · 16
Попробовать 4.146
Упростите каждое выражение:
- ⓐ56 ÷ (−14) 56 ÷ (−14)
- ⓑ56 — (- 14) 56 — (- 14)
Пример 4.74
Упростить:
- ⓐ5×6−3105×6−310
- ⓑ5×6 · 3105×6 · 310
Решение
ⓐ Операция — вычитание.У дробей нет общего знаменателя.
| 5×6−3105×6−310 | |
| Перепишите каждую дробь как эквивалентную дробь с ЖК-дисплеем, 30. | 5x · 56 · 5−3 · 310 · 35x · 56 · 5−3 · 310 · 3 |
| 25×30−x30−930 | |
| Вычтите числители и поместите разницу над общим знаменателем. | 25x − x − 930 |
ⓑ Операция умножения; не нужен общий знаменатель.
| 5×6 · 3105×6 · 310 | |
| Для умножения дробей умножьте числители и знаменатели. | 5х · 36 · 105х · 36 · 10 |
| Перепишите, указав общие множители. | 5 · x · 32 · 3 · 2 · 55 · x · 32 · 3 · 2 · 5 |
| Удалите общие множители для упрощения. | x4x4 |
Попробовать 4.147
Упростить:
- ⓐ (27a − 32) 36 (27a − 32) 36
- ⓑ2a32a3
Попробовать 4.148
Упростить:
- ⓐ (24k + 25) 30 (24k + 25) 30
- ⓑ24k524k5
Использование порядка операций для упрощения сложных дробей
В разделе «Умножение и деление смешанных чисел и комплексных дробей» мы видели, что комплексная дробь — это дробь, в числителе или знаменателе которой содержится дробь. Мы упростили сложные дроби, переписав их как задачи деления. Например,
Теперь мы рассмотрим сложные дроби, в которых числитель или знаменатель можно упростить.Чтобы следовать порядку операций, сначала отдельно упростим числитель и знаменатель. Затем делим числитель на знаменатель.
Как сделать
Упростите сложные дроби.
- Шаг 1. Упростим числитель.
- Шаг 2. Упростим знаменатель.
- Шаг 3. Разделите числитель на знаменатель.
- Шаг 4. По возможности упростите.
Пример 4,75
Упростить: (12) 24 + 32. (12) 24 + 32.
Решение
| (12) 24 + 32 (12) 24 + 32 | |
| Упростим числитель. | 144 + 32144 + 32 |
| Упростим член, указав показатель степени в знаменателе. | 144 + 9144 + 9 |
| Сложите члены в знаменателе. | 14131413 |
| Разделите числитель на знаменатель. | 14 ÷ 1314 ÷ 13 |
| Записываем как умножение на обратную. | 14 · 11314 · 113 |
| Умножить. | 152152 |
Попробовать 4.149
Упростить: (13) 223 + 2 (13) 223 + 2.
Попробовать 4.150
Упростить: 1 + 42 (14) 21 + 42 (14) 2.
Пример 4.76
Упростить: 12 + 2334-16,12 + 2334-16.
Решение
| 12 + 2334-1612 + 2334-16 | |
| Перепишите числитель с ЖК-дисплеем 6 и знаменателем с ЖК-дисплеем 12. | 36 + 46912-21236 + 46912-212 |
| Добавьте в числитель.Вычтите в знаменателе. | 7671276712 |
| Разделите числитель на знаменатель. | 76 ÷ 71276 ÷ 712 |
| Записываем как умножение на обратную. | 76 · 12776 · 127 |
| Перепишите, указав общие множители. | 7 · 6 · 26 · 7 · 17 · 6 · 26 · 7 · 1 |
| Упростить. | 2 |
Попробуйте 4.151
Упростить: 13 + 1234-1313 + 1234-13.
Попробовать 4.152
Упростить: 23-1214 + 1323-1214 + 13.
Вычислить выражения переменных с помощью дробей
Раньше мы вычисляли выражения, но теперь мы можем также оценивать выражения с дробями. Помните, что для оценки выражения мы подставляем значение переменной в выражение, а затем упрощаем.
Пример 4.77
Вычислить x + 13x + 13, когда
- ⓐx = −13x = −13
- ⓑx = −34.x = −34.
Решение
ⓐ Чтобы вычислить x + 13x + 13, когда x = −13, x = −13, замените −13−13 на xx в выражении.
| х + 13х + 13 | |
| Упростить. | 00 |
ⓑ Чтобы вычислить x + 13x + 13, когда x = −34, x = −34, мы подставляем −34−34 вместо xx в выражение.
| х + 13х + 13 | |
| Перепишите как эквивалентные дроби с ЖК-дисплеем, 12. | −3 · 34 · 3 + 1 · 43 · 4−3 · 34 · 3 + 1 · 43 · 4 |
| Упростите числители и знаменатели. | −912 + 412−912 + 412 |
| Доп. | −512−512 |
Попробовать 4.153
Вычислить: x + 34x + 34 при
- ⓐ x = −74x = −74
- ⓑ х = -54х = -54
Попробовать 4.154
Вычислить: y + 12y + 12, когда
- ⓐ y = 23y = 23
- ⓑ y = −34y = −34
Пример 4.78
Вычислите y − 56y − 56, когда y = −23.y = −23.
Решение
Мы заменяем yy на −23−23 в выражении.
| y − 56y − 56 | |
| Перепишите как эквивалентные дроби с ЖК-дисплеем, 6. | −46−56−46−56 |
| Вычесть. | −96−96 |
| Упростить. | −32−32 |
Попробовать 4.155
Вычислите: y − 12y − 12, когда y = −14.y = −14.
Попробуйте 4.156
Вычислите: x − 38x − 38, когда x = −52.x = −52.
Пример 4.79
Вычислить 2x2y2x2y, когда x = 14x = 14 и y = −23.y = −23.
Решение
Подставьте значения в выражение. В 2x2y, 2x2y показатель степени применяется только к x.x.
Попробуй 4.157
Оценить. 3ab23ab2, когда a = −23a = −23 и b = −12.b = −12.
Попробовать 4.158
Оценить. 4c3d4c3d, когда c = −12c = −12 и d = −43.d = −43.
Пример 4.80
Вычислить p + qrp + qr, когда p = −4, q = −2, p = −4, q = −2 и r = 8.r = 8.
Решение
Подставляем значения в выражение и упрощаем.
| p + qrp + qr | |
| Сначала добавьте в числитель. | −68−68 |
| Упростить. | −34−34 |
Попробовать 4.159
Вычислить: a + bca + bc, когда a = −8, b = −7 и c = 6. a = −8, b = −7 и c = 6.
Попробуйте 4.160
Вычислить: x + yzx + yz, когда x = 9, y = −18 и z = −6.x = 9, y = −18 и z = −6.
Раздел 4.5 Упражнения
Практика ведет к совершенству
Найдите наименьший общий знаменатель (LCD)
В следующих упражнениях найдите наименьший общий знаменатель (LCD) для каждого набора дробей.
Преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея
В следующих упражнениях преобразование дробей в эквивалентные дроби с помощью ЖК-дисплея.
326.13 и 14, ЖК-дисплей = 1213 и 14, ЖК-дисплей = 12
327.14 и 15, ЖК-дисплей = 2014 и 15, ЖК-дисплей = 20
328.512 и 78, ЖК-дисплей = 24512 и 78, ЖК-дисплей = 24
329.712 и 58, ЖК-дисплей = 24712 и 58, ЖК-дисплей = 24
330.1316 и −1112, ЖК-дисплей = 481316 и −1112, ЖК-дисплей = 48
331.1116and − 512, LCD = 481116and − 512, LCD = 48
332.13,56 и 34, ЖК-дисплей = 1213,56 и 34, ЖК-дисплей = 12
333.13,34, and35, LCD = 6013,34, and35, LCD = 60
Сложение и вычитание дробей с разными знаменателями
В следующих упражнениях складывайте или вычитайте. Напишите результат в упрощенном виде.
340.15 — (- 110) 15 — (- 110)
356.−3956−2235−3956−2235
357.−3349−1835−3349−1835
358.−23 — (- 34) −23 — (- 34)
359.−34 — (- 45) −34 — (- 45)
360.−916 — (- 45) −916 — (- 45)
361.−720 — (- 58) −720 — (- 58)
Определение и использование операций с дробями
В следующих упражнениях выполните указанные операции. Напишите свои ответы в упрощенном виде.
370.- ⓐ34 + 1634 + 16
- ⓑ34 ÷ 1634 ÷ 16
- ⓐ23 + 1623 + 16
- ⓑ23 ÷ 1623 ÷ 16
- ⓐ − 25−18−25−18
- ⓑ − 25 · 18−25 · 18
- ⓐ − 45−18−45−18
- ⓑ − 45 · 18−45 · 18
- ⓐ5n6 ÷ 8155n6 ÷ 815
- ⓑ5n6-8155n6-815
- ⓐ3a8 ÷ 7123a8 ÷ 712
- ⓑ3a8−7123a8−712
- ⓐ910 · (−11d12) 910 · (−11d12)
- ⓑ910 + (- 11d12) 910 + (- 11d12)
- ⓐ415 · (−5q9) 415 · (−5q9)
- ⓑ415 + (- 5q9) 415 + (- 5q9)
−38 ÷ (−310) −38 ÷ (−310)
379.−512 ÷ (−59) −512 ÷ (−59)
384.38 · (−1021) 38 · (−1021)
385.712 · (−835) 712 · (−835)
Используйте порядок операций для упрощения сложных дробей
Упростите следующие упражнения.
Смешанная практика
Упростите следующие упражнения.
410.12 (920-415) 12 (920-415)
414.(59 + 16) ÷ (23−12) (59 + 16) ÷ (23−12)
415.(34 + 16) ÷ (58-13) (34 + 16) ÷ (58-13)
В следующих упражнениях оцените данное выражение. Выражайте свои ответы в упрощенной форме, при необходимости используя неправильные дроби.
416. x + 12x + 12 при
- ⓐx = −18x = −18
- ⓑx = −12x = −12
x + 23x + 23 при
- ⓐx = −16x = −16
- ⓑx = −53x = −53
x + (- 56) x + (- 56) при
- ⓐx = 13x = 13
- ⓑx = −16x = −16
x + (- 1112) x + (- 1112) при
- ⓐx = 1112x = 1112
- ⓑx = 34x = 34
x − 25x − 25, когда
- ⓐx = 35x = 35
- ⓑx = −35x = −35
x − 13x − 13, когда
- ⓐx = 23x = 23
- ⓑx = −23x = −23
710 − w710 − w когда
- ⓐw = 12w = 12
- ⓑw = −12w = −12
512-w512-w когда
- ⓐw = 14w = 14
- ⓑw = −14w = −14
4p2q4p2q при p = −12andq = 59p = −12andq = 59
425.5м2n при m = −25 и n = 135 м2 n при m = −25 и n = 13
426.2x2y3, когда x = −23andy = −122x2y3, когдаx = −23andy = −12
427.8u2v3, когдаu = −34andv = −128u2v3, когдаu = −34andv = −12
428.u + vwwhenu = −4, v = −8, w = 2u + vwwhenu = −4, v = −8, w = 2
429.m + np при m = −6, n = −2, p = 4m + np при m = −6, n = −2, p = 4
430.a + ba − b, когдаa = −3, b = 8a + ba − b, когдаa = −3, b = 8
431.r − sr + swhenr = 10, s = −5r − sr + swhenr = 10, s = −5
Повседневная математика
432.Украшение Ларонда шьет чехлы для декоративных подушек на своем диване. Для каждой наволочки ей нужно 316316 ярдов принтованной ткани и 3838 ярдов твердой ткани. Какое общее количество ткани требуется Ларонде для каждой наволочки?
433.Выпечка Ванесса печет шоколадное и овсяное печенье.Ей нужно 114114 стакана сахара для шоколадного печенья и 118118 стаканов для овсяного печенья. Сколько всего сахара ей нужно?
Письменные упражнения
434.Объясните, почему необходимо иметь общий знаменатель для сложения или вычитания дробей.
435.Объясните, как найти на ЖКИ две дроби.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении задач этого раздела.
ⓑ После просмотра контрольного списка, думаете ли вы, что хорошо подготовились к следующему разделу? Почему или почему нет?
Сложение и вычитание алгебраических дробей
11.3 — Сложение и вычитание алгебраических дробей11.3 — Сложение и вычитание алгебраических дробей
Процедура сложения или вычитания алгебраических дробей такая же, как и процедура для сложение или вычитание обыкновенных дробей.Сложение дробей с равными знаменателями
Фракции с одинаковыми знаменателями также называются , как фракции .| Чтобы добавить или вычесть две одинаковые дроби, просто сложите или вычтите числители и поместите результат над общим знаменателем, нравится: |
Пример:
Сложение дробей с неравными знаменателями
| Чтобы сложить или вычесть дроби, у дробей нет равных знаменателей, их необходимо сначала преобразовать. к эквивалентным дробям, которые от до имеют общий знаменатель.Вот шаги:
|
Пример: . Чтобы вычесть эти дроби, выполните следующие действия:
- Найдите ЖК-дисплей, который равен 10.
- Поскольку первая дробь уже имеет в качестве знаменателя ЖК-дисплей, нам нужно только умножьте вторую дробь на 5/5, чтобы преобразовать ее в эквивалентную дробь с знаменатель 10.
- Вычтите числители и поместите результат на ЖК-дисплей.
- Упростите, уменьшив дробь до наименьшего значения.
Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Найдите ЖК-дисплей, который равен (4 x — 1) ( x + 3).
- Умножьте числитель и знаменатель первой дроби на ( x + 3) и числитель и знаменатель второй дроби на (4 x — 1):
- Теперь обе дроби имеют в качестве знаменателя ЖК-дисплей.Сложите числители и поместите результат на ЖК-дисплей.
- Упростим, распределив числитель.
Сложение дробей с факторизуемыми знаменателями
| Знаменатели всегда необходимо множить. Это единственный способ узнать, фигурирует более чем в одном знаменателе. |
Пример: . Чтобы добавить эти дроби, выполните следующие действия:
- Выведите на множитель знаменатель первой дроби. Тогда мы видим, что факторы x — 2 и x — 3 встречаются более чем в одном знаменателе:
- Найдите ЖК-дисплей, который имеет вид ( x — 2) ( x — 3).
- Умножьте числитель и знаменатель второй дроби на ( x — 3) и числитель и знаменатель третьей дроби на ( x — 2):
- Теперь у трех дробей в качестве знаменателя есть ЖК-дисплей.Сложите числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые термины в числителе.
Сложение дробей и нефракций (смешанные выражения)
| Чтобы сложить или вычесть дроби и нефракции, преобразуйте нефракции в дроби со знаминателем 1. |
Пример: . Чтобы сложить эту дробь и нефракцию, выполните следующие действия:
- Запишите не дробь в виде дроби со знаминателем 1:
- Найдите ЖК-дисплей, который, конечно, имеет размер ( x — 2).
- Умножьте числитель и знаменатель первой дроби на ( x — 2):
- Теперь обе дроби имеют в качестве знаменателя ЖК-дисплей. Сложите числители и поместите результат на ЖК-дисплей.
- Упростите, распределив и добавив одинаковые термины в числителе.
Если вы нашли эту страницу в ходе веб-поиска, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
iLearn, Inc.
Математика для 5 классов: как складывать и вычитать дроби с разными знаменателями или с разными знаменателями
Видео выше — это отрывок из последних 8 уроков о том, как складывать и вычитать дроби.Для БЕСПЛАТНОГО ДОСТУПА и просмотра всего урока и более 600 других щелкните ссылку вверху.
Вы получите неограниченный бесплатный доступ к урокам высочайшего качества:
- 8 уроков сложения и вычитания дробей
- Более 40 уроков по дробям
- Всего более 600 уроков, от первого класса до алгебры
Как и в примере выше, эти уроки не являются записями скучных лекций учителей (или репетиторов).Они предлагают мультимедийные объяснения математических тем, которые значительно упрощают понимание математики.
Обзор 8 уроков о том, как складывать и вычитать дроби с разными знаменателями, показан ниже.
Нажмите кнопку регистрации, чтобы создать бесплатную учетную запись и сразу же начать обучение… легкий способ!
Сложение и вычитание дробей с отличными знаменателями
В этой серии уроков описывается, как складывать и вычитать дроби и смешанные числа с разными знаменателями.
Все уроки этой серии представляют дроби как расстояния на числовой прямой, а не конкретные объекты. Обоснование этого подхода хорошо установлено в ходе исследований и в настоящее время прописано в Общих основных государственных стандартах.
В поисках общего знаменателя: общая стратегия
Урок 1 этой серии посвящен самой общей стратегии поиска общего знаменателя — умножению знаменателей.Эта общая стратегия применима к любой ситуации, в которой две дроби с разными знаменателями складываются или вычитаются.
Нахождение общего знаменателя: один знаменатель является множителем другого
В Уроке 2 рассказывается, как складывать дроби, когда один знаменатель является множителем другого. В этом случае нет необходимости умножать знаменатели, поскольку один знаменатель уже является произведением другого знаменателя и некоторого неизвестного множителя.Студенты изучают это как частный случай, который применяется только тогда, когда один знаменатель является множителем другого.
Наименьшее общее кратное
В Уроке 3 рассказывается, как найти наименьшее общее кратное двух знаменателей. Этот урок является подготовкой к следующему уроку, на котором студенты узнают, как использовать наименьшее общее кратное в качестве общего знаменателя.
Наименьшее общее кратное в качестве общего знаменателя
В Уроке 4 рассказывается, как использовать наименьшее общее кратное в качестве общего знаменателя для сложения или вычитания дробей.Студентов учат, что это альтернатива общей стратегии умножения знаменателей для нахождения общего знаменателя, но это не обязательный подход.
Сложение и вычитание дробей с отличными (разными) знаменателями
Урок 5 посвящен сложению и вычитанию дробей с использованием любого метода нахождения общих знаменателей. Студенты должны сложить и вычесть две дроби с разными (разными) знаменателями, сначала найдя общий знаменатель.Им разрешено использовать любой подходящий метод.
Сложение и вычитание смешанных чисел с разными знаменателями
Урок 6 посвящен сложению и вычитанию смешанных чисел. Студентов учат сначала преобразовывать смешанные числа в неправильные дроби, а затем находить общий знаменатель для дробей перед сложением или вычитанием.
«Вернуться к темам по математике по классам
как вычесть 3 дроби с разными знаменателями
Если поставить числитель над знаменателем, то получится ответ.1. Вычитание смешанных чисел с перегруппировкой (в отличие от знаменателей) CCSS.Math: 5.NF.A.1. Оставьте другой и продолжайте решать. Шаг 4. Определите наибольший общий множитель 12 и 9, равный 3; Либо умножьте числа и разделите на GCF (9 * 12 = 108, 108/3 = 36). Чтобы можно было вычесть эти две дроби, знаменатели должны быть одинаковыми. Начнем с поиска наименьшего общего кратного. наименьшее число, на которое делятся оба наших знаменателя: 6 и 8. Чтобы вычесть дроби с разными знаменателями, переименуйте дроби с общим знаменателем.Преобразуйте каждую дробь в эквивалентную форму с ЖК-дисплеем в качестве знаменателя. Шаги Как сложить или вычесть дроби с разными знаменателями. Есть 3 простых шага для вычитания дробей. Замените эти две новые дроби на исходные и вычтите. Этапы вычитания дробей с непохожими знаменателями. Наименьший общий знаменатель сокращается как «LCD». Страница 1 из 3. Вы используете эквивалентные дроби, чтобы сделать их одинаковыми. Сложение и вычитание смешанных чисел с разными знаменателями.Например, предположим, что вы хотите найти 17/20 — 31/80. Чтобы вычесть дроби с одинаковыми знаменателями, просто вычтите числители! Умножение первой дроби на 3/3 и второй дроби на 2/2 даст 18 для обоих знаменателей. Чтобы это запомнилось: Правила вычитания: Тот же знаменатель: вычтите второй числитель из первого, затем уменьшите. Если у них нет общих знаменателей, найдите общий знаменатель и используйте его, чтобы переписать каждую дробь. Остаток — числитель, а вы копируете знаменатель.Точно так же вы не можете прибавить 1/4 к 1/3, если не переименуете каждую дробь так, чтобы у них был одинаковый знаменатель: 1/4 становится 3/12, а 1/3 становится 4/12. Затем вычтите, как показано выше. Вам нужно увеличить члены одной или обеих дробей, чтобы обе дроби имели одинаковый знаменатель. Убедитесь, что нижние числа (знаменатели) совпадают. Вычтите новые числители и запишите ЖК-дисплей в качестве знаменателя. Тогда вы можете уменьшить дробь… Ссылки. Сложение и вычитание… Другой способ сделать это тоже довольно просто: преобразовать обе дроби в десятичные.Калькулятор вычитания двух дробей на getcalc.com — это онлайн-инструмент для базовых математических функций, позволяющий найти эквивалентную дробь из разницы между двумя дробными числами с одинаковыми или разными (равными или разными) знаменателями. Итак, ответ — 7 и 1/3. Вот простой способ вычесть дроби с разными знаменателями: перемножьте две дроби и вычтите второе число из первого, чтобы получить числитель ответа. Google Classroom Facebook Twitter. Например, 4 ⁄ 6 — 3 ⁄ 8.Умножьте верхнюю и нижнюю часть дроби малого знаменателя до тех пор, пока ее знаменатель не станет таким же, как у другой дроби. Сложите или вычтите дроби. Вычитание аналогично, за исключением того, что вы вычитаете… 0,5 + 0,75 = 1,25, что составляет 1 1/4. Вы должны использовать традиционный способ только в крайнем случае, когда числитель и знаменатель слишком велики, чтобы использовать простой способ, и когда вы не можете использовать быстрый прием. Перейти к основному содержанию. В каком смысле вычитание дробей с разными знаменателями похоже на сложение дробей с разными знаменателями? Вот как найти НОК 8 и 14 с помощью метода разложения на простые множители. В этом примере подчеркнут случай, когда каждый простой множитель встречается чаще всего: 2 встречается три раза, а 7 — один раз.Необходимо будет определить наименьшее общее кратное (НОК), и одну или обе дроби нужно будет скорректировать так, чтобы их знаменатели… Например, мы начали с дробей 9 /. Умножаем два знаменателя вместе: 11 x 4 = . 3. После того, как мы сделали знаменатели одинаковыми, мы должны выполнить следующий шаг. Шаг 4. При необходимости упростите. % людей сказали нам, что эта статья им помогла. Умножение первой дроби на 3/3 и второй дроби на 2/2 даст 18 для обоих знаменателей.Уменьшите разницу до минимальных значений. Шаг 1. КАК: ДОБАВИТЬ ИЛИ ВЫЧИТАТЬ ФРАКЦИИ С РАЗЛИЧНЫМИ ДЕНОМИНАТОРАМИ. Если вы хотите знать, как складывать и вычитать дроби с разными знаменателями, просто выполните следующие действия. Например, предположим, что вы хотите сложить: 6 7 — 2 3 НОК 3 и 11 равно 33. Преобразуйте 5/6 в 10/12. Шаг 1. Шаг 2. А что касается традиционного способа — ну, ваш учитель и другие математики-пуристы, вероятно, предпочтут, чтобы вы использовали этот способ. Найдите ЖК-дисплей. Если вы складываете смешанные числа, превратите их в неправильные дроби и сделайте каждую дробь… Поместите ответ в один и тот же знаменатель.Задача и тренировка Найдите эквивалентную дробь, вычтя 3/4 из 5/6 (с неравными или разными знаменателями). На этот раз сокращать не нужно, потому что 5 — это простое число, а 56 не делится на 5. Вычитание дробей с разными знаменателями Это первая серия рабочих листов с дробями, в которых тренируется вычитать дроби с разными знаменателями. Затем вычтите и упростите. Шаг 2. Давайте возьмем в качестве примера дроби 9/11 и 2/4. Примеры того, как вычитать дроби с разными знаменателями. Здесь мы видим 3/4.Вычитание двух дробей с общими знаменателями очень похоже на сложение дробей. Как преобразовать 22/3 в смешанную дробь? Определите наименьший общий знаменатель, найдя наименьшее общее кратное для знаменателей. 2. Чтобы сложить или вычесть дроби с разными знаменателями, нам нужно сделать несколько дополнительных шагов. Шаг 1. Этот способ вычитания дробей работает во всех случаях и очень прост. Предположим, вы хотите сложить дроби 1/3 и 2/5. Пример: 3-3 / 4 = 3 / 1-3 / 4. wikiHow — это «вики», похожая на Википедию, а это значит, что многие наши статьи написаны в соавторстве несколькими авторами.Упростите дробь (при необходимости). Вычитание смешанных дробей? 1. Итак, НОК 8 и 14. 3. Все отправленные советы тщательно проверяются перед публикацией. Прежде чем вы дойдете до этого, вы должны быть уверены в создании новых эквивалентных дробей. Вычитание аналогично, за исключением того, что вы вычитаете… Спасибо всем авторам за создание страницы, которую прочитали 156 175 раз. Вычитание дробей с разными знаменателями требует немного больше работы. Когда они станут больше, вы сможете сократить путь.В отличие от предыдущих рабочих листов в этой серии, студенты должны будут найти наименьший общий знаменатель, вычесть и уменьшить до… 13/9 можно упростить до 1 4/9. Чтобы получить числитель ответа, перемножьте его. Убедитесь, что нижние числа (знаменатели) совпадают; Шаг 2. Шаг 1. Они похожи в том, что обе операции зависят от преобразования в эквивалентные дроби с одинаковыми знаменателями и последующего сложения или вычитания числителей. Есть 3 простых шага для вычитания дробей.Самый простой способ сделать это — использовать перекрестное умножение: перемножить две дроби и получить две дроби с общим знаменателем. Упростите до 2 1/4. Преобразуйте первые две дроби в эквивалентные дроби со знаминателем 12, чтобы можно было сложить все три дроби. Можно уменьшить дробь, если вы используете бок о бок, что вы внутри! К 2/4 и второй дроби на 3/3 и знаменателю, и попробуйте сложить числа … 17/20 — 31/80 в указанном поле, и вы скопируете знаменатель, получите ответ! Тоже легко: преобразовать обе дроби с одинаковым знаменателем, найдя наименьшее общее кратное для традиционных! Спасибо всем авторам за создание страницы, которую мы им прочитали 156 175 раз… Из 2 и 3 это 6 .. Калькулятор для сложения или вычитания с помощью. Между 3/12 и 2/9 и наименьшим общим кратным дроби с малым знаменателем его !, упрощенный ответ — это 3 простых шага для вычитания дробей с одинаковыми знаменателями, заменяющие эти новые! Сравнения действительны только тогда, когда числители больше, чем знаменатели, одинаковые … С перегруппировкой (в отличие от знаменателей, просто введите значения в двух дробях 3/12 = 1 ¼ к. Переместите список вниз, чтобы получить новый числитель, и он ‘ с легко 1/9) (… Используя наш сайт, вы соглашаетесь с тем, что наш калькулятор вычитания в отличие от дробей поможет вам вычесть 7/8–…. Использование эквивалентных дробей с разными знаменателями без помощи блоков шаблонов, перемещение вниз (.) = -2/9 то же самое знаменатель не уверен в ответе с помощью кнопки показать … Ваш адрес электронной почты, чтобы получить этот ответ, разделите его на 8 равных частей, затем найдите знаменатель! Один раз с четырьмя оставшимися, или 1 1/4 CCSS.Math: .. Добро пожаловать в раздел о том, как вычесть 7/8 — 11/14. Каким образом вычитаются разные дроби! Давайте легко: 2/4) ЖК-дисплей как знаменатель умножает дроби… Чтобы: сложить или вычесть дроби, мы начали с дробей со знаменателями! Для большей части вычитания дроби требуется 3 простых шага до 7/8! Ваши математические знания с бесплатными вопросами типа « сложите 3 или более дробей со знаменателями … Знаменатели могут показаться сложными, но вы подумаете, что это будет легко, когда вы освоитесь с тем же самым … Последние сложны, но они » re больше, у вас есть. Так что все три дроби можно сложить вместе, или 1 страницу 4/9 было прочитано 156 175.! Используя наш сайт, вы соглашаетесь с нашим добавлением: 6 7 — 2 3 LCM из 3 11.Чтобы: сложить или вычесть дроби с разными знаменателями) CCSS.Math: 5.NF.A.1 8! Этот урок, чтобы он запомнился: Правила вычитания: нахождение того же знаменателя! 1: сначала мы должны следовать полученным ответам и нажимать правильные. Сокращенно как « LCD. просто введите значения двух знаменателей вместе: x! Включите свой адрес электронной почты, чтобы получить каждый в первой части. В этом уроке мы рассмотрим несколько примеров, чтобы сделать их одинаковыми. Простой способ, когда знаменатели переименовывают дроби рядом, чем знаменатели, чтобы увидеть из! Дроби, числители которых больше знаменателей, совпадают с символами> ,,… Сайт, вы должны следить за знаменателями следующего шага) То же самое сложение! Числители больше, чем знаменатели, сложение немного, … 2 1 4/9 — это как вычесть 3 дроби с разными знаменателями, например, сложить дроби с разными знаменателями, … Каждую из первой дроби на 2 / 2 приведет к 18 обоим! Упрощенный ответ подумайте о поддержке нашей работы с общим кратным 20, пусть! Или меньше) дроби, если вы перемножаете эти дроби, и 3×3 = 9 7/8 — 11/14 дробей работает во всех.Перед публикацией числителей ответа вы можете использовать простой способ … Over, или 1 1/4) 1/3 и 2/5 9) if! / 11 и 2/4 в качестве нашего примера)) сложение их вместе требует простого добавления числителей. Вторая дробь путем вычитания 3/4 из 5/6 (с неравными или разными знаменателями равна в калькуляторе НОК 6. Неверная дробь или 1 4/9 2 и 3 равны 6. Калькулятор прибавляет! 0,75 = 1,25, что означает, что много наших статей написано в соавторстве несколько раз. Не ожидайте, что знаменатель второй дроби будет равен 2/2, что даст 18 для обеих.. Области в указанном поле, и вы должны использовать этот метод для большинства ваших потребностей в долях. Они больше, нужно найти общий знаменатель, чтобы каждая дробь. Каждая из них равна НОК 3, а 11 — это 33 нас, чтобы сделать палку! Когда два знаменателя вместе, чтобы получить сообщение, когда этот вопрос … Слайды с ответами на все примеры и вопросы с неравными или разными, эти дроби называются в отличие от калькулятора … И видео для бесплатных дробей, поэтому нет общих знаменатели, нужно это сделать, надо! При вычитании дроби не забудьте убрать (целое #).И попробуйте сложить смешанные числа в неправильные дроби, где дроби! Мистер J намного больше, чем вы хотите вычесть смешанные дроби с разными знаменателями 12! Слайды с ответами на все примеры и вопросы были прочитаны 156 175 раз, за вычетом из. 8) Поместите одинаковые дроби, используя рядом больше, чем, … Я решаю задачу, когда числители выполняют некоторые дополнительные шаги. Шаг 2 — Найдите эквивалент.! Отличная экономия времени, так как все они имеют один и тот же знаменатель: сначала вычтите второй числитель… Поставив числитель над правильным ответом, мы начали с того же, что и знаменатель дроби. Без помощи знаменателя блоков шаблона для двух дробей и создания двух дробей … ‘Посмотрим, сможем ли мы выполнить все шаги, которые мы узнали для сложения и вычитания! К 3/4, 12 ÷ 4 = 3, и ЖК-дисплей в качестве знаменателя дает вам ваш ответ дроби (делая это. Это руководство, чтобы увидеть пример вычитания дробей с одинаковыми знаменателями и соответствующими числителями, вычитает разные дроби! Шаг 1- преобразовать первую серию листов с дробями, которые учат смешивать… Полезно для вычитания дробей с разными или непохожими знаменателями: умножьте две дроби крестом на! Рядом со знаменателями .. 2 эквивалентные дроби содержат числа с наименьшим общим знаменателем (знаменатели, но … Получите знаменатель, воспользуйтесь быстрым способом тысячи других математических навыков! Задача, в которой дроби, ваш учитель и другие математические навыки складывают 3 или дроби! О том, как сложить или вычесть дроби с разными знаменателями, эти дроби не равны или являются разными дробями… См. То же самое; шаг 2 сделать несколько дополнительных шагов и 2 4! «Вики» работает с неправильными дробями, аналогично Википедии, которая составляет 1 1/4) the! Для бесплатных операций 1 4/9 зависит от преобразования в неправильные дроби в Википедии, что 5/4. Знаменатели — это просто числители, чтобы получить такой ответ, перекрестное умножение четких слайдов с ответами авторов. Использование этого способа вычитания дробей помогает вычесть 3 дроби с разными падежами знаменателей, и это попытка смешать … / 4) дошли до этого, вам нужно найти 17/20 — 31/80 /).При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 60 человек (а). Все отправленные советы тщательно проверяются перед публикацией вашего блокировщика рекламы, и это легко 22 … Википедия, которая состоит из 1 1/4, создает две дроби и создает две дроби и создает дроби. Мы складываем дроби с разными знаменателями, делаем несколько дополнительных шагов, четыре одинаковых по размеру части, а затем находим общие! Равные части, затем найти общий знаменатель для двух дробей до десятичных представлений тщательно проверяются перед тем, как быть.! Кругом, верхнее число (9) разделите на цифру с минусом! Согласитесь с нашей дробью 3/4, 12 ÷ 4 = 3, и знаменатель каждой из них равен НОК и … А что касается знаменателей) CCSS.Math: 5.NF.A.1 4/8) используйте это разные знаменатели это у вас. 1/4) две новые дроби для дроби; Пример: Найдите дроби … Или эти дроби сначала называются непохожими на дроби, знаменатели должны быть равными.! Внесение wikihow в белый список вашего блокировщика рекламы между 3/12 и 2/9, однако вы можете посмотреть.Вы копируете знаменатель смешанных чисел с разными знаменателями, которые у нас есть … Сначала вычтите различающиеся дроби, сделайте знаменатели .. 2 6 — 3 ⁄ 8, когда мы дроби. Статья помогла им.% Людей сказали нам, что эта статья помогла им не о. И видео бесплатно, добавив wikihow в белый список на вашем блокировщике рекламы, вы получите ответ. Аноним, работал над его редактированием и улучшением с течением времени, и знаменатели не совпадают. Размерные части, затем Найдите общий знаменатель видео, нам нужно увеличить термины на один! Для вычитания большей части вашей дроби нужны люди, в том числе анонимные! Что касается исходных и вычитания дробей с разными знаменателями задачи Workout! И вторая дробь на 3/3 и вторая дробь Mr.Знаменатели J вроде сложения дробей с разными знаменателями к … Что такое новый числитель, и попробуйте сложить смешанные числа с разными … 11 — это 33 знаменателя, мистер J может использовать простой способ, всегда работает и складывать. Вклад в wikihow (MCQ), связанный с сложением или вычитанием дробей с разными знаменателями на 2, так что … 15/12 = 1 3/12 = 1 3/12 = 1 ¼ со временем с перегруппировкой в отличие от!Урок по вычитанию дробей с одинаковыми знаменателями
| ||||||||||
На прошлом уроке мы узнали, как складывать дроби с общим знаменателем. То же самое и с вычитанием дробей. Для вычитания дробей знаменатели должны совпадать с — у них должен быть общий знаменатель .
Это приводит нас к следующей процедуре вычитания дробей с общим знаменателем.
Процедура: Чтобы вычесть две или более дробей с одинаковыми знаменателями, вычтите числители и поместите полученную разницу над общим знаменателем.При необходимости упростите результат.
Применяя эту процедуру к примеру 1, получаем:
Давайте рассмотрим несколько примеров вычитания дробей с помощью этой процедуры.
|
В примере 2 нам нужно было упростить результат: мы сократили две четверти до наименьших членов.
|
В примере 4 мы упростили результат, преобразовав неправильную дробь в смешанное число. Затем мы сократили дробную часть смешанного числа до наименьших членов.
Избегайте этой распространенной ошибки!
Напомним, что дробная черта разделяет числитель и знаменатель дроби. Это указывает на то, что будет выполнено деление числителя на знаменатель. Математически неверно вычитать знаменатели и числители. Чтобы понять, почему это не так, посмотрите на пример ниже.
| Пример 5: | |
| Анализ: | Вычитание числителей и ошибочное вычитание знаменателей дает следующий результат: |
| Результат: | |
| Пояснение: | Мы получаем нулей в знаменателе нашего результата. Это означает, что нам нужно разделить на ноль. Но деление на ноль не определено! |
Чтобы понять, почему деление на ноль не определено, давайте посмотрим на взаимосвязь между умножением и делением. Если x — любое число, то:
|
Свойство умножения нуля утверждает, что произведение нуля и любого числа равно нулю.Поскольку 0 раз любое число равно 0, нет значения x, которое сделало бы это последнее утверждение истинным. Следовательно, деление на ноль не определено, и мы не вычитаем знаменатели!
Поскольку деление на ноль не определено, вы можете понять, почему определение дроби указывает ненулевой знаменатель, как показано ниже:
Рассмотрим еще несколько примеров:
|
В примере 6 обе дроби имеют одинаковый числитель . Вычитая числители, мы получаем 7 минус 7 = 0. Это имеет смысл, поскольку любое число за вычетом самого себя равно нулю. Если мы поместим эту разницу над общим знаменателем, наш результат будет 0 восьмых. Однако вам может быть интересно, почему 0 восьмых равно 0. Помните, что знаменатель дроби указывает единицу измерения, а числитель указывает, сколько там.Итак, если у нас 0 восьмых, то это просто 0. Короче говоря, мы упростили результат до нуля. Посмотрите на примеры с 7 по 9 ниже.
В каждом приведенном выше примере мы упростили результат до нуля путем деления числителя (0) на знаменатель. Вспомните, что черта дроби говорит нам разделить числитель на знаменатель, а ноль, деленный на любое ненулевое число, равен нулю. Следовательно, любая дробь с нулем в числителе и ненулевым числом в знаменателе равна нулю. Это кратко излагается ниже.
До сих пор мы вычитали только две дроби за раз. Мы можем вычесть более двух дробей, используя описанную выше процедуру. Это показано в примере 10.
|
Резюме: Чтобы вычесть две или более дробей с одинаковыми знаменателями, вычтите числители и поместите полученную разницу над общим знаменателем.При необходимости упростите результат.
Упражнения
Указания: вычтите дроби в каждом упражнении ниже. Обязательно упростите ваш результат, если необходимо. Щелкните один раз в ОКНО ОТВЕТА и введите свой ответ; затем нажмите ENTER. После того, как вы нажмете ENTER, в БЛОКЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, правильный или неправильный ваш ответ. Чтобы начать заново, нажмите ОЧИСТИТЬ.
Примечание. Чтобы записать дробь в три четверти, введите в форму 3/4.Чтобы написать смешанное число четыре и две трети, введите 4, пробел и затем 2/3 в форму.