Вычитание дробей через калькулятор онлайн

Дробь – это одна из классических форм для выполнения математических операций, с которой можно решать самые разные задачи. Дробная черта используется для того, чтобы выделить операцию деления. Сама дробь состоит из двух частей – числителя и знаменателя. Правильные дроби используются для обозначения таких чисел, где числитель меньше знаменателя. Неправильные дроби используются для обозначения дробей, где знаменатель меньше числителя. Смешанные дроби также содержат целую часть, которая также принимает участие в математических операциях.

Вычитание дробей – это базовая процедура, которая используется для того, чтобы получить искомый результат с минимальными затратами. Если следовать всем базовым правилам, то выполнить математическую операцию не составит никакого труда. Важно внимательно ознакомиться и со свойствами данных чисел. Если знать эти параметры, то можно легко выполнить операции, минимизируя возможные дополнительные затраты в процессе. Также следует обратить внимание на основное свойство дроби, когда при умножении на одно и то же число числитель и знаменатель остаются одинаковыми, не теряя свои значения.

Среди прочих основных особенностей дробей следует обратить внимание на такие:

• Можно привести несколько дробей к единому знаменателю. Для этого нужно числитель обязательно умножить на знаменатель второго числа.
• Также можно умножить знаменатель первой дроби на числитель второй.
• Чтобы привести результат к единому знаменателю, можно оба знаменателя умножить.

Как видно, операции приведения дроби к единому знаменателю выполняются по базовым правилам. С помощью онлайн-калькулятора вы сможете легко и быстро выполнить операцию за считанные минуты с минимальными дополнительными усилиями и затратами.

Свойства вычитания дробей

Процесс, как вычесть дроби, выполняется по базовой формуле, поэтому выполнить действие можно, следуя рекомендациям. Для того, чтобы получить желаемый результат, необходимо обратить внимание на такие базовые правила:

• Для начала необходимо посмотреть, совпадает ли дробная часть обеих дробей. Если совпадает, то отнимать их можно по простому правилу. Эта процедура выполняется по соответствующему алгоритму.
• Если знаменатель у дробей отличается, тогда необходимо привести дроби к общему знаменателю. Обычно этот процесс проводится по правилу. Например, можно умножить знаменатель друг на друга.
• Далее для выполнения вычитания необходимо отнять числители. При этом знаменатель остаются прежним.
• Если число позволяет, то можно сократить числитель и знаменатель на единое значение. Также можно оставить результат без каких-либо изменений, если не требуется проводить дополнительные транзакции.

Операции с дробями выполняются в соответствии с определенными алгоритмами. Если следовать правилам, то результат получится правильным без каких-либо дополнительных затрат. Также можно воспользоваться калькулятором вычитания дробей для того, чтобы получить искомый результат. Ниже будут представлены базовые примеры выполнения классических операций вычитания с дробями, которые можно выполнить самостоятельно или при помощи простого калькулятора.

Вычитание дробей с одинаковыми знаменателями

Это наиболее простой и распространенный пример выполнения вычитания двух дробей. Например, можно легко выполнить вычитание дробей с одинаковыми знаменателями. Для этого нужно просто отнять числители двух дробей, а знаменатель оставить таким же. Такая процедура выполняется максимально просто и без особых усилий. Для получения результата необходимо обратить внимание на такой пример:

2/3 – 1/3 = 1/3.

В результате были отняты числа числителя, на знаменатель остался одинаковым. При необходимости можно сократить результат, если это позволяет ситуация. Можно оставить результат таким же с минимальными усилиями и без дополнительных затрат для пользователей. Также можно воспользоваться онлайн-калькулятором, если необходимо выполнить несколько операций.

Вычитание смешанных дробей с одинаковыми знаменателями

Если необходимо выполнить вычитание смешанных дробей с одинаковыми знаменателями, достаточно выполнить базовую операцию с минимальными дополнительными усилиями. Для выполнения операции необходимо преобразовать дроби в неправильные, после чего отнять числители. При этом знаменатель остается таким же. Далее нужно сократить дробь при необходимости, если того требует ситуация. Для поиска разницы можно рассмотреть такой пример:

1 2/3 – 1 1/3 = 5/3 – 4/3 = 1/3.

Как видно, процесс решения не потребует особых усилий. Для этого можно воспользоваться соответствующей формулой. Достаточно следовать правилу, а также внимательно преобразовывать неправильные дроби. Результат также можно преобразовать к неправильной дроби или же оставить таким, какой он есть, если сокращение или преобразование не требуется.

Вычитание дробей с разными знаменателями

Если нужно выполнить выполнить вычитание с разными знаменателями, тогда необходимо их привести к единому знаменателю. Обычно приведение к единому знаменателю происходи к большему значению. После этого отнимают числители по обычному правилу. Далее процесс ничем не отличается от классического. Необходимо просто отнять числители и получить результат. Конечное число можно сократить при необходимости или же преобразовать в смешанную дробь. В качестве примера можно рассмотреть такой пример:

5/6 – 1/2 = 5/6 – 3/6 = 2/6 = 1/3.

Как видно, в этом примере дроби были приведены к единому знаменателю. Далее была выполнена операция вычитания числителей. После этого результат был сокращен на 2. С помощью онлайн-калькулятора можно выполнить данную транзакцию намного быстрее и эффективнее.

Вычитание из обыкновенной дроби натурального числа

Если нужно выполнить вычитание обыкновенной дроби и числа, необходимо учитывать некоторые базовые правила. Для начала необходимо обязательно провести преобразование натурального числа в дробь. Далее вычитание выполняется по базовому правилу, не требуя никаких особых правил или соблюдения тонкостей. Сама процедура выполняется достаточно быстро. Ниже представлен такой пример, который можно использовать в качестве шаблона для выполнения соответствующей операции:

2 2/3 – 2 = 8/3 – 6/3 = 2/3.

Как видно, для начала дробь была преобразована в неправильную. После этого была выполнена операция вычитания по общему правилу. Весь результат был приведен к общему знаменателю. При этом для выполнения операции были вычтены элементы числителя обоих чисел. При необходимости результат можно сократить или преобразовать в неправильную дробь. Этот процесс можно выполнить максимально быстро. Если воспользоваться онлайн-калькулятором, можно снизить затраты.

Вычитание из числа обыкновенной дроби

Если необходимо вычесть из обычного числа дробь, тогда необходимо это число обязательно преобразовать в дробь. Также нужно привести оба значения к единому знаменателю. Это необходимо для того, чтобы выполнить дальнейшую операцию вычитания в соответствии с базовыми правилами. Обычно эта процедура выполняется максимально быстро. Ниже представлен такой пример, которым можно воспользоваться для того, чтобы быстро получить искомое значение:

5 – 2/3 = 15/3 – 2/3 = 13/3 = 4 1/3.

Теперь нужно объяснить данный пример. Для начала число было приведено к дроби с использованием единого знаменателя с обыкновенной дробью. Далее Были вычтены числители по общему правилу. После этого результат был преобразован в смешанную дробь для того, чтобы упростить его отображение в соответствии с общими правилами. При необходимости дроби также можно сократить, если того требует ситуация. Также можно выполнить операцию намного быстрее и эффективнее, если использовать онлайн-калькулятор. Этот процесс практически не требует затрат, а также позволяет быстро получить результат и использовать его для достижения других вспомогательных задач.

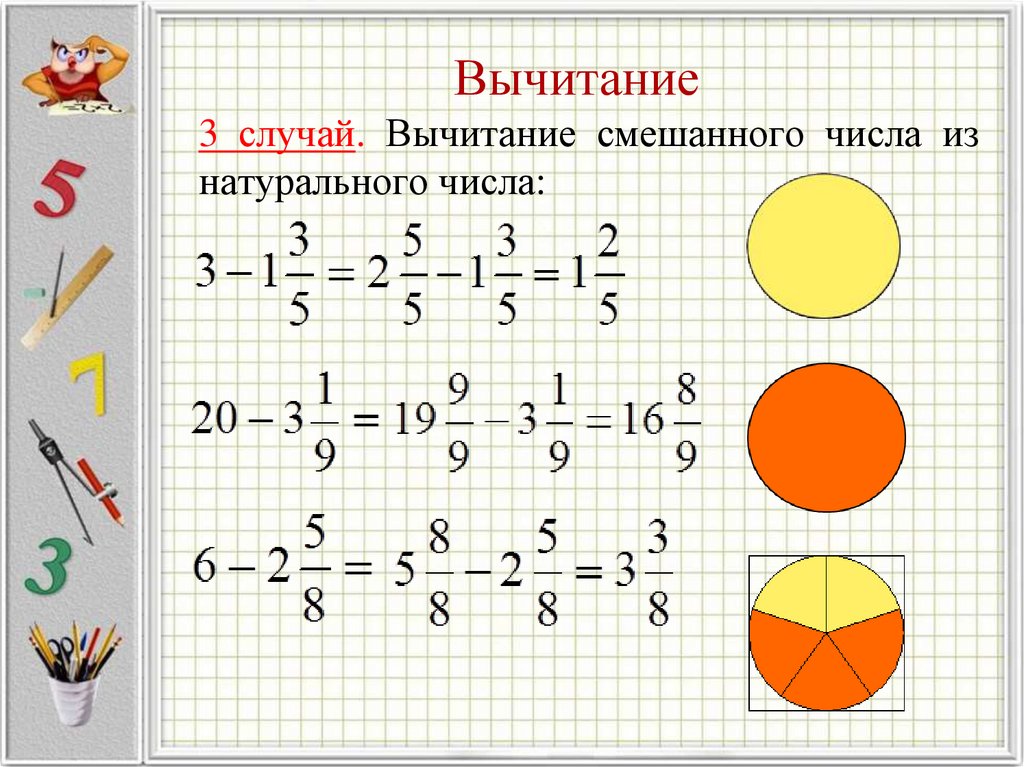
Вычитание смешанного числа из целого числа

Если нужно отнимать от целого числа смешанное, необходимо следовать определенным правилам, среди которых выделяют такие:

• для начала необходимо преобразовать целое число в дробь;
• также нужно обязательно преобразовать обе дроби к единому знаменателю для простоты выполнения операции вычитания;
• также можно уменьшить значение целой части для того, чтобы упростить выполнение процедуры вычитания;
• далее отдельно выполняется вычитание числителей рассматриваемых дробей;
• при необходимости можно также отнять целую часть для того, чтобы проще выполнить операцию с дробями;
• полученную дробь нужно обязательно сократить и преобразовать в смешанное число при необходимости.

В качестве примера необходимо рассмотреть такую задачу:

2 1/2 – 1 1/3 = 1 + 3/6 – 2/6 = 1 1/6.

Чтобы упростить себе задачу, можно выполнить вычитание дробей онлайн. Это будет намного проще и эффективнее, что позволит решить задачу любой сложности с минимальными усилиями и без дополнительных затрат.

Правила работы с дробями достаточно сложно и проблематично помнить всегда. Достаточно разбираться с базовыми функциями и особенностями для того, чтобы намного быстрее получить искомый результат. Каждый сможет легко воспользоваться всеми правилами и инструментами онлайн. С помощью калькулятора можно намного быстрее выполнить операцию с минимальными усилиями и затратами. Операция выполняется всего в несколько кликов. Достаточно ввести числа, выполнить операцию, после чего результат не заставит себя долго ждать.

Сложение и вычитание дробей. Додавання і віднімання дробів

Описание курса Элементарная математика Умножение и его свойства. Множення та його властивості Деление и его свойства. Ділення і його властивості Умножение и деление в столбик Дроби, задачи на нахождение частей от целого Найти наименьшее общее кратное (НОК) Привести дробь к наименьшему общему знаменателю Нахождение целого по его части Скорость поедания яблока Сложение и вычитание простых дробей Сложение и вычитание дробей. Додавання і віднімання дробів Вычислить выражение с простыми и десятичными дробями Проценты Нахождение процентов от суммы Задачи на нахождение процентов Задачи про втекающую в бассейн воду Задачи на тему «Найти число», «Найти два числа» Задачи на нахождение двух чисел Задачи на нахождение двух чисел (часть 2) Найти трехзначное число Задачи о прохождении пути Задача про велосипедистов Задача про туриста Нахождение общей величины пройденного пути Задачи про лодку и течение реки Задачи с решением элементарных уравнений Задача про бросание гранаты Корни и степени, возведение в степень, извлечение корня Дробь в степени числа. Нахождение дробной степени числа Операции с корнями на основе ствойств степени Квадратный корень. Квадратний корінь Свойства квадратного корня. Властивості квадратного кореня Таблица степеней натуральных чисел Показательная функция. Показова функція Функции Область определения функции Эллипс Свойства бесконечно малых и бесконечно больших функций Уравнения Простейшие уравнения Квадратные уравнения Неравенства (Нерівності) Решаем неравенства Векторы Трехмерное пространство Равенство векторов. Рiвнiсть векторiв Логарифм Дифференциальное исчисление Что такое производная. Практический смысл производной Правила дифференцирования Таблица производных простых функций Таблица производных экспоненциальных и логарифмических функций Таблица производных тригонометрических функций Производная числа Производная дроби Производная корня Нахождение экстремума функции Комбинаторика Найти количество возможных комбинаций Теория вероятности Вероятность появления карт Вероятность наступления события Вероятность одновременного прихода пароходов Тесты (1) См. также: более простой уровень — сложение и вычитание простых дробей для младших классов. Сложение (вычитание) дробей производится по правилам сложения (вычитания) обыкновенных дробей. Слагаемыми, уменьшаемым и вычитаемым в числителе или знаменателе дроби могут быть любые рациональные числа или выражения с переменными. Исключения составляют число 0 и выражения, обращающие знаменатель в нуль. Правило: Чтобы сложить (вычесть) дроби с одинаковым знаменателем, не равным нулю, нужно сложить (вычесть) их числители и оставить тот же знаменатель. Чтобы сложить (вычесть) дроби с разными знаменателями, не равными нулю, нужно найти общий знаменатель дробей и дополнительные множители. Умножить числители на дополнительные множители и взять произведения слагаемыми (от первого произведения вычесть второе), оставить общий знаменатель под суммой (разностью). Рассмотрим сложение и вычитание дробей на примерах: Додавання (віднімання) дробів проводиться за правилами складання (віднімання) звичайних дробів. Доданками, зменшуваним і від’ємником в чисельнику або знаменнику дробу можуть бути будь-які раціональні числа або вирази зі змінними. Винятки становлять число 0 і вирази, які звертають знаменник в нуль. Правило: Щоб додати (відняти) дроби з однаковим знаменником, не рівним нулю, треба додати (відняти) їх чисельники і знаменник залишити той самий. Щоб додати (відняти) дроби з різними знаменниками, не рівними нулю, потрібно знайти спільний знаменник дробів і додаткові множники. Помножити чисельники на додаткові множники і взяти добуток складовими (від першого добутку відняти другий), залишити спільний знаменник під сумою (різницею). Розглянемо додавання і віднімання дробів на прикладах: ЗАДАЧА 1: Сумма дробей, у которых знаменатели одинаковые (произведение одночлена на многочлен), а числители: у первой дроби – многочлен, у второй дроби – одночлен. ЗАВДАННЯ 1: Сума дробів, у яких однакові знаменники (добуток одночлена на багаточлен), а чисельники: у першому дробу — багаточлен, у другому — одночлени. Так как знаменатели дробей одинаковые, то сложим числители дробей и подпишем тот же знаменатель. В числителе выражение x2+y2+2xy можно заменить по формулам сокращенного умножения на квадрат двучлена, так как, используя переместительный закон сложения, трехчлен можно записать как  x2+2xy+y2. Так як знаменники дробів однакові, то складемо чисельники дробів і підпишемо той же знаменник. В чисельнику виразу x2+y2+2xy можна замінити за формулами скороченого множення на квадрат двочлена, так як, використовуючи переміщуючий закон додавання, тричлен можна записати як x2+2xy+y2. при а≠0, х≠-у. Квадрат любого основания есть произведение двух одинаковых сомножителей, поэтому в числителе вместо квадрата суммы пишем произведение одинаковых двучленов, один из которых можно сократить с таким же двучленом в знаменателе. Сумма имеет смысл при любых а, кроме а=0, х=-у. при а≠0, х≠-у. Квадрат будь-якої основи є добуток двох однакових співмножників, тому в чисельнику замість квадрата суми пишемо добуток однакових двочленів, один з яких можна скоротити з таким же двочленом в знаменнику. Сума має сенс при будь-яких а, крім а=0, х=-у. ЗАДАЧА 2: Разность двух алгебраических дробей с одинаковыми знаменателями. Числители и знаменатели обеих дробей – многочлены. ЗАДАЧА 2: Різниця двох алгебраїчних дробів з однаковими знаменниками. Чисельники і знаменники обох дробів — багаточлени. В числителе полученной дроби приведем подобные, а в знаменателе трехчлен заменим по формуле сокращенного умножения на квадрат разности, который можно записать как произведение двух одинаковых множителей: У чисельнику отриманого дробу наведемо подібні, а в знаменнику тричлен змінимо за формулою скороченого множення на квадрат різниці, який можна записати як добуток двох однакових множників: при a-b≠0. Числитель и знаменатель имеют одинаковый множитель-двучлен, на который их можно по основному свойству дроби сократить. Решение будет верным при всех значениях а и в, кроме а=в. при a-b≠0. Чисельник і знаменник мають однаковий множник-двочлен, на який їх можна за основною властивістю дробу скоротити. Рішення буде вірним при всіх значеннях а ів, крім а=в. ЗАДАЧА 3: Сумма двух дробей с одинаковыми знаменателями, которые представлены одночленами в числителях и многочленом – в знаменателях. ЗАДАЧА 3: Сума двох дробів з однаковими знаменниками, які представлені одночленами в чисельниках і багаточленом — в знаменниках. В числителе сумма кубов заменяем по формуле сокращенного умножения на произведение двучлена и трехчлена. Сократим общий двучлен числителя и знаменателя по основному свойству дроби. Результатом является целое выражение: У чисельнику суму кубів замінюємо за формулою скороченого множення на добуток двочлена і тричлена. Скоротимо загальний двочлен чисельника та знаменника за основною властивістю дробу. Результатом є цілий вираз: при a≠-b. при a≠-b. ЗАДАЧА 4:Разность дробей с разными знаменателями, у которых числители и знаменатели – одночлены. ЗАДАЧА 4:Різницю дробів з різними знаменниками, у яких чисельники і знаменники — одночлени. при х≠0, у≠0. Найдем общий знаменатель дробей как произведение оснований с наибольшими показателями степеней. Проставим дополнительные множители. Умножим одночлены числителей на их дополнительные множители и запишем произведения разностью одночленов, а в знаменателе – общий знаменатель. Из числителя выносим общий множитель (2) и записываем числитель как произведение одночлена на многочлен. Дальнейшее преобразование невозможны, дробь имеет решения при всех значениях переменных, кроме х=у=0. при х≠0, у≠0. Знайдемо загальний знаменник дробів як добуток основ з найбільшими показниками ступенів. Проставимо додаткові множники. Помножимо одночлени чисельників на їх додаткові множники і запишемо добутки різницею одночленів, а в знаменнику — загальний знаменник. З чисельника виносимо загальний множник (2) і записуємо чисельник як добуток одночлена на багаточлен. Подальші перетворення неможливі, дріб має рішення при всіх значеннях змінних, крім х=у=0. ЗАДАЧА 5: Сумма дробей с разными знаменателями, у которых числители и знаменатели – многочлены. ЗАДАЧА 5: Сума дробів з різними знаменниками, у яких чисельники і знаменники — багаточлени. Общий знаменатель дробей равен произведению их знаменателей. Проставим дополнительные множители, умножим числители на их дополнительные множители и произведения возьмем суммой. Подпишем под числителем общий знаменатель. Перемножим в числителях многочлены и запишем одним многочленом. В знаменателе произведение двучленов по формуле сокращенного умножения переведем в многочлен (разность квадратов): Спільний знаменник дробів дорівнює добутку їх знаменників. Проставимо додаткові множники, помножимо чисельники на їх додаткові множники і добутки візьмемо сумою. Підпишемо під чисельником спільний знаменник. Перемножимо в чисельниках багаточлени і запишемо одним багаточленом. У знаменнику твір двочленів за формулою скороченого множення переведемо в багаточлен (різниця квадратів): Приведем подобные слагаемые в числителе: Наведемо подібні доданки в чисельнику: при х2-у2≠0. Получилась дробь, у которой в числителе и знаменателе двучлены. Из числителя можно вынести общий множитель (2), но это не упростит дробь. Все действительные значения неизвестных будут решением дроби, кроме х=±у, что обращает знаменатель в 0. при х2-у2≠0. Вийшов дріб, у якому в чисельнику і знаменнику двочлени. З чисельника можна винести спільний множник (2), але це не спростить дріб. Всі дійсні значення невідомих будуть рішенням дробу, крім х=±у, що звертає знаменник на 0. См. также: более простой уровень — сложение и вычитание простых дробей для младших классов. 0    Сложение и вычитание простых дробей | Описание курса | Вычислить выражение с простыми и десятичными дробями      Обсудить на форуме Записаться на курсы Обратиться к консультанту Пройти тест Полный список курсов обучения Бесплатные видеоуроки Нужна информация!

Сложение и вычитание дробей: сходство и отличие знаменателей

Основные математические процедуры сложения и вычитания также применимы к дробям. Поскольку в каждой ситуации мы предпринимаем разные шаги, очень важно понять, имеют ли дроби одинаковые или разные знаменатели, чтобы легко складывать и вычитать дроби. При решении задач на сложение и вычитание дробей связь этих понятий является ключевым критерием для получения правильного решения.

Дроби являются составной частью большего целого. Дроби можно решать с помощью основных арифметических методов. В результате дроби можно складывать, вычитать, умножать и делить. Давайте рассмотрим дроби, прежде чем переходить к сложению дробей.

Подобные дроби: Две или более дроби, в которых один и тот же знаменатель, известны как «подобные дроби». Например, 3/7, 4/7, 8/7 и т. д. похожи на дроби. Обратите внимание, что 7/7 не является подобной дробью, потому что ее можно упростить до . В отличие от дробей: . Когда знаменатель между 2 или более дробями не совпадает, дроби называются, в отличие от дробей. Например, 1/7, 5/6, ⅔ и т. д. не похожи на дроби.

В этой статье мы научимся складывать и вычитать похожие и разные дроби.

Table of Content

Вычитание фракций

вычитание фракций с не в отличие от знамениторов

Добавление, такие как фракции

Добавляя фракции с непревзойденными знаменателями

Установки фракции

.

. и Вычитание дробей с одинаковыми знаменателями

Сложение одинаковых дробей

Сложение дробей с одинаковыми дробями очень просто и точно так же, как сложение целых чисел. Прочтите шаги ниже, чтобы узнать, как складывать дроби:

Шаг 1: Запишите одинаковые дроби правильно, используя символ «+».

Шаг 2: Так как знаменатель у сложенных дробей один и тот же, то и в полученной дроби будет тот же знаменатель.

Шаг 3: Добавьте числители.

Шаг 4: Запишите ответ в форме a/b. Где а — сумма числителя, а b — знаменатель слагаемых.

Пример: Добавить 11/3 к 4/3 

Решение: Внимательно прочитав шаги и применив их к этому вопросу, мы получим:                

Шаг 1: 11/3 + 4/3

Шаг 2: Знаменатель ответа будет 3. Так как они как функции.

Шаг 3: 11 + 4 = 15 (добавление числителя)

Шаг 4: Запись полученной дроби: 15/3 

Мы видим, что в 15/3 15 можно разделить 5 раз на 3. Таким образом, результат равно 5. Если возможно, всегда упрощайте свои ответы.

Вычитание одинаковых дробей

Вычитание двух или более дробей с одинаковыми знаменателями аналогично сложению дробей, описанному выше. Шаги, связанные с вычитанием дробей с равными знаменателями, следующие:

Шаг 1: Запишите одинаковые дроби по порядку с символами «-» между ними.

Шаг 2: Знаменатель результата будет таким же, как знаменатель вычитаемых дробей.

Шаг 3: Соответственно вычтите числа в числителях.

Шаг 4: Запишите ответ в форме a/b. Где а — разница между числителем и b — знаменателем.

Пример: Вычесть 3/7 на 9/7.

Решение: Внимательно выполните описанные выше действия→           

Шаг 1: 9/7 – 3/7

Шаг 2: Поскольку они подобны функциям, знаменатель ответа будет равен 7.

Шаг 3: 9 – 3 = 6 (вычитание числителя)

Шаг 4: Запись полученной дроби: 6/7.

Если разность числителей отрицательное число, то дробь записывается в виде -a/b.

На этом заканчивается понятие о том, как складывать и вычитать дроби, когда знаменатели одинаковы. Далее мы научимся складывать и вычитать дроби с разными знаменателями.

Как складывать и вычитать дроби с разными знаменателями

Складывать дроби с разными знаменателями

Складывать дроби с разными знаменателями — довольно сложная задача. Это не так просто, как сложение «подобных дробей», потому что знаменатели здесь имеют разную величину. Результирующий знаменатель в этом случае представляет собой LCM (наименьшее общее кратное) знаменателей. См. шаги ниже, чтобы понять, как решать разные дроби:

Шаг 1: Правильно запишите одинаковые дроби со знаком «+».

Шаг 2: Найдите результирующий знаменатель, найдя НОК знаменателей.

Шаг 3: Умножьте числители в соответствии с НОК. Сложите соответствующие числа, чтобы получить значение результирующего числителя.

Шаг 4: Запишите результат в форме a/b. Где a — это сумма числителя, а b — знаменатель (НОК).

Пример: Сложите дроби, указанные как 5/4 и 2/9.

Решение: Мы решим это, используя пошаговый подход, упомянутый выше:

Шаг 1: 5/4 + 2/9

Шаг 2: Поскольку они не являются дробями, мы должны найти НОК чисел 4 и 9. 36 — это НОК чисел 4 и 9.

Шаг 3: Теперь, соответственно умножаем числители. Для 5/4 4 делится на 36 девяток; следовательно, мы умножим 5 на 9 = 45. Точно так же для 2/9 9 делит 36 четыре раза; следовательно, 2 умножается на 4 = 8. Теперь мы добавляем 45 и 8 = 45 + 8 = 53.

Шаг 4: Таким образом, полученная дробь равна 53/36. Его нельзя упростить; следовательно, дробь остается 53/36.

LCM берется, чтобы превратить их, в отличие от дробей, в подобные дроби. В остальном процедура остается прежней.

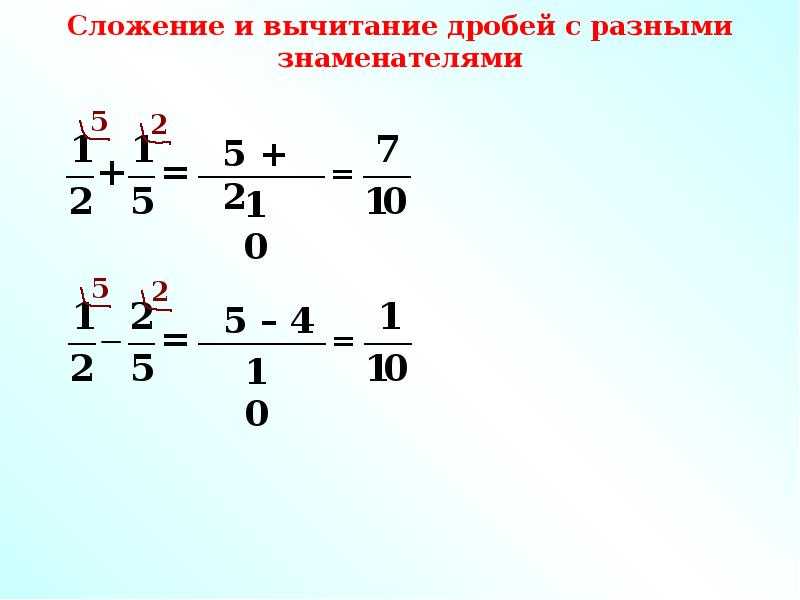
Вычитание дробей с разными знаменателями

Вычитание дробей с разными знаменателями — еще одно сложное, но важное арифметическое понятие дробей. Это следует той же процедуре, что и сложение, в отличие от дробей. Единственное изменение состоит в том, что здесь мы находим разницу, а не суммируем. Пошаговый подход к вычитанию двух разных дробей:

Шаг 1: Запишите одинаковые дроби правильно, используя знак вычитания «-».

Шаг 2: Результирующий знаменатель вычисляется путем нахождения НОК знаменателей.

Шаг 3: Соответственно умножьте числители на НОК. Сложите результаты, чтобы найти значение получившихся числителей.

Шаг 4: Результат должен быть записан в форме a/b. Где a — разница числителя, а b — НОК знаменателя.

Пример: Вычтите дроби 3/4 и 1/8

Решение: Мы решим это, используя пошаговый подход, упомянутый выше:

Шаг 1: 3/4 – 1/8

Шаг 2: Поскольку они в отличие от дробей, мы должны найти НОК 4 и 8. 8 — это НОК, потому что 4 x 2 = 8 и 8 x 1 = 8.

Шаг 3: Теперь умножим числители соответственно. Для 3/4 4 делит 8 два раза; следовательно, мы умножим 3 на 2 = 6. Точно так же для 1/8 8 делится на 1 раз; следовательно, 1 умножается на 1 = 1. Теперь мы вычитаем 6 и 1 = 6 – 1 = 5,

Шаг 4: Таким образом, полученная дробь равна 5/8.

Иногда вы можете обнаружить, что LCM является одним из знаменателей. Это возможно, когда знаменатели кратны друг другу. Наибольшее кратное становится знаменателем.

Сложение и вычитание дробей с целыми числами

Мы научились складывать или вычитать дробь из другой дроби. Теперь давайте научимся складывать и вычитать дроби с целыми числами. Старайтесь всегда составлять дроби в форме, неподходящей для арифметических операций. Хитрость сложения или вычитания дроби и целого числа заключается в том, чтобы преобразовать целое число в дробь. Это можно сделать, поставив 1 в знаменателе целого числа.

Целое число и дробь можно складывать или вычитать, используя процедуру, описанную для разных дробей .

Пример: Сложите 6/5 и 11 

Решение: Шаг 1. Преобразуйте 11 в дробную форму как 11/1.

              Шаг 2. НОК 6/5 и 11/1 равен 5. Поскольку 5 кратно 1. Сложите числители  

                           6 + 55 = 61,

               Шаг 4. Полученная дробь равна 61/5.

Обратите внимание, что НОК в случае сложения и вычитания двух дробей всегда является большим числом. Это связано с тем, что каждое число кратно 1. 

Важные напоминания:

• Чтобы суммировать разные дроби, выполните следующие действия:

а) Используя НОК знаменателя, преобразовать данные дроби в подобные дроби.

b) Определите соответствующие дроби следующих дробей с НОК в качестве знаменателя.

c) Сложите числители, не изменяя знаменатель.

• Никогда по отдельности не вычитайте и не суммируйте числители и знаменатели разных дробей. Это приведет к ошибочному результату. Следуйте правилам, упомянутым в каждом разделе этой статьи.
• Не обязательно находить НОК знаменателей при сложении или вычитании, в отличие от дробей. Подойдет любой стандартный множитель. Таким образом, мы можем получить общее кратное, перемножив два знаменателя. Хотя это дает более крупные числа, его можно свести к простейшей форме.

Часто задаваемые вопросы

1. Как складывать и вычитать дроби?

 Чтобы сложить дробь, просто сложите числители. Чтобы вычесть дробь, нужно просто вычесть знаменатели. Например: чтобы сложить одну треть и две трети, умножьте 1 на 2, а затем умножьте 3 на 3. Сложите эти два числа вместе, чтобы получить 7/9. Если вы хотите вычесть одну треть из двух третей, умножьте 1 на 2, а затем снова умножьте 3 на 3. Затем вычтите два числа, которые вы только что перемножили, — в данном случае 6/9..

2. Как складывать и вычитать дроби с разными знаменателями?

Сложение и вычитание дробей с разными знаменателями — это простой процесс, который требует сложения или вычитания числителей, умножения знаменателей на одно и то же число, а затем повторного сложения или вычитания полученных числителей.

3. Как складывать и вычитать дроби с целыми числами?

Чтобы складывать и вычитать дроби с целыми числами, сначала нужно преобразовать каждую дробь в дробь с тем же знаменателем. Например, если бы вам нужно было сложить 1/2 + 1/4, вы бы преобразовали их оба в 3/4, разделив оба на 2. Затем вы бы сложили их вместе, как если бы они были целыми числами. Чтобы вычесть одну дробь из другой, это похоже — просто убедитесь, что знаменатели для обеих одинаковы для начала!

4. Как складывать и вычитать дроби со смешанными числами?

 Чтобы складывать или вычитать дроби со смешанными числами, сначала нужно преобразовать их в неправильные дроби. Для этого вы делите большую часть на меньшую, а затем умножаете результат на 100%. Затем вы можете добавить или вычесть, как обычно.

5. Каковы правила сложения и вычитания дробей?

Правило сложения и вычитания дробей довольно простое:

1) Если знаменатели одинаковы, сложите числители вместе и напишите это над знаменателем первой дроби.

2) Если знаменатели не равны, нужно их умножить на какое-нибудь общее число (то есть на такое число, на которое оба знаменателя делятся без остатка). Затем добавьте или вычтите, как обычно.

Сложение и вычитание смешанных чисел

В этом разделе рассматриваются следующие темы:

1. Модель сложения смешанных чисел с общим знаменателем
2. Сложение смешанных чисел с общим знаменателем
3. Модель вычитания смешанных чисел
4. Вычитание смешанных чисел с общим знаменателем
5. Сложение и вычитание смешанных чисел с разными знаменателями

4.6.1 Модель сложения смешанных чисел с общим знаменателем

До сих пор мы складывали и вычитали правильные и неправильные дроби, но не смешанные числа. Давайте начнем с размышлений о сложении смешанных чисел с помощью денег.

Если у Рона есть $1$ доллара и $1$ квартал, у него есть $1\frac{1}{4}$ доллара.

Если у Дона есть $2$ долларов и $1$ квартал, у него есть $2\frac{1}{4}$ долларов.

Что, если Рон и Дон соединит свои деньги? У них были бы доллары по 3 доллара и четвертак по 2 доллара. Они добавляют доллары и добавляют четвертак. Это составляет 3 долларов США \frac{2}{4}$ долларов. Поскольку две четверти — это полдоллара, у них будет 3 с половиной доллара или 3 \frac{1}{2}$ доллара.

$\large 1 \frac{1}{4}$

$\large +2 \frac{1}{4}$

____________

$\large 3 \frac{2}{4} = 3 \frac{1}{2}$

Когда вы добавляли доллары, а затем добавляли четверти, вы складывали целые числа, а затем добавляли дроби.

$\large 1 \frac{1}{4} + 2 \frac{1}{4}$

Мы можем использовать дробные круги для моделирования этого же примера:

		$1 \frac{1 {4} + 2 \frac{1}{4}$
Начните с $1 \frac{1}{4}$.	один целый и один $\frac{1}{4}$ штук		$1 \frac{1}{4}$
Добавьте еще $2 \frac{1}{4}$.	два целых и один $\frac{}{4}$ штук		$+2 \frac{1}{4}$ ________
Сумма:	три целых и два $\frac{1}{4}$		$3 \frac{2}{4} = 3 \frac{1}{2 }$

Пример 1

Модель $2 \frac{1}{3} + 1 \frac{2}{3}$ и укажите сумму.

Решение

два целых числа и один $\frac{1}{3}$		$2 \frac{1}{3}$
плюс одно целое и два $\frac{1 {3}$s		$+1 \frac{2}{3}$ ________
сумма равна трем целым и трем $\frac{1}{3}$s		$3 \frac{3}{3} = 4$

Это то же самое, что $4$ всего. Итак, $2 \frac{1}{3} + 1 \frac{2}{3} = 4$

Пример 2

Модель $1 \frac{3}{5} + 2 \frac{3}{ 5}$ и представить сумму в виде смешанного числа.

Решение

Мы будем использовать дробные круги, целые круги для целых чисел и $\frac{1}{5}$ кусков для дробей.

одно целое и три $\frac{1}{5}$s		$1 \frac{3}{5}$
плюс два целых и три $\frac{1}{ 5}$ с.		$+2 \frac{3}{5}$ ________
сумма равна трем целым и шести $\frac{1}{5}$s		$3 \frac{6}{ 5} = 4 \frac{1}{5}$

Сложив целые круги и пятые части, мы получили сумму $3 \frac{6}{5}$.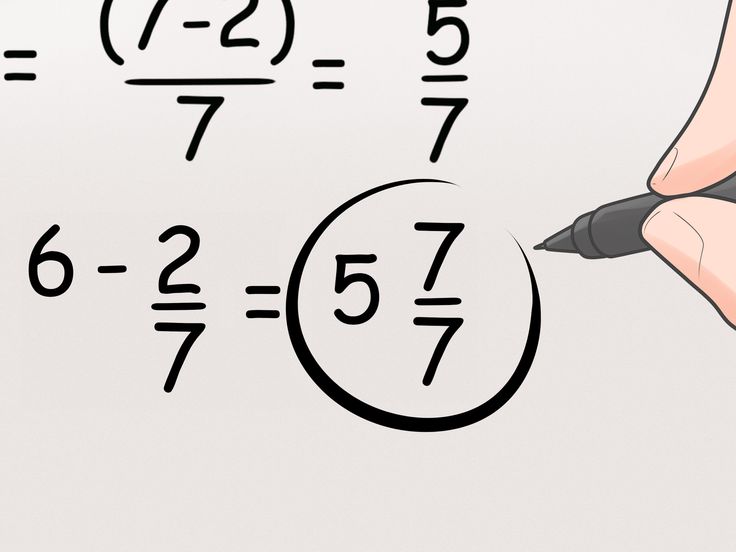 Мы видим, что $\frac{6}{5}$ эквивалентно $1 \frac{1}{5}$, поэтому мы добавляем это к $3$, чтобы получить $4 \frac{1}{5}$.

4.6.2 Сложение смешанных чисел

Моделирование с помощью кругов дробей помогает проиллюстрировать процесс сложения смешанных чисел: мы складываем целые числа и складываем дроби, а затем, если возможно, упрощаем результат.

КАК: Сложите смешанные числа с общим знаменателем.

1. Сложите целые числа.
2. Сложите дроби.
3. Упростите, если возможно.

Пример 3

Добавить: $3 \frac{4}{9} + 2 \frac{2}{9}$.

Решение

	$3 \frac{4}{9} + 2 \frac{2}{9}$
Сложите целые числа.
Сложите дроби.
Упростите дробь.

В примере 3 сумма дробей была правильной дробью. Теперь рассмотрим пример, где сумма является неправильной дробью.

Пример 4

Найдите сумму: $9 \frac{5}{5} + 5 \frac{7}{9}$.

Решение

	$9 \frac{5}{5} + 5 \frac{7}{9}$
Сложите целые числа, а затем сложите дроби.	$9 \frac{5}{9}$ $+5 \frac{7}{9}$ ________ $14 \frac{12}{9}$
Переписать $\frac{12}{ 9}$ как неправильная дробь.	14 $ + 1 \frac{3}{9}$
Доп.	15 $\frac{3}{9}$
Упрощение.	$15 \frac{1}{3}$

Альтернативным методом сложения смешанных чисел является преобразование смешанных чисел в неправильные дроби, а затем сложение неправильных дробей. Этот метод обычно пишется горизонтально.

Пример 5

Сложите путем преобразования смешанных чисел в неправильные дроби: $3 \frac{7}{8} + 4 \frac{3}{8}$.

Решение

	$3 \frac{7}{8} + 4 \frac{3}{8}$
Преобразование в неправильные дроби.	$\frac{31}{8} + \frac{35}{8}$
Сложите дроби.	$\frac{31+35}{8}$
Упростите числитель.	$\frac{66}{8}$
Перепишите как смешанное число.	$8 \frac{2}{8}$
Упростите дробь.	$8 \frac{1}{4}$

Поскольку задача была задана в виде смешанного числа, запишем сумму в виде смешанного числа.

В таблице ниже сравниваются два метода сложения на примере выражения $3 \frac{2}{5} + 6 \frac{4}{5}$. Какой путь вы предпочитаете? Смешанные числа 5}$
$9 +\frac{6}{5}$
$9 +1 \frac{1}{5}$
$10 \frac{1}{5}$ $3 \frac{2}{5} + 6 \frac{4}{5}$
$\frac{17}{5} + \frac{34}{5}$
$\frac{51}{5}$
$10 \frac{1}{5}$

с общим знаменателем. Предположим, вы только что испекли целую пиццу и хотите отдать половину пиццы своему брату. Что нужно сделать с пиццей, чтобы отдать ему половину? Вы должны разрезать его как минимум на две части. Тогда вы можете дать ему половину.

Мы будем использовать дробные круги (пиццы!), чтобы визуализировать процесс.

Начните с одного целого.

Алгебраически вы должны написать:

Пример 6

Используйте модель для вычитания: $1-\frac{1}{3}$.

Решение

Что, если мы начнем с более чем одного целого? Давай выясним.

Пример 8

Используйте модель для вычитания: $2-\frac{3}{4}$.

Решение

В следующем примере мы вычтем более одного целого.

Пример 9

Используйте модель для вычитания: $2-1 \frac{2}{5}$.

Решение

Что делать, если вы начинаете со смешанного числа и вам нужно вычесть дробь? Подумайте о такой ситуации: вам нужно положить три четвертака в парковочный счетчик, но у вас есть только купюра в $\$1$ и одна четвертак. Что ты можешь сделать? Вы можете разменять долларовую купюру на четвертинки по 4 доллара США. Стоимость 4-долларовой монеты такая же, как у одной долларовой банкноты, но 4-долларовая монета более полезна для парковочного счетчика. Теперь вместо купюры в $\$1 и одной четверти у вас есть 5$ четверти, и вы можете положить 3$ четверти в счетчик.

Это моделирует то, что происходит, когда мы вычитаем дробь из смешанного числа. Мы вычли три четверти из одного доллара и одну четверть.

Мы также можем смоделировать это с помощью дробных кругов, как мы делали для сложения смешанных чисел.

Пример 10

Используйте модель для вычитания: $1 \frac{1}{4} – \frac{3}{4}$.

Решение

Перепишите вертикально. Начните с одного целого и одной четверти.
Поскольку дроби имеют знаменатель $4$, разрежьте целое на части по $4$. Теперь у вас есть $\frac{4}{4}$ и $\frac{1}{4}$, что равно $\frac{5}{4}$.
Уберите $\frac{3}{4}$. Осталось $\frac{1}{2}$.

4.6.4 Вычитание смешанных чисел с общим знаменателем

Теперь вычтем смешанные числа без использования модели. Но это может помочь представить модель в уме, когда вы читаете шаги.

КАК: Вычитать смешанные числа с общими знаменателями.

1. Перепишите задачу в вертикальной форме.
2. Сравните две дроби.
   • Если верхняя дробь больше нижней, перейти к шагу 3.
   • Если нет, то в верхнем смешанном числе взять одно целое и прибавить его к дробной части, получив смешанное число с неправильной дробью.
3. Вычтите дроби.
4. Вычтите целые числа.
5. Упростите, если возможно.

Пример 11

Найдите разницу: $5 \frac{3}{5} – 2 \frac{4}{5}$.

Решение

Перепишите задачу в вертикальной форме.
Так как $\frac{3}{5}$ меньше, чем $\frac{4}{5}$, возьмите $1$ из $5$ и добавьте его к $\frac{3}{ 5}$ : $( \frac{5}{5} + \frac{3}{5} = \frac{8}{5} )$
Вычтите дроби.
Вычесть целые части. Результат в простейшей форме.

Так как задача была дана со смешанными числами, мы оставляем результат как смешанные числа.

Точно так же, как мы делали это со сложением, мы могли вычитать смешанные числа, преобразовывая их сначала в неправильные дроби. Мы должны записать ответ в той форме, в которой он был задан, поэтому, если нам дали смешанные числа для вычитания, мы запишем ответ как смешанное число.

КАК: Вычесть смешанные числа с общим знаменателем как неправильную дробь.

1. Перепишите смешанные числа в виде неправильных дробей.
2. Вычтите числители.
3. Запишите ответ в виде смешанного числа, по возможности упростив дробную часть.

Пример 12

Найдите разницу путем преобразования в неправильные дроби:

$9 \frac{6}{11} – 7 \frac{10}{11}$.

Раствор

	$9 \frac{6}{11} – 7 \frac{10}{11}$
Перепишите в виде неправильных дробей.	$\frac{105}{11} – \frac{87}{11}$
Вычесть числители.	$\frac{18}{11}$
Перепишите как смешанное число.	$1 \frac{7}{11}$

4.6.5 Сложение и вычитание смешанных чисел с разными знаменателями

Чтобы сложить или вычесть смешанные числа с разными знаменателями, мы сначала преобразуем дроби в эквивалентные дроби с ЖК. Затем мы можем выполнить все шаги, которые мы использовали выше для сложения или вычитания дробей с одинаковыми знаменателями.

Пример 13

Добавьте: $2 \frac{1}{2} + 5 \frac{2}{3}$.

Решение

Поскольку знаменатели разные, мы перепишем дроби как эквивалентные дроби с ЖК-дисплеем, $6$. Потом добавим и упростим.

Мы запишем ответ как смешанное число, потому что в задаче нам дали смешанные числа.

Пример 14

Вычесть: $4 \frac{3}{4} – 2 \frac{7}{8}$.

Раствор

Так как знаменатели дробей разные, мы перепишем их как эквивалентные дроби с ЖК $8$. Оказавшись в таком виде, мы будем вычитать. Но сначала нам нужно занять 1 доллар.

Нам дали смешанные числа, поэтому мы оставляем ответ как смешанное число.

Пример 15

Вычесть: $3 \frac{5}{11} – 4 \frac{3}{4}$.

Решение

Мы видим, что ответ будет отрицательным, так как мы вычитаем 4$ из 3$. Как правило, когда мы знаем, что ответ будет отрицательным, легче вычитать неправильные дроби, а не смешанные числа.

	$3 \frac{5}{11} – 4 \frac{3}{4}$
Изменить эквивалентные дроби с помощью ЖК-дисплея.	$3 \frac{5 \cdot 4}{11 \cdot 4} – 4 \frac{3 \cdot 11}{4 \cdot 11}$ $3 \frac{20}{44} – 4 \frac{33 {44}$
Перепишите в виде неправильных дробей.	$\frac{152}{44} – \frac{209}{44}$
Вычесть.	$- \frac{57}{44}$
Перепишите как смешанное число.	$ -1 \ frac {13} {44} $

8.