задачи, примеры, упражнения, правило в 2022 году

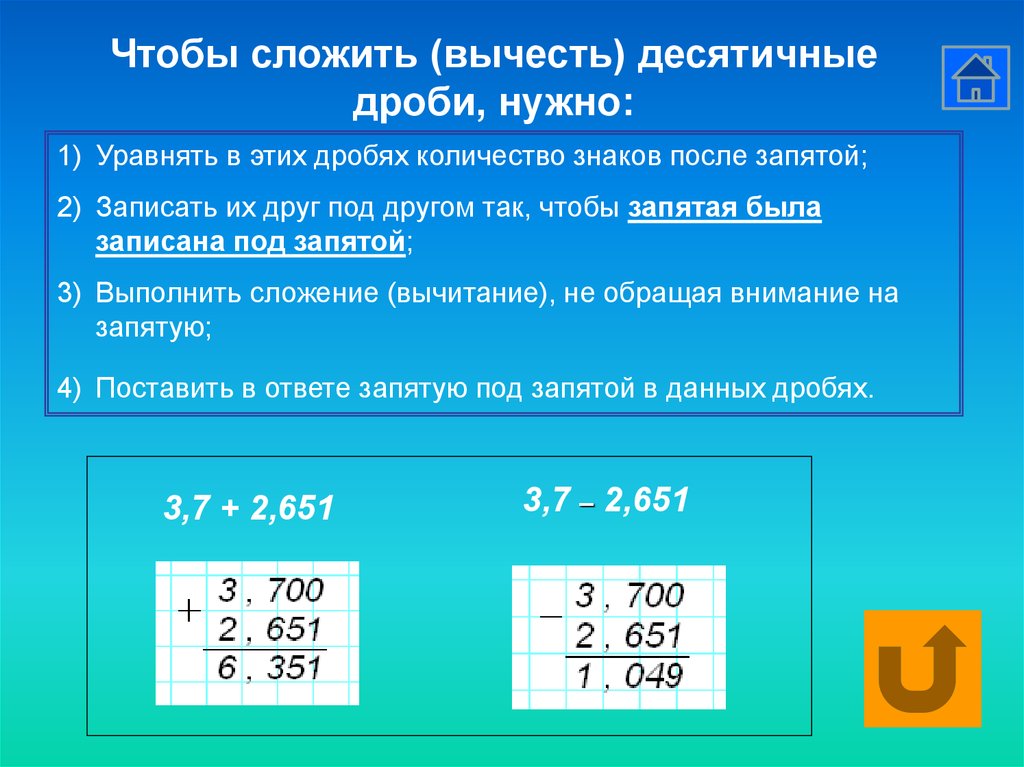
Сложение десятичных дробей. Примеры

Сложение десятичных дробей практически не отличается от нахождения суммы натуральных чисел. Для данного действия также выполняются переставной и связующий законы сложения. Сложность состоит только в правильном сопоставлении разрядов слагаемых. Поэтому можно выделить такое правило и порядок добавления десятичных дробей в столбик:

1. Десятичные дроби записываем друг под другом так, чтобы десятичная запятая и разряды одинаковых слагаемых были правильно сопоставлены и находились на одной вертикальной прямой
2. Для того чтобы слагаемые имели одинаковое количество цифр, справа от десятичных знаков можно дописать нули (если нужно)
3. Выполняем сложение по разрядам, начиная справа. Десятичную запятую (десятичный разделитель) в сумме ставят в том вертикальном столбце, в котором она находится в слагаемых.

Рассмотрим сложение десятичных дробей на примерах.

Пример. Сложить дроби 1,23 и 4,15

В данном примере количество цифр после запятой в двух слагаемых одинаково. Записываем в столбик, чтобы десятичные запятые находились в одном вертикальном столбце. Начинаем добавлять с сотых: 3 сотых плюс 5 сотых, получим 8 сотых; 2 десятых плюс 1 десятое – получили 3 десятых. Переписываем запятую и суммируем целые части: 1 + 4 = 5. Следовательно, суммой слагаемых будет число 5,38      

Пример. Найти сумму десятичных дробей 12,873 и 8,445

Начинаем выполнять сложение поразрядно справа: 3 тысячные + 5 тысячных = 8 тысячных, записываем 8; 7 сотых + 4 сотых = 11 сотых, записываем 1, а 1 десятую запоминаем или надписываем над разрядом десятых. 8 десятых + 4 десятых = 12 десятых и добавляем 1 десятую (перенесенную из сотового разряда), получим 13 десятых или 1 единица и 3 десятых, записываем 3, а единицу запоминаем или надписываем над целыми единицами. Поскольку добавление дробной части завершено, ставим десятичную запятую перед цифрой 3 в сумме.

Добавляем целую часть, начиная с единиц: 2 + 8 + 1 (перенесенное из разряда десятых) = 11, записываем 1 и 1 десяток надписываем над разрядом десятков. В разряде десятков суммируем 1+1 (перенесенная из разряда единиц) + 0 (во втором слагаемом отсутствует разряд десяток) = 2. Получили сумму 21,318

Пример. Найти сумму десятичных дробей 3,562 и 42,3

В данном примере самое важное – правильно записать сложение в столбик, поскольку слагаемые имеют разное количество цифр в целой и дробной частях.

Правильная запись будет выглядеть:

На месте сотых и тысячных второго слагаемого для удобства можно записывать нули, ведь данные разряды отсутствуют.

Правило сложения натурального числа и десятичной дроби

Поскольку натуральное число не имеет десятичной запятой, для правильной записи действия сложения ставим десятичную запятую справа от натурального числа.

Пример. Найти сумму 6,72 и 25

В данном примере мы поставили запятую после числа 25 и дописали два нуля в разряде десятых и сотых.

Пример. Найти сумму числа 36 и десятичной дроби 5,42

По такому же принципу выполняется сложение трех и более десятичных дробей.

Задачи на сложение десятичных дробей

Задача. В первый день поездки Маркиян проехал на велосипеде 5,2 км, на второй день – 6,45 км. Сколько километров проехал парень за 2 дня?

Решение:

5,2 км + 6,45 км = 11, 65 км.

Кроме того, выполнить сложение можно следующим способом:

5 км 200 м + 6 км 450 м = 11 км 650 м = 11,65 км

Ответ: 11,65 км

Задача. Мама купила 3,8 кг мандарин и 5,25 кг апельсин. Сколько фруктов купила мама?

Чтобы найти вес фруктов, нужно прибавить вес мандарин и апельсин, то есть найти сумму 3,8 + 5,25

Вычитание десятичных дробей

Как и при сложении, вычитание десятичных дробей происходит по принципу вычитания натуральных чисел.

Алгоритм и правило вычитания десятичных дробей являются следующим:

1. Вычитаемое подписываем под уменьшаемым таким образом, чтобы десятичные запятые и соответствующие разряды находились друг под другом в одном вертикальном столбце. Если в компонентах вычитания разное количество цифр или отсутствует определенный разряд, справа можно дописать или мысленно прибавить нули.
2. Выполняем вычитание по разрядам, начиная справа. Десятичную запятую в разности ставим в том же вертикальном столбике, где она находится в уменьшаемом и вычитаемом.

Начнем с простых примеров на вычитание десятичных дробей.

Пример. Найти разницу десятичных дробей 8,96 и 3,42

Записываем вычитаемое 3,42 под уменьшаемым 8,96, чтобы запятая и соответствующие разряды были в одном вертикальном столбце.

Начинаем вычитание справа: 6 сотых – 2 сотых = 4 сотых, 9 десятых – 4 десятых = 5 десятых. Ставим десятичную запятую и переходим к вычитанию целых частей: 8 – 3 = 5. Следовательно, разница дробей составит: 5,54

Пример. Найти разницу десятичных дробей 21,156 и 8,482

Начинаем вычитание справа: 6 тысячных минус 2 тысячные равно 4 тысячные, от 5 сотых нельзя вычесть 8 сотых, поэтому берем 1 десятую из разряда десятых и раздробим ее, получив 15 сотых. Ставим точку (звезду) над цифрой 1, чтобы не забыть о «заимствовании» 1 десятой. Поскольку мы забрали 1 десятую, в разряде десятых осталось 0, одалживаем из разряда целых 1 единицу, раздробим ее на десятые, выполним вычитание 10 десятых – 4 десятых = 6 десятых. Перед цифрой 6 в разности ставим запятую, ведь мы завершили вычитание дробной части. В разряде единиц вместо 1 у нас осталось 0 единиц, ведь 1 единицу мы одолжили разряду десятых. Поэтому одалживаем 1 десяток из разряда десяток и дробим его, получим 10 единиц – 8 единиц = 2 единицы. В разряде десяток уменьшаемого остается 2 – 1 = 1 десяток, вычитаемый не содержит разряда десяток, поэтому в разность записываем 1 десяток.

Таким образом, 21,156 – 8,482 = 12,674

Пример. Найти разницу десятичных дробей 41,4 и 7,257

Поскольку уменьшаемое содержит 1 цифру после запятой, а вычитатель – 3 цифры, то для удобства вычитания допишем два нуля к уменьшаемому справа. После этого выполним вычитание: 41,400-7,257.

Пример. Найти разницу дробей 11,3 и 4,128 двумя способами – как вычитание десятичных дробей и как вычитание обыкновенных дробей.

Сначала запишем десятичные дроби в виде обыкновенных:

Выполним вычитание обыкновенных дробей

Превратим обыкновенную дробь в десятичную

Вычтем десятичные дроби:

На этом примере мы видим, что отнимать десятичные дроби намного проще и быстрее, чем обыкновенные.

Задачи на вычитание десятичных дробей. Примеры

Задача. Папа купил конфеты и фрукты. За фрукты он заплатил 114,8 грн., а за конфеты – 71,35 грн. На сколько конфеты дешевле фруктов?

Решение. Чтобы найти, на сколько цукерки дешевле, нужно выполнить вычитание:

Выполнить вычитание также удобно в столбик:

Ответ: конфеты дешевле фруктов на 43,45 грн.

Задача. В первый день похода Игорь прошел 3,42 км, а на второй – всего 980 м. На сколько меньше парень прошел на второй день?

Решение:

 

Ответ: на второй день Игорь прошел на 2,44 км меньше, чем в первый

Математика. Десятичные дроби: сложение, вычитание, умножение.

Проводить расчеты с дробями, прямо скажем, довольно утомительно, особенно когда требуется складывать и вычитать дроби с разными знаменателями. Но если уж без дробей совсем нельзя обойтись, то, может быть, можно как-нибудь договориться о том, чтобы хотя бы знаменатели у них всегда были одинаковыми? Заманчивая идея, не правда ли? Конечно, универсального знаменателя на все случаи жизни подобрать не удастся, но некий порядок в знаменателях мы всё же можем навести. {-4}&\!\!\!\!=~\phantom{0}1{,}0009. \end{array}$

Замечание. Надо признаться, что запятая для этой роли подходит плохо. Как мы теперь будем отличать число $1{,}2$ от перечисления двух чисел, единицы и двойки: ${1, 2}$? Единственное отличие заключается в том, что в перечислении ${1, 2}$ после запятой стоит пробел, а в числе $1{,}2$ такого пробела нет. Но это, прямо скажем, не такое отличие, которое сразу бросается в глаза. Но такова традиция, получившая распространение в европейских странах, и нам придется ей следовать. Во избежание путаницы мы теперь будем использовать при перечислениях не запятую, а точку с запятой: ${1; 2}$. В англоязычной литературе и в языках программирования в качестве десятичного разделителя используют точку, что следует признать более удачным выбором.

Новый вид дробей, в написании которых используется запятая, называются десятичными — для того чтобы отличать их от дробей, с которыми мы имели дело ранее, называемых обыкновенными.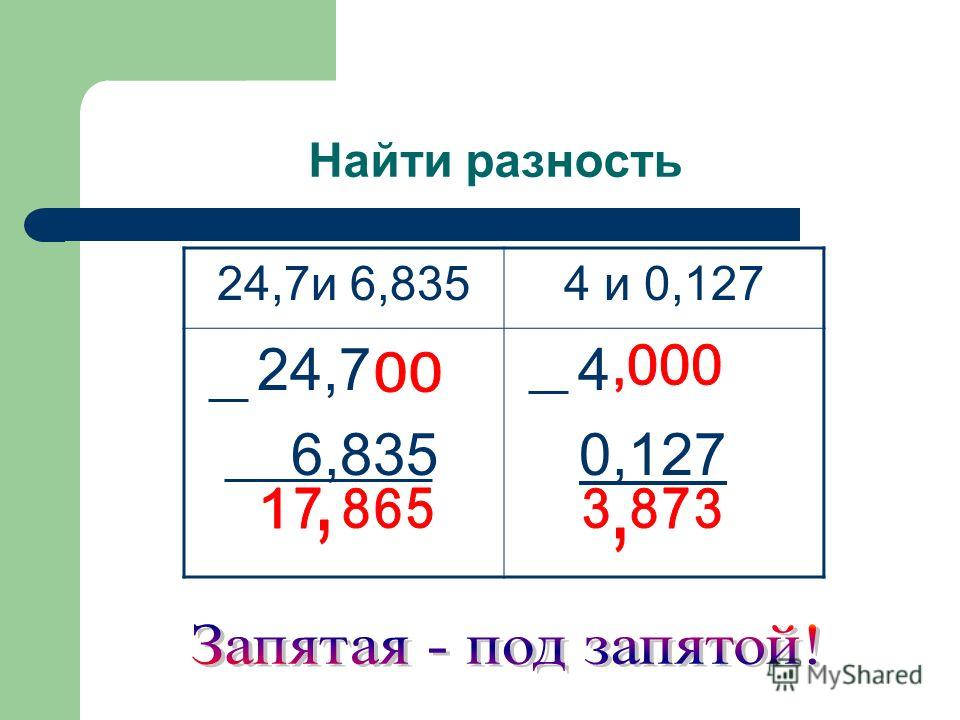 {-2}}$) и так далее.

Сложение и вычитание десятичных дробей делается очень просто, так как они легко приводятся к одному знаменателю. Например,

$\begin{align*} 0{,}432\phantom{.}\!&+ 0{,}1 =\\ 0{,}432\phantom{.}\!&+ 0{,}100 =\\ 0{,}532.\!&\phantom{+} \end{align*}$

Или же:

$\begin{align*} 0{,}432\phantom{.}\!&- 0{,}1 =\\ 0{,}432\phantom{.}\!&- 0{,}100 =\\ 0{,}332.\!&\phantom{+} \end{align*}$

Впрочем, вторые строчки в обеих этих цепочках равенств — совершенно лишние. Приписывать «недостающие» нули можно и мысленно. При сложении и вычитании столбиком запятые у чисел должны находиться одна под другой:

 

$+$	$3$	$2,$	$1$
		$0,$	$2$	$4$	$6$
	$3$	$2,$	$3$	$4$	$6$

Умножение десятичных дробей на $\boldsymbol{10^n}$

Мы уже знаем, что всякую десятичную дробь с дробной частью, не равной нулю, можно представить как

$a \cdot 10^k$,

где $a$ и $k$ — целые числа, причем ${k

$1234{,}0$. {k+n}$.

Если оба показателя степени, $k$ и $n$, больше нуля, то мы приходим к давно известному нам правилу умножения «круглых» чисел: мы отбрасываем поначалу все конечные нули, выполняем умножение без них, а потом к результату приписываем столько нулей, сколько мы раньше отбросили в обоих сомножителях вместе взятых. Например,

$3\underline{00} \cdot 5\underline{0} = 15\underline{000}$;

Это же правило формально действует и в том случае, когда один из показателей степени положителен, а другой равен нулю:

$3\underline{00} \cdot 5 = 15\underline{00}$;

Если оба показателя степени, $k$ и $n$, меньше нуля, то числа $x$ и $y$ являются дробными. Для них правило умножения таково: мы отбрасываем в их записи запятые, выполняем умножение как с целыми числами, а потом в ответе отделяем запятой столько знаков, сколько их было отделено в обоих сомножителях вместе взятых. Например,

$0{,}\underline{03} \cdot 0{,}\underline{5} = 0{,}\underline{015}$;

Это же правило формально действует и в том случае, когда один из показателей степени отрицателен, а другой равен нулю:

$0,\underline{03} \cdot 5 = 0{,}\underline{15}$;

Если же один из показателей степени положителен, а другой отрицателен, тогда мы имеем дело с умножением «круглого» числа на дробное. {k-n}}$. В случае когда $a$ делится нацело на $b$ результатом деления $x/y$ является десятичная дробь (возможно, с нулевой дробной частью).

Из «бесконечного» сборника типовых упражнений

Примечание: во всех приведенных ниже примерах деление сводится к делению нацело.

Примеры в два действия с десятичными дробями

Примеры в четыре действия с десятичными дробями

Примеры в семь действий с десятичными дробями («одноэтажная» запись)

То же («многоэтажная» запись, LaTeX)

Примеры с десятичными дробями на сокращение «большой» дроби («одноэтажная запись»)

То же («многоэтажная» запись, LaTeX)

 

Вычитание десятичных знаков – шаги, примеры и диаграммы

Некоторые параметры, с которыми мы сталкиваемся в повседневной жизни, такие как лекарства, химикаты или валюта, не являются целыми числами. Они десятичные. Однако мы все равно делаем расчеты с такими числами. Здесь мы научимся вычитать десятичные числа. Пример показан ниже, где мы будем вычитать десятичные дроби.

Шаги для вычитания десятичных знаков

Пример показан на диаграмме ниже, где мы используем три простых шага при вычитании двух одинаковых десятичных знаков (количество цифр после запятой одинаково).

Вычитание десятичных чисел

Давайте узнаем, как вычитать десятичное число из другого десятичного числа.

1. Запишите десятичные числа одно под другим в столбцы так, чтобы их десятичные знаки были выровнены.
2. Поставьте дополнительные нули на пустые места, чтобы сделать длину чисел одинаковой, если это необходимо.
3. Вычитание в столбцах как обычно.
4. Запишите результат ниже. Перетащите десятичную точку в ту же позицию в разнице.

Вычитание десятичных дробей с перегруппировкой

Вычтем два десятичных числа 5,64 и 3,89. Здесь 9 больше 4 на сотом месте. Таким образом, мы будем занимать 1 из 6 на десятом месте. Так что будем мысленно вычитать из 14 9 вместо 4. На схеме показан способ.

Вычитание десятичных дробей с перегруппировкой

Попробуем другое вычитание. Здесь мы будем делать перегруппировку мысленно, не записывая переносы.

Десятичное вычитание

Давайте научимся вычитать два разных десятичных знака.

Вычитание непохожих десятичных дробей

Здесь мы вычтем два непохожих десятичных дроби разной длины, используя все четыре шага, упомянутые выше в этой главе. Числа имеют разное количество знаков после запятой.

Вычитание в отличие от десятичных дробей

На приведенной выше диаграмме мы также мысленно задействовали техники перегруппировки, где это было необходимо. Всякий раз, когда в вычитаемых есть нули, мы перегруппировываем в соответствии с требованием.

Другой пример показан ниже, где большее десятичное число имеет меньшую длину. Меньшее десятичное число имеет больше цифр после запятой.

Как вычитать десятичные дроби

Нет необходимости ставить нули, если десятичные дроби имеют одинаковую длину, т. е. количество цифр после запятой одинаковое.

Вычитание целых чисел и десятичных дробей

Десятичная дробь из целого числа

Показан еще один пример вычитания десятичной дроби из целого числа.

Вычитание десятичных дробей из целых чисел

Целое число из десятичной дроби

Показан еще один пример, где мы вычитаем целое число из десятичной дроби.

Как вычитать десятичные дроби из целых чисел

Давайте научимся вычитать десятичные дроби с перегруппировкой на простом примере.

Решенные примеры

25,75 – 18,42

Решение:

Сначала запишем числа в столбцы с десятичными точками.
25,75 – 18,42
Длина двух чисел одинакова. Так что ноль не нужен.
Мы просто вычтем.
25,75 – 18,42
= 7,33

5,8 – 2,365

Решение:

Сначала запишем числа в столбцах с десятичной точкой.
Длина чисел не одинакова. Ставим нули там, где это необходимо.
5,800 – 2,365
= 3,435

15 – 12,42

Решение:

Сначала запишем числа в столбцы с выравниванием.
В целом числе 15 поставим нули везде, где это необходимо.
15.00 – 12.42
= 2,58

32,109 – 26

Решение:

Запишите числа столбиками, выровняв точки.
Ставим нули там, где это необходимо.
32.109 – 26.000
= 6.109

Вычитание десятичных дробей – Common Core: Математика для 5-го класса

All Common Core: Математические ресурсы для 5-го класса

7 Диагностических тестов 225 практических тестов Вопрос дня Карточки Учитесь по концепции

Common Core: Справка по математике для 5-го класса » Числа и операции в базе десяти » Сложение, вычитание, умножение и деление десятичных долей до сотых: CCSS.Math.Content.5.NBT.B.7 » Вычесть десятичные числа

Вычесть:

Возможные ответы:

Правильный ответ:

Объяснение:

Мы можем использовать десятичные числа, чтобы решить эту задачу. Давайте посмотрим, что представляют собой наши блоки с основанием 10, используя целое число 9.0003

Когда мы собираем это вместе, мы добавляем:

Чтобы использовать блоки с основанием 10 для сложения десятичных чисел, нам нужно немного по-другому думать о блоках с основанием 10. Мы думаем о блоке сотен как о едином целом. Десятки блокируются как десятые, потому что вам понадобится десять из них, чтобы составить одно целое. Наконец, блоки единиц представляют собой сотые доли, потому что вам потребуется сотня из них, чтобы составить одно целое: 

Давайте рассмотрим эту задачу:

Во-первых, мы хотим представить блоками четыре десятых и пять блоков сотых:

Далее мы хотим отнять , что означает отнять одну из десятых и одну из сотых:

Мы видим, что теперь у нас есть блоки из трех десятых и четырехсотых блоков, что означает, что наш ответ

Сообщить об ошибке

Вычесть следующее:

Возможные ответы:

Правильный ответ:

6

Объяснение:

Мы можем использовать десятичные числа, чтобы решить эту задачу. Давайте посмотрим, что представляют собой наши блоки с основанием 10, используя целое число 9.0003

Когда мы собираем это вместе, мы добавляем:

Чтобы использовать блоки с основанием 10 для сложения десятичных чисел, нам нужно немного по-другому думать о блоках с основанием 10. Мы думаем о блоке сотен как о едином целом. Десятки блокируются как десятые, потому что вам понадобится десять из них, чтобы составить одно целое. Наконец, блоки единиц представляют собой сотые доли, потому что вам потребуется сотня из них, чтобы составить одно целое:

Давайте рассмотрим эту задачу:

Во-первых, мы хотим представить блоками из пяти десятых и шестисотых блоков:

 

Далее мы хотим убрать , что означает отнять три десятых и пять сотых: ответ 

Сообщить об ошибке

Вычесть:

Возможные ответы:

Правильный ответ:

2

2

2 Объяснение:

Вычитание десятичных дробей аналогично вычитанию обычных чисел. Но вы должны помнить свой десятичный знак в своем ответе:

Отчет о ошибке

Вычитание:

Возможные ответы:

Правильный ответ:

Объяснение:

Вычитание десятичных дробей аналогично вычитанию обычных чисел. Но вы должны помнить свой десятичный знак в своем ответе:

        

Сообщить об ошибке

Вычесть:

Возможные ответы:

Правильный ответ:

Объяснение:

Вычитание десятичных дробей аналогично вычитанию обычных чисел. Но вы должны помнить о своем десятичном значении в своем ответе:

Отчет о ошибке

Вычитание:

Возможные ответы:

Правильный ответ:

6644. Объяснение:

Мы можем использовать десятичные числа, чтобы решить эту задачу. Давайте посмотрим, что представляют собой наши блоки с основанием 10, используя целое число 9.0003

Когда мы собираем это вместе, мы добавляем:

Чтобы использовать блоки с основанием 10 для сложения десятичных чисел, нам нужно немного по-другому думать о блоках с основанием 10. Мы думаем о блоке сотен как о едином целом. Десятки блокируются как десятые, потому что вам понадобится десять из них, чтобы составить одно целое. Наконец, блоки единиц представляют собой сотые доли, потому что вам потребуется сотня из них, чтобы составить одно целое:

Давайте рассмотрим эту задачу:

Во-первых, мы хотим представить блок с одной десятой и пятью сотыми:

Далее мы хотим убрать , что означает убрать ни одну из десятых и две сотые доли:

Мы видим, что теперь у нас есть блок с одной десятой и блок с тремя сотыми, что означает, что наш ответ

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Вычитание десятичных дробей аналогично вычитанию целых чисел. Но вы должны помнить свой десятичный знак в своем ответе.

 

Вы начинаете вычитать с крайнего правого числа, которое в данном случае является сотым разрядом. Вы не можете взять у кого-то, поэтому мы должны занять десятую часть с десятого места.  становится    , и мы переносим эту десятую в сотую, образуя а .

 

Затем вычтите десятые разряды.

Десятичная запятая будет перенесена вниз и останется между десятыми и единицами.

Последняя часть вычитания — разряд единиц.

Окончательный ответ

Сообщить об ошибке Объяснение:

Вычитание десятичных дробей аналогично вычитанию целых чисел. Но вы должны помнить свой десятичный знак в своем ответе.

Вы начинаете вычитать с крайнего правого числа, которое в данном случае является сотым разрядом.

Затем вычтите разряд десятых 

Десятичный разряд будет перенесен вниз и останется между разрядом десятых и разрядом единицы.

Последняя часть вычитания — разряд единиц.

Сообщить об ошибке

Возможные ответы:

Правильный ответ:

Объяснение:

Вычитание десятичных дробей аналогично вычитанию целых чисел. Но вы должны помнить свой десятичный знак в своем ответе.

 

Вы начинаете вычитать с крайнего правого числа, которое в данном случае является сотым разрядом.

Далее вычитаем десятые разряды.

Десятичная дробь будет перенесена вниз и останется между десятыми и единицами.

Последняя часть вычитания — разряд единиц.

Окончательный ответ:

Сообщить об ошибке Объяснение:

Вычитание десятичных дробей аналогично вычитанию целых чисел. Но вы должны помнить свой десятичный знак в своем ответе.

 

Вы начинаете вычитать с крайнего правого числа, которое в данном случае является сотым разрядом.