Умножить на 0,5. Умножение дроби на число. Умножение дробей на целое число.
- Альфашкола
- Статьи
- Как легко умножить на 0,5
В этой статье ты узнаешь как легко умножить любое число на \(0,5\), для этого тебе даже не понадобится калькулятор. \(0,5-\) это десятичная дробь, приведём её к виду обыкновенной дроби:
При умножении на \(0,5\) можно заменить умножением на \(\frac{1}{2}\). Обратная дробь одной пятой \(-2\) То есть для того чтобы умножить на \(0,5\) надо разделить на \(2.\) Легко не так ли?
Пример 1. Умножьте \(10\) на \(0,5\).
Решение: \(10*0,5=10*\frac{1}{2}=10:2=5\)
Ответ: \(5\).
Пример 2. Умножьте \(30\) на \(0,5\)
Умножьте \(30\) на \(0,5\)
Решение: \(30*0,5=30*\frac{1}{2}=30:2=15\)
Ответ: \(15\).
Пример 2. Умножьте \(34\) на \(0,5\).
Решение: \(34*0,5=34*\frac{1}{2}=34:2=17\)
Ответ: \(17\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Владлен Николаевич Березовский
Репетитор по математике
Стаж (лет)
Образование:
Национальная академия дополнительного профессионального образования
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому языку 5 — 11 классов. Моя фишка, как преподавателя в том, что своих учеников я погружаю в английскую речь сразу же с первого урока, уча их переводить выражения — от самых простых до сложных, с использованием одновременно нескольких времён, конструкций и прочего. Тем не менее, стараюсь не грузить грамматическими тестами. Тематика переводимых предложений, в своем большинстве, жизненная, поскольку простое лексическое наполнение намного легче запоминается. Практикую метод запоминания слов «Мнемотехника» с интервальными повторениями, что помогает человеку усвоить намного больше материала. Однако, за понятием «больше», приоритетом считаю «качественнее». Присоединяйтесь. Жду вас на своих интересных уроках!
Моя фишка, как преподавателя в том, что своих учеников я погружаю в английскую речь сразу же с первого урока, уча их переводить выражения — от самых простых до сложных, с использованием одновременно нескольких времён, конструкций и прочего. Тем не менее, стараюсь не грузить грамматическими тестами. Тематика переводимых предложений, в своем большинстве, жизненная, поскольку простое лексическое наполнение намного легче запоминается. Практикую метод запоминания слов «Мнемотехника» с интервальными повторениями, что помогает человеку усвоить намного больше материала. Однако, за понятием «больше», приоритетом считаю «качественнее». Присоединяйтесь. Жду вас на своих интересных уроках!
Улбала Жиентаевна Клетченко
Репетитор по математике
Стаж (лет)
Образование:
Челябинский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-9 классов.
Роман Михайлович Мясников
Репетитор по математике
Стаж (лет)
Образование:
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-9 классов. Докажу, что математика — это просто.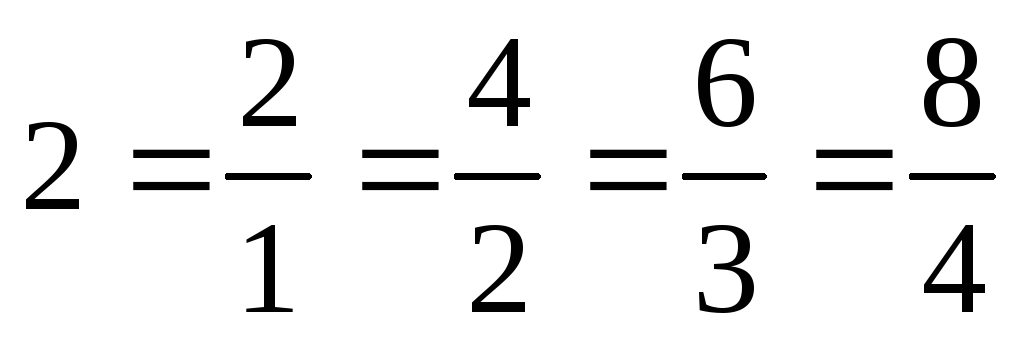
Похожие статьи
- НОК
- Экономический факультет МГУ: экзамены, ЕГЭ, проходной балл
- Факультет Мировой Экономики НИУ ВШЭ
- РУДН: прикладная математика и информатика (очно / заочно)
- Решение задач ЕГЭ на механический смысл производной
- Задачи на вклад в банк
- ЕГЭ по математике, профильный уровень. Неравенства
- ЕГЭ по математике, базовый уровень. Преобразование алгебраических выражений
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Как смешанное число умножить на число — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Как смешанное число умножить на число
Умножение смешанного числа на натуральное можно выполнять по-разному. Рассмотрим различные способы и выберем для себя, как смешанное число умножить на число натуральное удобнее.
Рассмотрим различные способы и выберем для себя, как смешанное число умножить на число натуральное удобнее.
1 способ
Чтобы умножить смешанное число на натуральное число, можно смешанное число превратить в неправильную дробь и умножить ее по правилу умножения дроби на число.
Например,
Решение:
Смешанное число переводим в неправильную дробь и умножаем по правилу умножения дроби на число (то есть числитель умножаем на это число, а знаменатель оставляем без изменений). Сокращаем 10 и 5 на 5 и умножаем получившиеся результаты. Поскольку в знаменателе единица, ответ — целое число.
Смешанное число записываем в виде неправильной дроби и умножаем. Сокращаем 3 и 9 на 3. Поскольку в результате получили неправильную дробь, выделяем целую часть.
Смешанное число превращаем в неправильную дробь и умножаем.
Из полученной неправильной дроби выделяем целую часть.
Смешанную дробь переводим в неправильную дробь. Сокращаем 11 и 11. Полученный результат — целое число.
2 способ — с помощью распределительного свойства умножения относительно сложения.
Чтобы умножить смешанное число на целое, можно умножить на это число отдельно целую часть, отдельно — дробную часть и полученные произведения сложить.
Рассмотрим, как смешанное число умножить на число целое с помощью распределительного свойства. Берем те же примеры.
Второй способ удобен в тех случаях, когда знаменатель дробной части и целое число можно сократить.
Теперь, когда мы рассмотрели оба способа, вы можете выбрать для себя, как смешанное число умножить на натуральное число вам удобнее, и в дальнейшем использовать любой из них.
Умножение дробей и смешанных чисел.
Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)
Умножение дробей и смешанных чисел. Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)
Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)
Главное замечание по теме от проекта DPVA.info: Дети часто путают действия с правильыми дробями (это такие дроби, где числитель меньше знаменателя) и со смешанными числами (состоящими из целой и дробной части).
Умножение правильных дробей и смешанных чисел на натуральное число: Чтобы умножить правильную дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения. Для того, чтобы умножить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее числитель умножить на это число, а знаменатель оставить без изменения, после чего выделить целую часть.
Умножение дробей : Чтобы умножить дробь на дробь, надо 1) найти произведение числителей и произведение знаменателей этих дробей.
2) первое произведение записать числителем, второе — знаменателем.
Умножение смешанных чисел: Для того, чтобы выплнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Деление правильных дробей и смешанных чисел на натуральное число: Чтобы разделить правильную дробь на натуральное число, надо ее знаменатель умножить на это число, а числитель оставить без изменения. Для того, чтобы разделить смешанное число на натуральное число, можно смешанное число предстваить в виде неправильной дроби, а затем ее знаменатель умножить на это число, а числитель оставить без изменения, после чего выделить целую часть.
Памятка: Взаимно обратные числа это числа, произведение которых равно 1. Например: дроби 71/17 и 17/71 взаимно обратны. Делимое — то, что делят. Делитель — то, на что делят.
Деление дробей: Для того, чтобы разделить одну дробь на другую, надо делимое умножить на число обратное делителю.
Деление смешанных чисел: Для того, чтобы выполнить деление смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом деления дробей.
Умножение дробей.
Навигация по странице:
Умножение дроби на натуральное число.
Определение.
Чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же.
Примеры умножения дроби на натуральное число
Пример 1.
Найти произведение дроби и натурального числа:
| 3 | · 2 | = | 3 · 2 | = | 6 |
| 7 | 7 | 7 |
Пример 2.
Найти произведение дроби и натурального числа:
| 1 | · 4 | = | 4 | = | 2·2 | = | 2 |
| 2 | 2 | 2 |
Умножение обыкновенных дробей.
Примеры умножения обыкновенных дробей
Пример 3.
Найти произведение двух дробей:
| 3 | · | 2 | = | 3 · 2 | = | 6 |
| 7 | 5 | 7 · 5 | 35 |
Пример 4.
Найти произведение двух дробей:
| 10 | · | 3 | = | 10 · 3 | = | 2 · 5 · 3 | = | 5 | = | 5 |
| 9 | 4 | 9 · 4 | 2 · 2 · 3 · 3 | 2 · 3 | 6 |
Смотрите также:
Умножение смешанных чисел.
Примеры умножения смешанных чисел
Пример 5. Найти произведение двух смешанных чисел:
| 2 | 1 | · | 1 | 2 | = | 2 · 2 + 1 | · | 1 · 3 + 2 | = | 5 | · | 5 | = | 5 · 5 | = | 25 | = | 6 · 4 + 1 | = 4 | 1 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 · 3 | 6 | 6 | 6 |
Пример 6.
Найти произведение смешанного числа и целого числа:
| 4 | 1 | · | 6 | = | 4 · 3 + 1 | · | 6 | = | 13 · 6 | = | 26 |
| 3 | 3 | 3 |
Пример 7.
Найти произведение смешаного числа и обыкновенной дроби:
| 2 | 1 | · | 3 | = | 2 · 7 + 1 | · | 3 | = | 15 | · | 3 | = | 15 · 3 | = | 3 · 3 | = | 9 | = | 7 + 2 | = 1 | 2 |
| 7 | 5 | 7 | 5 | 7 | 5 | 7 · 5 | 7 | 7 | 7 | 7 |
Смотрите также:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Смешанные числа (дроби), формулы и онлайн калькуляторы
Определение
Число, записанное в виде суммы натурального числа и правильной дроби, называется смешанным числом.
Рациональная дробь называется правильной, если ее числитель меньше знаменателя. Если же числитель дроби равен или больше ее знаменателя, то дробь называется неправильной.
Пример
$\frac{3}{5}$ — правильная дробь;
$\frac{5}{3}$ — неправильная дробь.
Правильная дробь меньше единицы, неправильная — больше или равна единице.
Слишком сложно?
Смешанные числа (дроби) не по зубам? Тебе ответит эксперт через 10 минут!
Если деление выполняется с остатком, то неполное частное дает искомое целое число, остаток стает числителем искомой дробной части, а знаменатель совпадает со знаменателем неправильной дроби.
Пример
Задание. Представить неправильную дробь $\frac{16}{5}$ в виде суммы целого числа и правильной дроби.
Решение. Делим 16 на 5, получаем частное 3 и остаток 1. То есть $\frac{16}{5}=3+\frac{1}{5}$
Данное выражение можно было получить и так:
$\frac{16}{5}=\frac{15+1}{5}=\frac{15}{5}+\frac{1}{5}=3+\frac{1}{5}$
Число, записанное в виде суммы натурального числа и правильной дроби, называется смешанным числом.
Пример
$\frac{16}{5}=3+\frac{1}{5}=3 \frac{1}{5}$
Число $3 \frac{1}{5}$ является смешанным числом или смешанной дробью.
Чтобы представить смешанное число в виде неправильной дроби, нужно умножить его целую часть на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.
Пример
Задание. Записать смешанное число $4 \frac{3}{5}$ в виде неправильной дроби.
Решение. $4 \frac{3}{5}=\frac{4 \cdot 5+3}{5}=\frac{23}{5}$
Читать следующую тему: десятичные дроби.
Умножение и деление смешанных чисел. Дроби. Умножение и деление дробей
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя.
Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.
Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.
Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.
Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.

Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.
Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.
Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.
Умножение дробей с разными знаменателями
Изначально стоит определить разновидности дробей :
- правильные;
- неправильные;
- смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.
При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:
a/ b * c/ d = a*c / b*d.
Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.
Стоит рассмотреть умножение дробей с разными знаменателями на примерах:
- 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
- 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.
Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:
1 4/ 11 =1 + 4/ 11.
Как происходит перемножение
Предлагается несколько примеров для рассмотрения.
2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.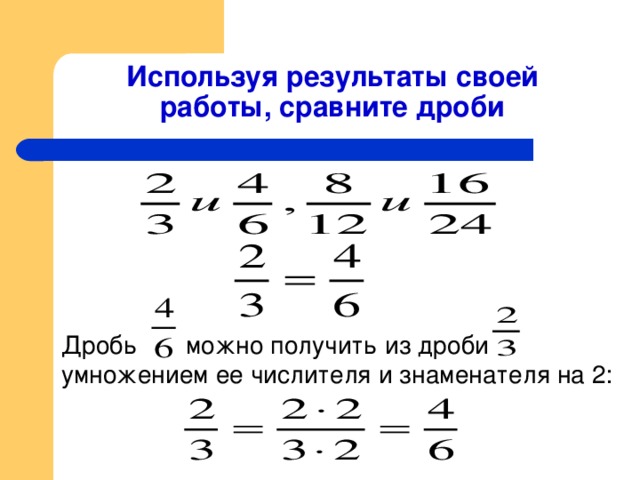
В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:
a * b/ c = a*b / c.
По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:
4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.
Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:
d * e/ f = e/ f: d.
Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.
Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:
1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.
В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:
a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.
Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».
Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.
В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.
Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.
В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.
Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
\(\bf \frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}\\\)
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.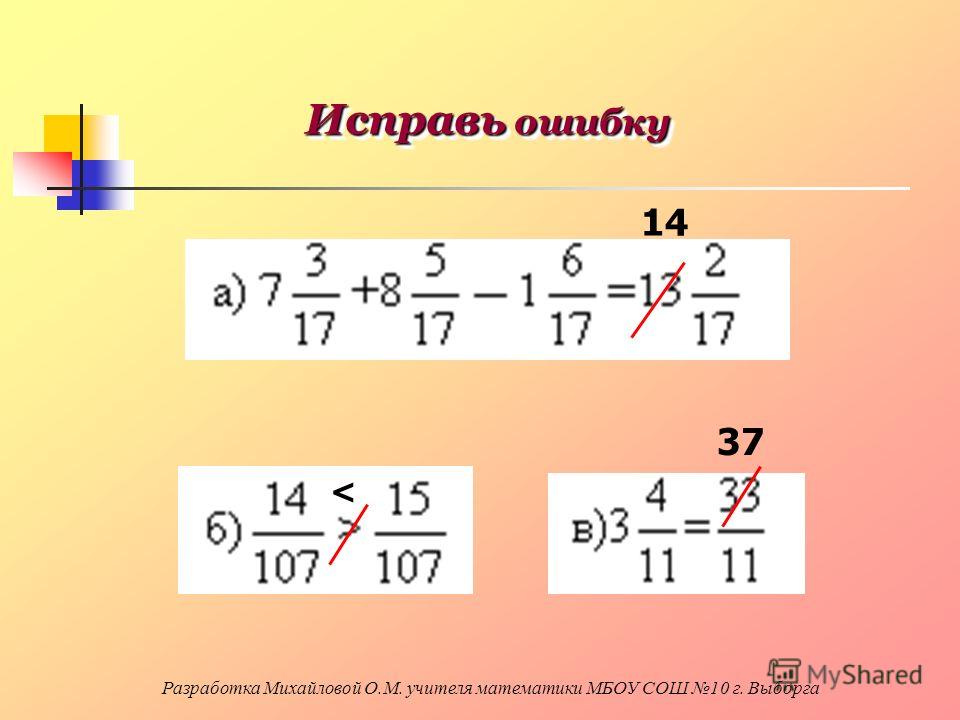
\(\frac{6}{7} \times \frac{2}{3} = \frac{6 \times 2}{7 \times 3} = \frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\)
Дробь \(\frac{12}{21} = \frac{4 \times 3}{7 \times 3} = \frac{4}{7}\\\) сократили на 3.
Умножение дроби на число.
Для начала вспомним правило, любое число можно представить в виде дроби \(\bf n = \frac{n}{1}\) .
Воспользуемся этим правилом при умножении.
\(5 \times \frac{4}{7} = \frac{5}{1} \times \frac{4}{7} = \frac{5 \times 4}{1 \times 7} = \frac{20}{7} = 2\frac{6}{7}\\\)
Неправильную дробь \(\frac{20}{7} = \frac{14 + 6}{7} = \frac{14}{7} + \frac{6}{7} = 2 + \frac{6}{7}= 2\frac{6}{7}\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
\(\frac{2}{5} \times 3 = \frac{2 \times 3}{5} = \frac{6}{5} = 1\frac{1}{5}\\\\\) \(\bf \frac{a}{b} \times c = \frac{a \times c}{b}\\\)
Умножение смешанных дробей.

Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Пример:
\(2\frac{1}{4} \times 3\frac{5}{6} = \frac{9}{4} \times \frac{23}{6} = \frac{9 \times 23}{4 \times 6} = \frac{3 \times \color{red} {3} \times 23}{4 \times 2 \times \color{red} {3}} = \frac{69}{8} = 8\frac{5}{8}\\\)
Умножение взаимно обратных дробей и чисел.
Дробь \(\bf \frac{a}{b}\) является обратной для дроби \(\bf \frac{b}{a}\), при условии a≠0,b≠0.
Дроби \(\bf \frac{a}{b}\) и \(\bf \frac{b}{a}\) называются взаимно обратными дробями. Произведение взаимно обратных дробей равно 1.
\(\bf \frac{a}{b} \times \frac{b}{a} = 1 \\\)
Пример:
\(\frac{5}{9} \times \frac{9}{5} = \frac{45}{45} = 1\\\)
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac{8}{9} \times \frac{7}{11}\) б) \(\frac{2}{15} \times \frac{10}{13}\)
Решение:
а) \(\frac{8}{9} \times \frac{7}{11} = \frac{8 \times 7}{9 \times 11} = \frac{56}{99}\\\\\)
б) \(\frac{2}{15} \times \frac{10}{13} = \frac{2 \times 10}{15 \times 13} = \frac{2 \times 2 \times \color{red} {5}}{3 \times \color{red} {5} \times 13} = \frac{4}{39}\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac{17}{23}\) б) \(\frac{2}{3} \times 11\)
Решение:
а) \(3 \times \frac{17}{23} = \frac{3}{1} \times \frac{17}{23} = \frac{3 \times 17}{1 \times 23} = \frac{51}{23} = 2\frac{5}{23}\\\\\)
б) \(\frac{2}{3} \times 11 = \frac{2}{3} \times \frac{11}{1} = \frac{2 \times 11}{3 \times 1} = \frac{22}{3} = 7\frac{1}{3}\)
Пример №3:
Напишите число обратное дроби \(\frac{1}{3}\)?
Ответ: \(\frac{3}{1} = 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac{104}{215} \times \frac{215}{104}\)
Решение:
а) \(\frac{104}{215} \times \frac{215}{104} = 1\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
Дробь \(\frac{2}{3}\) правильная, обратная ей дробь будет равна \(\frac{3}{2}\) – неправильная дробь. Ответ: нет.
б) практически при всех переборах дробей это условие не выполняется, но существуют некоторые числа, которые выполняют условие быть одновременно неправильной дробью. Например неправильная дробь \(\frac{3}{3}\) , обратная ей дробь равна \(\frac{3}{3}\). Получаем две неправильные дроби. Ответ: не всегда при определённых условиях, когда числитель и знаменатель равны.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac{3}{1}\), то обратная ей дробь будет \(\frac{1}{3}\). Дробь \(\frac{1}{3}\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac{1}{1} = \frac{1}{1} = 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac{4}{5}\) б) \(1\frac{1}{4} \times 3\frac{2}{7}\)
Решение:
а) \(4 \times 2\frac{4}{5} = \frac{4}{1} \times \frac{14}{5} = \frac{56}{5} = 11\frac{1}{5}\\\\ \)
б) \(1\frac{1}{4} \times 3\frac{2}{7} = \frac{5}{4} \times \frac{23}{7} = \frac{115}{28} = 4\frac{3}{7}\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Рассмотрим на примере. Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Возьмем смешанную дробь \(1\frac{1}{2}\), найдем для нее обратную дробь, для этого переведем ее в неправильную дробь \(1\frac{1}{2} = \frac{3}{2}\) . Обратная ей дробь будет равна \(\frac{2}{3}\) . Дробь \(\frac{2}{3}\) является правильной дробью. Ответ: взаимно обратные две дроби одновременно смешанными числами быть не могут.
Умножение дробей | Cubens
Умножение дробей
Умножение дроби на натуральное число
Чтобы умножить дробь на число, нужно числитель умножить на число, а знаменатель оставить без изменений.
Пример умножения дроби на натуральное число
Пример 1: Найти произведение дроби на натуральное число (умножить дробь на натуральное число): на
Ответ:
Умножение дробей с разными знаменателями
Чтобы добавить две обыкновенные дроби с разными знаменателями, нужно:
Пример умножения дробей с разными знаменателями
Пример 2: Перемножить две обыкновенные дроби с разными знаменателями: и
Ответ:
Умножение смешанных чисел
Чтобы умножить два смешанных числа, нужно:
Примеры сложения смешанных чисел
Пример 3: Умножить обыкновенную дробь на смешанное число: и
Ответ:
Пример 4 Умножить смешанное число на натуральное число: и
Ответ:
Пример 5: Умножить смешанные числа: и
Ответ:
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, следует:
Примеры умножения десятичных дробей
Пример 1: Перемножить дроби: 13,2 и 0,2.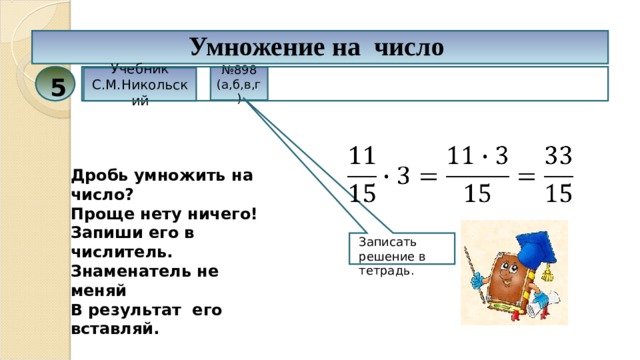
Выполнив умножение, не обращая внимания на запятые, получим: .
Отделим запятой справа столько цифр, сколько стоит после запятой в обоих множителях вместе, то есть две цифры .
Рассмотрим другие примеры умножения десятичных чисел:
Пример 2:
Пример 3:
Умножение десятичной дроби и натурального числа
Произведением десятичной дроби и натурального числа называют сумму слагаемых, каждый из которых равен данному десятичной дроби, а количество слагаемых равно этому натуральному числу.
Чтобыумножить десятичную дробь на натуральное число, нужно:
- умножить его на это число, не обращая внимания на запятую;
- в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.
Умножение десятичной дроби на 10, 100, 1000 и т.д.
Чтобыумножить десятичную дробь на 10,100,1000 и т.д., следует:
- надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.

Пример 4:
Если в результате получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.
Презентация «Умножение смешанных чисел» — математика, презентации
Классная работа.
Умножение
смешанных чисел
Цели обучения, которые достигаются на данном уроке
5.1.2.21
выполнять умножение обыкновенных дробей, смешанных чисел.
Цели урока:
закрепить умения применять правила умножения обыкновенных дробей при решении задач и примеров; активизировать деятельность учащихся через разнообразные виды самостоятельных работ .
Критерии оценивания
Учащиеся:
-знают правило умножения обыкновенных дробей;
-знают правило умножения смешанных чисел;
-умеют сокращать дроби;
-правильно применяют правила при умножении обыкновенных дробей и смешанных чисел;
-умеют записывать правильный ответ.
Домашнее задание
№ 581
Блиц опрос
1. Как умножить дробь на натуральное число?
2. По какому правилу выполняется умножение дробей?
3.Объясните, как выполнить умножение смешанных чисел ?
4. Какая дробь называется неправильной?
5. Как представить смешанное число в виде неправильной дроби?
6. Как сокращают дроби?
7. Какую дробь называют несократимой?
Математический диктант
13
27
8
3
28
1. Из дробей
Проверьте себя:
27
28
13
5
7
3
27
выпишите все правильные дроби.
28
7
Дескриптор: указывает правильные дроби .
41
23
12
6
9
2. Из дробей
6
12
41
41
23
11
12
5
12
23
5
выпишите все неправильные дроби.
Дескриптор: указывает неправильные дроби.
4
3. Представьте дробь в виде смешанного числа:
5
39
7
7
Дескриптор: записывает неправильную дробь в виде смешанного числа.
23
4. Представьте число в виде неправильной дроби:
5
3
4
5
Дескриптор:записывает смешанное число в виде неправильной дроби .
Монумент «Байтерек»
Групповая работа
Чтобы найти высоту этого сооружения, мы должны выполнить следующее задание:
Найти значение дроби:
Дескриптор:
-выполняет сложение смешанного и натурального чисел;
—переводит смешанное число в неправильную дробь;
-выполняет сокращение дробей при необходимости;
-находит произведение обыкновенных дробей.
В подземном уровне монумента «Байтерек» расположен аквариум, основание которого представляет собой часть кольца , образованного концентрическими окружностями. Найти объем аквариума:
Найти объем аквариума:
Дескриптор:
— переводит смешанное число в неправильную дробь;
-выполняет сокращение дробей при необходимости;
-находит произведение обыкновенных дробей.
Дворец Независимости
Здание Дворца Независимости состоит из трех этажей и имеет форму усеченной пирамиды. Найти протяженность первого этажа:
Дескриптор:
— переводит смешанное число в неправильную дробь;
-выполняет сокращение дробей при необходимости;
-находит произведение обыкновенных дробей.
Физкультминутка смешанное число – встаете, обыкновенная дробь – хлопаете, натуральное число – поднимаете руки вверх
1
90
23
Работа с учебником: №586
Применяя распределительное свойство умножения, вынесите общий множитель за скобки. Вычислите:
Дескриптор:
-находит общий множитель и выносит его за скобки;
-складывает либо вычитает дроби с одинаковыми знаменателями;
— складывает либо вычитает дроби с разными знаменателями;
-выполняет сокращение дробей при необходимости;
-находит произведение обыкновенных дробей.
Домашнее задание:
№ 587
повторить правила.
Рефлексия:
На стикерах записываем свои впечатления об уроке, пожелания и прикрепляем к макету «Байтерек».
( подсчитываем свои смайлики)
Как умножать дроби на смешанные числа
Перед умножением дробей вы конвертируете любые смешанные числа в неправильные дроби. Затем вы умножаете все дроби в своей задаче, упрощаете, если возможно, и, наконец, конвертируете обратно в смешанную числовую форму.
Преобразовать смешанное в неправильное
Чтобы преобразовать смешанное число в неправильную дробь, умножьте знаменатель на целое число и добавьте числитель. Например, в дроби 5 3/8 умножьте знаменатель 8 и целое число 5, затем добавьте числитель 3:
Ответ станет вашим новым числителем.Знаменатель останется прежним. В этом примере неправильная дробь — 43/8. Повторите этот процесс для всех смешанных чисел в вашем уравнении.
Умножение дробей
После преобразования всех дробей в неправильную форму дроби умножьте дроби, как в любой задаче умножения дробей. Сначала умножьте все числители. Затем умножьте все знаменатели. Запишите ответы в виде дробей, указав произведение числителя вверху и произведение знаменателя внизу.Для задачи 10/3 x 3/4 умножьте 10 и 3, чтобы найти числитель 30. Умножьте 3 и 4, чтобы найти знаменатель 12. Ваш ответ — 30/12.
Упростите ответ
Возможно, вам придется упростить ответ до самых низких значений. Упрощение на этом этапе упрощает обратное преобразование в смешанное число. Посмотрите на числитель и знаменатель и определите, может ли какое-либо число делиться на них обоих. Если они оба делятся более чем на одно число, ищите наибольшее число.В 48/18 оба числа делятся на 2, 3 и 6. Поскольку 6 является наибольшим, разделите оба числа на 6, чтобы получить 8/3.
Преобразовать обратно в смешанное число
Если ваш ответ является неправильной дробью, преобразуйте его обратно в смешанное число после упрощения. Вместо умножения на этот раз вы делите верхнее число на нижнее число. В неправильной дроби 32/5 разделите 32 на 5. Ваш ответ: 6 плюс остаток 2. 6 становится вашим целым числом. 2 становится числителем смешанного числа.Ваш знаменатель останется прежним, поэтому 32/5 станет 6 2/5.
Вместо умножения на этот раз вы делите верхнее число на нижнее число. В неправильной дроби 32/5 разделите 32 на 5. Ваш ответ: 6 плюс остаток 2. 6 становится вашим целым числом. 2 становится числителем смешанного числа.Ваш знаменатель останется прежним, поэтому 32/5 станет 6 2/5.
Обзор дробей
: смешанные числа и неправильные дроби
Purplemath
Если у вас большая вечеринка с пиццей и после этого у вас осталась одна пицца с ананасом и половина пиццы с анчоусами, вы бы сказали, что у вас есть «полторы» пиццы. «Полтора» — это стандартный разговорный английский способ выражения этого числа, он записывается как «1 1 / 2 ».Этот символ «1 1 / 2 » называется «смешанным числом», потому что он объединяет «обычное» число «1» с дробью « 1 / 2 ».
Хотя смешанные числа являются естественным выбором для разговорного английского языка (и поэтому хорошо подходят для ответов на словесные задачи), они, как правило, не самые простые дроби для вычисления. В алгебре вы почти всегда предпочитаете, чтобы дроби , а не были смешанными числами.
В алгебре вы почти всегда предпочитаете, чтобы дроби , а не были смешанными числами.
MathHelp.com
Вместо этого вы будете использовать так называемые «неправильные» дроби (также иногда называемые «вульгарными» дробями), когда верхнее число больше нижнего числа.
Стандартный способ преобразовать смешанное число в неправильную дробь — это умножить нижнее число на «обычное» число, добавить верхнее число и затем поместить его поверх исходного нижнего числа как новую дробь.
Например, чтобы преобразовать 1 1 / 2 в неправильную дробь, выполните следующие действия:
Я умножил нижние 2 на «обычную» 1, а затем добавил 1 сверху, получив 3. Затем я положил эти 3 поверх 2 снизу.
Чтобы выполнить преобразование, я умножу знаменатель (16) на целое число (2), чтобы получить 32.Затем я добавлю числитель (3) к 32, чтобы получить новый числитель (35). Знаменатель останется прежним; а именно, 16.
Для преобразования я умножу знаменатель (5) на целое число (6), чтобы получить 30. Затем я добавлю числитель (2) к 30, чтобы получить новый числитель (32).Знаменатель останется прежним; а именно 5.
Затем я добавлю числитель (2) к 30, чтобы получить новый числитель (32).Знаменатель останется прежним; а именно 5.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании процентов в десятичные числа. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Щелкните здесь, чтобы перейти прямо на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)
Чтобы перейти от неправильной дроби к смешанному числу, вы помните, что «дроби — это деление», и применяете длинное деление, чтобы найти частное целого числа плюс остаток. Другими словами, вы делите верхнее число на нижнее число. Все, что вы видите поверх символа деления, является частным и является частью вашего «обычного числа» смешанного числа. Каким бы ни был ваш остаток, положите это число поверх числа, на которое вы делили; это дробная часть вашего смешанного числа.
Примечание. Когда вы конвертируете неправильную дробь в смешанные числа, не продолжайте длинное деление на десятичные разряды , а не . Просто найдите частное и остаток. Тогда остановись.
Сначала я делаю полные числа, чтобы найти целую часть (являющуюся частным) и остаток:
Частное сверху — 11, так что это будет целая часть смешанного числа.Поскольку остаток равен 1, а я делю на 4, дробная часть будет равна 1 / 4 .
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании неправильной дроби в смешанное число. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Щелкнув «Нажмите, чтобы просмотреть шаги» на экране ответа виджета, вы перейдете на сайт Mathway для платного обновления.)
Эта процедура отлично работает с рациональными выражениями (полиномиальные дроби). Вы можете увидеть это в примере ниже (или же можете сразу перейти к умножению обычных дробей):
Вы можете увидеть это в примере ниже (или же можете сразу перейти к умножению обычных дробей):
Сначала проделайте длинное деление, чтобы найти правильную часть многочлена и остаток:
Полином сверху равен « x + 1», а остаток равен –1. Поскольку вы делите на « x + 2», дробная часть будет «(–1) / ( x + 2)»:
URL: https: // www.purplemath.com/modules/fraction2.htm
4.2: Правильные дроби, неправильные дроби и смешанные числа
Цели обучения
- уметь различать правильные дроби, неправильные дроби и смешанные числа
- уметь преобразовывать неправильную дробь в смешанное число
- уметь преобразовывать смешанное число в неправильную дробь
Теперь, когда мы знаем, что такое положительные дроби, мы рассматриваем три типа положительных дробей: правильные дроби, неправильные дроби и смешанные числа.
Положительные правильные дроби
Определение: положительная правильная фракция
Дроби, в которых целое число в числителе строго меньше целого числа в знаменателе, называются положительными собственными дробями .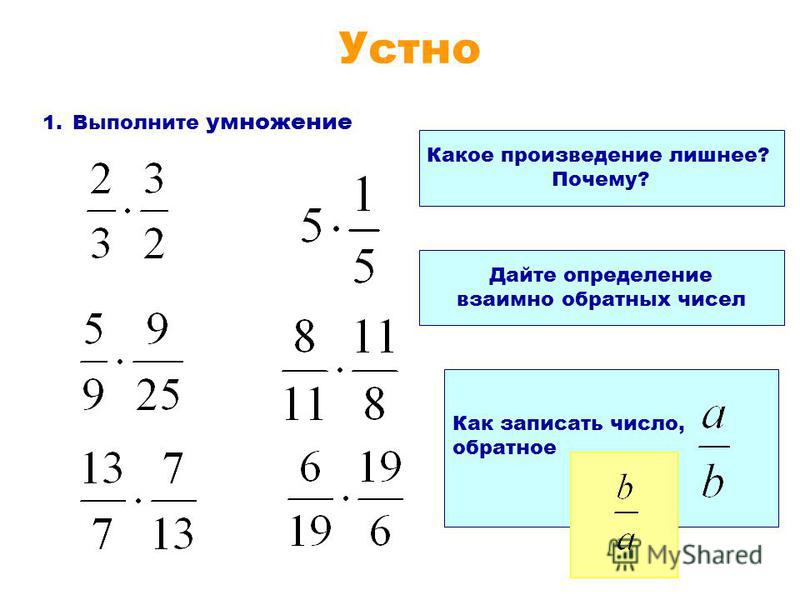 На числовой строке правильные дроби расположены в интервале от 0 до 1. Положительные собственные дроби всегда меньше единицы.
На числовой строке правильные дроби расположены в интервале от 0 до 1. Положительные собственные дроби всегда меньше единицы.
Закрашенный кружок в позиции 0 указывает, что 0 включен, в то время как белый кружок в позиции 1 указывает, что 1 не включен.
Некоторые примеры положительных собственных дробей:
\ (\ dfrac {1} {2} \), \ (\ dfrac {3} {5} \), \ (\ dfrac {20} {27} \) и \ (\ dfrac {106} {255 } \)
Обратите внимание, что \ (1
Положительные неправильные фракции
Определение: положительные неправильные дроби
Дроби, в которых целое число в числителе больше или равно целому числу в знаменателе, называются положительными неправильными дробями .В числовой строке неправильные дроби лежат справа (включительно) от 1. Положительные неправильные дроби всегда больше или равны 1.
Примеры положительных неправильных дробей:
\ (\ dfrac {3} {2} \), \ (\ dfrac {8} {5} \), \ (\ dfrac {4} {4} \) и \ (\ dfrac {105} {16 } \)
Обратите внимание, что \ (3 \ ge 2, 8 \ ge 5, 4 \ ge 4 \) и \ (105 \ ge 16 \).
Положительные смешанные числа
Определение: смешанные положительные числа
Число в форме \ (\ text {ненулевое целое число} + \ text {правильная дробь} \) называется положительным смешанным числом .Например, 2 \ (\ dfrac {3} {5} \) — смешанное число. В числовой строке смешанные числа расположены в интервале справа от (включительно) 1. Смешанные числа всегда больше или равны 1.
Связь положительных неправильных дробей и положительных смешанных чисел
Связь между неправильными дробями и смешанными числами подтверждается двумя фактами. Во-первых, неправильные дроби и смешанные числа расположены в одном интервале числовой строки.Второй факт, что смешанные числа представляют собой сумму натурального числа и дроби, можно увидеть, сделав следующие наблюдения.
Разделите все количество на 3 равные части.
Теперь рассмотрим следующие примеры, наблюдая за соответствующими заштрихованными областями.
В заштрихованной области две трети или \ (\ dfrac {2} {3} \).
\ (2 (\ dfrac {1} {3}) = \ dfrac {2} {3} \)
Есть 3 одной трети, или \ (\ dfrac {3} {3} \), или 1.
\ (3 (\ dfrac {1} {3}) = \ dfrac {3} {3} \) или 1
Таким образом,
\ (\ dfrac {3} {3} = 1 \)
Неправильная дробь = целое число.
Есть 4 1/3, или \ (\ dfrac {4} {3} \), или 1 и \ (\ dfrac {1} {3} \).
\ (4 (\ dfrac {1} {3}) = \ dfrac {4} {3} \) или 1 и \ (\ dfrac {1} {3} \)
Термины 1 и \ (\ dfrac {1} {3} \) могут быть представлены как \ (1 + \ dfrac {1} {3} \) или \ (1 \ dfrac {1} {3} \)
Таким образом,
\ (\ dfrac {4} {3} = 1 \ dfrac {1} {3}.\)
правильная дробь = смешанное число.
Есть 5 1/3, или \ (\ dfrac {5} {3} \), или 1 и \ (\ dfrac {2} {3} \).
\ (5 (\ dfrac {1} {3}) = \ dfrac {5} {3} \) или 1 и \ (\ dfrac {2} {3} \)
Термины 1 и \ (\ dfrac {2} {3} \) могут быть представлены как \ (1 + \ dfrac {2} {3} \) или \ (1 \ dfrac {2} {3} \).
Таким образом,
\ (\ dfrac {5} {3} = 1 \ dfrac {2} {3} \).
Неправильная дробь = смешанное число.
Есть 6 1/3, или \ (\ dfrac {6} {3} \), или 2.
\ (6 (\ dfrac {1} {3}) = \ dfrac {6} {3} = 2 \)
Таким образом,
\ (\ dfrac {6} {3} = 2 \)
Неправильная дробь = целое число.
Следующий важный факт проиллюстрирован предыдущими примерами.
Смешанное число = натуральное число + правильная дробь
Смешанное число — это сумма натурального числа и дроби. Смешанное число = (натуральное число) + (правильная дробь)
Например, \ (1 \ dfrac {1} {3} \) можно выразить как \ (1 + \ dfrac {1} {3} \). Дробь \ (5 \ dfrac {7} {8} \) может выражаться как \ (5 + \ dfrac {7} {8} \).
Важно отметить, что такое число, как \ (5 + \ dfrac {7} {8} \), не указывает на умножение , а не . Чтобы указать умножение, нам нужно будет использовать символ умножения (например, \ (\ cdot \))
Пример \ (\ PageIndex {1} \)
\ (5 \ dfrac {7} {8} \) означает \ (5 + \ dfrac {7} {8} \), а не \ (5 \ cdot \ dfrac {7} {8} \), что означает 5-кратное \ (\ dfrac {7} {8} \) или 5 умноженное на \ (\ dfrac {7} {8} \).
Таким образом, смешанные числа могут быть представлены неправильными дробями, а неправильные дроби могут быть представлены смешанными числами.
Преобразование неправильных дробей в смешанные числа
Чтобы понять, как можно преобразовать неправильную дробь в смешанное число, давайте рассмотрим дробь \ (\ dfrac {4} {3} \).
\ (\ begin {array} {rcl} {\ dfrac {4} {3}} & = & {\ underbrace {\ dfrac {1} {3} + \ dfrac {1} {3} + \ dfrac {1 } {3}} _ {1} + \ dfrac {1} {3}} \\ {} & = & {1 + \ dfrac {1} {3}} \\ {} & = & {1 \ dfrac { 1} {3}} \ end {array} \)
Мы можем проиллюстрировать процедуру преобразования неправильной дроби в смешанное число на этом примере.Однако преобразование проще, чем , выполняется делением числителя на знаменатель и использованием результата для записи смешанного числа.
Преобразование неправильной дроби в смешанное число
Чтобы преобразовать неправильную дробь в смешанное число, разделите числитель на знаменатель.
Целая часть смешанного числа является частным.
Дробная часть смешанного числа — это остаток от делителя (знаменателя неправильной дроби).
Образец набора A
Преобразует каждую неправильную дробь в соответствующее смешанное число.
\ (\ dfrac {5} {3} \) Разделить 5 на 3.
Решение
Несобственная дробь \ (\ dfrac {5} {3} = 1 \ dfrac {2} {3} \).
Образец набора A
\ (\ dfrac {46} {9} \) Разделим 46 на 9.
Решение
Несобственная дробь \ (\ dfrac {46} {9} = 5 \ dfrac {1} {9} \).
Образец набора A
\ (\ dfrac {83} {11} \) Разделим 83 на 11.
Решение
Несобственная дробь \ (\ dfrac {83} {11} = 7 \ dfrac {6} {11} \).
Образец набора A
\ (\ dfrac {104} {4} \) Разделим 104 на 4.
Решение
\ (\ dfrac {104} {4} = 26 \ dfrac {0} {4} = 26
Несобственная дробь \ (\ dfrac {104} {4} = 26 \).
Практический набор A
Преобразует каждую неправильную дробь в соответствующее смешанное число.
\ (\ dfrac {9} {2} \)
- Ответ
\ (4 \ dfrac {1} {2} \)
Практический набор A
\ (\ dfrac {11} {3} \)
- Ответ
\ (3 \ dfrac {2} {3} \)
Практический набор A
\ (\ dfrac {14} {11} \)
- Ответ
\ (1 \ dfrac {3} {11} \)
Практический набор A
\ (\ dfrac {31} {13} \)
- Ответ
\ (2 \ dfrac {5} {13} \)
Практический набор A
\ (\ dfrac {79} {4} \)
- Ответ
\ (19 \ dfrac {3} {4} \)
Практический набор A
\ (\ dfrac {496} {8} \)
- Ответ
62
Преобразование смешанных чисел в неправильные дроби
Чтобы понять, как преобразовать смешанное число в неправильную дробь, вспомним
смешанное число = (натуральное число) + (правильная дробь)
и рассмотрите следующую диаграмму.
Напомним, что умножение описывает повторное сложение.
Обратите внимание, что \ (\ dfrac {5} {3} \) можно получить из \ (1 \ dfrac {2} {3} \), используя умножение следующим образом.
Умножить: \ (3 \ cdot 1 = 3 \)
Складываем: \ (3 + 2 = 5 \). Поместите 5 над 3: \ (\ dfrac {5} {3} \)
В этом примере проиллюстрирована процедура преобразования смешанного числа в неправильную дробь.
Преобразование смешанного числа в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь,
Умножьте знаменатель дробной части смешанного числа на целую часть числа.
К этому произведению добавьте числитель дробной части.
Поместите этот результат над знаменателем дробной части.
Образец набора B
Преобразует каждое смешанное число в неправильную дробь.
\ (5 \ dfrac {7} {8} \)
Решение
- Умножить: \ (8 \ cdot 5 = 40 \)
- Складываем: \ (40 + 7 = 47 \)
- Поместите 47 над 8: \ (\ dfrac {47} {8} \)
Таким образом, \ (5 \ dfrac {7} {8} = \ dfrac {47} {8} \).
Образец набора B
\ (16 \ dfrac {2} {3} \)
Решение
- Умножить: \ (3 \ cdot 16 = 48 \).
- Складываем: \ (48 + 2 = 50 \)
- Поместите 50 над 3: \ (\ dfrac {50} {3} \)
Таким образом, \ (16 \ dfrac {2} {3} = \ dfrac {50} {3} \)
Практический набор A
Преобразует каждое смешанное число в соответствующую неправильную дробь.
\ (8 \ dfrac {1} {4} \)
- Ответ
\ (\ dfrac {33} {4} \)
Практический набор A
\ (5 \ dfrac {3} {5} \)
- Ответ
\ (\ dfrac {28} {5} \)
Практический набор A
\ (1 \ dfrac {4} {15} \)
- Ответ
\ (\ dfrac {19} {15} \)
Практический набор A
\ (12 \ dfrac {2} {7} \)
- Ответ
\ (\ dfrac {86} {7} \)
Упражнения
Для следующих 15 задач определите каждое выражение как правильную дробь, неправильную дробь или смешанное число.
Упражнение \ (\ PageIndex {1} \)
\ (\ dfrac {3} {2} \)
- Ответ
неправильная дробь
Упражнение \ (\ PageIndex {2} \)
\ (\ dfrac {4} {9} \)
Упражнение \ (\ PageIndex {3} \)
\ (\ dfrac {5} {7} \)
- Ответ
собственная фракция
Упражнение \ (\ PageIndex {4} \)
\ (\ dfrac {1} {8} \)
Упражнение \ (\ PageIndex {5} \)
\ (6 \ dfrac {1} {4} \)
- Ответ
смешанное число
Упражнение \ (\ PageIndex {6} \)
\ (\ dfrac {11} {8} \)
Упражнение \ (\ PageIndex {7} \)
\ (\ dfrac {1,001} {12} \)
- Ответ
неправильная дробь
Упражнение \ (\ PageIndex {8} \)
\ (191 \ dfrac {4} {5} \)
Упражнение \ (\ PageIndex {9} \)
\ (1 \ dfrac {9} {13} \)
- Ответ
смешанное число
Упражнение \ (\ PageIndex {10} \)
\ (31 \ dfrac {6} {7} \)
Упражнение \ (\ PageIndex {11} \)
\ (3 \ dfrac {1} {40} \)
- Ответ
смешанное число
Упражнение \ (\ PageIndex {12} \)
\ (\ dfrac {55} {12} \)
Упражнение \ (\ PageIndex {13} \)
\ (\ dfrac {0} {9} \)
- Ответ
собственная фракция
Упражнение \ (\ PageIndex {14} \)
\ (\ dfrac {8} {9} \)
Упражнение \ (\ PageIndex {15} \)
\ (101 \ dfrac {1} {11} \)
- Ответ
смешанное число
Для следующих 15 задач преобразуйте каждую неправильную дробь в соответствующее смешанное число.
Упражнение \ (\ PageIndex {16} \)
\ (\ dfrac {11} {6} \)
Упражнение \ (\ PageIndex {17} \)
\ (\ dfrac {14} {3} \)
- Ответ
\ (4 \ dfrac {2} {3} \)
Упражнение \ (\ PageIndex {18} \)
\ (\ dfrac {25} {4} \)
Упражнение \ (\ PageIndex {19} \)
\ (\ dfrac {35} {4} \)
- Ответ
\ (8 \ dfrac {3} {4} \)
Упражнение \ (\ PageIndex {20} \)
\ (\ dfrac {71} {8} \)
Упражнение \ (\ PageIndex {21} \)
\ (\ dfrac {63} {7} \)
- Ответ
9
Упражнение \ (\ PageIndex {22} \)
\ (\ dfrac {121} {11} \)
Упражнение \ (\ PageIndex {23} \)
\ (\ dfrac {165} {12} \)
- Ответ
\ (13 \ dfrac {9} {12} \) или \ (13 \ dfrac {3} {4} \)
Упражнение \ (\ PageIndex {24} \)
\ (\ dfrac {346} {15} \)
Упражнение \ (\ PageIndex {25} \)
\ (\ dfrac {5,000} {9} \)
- Ответ
\ (555 \ dfrac {5} {9} \)
Упражнение \ (\ PageIndex {26} \)
\ (\ dfrac {23} {5} \)
Упражнение \ (\ PageIndex {27} \)
\ (\ dfrac {73} {2} \)
- Ответ
\ (36 \ dfrac {1} {2} \)
Упражнение \ (\ PageIndex {28} \)
\ (\ dfrac {19} {2} \)
Упражнение \ (\ PageIndex {29} \)
\ (\ dfrac {316} {41} \)
- Ответ
\ (7 \ dfrac {29} {41} \)
Упражнение \ (\ PageIndex {30} \)
\ (\ dfrac {800} {3} \)
Для следующих 15 задач преобразуйте каждое из смешанных чисел в соответствующую неправильную дробь.
Упражнение \ (\ PageIndex {31} \)
\ (4 \ dfrac {1} {8} \)
- Ответ
\ (\ dfrac {33} {8} \)
Упражнение \ (\ PageIndex {32} \)
\ (1 \ dfrac {5} {12} \)
Упражнение \ (\ PageIndex {33} \)
\ (6 \ dfrac {7} {9} \)
- Ответ
\ (\ dfrac {61} {9} \)
Упражнение \ (\ PageIndex {34} \)
\ (15 \ dfrac {1} {4} \)
Упражнение \ (\ PageIndex {35} \)
\ (10 \ dfrac {5} {11} \)
- Ответ
\ (\ dfrac {115} {11} \)
Упражнение \ (\ PageIndex {36} \)
\ (15 \ dfrac {3} {10} \)
Упражнение \ (\ PageIndex {37} \)
\ (8 \ dfrac {2} {3} \)
- Ответ
\ (\ dfrac {26} {3} \)
Упражнение \ (\ PageIndex {38} \)
\ (4 \ dfrac {3} {4} \)
Упражнение \ (\ PageIndex {39} \)
\ (21 \ dfrac {2} {5} \)
- Ответ
\ (\ dfrac {107} {5} \)
Упражнение \ (\ PageIndex {40} \)
\ (17 \ dfrac {9} {10} \)
Упражнение \ (\ PageIndex {41} \)
\ (9 \ dfrac {20} {21} \)
- Ответ
\ (\ dfrac {209} {21} \)
Упражнение \ (\ PageIndex {42} \)
\ (5 \ dfrac {1} {16} \)
Упражнение \ (\ PageIndex {43} \)
\ (90 \ dfrac {1} {100} \)
- Ответ
\ (\ dfrac {9001} {100} \)
Упражнение \ (\ PageIndex {44} \)
\ (300 \ dfrac {43} {1,000} \)
Упражнение \ (\ PageIndex {45} \)
\ (19 \ dfrac {7} {8} \)
- Ответ
\ (\ dfrac {159} {8} \)
Упражнение \ (\ PageIndex {46} \)
Почему \ (0 \ dfrac {4} {7} \) не считается смешанным числом?
Подсказка:
См. Определение смешанного числа.
Определение смешанного числа.
Упражнение \ (\ PageIndex {47} \)
Почему 5 считается смешанным числом?
Подсказка:
См. Определение смешанного числа.
- Ответ
… потому что его можно записать как \ (5 \ dfrac {0} {n} \), где \ (n \) — любое положительное целое число.
Проблемы с калькулятором
Для следующих 8 задач используйте калькулятор для преобразования каждого смешанного числа в соответствующую неправильную дробь.
Упражнение \ (\ PageIndex {48} \)
\ (35 \ dfrac {11} {12} \)
Упражнение \ (\ PageIndex {49} \)
\ (27 \ dfrac {5} {61} \)
- Ответ
\ (\ dfrac {1,652} {61} \)
Упражнение \ (\ PageIndex {50} \)
\ (83 \ dfrac {40} {41} \)
Упражнение \ (\ PageIndex {51} \)
\ (105 \ dfrac {21} {23} \)
- Ответ
\ (\ dfrac {2,436} {23} \)
Упражнение \ (\ PageIndex {52} \)
\ (72 \ dfrac {605} {606} \)
Упражнение \ (\ PageIndex {53} \)
\ (816 \ dfrac {19} {25} \)
- Ответ
\ (\ dfrac {20,419} {25} \)
Упражнение \ (\ PageIndex {54} \)
\ (708 \ dfrac {42} {51} \)
Упражнение \ (\ PageIndex {55} \)
\ (6,012 \ dfrac {4,216} {8,117} \)
- Ответ
\ (\ dfrac {48,803,620} {8,117} \)
Упражнения для обзора
Упражнение \ (\ PageIndex {56} \)
Округлите 2 614 000 до ближайшей тысячи.
Упражнение \ (\ PageIndex {57} \)
Найдите товар. \ (1,004 \ cdot 1,005 \)
- Ответ
1 009 020
Упражнение \ (\ PageIndex {58} \)
Определите, делится ли 41826 на 2 и 3.
Упражнение \ (\ PageIndex {59} \)
Найдите наименьшее общее кратное 28 и 36.
- Ответ
252
Упражнение \ (\ PageIndex {60} \)
Укажите числитель и знаменатель дроби \ (\ dfrac {12} {19} \).
Как умножить дроби: 7 удивительных упражнений, которые стоит попробовать
Поздравляем! Вы преуспели в обучении умножению (за шесть простых шагов). Но теперь пришло время научить ваших учеников умножать дроби. Глубокие вдохи. Учителя и ученики могут утверждать, что эта концепция более устрашающая, чем переход от вычитания и сложения к умножению. К счастью, существуют стратегии, которые должны сделать обучение умножению дробей намного более легким для понимания — и мы составили их для вас в ясной форме. вырезать направляющую.В этой статье вы найдете: Но сначала напомню.
вырезать направляющую.В этой статье вы найдете: Но сначала напомню.
Что такое умножение? Проще говоря, умножение складывает одно и то же число снова и снова . Хорошие новости для ваших учеников: если они могут складывать, они могут умножать! Вместо того, чтобы писать 1 + 1 + 1 + 1 , есть гораздо более быстрый способ чтобы написать эту сложную задачу: 1 × 4 . Вот некоторые примеры: Кредит: класс мисс Жираф [/ caption] Помимо умножения целых чисел, вы также можете умножать на целые числа, десятичные дроби и, сегодня, дробей .
Определение трех типов дробей Дробь обычно состоит из двух частей:
- Числитель — верхнее число , которое указывает, сколько частей (целого) у вас есть.
- Знаменатель — нижнее число , которое относится к общему количеству частей, составляющих целое.
Предоставлено: Бретт Берри [/ caption]
1. Правильные дроби У правильной дроби числитель меньше знаменателя.Например: ½, ⅔, ¾, ⅘, ⅚
Правильные дроби У правильной дроби числитель меньше знаменателя.Например: ½, ⅔, ¾, ⅘, ⅚
2. Неправильные дроби Несмотря на схожую структуру, неправильная дробь имеет числитель больше , чем знаменатель. Примечание : когда числитель равен знаменателю, это считается «неправильным», потому что вы можете преобразовать его в целое число. То же правило применяется к неправильным дробям, таким как ²⁶⁄₁₃, которые при уменьшении становятся целыми (т. Е. Двумя). Например: ³⁄₂, ⁵⁄₃, ⁷⁄₆, ¹¹⁄₁₀, ⁸⁄₈
3. Смешанные дроби В отличие от первых двух, смешанная дробь состоит из правильной дроби и целого числа.Например: 3 ½, 7 ⅔, 2 ¾, 6 ⅘, 1 Хорошо, так что эти странные числа, как-то связанные с пиццей, существуют. Но каковы правила умножения дробей?
Как умножать дроби Хорошие вещи бывают тройками, в том числе три простых шага, которым должны следовать ваши ученики при обучении умножению дробей:
- Умножение числителей ( верхние числа )
- Умножение знаменателей ( нижние числа )
- При необходимости упростите или уменьшите дробь
И прежде чем ваши увлеченные ученики спросят, да — в отличие от сложения дробей, вы можете умножить две дроби на различных знаменателя . Давайте вместе рассмотрим пример! Модели площадей для дробного умножения Идеально подходящие для визуальных учеников в вашем классе, модель площадей эффективно иллюстрирует, как выглядит одна часть, умноженная на другую (или «из»). Как вы можете видеть на иллюстрации ниже, создавая модель площади умножить дробь легко:
Давайте вместе рассмотрим пример! Модели площадей для дробного умножения Идеально подходящие для визуальных учеников в вашем классе, модель площадей эффективно иллюстрирует, как выглядит одна часть, умноженная на другую (или «из»). Как вы можете видеть на иллюстрации ниже, создавая модель площади умножить дробь легко:
Фото: госпожаКоггинс [/ caption] Запоминающееся напоминание О! И если ваши ученики когда-нибудь забудут шаги, просто напомните им спеть эту песню:
Умножение дробей? Это не большая проблема.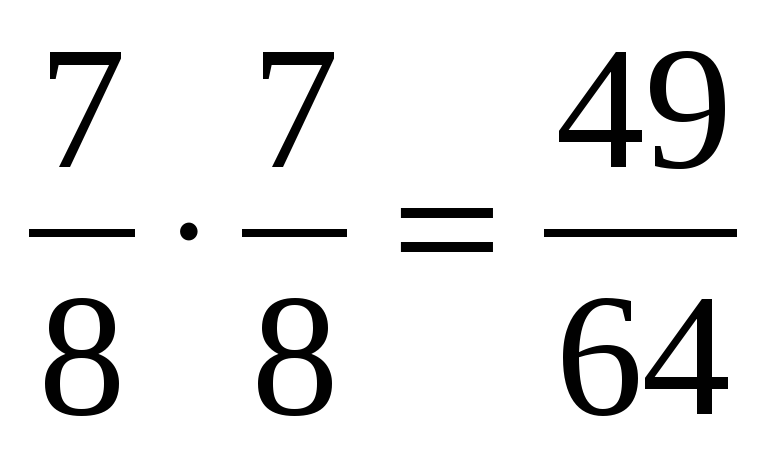 Сделайте верхний раз верхний поверх нижнего, умноженный на нижний. И прежде чем попрощаться, не забудьте упростить!
Сделайте верхний раз верхний поверх нижнего, умноженный на нижний. И прежде чем попрощаться, не забудьте упростить!
Умножение дробей на целые числа Предоставлено: Эрика Наджера [/ caption] Умножение целых чисел и дробей может озадачить ваших учеников.Почему? Потому что кажется, что есть только одна дробь вместо двух, но когда ученики учатся умножать дроби на целые числа, они могут переписывать их как дроби. Вместо 4, например, превратите его в дробь ⁴⁄₁. Теперь умножать проще и понятнее. Например, они могут переписать 2 × ⁵⁄₁₃:
Решить : 2 × ⁄₁₃ Перепишите целое число как дробь : ²⁄₁ × ⁵⁄₁₃ Умножение числителей : 2 × 5 = 10 Умножаем знаменатели : 1 × 13 = 13 Новая дробь : ¹⁰⁄₁₃
Примечание : Если учащиеся борются с целыми числами, объясните, что они могут рассматривать целое число как верхнее число, а нижнее число всегда равно единице.
Умножение неправильных дробей Предоставлено: Miranda Weenusk [/ caption] Вы умножаете неправильные дроби так же, как правильные. Однако иногда ученики могут получать неправильные дроби. Возьмем для примера эту задачу:
Решите : ⁄₃ × ⁷⁄₆ Умножение числителей : 5 × 7 = 35 Умножить знаменатели : 3 × 6 = 18 Новая дробь : ³⁵⁄₁₈
Если учащиеся знакомы со смешанными дробями, они могут изменить неправильную дробь на смешанную.В данном случае это смешанное число будет 1 ⁄₁₈, но вы можете узнать больше о смешанных числах ниже!
Умножение смешанных дробей Перед тем, как научить студентов умножать дроби на смешанные числа, им необходимо знать три шага:
- Преобразование любых смешанных дробей в неправильные дроби
- Умножение неправильных дробей
- Преобразование конечного произведения обратно в смешанное число
Чтобы выполнить первый шаг, научите своих учеников , как составить смешанное число «MAD» . Предоставлено: Fabulous Finch Facts [/ caption] Помните: смешанное число состоит из целого числа и правильной дроби. Чтобы завершить первый шаг и преобразовать смешанную дробь в неправильную, вам необходимо:
Предоставлено: Fabulous Finch Facts [/ caption] Помните: смешанное число состоит из целого числа и правильной дроби. Чтобы завершить первый шаг и преобразовать смешанную дробь в неправильную, вам необходимо:
- Найти новый числитель — Умножить целое число на знаменатель, затем прибавить к нему исходный числитель.
- Оставить тот же знаменатель — знаменатель не изменится.
Отсюда полезное сокращение:
M в конечном итоге A dd D enominator
Шаг второй, умножьте неправильные дроби, как мы проиллюстрировали перед этим разделом.Шаг третий: преобразуйте неправильную дробь обратно в смешанное число. Вот небольшой стишок, который поможет вашим ученикам запомнить, как это делать:
С неправильной дробью, дивизия — это действие!
Предоставлено: Heather’s Show and Tell [/ caption] Давайте воспользуемся примером, изображенным ранее: ⁄₅. Если деление — это действие, вам нужно разделить числитель (16) на знаменатель (5) и посмотреть, есть ли остаток.Пять переходит в 16 три раза равномерно , в сумме получается 15. Это означает, что целая числовая часть смешанного числа будет три . Но это не делится идеально, что вы можете увидеть по остатку от . . Таким образом, дробная часть смешанного числа — это остаток от знаменателя исходной дроби (⅕). Как выглядит смешанная дробь, это 3 ⅕ . Для более наглядного пошагового руководства по умножению смешанных чисел посмотрите это четырехминутное видео из Khan Academy:
Если деление — это действие, вам нужно разделить числитель (16) на знаменатель (5) и посмотреть, есть ли остаток.Пять переходит в 16 три раза равномерно , в сумме получается 15. Это означает, что целая числовая часть смешанного числа будет три . Но это не делится идеально, что вы можете увидеть по остатку от . . Таким образом, дробная часть смешанного числа — это остаток от знаменателя исходной дроби (⅕). Как выглядит смешанная дробь, это 3 ⅕ . Для более наглядного пошагового руководства по умножению смешанных чисел посмотрите это четырехминутное видео из Khan Academy:
И это то, что вам нужно знать при умножении дробей и смешанных чисел.
Две основные ошибки, которые делают ученики при умножении дробей Хотя некоторые ученики быстро усваивают уроки умножения дробей, другие могут столкнуться с трудностями при использовании этих новых концепций. Более ранние учителя улавливают эти заблуждения, тем скорее ученики смогут извлечь уроки и исправить свои ошибки. к практическому руководству What Works Clearinghouse Института педагогических наук «Разработка эффективных инструкций по дробям для от детского сада до 8-го класса» — это одни из наиболее распространенных заблуждений в отношении обучения умножению дробей.
Более ранние учителя улавливают эти заблуждения, тем скорее ученики смогут извлечь уроки и исправить свои ошибки. к практическому руководству What Works Clearinghouse Института педагогических наук «Разработка эффективных инструкций по дробям для от детского сада до 8-го класса» — это одни из наиболее распространенных заблуждений в отношении обучения умножению дробей.
1. Вера в то, что целые числа имеют тот же знаменатель, что и дроби в задаче Группа из восьми экспертов гида признала, что это заблуждение может побудить учащихся взять задачу, например, 4 -, и переписать ее как ⁄₈ — ⅜, так как неправильный ответ ⅛. При представлении смешанного числа учащиеся с таким неправильным представлением могут добавить целое число в числитель, как в ³¹⁄₃ × ⁶⁄₇ = (³⁄₃ + ⅓) × ⁶⁄₇ = ⁴ ⁄₃ × ⁶⁄₇ = ²⁴⁄₂₁. Помощь учащимся в понимании взаимосвязи между смешанными числами и неправильными дробями, а также в том, как переводить одно в другое, имеет решающее значение для работы с дробями.
Как помочь вашим ученикам Избегайте соблазна взорвать базовые уроки. Найдите время, которое нужно вашим ученикам, чтобы помочь им понять взаимосвязь между неправильными дробями и смешанными числами и как преобразовать их из одного в другое. Предоставлено: Once Upon a Creative Classroom [/ caption]
2. Оставить знаменатель неизменным Студенты могут совершить ошибку, забыв умножить равные знаменатели.Вероятно, это связано с тем, что вам не нужно касаться равных знаменателей при сложении дробей. Например, они могут увидеть ⅔ × ⅓ и неправильно ответить ⅔ вместо ²⁄₉.
Как помочь своим ученикам В практическом руководстве члены экспертной группы предлагают «объяснить концептуальную основу умножения дроби, используя единичные дроби (например, ½ × ½ = половина половины = ¼)». В частности, учителя могут показать что проблема ½ × ½ на самом деле спрашивает, что такое ½ от ½, что подразумевает, что произведение должно быть меньше любой умножаемой дроби. Вербализация этого заблуждения полезна, но особенно эффективна визуализация. Войдите во фракционную стену ! Дробные стены — отличный способ помочь ученикам увидеть, как в данном случае выглядит абстрактная половина из половины (то есть одна четверть).
Вербализация этого заблуждения полезна, но особенно эффективна визуализация. Войдите во фракционную стену ! Дробные стены — отличный способ помочь ученикам увидеть, как в данном случае выглядит абстрактная половина из половины (то есть одна четверть).
Поболтайте со своей суперзвездой @ rudstony4 в эти выходные! Посмотрите вместе на Стену дробей … спросите их о нашем ключевом словарном запасе … НОМЕР, ЗНАЧИТЕЛЬ, СМЕШАННОЕ ЧИСЛО, ЭКВИВАЛЕНТ … сколько они могут вам объяснить ?! #rudstonmaths рис.twitter.com/V02vgd9SYV
— Класс 4 (@ Rudstony4) 1 февраля 2019 г.
Теперь вы знаете о проблемах многих учеников, когда учились умножать дроби, что дальше? Давайте рассмотрим, как закрепить уроки дроби — и почему рабочие листы могут быть не лучшей стратегией.
Смерть рабочих листов? Доктор Стивен Камарата, специалист по развитию детей и отклонениям в развитии, считает, что естественное любопытство детей идет под откос. В эссе для Psychology Today он выразил недовольство предположением, что заполнение рабочих листов напрямую связано с улучшением обучения.
В эссе для Psychology Today он выразил недовольство предположением, что заполнение рабочих листов напрямую связано с улучшением обучения.
Но данные о достижениях в США по сравнению с остальным миром говорят об обратном. По иронии судьбы, по мере того, как все больше и больше листов вводятся в ранние и ранние классы и становятся все более механическими, скучная домашняя работа вынуждает развивающиеся умы, успеваемость учащихся в США продолжает снижаться.
Источник: Источник: NAEP Data Explorer, Национальный центр статистики образования [/ caption] Отчет Pew Center for Research указал на снижение и без того удручающих оценок достижений в США.Д-р Камарата подчеркнул:
Только 34% четвероклассников и 27% восьмиклассников были оценены как владеющие математикой в 2011 году, и этот показатель снизился до 33% для четвероклассников и 25% для восьмиклассников в 2015 году (последние данные Невозможно положительно повлиять на эти результаты: в настоящее время более двух третей четвероклассников и трое из четырех восьмиклассников не владеют математикой .Это 38-е место в мире.
Означает ли это, что школы должны обходиться без рабочих листов? Не обязательно.Корреляция — это не причинная связь. Фактически, многие учителя и ученики добились успеха с рабочими таблицами. Однако преподаватели должны понимать, что образование быстро меняется — от рабочих листов к классным технологиям. Итак, вот несколько творческих способов научить умножению дробей — без рабочих листов!
7 Интересные примеры для обучения студентов умножению дробей
1. Prodigy Prodigy — это бесплатная математическая игра по учебной программе, которую используют более миллиона учителей и 50 миллионов студентов по всему миру.Он предлагает материалы по всем основным математическим темам с 1-го по 8-й класс. Что касается умножения дробей, Prodigy может помочь студентам научиться:
- Умножать дробь на целое число
- Умножать две дроби
- Умножать целое число на пропущенную дробь
- Умножать две дроби с помощью словесных задач
- И многое другое
Практическое исследование 2018 года показало, что школы, использующие Prodigy, лучше справлялись со стандартизированными тестами и получили более высокие результаты. Игра Prodigy отправит ваших учеников в увлекательное и познавательное путешествие, вдохновленное фэнтези.
Игра Prodigy отправит ваших учеников в увлекательное и познавательное путешествие, вдохновленное фэнтези.
2. Перекидные дроби Предоставлено: MathFileFolderGames [/ caption] Для этого задания разделите учащихся на группы по четыре человека. Затем они разделятся на команды по два человека, одна из которых будет игроком А, а другая — игроком Б. Раздайте каждой группе колоду перетасованных карт (тузы = 1, валеты = 10, дамы = 11 и короли = 12).Как показано на картинке выше, каждый ученик рисует карточку с числителем (над карандашом) и карточку со знаменателем (под карандашом). Оба игрока А перепишут и умножат дроби на бумаге, а затем, если возможно, упростят произведение. После того, как они ответят, игроки Б. сделают то же самое. В зависимости от вашего расписания вы можете назначить всю колоду или дать учащимся таймер, чтобы они выполнили столько, сколько они могут. Попросите учащихся сдать свои листы ответов после задания для отметьте, или ответьте на 10+ вопросов вместе в классе. Примечание : Вы также можете назвать эту игру «Slam-it fractions», заменив карты и карандаши на домино.
Примечание : Вы также можете назвать эту игру «Slam-it fractions», заменив карты и карандаши на домино.
3. Умножение дроби BINGO Кредит: jimmiehomeschoolmom [/ caption] Каждый ученик получает заполненную дробью карточку бинго вместе с небольшими листами бумаги (или «фишками бинго») с соответствующими задачами умножения дробей. Когда вы говорите «ИДТИ», они могут начать решать каждую задачу одну за другой, закладывая фишку. поверх правильной дроби.Вам решать, хотите ли вы, чтобы они заполнили линию или всю карту бинго. Вы также можете выбрать, будут ли ответы на карточку бинго упрощенными. Для простоты вы можете дать всем одну и ту же карточку бинго с одинаковыми вопросами. Таким образом, вы сможете потом решать каждую проблему и вместе решать, как ее решать. Примечание : Вы можете использовать этот и последующие примеры в качестве формирующих оценок для оценки успеваемости учащихся и раннего выявления заблуждений.
4. Задачи со словами
Сегодняшние пятиклассники много размышляли над математикой. ❤️Они работали над концептуальным пониманием умножения дроби на целое число. @svmimac @BuenaVistaWCSD pic.twitter.com/Bg7HapJc82
— Келлианна Боксер (@BVBockser) 25 января 2019 г.
Задачи со словами — прекрасный способ сделать уроки математики актуальными для жизни ваших учеников. Умение умножать дроби может показаться им чуждым, но простая история может полностью изменить их точку зрения. примерно о дробях, а о математике в целом.Вот пример проблемы со словом:
У вас есть ½ пакета чипсов в шкафу, но вы съели ½ из них после обеда. Сколько всего пакета вы съели? (Не сводите свой ответ к минимуму.)
Конечно, это простой пример. Но секунду назад эта дробь была просто числом выше и ниже короткой линии.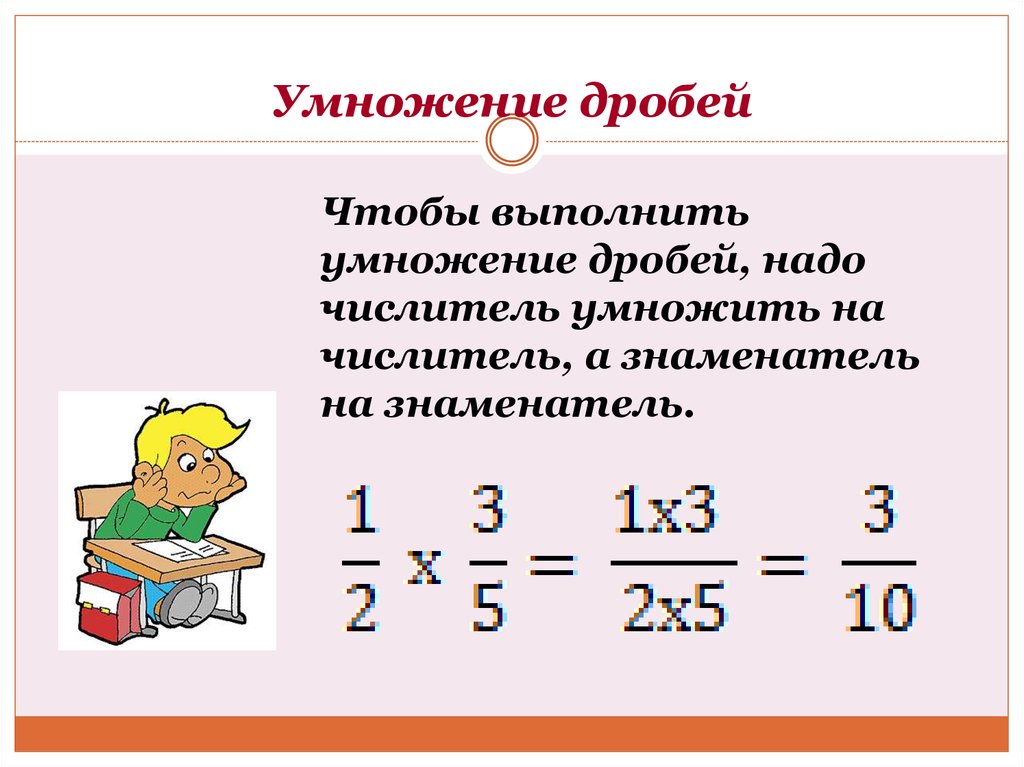 Однако теперь эта «повседневная» проблема слов сделала умножение дробей применимым к реальной жизни.
Однако теперь эта «повседневная» проблема слов сделала умножение дробей применимым к реальной жизни.
5. Война фракций Предоставлено: Шерри Фишер [/ caption] Это занятие для двух человек адаптировано из карточной игры «Война. Примечание : Многие учителя отходят от решения задач на основе скорости, потому что это не обязательно демонстрирует понимание учащимися. В вашем классе также могут быть дети, которые нервничают из-за необходимости быстро заниматься математикой и поэтому не успевают. Итак, лучше всего оценить свой класс, прежде чем играть в эту версию. Сидя бок о бок, у каждого ученика будет половина колоды карт фракций (которую вы можете скачать здесь). Перевернув стопку карт, каждый ученик одновременно вытянет карту .Первый ученик, правильно умноживший две дроби, добавляет эти карты в свою колоду. Студент побеждает, если в итоге у него в руке оказывается вся колода карт дробей или у него есть большинство карт в конце, например, 20. Более того, быстрое размышление на месте этого упражнения с дробями может помочь улучшить умственные математические навыки ваших учеников. В качестве альтернативы вы можете запустить версию этой игры, позволяющую всем играть против вас. Кому не нравится возможность перехитрить своего учителя !? Разделите ваш класс на пять групп.Вы перейдете в первую группу и встретитесь с одним вопросом, прежде чем переходить ко второй группе и так далее. Помните: цель этой версии не в том, чтобы отвечать перед учениками, а в том, чтобы помочь им развить умственные математические способности. Это позволяет ученикам отвечать коллективно, чтобы не выделять детей, которые могут испытывать трудности с умственной математикой.
Более того, быстрое размышление на месте этого упражнения с дробями может помочь улучшить умственные математические навыки ваших учеников. В качестве альтернативы вы можете запустить версию этой игры, позволяющую всем играть против вас. Кому не нравится возможность перехитрить своего учителя !? Разделите ваш класс на пять групп.Вы перейдете в первую группу и встретитесь с одним вопросом, прежде чем переходить ко второй группе и так далее. Помните: цель этой версии не в том, чтобы отвечать перед учениками, а в том, чтобы помочь им развить умственные математические способности. Это позволяет ученикам отвечать коллективно, чтобы не выделять детей, которые могут испытывать трудности с умственной математикой.
6. Пищевые фракции
Удивительно, как дети увлекаются, когда речь идет о ЕДА! Цель: найти любимый рецепт, а затем рассчитать каждый ингредиент для всех 90 пятиклассников! Им это нравится! Подлый способ попрактиковаться в умножении дробей.
— Эмили Либберт (@EmilyLibbert) 24 января 2019 г.😉 @Falcons_BMS #FalconsInFlight pic.twitter.com/M6Rg7zaXXQ
Дети любят поесть — это не секрет! Так почему бы не включить это в свой план урока? Учительница в твите выше заставила своих детей попрактиковаться в умножении дробей, преобразовывая рецепты вкусных блюд. Вы можете попросить каждого ученика выбрать свою любимую еду и умножить ингредиенты, чтобы накормить весь класс. Стимул тоже может помочь! Например, после того, как все переработали свою любимую еду, выберите безопасную закуску, которая понравится классу.Поднимите оригинальный рецепт. Теперь пусть ваши ученики поработают вместе над умножением ингредиентов, и, если они сделают это правильно, весь класс получит домашнюю (или купленную в магазине) выпечку!
7) Вымпел дробной части Предоставлено: Scaffolded Math [/ caption] Вырежьте для каждого ученика листы бумаги в форме ленты или треугольника. Вверху напишите «Я могу умножить…». Ниже вы будете включать:
Вверху напишите «Я могу умножить…». Ниже вы будете включать:
- Модель площади, иллюстрирующую дроби, которые они умножают
- Сама задача умножения (с местом для демонстрации их работы)
- Пробел в внизу: «Мой продукт сокращается до… »
После того, как каждый ученик завершит и украсит свой вымпел умножения дроби, приклейте его или скотчем к веревочке! Это активное учебное задание не только поможет научиться умножать дроби, но и придаст вашим ученикам уверенность. Это , их работают на стене, задача , которую они решили, и , все могут ее увидеть. Это будет выглядеть примерно так:
Хотите научить своих учеников умножать дроби сейчас? Надеемся на это! Умножение дробей может оказаться непростой задачей — выучить и научить . Надеемся, что тщательная разбивка по различным типам дробей, их умножение и увлекательное обучение помогут обогатить опыт преподавания и обучения ваших учеников, соответственно.
Надеемся, что тщательная разбивка по различным типам дробей, их умножение и увлекательное обучение помогут обогатить опыт преподавания и обучения ваших учеников, соответственно.
Читать далее: Как разделить дроби за 3 простых шага
Умножение смешанных чисел
(«Смешанные дроби» также называются «Смешанные числа»)
Для умножения смешанных дробей:
Пример: Что такое 1
3 8 × 3?
Подумайте о пицце.
| 1 3 8 — это 1 пицца и 3 восьмых другой пиццы. |
Сначала преобразуйте смешанную дробь (1 3 8 ) в неправильную дробь ( 11 8 ):
Разрежьте всю пиццу на восемь частей, а сколько у вас всего восьмых? 1 лот из 8 плюс 3 восьмых = 8 + 3 = 11 восьмых. |
Теперь умножьте это на 3:
И, наконец, преобразовать в смешанную дробь (только потому, что исходная дробь была в такой форме):
А вот как это выглядит в одной строке:
1 3 8 × 3 = 11 8 × 3 1 = 33 8 = 4 1 8
Другой пример: Что такое 1
1 2 × 2 1 5 ?
Выполните шаги, указанные выше:
- преобразовать в неправильные дроби
- Умножение дробей
- преобразовать результат обратно в смешанные дроби
Шаг за шагом:
Преобразовать смешанные дроби в неправильные:
1 1 2 = 2 2 + 1 2 = 3 2
2 1 5 = 10 5 + 1 5 = 11 5
Умножение дробей (верхние числа умножаются, нижние числа умножаются):
3 2 × 11 5 = 3 × 11 2 × 5 = 33 10
Преобразовать в смешанное число
33 10 = 3 3 10
Если вы умен, вы можете сделать все в одной строке, например:
1 1 2 × 2 1 5 = 3 2 × 11 5 = 33 10 = 3 3 10
Еще один пример: Что такое 3
1 4 × 3 1 3 ?
Преобразовать смешанные в неправильные дроби:
3 1 4 = 13 4
3 1 3 = 10 3
Умножить
13 4 × 10 3 = 130 12
Преобразовать в смешанное число:
130 12 = 10 10 12
И упростить:
10 10 12 = 10 5 6
Вот он в одной строке:
3 1 4 × 3 1 3 = 13 4 × 10 3 = 130 12 = 10 10 12 = 10 5 6
У этого есть минусы: что такое −1
5 9 × −2 1 7 ?
Преобразовать смешанные в неправильные дроби:
1 5 9 = 9 9 + 5 9 = 14 9
2 1 7 = 14 7 + 1 7 = 15 7
Затем умножьте неправильные дроби (Примечание: отрицательное умножение на отрицательное дает положительный результат) :
−14 9 × −15 7 = −14 × −15 9 × 7 = 210 63
Теперь мы можем упростить. Здесь мы используем два шага, сначала на 7 (21 и 63 оба кратны 7), затем снова на 3. Но это можно сделать за один шаг, разделив на 21:
Здесь мы используем два шага, сначала на 7 (21 и 63 оба кратны 7), затем снова на 3. Но это можно сделать за один шаг, разделив на 21:
.
210 63 = 30 9 = 10 3
Наконец преобразовать в смешанную дробь (потому что это был стиль вопроса):
10 3 = (9 + 1) 3 = 9 3 + 1 3 = 3 1 3
мдф
мдф
Умножение и деление дробей и смешанных чисел
Вот картинка, которая иллюстрирует правило умножения дроби
2/3 х 3/4 = 6/12
Результат можно выразить просто, сказав, что мы умножаем верхушки, а низы умножаем.Конечно, ответ может быть уменьшенный
6/12 = 1/2
Мы могли сказать, что 3 идут вверху и внизу, потому что
мы можем видеть 3, идущих вверх и вниз в
исходная проблема. Мы могли бы сначала умножить, а затем отменить, или мы могли бы
сначала отмените, а затем умножьте.
Мы могли бы сначала умножить, а затем отменить, или мы могли бы
сначала отмените, а затем умножьте.
Такой рисунок можно также использовать для иллюстрации умножения смешанные числа.
Есть два способа увидеть это. Следует заметить, что там это 1 x 2 = 2 в верхнем левом углу, есть 1 x 1/2 = 1/2 в вверху справа есть 2 x 3/4 = 6/4 = 11/2 внизу слева и 1/2 x 3/4 = 3/8 в правом нижнем углу.
Это показывает, что для правильного умножения смешанных чисел необходимо нужно использовать ФОЛЬГУ.Это также показывает, что, вероятно, проще выражайте числа, используя неправильные дроби.
и
т.
С
мы видим, что получаются те же результаты.
Если вы посмотрите на картинку, то в ней 8 маленьких прямоугольников. каждая квадратная единица, поэтому каждый прямоугольник равен 1/8 квадратной единицы.Там 5 прямоугольников, идущих по горизонтали на картинке, и 7 прямоугольников идем вертикально, так что на картинке 5×7 = 35/8.
Эти типы изображений нелегко адаптировать для использования в
иллюстрирующие деление на фракции. Есть такая картинка, которая
может использоваться для иллюстрации как умножения, так и деления
фракции.
Есть такая картинка, которая
может использоваться для иллюстрации как умножения, так и деления
фракции.
У нас есть 2 и 1/2 1 и 3/4, проложенные встык, выходя на 4 и 3/8.Это также изображение
, поскольку 4 и 3/8 делится на 2 и 1/2 равных части. На с другой стороны, поскольку мы видим, что 1 и 3/4 переходят в 4 и 3/8, 2 и 1/2 раз это также изображение
Как правило, один из этих типов изображений подходит для все три упражнения в семье. Настоящее преимущество использования этого типа изображения, иллюстрирующего этот тип проблемы разделения, с что-то вроде
Так как 3/4 меньше 1, требуется больше 3/4, чтобы перейти к 2 и 1/2, чем единицы.Это иллюстрирует, как, когда делитель меньше 1, ответ на проблему деления больше, чем дивиденды.
Мы могли бы также использовать идею пропущенных слагаемых, чтобы объяснить это. Подход неизвестного фактора довольно популярен. Рассмотрим следующая проблема.
Давайте притворимся, что не знаем ответа.
Ответ на проблему деления — это то, что нужно умножить
делитель на, чтобы получить дивиденд.
Возможно изготовление? который будет работать, а именно.
Это будет работать; потому что если мы проверим, мы увидим
Заключаем
С левой стороны приведенное выше уравнение вправо: инвертировать делитель и умножить.
После того, как учащиеся познакомятся с инвертированием и умножением техники, изображения могут быть использованы, чтобы проиллюстрировать, почему это работает. Вот изображение следующего упражнения.
Мы могли бы спросить, сколько раз 3/4 переходит в 21/2?
На картинке мы видим, что 3 2 и 1/2 выйдут на 2 и 1/4, остается 1/4, что составляет 1/3 от 3/4, чтобы получить 2 и 1/2.
На самом деле здесь проиллюстрирована техника инвертирования и умножения. Обратите внимание, что у нас есть 2 и 1/2 группы по 4, чтобы определить, сколько четверти там в 2 и 1/2, поэтому мы умножаем 2 и 1/2 на 4, и что эти кварталы делятся на группы по 3 человека, когда мы посмотреть, сколько 3/4 нужно выложить встык, чтобы получить 2 и 1/2.
В этом подходе 3/4 — это коэффициент, а ответ — 3 и
1/3 — это база. Можно нарисовать картину проблемы
где 3/4 — это база, а 31/3 — это ставка.
Можно нарисовать картину проблемы
где 3/4 — это база, а 31/3 — это ставка.
Если 3/4 — это основание, количество штук, то ответ будет ставка, сумма в одном штуке. Затем ответ находится над 1 на вторая числовая строка. На этой картинке мы видим, что мы деление на 3 и умножение на 4. На этом рисунке показан еще один объяснение.Переход от смешанных чисел к неправильным дробям и выразить задачу деления дробью
Затем умножьте верхнюю и нижнюю часть дроби на 4/3.
Нижняя часть отменяется, и мы получаем ответ
.
На картинке мы видим, что 2, 1/2 и 3/4 являются умножается на 4/3.Похоже, мы сначала делим на 3 и затем умножая на 4. Хотя учащиеся могут посчитать более естественным сначала умножьте на 4, а потом поделите на 3, картинка немного более неуклюже.
Если умножить 2 и 1/2 и 3/4 на 4, 2 и 1/2
x 4 = 10 и (3/4) x 4 = 3. На этом этапе мы видим, что 10 выстроились в линию.
над 3. Теперь, чтобы узнать, сколько в 1 штуке, нам нужно
разделить на 3.
Умножение дробей и смешанных чисел
Умножение дробей
Если у вашей подруги четверть пирога, а она дает вам половину, сколько пирога у вас есть? Или, другими словами, какая половина от четверти? Или, чтобы выразить это в математической записи:
1 /2 x 1 /4 =?
Чтобы получить ответ, умножьте числители (верхние части) и знаменатели (нижние части) по отдельности.
В этом случае сначала мы умножаем числители:
1 x 1 = 1
Затем мы умножаем знаменатели:
2 x 4 = 8
В ответе числитель равен 1, а знаменатель — 8. Другими словами:
1 /2 x 1 /4 = 1 x 1 /2 x 4 = 1 /8
У вас одна восьмая часть пирога.
Другой пример
Попробуем другой.
2 /9 x 3 /4 =?
Сначала умножаем числители:
2 x 3 = 6
Затем умножаем знаменатели:
9 x 4 = 36
В ответе числитель 6 и знаменатель 36. Другими словами:
Другими словами:
2 /9 x 3 /4 = 2 x 3 /9 x 4 = 6 /36
Это можно дополнительно уменьшить:
6 6 /36 6 = 1 /6
(См. Уменьшение дробей.)
Умножение смешанных чисел
Чтобы умножить два смешанных числа или смешанное число и дробь, сначала преобразуйте каждое смешанное число в дробь.
Умножение дробей.
Навигация по странице:
- Умножение дроби на натуральное число
- Умножение обыкновенных дробей
- Умножение смешанных чисел
Умножение дроби на натуральное число.
Определение.
Чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же.
Примеры умножения дроби на натуральное число
Пример 1.
Найти произведение дроби и натурального числа:
| 3 | · 2 | = | 3 · 2 | = | 6 |
| 7 | 7 | 7 |
Пример 2.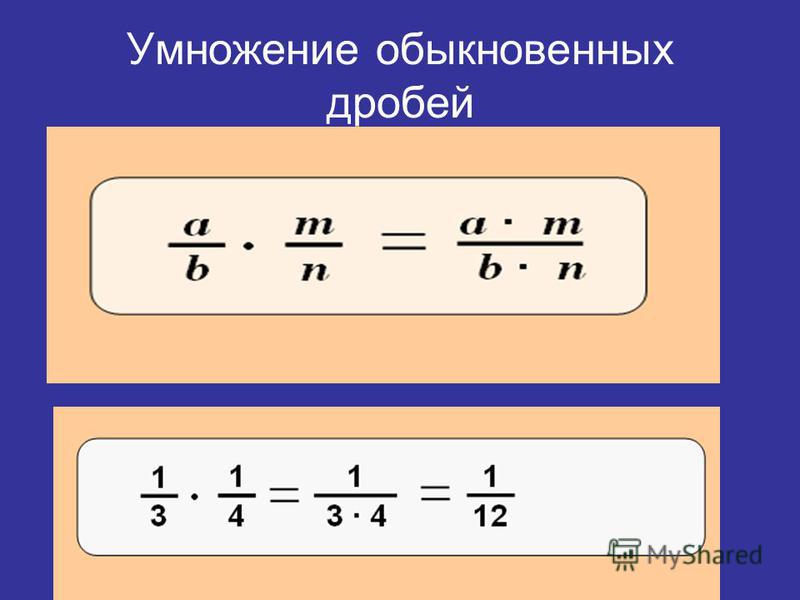
Найти произведение дроби и натурального числа:
| 1 | · 4 | = | 4 | = | 2·2 | = | 2 |
| 2 | 2 | 2 |
Умножение обыкновенных дробей.
Определение.
- Чтобы умножить две обыкновенные дроби, надо
- перемножить числители и знаменатели дробей;
- сократить полученную дробь.
Примеры умножения обыкновенных дробей
Пример 3.
Найти произведение двух дробей:
| 3 | · | 2 | = | 3 · 2 | = | 6 |
| 7 | 5 | 7 · 5 | 35 |
Пример 4.
Найти произведение двух дробей:
| 10 | · | 3 | = | 10 · 3 | = | 2 · 5 · 3 | = | 5 | = | 5 |
| 9 | 4 | 9 · 4 | 2 · 2 · 3 · 3 | 2 · 3 | 6 |
Смотрите также:
Онлайн калькулятор дробей
Упражнения на тему умножение двух обыкновенных дробей
Умножение смешанных чисел.

Определение.
- Чтобы умножить два смешанные числа, надо:
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- Если получилась неправильная дробь преобразовать неправильную дробь в смешанную.
Примеры умножения смешанных чисел
Пример 5.
Найти произведение двух смешанных чисел:
| 2 | 1 | · | 1 | 2 | = | 2 · 2 + 1 | · | 1 · 3 + 2 | = | 5 | · | 5 | = | 5 · 5 | = | 25 | = | 6 · 4 + 1 | = 4 | 1 |
| 2 | 3 | 2 | 3 | 2 | 3 | 2 · 3 | 6 | 6 | 6 |
Пример 6.
Найти произведение смешанного числа и целого числа:
| 4 | 1 | · | 6 | = | 4 · 3 + 1 | · | 6 | = | 13 · 6 | = | 26 |
| 3 | 3 | 3 |
Пример 7.
Найти произведение смешаного числа и обыкновенной дроби:
| 2 | 1 | · | 3 | = | 2 · 7 + 1 | · | 3 | = | 15 | · | 3 | = | 15 · 3 | = | 3 · 3 | = | 9 | = | 7 + 2 | = 1 | 2 |
| 7 | 5 | 7 | 5 | 7 | 5 | 7 · 5 | 7 | 7 | 7 | 7 |
Смотрите также:
Онлайн калькулятор дробей
Упражнения на тему умножение двух смешанных чисел
Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь
Онлайн калькуляторы дробей
Онлайн упражнения с дробями
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Умножение дробей с натуральными числами.
 Правило умножения дробей на целые числа
Правило умножения дробей на целые числаГлавная > Шторы > Умножение дробей с натуральными числами. Правило умножения дробей на целые числа
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Запишем сначала основное правило:
Определение 1
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a / b и c / d это можно выразить как a b · c d = a · c b · d .
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 1 4 и 1 8 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8 · 4 = 32).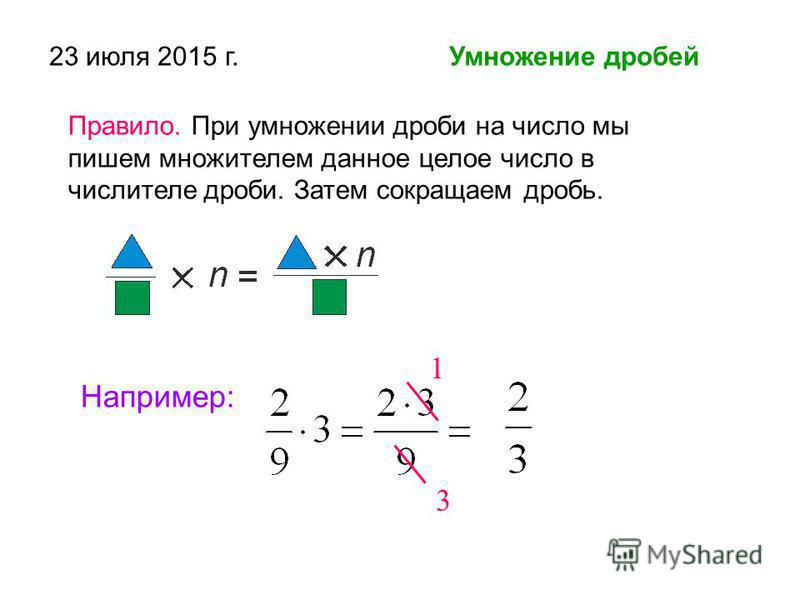 Соответственно, площадь каждого из них будет равна 1 32 от площади всей фигуры, т.е. 1 32 кв. единицы.
Соответственно, площадь каждого из них будет равна 1 32 от площади всей фигуры, т.е. 1 32 кв. единицы.
У нас получился закрашенный фрагмент со сторонами, равными 5 8 числовой единицы и 3 4 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 5 8 · 3 4 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15 , значит, общая площадь составляет 15 32 квадратных единиц.
Поскольку 5 · 3 = 15 и 8 · 4 = 32 , мы можем записать следующее равенство:
5 8 · 3 4 = 5 · 3 8 · 4 = 15 32
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как a b · c d = a · c b · d . Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Пример 1
Умножьте 7 11 на 9 8 .
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9 . У нас получилось 63 . Затем вычислим произведение знаменателей и получим: 11 · 8 = 88 . Составим их двух чисел ответ: 63 88 .
Все решение можно записать так:
7 11 · 9 8 = 7 · 9 11 · 8 = 63 88
Ответ: 7 11 · 9 8 = 63 88 .
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2
Вычислите произведение дробей 4 15 и 55 6 .
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
4 15 · 55 6 = 4 · 55 15 · 6 = 220 90
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10 .
Выполним сокращение дроби: 220 90 НОД (220 , 90) = 10 , 220 90 = 220: 10 90: 10 = 22 9 .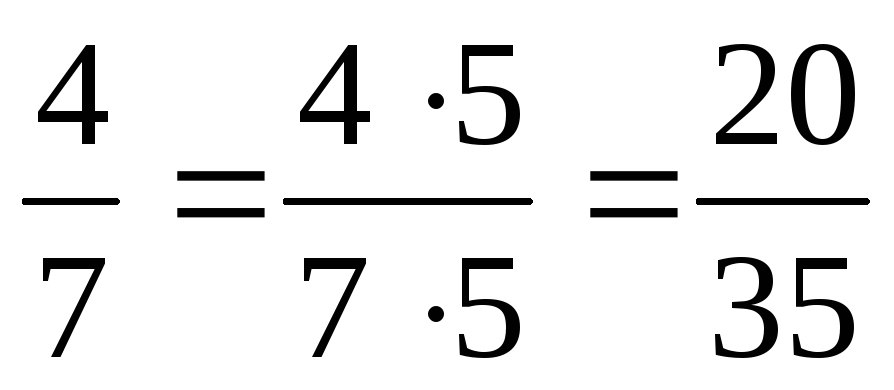 В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 22 9 = 2 4 9 .
В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 22 9 = 2 4 9 .
Ответ: 4 15 · 55 6 = 2 4 9 .
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a · c b · d . Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3
Вычислите произведение 4 15 · 55 6 .
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
4 15 · 55 6 = 4 · 55 15 · 6
Поскольку как 4 = 2 · 2 , 55 = 5 · 11 , 15 = 3 · 5 и 6 = 2 · 3 , значит, 4 · 55 15 · 6 = 2 · 2 · 5 · 11 3 · 5 · 2 · 3 .
2 · 11 3 · 3 = 22 9 = 2 4 9
Ответ : 4 15 · 55 6 = 2 4 9 .
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
a b · c d = c d · a b = a · c b · d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби a b на натуральное число n можно записать в виде формулы a b · n = a · n b .
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
a b · n = a b · n 1 = a · n b · 1 = a · n b
Поясним нашу мысль конкретными примерами.
Пример 4
Вычислите произведение 2 27 на 5 .
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10 . В силу правила, указанного выше, мы получим в результате 10 27 . Все решение приведено в этой записи:
2 27 · 5 = 2 · 5 27 = 10 27
Ответ: 2 27 · 5 = 10 27
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Пример 5
Условие: вычислите произведение 8 на 5 12 .
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 5 12 · 8 = 5 · 8 12 = 40 12 . Итоговая дробь имеет признаки делимости на 2 , поэтому нам нужно выполнить ее сокращение:
НОК (40 , 12) = 4 , значит, 40 12 = 40: 4 12: 4 = 10 3
Теперь нам осталось только выделить целую часть и записать готовый ответ: 10 3 = 3 1 3 .
В этой записи можно видеть все решение целиком: 5 12 · 8 = 5 · 8 12 = 40 12 = 10 3 = 3 1 3 .
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 5 12 · 8 = 3 1 3 .
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
a b · n = n · a b = a · n b
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6
Умножьте четыре обыкновенные дроби 1 20 , 12 5 , 3 7 и 5 8 .
Решение: для начала сделаем запись произведения. У нас получится 1 20 · 12 5 · 3 7 · 5 8 . Нам надо перемножить между собой все числители и все знаменатели: 1 20 · 12 5 · 3 7 · 5 8 = 1 · 12 · 3 · 5 20 · 5 · 7 · 8 .
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 1 · (2 · 2 · 3) · 3 · 5 2 · 2 · 5 · 5 · 7 (2 · 2 · 2) = 3 · 3 5 · 7 · 2 · 2 · 2 = 9 280
Ответ: 1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 9 280 .
Пример 7
Перемножьте 5 чисел 7 8 · 12 · 8 · 5 36 · 10 .
Решение
Для удобства мы можем сгруппировать дробь 7 8 с числом 8 , а число 12 с дробью 5 36 , поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
7 8 · 12 · 8 · 5 36 · 10 = 7 8 · 8 · 12 · 5 36 · 10 = 7 · 8 8 · 12 · 5 36 · 10 = 7 1 · 2 · 2 · 3 · 5 2 · 2 · 3 · 3 · 10 = = 7 · 5 3 · 10 = 7 · 5 · 10 3 = 350 3 = 116 2 3
Ответ: 7 8 · 12 · 8 · 5 36 · 10 = 116 2 3 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.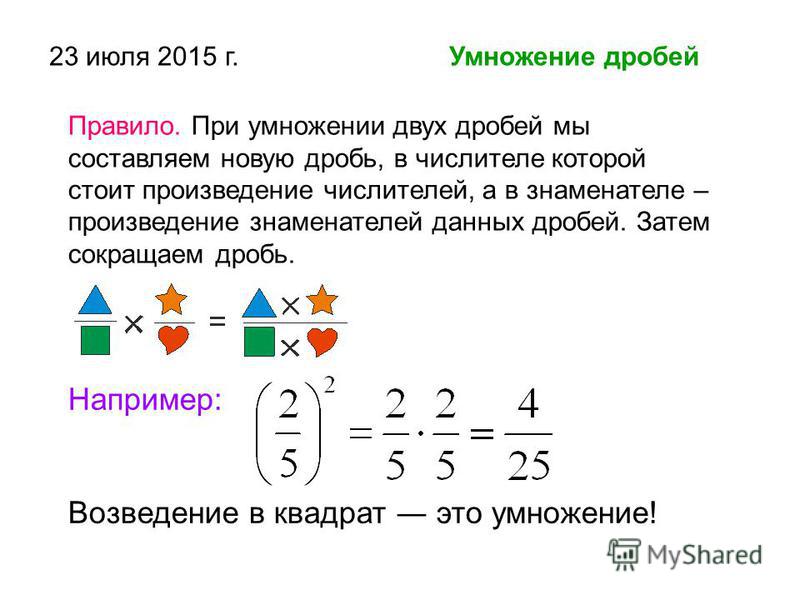
Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.
Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.
Обозначение:
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.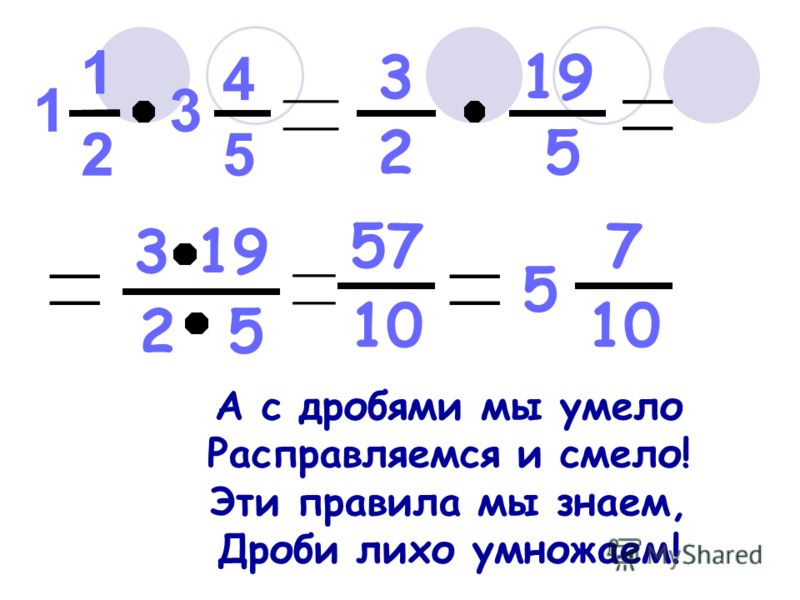
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
- Плюс на минус дает минус;
- Минус на минус дает плюс.
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
- Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
- Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Так делать нельзя!
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Правильное решение:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято.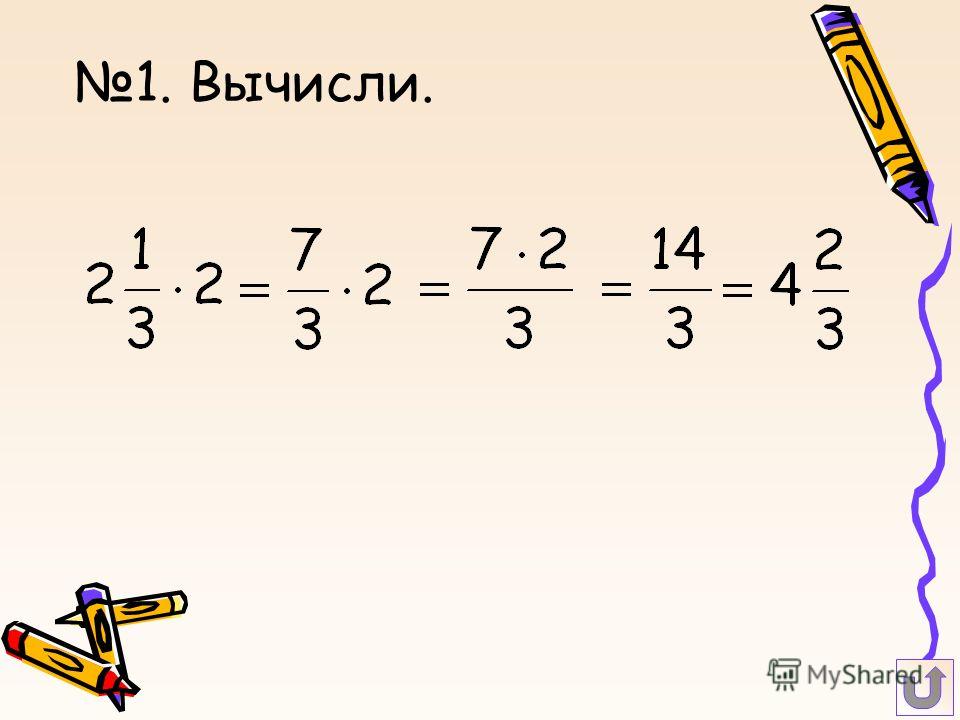 Числитель пишется над дробной чертой, знаменатель — под ней.
Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.
Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
Умножение обыкновенных дробей
Рассмотрим пример.
Пусть на тарелке лежит $\frac{1}{3}$ часть яблока. Нужно найти $\frac{1}{2}$ часть от нее. Необходимая часть является результатом умножения дробей $\frac{1}{3}$ и $\frac{1}{2}$. Результат умножения двух обыкновенных дробей — это обыкновенная дробь.
Умножение двух обыкновенных дробей
Правило умножения обыкновенных дробей:
Результатом умножения дроби на дробь является дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей:
Пример 1
Выполнить умножение обыкновенных дробей $\frac{3}{7}$ и $\frac{5}{11}$.
Решение.
Воспользуемся правилом умножения обыкновенных дробей:
\[\frac{3}{7}\cdot \frac{5}{11}=\frac{3\cdot 5}{7\cdot 11}=\frac{15}{77}\]
Ответ: $\frac{15}{77}$
Если в результате умножения дробей получается сократимая или неправильная дробь, то нужно ее упростить.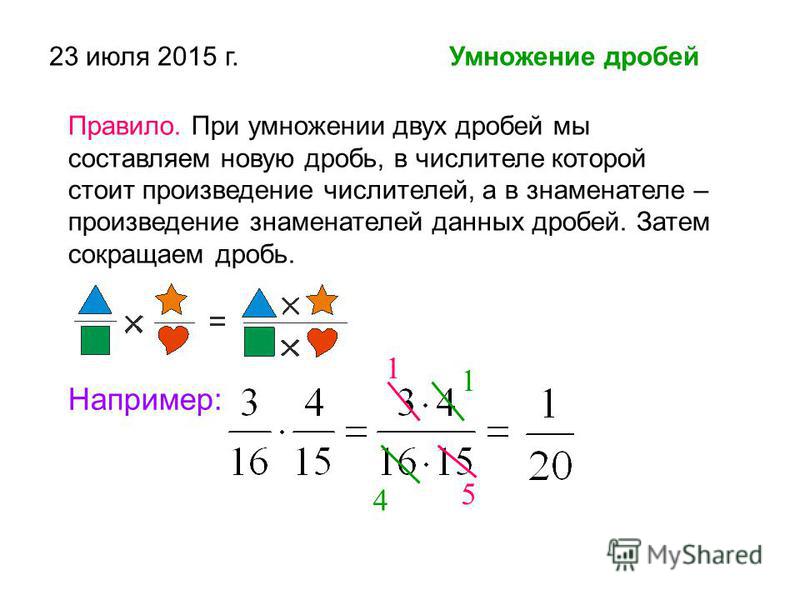
Пример 2
Выполнить умножение дробей $\frac{3}{8}$ и $\frac{1}{9}$.
Решение.
Используем правило умножения обыкновенных дробей:
\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}\]
В результате получили сократимую дробь (по признаку деления на $3$. Числитель и знаменатель дроби разделим на $3$, получим:
\[\frac{3}{72}=\frac{3:3}{72:3}=\frac{1}{24}\]
Краткое решение:
\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}=\frac{1}{24}\]
Ответ: $\frac{1}{24}.$
При умножении дробей сокращать числители и знаменатели можно до нахождения их произведения. При этом числитель и знаменатель дроби раскладывается на простые множители, после чего сокращаются повторяющиеся множители и находится результат.
Пример 3
Вычислить произведение дробей $\frac{6}{75}$ и $\frac{15}{24}$.
Решение.
Воспользуемся формулой умножения обыкновенных дробей:
\[\frac{6}{75}\cdot \frac{15}{24}=\frac{6\cdot 15}{75\cdot 24}\]
Очевидно, что в числителе и знаменателе есть числа, которые попарно можно сократить на числа $2$, $3$ и $5$. Разложим числитель и знаменатель на простые множители и произведем сокращение:
Разложим числитель и знаменатель на простые множители и произведем сокращение:
\[\frac{6\cdot 15}{75\cdot 24}=\frac{2\cdot 3\cdot 3\cdot 5}{3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3}=\frac{1}{5\cdot 2\cdot 2}=\frac{1}{20}\]
Ответ: $\frac{1}{20}.$
При умножении дробей можно применять переместительный закон:
Умножение обыкновенной дроби на натуральное число
Правило умножения обыкновенной дроби на натуральное число:
Результатом умножения дроби на натуральное число является дробь, у которой числитель равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби:
где $\frac{a}{b}$ — обыкновенная дробь, $n$ — натуральное число.
Пример 4
Выполнить умножение дроби $\frac{3}{17}$ на $4$.
Решение.
Воспользуемся правилом умножения обыкновенной дроби на натуральное число:
\[\frac{3}{17}\cdot 4=\frac{3\cdot 4}{17}=\frac{12}{17}\]
Ответ: $\frac{12}{17}. $
$
Не стоит забывать о проверке результата умножения на сократимость дроби или на неправильную дробь.
Пример 5
Умножить дробь $\frac{7}{15}$ на число $3$.
Решение.
Воспользуемся формулой умножения дроби на натуральное число:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}\]
По признаку деления на число $3$} можно определить, что полученную дробь можно сократить:
\[\frac{21}{15}=\frac{21:3}{15:3}=\frac{7}{5}\]
В результате получили неправильную дробь. Выделим целую часть:
\[\frac{7}{5}=1\frac{2}{5}\]
Краткое решение:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}=\frac{7}{5}=1\frac{2}{5}\]
Сократить дроби также можно было заменой чисел в числителе и знаменателе на их разложения на простые множители. В таком случае решение можно было записать так:
\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{7\cdot 3}{3\cdot 5}=\frac{7}{5}=1\frac{2}{5}\]
Ответ: $1\frac{2}{5}. $
$
При умножении дроби на натуральное число можно использовать переместительный закон:
Деление обыкновенных дробей
Операция деления является обратной к умножению и результатом ее является дробь, на которую нужно умножить известную дробь чтобы получить известное произведение двух дробей.
Деление двух обыкновенных дробей
Правило деления обыкновенных дробей: Очевидно, что числитель и знаменатель полученной дроби можно разложить на простые множители и произвести сокращение:
\[\frac{8\cdot 35}{15\cdot 12}=\frac{2\cdot 2\cdot 2\cdot 5\cdot 7}{3\cdot 5\cdot 2\cdot 2\cdot 3}=\frac{2\cdot 7}{3\cdot 3}=\frac{14}{9}\]
В результате получили неправильную дробь, из которой выделим целую часть:
\[\frac{14}{9}=1\frac{5}{9}\]
Ответ: $1\frac{5}{9}.$
Содержание урока
Сложение дробей с одинаковыми знаменателямиСложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями
- Сложение дробей с разными знаменателями
Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3 . Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить без изменения;
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1 . Сложим дроби и
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2.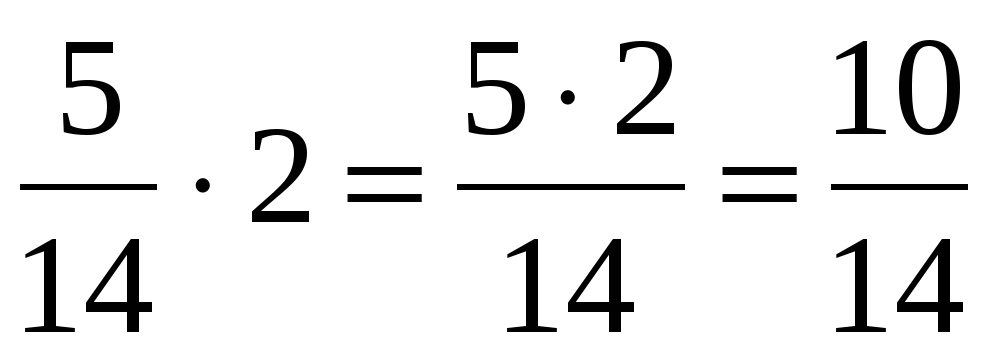 Найти значение выражения .
Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателямиВычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку.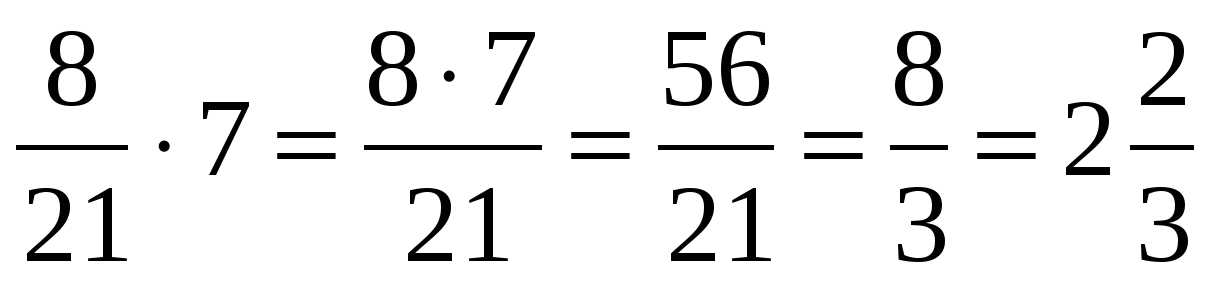 Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.
Пример 1 . Умножить дробь на число 1 .
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2 . Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Умножение дробейЧтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Найти значение выражения .
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2 . Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дробиЛюбое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числаСейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих.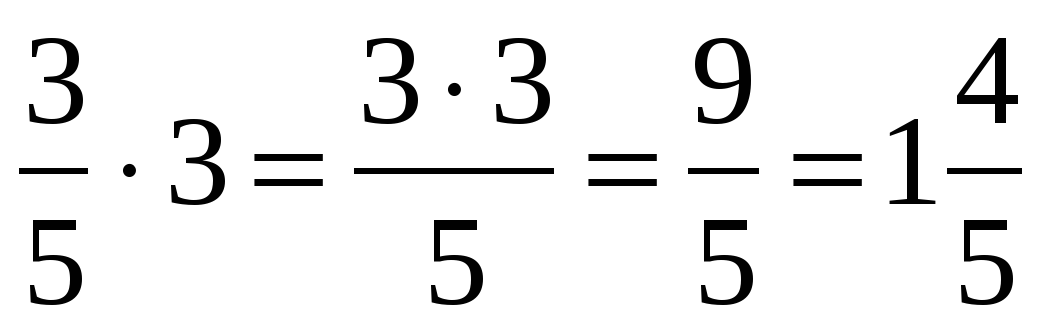 Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2 . Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
| Табличка на двери |
Как умножать десятичные цифры. Умножение десятичных дробей: правила, примеры, решения
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Содержание урока
Сложение десятичных дробейКак мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой» .
В школе это требование называют «запятая под запятой» .
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой» :
Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5
3,2 + 5,3 = 8,5
На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Разряды в десятичных дробяхУ десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345
Сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345 .
При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой» . Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
3,51 + 1,22 = 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти . В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
Значит значение выражения 2,65 + 3,27 равно 5,92
2,65 + 3,27 = 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
9,5 + 2,8 = 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5 . Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Вычитание десятичных дробейПри вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4 . Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,23 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
Умножение десятичных дробейУмножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
2,5 × 1,5 = 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Умножение десятичной дроби на обычное числоИногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
2,54 × 2 = 5,08
Умножение десятичных дробей на 10, 100, 1000Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
2,88 × 10 = 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
2,88 × 10 = 28,8
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
2,88 × 100 = 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Умножение десятичных дробей на 0,1 0,01 и 0,001Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
3,25 × 0,1 = 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
3,25 × 0,1 = 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице» , то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь равна 0,5
Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4: 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4: 5 равно 0,8
Пример 3. Найти значение выражения 5: 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5: 125 равно 0,04
Деление чисел без остатка
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
9: 5 = 1,8
Пример 2 . Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено. Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8: 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8: 2 равно 2,4
Пример 2. Найти значение выражения 8,43: 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43: 3 равно 2,81
Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9: 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2 ) : (3 × 2 ) = 18: 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17.
На самом деле внутри этого процесса происходило умножение на 10. Вот как это выглядело:
5,91 × 10 = 59,1
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и . Например, разделим 2,1 на 10. Решим этот пример уголком:
Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1: 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1: 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1: 1000 = 0,0021
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и . В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
Значит значение выражения 6,3: 0,1 равно 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3: 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
Переносим запятую вправо на одну цифру и получаем 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3: 0,001 = 6300
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Умножение десятичных дробей происходит в три этапа.
Десятичные дроби записывают в столбик и умножают как обыкновенные числа.
Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.
В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.
Как умножать десятичные дроби
Записываем десятичные дроби в столбик и умножаем их как натуральные числа, не обращая внимания на запятые. То есть 3,11 мы рассматриваем как 311 , а 0,01 как 1 .
Получили 311 . Теперь считаем количество знаков (цифр) после запятой у обеих дробей. В первой десятичной дроби два знака и во второй — два. Общее количество цифр после запятых:
Отсчитываем справа налево 4 знака (цифры) у полученного числа. В полученном результате цифр меньше, чем нужно отделить запятой. В таком случае нужно слева приписать недостающее число нулей.
У нас не хватает одной цифры, поэтому приписываем слева один ноль.
При умножении любой десятичной дроби на 10; 100; 1000 и т.д. запятая в десятичной дроби перемещается вправо на столько знаков, сколько нулей стоит после единицы.
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо в этой дроби перенести запятую влево на столько знаков, сколько нулей стоит перед единицей.
Считаем и ноль целых!
- 12 · 0,1 = 1,2
- 0,05 · 0,1 = 0,005
- 1,256 · 0,01 = 0,012 56
- не обращая внимания на запятые, выполнить умножение по всем правилам умножения столбиком натуральных чисел;
- в полученном числе отделить десятичной запятой столько цифр справа, сколько десятичных знаков в обоих множителях вместе, при этом если в произведении не хватает цифр, то слева нужно дописать нужное количество нулей.

Чтобы понять, как умножать десятичные дроби, рассмотрим конкретные примеры.
Правило умножения десятичных дробей
1) Умножаем, не обращая внимания на запятую.
2) В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе.
Найти произведение десятичных дробей:
Чтобы умножить десятичные дроби, умножаем, не обращая внимания на запятые. То есть мы умножаем не 6,8 и 3,4, а 68 и 34. В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе. В первом множителе после запятой одна цифра, во втором — тоже одна. Итого, отделяем после запятой две цифры.Таким образом, получили окончательный ответ: 6,8∙3,4=23,12.
Умножаем десятичные дроби, не принимая во внимание запятую. То есть фактически вместо умножения 36,85 на 1,14 мы умножаем 3685 на 14. Получаем 51590. Теперь в этом результате надо отделить запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой две цифры, во втором — одна. Итого, отделяем запятой три цифры. Поскольку в конце записи после запятой стоит нуль, в ответ мы его не пишем: 36,85∙1,4=51,59.
Теперь в этом результате надо отделить запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой две цифры, во втором — одна. Итого, отделяем запятой три цифры. Поскольку в конце записи после запятой стоит нуль, в ответ мы его не пишем: 36,85∙1,4=51,59.
Чтобы умножить эти десятичные дроби, умножим числа, не обращая внимания на запятые. То есть умножаем натуральные числа 2315 и 7. Получаем 16205. В этом числе нужно отделить после запятой четыре цифры — столько, сколько их в обоих множителях вместе (в каждом — по два). Окончательный ответ: 23,15∙0,07=1,6205.
Умножение десятичной дроби на натуральное число выполняется аналогично. Умножаем числа, не обращая внимания на запятую, то есть 75 умножаем на 16. В полученном результате после запятой должно стоять столько же знаков, сколько их в обоих множителях вместе — один. Таким образом, 75∙1,6=120,0=120.
Умножение десятичных дробей начинаем с того, что умножаем натуральные числа, так как на запятые не обращаем внимания. После этого отделяем после запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой два знака, во втором — тоже два. Итого, в результате после запятой должно стоять четыре цифры: 4,72∙5,04=23,7888.
После этого отделяем после запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой два знака, во втором — тоже два. Итого, в результате после запятой должно стоять четыре цифры: 4,72∙5,04=23,7888.
И еще пара примеров на умножение десятичных дробей:
www.for6cl.uznateshe.ru
Умножение десятичных дробей, правила, примеры, решения.
Переходим к изучению следующего действия с десятичными дробями, сейчас мы всесторонне рассмотрим умножение десятичных дробей . Сначала обговорим общие принципы умножения десятичных дробей. После этого перейдем к умножению десятичной дроби на десятичную дробь, покажем, как выполняется умножение десятичных дробей столбиком, рассмотрим решения примеров. Дальше разберем умножение десятичных дробей на натуральные числа, в частности на 10, 100 и т.д. В заключение поговорим об умножении десятичных дробей на обыкновенные дроби и смешанные числа.
Сразу скажем, что в этой статье мы будем говорить лишь об умножении положительных десятичных дробей (смотрите положительные и отрицательные числа). Остальные случаи разобраны в статьях умножение рациональных чисел и умножение действительных чисел .
Остальные случаи разобраны в статьях умножение рациональных чисел и умножение действительных чисел .
Навигация по странице.
Общие принципы умножения десятичных дробей
Обсудим общие принципы, которых следует придерживаться при проведении умножения с десятичными дробями.
Так как конечные десятичные дроби и бесконечные периодические дроби являются десятичной формой записи обыкновенных дробей, то умножение таких десятичных дробей по сути является умножением обыкновенных дробей. Иными словами, умножение конечных десятичных дробей , умножение конечной и периодической десятичных дробей , а также умножение периодических десятичных дробей сводится к умножению обыкновенных дробей после перевода десятичных дробей в обыкновенные.
Рассмотрим примеры применения озвученного принципа умножения десятичных дробей.
Выполните умножение десятичных дробей 1,5 и 0,75 .
Заменим умножаемые десятичные дроби соответствующими обыкновенными дробями. Так как 1,5=15/10 и 0,75=75/100 , то. Можно провести сокращение дроби, после чего выделить целую часть из неправильной дроби, а удобнее полученную обыкновенную дробь 1 125/1 000 записать в виде десятичной дроби 1,125 .
Так как 1,5=15/10 и 0,75=75/100 , то. Можно провести сокращение дроби, после чего выделить целую часть из неправильной дроби, а удобнее полученную обыкновенную дробь 1 125/1 000 записать в виде десятичной дроби 1,125 .
Следует отметить, что конечные десятичные дроби удобно умножать столбиком, об этом способе умножения десятичных дробей мы поговорим в следующем пункте.
Рассмотрим пример умножения периодических десятичных дробей.
Вычислите произведение периодических десятичных дробей 0,(3) и 2,(36) .
Выполним перевод периодических десятичных дробей в обыкновенные дроби:
Тогда. Можно полученную обыкновенную дробь перевести в десятичную дробь:
Если среди умножаемых десятичных дробей присутствуют бесконечные непериодические, то все умножаемые дроби, в том числе конечные и периодические, следует округлить до некоторого разряда (смотрите округление чисел ), после чего выполнять умножение полученных после округления конечных десятичных дробей.
Выполните умножение десятичных дробей 5,382… и 0,2 .
Сначала округлим бесконечную непериодическую десятичную дробь, округление можно провести до сотых, имеем 5,382…≈5,38 . Конечную десятичную дробь 0,2 округлять до сотых нет необходимости. Таким образом, 5,382…·0,2≈5,38·0,2 . Осталось вычислить произведение конечных десятичных дробей: 5,38·0,2=538/100·2/10= 1 076/1 000=1,076 .
Умножение десятичных дробей столбиком
Умножение конечных десятичных дробей можно выполнять столбиком, аналогично умножению столбиком натуральных чисел.
Сформулируем правило умножения десятичных дробей столбиком . Чтобы умножить десятичные дроби столбиком, надо:
Рассмотрим примеры умножения десятичных дробей столбиком.
Выполните умножение десятичных дробей 63,37 и 0,12 .
Проведем умножение десятичных дробей столбиком. Сначала умножаем числа, не обращая внимания на запятые:
Осталось в полученном произведении поставить запятую. Ей нужно отделить 4 цифры справа, так как в множителях в сумме четыре десятичных знака (два в дроби 3,37 и два в дроби 0,12). Цифр там хватает, поэтому нулей слева дописывать не придется. Закончим запись:
В итоге имеем 3,37·0,12=7,6044 .
Вычислите произведение десятичных дробей 3,2601 и 0,0254 .
Выполнив умножение столбиком без учета запятых, получаем следующую картину:
Теперь в произведении нужно отделить запятой 8 цифр справа, так как общее количество десятичных знаков умножаемых дробей равно восьми. Но в произведении только 7 цифр, поэтому, нужно слева приписать столько нулей, чтобы можно было отделить запятой 8 цифр. В нашем случае нужно приписать два нуля:
На этом умножение десятичных дробей столбиком закончено.
Умножение десятичных дробей на 0,1, 0,01, и т.д.
Довольно часто приходится умножать десятичные дроби на 0,1 , 0,01 и так далее. Поэтому целесообразно сформулировать правило умножения десятичной дроби на эти числа, которое следует из рассмотренных выше принципов умножения десятичных дробей.
Итак, умножение данной десятичной дроби на 0,1 , 0,01 , 0,001 и так далее дает дробь, которая получается из исходной, если в ее записи перенести запятую влево на 1 , 2 , 3 и так далее цифр соответственно, при этом если не хватает цифр для переноса запятой, то нужно слева дописать необходимое количество нулей.
Например, чтобы умножить десятичную дробь 54,34 на 0,1 , надо в дроби 54,34 перенести запятую влево на 1 цифру, при этом получится дробь 5,434 , то есть, 54,34·0,1=5,434 . Приведем еще один пример. Умножим десятичную дробь 9,3 на 0,0001 . Для этого нам нужно в умножаемой десятичной дроби 9,3 перенести запятую на 4 цифры влево, но запись дроби 9,3 не содержит такого количества знаков. Поэтому нам нужно в записи дроби 9,3 слева приписать столько нулей, чтобы можно было беспрепятственно осуществить перенос запятой на 4 цифры, имеем 9,3·0,0001=0,00093 .
Поэтому нам нужно в записи дроби 9,3 слева приписать столько нулей, чтобы можно было беспрепятственно осуществить перенос запятой на 4 цифры, имеем 9,3·0,0001=0,00093 .
Заметим, что озвученное правило умножения десятичной дроби на 0,1, 0,01, … справедливо и для бесконечных десятичных дробей. К примеру, 0,(18)·0,01=0,00(18) или 93,938…·0,1=9,3938… .
Умножение десятичной дроби на натуральное число
По своей сути умножение десятичных дробей на натуральные числа ничем не отличается от умножения десятичной дроби на десятичную дробь.
Конечную десятичную дробь умножать на натуральное число удобнее всего столбиком, при этом следует придерживаться правил умножения столбиком десятичных дробей, рассмотренных в одном из предыдущих пунктов.
Вычислите произведение 15·2,27 .
Проведем умножение натурального числа на десятичную дробь столбиком:
При умножении периодической десятичной дроби на натуральное число, периодическую дробь следует заменить обыкновенной дробью.
Умножьте десятичную дробь 0,(42) на натуральное число 22 .
Сначала переведем периодическую десятичную дробь в обыкновенную дробь:
Теперь выполним умножение: . Этот результат в виде десятичной дроби имеет вид 9,(3) .
А при умножении бесконечной непериодической десятичной дроби на натуральное число нужно предварительно провести округление.
Выполните умножение 4·2,145… .
Округлив до сотых исходную бесконечную десятичную дробь, мы придем к умножению натурального числа и конечной десятичной дроби. Имеем 4·2,145…≈4·2,15=8,60 .
Умножение десятичной дроби на 10, 100, …
Довольно часто приходится умножать десятичные дроби на 10, 100, … Поэтому целесообразно подробно остановиться на этих случаях.
Озвучим правило умножения десятичной дроби на 10, 100, 1 000 и т.д. При умножении десятичной дроби на 10, 100, … в ее записи нужно перенести запятую вправо на 1, 2, 3, … цифры соответственно и отбросить лишние нули слева; если в записи умножаемой дроби не хватает цифр для переноса запятой, то нужно дописать необходимое количество нулей справа.
Умножьте десятичную дробь 0,0783 на 100 .
Перенесем в записи дроби 0,0783 на две цифры вправо, при этом получим 007,83 . Отбросив два нуля слева, получаем десятичную дробь 7,38 . Таким образом, 0,0783·100=7,83 .
Выполните умножение десятичной дроби 0,02 на 10 000 .
Чтобы умножить 0,02 на 10 000 , нам нужно перенести запятую на 4 цифры вправо. Очевидно, в записи дроби 0,02 не хватает цифр для переноса запятой на 4 цифры, поэтому допишем несколько нулей справа, чтобы можно было осуществить перенос запятой. В нашем примере достаточно дописать три нуля, имеем 0,02000 . После переноса запятой получим запись 00200,0 . Отбросив нули слева, имеем число 200,0 , которое равно натуральному числу 200 , оно и является результатом умножения десятичной дроби 0,02 на 10 000 .
Озвученное правило справедливо и для умножения бесконечных десятичных дробей на 10, 100, … При умножении периодических десятичных дробей нужно быть аккуратными с периодом дроби, которая является результатом умножения.
Умножьте периодическую десятичную дробь 5,32(672) на 1 000 .
Перед умножением распишем периодическую десятичную дробь как 5,32672672672… , это нам позволит не допустить ошибки. Теперь перенесем запятую вправо на 3 знака, имеем 5 326,726726… . Таким образом, после умножения получается периодическая десятичная дробь 5 326,(726) .
5,32(672)·1 000=5 326,(726) .
При умножении бесконечных непериодических дробей на 10, 100, … нужно предварительно провести округление бесконечной дроби до некоторого разряда, после чего проводить умножение.
Умножение десятичной дроби на обыкновенную дробь или смешанное число
Для умножения конечной десятичной дроби или бесконечной периодической десятичной дроби на обыкновенную дробь или смешанное число, нужно десятичную дробь представить в виде обыкновенной дроби, после чего провести умножение.
Проведите умножение десятичной дроби 0,4 на смешанное число.
Так как 0,4=4/10=2/5 и, то. Полученное число можно записать в виде периодической десятичной дроби 1,5(3) .
При умножении бесконечной непериодической десятичной дроби на обыкновенную дробь или смешанное число, обыкновенную дробь или смешанное число следует заменить десятичной дробью, после чего провести округление умножаемых дробей и закончить вычисления.
Так как 2/3=0,6666… , то. После округления умножаемых дробей до тысячных, приходим к произведению двух конечных десятичных дробей 3,568 и 0,667 . Выполним умножение в столбик:
Полученный результат следует округлить до тысячных, так как умножаемые дроби были взяты с точностью до тысячных, имеем 2,379856≈2,380 .
www.cleverstudents.ru
29. Умножение десятичных дробей. Правила
Найдем площадь прямоугольника со сторонами равными
1,4 дм и 0,3 дм. Переведем дециметры в сантиметры:
1,4 дм = 14 см; 0,3 дм = 3 см.
Теперь вычислим площадь в сантиметрах.
S = 14 3 = 42 см 2 .
Переведем квадратные сантиметры в квадратные
дециметры:
д м 2 = 0,42 д м 2 .
Значит, S = 1,4 дм 0,3 дм = 0,42 дм 2 .
Умножение двух десятичных дробей выполняется так:
1) числа перемножаются без учета запятых.
2) запятая в произведении ставится так, чтобы отделить справа
столько же знаков, сколько отделено в обоих множителях
вместе взятых. Например:
1,1 0,2 = 0,22 ; 1,1 1,1 = 1,21 ; 2,2 0,1 = 0,22 .
Примеры умножения десятичных дробей в столбик:
Вместо умножения любого числа на 0,1 ; 0,01 ; 0,001 ,
можно разделить это число на 10 ; 100 ; или 1000 соответственно.
Например:
22 0,1 = 2,2 ; 22: 10 = 2,2 .
При умножении десятичной дроби на натуральное число, мы должны:
1) перемножить числа, не обращая внимания на запятую;
2) в полученном произведении поставить запятую так, чтобы справа
от нее было столько же цифр, сколько в десятичной дроби.
Найдем произведение 3,12 10 . По указанному выше правилу
сначала умножаем 312 на 10 . Получим: 312 10 = 3120 .
А теперь отделяем запятой две цифры справа и получаем:
3,12 10 = 31,20 = 31,2 .
Значит, при умножении 3,12 на 10 мы перенесли запятую на одну
цифру вправо. Если умножить 3,12 на 100 , то получим 312 , то есть
запятую перенесли на две цифры вправо.
3,12 100 = 312,00 = 312 .
При умножении десятичной дроби на 10 , 100 , 1000 и т. д., надо
в этой дроби перенести запятую вправо на столько знаков, сколько нулей
стоит в множителе. Например:
0,065 1000 = 0065, = 65 ;
2,9 1000 = 2,900 1000 = 2900, = 2900 .
Задачи на тему «Умножение десятичных дробей»
school-assistant.ru
Сложение, вычитание, умножение и деление десятичных дробей
Сложение и вычитание десятичных дробей аналогично сложению и вычитанию натуральных чисел, но с определенными условиями.
Правило. производится по разрядам целой и дробной части как натуральных чисел.
При письменном сложении и вычитании десятичных дробей запятая, отделяющая целую часть от дробной, должна находиться у слагаемых и суммы или у уменьшаемого, вычитаемого и разности в одном столбце (запятая под запятой от записи условия до конца вычисления).
Сложение и вычитание десятичных дробей в строку:
243,625 + 24,026 = 200 + 40 + 3 + 0,6 + 0,02 + 0,005 + 20 + 4 + 0,02 + 0,006 = 200 + (40 + 20) + (3 + 4)+ 0,6 + (0,02 + 0,02) + (0,005 + 0,006) = 200 + 60 + 7 + 0,6 + 0,04 + 0,011 = 200 + 60 + 7 + 0,6 + (0,04 + 0,01) + 0,001 = 200 + 60 + 7 + 0,6 + 0,05 + 0,001 = 267,651
843,217 — 700,628 = (800 — 700) + 40 + 3 + (0,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + (1,2 — 0,6) + (0,01 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + (0,11 — 0,02) + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,09 + (0,007 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + (0,017 — 0,008) = 100 + 40 + 2 + 0,5 + 0,08 + 0,009 = 142,589
Сложение и вычитание десятичных дробей в столбик:
Сложение десятичных дробей требует верхней дополнительной строки для записи чисел, когда сумма разряда переходит через десяток. Вычитание десятичных дробей требует верхней дополнительной строки для того, чтобы отметить разряд, в котором одалживается 1.
Если справа от слагаемого или уменьшаемого не хватает разрядов дробной части, то справа в дробной части можно дописывать столько нулей (увеличивать разрядность дробной части), сколько разрядов в другом слагаемом или уменьшаемом.
Умножение десятичных дробей производится так же, как и умножение натуральных чисел, по тем же правилам, но в произведении ставится запятая по сумме разрядов множителей в дробной части, считая справа налево (сумма разрядов множителей — это количество разрядов после запятой у множителей, вместе взятых).
При умножении десятичных дробей в столбик первая справа значащая цифра подписывается под первой справа значащей цифрой, как и в натуральных числах:
Запись умножения десятичных дробей в столбик:
Запись деления десятичных дробей в столбик:
Подчеркнутые знаки — это знаки, за которые переносится запятая, потому что делитель должен быть целым числом.
Правило. При делении дробей делитель десятичной дроби увеличивается на столько разрядов, сколько разрядов в дробной его части. Чтобы дробь не изменилась, на столько же разрядов увеличивается и делимое (в делимом и делителе запятая переносится на одно и то же число знаков). Запятая ставится в частном на том этапе деления, когда целая часть дроби разделена.
Чтобы дробь не изменилась, на столько же разрядов увеличивается и делимое (в делимом и делителе запятая переносится на одно и то же число знаков). Запятая ставится в частном на том этапе деления, когда целая часть дроби разделена.
Для десятичных дробей, как и для натуральных чисел, сохраняется правило: на ноль десятичную дробь делить нельзя!
Вы уже знаете, что a * 10 = a + a + a + a + a + a + a + a + a + a. Например, 0,2 * 10 = 0,2 + 0,2 + 0,2 + 0,2 + 0,2 + 0,2 + 0,2 + 0,2 + 0,2 + 0,2 . Несложно догадаться, что эта сумма равна 2, т.е. 0,2 * 10 = 2 .
Аналогично можно убедиться, что:
5,2 * 10 = 52 ;
0,27 * 10 = 2,7 ;
1,253 * 10 = 12,53 ;
64,95 * 10 = 649,5 .
Вы, наверное, догадались, что при умножении десятичной дроби на 10 надо в этой дроби перенести запятую вправо на одну цифру.
А как умножить десятичную дробь на 100 ?
Имеем: a * 100 = a * 10 * 10 . Тогда:
2,375
* 100
= 2,375
* 10
* 10
= 23,75
* 10
= 237,5
.
Рассуждая аналогично, получаем, что:
3,2 * 100 = 320 ;
28,431 * 100 = 2843,1 ;
0,57964 * 100 = 57,964 .
Умножим дробь 7,1212 на число 1 000 .
Имеем: 7,1212 * 1 000 = 7,1212 * 100 * 10 = 712,12 * 10 = 7121,2 .
Эти примеры иллюстрируют следующее правило.
Чтобы умножить десятичную дробь на 10, 100, 1 000 и т.д., надо в этой дроби перенести запятую вправо соответственно на 1, 2, 3 и т.д. цифры .
Итак, если запятую перенести вправо на 1, 2, 3 и т.д. цифры, то дробь увеличится соответственно в 10, 100, 1 000 и т.д. раз.
Следовательно, если запятую перенести влево на 1, 2, 3 и т.д. цифры, то дробь уменьшится соответственно в 10, 100, 1 000 и т.д. раз .
Покажем, что десятичная форма записи дробей дет возможность умножать их, руководствуясь правилом умножения натуральных чисел.
Найдем, например, произведение 3,4
* 1,23
. Увеличим первый множитель в 10
раз, а второй − в 100
раз. Это означает, что мы увеличили произведение в 1
000
раз.
Это означает, что мы увеличили произведение в 1
000
раз.
Следовательно, произведение натуральных чисел 34 и 123 в 1 000 раз больше искомого произведения.
Имеем: 34 * 123 = 4182 . Тогда для получения ответа надо число 4 182 уменьшить в 1 000 раз. Запишем: 4 182 = 4 182,0 . Перенося запятую в числе 4 182,0 на три цифры влево, получим число 4,182 , которое в 1 000 раз меньше числа 4 182 . Поэтому 3,4 * 1,23 = 4,182 .
Этот же результат можно получить, руководствуясь следующим правилом.
Чтобы перемножить две десятичные дроби, надо:
1 ) умножить их как натуральные числа, не обращая внимания на запятые;
2 ) в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
В тех случаях, когда произведение содержит меньше цифр, чем требуется отделить запятой, слева перед этим произведение дописывают необходимое количество нулей, а затем переносят запятую влево на нужное количество цифр.
Например, 2 * 3 = 6, тогда 0,2 * 3 = 0,006 ; 25 * 33 = 825, тогда 0,025 * 0,33 = 0,00825 .
В тех случаях, когда один из множителей равен 0,1 ; 0,01 ; 0,001 и т.д., удобно пользоваться следующим правилом.
Чтобы умножить десятичную дробь на 0,1 ; 0,01 ; 0,001 и т.д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т.д. цифры .
Например, 1,58 * 0,1 = 0,158 ; 324,7 * 0,01 = 3,247 .
Свойства умножения натуральных чисел выполняются и для дробных чисел:
ab = ba − переместительное свойство умножения,
(ab) с = a(b с) − сочетательное свойство умножения,
a(b + с) = ab + ac − распределительное свойство умножения относительно сложения.
В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.
Что такое дробь?
Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.
Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.
Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.
Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.
Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.
Разновидности дробей
Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.
Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.
Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.
Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.
Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.
Пример . Представить дробь 7 21 / 1000 в десятичной записи.
Алгоритм перевода неправильной дроби в смешанное число и наоборот
Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:
- разделить числитель на имеющийся знаменатель;
- в конкретном примере неполное частное — целое;
- и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .
Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .
Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:
- целая часть умножается на знаменатель дробного выражения;
- полученное произведение прибавляется к числителю;
- результат записывается в числителе, знаменатель остается неизменным.
Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .
Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.
Ответ : 98 / 10.
Умножение дробей обыкновенных
Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.
Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.
Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .
Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .
Умножение дробей десятичных
Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:
- две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
- нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
- подсчитать количество цифр после знака запятой в каждом из чисел;
- в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
- если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.
Решение .
Умножение смешанных дробей
Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:
- перевести числа в смешанном виде в неправильные дроби;
- найти произведение числителей;
- найти произведение знаменателей;
- записать получившийся результат;
- максимально упростить выражение.
Пример . Найти произведение 4½ и 6 2 / 5.
Умножение числа на дробь (дроби на число)
Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.
Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:
- записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
- найти произведение, несмотря на запятую;
- в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.
Пример . Вычислить произведение 5 / 8 и 12.
Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.
Ответ : 7 1 / 2.
Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.
Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.
Пример . Найти произведение 9 5 / 6 и 9.
Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.
Ответ : 88 1 / 2.
Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001
Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.
Пример 1 . Найти произведение 0,065 и 1000.
Решение . 0,065 х 1000 = 0065 = 65.
Ответ : 65.
Пример 2 . Найти произведение 3,9 и 1000.
Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.
Ответ : 3900.
Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.
Пример 1 . Найти произведение 56 и 0,01.
Решение . 56 х 0,01 = 0056 = 0,56.
Ответ : 0,56.
Пример 2 . Найти произведение 4 и 0,001.
Решение . 4 х 0,001 = 0004 = 0,004.
Ответ : 0,004.
Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.
Чтобы понять, как умножать десятичные дроби, рассмотрим конкретные примеры.
Правило умножения десятичных дробей
1) Умножаем, не обращая внимания на запятую.
2) В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе.
Примеры .
Найти произведение десятичных дробей:
Чтобы умножить десятичные дроби, умножаем, не обращая внимания на запятые. То есть мы умножаем не 6,8 и 3,4, а 68 и 34. В результате отделяем после запятой столько цифр, сколько их после запятых в обоих множителях вместе. В первом множителе после запятой одна цифра, во втором — тоже одна. Итого, отделяем после запятой две цифры.Таким образом, получили окончательный ответ: 6,8∙3,4=23,12.
Умножаем десятичные дроби, не принимая во внимание запятую. То есть фактически вместо умножения 36,85 на 1,14 мы умножаем 3685 на 14. Получаем 51590. Теперь в этом результате надо отделить запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой две цифры, во втором — одна. Итого, отделяем запятой три цифры. Поскольку в конце записи после запятой стоит нуль, в ответ мы его не пишем: 36,85∙1,4=51,59.
Чтобы умножить эти десятичные дроби, умножим числа, не обращая внимания на запятые. То есть умножаем натуральные числа 2315 и 7. Получаем 16205. В этом числе нужно отделить после запятой четыре цифры — столько, сколько их в обоих множителях вместе (в каждом — по два). Окончательный ответ: 23,15∙0,07=1,6205.
Умножение десятичной дроби на натуральное число выполняется аналогично. Умножаем числа, не обращая внимания на запятую, то есть 75 умножаем на 16. В полученном результате после запятой должно стоять столько же знаков, сколько их в обоих множителях вместе — один. Таким образом, 75∙1,6=120,0=120.
Таким образом, 75∙1,6=120,0=120.
Умножение десятичных дробей начинаем с того, что умножаем натуральные числа, так как на запятые не обращаем внимания. После этого отделяем после запятой столько цифр, сколько их в обоих множителях вместе. В первом числе после запятой два знака, во втором — тоже два. Итого, в результате после запятой должно стоять четыре цифры: 4,72∙5,04=23,7888.
Как умножить дробь на целое число
Как умножить дробь на целое число
Чтобы умножить дробь на целое число:
- Умножить числитель дроби на целое число.
- Оставьте знаменатель прежним.
- Упростите дробь, если это возможно.
Например, умножьте 5 × 2 / 7 .
Числитель дроби — число сверху, равное 2.
Мы умножаем 2 на 5, но сохраняем знаменатель 7 равным 7.
5 × 2 / 7 = 10 / 7 .
Упрощаем, если это возможно. Поскольку дробь неправильная, мы можем преобразовать ее в смешанное число.
Поскольку дробь неправильная, мы можем преобразовать ее в смешанное число.
10 / 7 означает 10 ÷ 7, что составляет 1 остаток 3. Следовательно, дробь может быть записана как 1 3 / 7 .
Альтернативный метод умножения дроби на целое число
Чтобы умножить дробь на целое число:
- Запишите целое число как дробь от 1.
- Умножить числители.
- Умножить знаменатели..
- Упростите, если возможно.
Например, умножьте 4 × 1 / 2 .
Первый шаг — записать 4 как 4 / 1 .
Второй шаг — умножить числители: 4 × 1 = 4. Числитель ответа равен 4.
Третий шаг — умножить знаменатели: 1 × 2 = 2. Знаменатель ответа равен 2.
Следовательно, 4 × 1 / 2 = 4 / 2 .
Наконец, упростите дробь, разделив и числитель, и знаменатель на одно и то же значение. Мы можем разделить 4 и 2 на 2, поэтому 4 / 2 упрощается до 2 / 1 . 2 / 1 то же, что и 2.
Мы можем разделить 4 и 2 на 2, поэтому 4 / 2 упрощается до 2 / 1 . 2 / 1 то же, что и 2.
Следовательно, 4 × 1 / 2 = 2.
Мы также знаем, что половина 4 равна 2.
Как умножить дробь на целое число в простейшей форме
Чтобы умножить дробь на целое число, умножьте числитель на целое число. Чтобы записать этот ответ в простейшей форме, разделите числитель и знаменатель на наибольшее число, которое точно делится на оба.
Например, вычислите 2 × 3 / 10 в простейшей форме.
Первый шаг — умножить числитель дроби на целое число. 2 × 3 = 6 и, следовательно, 2 × 3 / 10 = 6 / 10 .
Второй шаг — упростить дробь, разделив числитель и знаменатель на наибольшее число, которое делится на оба.
И 6, и 10 можно разделить на 2. 6 / 10 упрощается до 3 / 5 .
Следовательно, 2 × 3 / 10 в простейшей форме: 3 / 5 .
Умножение дроби на целое число можно также рассчитать, разделив знаменатель на целое число.
10 — знаменатель, а 10 ÷ 2 = 5 — новый знаменатель. Это работает только в том случае, если знаменатель дроби можно разделить на целое число.
Как умножить смешанное число на целое
Чтобы умножить смешанное число на целое число:
- Преобразуйте смешанное число в неправильную дробь.
- Умножить числитель неправильной дроби на целое число.
- Упростите, если возможно, и преобразуйте обратно в смешанное число.
Например, умножьте 2 × 1 2 / 3 .
Шаг 1. Превратите смешанное число в неправильную дробь.
Оставьте знаменатель прежним.
Чтобы найти новый числитель, умножьте целое число смешанного числа на знаменатель, а затем добавьте числитель.
Знаменатель равен 3. Числитель находится путем умножения 1 и 3, чтобы получить 3, а затем прибавления 2, чтобы получить 5.
1 2 / 3 = 5 / 3 .
Шаг 2. Умножьте числитель неправильной дроби на целое число.
Мы умножаем 2 × 5 = 10 и, таким образом, 2 × 5 / 3 = 10 / 3 .
Последний шаг — упростить и снова записать смешанное число.
10 / 3 = 3 1 / 3 .
Следовательно, 2 × 1 2 / 3 = 3 1 / 3
Умножение дроби на целое число с использованием числовой строки
Отметьте дробь на числовой прямой. Чтобы умножить его на целое число, прибавьте к той же дроби столько раз, сколько требуется для умножения.
Например, вот 5 × 1 / 8 в числовой строке.
Разбиваем каждое целое число на восьмые и считаем пять из них.
5 × 1 / 8 = 5 / 8 .
Вот еще один пример с неправильной дробью или смешанным числом.
Вычислите 5 × 1 / 3 , используя числовую прямую.
Разобьем каждое целое число на трети. Затем мы отсчитываем пять таких прыжков на нашей числовой прямой.
5 × 1 / 3 = 5 / 3 .
В качестве смешанного числа это 1 2 / 3 .
Умножение дроби на целое число с использованием моделей
Модели можно использовать для обучения процессу умножения дробей на целые числа.
Вот модель дроби 1 / 3 . Чтобы умножить его на 2, мы имеем в два раза больше частей.
Мы видим, что теперь у нас есть 2 / 3 заштриховано.
Вот еще один пример использования модели для умножения 1 / 4 на 3.
Если мы умножим 1 / 4 на 3, то получим 3 / 4 .
Модели полезны при умножении дробей и целых чисел, потому что мы видим, что знаменатель дроби не меняется, потому что количество частей в модели остается прежним.
Словесные задачи на умножение дробей и целых чисел
Вот несколько примеров текстовых задач на умножение дробей и целых чисел.
Q1. Я проезжаю 1 / 3 километр каждый день. Сколько километров я проеду за 5 дней?
Ответ: 1 / 3 × 5 = 5 / 3 .
Q2. На вечеринку каждому человеку нужно 3 / 4 литра напитка. Всего приходит 10 человек. Сколько литров напитка нужно купить?
Ответ: 3 / 4 × 10 = 30 / 4 .
Q3. Аккумулятор моего телефона заряжается на 3 / 100 каждую минуту. Какую долю он зарядит за 7 минут?
Какую долю он зарядит за 7 минут?
Ответ: 3 / 100 × 7 = 21 / 100 .
Умножение дробей на целые числа
Для умножение дробей на целые числа, целое число записывается в виде дроби, а затем умножается на заданную дробь по правилам умножения дробей. При умножении дробей на целые числа следует также помнить, что данные дроби должны быть в виде правильной дроби или неправильной дроби. Давайте узнаем больше об умножении дробей на целые числа вместе с некоторыми примерами.
| 1. | Что такое умножение дробей на целые числа? |
| 2. | Как умножать дроби на целые числа? |
| 3. | Как умножать смешанные дроби на целые числа? |
| 4. | Часто задаваемые вопросы об умножении дробей на целые числа |
Что такое умножение дробей на целые числа?
Умножение дробей на целые числа аналогично многократному сложению, когда дробь прибавляется столько же раз, сколько и целое число. Для умножения дробей мы сначала умножаем числители, затем умножаем знаменатели и, наконец, приводим полученную дробь к наименьшему порядку. Однако, когда нам нужно умножить дроби на целые числа, мы записываем целое число в виде дроби, записывая 1 в качестве ее знаменателя. После этого шага мы можем умножить его, используя те же правила. Например, когда мы умножаем дробь a/b × c/d, мы получаем (a × c)/(b × d). Это правило применимо и при умножении дробей на целые числа.
Для умножения дробей мы сначала умножаем числители, затем умножаем знаменатели и, наконец, приводим полученную дробь к наименьшему порядку. Однако, когда нам нужно умножить дроби на целые числа, мы записываем целое число в виде дроби, записывая 1 в качестве ее знаменателя. После этого шага мы можем умножить его, используя те же правила. Например, когда мы умножаем дробь a/b × c/d, мы получаем (a × c)/(b × d). Это правило применимо и при умножении дробей на целые числа.
Как умножать дроби на целые числа?
Умножение дробей на целые числа — простая идея. Нам просто нужно преобразовать целое число в дробь, написав 1 в качестве знаменателя и написав целое число в качестве числителя. Затем оно умножается на заданную дробь. После их умножения окончательный результат должен быть в виде правильной дроби или смешанной дроби. Если в результате получается неправильная дробь, преобразуем ее в смешанную дробь. Давайте разберемся с шагами на примере.
Пример: Умножить 1/8 × 5
Решение: Здесь 1/8 — дробь, а 5 — целое число.
- Шаг 1: Преобразуйте целое число в дробь, написав 1 в качестве знаменателя. Это означает, что 5 записывается как 5/1 .
- Шаг 2: Умножьте числители. Здесь 1 × 5 = 5
- Шаг 3: Умножьте знаменатели. Здесь 8 × 1 = 8
- Шаг 4: При необходимости упростите и сократите продукт. Если в результате получится неправильная дробь, мы преобразуем ее в смешанную дробь. Итак, товар 5/8
Давайте посмотрим на другой пример, чтобы лучше понять это.
Пример 2: Умножьте 5 × 3/10.
Решение: Здесь 5 — целое число, а 3/10 — правильная дробь.
- Шаг 1: Преобразуем целое число 5 в дробь, написав 1 в знаменателе. Это означает, что 5 записывается как 5/1.
- Шаг 2: Умножьте числители обеих дробей. 5/1 × 3/10 = 5 × 3 = 15,
- Шаг 3: Умножьте знаменатели обеих дробей.
 5/1 × 3/10 = 1 × 10 = 10,
5/1 × 3/10 = 1 × 10 = 10, - Шаг 4: Упростите дроби. 5/1 × 3/10 = 15/10. Мы можем еще упростить это, так как и 15, и 10 можно разделить на 5. Это означает, что (15 ÷ 5) / (10 ÷ 5) = 3/2. Следовательно, 5 × 3/10 = 3/2 = \(1\dfrac{1}{2}\)
Как умножать смешанные дроби на целые числа?
Чтобы умножать смешанные дроби на целые числа, мы преобразуем смешанную дробь в неправильную дробь, а затем умножаем ее на целое число.
Пример: Умножить \(1\dfrac{2}{5}\) на 10.
Решение: Посмотрим, как умножить заданную смешанную дробь на целое число.
- Шаг 1: Сначала преобразуем смешанную дробь в неправильную. Это означает, что \(1\dfrac{2}{5}\) = 7/5.
- Шаг 2: Затем преобразуйте целое число 10 в дробь. Это означает, что 10 = 10/1. Это составляет 7/5 × 10/1 .
- Шаг 3: Умножьте числители обеих дробей.
 7 × 10 = 70. Перемножьте знаменатели обеих дробей. Это означает, что 5 × 1 = 5, .
7 × 10 = 70. Перемножьте знаменатели обеих дробей. Это означает, что 5 × 1 = 5, . - Шаг 4: Упростите и сократите дробь, то есть 70/5 = (70 ÷ 5) / (5 ÷ 5) = 14/1. Следовательно, \(1\dfrac{2}{5}\) × 10 = 14,
☛ Похожие статьи
- Умножение смешанных дробей
- Деление дробей
- Сокращение дробей
- Сложение и вычитание дробей
- Формула фракций
Примеры умножения дробей на целые числа
Пример 1: Умножьте дробь на целое число: 1/3 × 15
Решение:
Умножим дробь на целое число,
1/3 × 15 = 1/3 × 15/1 = (1 × 15) / (3 × 1) = 15/3 = 5.
Следовательно, 1/3 × 15 = 5
Пример 2: Найдите произведение после умножения дроби на целое число: 3/4 × 4
Решение:
Для умножения дробей на целые числа нам нужно преобразовать целое число в дробь, написав 1 в качестве ее знаменателя.

3/4 × 4 = 3/4 × 4/1 = (3 × 4) / (4 × 1) = 12/4 = 3.
Следовательно, 3/4 × 4 = 3
Пример 3: Найдите произведение целого числа 6 и смешанной дроби \(3\dfrac{4}{7}\)
Решение:
Сначала преобразуем смешанную дробь в правильную дробь .
\(3\dfrac{4}{7}\) = [(7 × 3) + 4] / 7 = 25/7
Преобразуем целое число в дробь,
6 = 6/1
Теперь давайте умножим дробь на целое число,
6/1 × 25/7 = (6 × 25) / (1 × 7) = 150/7
Получив результат, мы преобразуем его в смешанная фракция.
150/7 = \(21\dfrac{3}{7}\).
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Записаться на бесплатный пробный урок
Практические вопросы по умножению дробей на целые числа
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об умножении дробей на целые числа
Что означает умножение дробей на целые числа?
Умножение дробей на целые числа считается повторным сложением, когда дробь прибавляется столько же раз, сколько и целое число. Умножение дробей с целыми числами выполняется по тем же правилам умножения, где числители умножаются вместе, затем знаменатели умножаются вместе, а затем они уменьшаются, чтобы получить произведение.
Умножение дробей с целыми числами выполняется по тем же правилам умножения, где числители умножаются вместе, затем знаменатели умножаются вместе, а затем они уменьшаются, чтобы получить произведение.
Как умножать дроби на целые числа?
Чтобы умножать дроби на целые числа, мы используем следующие шаги.
- Шаг 1: Преобразуйте целое число в дробь, написав 1 в качестве знаменателя.
- Шаг 2: После этого нам нужно умножить две дроби. Итак, мы используем правило умножения дробей, чтобы умножить дроби.
- Шаг 3: Это означает, что сначала перемножаются числители, а затем перемножаются знаменатели.
- Шаг 4: Наконец, продукт упрощается или сокращается, если это необходимо.
Как умножать смешанные дроби на целые числа?
Следующие шаги показывают, как умножать смешанные дроби на целые числа:
- Шаг 1: Преобразуйте смешанную дробь в неправильную дробь.
- Шаг 2: Преобразуйте целое число в дробь со знаменателем 1.

- Шаг 3: Умножьте числители.
- Шаг 4: Умножьте знаменатели.
- Шаг 5: Упростите окончательный результат до минимума.
Как умножать неправильные дроби на целые числа?
Для умножения неправильных дробей на целые числа используются те же правила умножения. Это означает, что целое число записывается в виде дроби, а затем умножается на неправильную дробь. Числители перемножаются, затем знаменатели перемножаются, а затем при необходимости упрощаются.
Как умножить 3 дроби на целые числа?
Чтобы умножить 3 дроби на целые числа, мы используем следующие шаги. Умножим 4/5 × 10/6 × 1/4 × 25.
- Шаг 1: Здесь 25 — целое число, а остальные дроби, поэтому мы преобразуем целое число в дробь, написав его знаменатель равен 1. Это означает, что 25 записывается как 25/1 .
- Шаг 2: Теперь у нас есть 4 дроби для умножения. Итак, мы используем правило умножения дробей, чтобы умножить все эти дроби. 4/5 × 10/6 × 1/4 × 25/1
- Шаг 3: Это означает, что сначала перемножаются числители, а затем перемножаются знаменатели.
 Здесь произведение числителей будет 4 × 10 × 1 × 25 = 1000. Произведение знаменателей будет 5 × 6 × 4 × 1 = 120.
Здесь произведение числителей будет 4 × 10 × 1 × 25 = 1000. Произведение знаменателей будет 5 × 6 × 4 × 1 = 120. - Шаг 4: Дробь, которую мы получаем в результате произведения, равна 1000/120. Наконец, произведение упрощается или сокращается, это означает, что 1000/120 = 25/3 = \(8\dfrac{1}{3}\)
Как умножать отрицательные дроби на целые числа?
Для умножения отрицательных дробей на целые числа используются те же правила умножения. Это означает, что целое число записывается в виде дроби, а затем умножается на отрицательную дробь. Числители перемножаются, затем знаменатели перемножаются, а затем при необходимости упрощаются. Однако следует помнить, что произведение будет иметь знак, соответствующий знаку, данному в дроби. Это означает, что если отрицательную дробь умножить на целое положительное число, произведение будет иметь отрицательный знак. Например, -6/4 × 5 = -6/4 × 5/1. Теперь мы можем перемножить числители и знаменатели, чтобы получить -30/4, что в дальнейшем будет уменьшено до -15/2.
Что такое правило умножения дробей?
Умножение дробей осуществляется двумя простыми способами. Сначала умножьте числители, а затем знаменатели обеих дробей, чтобы получить результирующую дробь. Затем нам нужно упростить полученную дробь, чтобы получить произведение. При необходимости его можно еще уменьшить. Это можно понять на простом примере. 2/6 × 4/7 = (2 × 4)/(6 × 7) = 8/42 = 4/21.
Скачать БЕСПЛАТНЫЕ учебные материалы
Умножение дробей на целые числа
Как умножать дроби на целые числа
Нужно научиться умножать дроби на целые числа? Или как делить дроби на целые числа? Процесс, вероятно, проще, чем вы думаете! Мы разбираем 4 простых шага для умножения дробей на целые числа, а также один дополнительный шаг для деления дробей и целых чисел. Изучите этот важный математический навык, а затем проверьте свои знания, пройдя наш тест в конце этого руководства.
Как умножать дроби на целые числа: 4 шага
Умножение дробей на целые числа может показаться пугающим, но на самом деле процесс довольно прост: нужно выполнить всего четыре шага. Мы проведем вас через каждый из шагов с нашим первым примером вопроса, а затем предоставим два дополнительных примера, чтобы вы хорошо поняли, как умножать дроби на целые числа.
Мы проведем вас через каждый из шагов с нашим первым примером вопроса, а затем предоставим два дополнительных примера, чтобы вы хорошо поняли, как умножать дроби на целые числа.
Пример вопроса 1: ⅜ x 6
Шаг 1. Превратите целое число в дробь
Ваш первый шаг — превратите целое число в дробь. Это легко: вы просто присваиваете ей знаменатель, равный 1. Итак, в нашем примере 6 становится 6 / 1 . Это верно, потому что 6, разделенное на 1 группу, по-прежнему равно 6. Это верно для любого целого числа: 3 = 3 / 1 , 17 = 17 / 1 и т. д.
Теперь у нас есть ⅜ x 6 / 1
Шаг 2: Умножение числителей
Затем мы умножаем два числителя (верхнее число в дроби).
3 x 6 = 18, так что теперь у нас есть числитель для нашего ответа: 18 /__
Шаг 3. Умножьте знаменатели
Теперь умножьте два знаменателя (нижнее число в дроби). Когда вы умножаете дробь на целое число, это будет легко, потому что вы просто умножаете на 1.
Когда вы умножаете дробь на целое число, это будет легко, потому что вы просто умножаете на 1.
8 x 1 = 8.
Добавьте его к нашему ответу, чтобы получить: 18 /8. Ну вот!
Шаг 4. Упрощение
Но мы еще не закончили. Можно было бы упростить дробь. Простейшая форма дроби — это когда верх и низ дроби представляют собой наименьшие целые числа, которыми они могут быть. Например, дробь 18 /8 не является простейшей, потому что ее можно сократить до 9 /4, разделив верхние и нижние части дроби на 2,9.0007
9 /4 — это дробь в ее простейшей форме, но вы можете предпочесть преобразовать ее в смешанное число, поскольку 9 /4 больше 1.
4 дважды входит в число 9 с остатком 1. , поэтому ответ также можно записать как 2 ¼.
Вы также можете указать ответ в виде десятичной дроби. У нас есть целое руководство по преобразованию дробей в десятичные (и наоборот), но вот как это сделать просто. 2 остается прежним, так как это целое число. Вы, наверное, уже знаете, что ¼ равно 0,25, так что это становится значением справа от десятичной дроби для окончательного ответа 2,25.
2 остается прежним, так как это целое число. Вы, наверное, уже знаете, что ¼ равно 0,25, так что это становится значением справа от десятичной дроби для окончательного ответа 2,25.
Шаг 1: 4 /1 x ⅖
Шаг 2: 4 x 2 = 8
Шаг 3: 5 x 1 = 5
Шаг. 4: Наш ответ, 8 /5, не может быть далее упрощен как неправильная дробь (где числитель больше знаменателя), но его можно преобразовать в смешанное число. 5 входит в 8 один раз, а осталось 3, поэтому ответ смешанного числа равен 1 ⅗.
Чтобы перевести ⅗ в десятичную дробь, сначала нам нужно привести знаменатель к значению 10. Для этого достаточно обе части дроби умножить на 2, получив 6 /10. Теперь мы хотим, чтобы знаменатель был равен 1, чтобы избавиться от дроби, поэтому мы делим каждую часть дроби на 10. Это дает нам ,6 /1, что также равно всего 0,6. Объедините это с целым числом (1) из ответа, и ваш окончательный ответ в десятичной форме будет 1,6.
Пример вопроса 3: 5 x 2 3 /7
Шаг 1. Дробь представляет собой смешанное число, поэтому сначала нам нужно преобразовать ее в неправильную дробь. Помните, что при сложении или вычитании дробей знаменатели должны быть одинаковыми. Чтобы у целого числа 2 был один и тот же знаменатель, разделите его на 9.0017 2 /1, затем умножьте верх и низ на 7. Вы получите 14 /7, что при сложении с 3 /7 равно 17 /7. Сделайте 5 тоже дробью. Теперь у нас есть: 5 /1 x 17 /7
Шаг 2: 5 x 17 = 85
Шаг 3: 7 x 1 = 7
Шаг 4: Теперь у нас есть 85 /7. Его нельзя упростить, но можно превратить в смешанное число. 7 входит в число 85 двенадцать раз с остатком 1. Наш окончательный ответ: 12 1 /7, или 12,14 в десятичной форме.
5 шагов к делению дробей на целые числа (и наоборот)
Деление двух дробей аналогично умножению на обратную дробь второй дроби. Это означает, что, как только вы освоите умножение дробей на целые числа, вы практически знаете, как делить дроби на целые числа!
Это означает, что, как только вы освоите умножение дробей на целые числа, вы практически знаете, как делить дроби на целые числа!
Ниже мы проведем вас по шагам и объясним два примера: в одном вы делите дробь на целое число (используя те же значения, что и в примере № 1 выше), а в другом — целое число делите на дробь.
Пример вопроса 4: ⅜ / 6
Шаг 1. Превратите целое число в дробь a 1 в знаменателе: 6 /1
Шаг 2. Переверните второе число
Это дополнительный шаг, необходимый для деления дробей. Сейчас у нас есть ⅜ / 6 /1. Переверните второе число и измените знак деления на знак умножения: ⅜ x ⅙ 9.0007
Как только вы это сделаете, вы проработаете проблему так же, как и в приведенных выше примерах.
Шаг 3: Умножением числителей
3 x 1 = 3
Шаг 4: Умноженные знаменатели
8 x 6 = 48
.
Не забывайте упрощать! Мы можем разделить и числитель, и знаменатель на 3, что даст нам окончательный ответ 1 /16 или 0,0625.
Шаг 1: 4 /1 /⅖
Шаг 2: 4 /1 x 5 /2
Шаг 3: 4 x 5 =. 20
Шаг 4: 1 x 2 = 2
Шаг 5: 20 /2 упрощается до 10!
3 совета, как избежать ошибок
Теперь вы знаете, как умножать дроби с целыми числами, а также как делить дроби с целыми числами. проблемы, даже если вы хорошо понимаете концепции. Сократите свои шансы на ошибку, следуя этим трем советам.
#1: Знайте, ожидать ли большое или малое число
Один из лучших способов проверить и избежать глупых ошибок — быстро узнать, не отличается ли ваш ответ от ожидаемого. Когда вы делите или умножаете дроби и целые числа, вы можете ожидать определенных закономерностей.
Ответ, скорее всего, будет > 1
- Дробь, умноженная на целое число
- Целое число, умноженное на дробь
- Целое число разделить на дробь
Ответ, скорее всего, будет < 1
- Дробь, деленная на целое число
Очевидно, что знание этого трюка не только даст вам правильный ответ, но если вы решаете задачу типа ⅖ / 4 и получаете число больше 1, вы можете быть уверены, что вам следует вернуться назад. и перепроверьте свою работу.
и перепроверьте свою работу.
#2: Порядок в числителях и знаменателях
Можно легко перепутать числители и знаменатели, особенно при делении и переворачивании дробей. Большинство ошибок совершается, когда люди умножают неправильные числа или помещают ответ числителя в место знаменателя (или наоборот).
Чтобы избежать этого, следите за чистотой своей работы и всегда четко указывайте, что такое числитель и что такое знаменатель. Например, после умножения числителей добавьте тире под своим ответом (например, 4 /___), чтобы вы помнили, что вы только что решили, и что следующее значение, которое вы вычислите, будет знаменателем.
#3: Всегда упрощайте
Как только вы закончите умножение и запишете свой ответ, у вас может возникнуть соблазн сразу перейти к следующему вопросу. Потратьте дополнительные несколько секунд, чтобы посмотреть, можно ли упростить ваш ответ. Некоторые преподаватели будут снимать баллы за правильные, но не упрощенные ответы, а вы точно не хотите получать отчисления после того, как выполнили всю работу правильно! Упростите, насколько это возможно, и, если значение вашей дроби больше 1, преобразуйте ее в смешанное число, если это то, что предпочитает ваш учитель (у некоторых другие предпочтения, поэтому попросите убедиться, что вы делаете все шаги, необходимые для ).
Тест: Деление и умножение дробей на целые числа
Готовы проверить свои знания о том, как умножать дроби на целые числа? В этом разделе десять вопросов. Для каждого вы будете умножать дроби на целые числа или делить дроби на целые числа. Попробуйте их, а затем проверьте свои ответы с помощью приведенного ниже ключа.
№1: 5 x 4 /3
№2: 2 /9 x 11
#3: 12 x ⅕
#4: ½ / 3
#5: 4 /9 x 7
#6: ⅞ x 2
#7: 8 / ⅔ 0 7
7 900 /12 x 5
#9: 5 / 4 /7
#10: 4 /15 x
Ключ ответа
#1: 6 ⅔
#2: 2 4 /9
#3: 2 ⅖
#4: ⅙
#5: 3 1 /9
#6: 1 ¾
#7: 12
#8: 2 1 /12
#9: 8 ¾
#10: 2 6 /15
Что дальше?
Хотите узнать больше о десятичных дробях, дробях и процентах? Ознакомьтесь с 3 шагами по преобразованию десятичных дробей в дроби (и обратно)
. Если вы не знаете, какие уроки математики в средней школе вам следует посещать, это руководство поможет вам определить свое расписание, чтобы быть уверенным, что вы готовы к колледжу. !
Если вы не знаете, какие уроки математики в средней школе вам следует посещать, это руководство поможет вам определить свое расписание, чтобы быть уверенным, что вы готовы к колледжу. !
Теперь, когда вы стали экспертом в делении и умножении дробей, научитесь переводить градусы Цельсия в градусы Фаренгейта!
Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!
Наша база данных проверенных преподавателей включает в себя ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.
У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!
Кристин Сарикас
Об авторе
Кристин окончила Мичиганский государственный университет со степенью в области экологической биологии и географии и получила степень магистра в Университете Дьюка. В старшей школе она набрала 99-й процентиль по SAT и была названа финалистом национальных заслуг. Она преподавала английский язык и биологию в нескольких странах.
В старшей школе она набрала 99-й процентиль по SAT и была названа финалистом национальных заслуг. Она преподавала английский язык и биологию в нескольких странах.
Умножение дробей на целые числа
Умножение дробей на целое число является простой операцией. Это одно из основных понятий, которым учат в младших классах. Его учат повышать арифметические способности учащихся. Учащиеся часто путаются при умножении и делении дробей. В этой статье будут рассмотрены методы умножения дроби на целое число с некоторыми примерами.
Прежде чем научиться умножать дробь на целое число, давайте рассмотрим некоторые основные термины, которые мы будем использовать при умножении. Вы хорошо знаете, что такое дроби? Дроби, как правило, представляют собой числа, представленные в виде p/q. Например, 2/3, 9/2 и т. д. Вы должны понимать, что дробное число состоит из двух частей. Часть над «тире» является числителем, а число под «тире» называется знаменателем. К дробям можно применять все типы математических операций.
Если вы разделите числитель на знаменатель, вы получите либо целое число, либо десятичное число. Это уже не дробь. Таким образом, значение никогда не может быть дробью, если форма не равна p/q.
Чтобы сначала научиться умножать дробь на целое число, нам нужно научиться умножать дробь на другую дробь. Сообщите нам о том же в статье.
Допустим, у нас есть две дроби: d/c и j/k. Чтобы умножить эти дроби, вам нужно правильно записать их друг против друга. Затем посмотрите числители и знаменатели дробей. Умножьте числители вместе (d x j) = x. Запишите результат умножения числителей в разных дробях, скажем, «х».
Аналогичным образом умножьте знаменатели дробей. Запишите мультипликативный результат знаменателя под результирующим числителем, (c x k) = y. Таким образом, умножение двух дробей может быть представлено как:
d/c x j/k = (d x j) / (c x k) = x/y
Давайте рассмотрим пример для лучшего понимания.
Пример 1: Умножьте дроби ⅘ и 3/7.
Решение: Посмотрите на пошаговое решение ниже→
Шаг 1: Запишите числа вместе, используя символ умножения.
4/5 x 3/7
Шаг 2. Умножьте числители и запишите результат в виде новой дроби.
(4 x 3) = 12
Шаг 3: Теперь умножьте знаменатели и запишите их под результирующим числителем, используя тире.
(5 x 7) = 35
Шаг 4: Правильно расставьте дробь: 12/35.
Дробь после умножения 4/5 на 3/7 равна 12/35. Если числа в дробях кратны какому-то меньшему числу, то можно легко сократить дробь в более простой форме. Единственное условие — если числитель делить на любое число «а», то нужно делить и знаменатель на то же число «а».
Пример 2: Упростите дробь 12/9.
Решение: Мы видим, что числитель = 12 и знаменатель = 9 кратны 3. Следовательно, мы должны разделить числитель на 3 и знаменатель на 3. Это дает нам
12/ 3 = 4
9 /3 = 3
Следовательно, результирующая дробь равна 4/3, что является неправильной функцией.
Теперь мы научились умножать две дроби. В этом разделе вы узнаете, как умножить дробь на целое число. Предположим, у нас есть дроби d/c и целое число «k». Первый шаг к умножению дроби и целого числа всегда начинается с правильного написания их друг против друга со знаком умножения. У нас нет формы «p/q» в случае целых чисел. Следовательно, мы сначала преобразуем число в дробную форму. Для этого поставьте тире под целым числом с 1 в знаменателе. Теперь у нас есть целое число в форме p/q.
Теперь проделываем те же шаги, что и в части умножения дроби. Теперь посмотрите на числители и знаменатели дробей и целого числа. Умножьте числители на целое число «k», таким образом, (d x k) = x. Теперь умножьте знаменатель дроби на 1 (потому что знаменатель целого числа равен 1). Это дает (с х 1 = с). Таким образом, умножение двух дробей можно представить как:
d/c x k/1 = (d x k) / (c x 1) = x/c
В случае умножения дробей на целые числа знаменатель дроби сохраняется. Таким образом, всякий раз, когда вы встречаете такой тип умножения, ставьте знаменатель как дробь и умножайте числитель.
Таким образом, всякий раз, когда вы встречаете такой тип умножения, ставьте знаменатель как дробь и умножайте числитель.
Пример 1: Умножьте дробь 5/11 на 6.
Решение: Посмотрите на приведенное ниже пошаговое решение→
Шаг 1: Запишите числа вместе, используя символ умножения.
5/11 x 6
Шаг 2. Преобразуйте целое число в дробную форму.
5/11 x 6/1
Шаг 3: Умножьте числители и запишите результат
5 x 6 = 30
(11 x 1) = 11
Шаг 5: Расставьте дробь в правильной форме: 30/11.
Альтернативный метод
Шаг 1. Запишите числа в виде 5/11 x 6.
Шаг 2. Поскольку мы знаем, что в таких случаях знаменатель не изменится, нам нужно умножить числители.
Шаг 3: Умножьте числители = 5 x 6 = 30
Шаг 4: Запишите результаты в дробной форме = 30/11
Надеюсь, теперь вопрос о том, как я умножаю дроби на целое число, ясен. Далее рассмотрим очень интересную идею.
Далее рассмотрим очень интересную идею.
Пример 2: Умножить 11 на 3/11
Решение: Первым шагом всегда будет правильное упоминание чисел с символом умножения. Следовательно,
11 x 3/11
Следуя шагам, описанным выше, мы получаем результирующую дробь как 33/11 = 3
. Но мы можем заметить, что если мы исключим 11 с самого начала, мы все равно получим ответ как 3.
Таким образом, из этого примера мы получаем очень важное понятие. Давайте узнаем об этом дальше.
Особый случай
Как указано в приведенном выше примере. Предположим, дробь умножается на целое число, которое либо кратно знаменателю, либо равно знаменателю. В этом случае вы можете исключить или уменьшить числа до фактического умножения. Поймите это на примерах ниже:
Пример 1: Умножьте 1/7 на 7.
Решение: Сначала запишем числа в правильном формате.
1/7 x 7
Мы видим, что целое число и знаменатели совпадают. Следовательно, мы можем исключить их и получить ответ в виде числителя дроби.
Следовательно, мы можем исключить их и получить ответ в виде числителя дроби.
Здесь 7 исключает 7, и ответ равен 1.
Пример 2: Умножьте 3/7 на 21.
Решение: Первоначально правильно отформатировав умножение
3/7 x 21 9000 знаменатель и целые числа кратны 7. Следовательно, мы приводим их к наименьшей форме. 7, деленное само на себя, становится 1, а 21, деленное на 7, становится 3. Теперь у нас осталось 3 x 3 в числителе. Следовательно, ответ на этот вопрос 9.
Умножение дроби на нольКак мы все знаем, целые числа представляют собой набор действительных чисел, начинающихся с нуля и простирающихся до положительной бесконечности. Мы уже видели все случаи, что происходит при умножении дроби на целое число. Если умножить дробь на 1, получится само число. Но что происходит, когда вы умножаете дробь на ноль.
Мы знаем, что все, что умножается на ноль, равно 0. Следовательно, когда дробь умножается на ноль, результирующая дробь равна нулю или 0/1.
Пример: Умножить 22/17 на 0.
Решение: Записав дроби в правильной форме, получим
22/7 x 0
Поскольку мы знаем, что число, умноженное на ноль, равно 0. Следовательно ,
22/7 x 0 = 0
Что произойдет, если мы умножим число на обратную величину нуля?
Обратное число — это когда числители и знаменатели меняются местами. Поскольку 0 = 0/1, следовательно, его обратная величина равна 1/0. Предположим, у нас есть дробь «a/b». Используя шаги, которые мы изучили до сих пор, a x 1 = a и b x 0 = 0. Следовательно, результирующая дробь равна a/0. В математике 1/0 или что-либо, деленное на ноль, не определяется. Следовательно, мы не можем умножить число на обратную величину нуля.
Пример умножения дроби на целое число Словесная задача: Джилл готовит домашний горячий шоколад. Она использует одну четвертую чайную ложку смеси для горячего шоколада, чтобы приготовить 1 чашку горячего шоколада. Подсчитайте количество чайных ложек, необходимое для приготовления 10 чашек горячего шоколада?
Подсчитайте количество чайных ложек, необходимое для приготовления 10 чашек горячего шоколада?
Решение: чайных ложек на 1 чашку = ¼
чайных ложек на 10 чашек = ¼ x 100004 Мы можем уменьшить его на 2,
→ 5/2
Следовательно, количество чайных ложек, необходимых для приготовления 10 чашек горячего шоколада, равно 5/2.
Концепция умножения в целых числах и фракциях (определение, типы и примеры)
Содержание
- Целые числа
- Фракция
- Умножение доли на целое число
- Умножение и целое число
- Часто задаваемые вопросы
Набор чисел без дробей, десятичных знаков или даже отрицательных целых чисел называется целым числом. Он состоит из набора положительных целых чисел и нулей. Набор целых чисел состоит из натуральных чисел, включая ноль (0). В математике этот набор целых чисел задается как {0, 1, 2, 3, …}, который обозначается буквой W.
W = {0, 1, 2, 3, 4, …}
Дроби являются частями целого или набора, равного по размеру. Каждая часть целого, разделенная на равные части, есть часть целого. Дробь состоит из двух частей. Числитель — это число в верхней части строки. Он указывает, сколько равных частей было взято из всей коллекции или целого. Число под чертой является знаменателем. Он отображает общее количество равных частей, которые можно разделить на целое, или общее количество равных частей в коллекции.
Например, апельсин разделен на две равные по размеру части. В результате каждая часть равна половине \((\frac{1}{2})\).
Чтобы умножить дробь на целое число, выполните следующие действия:
1. Целое число имеет единицу в знаменателе, поэтому запишите его в виде дроби.
2. Умножить целое на числитель.
3. При необходимости упростите. Попробуйте записать свой ответ в виде смешанного числа, если оно больше единицы.
Например , \(\frac{1}{5}\times 3 = ?\)
Для начала преобразуйте целое число в дробь с единицей в знаменателе.
\(3 = \frac{3}{1}\)
Теперь перемножьте числители и знаменатели.
\(\frac{1}{5}\times \frac{3}{1} = \frac{1\times 3}{5\times 1} = \frac{3}{5}\)
Наконец, упростите. Поскольку \(\frac{3}{5}\) не больше 1, не меняйте его на смешанное число.
Итак, \(\frac{1}{5}\times 3=\frac{3}{5}\)
- Когда вы умножаете дробь на целое число, это похоже на многократное сложение.
Посмотрите на приведенный выше пример \(\frac{1}{5}\times 3\). Это то же самое, что и \(\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\).
Помните, что \(\frac{1}{5}\times \frac{3}{1}=\frac{1\times 3}{5\times 1}=\frac{3}{5} \). Есть три части, каждая из которых составляет пятую часть целого.
Примеры умножения целых чисел и дробей с помощью числовой прямой:
1. У вас есть четыре галлона краски, и вы используете 3 4 галлонов из него. Сколько краски вы использовали?
Решение:
Переформулировать вопрос — хороший способ подумать над ним.
Что такое \(\frac{3}{4}\times 4?\) (или) \(\frac{3}{4}\times 4=?\)
Шаг 1: Использование числа линии, мы должны умножить дробь \(\frac{3}{4}\) на целое число 4. Сначала нарисуйте линию и поставьте решетку. Предположим, что каждая решетка представляет собой \(\frac{3}{4}\). Таким образом, разделы будут \(\frac{3}{4}\), \(\frac{6}{4}\), \(\frac{9{4}\), \(\frac{12}{4}\) и \(\frac{15}{4}\).
Шаг 2: Теперь, \(\frac{3}{4}\) умножить на 1 означает, что мы должны сделать один прыжок, чтобы добраться до \(\frac{3}{4}\) из 0 на числовой прямой, так что \(\frac{3}{4}\) умножить на 1 будет \(\frac{3}{4}\).
И \(\frac{3}{4}\) умножить на 2 означает, что нам нужно сделать два прыжка, чтобы добраться до \(\frac{6}{4}\) от 0 на числовой прямой так, чтобы \(\frac{3}{4}\) умножить на 2 будет \(\frac{6}{4}\).
Кроме того, \(\frac{3}{4}\) умножить на 3 означает, что нам нужно сделать три прыжка, чтобы добраться до \(\frac{9}{4}\) от 0 на числовой прямой так, чтобы \( \frac{3}{4}\) умножить на 3 будет \(\frac{9}{4}\).
Аналогично, \(\frac{3}{4}\) умножить на 4 означает, что нам нужно сделать четыре прыжка, чтобы добраться до \(\frac{12}{4}\) от 0 на числовой прямой, поэтому что \(\frac{3}{4}\) умножить на 4 будет \(\frac{12}{4}\).
Шаг 3: Каждая часть равна \(\frac{3}{4}\) галлонам, и вы использовали 4 из них. Записывается как умножение,
у нас есть \(\frac{3}{4}\times4=\frac{12}{4}\) или 3 (наблюдая за числовой прямой)
Следовательно, вы использовали \(\frac{12 {4}\) или 3 галлона краски.
Умножить числитель дроби на целое число. Затем напишите произведение над знаменателем. Общий множитель — это множитель, который является общим для двух или более целых чисел. Например, 2 и 4 делят 2 как общий множитель.
Алгебраическая формула: \(\text{целое число}\times \frac{числитель}{знаменатель}=\frac{\text{целое число}\times \text{числитель}}{знаменатель}\), где знаменатель никогда не равняется 0,9Пример 1
\(2\times\frac{7}{8}\)
\(=\frac{2\times 7}{8}\)( Умножьте числитель на целое число, затем запишите произведение над знаменатель)
\(=\frac{14}{8}\)
\(=\frac{7}{4}\) или \(1\frac{3}{4}\) (упрощенно)
Итак, произведение \(1\frac{6}{8}\)
пример 2 }\)
\(=\frac{9\times 2}{3}\) ( Умножьте числитель на целое число, затем запишите произведение над знаменателем)
\(=\frac{18}{3 }\)
\(=6\) (упрощенно)
Итак, произведение равно \(6\).
Пример 3 : Вода составляет примерно \(\frac{6}{10}\) веса арбуза. Арбуз весит 30 фунтов. в целом. Сколько воды содержит арбуз?
Решение:
Чтобы найти \(\frac{6}{10}\) 30, умножьте.
\(30\times\frac{6}{10}\)
\(=\frac{30\times 6}{10}\) (Умножьте числитель на целое число, произведение запишите над знаменателем )
\(= 18\) (упрощенно)
Итак, арбуз содержит \(18\) фунтов воды.
Часто задаваемые вопросы
Что означает целое число?
Набор чисел без дробей, десятичных знаков и даже отрицательных целых чисел называется целым числом. Он состоит из набора положительных целых чисел и нулей. В качестве альтернативы целые числа могут быть определены как набор неотрицательных целых чисел. Набор натуральных чисел плюс число 0 в совокупности известны как целые числа.
Что означает дробь?
Фракции — это части целого или набора, равные по размеру. Каждая часть целого, разделенная на равные части, есть часть целого. Дробь состоит из двух частей. Числитель — это число в верхней части строки. Он указывает, сколько равных частей было взято из всей коллекции или целого.
Каждая часть целого, разделенная на равные части, есть часть целого. Дробь состоит из двух частей. Числитель — это число в верхней части строки. Он указывает, сколько равных частей было взято из всей коллекции или целого.
Что мы подразумеваем под умножением дробей на целые числа?
Умножение дробей на целые числа относится к многократному сложению, поскольку дробь умножается столько же раз, сколько и целое число. Те же правила умножения применяются при умножении дробей с целыми числами: числители умножаются вместе, затем знаменатели умножаются вместе и, наконец, произведение уменьшается.
Посмотрите другие наши курсы
Умножение дробей на целые числа
Этот урок научит вас умножать дроби на целые числа на основе визуальных моделей. Мы просто находим общее количество штук путем умножения, то есть вы умножаете целое число и верхнее число (числитель) дроби. В уроке также много текстовых задач.
В видео ниже я учу умножать дроби на целые числа, что является довольно простой концепцией. Вам просто нужно помнить, что 4 х (2/3) не рассчитывается как (4 х 2) / (4 х 3). В визуальной модели вы можете раскрасить две трети четыре раза, чтобы получить ответ. Я также показываю интересную связь между (1/3) x 5 или одной третью пяти кругов и 5 x (1/3), или пятью копиями 1/3.
Вам просто нужно помнить, что 4 х (2/3) не рассчитывается как (4 х 2) / (4 х 3). В визуальной модели вы можете раскрасить две трети четыре раза, чтобы получить ответ. Я также показываю интересную связь между (1/3) x 5 или одной третью пяти кругов и 5 x (1/3), или пятью копиями 1/3.
Сколько пятых в общий?
12/5 равно 2 2/5. |
|
1. Несколько раз раскрасьте части, чтобы решить
умножения. Дайте ответ в виде смешанного числа .
Дайте ответ в виде смешанного числа .
|
| ||||||
|
|
2. Заполните.
Заполните.
а.
| б.
| г.
|
Решите, например, с помощью чертежа.
3. Высокие стаканы Эрики вмещают 3/8 литра каждый.
Сколько воды ей нужно, чтобы заполнить
четыре из них?
| 4. Марлен хочет утроить этот рецепт (сделать три раза). Сколько ей понадобится каждого ингредиента? |
|
| Чтобы умножить целое число на дробь, найдите общее количество «частей» (путем умножения). Это означает, что вы умножаете целое число и верхнее число (числитель) фракции. | |||||||||||||
| |||||||||||||
Пример 2. Умножение можно выполнять в любом порядке. (Другими словами, умножение равно коммутативный .)
|
5. Решить. Дайте свой ответ в самых низких терминах (упрощенное) и как смешанное число. Изучите пример.
|
| ||||||||||||
|
| ||||||||||||
|
| ||||||||||||
|
| ||||||||||||
|
|
6. Уильям спросил 20 пятиклассников, сколько времени
они потратили на работу по дому / работу по дому накануне. Он
затем округли ответы до ближайшей 1/8 часа.
линейный график показывает его результаты. Каждая отметка x
соответствует одному пятикласснику.
а. Исключить трех учеников, которые сделали меньше всего работу по дому и троих, которые сделали больше всего, и введите:
Большинство учащихся использовали
___________ и __________ часов на работу по дому и работу по дому.
б. Среднее значение для этих данных составляет 7/8 часов. Использовать это
как рассчитать
много часов 20 пятого
всего грейдеров, используемых для работы по дому.
| НАПОМИНАНИЕ Дробь от число означает что дробь РАЗ
число. |
| |||||||||
Теперь вы уже научились находить 3/10 от 120 долларов США при использовании подразделения :
Оба метода по существу одинаковы: вы делите на 10 и умножаете на 3, только в двух разных порядках. | ||||||||||
7. Найдите следующие количества.
а. 2/5 из 35 фунтов
б. 4/9 из 180 км
8. Папа строит полку длиной 4 метра. Он хочет использовать
2/5 из них для
садовые принадлежности и остальное для инструментов.
Какова длина этих двух частей
полка?
( Подсказка: использование сантиметров может помочь. )
9. а. Джанет и Сэнди заработали 81 доллар за работу во дворе. Они разделили
деньги неравномерно, так что 2/3 досталось Джанет, а Сэнди
получил
остальные. Сколько денег получила каждая девочка?
б. Что произойдет, если сумма, которую они заработали, составляет 80 долларов?
10.
Энди нарисовал на бумаге прямоугольник размером 5 на 4 дюйма. Затем он начертил
Затем он начертил
второй прямоугольник, длина и ширина которого составляла 3/4 длины и ширины первого.
один.
а. Какой длины и ширины была секунда Энди? прямоугольник?
б. Нарисуйте оба прямоугольника (на отдельной бумаге).
| Эпилог: Есть кое-что интересное в умножении «дроби на целое».
номер» или умножение «целого числа на дробь». Давайте сравним. | ||||||||||
|
из которых получается 3 целых пирога. | |||||||||
в любом порядке. Но они означают разные вещи (четвертая часть 12 и 12 копий 1/4). | ||||||||||
11. Заполните недостающие части.
| а. Две пятых от 10 | 10 копий 2/5 | |||||||||
что равно . |
что равно . |
| б. А ______________ часть 5 | 5 копий 1/3 | |||||||||
что равно . |
что равно . |
| в. ____________________ из 7 | 7 экз. |

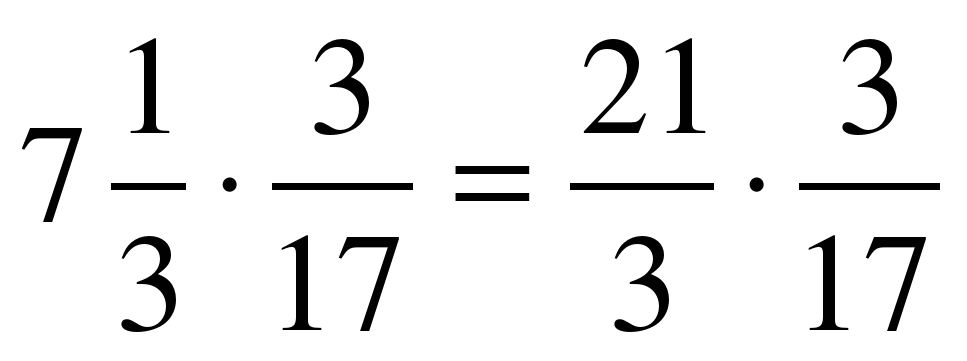


 Это 38-е место в мире.
Это 38-е место в мире. 😉 @Falcons_BMS #FalconsInFlight pic.twitter.com/M6Rg7zaXXQ
😉 @Falcons_BMS #FalconsInFlight pic.twitter.com/M6Rg7zaXXQ

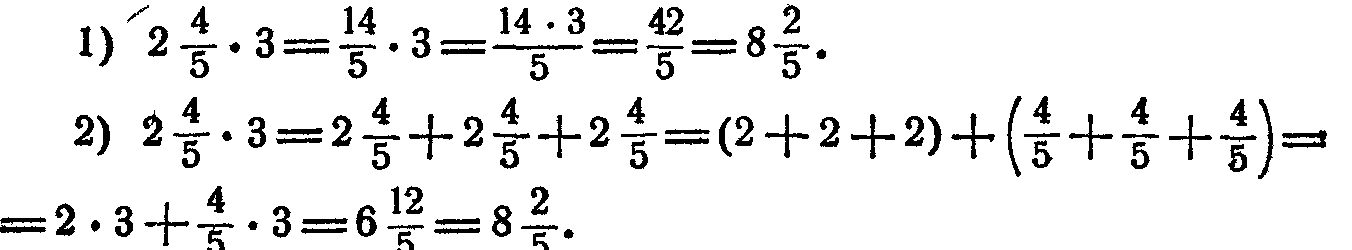
 Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.
