Как умножать натуральное число на дробь?

Как умножать натуральное число на дробь?

Итак, чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это натуральное число, а знаменатель оставить тот же. Например: Вычислим произведение четырёх пятых и трёх. Умножение можно заменить сложением, то есть три раза сложить дробь четыре пятых.

Как умножить дробь на дробь с разными знаменателями?

Чтобы умножить дробь на дробь, надо:

1. числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;
2. знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;

Как умножить число на десятичную дробь?

Чтобы умножить десятичную дробь на натуральное число, надо: 1) умножить её на это число, не обращая внимания на запятую; 2) в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби. Например, надо вычислить 3,2*5.

Как правильно умножать числа с запятыми?

Чтобы умножить десятичную дробь на 0,1, 0,01, 0,001, нужно перенести запятую в дроби влево на столько знаков, сколько нулей стоит перед единицей. Ноль целых — тоже считаем. Если цифр не хватает — просто дописываем дополнительный ноль — один или несколько — после запятой.

Как умножить десятичную дробь на смешанное число?

Для умножения конечной десятичной дроби или бесконечной периодической десятичной дроби на обыкновенную дробь или смешанное число, нужно десятичную дробь представить в виде обыкновенной дроби, после чего провести умножение. Проведите умножение десятичной дроби 0,4 на смешанное число . Так как 0,4=4/10=2/5 и , то .

Как умножить на 0 2?

Как легко умножить на 0,2 При умножении на 0,2 можно заменить умножением на 15. Обратная дробь одной пятой −5 То есть для того чтобы умножить на 0,2 надо разделить на 5.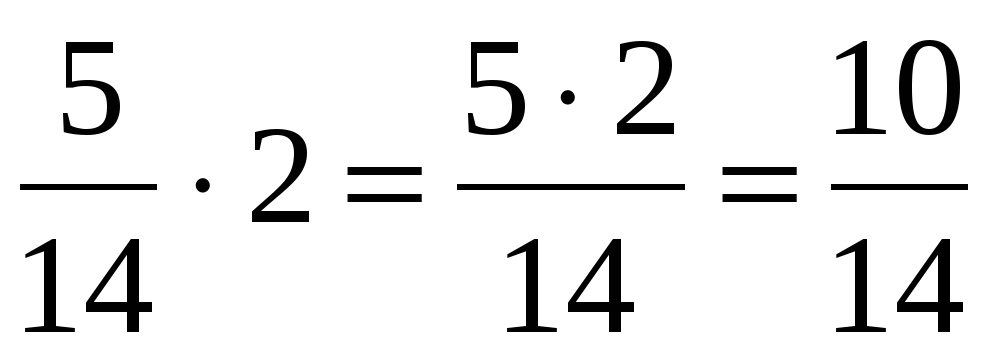

Как умножить десятичную дробь на 0 1 на 0 01 на 0 001?

Чтобы умножить число на 0,1, 0,01, 0,001 и т. д., надо: 1….Например, необходимо выполнить умножение: 4,7*0,001.

1. Перед единицей во втором множителе стоит 3 нуля.
2. Переносим запятую в числе 4,7 на 3 знака влево. Проблема — цифр не хватает.
3. Впереди пишем 3 нуля.
4. Итак, 4,7*0,001=0,0047.

Как умножить на 0001?

умножение числа на 0,001 можно заменить его делением на 1000. Чтобы умножить число на 0,001, надо запятую в записи этого числа перенести на три знака влево.

Как умножать целые числа на Нецелые?

Умножение десятичных дробей

1. Десятичные дроби записывают в столбик и умножают как обыкновенные числа.
2. Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.
3. В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.

Как умножить на ноль?

Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения. Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует.

Что будет если ноль делить на ноль?

Разделить 0 на 0 — значит, подобрать такое число, что если умножить его на 0, получится 0. … На самом деле подойдет любое число; ведь любое число, умноженное на ноль, дает ноль. Мы не можем выбрать какой-то один результат, поэтому говорят, что результат деления ноля на ноль не определен.

Сколько будет если поделить на 0?

При делении 0 на любое число получается 0: 0 : a = 0, где a — любое число, кроме нуля. Обрати внимание! На ноль делить нельзя!

Что значит одно число разделить на другое?

Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом. Деление можно представить, как неоднократно повторяемое вычитание.

Правила умножения и деления смешанных чисел. Деление смешанных чисел. Формула умножения дробей

В этой статье мы разберем умножение смешанных чисел . Сначала озвучим правило умножения смешанных чисел и рассмотрим применение этого правила при решении примеров. Дальше поговорим об умножении смешанного числа и натурального числа. Наконец, научимся выполнять умножение смешанного числа и обыкновенной дроби.

Навигация по странице.

Умножение смешанных чисел.

Умножение смешанных чисел можно свести к умножению обыкновенных дробей . Для этого достаточно выполнить перевод смешанных чисел в неправильные дроби .

Запишем правило умножения смешанных чисел :

• Во-первых, умножаемые смешанные числа нужно заменить неправильными дробями;
• Во-вторых, нужно воспользоваться правилом умножения дроби на дробь.

Рассмотрим примеры применения этого правила при умножении смешанного числа на смешанное число.

Пример.

Выполните умножение смешанных чисел и .

Решение.

Сначала представим умножаемые смешанные числа в виде неправильных дробей: и . Теперь мы можем умножение смешанных чисел заменить умножением обыкновенных дробей: . Применив правило умножения дробей, получаем . Полученная дробь несократима (смотрите сократимые и несократимые дроби), но она неправильная (смотрите правильные и неправильные дроби), поэтому, для получения окончательного ответа осталось выполнить выделение целой части из неправильной дроби : .

Запишем все решение в одну строку: .

Ответ:

.

Для закрепления навыков умножения смешанных чисел рассмотрим решение еще одного примера.

Пример.

Выполните умножение .

Решение.

Смешные числа и равны соответственно дробям 13/5 и 10/9 . Тогда . На этом этапе самое время вспомнить про сокращение дроби : заменим все числа в дроби их разложениями на простые множители, и выполним сокращение одинаковых множителей .

Ответ:

Умножение смешанного числа и натурального числа

После замены смешанного числа неправильной дробью, умножение смешанного числа и натурального числа приводится к умножению обыкновенной дроби и натурального числа .

Пример.

Выполните умножение смешанного числа и натурального числа 45 .

Решение.

Смешанное число равно дроби , тогда . Заменим числа в полученной дроби их разложениями на простые множители, произведем сокращение, после чего выделим целую часть: .

Ответ:

Умножение смешанного числа и натурального числа иногда удобно проводить с использованием распределительного свойства умножения относительно сложения. В этом случае произведение смешанного числа и натурального числа равно сумме произведений целой части на данное натуральное число и дробной части на данное натуральное число, то есть, .

Пример.

Вычислите произведение .

) и знаменатель на знаменатель (получим знаменатель произведения).

Формула умножения дробей:

Например:

Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби . Если получится сократить дробь, то вам легче будет дальше производить расчеты.

Деление обыкновенной дроби на дробь.

Деление дробей с участием натурального числа.

Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:

Умножение смешанных дробей.

Правила умножения дробей (смешанных):

• преобразовываем смешанные дроби в неправильные;
• перемножаем числители и знаменатели дробей;
• сокращаем дробь;
• если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.

Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.

Второй способ умножения дроби на натуральное число.

Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.

Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.

Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.

Многоэтажные дроби.

В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:

Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:

Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.

Обратите внимание, например:

При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:

Практические советы при умножении и делении дробей:

1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко.

Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.

2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.

3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.

4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.

5. Единицу на дробь делим в уме, просто переворачивая дробь.

Тема урока: «Умножение и деление смешанных дробей»

Цель: выработать у учащихся умение и навыки применения правила умножения и деления смешанных дробей;

развитие аналитического мышления учащихся, формирование умения у учащихся выделять главное и обобщать.

Задачи: повторить правило умножения и деления обыкновенных дробей.

Проверить умения применения правила умножения и деления обыкновенных дробей,

правило умножения дроби на натуральное число и обратно. Проверить умение переводить неправильную дробь в смешанное число и обратно.

Вывести новое правило и алгоритм умножение и деления смешанных чисел.

Отработать новое правило на выполнении заданий.

Предметные результаты: алгоритм умножения и деления смешанных дробей(памятка)

Метапредметные и личностные результаты :

Регулятивные УУД: постановка цели; план, получение результата

Познавательные УУД: общеучебные, логические, постановка и решение проблемы

Коммуникативные УУД: работа в парах

Оборудование: учебник математики 6 класс

Раздаточный материал.

Проектор.

Ход урока:

I .Проблемная ситуация и актуализация знаний

1.Опрос детей на повторение изученного материала по теме умножение и деление дробей (алгоритм выполнения, правило умножения дроби на натуральное число).

2. Иллюстрация примеров на проекторе. Виды обыкновенных дробей. Как из неправильной дроби получить смешанную и обратно.

3.По окончании опроса самостоятельная работа включающая примеры на умножение и деление обыкновенных дробей и содержащая два примера на умножение и деление смешанных дробей, где дети сталкиваются с проблемой. Правильные ответы для сверки с учащимися отражаются на проекторе.

4. Обсуждение проблемы. Вывести на тему урока.

II .Совместное открытие знаний.

1/Предлагается обсуждение в парах, для озвучивания версии решения возникшей проблемы. Версии записать на школьной доске. Как узнать какая же из версий правильная?

2/Предложить ученикам обратиться к учебнику на соответствующей теме.

3/Выполнить ознакомительное чтение, найти нужный абзац и изучить его для составления алгоритма умножения и деления смешанных дробей. Контроль над выполнением задания.

4/Прослушать версии составить из главного общий алгоритм. Отразить его на проекторе и раздать ученикам в виде памятки.

III .Самостоятельное применение знаний

1/Вернуться к проблеме с решением примеров из самостоятельной работы и применяя полученный алгоритм решить их. Проверить в парах. Результаты отразить на проекторе для сверки.

2/ Дать задание из учебника. Контроль выполнения.

IV. Итог урока

Начать с проблемы возникшей в начале урока, проговорить пути ее решения и полученный результат.

Оценивание работы учащихся.

Задание для домашней работы.

Затем действуем по правилу: первую дробь умножаем на дробь, обратную ко второй (то есть на перевернутую дробь, у которой числитель и знаменатель меняются местами). При умножении дробей числитель умножаем на числитель, знаменатель — на знаменатель.

Рассмотрим примеры на деление смешанных чисел.

Деление смешанных чисел начинаем с перевода их в неправильные дроби. Затем делим полученные дроби. Для этого первую дробь умножаем на перевернутую вторую. 20 и 25 на 5, 3 и 9 — на 3. Получили неправильную дробь, поэтому необходимо .

Смешанные числа переводим в неправильные дроби. Далее по правилу деления дробей первое число оставляем и умножаем его на число, обратное ко второму. Сокращаем 15 и 25 на 5, 8 и 16 — на 2. Из полученной неправильной дроби выделяем целую часть.

Смешанные числа заменяем неправильными дробями и делим их. Для этого первую дробь переписываем без изменений и умножаем на перевернутую вторую. Сокращаем 18 и 36 на 18, 35 и 7 — на 7. В результате — неправильная дробь. Выделяем из нее целую часть.

целых чисел | MS GARCIA MATH

Натуральные числа — это счетные числа {1, 2, 3, …} (целые неотрицательные числа) или десятичная. Целые числа включают все натуральные числа и ноль.

Целые числа — это натуральные числа и их отрицательные значения {… −3, −2, −1, 0, 1, 2, 3, …}.

 

 

 

Положительное число  – это число, большее нуля. В бизнесе положительные числа использовались для обозначения активов.

Отрицательное число  – это действительное число, меньшее нуля. Такие числа часто используются для обозначения дефицита.

Отрицательные числа имеют множество применений в бизнесе и личных финансах. Пример: Как мы можем иметь меньше, чем ничего? Когда мы в долгах.

Два числа, имеющие одинаковую величину, но противоположные по знаку, называются Противоположные числа . Пример: +5 и -5 являются противоположными числами

Абсолютное значение (или модуль) |a| целого числа a является числовым значением a без учета знака. Пример:   |-5|  = 5

Теперь рассмотрим четыре основные операции с целыми числами: сложение, вычитание, умножение и деление.

Разрядное значение

WN01 Place_value

в 10 базовых операциях с целым номером 1

IN11 Basic_operations с целым номером 2

WN02 RUGE

8 WN3468 WN02 RUGE

WN3468 WN02 RUGE

WN3468 WN02 . WN36  Задачи на денежные слова

WN37  Квадратный корень из N

WN48  Разрядное значение (единица)

WN49 Значение места (единица)

WN50 Значение места (напишите свой номер)

BS01 Basic Skills

Реальные цифры (Помощь)

Place Value Value). Система счисления

Система счисления — это система представления чисел.

Натуральные числа (N).  [Числа, часто встречающиеся в природе]. Это числа {1, 2, 3, 4, 5, …}

Целые числа (W). Это набор натуральных чисел плюс ноль, т. е. {0, 1, 2, 3, 4, 5, …}.

Целые числа (Z). Это множество всех целых чисел плюс все отрицательные (или обратные) числа натуральных чисел, т. е. {… , -2, -1, 0, 1, 2, …}

Рациональные числа (Q). Это набор всех дробей, где верхние и нижние числа являются целыми числами; например, ¼, ½, ¾,… [Примечание: знаменатель не может быть равен нулю].

Вещественные числа ( р). В этот набор входят все числа, которые можно записать в виде десятичной дроби. Сюда входят дроби, записанные в десятичной форме, например, 0,5, 2,5 и т. д. Сюда также входят все иррациональные числа, такие как π, e , √2 и т.  д. Каждое действительное число соответствует точке на числовой прямой.

При обратном счете от нуля получается отрицательных чисел . Отрицательные числа используются для представления величины убытка или дефицита, например: «банк регистрирует депозиты как положительные числа, а снятие средств — как отрицательные числа».

Иррациональные числа — это действительные числа, которые нельзя записать в виде простой дроби. Иррациональные числа имеют десятичные расширения, которые не заканчиваются и не становятся периодическими. Examples  (π = 3.1415926535897932384626433832795…),  e , also known as Euler’s number  (e=2.718281828459045235360…),  the Square Root of 2, written as √2,  (√2 = 1.41421356237…), etc.

Real Number Voc

Расширение словарного запаса с использованием модели Frayer.

Шаблон Frayer

Создайте графический органайзер (модель Frayer) для следующих словарных слов: целое число, абсолютное значение, противоположное, рациональное число.

(сохраните копию в своем блокноте)

Ваша способность понимать математические задачи может быть улучшена с помощью ведения математических журналов. Обязательно укажите всю необходимую информацию. Помните: покажите свою работу и ответы в своем математическом журнале!

 

Умножение дробей на целые числа

Когда вы объединяете термины «умножение» и «дробь» в одном стандарте, это может звучать немного обескураживающе. К счастью, если учащиеся имеют четкое представление об умножении и дробях, это вполне естественно для учащихся. Этот пост включает в себя некоторые из моих любимых уроков для обучения студентов умножению дробей на целые числа.

Начните с понятия

Как и с большинством понятий фракций, я начинаю с обучения понятию с помощью Жезлов Кюизенера. Если коричневый стержень представляет собой целое, учащиеся должны сначала определить, какого цвета стержень является восьмым. Затем учащиеся будут использовать многократное сложение, чтобы найти сумму трех групп одной восьмой.

Проходит мимо долей единиц, а также меняет порядок множителей в числовом предложении на обратный. Студентам слишком легко думать, что есть только один способ представить контент или решить проблемы.

Умножение в контексте

Как и в случае с другими математическими понятиями, важно включать текстовые задачи, чтобы придать понятию контекст. После введения понятия умножения дробей на целые числа я предлагаю учащимся решить задачи на умножение слов. При необходимости учащиеся могут использовать манипуляторы. Однако на этом этапе хорошо, если учащиеся переходят к графическим представлениям.

Алгоритм умножения

Одно из заблуждений, которое может возникнуть у учащихся, состоит в том, что операция умножения всегда дает больший результат. Хотя это верно для целых чисел, это неверно для умножения дробей. В этом задании учащиеся используют модели площадей, чтобы начать понимать алгоритм умножения дробей. Студенты также увидят, что произведение не всегда увеличивается при умножении целого числа на дробь.

В этом упражнении учащиеся решают четыре задачи на умножение дробей, которые требуют от учащихся моделировать свою работу с помощью модели площади. После того, как учащиеся покажут, как проблема может быть представлена ​​с помощью модели области, они должны дать письменное объяснение.

Решение задач

Остальные мои уроки, посвященные умножению дроби на целое число, представляют собой уроки решения задач, на которых учащиеся применяют то, что они уже изучили, в ситуациях решения задач.

Я стараюсь избегать спешки на конкретных и иллюстрированных стадиях обучения. Легко перейти к полностью абстрактным заданиям, но учащимся нужно время для работы с несколькими представлениями, чтобы закрепить свое понимание.

На протяжении этих уроков повторяйте различные стратегии решения задач, такие как составление таблицы или работа в обратном порядке, так как учащиеся, скорее всего, будут использовать эти стратегии в задачах решения задач. Несмотря на то, что учащимся поначалу может быть трудно начать выполнять эти задачи, решение проблем будет способствовать развитию навыков критического мышления, а также применению и концептуальному пониманию дробей.