Умножение дробей | Cubens
Умножение дробей
Умножение дроби на натуральное число
Чтобы умножить дробь на число, нужно числитель умножить на число, а знаменатель оставить без изменений.
Пример умножения дроби на натуральное число
Пример 1: Найти произведение дроби на натуральное число (умножить дробь на натуральное число): на
Ответ:
Умножение дробей с разными знаменателями
Чтобы добавить две обыкновенные дроби с разными знаменателями, нужно:
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
Пример умножения дробей с разными знаменателями
Пример 2: Перемножить две обыкновенные дроби с разными знаменателями: и
Ответ:
Умножение смешанных чисел
Чтобы умножить два смешанных числа, нужно:
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- Если был получен неправильный дробь нужно преобразовать неправильный дробь в смешанный.
Примеры сложения смешанных чисел
Пример 3: Умножить обыкновенную дробь на смешанное число: и
Ответ:
Пример 4 Умножить смешанное число на натуральное число: и
Ответ:
Пример 5: Умножить смешанные числа: и
Ответ:
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, следует:
- выполнить умножение, не обращая внимания на запятые;
- отделить запятой столько цифр справа, сколько их после запятой в обоих множителях вместе.
Примеры умножения десятичных дробей
Пример 1: Перемножить дроби: 13,2 и 0,2.
Выполнив умножение, не обращая внимания на запятые, получим: .
Отделим запятой справа столько цифр, сколько стоит после запятой в обоих множителях вместе, то есть две цифры .
Рассмотрим другие примеры умножения десятичных чисел:
Пример 2:
Пример 3:
Умножение десятичной дроби и натурального числа
Произведением десятичной дроби и натурального числа называют сумму слагаемых, каждый из которых равен данному десятичной дроби, а количество слагаемых равно этому натуральному числу.
Чтобыумножить десятичную дробь на натуральное число, нужно:
- умножить его на это число, не обращая внимания на запятую;
- в полученном произведении отделить запятой столько цифр справа, сколько их отделено запятой в десятичной дроби.
Умножение десятичной дроби на 10, 100, 1000 и т.д.
Чтобыумножить десятичную дробь на 10,100,1000 и т.д., следует:
- надо в этой дроби перенести запятую на столько цифр вправо, сколько нулей стоит в множителе после единицы.
Пример 4:
Если в результате получается меньше цифр, чем надо отделить запятой, то впереди пишут нуль или несколько нулей.
Онлайн урок: Умножение дробей по предмету Математика 6 класс
В этом уроке мы научимся умножать дробь на натуральное число, разберемся с перемножением двух дробей и поймем, в чем заключается алгоритм умножения смешанных чисел.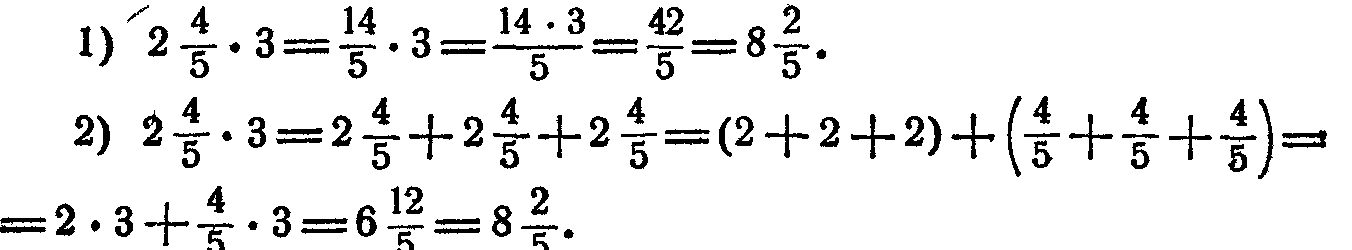
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Вполне типичная ситуация из жизни: человек покупает в магазине 5 упаковок товара, в каждой содержится по \(\mathbf{\frac{2}{3}}\) килограмм товара.
В таких и многих других случаях, необходимо уметь умножить дробь на натурально число.
В нашем случае нужно умножить \(\mathbf{\frac{2}{3}}\) на 5.
Результат умножения дроби и натурального числа будет дробь, числитель которой будет равен произведению числителя дроби и натурального числа, а знаменатель — знаменателю дроби.
То есть в нашем примере:
2 умножим на 5, получим 10.
Запишем результат: \(\mathbf{\frac{10}{3}}\)
Заметьте, что дробь получилась неправильной, то есть числитель больше знаменателя. Для красоты ответа стоит выделить целую часть также, как мы это делали в прошлом уроке.
На всякий случай повторим:
- разделите числитель нацело на знаменатель
- запишите частное в целую часть
- остаток запишите в числитель дробной части
Ответ будет: \(\mathbf{3\frac{1}{3}}\)
Приведем еще несколько примеров:
\(\mathbf{\frac{3}{4}\cdot4=\frac{3\cdot4}{4}=3}\)
Этот пример показывает, что имеет смысл сначала записать произведение, не считая его значение. Тогда можно сократить результат и потом уже досчитать.
\(\mathbf{\frac{4}{7}\cdot5=\frac{4\cdot5}{7}=\frac{20}{7}=2\frac{6}{7}}\)
В этом примере снова потребовалось выделить целую часть.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum
enim
fugit magni nihil odit provident quaerat.
Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
После того, как мы научились умножать дробь на натуральное число, пора переходить к умножению дроби на дробь.
Алгоритм весьма схож. Ответом снова будет дробь:
- в числителе будет стоять произведение числителей изначальных дробей
- в знаменателе будет стоять произведение знаменателей
Рассмотрим подробнее на примере: пусть нам надо перемножить \(\mathbf{\frac{3}{4}}\) и \(\mathbf{\frac{2}{7}}\).
Числители здесь это 3 и 2, их произведение равняется 6.
Знаменатели: 4 и 7, их произведение дает 28.
Тогда ответом будет дробь: \(\mathbf{\frac{6}{28}}\)
Возникает естественное желание сократить эту дробь. Сократим числитель и знаменатель на 2, в итоге ответ будет выглядеть так:\(\mathbf{\frac{6}{7}}\)
Сформулируем алгоритм умножения двух дробей:
- перемножаем числители
- перемножаем знаменатели
- пишем результат первого действия в числитель ответа, результат второго действия в знаменатель
Примеры:
\(\mathbf{\frac{5}{8}\cdot\frac{2}{3}=\frac{5\cdot2}{8\cdot3}=\frac{5}{4\cdot3}=\frac{5}{12}}\)
Здесь мы прибегли к сокращению, убрав из числителя двойку и поделив восьмерку в знаменателе на 2.
\(\mathbf{\frac{1}{5}\cdot\frac{7}{9}=\frac{1\cdot7}{5\cdot9}=\frac{7}{45}}\)
\(\mathbf{\frac{4}{9}\cdot\frac{5}{6}=\frac{4\cdot5}{9\cdot6}=\frac{2\cdot5}{9\cdot3}=\frac{10}{27}}\)
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Прежде чем рассмотреть умножение смешанного числа на смешанное, рассмотрим случай, в котором мы умножаем смешанное число на натуральное.
Существует два способа умножения смешанного числа на натуральное, рассмотрим их по порядку.
1. В первом способе мы преобразуем смешанное число к неправильной дроби, а дальше выполняем умножение дроби на натуральное число, которое мы рассмотрели в начале урока.
Например, надо решить такой пример:
\(\mathbf{1\frac{2}{7}\cdot4}\)
Домножаем целую часть смешанного числа на его знаменатель и прибавляем к числителю:
\(\mathbf{1\frac{2}{7}=\frac{1\cdot7+2}{7}=\frac{9}{7}}\)
Теперь по правилу умножения дроби на натуральное число, перемножим числитель дроби и натуральное число, а знаменатель оставим тем же самым:
\(\mathbf{\frac{9}{7}\cdot4=\frac{9\cdot4}{7}=\frac{36}{7}}\)
Остается, как и в остальных случаях, выделить целую часть:
\(\mathbf{\frac{36}{7}=5\frac{1}{7}}\)
И еще немного примеров:
\(\mathbf{3\frac{1}{4}\cdot3=\frac{3\cdot4+1}{4}\cdot3=\frac{13}{4}\cdot3=\frac{13\cdot3}{4}=\frac{39}{4}=9\frac{3}{4}}\)
\(\mathbf{2\frac{3}{8}\cdot5=\frac{2\cdot8+3}{8}\cdot5=\frac{19}{8}\cdot5=\frac{19\cdot5}{8}=\frac{95}{8}=11\frac{7}{8}}\)
2.
Второй способ заключается в том, что смешанное число представляем как сумму натурального числа и правильной дроби. По очереди умножаем их на натуральное число и складываем результаты.
Вспомним распределительное свойство умножения относительно сложения:
\(\mathbf{a\cdot(b+c)=a\cdot b+a\cdot c}\)
То есть если нам надо умножить сумму двух чисел на третье, мы можем сначала перемножить первое и третье, потом второе и третье и сложить результаты.
Возникает вопрос: как это поможет в нашем случае?
Ответ: можно представить смешанное число как сумму его целой и дробной частей.
Например:
\(\mathbf{5\frac{2}{3}=5+\frac{2}{3}}\)
Если нам надо умножить смешанное число на натуральное, можно сначала представить смешанное число как сумму натурального числа и правильной дроби, затем по очереди умножить их на натуральное число и сложить результаты.
Для понимания решим такой пример:
\(\mathbf{5\frac{2}{3}\cdot8}\)
Представляем смешанное число в виде суммы:
\(\mathbf{5\frac{2}{3}\cdot8=(5+\frac{2}{3})\cdot8}\)
Расписываем выражение по распределительному свойству:
\(\mathbf{(5+\frac{2}{3})\cdot8=5\cdot8+\frac{2}{3}\cdot8}\)
Производим умножения:
\(\mathbf{5\cdot8+\frac{2}{3}\cdot8=40+\frac{16}{3}}\)
Остается преобразовать неправильную дробь в смешанное число и сложить с полученным натуральным:
\(\mathbf{40+\frac{16}{3}=40+5\frac{1}{3}=45\frac{1}{3}}\)
Также дадим еще парочку примеров на это правило:
\(\mathbf{3\frac{8}{9}\cdot2=(3+\frac{8}{9})\cdot2=3\cdot2+\frac{8}{9}\cdot2=6+\frac{8\cdot2}{9}=6+\frac{16}{9}=6+1\frac{7}{9}=7\frac{7}{9}}\)
\(\mathbf{8\frac{5}{7}\cdot3=(8+\frac{5}{7})\cdot3=8\cdot3+\frac{5}{7}\cdot3=24+\frac{5\cdot3}{7}=24+\frac{15}{7}=24+2\frac{1}{7}=26\frac{1}{7}}\)
Второй способ часто оказывается более удобным, так как в нем мы работаем с меньшими по величине числами.
Теперь вы знаете два способа перемножения смешанных и натуральных чисел. Выбирайте наиболее удобный для вас!
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Перейдем к умножению двух смешанных чисел.
Если говорить коротко, то надо преобразовать смешанные числа в неправильные дроби и проделать все действия для умножения дробей.
Распишем все это подробно.
Допустим, мы хотим посчитать произведение \(\mathbf{3\frac{1}{2}}\) и \(\mathbf{2\frac{2}{3}}\)
Сначала преобразуем смешанные числа в неправильные дроби.
Для этого перемножаем целую часть смешанного числа и его знаменатель и прибавляем к числителю, знаменатель оставляем без изменений.
\(\mathbf{3\frac{1}{2}=\frac{3\cdot2+1}{2}=\frac{7}{2}}\)
\(\mathbf{2\frac{2}{3}=\frac{2\cdot3+1}{3}=\frac{7}{3}}\)
Теперь пойдем по алгоритму произведения дробей.
Перемножим числители: \(\mathbf{7\cdot7=49}\)
Перемножим знаменатели: \(\mathbf{2\cdot3=6}\)
Подставим это в дробь: \(\mathbf{\frac{49}{6}}\)
Теперь остается выделить целую часть: \(\mathbf{\frac{49}{6}=8\frac{1}{6}}\)
Это и будет решением нашего примера.
Еще немного примеров:
\(\mathbf{7\frac{2}{9}\cdot2\frac{1}{4}=\frac{7\cdot9+2}{9}\cdot\frac{2\cdot4+1}{4}=\frac{65}{9}\cdot\frac{9}{4}=\frac{65\cdot9}{9\cdot4}=\frac{65}{4}=16\frac{1}{4}}\)
\(\mathbf{4\frac{2}{5}\cdot3\frac{3}{8}=\frac{4\cdot5+2}{5}\cdot\frac{3\cdot8+3}{8}=\frac{22}{5}\cdot\frac{27}{8}=\frac{22\cdot27}{5\cdot8}=\frac{11\cdot27}{5\cdot4}=\frac{297}{20}=14\frac{17}{20}}\)
\(\mathbf{2\frac{1}{2}\cdot1\frac{2}{3}=\frac{2\cdot2+1}{2}\cdot\frac{1\cdot3+2}{3}=\frac{5}{2}\cdot\frac{5}{3}=\frac{5\cdot5}{2\cdot3}=\frac{25}{6}=4\frac{1}{6}}\)
Lorem ipsum dolor sit amet, consectetur adipisicing elit.
Adipisci autem beatae consectetur corporis
dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore
voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
Мы уже привыкли работать с обычными и десятичными дробями.
Также мы довольно неплохо умеем читать римские цифры, которые часто используют на часах, для описания глав книги или подпунктов задач и теорем.
Тогда возникает естественный интерес: как в римской записи будут выглядеть дроби?
Оказывается, в Древнем Риме использовали двенадцатеричную систему дробей.
То есть у всех дробей в этой системе счисления знаменатель равен 12.
Это аналогично тому, как в десятичных дробях знаменатель кратен 10.
Медные монеты ассы, используемые в Древнем Риме, делились на 12 равных частей — унций.
Одной унции соответствовала одна точка: \(\mathbf{\cdot}\), двум унциям соответствовало две точки и так далее.
Lorem ipsum dolor sit amet, consectetur adipisicing elit. Adipisci autem beatae consectetur corporis dolores ea, eius, esse id illo inventore iste mollitia nemo nesciunt nisi obcaecati optio similique tempore voluptate!
Adipisci alias assumenda consequatur cupiditate, ex id minima quam rem sint vitae? Animi dolores earum enim fugit magni nihil odit provident quaerat. Aliquid aspernatur eos esse magnam maiores necessitatibus, nulla?
Эта информация доступна зарегистрированным пользователям
На приведенной выше картинке изображены монеты номиналом по 4 унции.
Также были специальные обозначения для \(\mathbf{\frac{1}{2}}\)- семис, \(\mathbf{\frac{1}{6}}\)- секстанс, \(\mathbf{\frac{1}{24}}\)- семиунция и так далее.
Для работы с такими сложными дробями римлянам приходилось прибегать к специальным таблицам.
Смотря на это, можно порадоваться: с нашей системой счисления работать гораздо удобнее.
Как умножать дроби на целые числа
Дроби-смысл числа | Математика | Умножение и деление дробей
Как умножать дроби на целые числа
Упражнение «Умножение дробей на целые числа» поможет учащимся понять, как умножать дроби на целые числа, используя числовую прямую и алгоритм.
Одним из моих любимых предметов в качестве учителя пятого класса были дроби. Я люблю учить дроби, и, что еще более безумно, я люблю учить их на числовой прямой. Это так аккуратно и организовано, и вы можете визуально видеть, что вы делаете.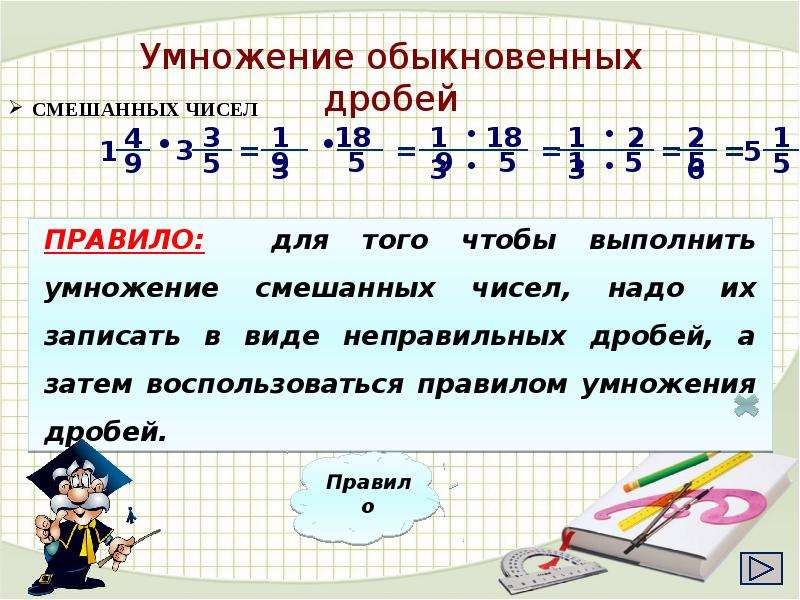
Оглавление
Я счастлив видеть, что все эти маленькие фракции выстраиваются в очередь!!
Обучение умножению дробей с помощью манипулятивных чисел
Обучение дробям на числовой прямой позволяет достичь того, в чем я твердо убежден. Я считаю, что учащиеся должны понимать, почему они что-то делают, а не просто знать, как выполнять алгоритм.
Я никогда не был силен в математике, когда учился в школе, но процесс обучения с помощью манипуляций, разложения чисел и рисования моделей принес понимание математики, о котором я никогда не думал.
Теперь мне это нравится.
Чтобы помочь вашим учащимся понять умножение дробей, этот пост содержит БЕСПЛАТНОЕ упражнение по умножению дробей, которое вы можете использовать для повторения или начала обучения умножению дробей на целое число с помощью числовой прямой.
Умножение дробей Упражнение
- Распечатайте интерактивную тетрадь.
- Затем попросите детей вклеить два средних ряда в свои математические журналы.
- Теперь разрежьте их по пунктирным линиям.
- Наконец, соберите несколько карандашей и маркеров, чтобы они могли заполнить этот интерактивный блокнот вместе с вами.
Умножение дробей на целые числа
В старших классах учащиеся хорошо знакомы с умножением. Надеюсь, к этому моменту ваши ученики понимают, что умножение — это быстрый способ выяснить, сколько у вас есть определенного предмета, если этот предмет был разделен на равные группы.
Им следует признать, что они могут решить задачу на умножение, пропуская счет или повторяя сложение, но это неэффективно по времени.
Если они это поймут, то умножение дробей на числовой прямой не составит для них труда.
Умножение дробей на целые числа: пример 1
Предположим, задача 2 x 3/5.
Учащиеся начинают с того, что строят числовую прямую в точке 0, а затем прибавляют пятые к каждому приращению.
Затем они начинают «прыгать» на три пятых…..и так два раза.
Это так просто.
Как умножить дробь на целое число: Пример 2
В этой задаче мы умножаем 2/3 на 3. Поэтому мы снова воспользуемся нашим знаменателем 3 и создадим в строке дроби с шагом 1/3.
Как только наша числовая строка будет заполнена, мы «прыгнем» на две трети, три раза. Мы закончим номером два…… ответом.
Так что, если у вашего ученика проблемы с дробями, попробуйте уйти от алгоритма и найти манипуляции, числовую прямую или модели, и пусть они исследуют. Вы можете быть поражены пониманием, которое начинает развиваться!!
Умножение дробей PDF
Ниже вы найдете задание по умножению дробей pdf. Вы можете загрузить PDF-файл, нажав кнопку загрузки, а затем распечатав его со своего устройства.
Умножение-фракций-на-числовую-линию-игру-1 #3 — 5 бесплатных распечаток#фракции#Умножение
Похожие сообщения
Как умножать дроби — пустышки
Автор: Марк Зегарелли и
Обновлено: 26 марта 2016 г.
Математика для реальной жизни Для чайников
Исследуйте книгу Купить на Amazon
Почему все в жизни не может быть таким же простым, как умножение дробей? Чтобы умножить две дроби, просто сделайте следующее: Умножьте два числителя на (верхние числа), чтобы получить числитель ответа; умножьте два знаменателя на (нижние числа), чтобы получить знаменатель ответа.
Когда вы умножаете две правильные дроби, ответ всегда будет правильной дробью, поэтому вам не нужно будет превращать его в смешанное число, но, возможно, вам придется уменьшить его.
Перед умножением проверьте, сможете ли вы исключить общие множители, которые появляются как в числителе, так и в знаменателе. (Этот процесс похож на сокращение дроби.) Когда вы убираете все общие множители перед умножением, вы получаете ответ, который уже приведен к самым низким условиям.
Примеры вопросов
Умножьте 2/5 на 4/9.
Умножьте два числителя (верхние числа), чтобы получить числитель ответа. Затем умножьте два знаменателя (нижние числа), чтобы получить знаменатель ответа:
В этом случае можно не уменьшать ответ.
Найти
Перед умножением обратите внимание, что числитель 4 и знаменатель 8 четны. Итак, разделите оба этих числа на 2 так же, как при сокращении дроби:
.Теперь числитель 2 и знаменатель 4 четные, поэтому повторите этот процесс:
На данный момент ни один числитель не имеет общего делителя ни с одним из знаменателей, так что вы готовы к умножению. Умножьте два числителя, чтобы получить числитель ответа. Затем умножьте два знаменателя, чтобы получить знаменатель ответа:
Поскольку вы отменили все общие множители перед умножением, этот ответ будет самым низким.
Практические вопросы
Умножьте 2/3 на 7/9.
Найти
Умножить 2/9 на 3/10.
