Как умножить число на дробь — «Семья и Школа»
Содержание
Как разделить число на дробь. Как разделить число на дробь правило. Целое число разделить на дробь пример.
- Альфашкола
- Статьи
- Как разделить число на дробь
Деление числа на дробь происходит по правилу: дробь меняет местами числитель и знаменатель, далее умножаем на число по правилу умножению числа на дробь : https://myalfaschool.ru/articles/kak-umnozhit-chislo-na-drob.
Пример 1. Разделите \(5:\frac{5}{12}\).
Решение:
Здесь мы сократили дробь на \(5\) и получили \(12\).
Ответ: \(12.\)
Пример 2. Разделите \(8:\frac{4}{5}\).
Разделите \(8:\frac{4}{5}\).
Решение:
Ответ: \(10\)
Пример 3. Разделите \(27:\frac{9}{5}\).
Решение:
Ответ: \(15.\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Марина Александровна Курилина
Репетитор по математике
Стаж (лет)
Образование:
БГУ , Институт Позитивных Технологий и Консалтинга
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 класса. Активно использую в своей работе не только знания математики., но и навыки консультанта-психолога, объединяя их для достижения желаемого результата.
Юлия Игоревна Ярош
Репетитор по математике
Стаж (лет)
Образование:
Брестский государственный университет имени А. С. Пушкина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку для 5-11 классов. Мне очень нравится преподавать русский язык, использовать индивидуальный подход на своих уроках, все мои уроки проходит в очень динамичной обстановки. Руководствуюсь комплексный подходов, всесторонним анализом текста, ученик осознает, что русский язык -это неразрывная система, понимает, как его разделы связаны между собой и функционируют друг с другом. Всегда нахожу подход к каждому ученику, выстраиваю доверительные отношения.
Виктория Анатольевна Луковская
Репетитор по математике
Стаж (лет)
Образование:
Таганрогский педагогический институт им. А.П. Чехова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 4-11 классов. Математика дисциплинирует и воспитывает ум, это основа для всех наук. Очень люблю работать с детьми! Уроки проходят в комфортной обстановке, к каждому ученику подхожу индивидуально, объясняю доступно и понятно. На занятиях применяю игровые приемы, схемы, графики и презентации, для того, чтобы учащимся было интересно.
Похожие статьи
- Пирамида
- Как решать уравнения с помощью пропорции?
- МИФИ: Прикладная математика и физика
- ЕГЭ по математике, базовый уровень. Простейшие уравнения (вариант 5)
- Летние идеи для занятия спортом
- Полезные физические упражнения для тех, кто долго сидит за учебниками: разминка для ног
- «Я не знаю, кем мне быть»: ответы на популярные вопросы старшеклассников
- Что такое конформизм или влияние чужого мнения на собственное поведение и мышление
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Умножение дробей.

Умножение дробей.
Навигация по странице:
- Умножение дроби на натуральное число
- Умножение обыкновенных дробей
- Умножение смешанных чисел
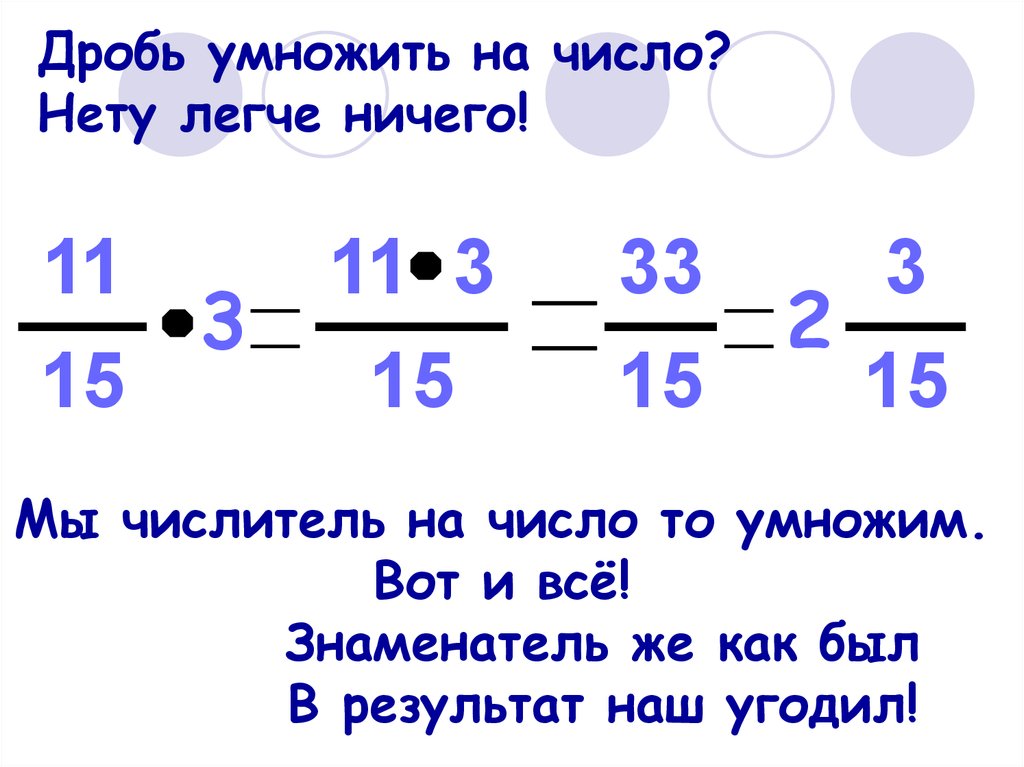
Умножение дроби на натуральное число.
Определение.
Чтобы умножить дробь на натуральное число, надо числитель умножить на число, а знаменатель оставить тем же.
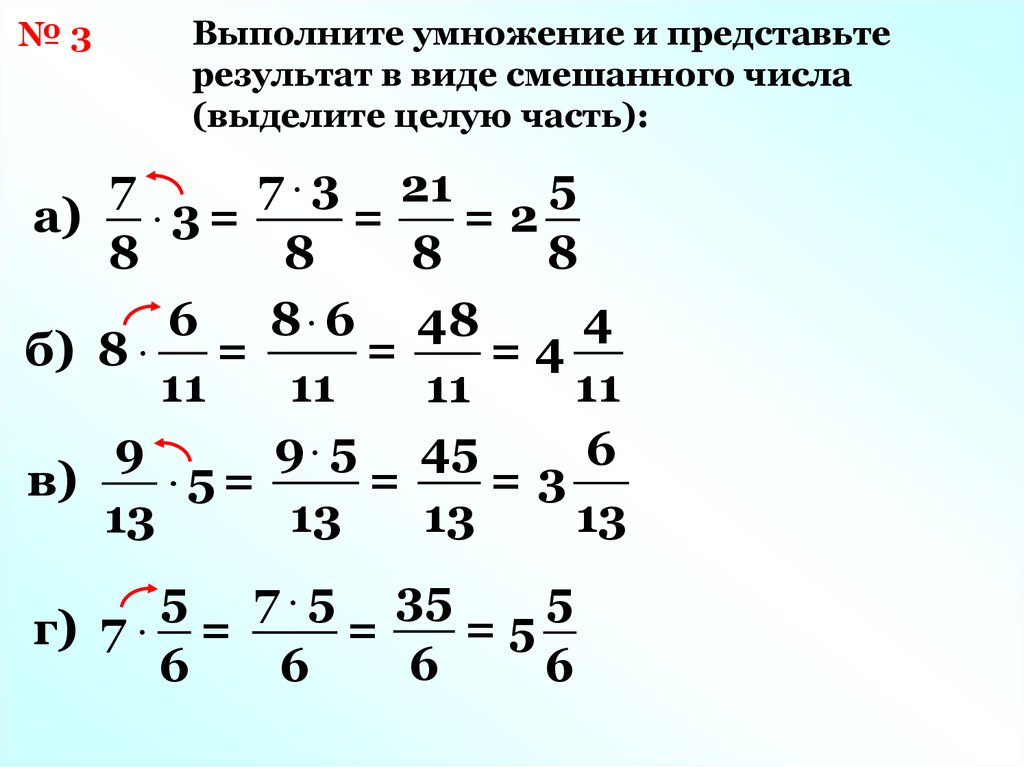
Примеры умножения дроби на натуральное число
Пример 1.
Найти произведение дроби и натурального числа:
| 3 | = | 3 · 2 | = | 6 | |
| 7 | 7 | 7 |
Пример 2.
Найти произведение дроби и натурального числа:
| 1 | · 4 | = | 4 | = | 2·2 | = | 2 |
| 2 | 2 | 2 |
Умножение обыкновенных дробей.

Определение.
- Чтобы умножить две обыкновенные дроби, надо
- перемножить числители и знаменатели дробей;
- сократить полученную дробь.
Примеры умножения обыкновенных дробей
Пример 3.
Найти произведение двух дробей:
| 3 | · | 2 | = | 3 · 2 | = | 6 |
| 7 | 5 | 7 · 5 | 35 |
Пример 4.
Найти произведение двух дробей:
| 10 | · | 3 | = | 10 · 3 | = | 2 · 5 · 3 | = | 5 | = | 5 |
| 9 | 4 | 9 · 4 | 2 · 2 · 3 · 3 | 2 · 3 | 6 |
Онлайн калькулятор дробей
Упражнения на тему умножение двух обыкновенных дробей
Умножение смешанных чисел.

Примеры умножения смешанных чисел
Пример 5.
Найти произведение двух смешанных чисел:
212 · 123 = 2 · 2 + 12 · 1 · 3 + 23 = 52 · 53 = 5 · 52 · 3 = 256 = 6 · 4 + 16 = 416
Пример 6.
Найти произведение смешанного числа и целого числа:
| 4 | 1 | · | 6 | = | 4 · 3 + 1 | · | = | 13 · 6 | = | 26 | |
| 3 | 3 | 3 |
Пример 7.
Найти произведение смешаного числа и обыкновенной дроби:
217 · 35 = 2 · 7 + 17 · 35 = 157 · 35 = 15 · 37 · 5 = 3 · 37 = 97 = 7 + 27 = 127
Онлайн калькулятор дробей
Упражнения на тему умножение двух смешанных чисел
Дроби Виды дробей (обыкновенная правильная, неправильная, смешанная, десятичная) Основное свойство дроби Сокращение дроби Приведение дробей к общему знаменателю Преобразование неправильной дроби в смешанное число Преобразование смешанного числа в неправильную дробь Сложение и вычитание дробей Умножение дробей Деление дробей Сравнение дробей Преобразование десятичной дроби в обыкновенную дробь
Онлайн калькуляторы дробей
Онлайн упражнения с дробями
Простая факторизация
Простые числа
Простое число:
целое число больше 1, которое можно не получить путем умножения других целых чисел
Первые несколько простых чисел: 2, 3, 5, 7, 11, 13, 17, 19 и 23,
и у нас есть диаграмма простых чисел, если вам нужно больше.
Если мы можем составить путем умножения других целых чисел, то это составное число .
Вот так:
2 — Prime, 3 — Prime, 4 — Composite (=2×2), 5 — Prime и так далее…
Факторы
«Коэффициенты» — это числа, которые нужно перемножить, чтобы получить другой номер:
Простая факторизация
«Факторизация простых чисел» — это нахождение числа , которое умножает простые числа , чтобы получить исходное число.
Вот несколько примеров:
Пример: Каковы простые делители числа 12?
Лучше всего начинать работу с наименьшего простого числа, которое равно 2, поэтому давайте проверим:
12 ÷ 2 = 6
Да, оно делится ровно на 2. Мы сделали первый шаг!
Но 6 не простое число, поэтому нужно идти дальше. Попробуем еще раз 2:
6 ÷ 2 = 3
Да, это тоже сработало. А 3 — это простое число, поэтому у нас есть ответ:
12 = 2 × 2 × 3
Как видите, на каждый делитель — это простое число , поэтому ответ должен быть правильным.
Примечание: 12 = 2 × 2 × 3 также может быть записано с использованием показателей степени как 12 = 2 2 × 3
Пример: Какова простая факторизация числа 147?
Можем ли мы разделить 147 точно на 2?
147 ÷ 2 = 73½
Нет, не может. Ответ должен быть целым числом, а 73½ — нет.
Попробуем следующее простое число число, 3:
147 ÷ 3 = 49
Это сработало, теперь попробуем разложить на множители 49.
Следующее простое число 5 не работает. Но 7 подходит, поэтому мы получаем:
49 ÷ 7 = 7
И это все, что нам нужно сделать, потому что все множители простые числа.
147 = 3 × 7 × 7
(или 147 = 3 × 7 2 с использованием показателей)
Пример: Какова простая факторизация числа 17?
Подожди… 17 — простое число .
Вот и все, что мы можем сделать.
17 = 17
Другой метод
Мы показали вам, как разложить на множители, начав с наименьшего простого числа и продвигаясь вверх.
Но иногда проще разбить число на любые множители , которые вы можете … затем разложить эти множители на простые числа.
Пример: Каковы простые делители числа 90?
Разбить 90 на 9 × 10
- Простые множители числа 9 3 и 3
- Простые делители числа 10 равны 2 и 5
Итак, простые делители числа 90 равны 3, 3, 2 и 5
Факторное дерево
И «Дерево множителей» может помочь: найти любые множители числа, затем множители этих чисел и т.д., пока мы не сможем больше множить.
Пример: 48
48 = 8 × 6 , поэтому запишем «8» и «6» ниже 48
Теперь мы продолжаем и делим 8 на 4 × 2
Затем 4 на 2 × 2
И, наконец, 6 на 3 × 2
Мы не можем найти больше
основные факторы.
Что показывает, что 48 = 2 × 2 × 2 × 2 × 3
(или 48 = 2 4 × 3 с использованием показателей)
Зачем искать Prime Factors?
Простое число можно разделить только на 1 или само на себя, поэтому оно не может учитываться дальше!
Любое другое целое число можно разбить на простые множители.
Это похоже на то, что простые числа являются основными строительными блоками всех чисел. |
Эта идея может быть очень полезна при работе с большими числами, например, в криптографии.
Криптография
Криптография — это изучение секретных кодов. Прайм-факторизация очень важна для людей, которые пытаются создавать (или взламывать) секретные коды на основе чисел.
Это потому, что разложение очень больших чисел на множители очень сложно и может занять много времени у компьютеров.
Если вы хотите знать больше, предметом является «шифрование» или «криптография».
Уникальный
И вот еще что:
Для любого числа существует только один (уникальный!) набор простых множителей.
Пример: простые делители числа 330 равны 2, 3, 5 и 11.0005
На самом деле эта идея настолько важна, что ее называют Фундаментальной теоремой арифметики .
Инструмент простой факторизации
Хорошо, у нас есть еще один метод… используйте наш Инструмент факторизации простых чисел, который может вычислять простые множители для чисел до 4 294 967 296.
370, 1055, 1694, 1695, 1696, 1697
Калькулятор простой факторизации
Базовый калькулятор
Поделись этим калькулятором и страницей
Калькулятор Используйте
Используйте этот калькулятор простых чисел, чтобы найти все простые делители заданного целого числа до 10 триллионов. Этот калькулятор представляет:
- Простые множители числа
- Разложение простых чисел в экспоненциальной форме
- CSV (значения, разделенные запятыми) список простых множителей
- Факторизация в дереве простых множителей
Для первых 5000 простых чисел этот калькулятор указывает индекс простого числа. n th Простое число обозначается как Prime[n], поэтому Prime[1] = 2, Prime[2] = 3, Prime[3] = 5 и так далее.
Ограничение на ввод числа для фактора меньше 10 000 000 000 000 (менее 10 триллионов или максимум 13 цифр).
Что такое простая факторизация?
Разложение числа на простые или целочисленные разложения — это разбиение числа на набор простых чисел, которые перемножаются, чтобы получить исходное число. Это также известно как первичное разложение.
Как найти разложение числа на простые множители
Мы рассмотрим два метода разложения на простые множители: поиск простых чисел путем пробного деления и использование простых чисел для создания дерева простых множителей.
Прайм-факторизация с помощью Trial Division
Допустим, вы хотите найти простые делители числа 100 с помощью пробного деления. Начните с проверки каждого целого числа, чтобы увидеть, делится ли оно на 100 и последующие частные, и если да, то как часто. Результирующий набор множителей будет простым, поскольку, например, когда 2 исчерпано, все числа, кратные 2, также исчерпаны.
Найдите простые делители числа 100:
- 100 ÷ 2 = 50; сохранить 2
- 50 ÷ 2 = 25; сохранить 2
- 25 ÷ 2 = 12,5, неравномерно, поэтому разделить на следующее наибольшее число, 3
- 25 ÷ 3 = 8,333, неравномерно, поэтому разделить на следующее наибольшее число, 4
- Но 4 кратно 2, так что это уже проверено, поэтому разделите на следующее наибольшее число, 5
- 25 ÷ 5 = 5; сохранить 5
- 5 ÷ 5 = 1; сохранить 5
Перечислите получившиеся простые множители в виде последовательности кратных 2 x 2 x 5 x 5 или в виде множителей с показателями степени 2 2 х 5 2 .
Примеры разложения простых чисел: множители и показатели
- Разложение числа 100 на простые множители равно 2 x 2 x 5 x 5 или 2 2 x 5 2
- Разложение числа 76 на простые множители равно 2 x 2 x 19 или 2 2 x 19 1
- Разложение числа 50 на простые множители равно 2 x 5 x 5 или 2 x 5 2
- Разложение числа 48 на простые множители равно 2 x 2 x 2 x 2 x 3 или 2 4 x 3 1
- Разложение числа 36 на простые множители равно 2 x 2 x 3 x 3 или 2 2 x 3 2
- Разложение числа 20 на простые множители равно 2 x 2 x 5 или 2 2 x 5 1
- Разложение числа 10 на простые множители равно 2 x 5 или 2 1 x 5 1
Дерево простых множителей
Используя дерево простой факторизации, чтобы увидеть работу, простое разложение 100 = 2 x 2 x 5 x 5 выглядит следующим образом:
2
25
Связанные калькуляторы
Список первых 1000 простых чисел см.
Основное свойство алгебраической дроби 8 класс онлайн-подготовка на Ростелеком Лицей
Основное свойство обыкновенной дроби
Вспомним основное свойство обыкновенной дроби: значение дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. Напомним, что деление числителя и знаменателя дроби на одно и то же отличное от нуля число называется сокращением.
Например: , при этом значение дробей не изменяется. Однако зачастую при применении данного свойства многие допускают стандартные ошибки:
1) — в приведенном примере допущена ошибка деления только одного слагаемого из числителя на 2, а не всего числителя. Правильная последовательность действий выглядит таким образом: или .
2) — здесь мы видим похожую ошибку, однако, кроме этого еще в результате деления получен 0, а не 1, что является еще более частой и грубой ошибкой.
Теперь необходимо перейти к рассмотрению алгебраической дроби. Вспомним это понятие из предыдущего урока.
Вспомним это понятие из предыдущего урока.
Определение. Рациональная (алгебраическая) дробь – дробное выражение вида , где – многочлены. – числитель, – знаменатель.
Алгебраические дроби являются, в некотором смысле, обобщением обыкновенных дробей и над ними можно проводить те же операции, что и над обыкновенными дробями.
Основное свойство алгебраической дроби
Основное свойство алгебраической дроби – и числитель, и знаменатель дроби можно умножать и делить на один и тот же многочлен (одночлен) или число, отличное от нуля. Это будет тождественное преобразование алгебраической дроби. Вспомним, что как и ранее, деление числителя и знаменателя дроби на одно и то же отличное от нуля выражение называется сокращением.
Основное свойство алгебраической дроби позволяет сокращать дроби и приводить их к наименьшему общему знаменателю.
Примеры сокращения обыкновенных дробей
Для сокращения обыкновенных дробей мы прибегали к основной теореме арифметики, разлагали и числитель, и знаменатель на простые множители.
Определение. Простое число – натуральное число, которое делится только на единицу и само себя. Все остальные натуральные числа называются составными. 1 не является ни простым, ни составным числом.
Пример 1. а), где множители, на которые разложены числители и знаменатели указанных дробей, являются простыми числами.
Ответ. ; .
Примеры сокращения алгебраических дробей
Следовательно, для сокращения дробей необходимо предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители. Т.е. следует владеть методами разложения многочленов на множители.
Пример 2. Сократить дробь а), б) , в) .
Решение. а) . Необходимо заметить, что в числителе находится полный квадрат, а в знаменателе разность квадратов. После сокращения необходимо указать, что , во избежание деления на ноль.
б) . В знаменателе выносится общий числовой множитель, что полезно делать практически в любом случае, когда это возможно. Аналогично с предыдущим примером указываем, что .
В знаменателе выносится общий числовой множитель, что полезно делать практически в любом случае, когда это возможно. Аналогично с предыдущим примером указываем, что .
в) . В знаменателе выносим за скобки минус (или, формально, ). Не забываем, что при сокращении .
Ответ. ;; .
Теперь приведём пример на приведение к общему знаменателю, делается это аналогично с обыкновенными дробями.
Приведение обыкновенных дробей к общему знаменателю
Пример 3. Привести к общему знаменателю дроби и .
Решение. Для нахождения наименьшего общего знаменателя необходимо найти наименьшее общее кратное (НОК) двух знаменателей, т.е. НОК(3;5). Иными словами, найти наименьшее число, которое делится на 3 и на 5 одновременно. Очевидно, что это число 15, записать это можно таким образом: НОК(3;5)=15 – это и будет общий знаменатель указанных дробей.
Чтобы преобразовать знаменатель 3 в 15, его необходимо умножить на 5, а для преобразования 5 в 15, его необходимо умножить на 3. По основному свойству алгебраической дроби следует умножить на те же числа и соответствующие числители указанных дробей.
По основному свойству алгебраической дроби следует умножить на те же числа и соответствующие числители указанных дробей.
и .
Ответ.; .
Пример 4. Привести к общему знаменателю дроби и .
Решение. Проведем аналогичные предыдущему примеру действия. Наименьшее общее кратное знаменателей НОК(12;18)=36. Приведем к этому знаменателю обе дроби:
и .
Ответ.; .
Сокращение сложных обыкновенных дробей
Теперь рассмотрим примеры, демонстрирующие применение техники сокращения дробей для их упрощения в более сложных случаях.
Пример 5. Вычислить значение дроби: а) , б) , в) .
а) . При сокращении пользуемся правилом деления степеней .
б) .
в) .
Сокращение сложных алгебраических дробей
После того, как мы повторили использование основного свойства обыкновенной дроби, можно перейти к рассмотрению алгебраических дробей.
Пример 6. Упростить дробь и вычислить при заданных значениях переменных: а) ; , б) ;
Решение. При подходе к решению возможен следующий вариант – сразу же подставить значения переменных и начать расчет дроби, но в таком случае решение сильно усложняется и необходимое на его решение время увеличивается, не говоря уже об опасности ошибиться в сложных вычислениях. Поэтому удобно сначала упростить выражение в буквенном виде, а затем уже подставить значения переменных.
а) . При сокращении на множитель необходимо проверить, не обращается ли он в ноль в указанных значениях переменных. При подстановке получаем , что дает возможность сокращения на данный множитель.
б) . В знаменателе выносим минус, как мы это уже делали в примере 2. При сокращении на снова проверяем не делим ли мы на ноль: .
Ответ. ; .
Приведение алгебраических дробей к общему знаменателю
Пример 7. Привести к общему знаменателю дроби а) и , б) и , в) и .
Решение. а) В данном случае подойдем к решению следующим образом: не будем пользоваться понятием НОК, как во втором примере, а просто умножим знаменатель первой дроби на знаменатель второй и наоборот – это позволит привести дроби к одинаковому знаменателю. Конечно же, не забываем при этом умножать и числители дробей на такие же выражения.
. В числителе раскрыли скобки, а в знаменателе воспользовались формулой разности квадратов.
. Аналогичные действия.
Видно, что такой способ позволяет умножить знаменатель и числитель одной дроби на тот элемент из знаменателя второй дроби, которого не хватает. С другой дробью проводятся аналогичные действия, и знаменатели приводятся к общему.
б) Проделаем аналогичные с предыдущим пунктом действия:
. Умножим числитель и знаменатель на тот элемент знаменателя второй дроби, которого не хватало (в данном случае на весь знаменатель).
. Аналогично.
в) . В данном случае мы умножили на 3 (множитель который присутствует в знаменателе второй дроби и отсутствует в первой).
.
Ответ. а) ; , б) ; , в) ; .
На данном уроке мы изучили основное свойство алгебраической дроби и рассмотрели основные задачи с его использованием. На следующем уроке мы более подробно разберем приведение дробей к общему знаменателю с использованием формул сокращенного умножения и метода группировки при разложении на множители.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- ЕГЭ по математике (Источник).
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Математика в школе: поурочные планы (Источник).

Домашнее задание
- №20, 22, 23, 26, 27, 29. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Сократить дробь: а) , б) , в) , г) .
- Привести дробь к знаменателю .
дробей | Прайм-факторизация | Нахождение общих знаменателей
Дроби | Прайм-факторизация | Поиск общих знаменателейЭто более сложный метод, но он всегда дает наименьший общий знаменатель, что упрощает последующую работу. легче найти числители равнозначных дробей.
Сначала вы записываете каждый из знаменателей как произведение его простых множителей.
Простое число — это просто число, которое делится только на себя и на 1. например. 1, 2, 3, 5, 7, 11 и т. д. — простые числа.
Множитель числа — это просто целое число, которое можно умножить на другое целое число, чтобы получить число.
например 4 x 5 = 20 , поэтому оба числа 4 и 5 являются множителями 20 .
5 — это простой делитель, потому что это тоже простое число.
Пример. 3/12 + 1/6 + 1/4
(вы, наверное, заметили, что 12 — это общий знаменатель, но мы докажем это, написав каждый знаменатель
как кратное своим простым множителям.)
- Простые множители, при умножении которых получается 12, таковы: 1 x 2 x 2 x 3 .
- (т. е. 1 х 2 х 2 х 3 = 12, и каждое из чисел 1, 2 и 3 — простые числа).
- Простые множители, при умножении которых получается 6, таковы: 1 x 2 x 3 .
- Простые множители, при умножении которых получается 4: 1 x 2 x 2 .
Сверху мы видим, что:
- Когда 12 выражается как кратное его простых множителей, одна 1, две двойки и одна 3 .
- Когда число 6 выражается как кратное его простым множителям, получается один 1, один 2 и один 3 .
- Когда 4 выражается как кратное его простых множителей, одна 1 и две двойки .

Затем мы определяем наибольшее количество раз появления каждого простого множителя для любого из знаменателей.
- Наибольшее количество единиц для любого из знаменателей равно 1, т. е. 1 .
- Наибольшее количество двоек для любого из знаменателей равно 2, т. е. 2, 2 .
- Наибольшее количество троек для любого из знаменателей равно 1, т. е. 3 .
Наконец, вы перемножаете эти числа вместе, чтобы получить наименьший общий знаменатель.
Это дает 1 x 2 x 2 x 3 = 12 .
то есть наименьший общий знаменатель равен 12 .
Пример.
- 5/12 — 2/10 .
- 1 х 2 х 2 х 3 = 12 .
- 1 х 2 х 5 = 10 .
- наибольшее количество единиц = один, 1 .
- наибольшее количество двоек = два, 2 2 .
- наибольшее количество троек = один, 3 .

- наибольшее количество 5s = один, 5 .
- 1 х 2 х 2 х 3 х 5 = 60 .
- 60 является общим знаменателем.
Расчет с эквивалентными дробями будет 25/60 — 12/60 = 13/60 .
Следовательно 5/12 — 2/10 = 13/60 .
Дробь 13/60 уже находится в низшей форме (нет числа, которое делится без остатка и на числитель, и на числитель).
знаменатель).
Умножений и разделительных фракций — минутная математика
4,2 Умножения и разделительных фракцийТемы, охватываемые в этом разделе:
- Упрощайте фракции
- Фракции
- . 1 Упрощение дробей
Работая с эквивалентными дробями, вы увидели, что существует множество способов записи дробей, имеющих одинаковое значение или представляющих одну и ту же часть целого. Как узнать, какой из них использовать? Часто мы будем использовать дробь, которая находится в упрощенная форма .

Дробь считается упрощенной, если в числителе и знаменателе нет общих множителей, кроме $1$. Если дробь имеет общие делители в числителе и знаменателе, мы можем привести дробь к ее упрощенной форме, удалив общие делители.
УПРОЩЕННАЯ ДробьДробь считается упрощенной, если в числителе и знаменателе нет общих множителей.
Например,
- $\frac{2}{3}$ упрощено, поскольку нет общих множителей для $2$ и $3$.
- $\frac{10}{15}$ не упрощается, поскольку $5$ является общим делителем 10$ и 15$.
Процесс упрощения дроби часто называют сокращением дроби . В предыдущем разделе мы использовали свойство Equivalent Fractions, чтобы найти эквивалентные дроби. Мы также можем использовать свойство Equivalent Fractions в обратном порядке, чтобы упростить дроби. Мы переписываем свойство, чтобы отображать обе формы вместе.
СВОЙСТВО ЭКВИВАЛЕНТНЫХ ДРОБЕЙЕсли $a,b,c$ числа, где $b \neq 0, c \neq 0$, то
$\frac{a}{b} = \frac{a \ cdot c}{b \cdot c}$ и $\frac{a \cdot c}{b \cdot c} = \frac{a}{b}$.

Обратите внимание, что $c$ — это общий множитель в числителе и знаменателе. Каждый раз, когда у нас есть общий множитель в числителе и знаменателе, его можно удалить.
КАК: Упростить дробь.- Перепишите числитель и знаменатель, чтобы показать общие множители. При необходимости разложите числитель и знаменатель на простые числа.
- Упростите, используя свойство эквивалентных дробей, удалив общие множители.
- Умножьте оставшиеся коэффициенты.
Упрощение: $\frac{10}{15}$.
РешениеЧтобы упростить дробь, мы ищем какие-либо общие делители в числителе и знаменателе.
Обратите внимание, что 5$ — это множитель как 10$, так и 15$. $\frac{10}{15}$ Разложите числитель и знаменатель на множители. Удалите общие множители. 
Упрощение. $\frac{2}{5}$ Чтобы упростить отрицательную дробь, мы используем тот же процесс, что и в примере 1. Не забудьте сохранить знак минус.
Пример 2Упрощение: $- \frac{18}{24}$.
РешениеМы замечаем, что множители $18$ и $24$ равны $6$. $- \frac{18}{24}$ Перепишите числитель и знаменатель, указав общий множитель. Удалить общие множители. Упрощение. 
$- \frac{3}{4}$ После упрощения дроби всегда важно проверить результат, чтобы убедиться, что числитель и знаменатель больше не имеют общих множителей. Помните, определение упрощенной дроби: дробь считается упрощенной, если в числителе и знаменателе нет общих множителей .
Когда мы упрощаем неправильную дробь, нет необходимости превращать ее в смешанное число.
Пример 3Упрощение: $- \frac{56}{32}$.
Решение
КАК: Упростить дробь.$- \frac{56}{32}$ Перепишите числитель и знаменатель, показав общие множители, $8$. 
Удаление общих факторов. Упрощение. $- \frac{7}{4}$ - Перепишите числитель и знаменатель, чтобы показать общие множители. При необходимости разложите числитель и знаменатель на простые числа.
- Упростите, используя свойство эквивалентных дробей, удалив общие множители.
- Умножьте оставшиеся коэффициенты.
Иногда бывает непросто найти общие множители числителя и знаменателя. Тогда хорошей идеей будет разложить числитель и знаменатель на простые числа.
Пример 4 (Возможно, вы захотите использовать метод дерева множителей для определения простых множителей.) Затем разделите общие множители, используя свойство «Эквивалентные дроби».
(Возможно, вы захотите использовать метод дерева множителей для определения простых множителей.) Затем разделите общие множители, используя свойство «Эквивалентные дроби».Упрощение: $\frac{210}{385}$.
РешениеИспользуйте факторные деревья для факторизации числителя и знаменателя. $\frac{210}{385}$ Перепишите числитель и знаменатель как произведение простых чисел. $\frac{210}{385} = \frac{2 \cdot 3 \cdot 5 \cdot 7}{5 \cdot 7 \cdot 11}$ Удалите общие множители. Упрощение. $\frac{2 \cdot 3}{11}$ Умножьте любые оставшиеся множители. $\frac{6}{11}$ Мы также можем упростить дроби, содержащие переменные.
Пример 5 Если переменная является общим множителем в числителе и знаменателе, мы удаляем ее так же, как и целочисленный множитель.
Если переменная является общим множителем в числителе и знаменателе, мы удаляем ее так же, как и целочисленный множитель.Упрощение: $\frac{5xy}{15x}$.
Решение
4.$\frac{5xy}{15x}$ Перепишите числитель и знаменатель, указав общие множители. $\frac{5 \cdot x \cdot y}{3 \cdot 5 \cdot x}$ Удалить общие делители. $\frac{\cancel{5} \cdot \cancel{x} \cdot \cancel{y}}{\cancel{3} \cdot \cancel{5} \cdot \cancel{x}}$ Упрощение. $\frac{y}{3}$  2.2 Умножение дробей
2.2 Умножение дробей Модель может помочь вам понять умножение дробей. Мы будем использовать фрагменты дробей для моделирования $\frac{1}{2} \cdot \frac{3}{4}$. Чтобы умножить $\frac{1}{2}$ и $\frac{3}{4}$, представьте $\frac{1}{2}$ из $\frac{3}{4}$.
Начните с дробных плиток на три четверти. Чтобы найти половину от трех четвертей, нам нужно разделить их на две равные группы. Поскольку мы не можем разделить три $\frac{1}{4}$ тайла поровну на две части, мы обмениваем их на меньшие тайлы.
Мы видим, что $\frac{6}{8}$ эквивалентно $\frac{3}{4}$. Взяв половину шести плиток $\frac{1}{8}$, мы получим три плитки $\frac{1}{8}$, что равно $\frac{3}{8}$.
Следовательно,
$\frac{1}{2} \cdot \frac{3}{4} = \frac{3}{8}$
Пример 6Использование диаграммы для моделирования $\ frac{1}{2} \cdot \frac{3}{4}$.
РешениеПервая тень в $\frac{3}{4}$ прямоугольника.
Мы возьмем $\frac{1}{2}$ этого $\frac{3}{4}$, поэтому сильно заштрихуем $\frac{1}{2}$ заштрихованной области.

Обратите внимание, что 3$ из 8$ штук сильно затенены. Это означает, что $\frac{3}{8}$ прямоугольника сильно затенены.
Следовательно, $\frac{1}{2}$ в $\frac{3}{4}$ равно $\frac{3}{8}$ или $\frac{1}{2} \cdot \ frac{3}{4} = \frac{3}{8}$
Посмотрите на результат, который мы получили от модели в примере 6. Мы обнаружили, что $\frac{1}{2} \cdot \frac{3 {4} = \frac{3}{8}$. Вы заметили, что мы могли бы получить один и тот же ответ, перемножив числители и умножив знаменатели?
$\frac{1}{2} \cdot \frac{3}{4}$ Умножьте числители и умножьте знаменатели. $\frac{1}{2} \cdot \frac{3}{4}$ Упростить. $\frac{3}{8}$ Это приводит к определению дробного умножения. Чтобы умножить дроби, мы умножаем числители и умножаем знаменатели. Тогда запишем дробь в упрощенной форме.
УМНОЖЕНИЕ ДОБЕЙЕсли $a,b,c$ и $d$ — числа, где $b \neq 0$, то
$\frac{a}{b} \cdot \frac{c}{d} = \ frac{ac}{bd}$
Пример 7Умножьте и запишите ответ в упрощенной форме: $\frac{3}{4} \cdot \frac{1}{5}$.
Решение
$\frac{3}{4} \cdot \frac{1}{5}$ Умножить числители; умножить знаменатели. $\frac{3 \cdot 1}{4 \cdot 5}$ Упрощение. $\frac{3}{20}$ Общих множителей нет, поэтому дробь упрощена.
При умножении дробей сохраняются свойства положительных и отрицательных чисел. В качестве первого шага рекомендуется определить знак произведения. В примере 8 мы умножим два отрицательных числа, поэтому произведение будет положительным.
Пример 8Умножьте и запишите ответ в упрощенной форме: $- \frac{5}{8} (- \frac{2}{3})$.
Решение
$- \frac{5}{8} (- \frac{2}{3})$ Знаки одинаковые, поэтому произведение положительное. Умножь числители, умножь знаменатели. $\frac{5 \cdot 2}{8 \cdot 3}$ Упростить. $\frac{10}{24}$ Найдите общие множители в числителе и знаменателе. Перепишите, показав общие факторы. $\frac{5 \cdot \cancel{2} }{12 \cdot \cancel{2} }$ Удалить общие факторы. $\frac{5}{12}$ Другой способ найти этот продукт заключается в удалении общих множителей ранее.
$- \frac{5}{8} (- \frac{2}{3})$ Определите знак произведения. Умножить. $\frac{5 \cdot 2}{8 \cdot 3}$ Показать общие множители, а затем удалить их. $\frac{5 \cdot \cancel{2} }{4 \cdot \cancel{2} \cdot 3}$ Умножьте оставшиеся коэффициенты. 
$\frac{5}{12}$ Мы получаем тот же результат.
Пример 9Умножьте и запишите ответ в упрощенной форме: $- \frac{14}{15} \cdot \frac{20}{21}$.
Решение$- \frac{14}{15} \cdot \frac{20}{21}$ Определить знак произведения; умножить. $- \frac{14}{15} \cdot \frac{20}{21}$ Есть ли общие множители в числителе и знаменателе? Мы знаем, что 7$ — это множитель 14$ и 21$, а 5$ — множитель 20$ и 15$.
Перепишите, указав общие факторы. $- \frac{2 \cdot \cancel{7} \cdot 4 \cdot \cancel{5} }{3 \cdot \cancel{5} \cdot 3 \cdot \cancel{7} }$ Удалите общие факторы. 
$- \frac{2 \cdot 4}{3 \cdot 3}$ Умножьте остальные множители. $- \frac{8}{9}$ При умножении дроби на целое число может быть полезно записать целое число в виде дроби. Любое целое число $a$ можно записать как $\frac{a}{1}$. Так, например, $3 = \frac{3}{1}$.
Пример 10Умножьте и запишите ответ в упрощенной форме:
- $\frac{1}{7} \cdot 56$
- $\frac{12}{5} (-20x)$
4.2.3 Найти обратные числаЧасть 1. $\frac{1}{4} \cdot 56$ Запишите $56$ в виде дроби. $\frac{1}{7} \cdot \frac{56}{1}$ Определить знак произведения; умножить. 
$\frac{56}{7}$ Упростить. Часть 2 $\frac{12}{5} ( \frac{-20x}{1} )$ Определить знак произведения; умножить. $- \frac{12 \cdot 20 \cdot x}{5 \cdot 1}$ Показать общие множители, а затем удалить их. $- \frac{12 \cdot 4 \cdot \cancel{5} x}{\cancel{5} \cdot 1}$ Умножить оставшиеся множители; упрощать. $-48x$ особым образом. Так же как $- \frac{10}{7}$ и $- \frac{7}{10}$. Вы видите, как? Помимо того, что они выглядят как перевернутые версии друг друга, если бы мы перемножили эти пары дробей, произведение составило бы $1$.

$\frac{2}{3} \cdot \frac{3}{2} = 1$ и $- \frac{10}{7} (- \frac{7}{10} ) = 1$
Такие пары чисел называются обратными.
ВЗАИМНОЕобратное дроби $\frac{a}{b}$ равно $\frac{b}{a}$, где $a \neq 0$ и $b \neq 0$ ,
Произведение числа и его обратного числа равно $1$.
$\frac{a}{b} \cdot \frac{b}{a} = 1$
Чтобы найти обратную дробь, мы инвертируем дробь. Это означает, что мы помещаем числитель в знаменатель, а знаменатель в числитель.
Чтобы получить положительный результат при умножении двух чисел, числа должны иметь одинаковый знак. Значит, обратные числа должны иметь один и тот же знак.
Чтобы найти обратную, сохраните тот же знак и инвертируйте дробь. Число ноль не имеет обратной величины. Почему? Число и его обратное умножение на $1$. Существует ли такое число $r$, что $0 \cdot r = 1$? Нет. Значит, у числа $0$ нет обратного числа.
Пример 11Найдите обратную величину каждого числа.
 Затем убедитесь, что произведение каждого числа на его обратное число равно 1 доллару США.
Затем убедитесь, что произведение каждого числа на его обратное число равно 1 доллару США.- $\frac{4}{9}$
- $- \frac{1}{6}$
- $- \frac{14}{5}$
- $7$
To находим обратные, сохраняем знак и инвертируем дроби.
часть 1 {4}$. Проверка: Умножьте число и его обратное число. $\frac{4}{9} \cdot \frac{9}{4}$ Умножить числители и знаменатели. $\frac{36}{36}$ Упростить. $ 1 $ ✓ ЧАСТЬ 2. . $. Упрощение. $-6$ Чек: $- \frac{1}{6} \cdot (-6)$ $ 1 $ ✓ . {14}$. Чек: $- \frac{14}{5} \cdot (- \frac{5}{14} )$ $\frac{70}{70}$ $1$✓ Часть 4. 
Найдите обратную величину 7$ Запишите 7$ в виде дроби. $\frac{7}{1}$ Запишите обратную величину $\frac{7}{1}$ $\frac{1}{7}$ Проверить: $7 \cdot ( \frac{1}{7} )$ $1$✓ В предыдущей главе мы работали с противоположностями и абсолютными значениями. В таблице ниже сравниваются противоположности, абсолютные значения и обратные величины.
Example 12Opposite Absolute Value Reciprocal has opposite sign is never negative has same sign, fraction inverts Fill in the chard for каждая дробь в левом столбце:
РешениеЧисло Противоположное Абсолютное значение Обратное $- \frac{3}{8}$ $\frac{1}{2}$ $\frac{9}{5}$ 9030 177$-5$ Чтобы найти противоположное, измените знак.
 Чтобы найти абсолютное значение, оставьте положительные числа одинаковыми, но возьмите противоположные отрицательные числа. Чтобы найти обратную, сохраните знак и инвертируйте дробь.
Чтобы найти абсолютное значение, оставьте положительные числа одинаковыми, но возьмите противоположные отрицательные числа. Чтобы найти обратную, сохраните знак и инвертируйте дробь.
Ранее мы моделировали это с помощью счетчиков. Сколько групп по 3$ можно составить из группы по 12$?Номер Напротив Абсолютное значение Взаимное $- \ frac {3} {8} $ $ 3}{8}$ $- \frac{8}{3}$ $\frac{1}{2}$ $- \frac{1}{2}$ $\ frac{1}{2}$ $2$ $\frac{9}{5}$ $- \frac{9}{5}$ $\frac{9}{5} $ $\frac{5}{9}$ $-5$ $5$ $5$ $- \frac{1}{5}$ Есть $4$ группы из $3$ счетчиков. Другими словами, в $12$ есть четыре $3$. Итак, 12$\дел 3 = 4$.
Как насчет деления дробей? Предположим, мы хотим найти частное: $\frac{1}{2} \div \frac{1}{6}$.
Пример 13 Нам нужно выяснить, сколько $\frac{1}{6}$ содержится в $\frac{1}{2}$. Мы можем использовать плитки дробей для моделирования этого деления. Начнем с того, что выстроим плитки половинной и шестой дроби, как показано на рисунке ниже. Обратите внимание, что в $\frac{1}{2}$ есть три плитки $\frac{1}{6}$, поэтому $\frac{1}{2} \div \frac{1}{6} = 3 $.
Нам нужно выяснить, сколько $\frac{1}{6}$ содержится в $\frac{1}{2}$. Мы можем использовать плитки дробей для моделирования этого деления. Начнем с того, что выстроим плитки половинной и шестой дроби, как показано на рисунке ниже. Обратите внимание, что в $\frac{1}{2}$ есть три плитки $\frac{1}{6}$, поэтому $\frac{1}{2} \div \frac{1}{6} = 3 $.Модель: $\frac{1}{4} \div \frac{1}{8}$.
РешениеМы хотим определить, сколько $\frac{1}{8}$ содержится в $\frac{1}{4}$. Начните с одной плитки $\frac{1}{4}$. Выровняйте плитки $\frac{1}{8}$ под плиткой $\frac{1}{4}$.
В $\frac{1}{4}$ есть два символа $\frac{1}{8}$.
Итак, $\frac{1}{4} \div \frac{1}{8} = 2$.
Пример 14Модель: $2 \div \frac{1}{4}$.
РешениеМы пытаемся определить, сколько $\frac{1}{4}$ содержится в $2$. Мы можем смоделировать это, как показано.
Поскольку в $2$ восемь $\frac{1}{4}$s, $2 \div \frac{1}{4} = 8$.

Давайте используем деньги для моделирования $2 \div \frac{1}{4}$ другим способом. Мы часто читаем $\frac{1}{4}$ как «четверть», и мы знаем, что четверть составляет одну четвертую часть доллара, как показано на рисунке ниже. Таким образом, мы можем думать о $2 \div \frac{1}{4}$ как о «Сколько четвертаков в двух долларах?» Один доллар равен 4 долларам США, поэтому 2 доллара – это 8 долларов США. Итак, снова $2 \div \frac{1}{4} = 8$.
Монета США, называемая четвертью, стоит одну четвертую доллара.Используя фрагменты дробей, мы показали, что $\frac{1}{2} \div \frac{1}{6} = 3$. Обратите внимание, что $\frac{1}{2} \cdot \frac{6}{1} = 3$ также. Как связаны $\frac{1}{6}$ и $\frac{6}{1}$ ? Они взаимозаменяемы. Это приводит нас к процедуре дробного деления.
ДРОБНОЕ ДЕЛЕНИЕЕсли $a, b, c$ и $d$ — числа, где $b \neq 0 , c \neq 0$ и $d \neq 0$, то
$\frac {a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c}$
Чтобы разделить дроби, умножьте первую дробь на величину, обратную второй.

Нам нужно сказать $b \neq 0 , c \neq 0$ и $d \neq 0$, чтобы убедиться, что мы не делим на ноль.
Пример 15Разделите и запишите ответ в упрощенной форме: $\frac{2}{5} \div (- \frac{3}{7} )$.
Решение$\frac{2}{5} \div (- \frac{3}{7} )$ Умножьте первую дробь на величину, обратную второй. $\frac{2}{5} (- \frac{7}{3} )$ Умножить. Произведение отрицательное. Пример 16 Разделите и запишите ответ в упрощенной форме: $\frac{2}{3} \div (\frac {n}{5} )$.
Решение$\frac{2}{3} \div (\frac{n}{5} )$ Умножьте первую дробь на величину, обратную второй. $\frac{2}{3} \cdot \frac{5}{n}$ Умножение. Пример 17 Разделите и запишите ответ в упрощенной форме: $- \frac{3}{4} \div (- \ дробь{7}{8} )$.
Решение$- \frac{3}{4} \div (- \frac{7}{8} )$ Умножьте первую дробь на величину, обратную второй. 
$- \frac{3}{4} \cdot (- \frac{8}{7} )$ Умножить. Не забудьте сначала определить знак. $\frac{3 \cdot 8}{4 \cdot 7}$ Перепишите, чтобы показать общие множители. $\frac{3 \cdot \cancel{4} \cdot 2}{\cancel{4} \cdot 7}$ Удалите общие множители и упростите. Пример 18 Разделите и запишите ответ в упрощенной форме: $\frac{7}{18} \div (\frac{ 14}{27} )$.
Решение$\frac{7}{18} \div (\frac{14}{27} )$ Умножьте первую дробь на обратную вторую. $\frac{7}{18} \cdot (\frac{14}{27} )$ Умножить. $\frac{7 \cdot 27}{18 \cdot 14}$ Перепишите, указав общие множители. $\frac{\cancel{7} \cdot \cancel{9} \cdot 3}{\cancel{9} \cdot 2 \cdot \cancel{7} \cdot 2}$ Удалить общие делители . $\frac{3}{2 \cdot 2}$ Упростить. 







 (Возможно, вы захотите использовать метод дерева множителей для определения простых множителей.) Затем разделите общие множители, используя свойство «Эквивалентные дроби».
(Возможно, вы захотите использовать метод дерева множителей для определения простых множителей.) Затем разделите общие множители, используя свойство «Эквивалентные дроби». Если переменная является общим множителем в числителе и знаменателе, мы удаляем ее так же, как и целочисленный множитель.
Если переменная является общим множителем в числителе и знаменателе, мы удаляем ее так же, как и целочисленный множитель. 2.2 Умножение дробей
2.2 Умножение дробей 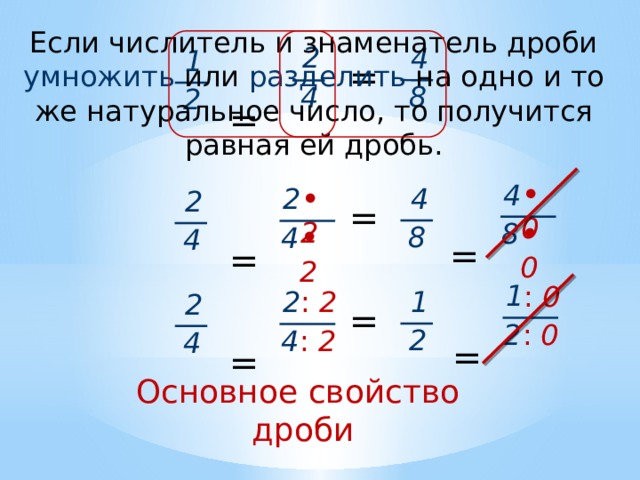


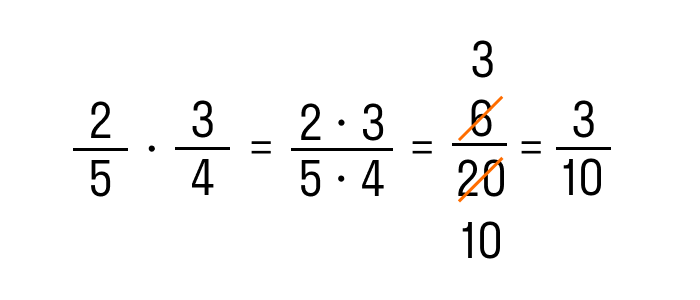


 Затем убедитесь, что произведение каждого числа на его обратное число равно 1 доллару США.
Затем убедитесь, что произведение каждого числа на его обратное число равно 1 доллару США.
 Чтобы найти абсолютное значение, оставьте положительные числа одинаковыми, но возьмите противоположные отрицательные числа. Чтобы найти обратную, сохраните знак и инвертируйте дробь.
Чтобы найти абсолютное значение, оставьте положительные числа одинаковыми, но возьмите противоположные отрицательные числа. Чтобы найти обратную, сохраните знак и инвертируйте дробь. Нам нужно выяснить, сколько $\frac{1}{6}$ содержится в $\frac{1}{2}$. Мы можем использовать плитки дробей для моделирования этого деления. Начнем с того, что выстроим плитки половинной и шестой дроби, как показано на рисунке ниже. Обратите внимание, что в $\frac{1}{2}$ есть три плитки $\frac{1}{6}$, поэтому $\frac{1}{2} \div \frac{1}{6} = 3 $.
Нам нужно выяснить, сколько $\frac{1}{6}$ содержится в $\frac{1}{2}$. Мы можем использовать плитки дробей для моделирования этого деления. Начнем с того, что выстроим плитки половинной и шестой дроби, как показано на рисунке ниже. Обратите внимание, что в $\frac{1}{2}$ есть три плитки $\frac{1}{6}$, поэтому $\frac{1}{2} \div \frac{1}{6} = 3 $.


