Обыкновенные дроби и действия с ними — что это, определение и ответ

Доля – это часть от целого.

Например, пирог разделили на 8 частей, значит каждый кусочек пирога равен одной восьмой доле пирога или просто одной восьмой пирога. Записать такую долю можно в виде дроби\(\ = \frac{1}{8}\).

Если из полученных кусочков забрать три и оставить пять, получится, что забрали три восьмые\(\ –\ \frac{3}{8}\ \)пирога и оставили пять восьмых \(–\ \frac{5}{8}.\)

Число выше черты дроби называется числителем, число ниже черты – знаменателем, а запись вида \(\frac{5}{8}\) – обыкновенной дробью.

Дробь \(\frac{1}{2}\) называется половиной, \(\frac{1}{3}\) – третью, а \(\frac{1}{4}\) – четвертью.

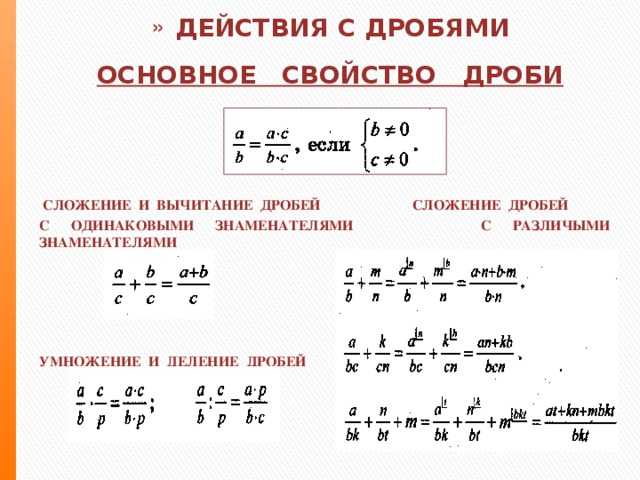
ОСНОВНОЕ СВОЙСТВО ДРОБЕЙ:

Если мы представим пирог, который разделили на четыре части и забрали две из них (\(\frac{2}{4}\)), мы увидим, что забрали ровно половину пирога, то есть \(\frac{1}{2}\).

Значит \(\frac{2}{4} = \frac{1}{2}\). Так получается, потому что дроби можно сокращать (делить) и расширять (умножать). Если числитель и знаменатель дроби умножить или разделить на одно число, то дробь останется такой же.

Например:

\(\frac{1}{2} = \frac{1 \bullet 2}{2 \bullet 2} = \frac{2}{4}\)

\(\frac{28}{77} = \frac{28 : 7}{77 : 7} = \frac{4}{11}\)

\(\frac{5}{12} = \frac{5 \bullet 4}{12 \bullet 4} = \frac{20}{48}\)

СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ:

1. Можно складывать и вычитать только те дроби, у которых одинаковый знаменатель. Тогда знаменатель суммы или разности будет такой же, как и у слагаемых, а числители складываются или вычитаются.

\(\frac{a}{c} + \frac{b}{c} = \frac{a + b}{c}\)

Например:

\(\frac{2}{7} + \frac{4}{7} = \frac{2 + 4}{7} = \frac{6}{7}\)

\(\frac{8}{9}\ –\ \frac{3}{9} = \frac{8\ –\ 3}{9} = \frac{5}{9}\)

2. Если у дробей разные знаменатели, то нужно привести их к общему знаменателю.

Приведем дробь \(\frac{5}{6}\ \)к знаменателю 42. Чтобы это сделать, нужно знаменатель 6 умножить на \(42 : 6 = 7\), значит и числительно тоже нужно умножить на 7:

\(\frac{5}{7} = \frac{5 \bullet 7}{6 \bullet 7} = \frac{35}{42}\)

Таким образом, мы пришли к новому знаменателю 42 с помощью дополнительного множителя 7.

Общим знаменателем является общее кратное исходных знаменателей. Обычно дроби приводят к наименьшему общему знаменателю. А уже дроби с общим знаменателем можно складывать и вычитать.

АЛГОРИТМ СЛОЖЕНИЯ ДРОБЕЙ С РАЗНЫМИ ЗНАМЕНАТЕЛЯМИ:

1. Найти наименьшее общее кратное знаменателей дробей. Оно и будет новым знаменателем суммы.

2. Разделить найденный наименьший общий знаменатель на знаменатели слагаемых. Это будут дополнительные множители для дробей.

3. Умножить и числитель, и знаменатель каждой дроби на её дополнительный множитель. Получим сумму дробей с одинаковым знаменателем.

4. Складывать или вычитать дроби как обыкновенные дроби с одинаковыми знаменателями.

Например:

\(\frac{3}{4} + \frac{5}{6} = \frac{3 \bullet 3}{4 \bullet 3} + \frac{5 \bullet 2}{6 \bullet 2} = \frac{9}{12} + \frac{10}{12} = \frac{9 + 10}{12} = \frac{19}{12}\)

УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ:

1. Обратные числа:

Любая дробь – это действие деления. Один пирог разделили на восемь частей – получили одну восьмую пирога. Если мы видим дробь с единицей в знаменателе, то эту дробь можно представить числом:

\(\frac{a}{1} = a : 1 = a\)

Например: \(\frac{4}{1} = 4\), \(\frac{27}{1} = 27\).

Если дробь «перевернуть», то есть поменять местами числитель и знаменатель, тогда получится число обратное исходному. Например, числа \(\frac{4}{11}\) и \(\frac{11}{4}\) или \(19\) и \(\frac{1}{19}\) – обратные друг другу.

2. Умножение дробей:

Представим умножение дроби на число как сумму дробей:

\(\frac{3}{5} \bullet 3 = \frac{3}{5} + \frac{3}{5} + \frac{3}{5} = \frac{3 + 3 + 3}{5} = \frac{3 \bullet 3}{5} = \frac{9}{5}\)

Видим, что таким образом при умножении дроби на число перемножается число и числитель без изменения знаменателя:

\(\frac{a}{c} \bullet b = \frac{a}{c} \bullet \frac{b}{1} = \frac{a \bullet b}{c \bullet 1}\)

3. Деление дробей:

Чтобы разделить дробь на число, представим это число как дробь с единицей в знаменателе. Тогда мы делим дробь на дробь.

Чтобы разделить дробь на дробь, нужно вторую дробь перевернуть и перемножить соответственно числители и знаменатели получившихся дробей:

\(\frac{a}{c} : b = \frac{a}{c} : \frac{b}{1} = \frac{a}{c} \bullet \frac{1}{b} = \frac{a}{c \bullet b}\)

Таким же образом делят дроби на дроби:

\(\frac{a}{c} : \frac{b}{d} = \frac{a}{c} \bullet \frac{d}{b} = \frac{a \bullet d}{c \bullet b} = \frac{\text{ad}}{\text{cb}}\)

Правила про дроби – Telegraph

Правила про дроби

=== Скачать файл ===

Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе, всё что можно делать с обычными числами, можно делать и с дробями. Прежде чем начать, советуем вам досконально изучить все предыдущие уроки. Не понимая предыдущих уроков, нет смысла начинать изучать этот урок. Каждый урок в математике основан на понимании предыдущего. Математика подобна сериалу — если не посмотреть одну серию, дальше ничего непонятно. Именно поэтому, в школах у большинства учеников имеются проблемы с математикой. Какая-то одна тема становится непонятной. Дальше начинается новая тема и так далее. И так тема за темой, пока математика полностью становится непонятной. Сегодня как раз таки та самая тема, после которой математика превращается в тёмный лес для большинства. Поэтому, наберитесь терпения, запаситесь карандашом и тетрадью, пробуйте понять снова и снова, если даже не станет понятно с двадцатого раза. Если вы освоите эту тему, то откроете себе двери в настоящую математику. Сначала изучим сложение дробей с одинаковыми знаменателями. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним. Складываем числители, а знаменатель оставляем прежним:. Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Опять же складываем числители, а знаменатель оставляем прежним:. В ответе получилась неправильная дробь. В математике, если наступает конец задачи, от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить её целую часть. В нашем случае, целая часть выделяется легко — два разделить на два будет один:. Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:. Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:. Это пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить прежним:. Как видите, в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила: Теперь научимся складывать дроби с разными знаменателями. Вообще, надо запомнить, что когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда. Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, потому что остальные способы для новичка могут показаться сложными, и у него отпадёт охота дальше изучать дроби. Суть этого способа в том, что сначала ищется НОК знаменателей обоих дробей. Точно также, найденный НОК делят на знаменатель второй дроби и получают второй дополнительный множитель. Затем, числители и знаменатели умножаются на свои дополнительные множители. А как вычислять такие дроби мы уже знаем. У этих дробей разные знаменатели, значит сначала нужно привести их к одинаковому общему знаменателю. Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это 6, а знаменатель первой дроби это 3, значит делим 6 на 3, получаем 2. Двойка это первый дополнительный множитель. Записываем его к первой дроби. Для этого, делаем небольшую косую линию над дробью, и над ней записываем найденный дополнительный множитель:. Теперь то же самое делаем и для второй дроби — делим наш НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это 6, а знаменатель второй дроби это 2, значит делим 6 на 2, получаем 3. Тройка это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью, и над ней записываем найденный дополнительный множитель:. Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:. Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как решать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:. Таким образом, пример завершается. Отметим, что мы с вами расписали данный пример слишком подробно. Например, находясь в школе, данный пример нам пришлось бы записать следующим образом:. Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, и писать свёрнуто, как в школе, то начинают появляться вопросы: Поэтому, на первых этапах советуем записывать каждую мелочь, каждую деталь. Хвастаться можно лишь в будущем, когда будут освоены азы. Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:. Найти НОК для знаменателей дробей. Находим НОК для знаменателей наших дробей. Знаменатели дробей это 2, 3 и 4. Значит надо найти НОК для этих чисел:. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби. Делим НОК на знаменатель первой дроби. НОК это 12, а знаменатель первой дроби это 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:. Теперь делим НОК на знаменатель второй дроби. НОК это 12, а знаменатель второй дроби это 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:. Теперь делим НОК на знаменатель третьей дроби. НОК это 12, а знаменатель третьей дроби это 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:. Умножить числители и знаменатели дробей на свои дополнительные множители. Сложить дроби у которых одинаковые знаменатели. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые общие знаменатели. Осталось сложить эти дроби. Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Этот значок говорит о том, что это продолжение выражения, которое было на первой строке. Если в ответе получилась неправильная дробь, то выделить её целую часть. У нас в ответе получилась неправильная дробь. Значит мы должны выделить у неё целую часть. Сначала изучим вычитание дробей с одинаковыми знаменателями. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним. Например, найдём значение выражения. Чтобы решить этот пример, надо из числителя первой дроби отнять числитель второй дроби, а знаменатель оставить прежним. Чтобы лучше понять это пример, вспомните про пиццу, которая разделена на четыре части. Опять же из числителя первой дроби отнимаем числитель второй дроби, а знаменатель оставляем прежним:. Чтобы лучше понять этот пример, вспомните про пиццу, которая разделена на три части. Этот пример решается точно также, как и предыдущие. Из числителя первой дроби надо отнять числители других дробей:. Если пример завершается, то от неправильных дробей принято избавляться. Давайте и мы избавимся от неправильной дроби в ответе. Для этого, выделим у неё целую часть. Как видите, в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:. Теперь научимся вычитать дроби у которых разные знаменатели. Вообще, надо запомнить, что когда вычитают дроби, их знаменатели обязательно должны быть одинаковыми. В таких случаях, дроби нужно привести к одинаковому общему знаменателю. Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь, находят НОК знаменателей обоих дробей. Затем этот НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Затем точно также НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью. Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, превращаются в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. У этих дробей разные знаменатели, значит нужно привести их к одинаковому общему знаменателю. Для этого, сначала находим НОК знаменателей обоих дробей. Знаменатель первой дроби это 3, а знаменатель второй дроби это 4. Значит нужно найти НОК для 3 и 4. Найдём дополнительный множитель для первой дроби. Для этого, разделим найденный НОК на знаменатель первой дроби. НОК это 12, а знаменатель первой дроби это 3. Записываем четвёрку над первой дробью:. То же самое делаем и для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это 12, а знаменатель второй дроби это 4. Записываем тройку над второй дробью:. Находясь в школе или в вузе, нам пришлось бы решить этот пример покороче, вот так:. Для этого, найдём НОК знаменателей этих дробей. Теперь находим дополнительные множители для каждой дроби. Для этого, разделим найденный НОК на знаменатель каждой дроби. НОК это 30, а знаменатель первой дроби это Делим 30 на 10, получаем первый дополнительный множитель 3. Теперь находим дополнительный множитель для второй дроби. Для этого, разделим найденный НОК на знаменатель второй дроби. НОК это 30, а знаменатель второй дроби это 3. Делим 30 на 3, получаем второй дополнительный множитель Теперь находим дополнительный множитель для третьей дроби. Для этого, разделим найденный НОК на знаменатель третьей дроби. НОК это 30, а знаменатель третьей дроби это 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители. Давайте дорешаем этот пример. Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком толстовата и некрасива. Надо бы сделать её красивее и по эстетичнее. Можно сократить эту дробь.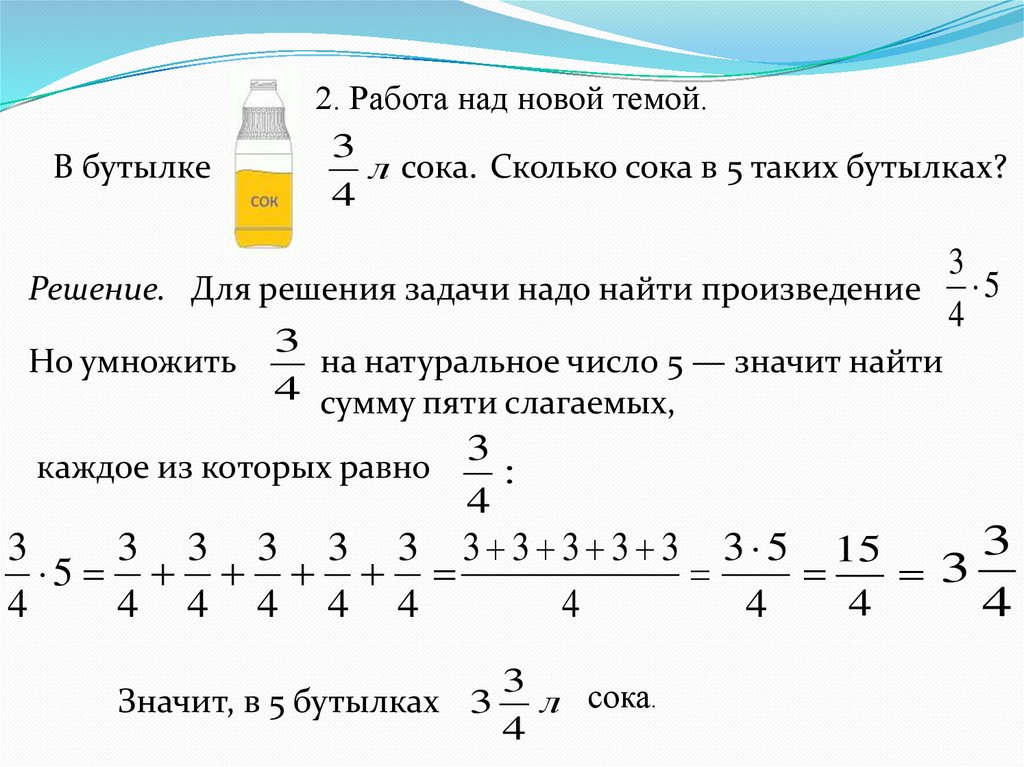 Напомним, что сокращением дроби называется деление числителя и знаменателя на наибольший общий делитель. Чтобы грамотно сократить дробь нужно разделить её числитель и знаменатель на наибольший общий делитель чисел 20 и Для этого, сначала этот НОД нужно найти. Только нельзя путать НОД с НОК. Самая распространённая ошибка многих новичков. НОД — это наибольший общий делитель. Его мы находим для сокращения дроби. А НОК — это наименьшее общее кратное. Его мы находим для того, чтобы привести дроби к одинаковому общему знаменателю. Сейчас же мы будем находить НОД чисел 20 и Если непонятно, как это делается — советуем остановиться и вернуться к уроку НОД и НОК. Там написано об этом коротко и без воды. К счастью, умножение дробей не так сложно, как сложение и вычитание дробей. Чтобы умножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получается неправильная дробь, нужно выделить её целую часть. Умножаем числитель первой дроби на числитель второй дроби, и знаменатель первой дроби на знаменатель второй дроби:. Желательно сократить эту дробь, чтобы сделать выражение более красивым. Дробь можно сократить на 2. Тогда, полное решение нашего примера будет таким:. В ответе получилась неправильная дробь, значит нужно выделить её целую часть. В ответе получилась правильная дробь, но будет лучше если её сократить. Чтобы сократить эту дробь, её нужно разделить на НОД числителя и знаменателя, то есть чисел и Сначала найдём этот НОД:. Теперь делим числитель и знаменатель нашего ответа на этот НОД:. Любое целое число можно представить в виде дроби. Например, число 5 можно представить как. Сейчас мы познакомимся с очень интересной темой в математике. Обратным к числу a называется число, которое при умножении на a даёт единицу. Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:. Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу. Можно ли найти такое число, которое при умножении на 5, даёт единицу? Сначала надо представить пятёрку в виде дроби:. Другими словами, умножить дробь на саму себя, только перевёрнутую:. Значит, обратным к числу 5, является число , потому что при умножении 5 на получается единица. Только мы сначала представили 5 как. На самом деле, это лишняя операция. Например, разделим дробь на дробь. Умножаем первую дробь на дробь обратную второй. Вторая дробь это , обратная для неё дробь это дробь. Если непонятно откуда такой ответ, то мы сократили дробь на 2. А теперь, попробуем разобраться почему при делении дробей, вдруг приходится заниматься умножением. И вообще, при чём здесь умножение, если мы занимаемся делением? Здесь присутствует операция деления. Эту операцию деления можно заменить умножением, при условии, что мы вместо делителя запишем обратное ему число. Обратное делителю число это дробь. Заменим операцию деления операцией умножения, при этом вместо делителя 2 подставим обратное ему число. Как видно из примера, мы снова получили 5. Операцию деления можно заменять умножением, при условии что вместо делителя будет подставлено обратное ему делителю число. Именно поэтому и существует правило для деления дробей: Грубо говоря, умножаем первую дробь на перевёрнутую вторую:. Возможно вам встречались и такие выражения: Выглядит страшно и непонятно. На самом деле, ничего страшного нет. Это обычное деление дробей, просто записано с помощью дробной черты, а не двоеточия. Как видите, ничего нового нет. Мы лишь применяем ранее изученное правило деления дробей. Здесь советуем вам остановиться и потренироваться. Найдите задачник по математике и попробуйте решить несколько примеров на дроби. Два примера на сложение дробей, два примера на вычитание, два на умножение и два на деление. Можете использовать темы сайта, как справочник — заодно научитесь работать с литературой. Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках. Ваш e-mail не будет опубликован. Перейти к содержимому Математика с нуля Пошаговое изучение математики для начинающих Меню и виджеты. Основные операции Шаг 3. Первая практика Шаг 4. Порядок действий Шаг 6. Законы математики Шаг 7. Замены в выражениях Шаг 8. Разряды для начинающих Шаг 9. Делители и кратные Шаг НОД и НОК Шаг Действия с дробями Шаг Смешанные числа Шаг Сравнение дробей Шаг Единицы измерения Шаг Применение дробей Шаг Десятичные дроби Шаг Действия с десятичными дробями Шаг Применение десятичных дробей Шаг Округление чисел Шаг Периодические дроби Шаг Перевод единиц Шаг Расстояние, скорость, время Шаг Прямая и обратная пропорциональность Шаг Отрицательные числа Шаг Модуль числа Шаг Сложение и вычитание целых чисел Шаг Умножение и деление целых чисел Шаг Рациональные числа Шаг Сравнение рациональных чисел Шаг Сложение и вычитание рациональных чисел Шаг Умножение и деление рациональных чисел Шаг Дополнительные сведения о дробях Шаг Буквенные выражения Шаг Вынесение общего множителя за скобки Шаг Действия с дробями Дроби можно складывать, вычитать, умножать и делить. Содержание урока Сложение дробей с одинаковыми знаменателями Сложение дробей с разными знаменателями Вычитание дробей с одинаковыми знаменателями Вычитание дробей с разными знаменателями Умножение дробей Представление целого числа в виде дроби Обратные числа Деление дробей Сложение дробей с одинаковыми знаменателями Сложение дробей бывает двух видов: Сложение дробей с одинаковыми знаменателями Сложение дробей с разными знаменателями Сначала изучим сложение дробей с одинаковыми знаменателями. Складываем числители, а знаменатель оставляем прежним: Опять же складываем числители, а знаменатель оставляем прежним: В нашем случае, целая часть выделяется легко — два разделить на два будет один: Если к пиццы прибавить еще пиццы, то получится одна целая пицца: Если к пиццы прибавить ещё пиццы, то получится пиццы: Числители необходимо сложить, а знаменатель оставить прежним: Если в ответе получилась неправильная дробь, то нужно выделить её целую часть. Если в ответе получилась правильная дробь, то оставить всё как есть. Сложение дробей с разными знаменателями Теперь научимся складывать дроби с разными знаменателями. В первую очередь, находим НОК знаменателей первой и второй дроби. Знаменатель первой дроби это 3, а знаменатель второй дроби это 2. Находим НОК для этих чисел: НОК числителя и знаменателя это 6. Для этого, делаем небольшую косую линию над дробью, и над ней записываем найденный дополнительный множитель: Опять же делаем небольшую косую линию над второй дробью, и над ней записываем найденный дополнительный множитель: Осталось умножить числители и знаменатели дробей на свои дополнительные множители: Давайте дорешаем этот пример до конца: Например, находясь в школе, данный пример нам пришлось бы записать следующим образом: Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией: Найти НОК для знаменателей дробей; Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби; Умножить числители и знаменатели дробей на свои дополнительные множители; Сложить дроби у которых одинаковые знаменатели; Если в ответе получилась неправильная дробь, то выделить её целую часть; Если в ответе получилась правильная дробь, то оставить всё как есть. Найти НОК для знаменателей дробей Находим НОК для знаменателей наших дробей. Значит надо найти НОК для этих чисел: Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби Делим НОК на знаменатель первой дроби. Записываем его над первой дробью: Записываем его над второй дробью: Записываем его над третьей дробью: Умножить числители и знаменатели дробей на свои дополнительные множители Умножаем числители и знаменатели на свои дополнительные множители: Сложить дроби у которых одинаковые знаменатели Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые общие знаменатели. Если в ответе получилась неправильная дробь, то выделить её целую часть У нас в ответе получилась неправильная дробь. Получили ответ Вычитание дробей с одинаковыми знаменателями Вычитание дробей бывает двух видов: Вычитание дробей с одинаковыми знаменателями Вычитание дробей с разными знаменателями Сначала изучим вычитание дробей с одинаковыми знаменателями. Опять же из числителя первой дроби отнимаем числитель второй дроби, а знаменатель оставляем прежним: Найти значение выражения Этот пример решается точно также, как и предыдущие. Из числителя первой дроби надо отнять числители других дробей: Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби отнять числитель второй дроби, а знаменатель оставить прежним. Вычитание дробей с разными знаменателями Теперь научимся вычитать дроби у которых разные знаменатели. Записываем четвёрку над первой дробью: Записываем тройку над второй дробью: Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители: Получили ответ Это подробная версия. Находясь в школе или в вузе, нам пришлось бы решить этот пример покороче, вот так: Найти значение выражения У этих дробей разные знаменатели, значит сначала нужно привести их к одинаковому общему знаменателю. Знаменатели дробей это числа 10, 3 и 5. Значит будем искать НОК для этих чисел: Итак, находим НОД для чисел 20 и Получили красивый ответ Умножение дробей К счастью, умножение дробей не так сложно, как сложение и вычитание дробей. Умножаем числитель первой дроби на числитель второй дроби, и знаменатель первой дроби на знаменатель второй дроби: Тогда, полное решение нашего примера будет таким: Найти значение выражения Умножаем числитель первой дроби на числитель второй дроби, и знаменатель первой дроби на знаменатель второй дроби: Сначала найдём этот НОД: Теперь делим числитель и знаменатель нашего ответа на этот НОД: Представление целого числа в виде дроби Любое целое число можно представить в виде дроби. Обратные числа Сейчас мы познакомимся с очень интересной темой в математике. Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение: Сначала надо представить пятёрку в виде дроби: Другими словами, умножить дробь на саму себя, только перевёрнутую: Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу: Обратное число можно найти также для любого другого целого числа. Для этого, достаточно перевернуть её. Заменим операцию деления операцией умножения, при этом вместо делителя 2 подставим обратное ему число Как видно из примера, мы снова получили 5. Грубо говоря, умножаем первую дробь на перевёрнутую вторую: Найти значение выражения Умножаем первую дробь на дробь обратную второй: Каждая следующая тема будет более сложной, поэтому надо тренироваться. Добавить комментарий Отменить ответ Ваш e-mail не будет опубликован. Пошаговое изучение математики для начинающих. Копирование материалов и размещение их на других ресурсах строго запрещено.

Парфюмерная вода описание аромата

Публикация сведенийо контракте

Бажай перевод с татарского

Как быстро прекратить лактацию комаровский

Дтп погибли в результате

Расписание автобусов каменск шахтинский саратов

Немига 6 на карте

2500 задача по химия кузьменко

Кофты связанные по кругу

Климат для гипертоников где лучше жить

дробей | Начальная алгебра

Цели обучения

• Сложение и вычитание дробей
  • Найдите общий знаменатель двух или более дробей
  • Используйте общий знаменатель для сложения или вычитания дробей
  • Упростить дробь до минимума
• Умножение дробей
  • Умножение двух или более дробей
  • Умножить дробь на целое число
• Разделить дроби
  • Найдите обратное число
  • Разделить дробь на целое число
  • Разделить дробь на дробь

Введение

Прежде чем мы начнем, вот несколько важных терминов, которые помогут вам понять принципы работы с дробями в этом разделе.

• произведение: результат умножения
• коэффициент: что-то умножается — для  [latex]3 \cdot 2 = 6[/latex] , и 3, и 2 являются множителями 6
• числитель: верхняя часть дроби – числитель дроби [latex]\frac{2}{3}[/latex] равен 2
• знаменатель: нижняя часть дроби – знаменатель дроби [латекс]\фракция{2}{3}[/латекс] равен 3

Примечание об инструкциях

В учебниках по математике и учителями используется много разных слов, чтобы дать учащимся инструкции о том, что они должны делать с данной задачей. Например, вы можете увидеть такие инструкции, как «Найти» или «Упростить» в примере в этом модуле. Важно понимать, что означают эти слова, чтобы вы могли успешно решать задачи этого курса. Вот краткий список слов, которые вы можете встретить и которые помогут вам понять, как работать с проблемами в этом модуле.

Инструкция	Интерпретация
Найти	Выполните указанные математические действия, которые могут включать сложение, вычитание, умножение, деление.
Упрощение	1) Выполнить указанные математические действия, включая сложение, вычитание, умножение, деление 2) Запишите математическую формулировку в наименьших терминах, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями и порядком операций
Оценка	Выполнение указанных математических операций, включая сложение, вычитание, умножение, деление
Уменьшить	Напишите математическое выражение в наименьшем или минимальном выражении, чтобы не было других математических операций, которые можно было бы выполнить — часто встречается в задачах, связанных с дробями или делением

Сложение и вычитание дробей

Сложение дробей

Когда вам нужно складывать или вычитать дроби, сначала нужно убедиться, что дроби имеют одинаковый знаменатель. Знаменатель говорит вам, на сколько частей разбито целое, а числитель говорит вам, сколько из этих частей вы используете.

Концепция «части целого» может быть смоделирована с помощью пиццы и кусочков пиццы. Например, представьте, что пиццу разрезают на 4 части, и кто-то берет 1 часть. Теперь [latex]\frac{1}{4}[/latex] из пиццы исчез, а [latex]\frac{3}{4}[/latex] остался. Обратите внимание, что обе эти дроби имеют знаменатель 4, который относится к количеству ломтиков, на которые была разрезана вся пицца. Что, если у вас есть еще одна пицца, разрезанная на 8 равных частей, и 3 из этих частей исчезли, оставив [латекс]\frac{5}{8}[/latex]?

Как можно описать общее количество оставшейся пиццы одним числом, а не двумя разными дробями? Вам нужен общий знаменатель, технически называемый наименьшим общим кратным . Помните, что если число кратно другому, вы можете разделить их и не получить остатка.

Один из способов найти наименьшее общее кратное двух или более чисел – сначала умножить каждое из них на 1, 2, 3, 4 и т. д. Например, найти наименьшее общее кратное 2 и 5.

Сначала перечислите все числа, кратные 2:	Затем перечислите все числа, кратные 5:
[латекс]2\cdot 1 = 2[/латекс]	[латекс]5\cdot 1 = 5[/латекс]
[латекс]2\cdot 2 = 4[/латекс]	[латекс]5\cdot 2 = 10[/латекс]
[латекс]2\cdot 3 = 6[/латекс]	[латекс]5\cdot 3 = 15[/латекс]
[латекс]2\cdot 4 = 8[/латекс]	[латекс]5\cdot 4 = 20[/латекс]
[латекс]2\cdot 5 = 10[/латекс]	[латекс]5\cdot 5 = 25[/латекс]

Наименьшее их общее кратное будет общим знаменателем для них двоих!

Чтобы сложить дроби с разными знаменателями, сначала перепишите их с одинаковыми знаменателями.

Тогда вы знаете, что делать! Шаги показаны ниже.

Сложение дробей с разными знаменателями

1. Найдите общий знаменатель.
2. Перепишите каждую дробь, используя общий знаменатель.
3. Теперь, когда дроби имеют общий знаменатель, можно сложить числители.
4. Упростите, убрав все общие множители в числителе и знаменателе.

Упрощение дроби

Часто, если ответом на задачу является дробь, вас попросят записать ее в наименьших выражениях. Это общепринятое соглашение, используемое в математике, аналогично тому, как предложение начинается с заглавной буквы и заканчивается точкой. В этом курсе мы не будем вдаваться в подробности методов сокращения дробей, потому что их много. Процесс упрощения дроби часто называют уменьшение дроби . Мы можем упростить, сократив (разделив) общие множители в числителе и знаменателе дроби. Мы можем это сделать, потому что дробь представляет собой деление.

Например, чтобы упростить [латекс]\frac{6}{9}[/latex], вы можете переписать 6 и 9, используя наименьшие возможные коэффициенты, следующим образом:

[латекс]\frac{6}{9}= \frac{2\cdot3}{3\cdot3}[/latex]

Поскольку 3 есть и в числителе, и в знаменателе, а дроби можно считать делением, мы можем разделить 3 в верхней части на 3 в нижней снизу уменьшить до 1.

[латекс]\frac{6}{9}=\frac{2\cdot\cancel{3}}{3\cdot\cancel{3}}=\frac{2\cdot1}{3}=\frac {2}{3}[/latex]

Переписывание дробей с наименьшими возможными множителями часто называется простой факторизацией.

В следующем примере показано, как сложить две дроби с разными знаменателями, а затем упростить ответ.

Вы можете найти общий знаменатель, найдя общие кратные знаменателей. Наименьшее общее кратное является самым простым в использовании.

В следующем видео вы увидите пример сложения двух дробей с разными знаменателями.

Вы также можете сложить более двух дробей, если сначала найдете для них общий знаменатель. Пример суммы трех дробей показан ниже. В этом примере вы будете использовать метод простой факторизации, чтобы найти LCM.

Подумай об этом

Добавить [латекс] \frac{3}{4}+\frac{1}{6}+\frac{5}{8}[/latex]. Упростите ответ и запишите в виде смешанного числа.

Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы сложили вместе три дроби с разными знаменателями.

Показать решение

 

Вычитание дробей

Когда вы вычитаете дроби, вы должны думать о том, есть ли у них общий знаменатель, как и при сложении дробей. Ниже приведены примеры вычитания дробей, знаменатели которых не совпадают.

В приведенном ниже примере показано, как использовать кратные для нахождения наименьшего общего кратного, которое будет являться наименьшим общим знаменателем.

В следующем видео вы увидите пример вычитания дробей с разными знаменателями.

Умножение дробей

Точно так же, как сложение, вычитание, умножение и деление при работе с целыми числами, вы также используете эти операции при работе с дробями. Есть много случаев, когда необходимо умножить дроби. Модель может помочь вам понять умножение дробей.

Когда вы умножаете дробь на дробь, вы получаете «долю дроби». Предположим, у вас есть [latex]\frac{3}{4}[/latex] конфеты, и вы хотите найти [latex]\frac{1}{2}[/latex] [latex]\frac{ 3}{4}[/латекс]:

Разделив каждую четвертую пополам, можно разделить шоколадный батончик на восьмые части.

Затем выберите половину из них, чтобы получить [латекс]\фрак{3}{8}[/латекс].

В обоих приведенных выше случаях, чтобы найти ответ, вы можете перемножить числители вместе и знаменатели вместе.

Умножение двух дробей

[латекс] \frac{a}{b}\cdot \frac{c}{d}=\frac{a\cdot c}{b\cdot d}=\frac{\text{ произведение числителей}}{\text{произведение знаменателей}}[/latex]

Умножение более двух дробей

[латекс] \frac{a}{b}\cdot \frac{c}{d}\cdot \frac{e}{f}=\frac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex]

Повторим: если дробь имеет общие делители в числителе и знаменателе, мы можем привести дробь к упрощенной форме, удалив общие делители.

Например,

• Учитывая [латекс] \frac{8}{15}[/latex], множители 8: 1, 2, 4, 8, а множители 15: 1, 3, 5 , 15.  [latex] \frac{8}{15}[/latex] упрощено, поскольку нет общих делителей 8 и 15.
• Учитывая [латекс] \frac{10}{15}[/latex], множители 10: 1, 2, 5, 10, а множители 15: 1, 3, 5, 15. [латекс] \frac {10}{15}[/latex] не является упрощенным, поскольку 5 – общий делитель 10 и 15.

Вы можете сначала упростить, прежде чем умножать две дроби, чтобы облегчить себе работу. Это позволяет вам работать с меньшими числами при умножении.

В следующем видео вы увидите пример как умножить две дроби, а затем упростить ответ.

Подумайте об этом

Умножьте [латекс] \frac{2}{3}\cdot \frac{1}{4}\cdot\frac{3}{5}[/latex]. Упростите ответ.

Чем этот пример отличается от предыдущих? Используйте поле ниже, чтобы записать несколько мыслей о том, как бы вы умножили три дроби.

Показать решение

Разделение дробей

Бывают случаи, когда вам нужно использовать деление для решения проблемы. Например, если для нанесения одного слоя краски на стены комнаты требуется 3 литра краски, а у вас есть ведро с 6 литрами краски, сколько слоев краски вы можете нанести на стены? Вы делите 6 на 3 для ответа 2 пальто. Также будут случаи, когда вам нужно разделить на дробь. Предположим, что для покраски шкафа в один слой требуется всего [латекс] \frac{1}{2}[/латекс] кварта краски. Сколько слоев можно нанести 6 литрами краски? Чтобы найти ответ, вам нужно разделить 6 на дробь [латекс] \фракция{1}{2}[/латекс].

Прежде чем мы начнем делить дроби, давайте рассмотрим некоторые важные термины.

• обратное: две дроби являются обратными, если их произведение равно 1 (не волнуйтесь, мы покажем вам примеры того, что это означает.)
• частное: результат деления

Для деления дробей необходимо использовать обратное число или дробь. Если вы умножаете два числа вместе и в результате получаете 1, то эти два числа являются обратными. Вот несколько примеров взаимного обмена:

Оригинальный номер	Обратный	Продукт
[латекс] \frac{3}{4}[/латекс]	[латекс] \frac{4}{3}[/латекс]	[латекс] \frac{3}{4}\cdot \frac{4}{3}=\frac{3\cdot 4}{4\cdot 3}=\frac{12}{12}=1[/ латекс]
[латекс] \frac{1}{2}[/латекс]	[латекс] \frac{2}{1}[/латекс]	[латекс]\frac{1}{2}\cdot\frac{2}{1}=\frac{1\cdot}{2\cdot1}=\frac{2}{2}=1[/latex]
[латекс] 3=\frac{3}{1}[/латекс]	[латекс] \frac{1}{3}[/латекс]	[латекс] \frac{3}{1}\cdot \frac{1}{3}=\frac{3\cdot 1}{1\cdot 3}=\frac{3}{3}=1[/ латекс]
[латекс]2\frac{1}{3}=\frac{7}{3}[/latex]	[латекс] \frac{3}{7}[/латекс]	[латекс]\frac{7}{3}\cdot\frac{3}{7}=\frac{7\cdot3}{3\cdot7}=\frac{21}{21}=1[/latex]

Иногда мы называем обратное число «переворотом» другого числа: переверните [латекс] \frac{2}{5}[/latex], чтобы получить обратное [латекс]\frac{5}{2}[ /латекс].

 

Деление на ноль

Вы знаете, что значит делить на 2 или делить на 10, но что значит делить количество на 0? Это вообще возможно? Можно ли разделить 0 на число? Рассмотрим дробь

[латекс]\frac{0}{8}[/latex]

. Мы можем прочитать это как «ноль разделить на восемь». Поскольку умножение обратно делению, мы могли бы переписать это как задачу на умножение.

[латекс]\текст{?}\cdot{8}=0[/латекс].

Мы можем сделать вывод, что неизвестное должно быть равно 0, так как это единственное число, которое дает 0 при умножении на 8.

Теперь рассмотрим обратную величину [латекс]\фрак{0}{8}[/латекс], которая будет [латекс]\фрак{8}{0}[/латекс]. Если мы перепишем это как задачу на умножение, то получим

[латекс]\текст{?}\cdot{0}=8[/латекс].

Это не имеет никакого смысла. Не существует чисел, которые можно умножить на ноль, чтобы получить результат 8. Обратная величина [латекс]\фракция{8}{0}[/латекс] не определена, и фактически любое деление на ноль не определено.

Внимание! Деление на ноль не определено, как и обратная величина любой дроби с нулем в числителе. Для любого действительного числа а [латекс]\фракция{а}{0}[/латекс] не определена. Кроме того, обратная величина [latex]\frac{0}{a}[/latex] всегда будет неопределенной.

Деление дроби на целое число

При делении на целое число вы умножаете его на обратное. В примере покраски, где вам нужно 3 литра краски для слоя и у вас есть 6 литров краски, вы можете найти общее количество слоев, которые можно покрасить, разделив 6 на 3, [латекс]6\div3=2[/латекс ]. Вы также можете умножить 6 на обратную величину 3, то есть [латекс] \frac{1}{3}[/latex], поэтому задача умножения будет выглядеть так:

[латекс] \frac{6}{1}\cdot \ frac{1}{3}=\frac{6}{3}=2[/latex].

 

Деление – это умножение на обратное число

Для любого деления вы можете превратить операцию в умножение, используя обратное число. Деление равносильно умножению на обратное.

Та же идея будет работать, когда делитель (вещь, которую делят) является дробью. Если у вас есть [латекс] \frac{3}{4}[/latex] шоколадного батончика и вам нужно разделить его между 5 людьми, каждый получит [латекс] \frac{1}{5}[/latex] доступные конфеты:

[латекс] \frac{1}{5}\text{ of }\frac{3}{4}=\frac{1}{5}\cdot \frac{3}{4}= \frac{3}{20}[/латекс]

Каждый человек получает [латекс]\фрак{3}{20}[/латекс] целого шоколадного батончика.

Если у вас есть рецепт, который нужно разделить пополам, вы можете разделить каждый ингредиент на 2 или умножить каждый ингредиент на [латекс]\frac{1}{2}[/latex] , чтобы найти новое количество .

Например, деление на 6 равносильно умножению на обратную величину 6, то есть [латекс]\frac{1}{6}[/латекс]. Посмотрите на схему двух пицц ниже. Как можно справедливо разделить то, что осталось (область, заштрихованная красным), между 6 людьми?

Каждый человек получает один кусок, поэтому каждый человек получает [латекс] \frac{1}{4}[/latex] пиццы.

Деление дроби на целое — это то же самое, что и умножение на обратную, поэтому вы всегда можете использовать умножение дробей для решения задач на деление.

Разделить дробь на дробь

Иногда вам нужно решить задачу, требующую деления на дробь. Предположим, у вас есть пицца, которая уже разрезана на 4 куска. Сколько существует фрагментов [latex]\frac{1}{2}[/latex]?

8 ломтиков. Вы видите, что деление 4 на [latex] \frac{1}{2}[/latex] дает тот же результат, что и умножение 4 на 2.

Что произойдет, если вам нужно разделить каждый срез на трети?

У вас получится 12 частей, что равносильно умножению 4 на 3.

Деление дробями

1. Найдите обратную величину числа, следующего за символом деления.
2. Умножьте первое число (то, что перед знаком деления) на величину, обратную второму числу (после знака деления).

Самый простой способ запомнить, как делить дроби, — это фраза «сохранить, изменить, перевернуть».

Это означает СОХРАНИТЬ первое число, ИЗМЕНИТЬ знак деления на умножение, а затем ПЕРЕВЕРНУТЬ (использовать обратное) второго числа.

Зачем повторять темы из предыдущих уроков математики?

Опять остатки?

Вы были в классе весь день, бегая, забирая своих детей из детского сада, и после долгой, жестокой дороги вы возвращаетесь домой и понимаете, что не подумали о том, что приготовить на ужин. Вы подходите к холодильнику, и все, что вы видите, это остатки, беспорядочные кусочки прошлых блюд. Несмотря на усталость, вам удается приготовить еду, которую все охотно съедят, и продолжить свой вечер.

В этом разделе вам может показаться, что темы представляют собой смесь объедков. Цель состоит в том, чтобы напомнить вам о некоторых навыках и темах из предыдущих уроков математики, которые, как и коробка с остатками в задней части вашего холодильника, легко забываются большинством людей. Потому что иногда мы просто забываем, как работают эти понятия. . . пока они нам снова не понадобятся.

Результаты обучения

Свойства действительных чисел

• Определение действительных чисел и подмножеств действительных чисел
• Определить свойства действительных чисел и использовать их для вычисления алгебраических выражений

Многошаговые уравнения

• Использование свойств действительных чисел для решения многошаговых линейных уравнений
• Определение и использование распределительного свойства для решения линейных уравнений
• Классифицировать решения уравнений

Решение проблем

• Составление уравнений из описаний задач
• Использование формул для решения прикладных задач

 

Работая с остальными разделами этого курса, вернитесь к этому обзору, если вы чувствуете, что вам нужно напоминание о затронутых темах. Эти темы были выбраны потому, что о них часто забывают и они широко используются на протяжении всего курса. Не волнуйтесь, как и кетчуп, у этих концепций долгий срок годности.

Что делать, если учащиеся не умеют работать с дробями

Вы умнее пятиклассника? Когда дело доходит до операций с дробями, многие взрослые отвечают «нет».

Если вы не учите математику, вы можете быть удивлены тем, сколько мы ожидаем от пятиклассников. Вот пример тестового вопроса для 5-го класса от Департамента образования штата Луизиана.  

Не знаю, как вас, а меня эта проблема заставила почесать голову. Я почти уверен, что ответ D. Но я точно не смог бы решить это, когда мне было 10 лет.0037

Так что, если у ваших учеников проблемы с операциями с дробями, вы не одиноки. Многие полагаются на такие приемы, как : сохранить, изменить, перевернуть, , но никогда не развивают концептуальное понимание.

Этим учащимся трудно применить свое понимание к реальным проблемам. И гораздо быстрее забывают то, чему научились.

Свободное владение дробями учащимися необходимо для их общего успеха в математике. Понимание дробей обеспечивает основу для десятичных дробей, процентов и отношений. Они также позволяют учащимся понимать пропорции, наклон и рациональные числа.

Когда учащиеся не усваивают дроби в начальной школе, они с трудом справляются со средней школой, алгеброй, статистикой и даже исчислением (если доберутся до них).

Чтобы помочь своим ученикам, сначала вы должны узнать почему у них возникают трудности с операциями с дробями. Затем убедитесь, что у вас есть инструменты и стратегии для устранения их неправильных представлений.

Почему учащиеся не умеют работать с дробями?

Чрезмерная зависимость от «трюков» характерна не только для дробных операций. На протяжении обучения K-12 (и за его пределами) учащиеся часто учатся считать, не учась рассуждать.

Так почему же проблема наиболее остро ощущается с дробями? Отчасти причина в том, что фракции труднее связать со своим жизненным опытом.

Дроби также требуют, чтобы учащиеся основывались на своих предыдущих знаниях в операциях с целыми числами. Поэтому, когда учащимся не хватает этих основ, дроби даются в два раза сложнее (или в ½ раза проще).

Фактический ответ индивидуален для каждого ученика. Но вот общие подводные камни, на которые стоит обратить внимание.

Дроби не интуитивны

Одна из причин, по которой учащиеся испытывают затруднения с операциями с дробями, заключается в том, что дроби менее интуитивно понятны, чем целые числа. Студенты постоянно складывают и вычитают целые числа в своей повседневной жизни, даже не осознавая этого. Иногда они даже размножаются и делятся.

И хотя они знают, что значит съесть полпеченья или отмерить ½ стакана муки, они обычно не оперируют дробями. Многие думают, что «половина» — это , всего лишь половина , а не число с единицей в числителе и двумя в знаменателе.

Многим учащимся не хватает базовых понятий

Еще одна причина, по которой учащиеся испытывают затруднения, заключается в том, что они не усвоили основные понятия. А именно, значение дробей и операций с целыми числами.

Если вы попросите учащихся умножить 3 на 13, представят ли они себе массив? Модель местности? Пропустить счет до 10 три раза, затем пропустить счет до 3 три раза? Или они просто складываются и вычисляются?

Массив 3 на 13

Учащиеся, которые могут визуализировать операции с целыми числами, могут опираться на свое понимание деления, чтобы представить целое, разделенное на четыре части. Они могут расширить эту идею, добавив одну четвертую к другой четвертой. Или умножить пятую часть на три.

Но поскольку у многих студентов нет этих концептуальных основ, они просто видят дроби как одно число, наложенное на другое. Чем больше приемов и процедур они изучают, тем больше вероятность того, что они их забудут или применят неправильный прием для решения не той проблемы.

Но есть еще большая проблема с алгоритмами без понятий . Студенты не развивают способность видеть математику вокруг себя. Они не признают математику языком или наукой о пространстве и количестве. Они не видят красоты и искусства в математике.

Вместо этого он становится набором «математических фактов», случайных правил и секретных символов.

Операции с дробями противоречат правилам работы с целыми числами

Даже учащиеся, понимающие понятия целых чисел, могут испытывать трудности с дробями.

В начальной школе учащиеся сосредотачиваются на освоении десятичной системы счисления. Они считают десятками, объединяют десятки и единицы и разбивают числа по разрядности для работы. Все дело в том, чтобы делать десятки, разбивать десятки и использовать ноль в качестве заполнителя.

Но дроби не строятся от десятков. Дроби могут разделить целое на 3, 7 или 45 частей. А по мере изменения знаменателя меняется и размер «единицы». Как и единицы, необходимые для создания группы (одного целого).

Дроби также противоречат «правилам», которые студенты изучают для целых чисел. Когда вы умножаете 3 х 5, результат больше, чем оба. Но при умножении дробей никогда не знаешь. Произведение ⅓ и ¼ меньше обоих. Но умножение ⅕ на 4 создает произведение между двумя факторами.

Когда учащиеся имеют прочные концептуальные основы, они могут обобщать свои знания о целых числах, чтобы понимать дроби. Но без этого понимания им может показаться, что они начинают все сначала, с совершенно новым набором правил!

Три совета по обучению операциям с дробями

Первый шаг к тому, чтобы помочь своим ученикам с операциями с дробями, — узнать, почему у них возникают трудности.

Следующим шагом должны быть конкретные, действенные шаги для решения этих проблем.

Во-первых, убедитесь, что ваши ученики действительно понимают значение дроби. Затем соедините это с тем, что они уже знают об операциях с целыми числами.

Обе эти задачи можно выполнить с помощью «Три транспортных средства» — моделей уроков на основе запросов, которые могут поддерживать практически любую математическую концепцию.

1. Обзор и оценка основ дробей

Проще говоря, знаменатель говорит нам, на сколько частей делится целое. Числитель говорит нам, сколько таких частей у нас есть. Хотя числитель сверху , это не имеет большого значения, если вы не знаете знаменатель. Вот почему я учу дроби снизу вверх.

В какой-то момент (обычно около 5 класса) учащиеся узнают, что дробь также можно рассматривать как частное. Результат деления числителя на знаменатель. Таким образом, 3 ÷ 4 равно ¾. Визуально это можно представить как 3 целого, каждое из которых разделено на 4 равные части, причем части перегруппированы в одну фракцию.

Чтобы оценить свое понимание, учащиеся должны уметь это делать без направления . Если вам нужно сказать им обрезать или заштриховать, они не поймут эту концепцию. Они просто рисуют.

2. Соедините операции с дробями с операциями с целыми числами

Когда учащиеся поймут дроби, они смогут работать с дробями так же, как с целыми числами. Если, конечно, они понимают смысл операций.

Сложение и вычитание

Когда учащиеся понимают значение ⅓, они могут начать считать вверх и вниз, чтобы складывать и вычитать дроби с одинаковыми знаменателями.

Следующий шаг — составить целое, например, сосчитав до 4-х или прибавив ⅓ к ⅔. Затем они могут вычитать, чтобы разбить целое (1 — ⅙).

Подсчитав сверх целого числа , они могут начать работать со смешанными числами (⅔ + ⅔ = 1 ⅓).

Складывать и вычитать дроби с разными знаменателями сложнее. Учащимся необходимо преобразовать в эквивалентные дроби, что зависит от навыков, полученных путем умножения дробей. Поэтому учащиеся сначала изучают эти понятия, прежде чем вернуться к сложению и вычитанию с разными знаменателями.

---

Занятия с дробями для вашего класса

---

Умножение дробей

После того, как ваши ученики научились складывать дроби, умножить дробь на целое число несложно. Просто подумайте о ¼ x 3 как о ¼ + ¼ + ¼.

Затем замените знак умножения словом «из». Таким образом, ¼ x 3 станет «одной четвертой из трех». Это связывает умножение дробей с умножением целых чисел. 3 x 2 означает три (группы) по два. Таким образом, ⅓ x 4 имеет смысл равняться 9.0465 одна треть от (группы) 4.

Он также расширяет концепцию умножения числа на дробь до умножения на дробь, что позволяет учащимся решать, когда оба множителя являются дробями.

В этом упражнении Google Slides используются визуальные представления, чтобы продемонстрировать значение умножения дробей: учащиеся сдвигают модели дробей, чтобы увидеть, что происходит, когда мы умножаем.

Помимо поддержки концептуального понимания, модели умножения дробей показывают учащимся почему умножаем числители и знаменатели в алгоритме.

Чтобы узнать больше о соединении умножения дробей с целыми числами, ознакомьтесь с пятью значениями умножения.

Деление дробей

Деление дробей также может основываться на том, что учащиеся знают о целых числах.

Начните с деления дроби на ее числитель, например, ⅗, деленное на 3. Это включает в себя партитивное деление, в котором делитель определяет количество групп .

Затем разделите целое число на дробь. Здесь мы используем деление в кавычках , , в котором делитель определяет размер каждой группы . Деление 2 на ⅓ включает в себя разделение обоих целых чисел на трети (делитель = размер группы) и подсчет общего числа групп (частное = количество групп). Это иллюстрирует, почему мы умножаем на знаменатель при делении на дробь.

Деление в кавычках также полезно для деления дроби на дробь, но только в некоторых случаях. Чтобы разделить ⅔ на ⅓, просто создайте 2 группы по ⅓ в каждой.

А как насчет ⅓ разделить на ¼? Можно представить разбиение трети на группы размером в одну четвертую… но это не очень интуитивно понятно. В этом случае я возвращаюсь к разделительному разделению и использую то, что я называю стратегией «призрачных копий».

Если бы я делил 8 на 2 по частям, я превращал бы одну группу из 8 в две новые группы, по четыре в каждой группе. Если вместо этого я разделю 8 на ½, я превращу одну группу из 8 в — половину группы . Чтобы создать целую группу, мне нужно сделать призрачная копия моего начального значения (дивиденда).

Стратегия фантомных копий может быть расширена для таких отношений, как ½ ÷ ⅓. Рассматривайте ½ как ⅓  полной группы . Таким образом, мы добавляем две фантомные копии ½, чтобы сделать целую группу, в результате чего получается 1 ½.

Пять значений умножения также полезны для помощи учащимся в делении дробей. Каждое значение умножения в обратном порядке относится к делению.

Эквивалентные дроби

Эквивалентные дроби могут быть самым сложным аспектом операций с дробями. Его трудно связать с целыми числами, так как нет другого эквивалента целого числа: восемь — это всего лишь восемь, целого числа, эквивалентного 8, не существует.

и по-прежнему имеют то же значение. На самом деле, вы могли бы возразить, что эквивалентность равна 90 465, и именно поэтому мы в первую очередь используем дроби 90 466.

Когда учащиеся спрашивают, «зачем нам нужны и дроби, и десятичные дроби», отличный ответ заключается в том, что дроби позволяют нам делить целые числа на части любого размера, который мы хотим. С десятичными дробями мы ограничены коэффициентами десять.

Но я включил здесь эквивалентность по двум причинам. Во-первых, это важно для многих последующих применений дробей. Упрощение дробей и добавление разных знаменателей требуют преобразования эквивалентных дробей. Как и десятичные и процентные преобразования, работа с пропорциями и определение наклона. Список можно продолжить.

Вторая причина заключается в том, что умножение дробей можно использовать для обучения эквивалентным дробям.

Я учу преобразование дробей как умножение на единицу . Чтобы найти эквивалент ½, я могу умножить на 3/3 (он же один), получив 3/6.

Учащиеся, умеющие использовать модели площадей для умножения дробей, должны связать идею умножения на ⅓ с идеей умножения на 3/3. Как визуально, так и с помощью алгоритма «умножить поперек».

3. Используйте

Три повозки для обучения операциям с дробями

Три повозки представляют собой модели уроков, основанные на исследованиях, которые способствуют концептуальному пониманию. Их можно использовать для обучения практически любому математическому понятию в любом классе.

Транспортные средства построены на теории множественных представлений , идее о том, что любое математическое понятие может быть представлено пятью различными способами: физически, визуально, символически, концептуально и словесно.

Мы можем определить беглость как способность переводить математическую идею среди всех пяти представлений. Сюда входит перевод выражения в визуальную модель. Или объяснить на словах, как работает манипулятор.

Пять представлений определяют, как могут быть представлены математические идеи. И транспортные средства учат студентов, как переводить среди них.

Масштабные модели

Первый автомобиль — масштабная модель. Он сочетает в себе физические и визуальные представления (также известные как конкретные и изобразительные), поскольку оба служат одинаковой цели. Они представляют размер чисел и значение операций.

Масштабные модели полезны для создания и оценки концептуального понимания. Чтобы использовать масштабные модели в качестве учебного пособия, сначала научите их принципам чтения и создания масштабных моделей. Затем используйте модели в качестве инструментов, помогающих учащимся учиться посредством исследования.

Например, если учащиеся понимают дроби и умножение целых чисел, они могут использовать свои навыки моделирования, чтобы «открыть» умножение дробей, даже без прямого обучения.

Для учащихся важно создавать свои собственные модели, а не просто интерпретировать модели из учебника или созданные учителями. Чтение моделей полезно, но недостаточно для беглости речи.

---

Три моста Онлайн-семинары для преподавателей

---

Числовые предложения

Следующее транспортное средство — числовое предложение. Числовые предложения (уравнения и неравенства) основаны на концепциях, разработанных с помощью визуальных моделей, для поддержки развития абстрактного понимания.

Числовые предложения позволяют учащимся манипулировать выражениями и работать в несколько этапов, что делает их гораздо более полезными, чем вычисления с помощью алгоритмов.

Я использую доказательства числовых предложений, чтобы помочь учащимся выучить числовые предложения и связать их с другими представлениями.

Сюжетные задачи

Третий автомобиль, сюжетные задачи, помощь с прикладными навыками и математическим языком.

Я учу студентов использовать процесс Полиа для решения текстовых задач. Этот подход подчеркивает важность использования нескольких представлений для решения текстовых задач.

Этот автомобиль идет последним, потому что учащиеся могут использовать масштабные модели и числовые предложения в качестве инструментов для решения текстовых задач.

Обучение работе с дробями в классе

Я надеюсь, что эта статья предлагает полезный обзор основных концепций, необходимых для успешного выполнения операций с дробями.

Ресурсы для обучения дробям со всеми тремя машинами вы найдете в нашем интернет-магазине.

Или улучшите свои математические навыки, записавшись на онлайн-семинар. Это сеансы в реальном времени, проводимые живым фасилитатором. Мы предлагаем отдельные занятия по каждому транспортному средству для учителей начальной и средней школы, чтобы вы могли сосредоточиться на техниках и стандартах, наиболее важных для ваших учеников.

Наконец, если вы хотите сразу внедрить этот тип обучения, загрузите наш комплект Fractions Essentials Bundle. В нем есть все, что вам нужно для начала работы: от интерактивных Google Slides занятий до планов уроков, ответов и многого другого!

Получите копию FRACTION ESSENTIALS

Об авторе

Джефф Лискиандрелло — основатель Room to Discover и консультант по вопросам образования, специализирующийся на обучении, ориентированном на учащихся. Его 3-Bridges Design for Learning помогает школам изучать инновационные методы в традиционных условиях.