Умножение в столбик — как умножать в столбик в 3 и 4 класс
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков.
- Однозначное — состоит из одного знака
- Двузначное — из двух
- Трехзначное — из трех и так далее.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитываются с конца.
Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
- В числе 429 содержится 0 тысяч, 4 сотни, 2 десятка и 9 единиц.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения1. От перестановки множителей местами произведение не меняется. 2. Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым. |
Важно помнить правило: умножение в столбик с нулями дает в результате ноль
- а * 0 = 0, где а — любое натуральное число.
Алгоритм умножения в столбик
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:
1. Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
2. Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.
3. Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.
Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.
4. После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
5. Складываем то, что нашли и получаем ответ.
Умножение на однозначное число
Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше.
Возьмем пример 234 * 2:
1. Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.
2. Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.
3. Ответ запишем под чертой:
Производить действия необходимо в следующей последовательности:
Умножение двух многозначных чисел
Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.
Рассмотрим пример 207 * 8063:
- Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:
- Последовательно перемножаем значения разрядов.
 Результатом является неполное произведение.
Результатом является неполное произведение.
- Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.
- По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:
- Далее складываем два произведения в столбик.
- Получившееся семизначное число — результат умножения исходных натуральных чисел.
Ответ: 8 063 * 207 = 1669041.
Примеры на умножение в столбик
Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.
Повтори тему — деление в столбик, она очень полезная!
Чтобы запомнить все правила, повторите метод сложения столбиком, так как один из этапов умножения состоит из сложения промежуточных результатов. А еще лучше — приходите заниматься увлекательной математикой в детскую школу Skysmart.
Вместо скучных параграфов ученики решают интерактивные задачки и головоломки с мгновенной автоматической проверкой, а еще чертят фигуры на онлайн-доске вместе с преподавателем.
Математика. Умножение «в столбик» | Сайт Леонида Некина
Главная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
До сих пор мы умели только умножать на счетах в пределах 24 × 24. Настало время научиться перемножать бóльшие числа, и не на счетах, а на бумаге — с помощью процедуры, которая называется умножением «в столбик».
Надо честно признаться: умножение «в столбик» — это одна из самых неприятных и нудных вещей во всей математике. Хуже нее только деление «уголком», которым мы тоже вскоре займемся. Как только мы освоим умножение «в столбик» и деление «уголком», мы можем смело утверждать, что самый трудный участок на пути изучения математики у нас остался позади.
Прежде всего нам понадобится таблица умножения в пределах от 2 × 2 до 9 × 9. Удобнее всего ее записать в таком виде:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | |
3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
Это так называемая таблица Пифагора. Здесь на пересечении строки, помеченной числом 3, и колонки, помеченной числом 5, стоит как раз произведение чисел 3∙5, то есть 15. Подобным же образом мы можем по этой таблице быстро найти произведение любых однозначных чисел (за исключением нуля и единицы, но умножать на ноль и единицу настолько легко, что никакая таблица не нужна).
Здесь на пересечении строки, помеченной числом 3, и колонки, помеченной числом 5, стоит как раз произведение чисел 3∙5, то есть 15. Подобным же образом мы можем по этой таблице быстро найти произведение любых однозначных чисел (за исключением нуля и единицы, но умножать на ноль и единицу настолько легко, что никакая таблица не нужна).
В школе эту таблицу заставляют учить наизусть. На мой взгляд, в этом нет никакой необходимости. Пусть она просто будет под рукой, и этого совершенно достаточно. По мере того как мы будем практиковаться в умножении «в столбик», она выучится сама собой.
Таблицу умножения на отдельном листе (в формате pdf) можно взять здесь.
Итак, приступим к умножению чисел. Для начала научимся умножать на однозначное число. Пусть нам надо вычислить
6879∙7.
Воспользовавшись свойствами умножения, которые мы проходили на прошлом уроке, мы можем написать:
6879∙7 =
(9 | + | 7∙10 | + | 8∙100 | + | 6∙1000)∙7 | = |
9∙7 | + | 7∙7∙10 | + | 8∙7∙100 | + | 6∙7∙1000 | = |
63 | + | 49∙10 | + | 56∙100 | + | 42∙1000 | = |
| 6 3 |
+ | 4 9 0 |
+ | 5 6 0 0 |
+ | 4 2 0 0 0 |
Перепишем это в виде упрощенной таблицы (очень похожей на ту, какую мы писали, когда учились сложению столбиком):
× | 6 | 8 | 7 | 9 |
|
|
| 7 | |
| 6 | 3 | ||
| 4 | 9 |
| |
| 5 | 6 |
| |
4 | 2 |
| ||
Теперь остается сложить числа под горизонтальной линией — и ответ готов:
× | 6 | 8 | 7 | 9 |
|
|
| 7 | |
| 6 | 3 | ||
| 4 | 9 |
| |
| 5 | 6 |
| |
4 | 2 |
| ||
| 1 | 1 |
|
|
4 | 8 | 1 | 5 | 3 |
Надо ли пояснять, откуда взялись маленькие единички над нашим ответом? Когда мы в разряде десятков сложили 6 и 9, то получили 15. Последнюю цифру этого числа (то есть пятерку) мы записали в ответе в разряде десятков, а первую цифру этого числа (то есть единицу) перенесли в следующий разряд в виде маленькой приподнятой единички. Потом в разряде сотен мы стали складывать 4 и 6, и не забыли добавить сюда же эту самую единичку. Получившееся число 11 тоже записали наискосок: вторую единицу покрупнее и пониже (в аккурат в строке ответа), а первую единицу поменьше и повыше.
Последнюю цифру этого числа (то есть пятерку) мы записали в ответе в разряде десятков, а первую цифру этого числа (то есть единицу) перенесли в следующий разряд в виде маленькой приподнятой единички. Потом в разряде сотен мы стали складывать 4 и 6, и не забыли добавить сюда же эту самую единичку. Получившееся число 11 тоже записали наискосок: вторую единицу покрупнее и пониже (в аккурат в строке ответа), а первую единицу поменьше и повыше.
Мы теперь, в принципе, умеем умножать на однозначное число. Но давайте подумаем над усовершенствованиями. Во-первых, перепишем нашу табличку в более компактном виде:
× | 6 | 8 | 7 | 9 |
|
|
| 7 | |
4 | 5 | 4 | 6 |
|
| 2 | 6 | 9 | 3 |
| 1 | 1 |
|
|
4 | 8 | 1 | 5 | 3 |
А во-вторых, подумаем над возможностью более радикального сокращения записи. Вернемся в исходное положение:
× | 6 | 8 | 7 | 9 |
|
|
| 7 |
В разряде единиц умножим 9 на 7. Результат 63 запишем, как и раньше, наискосок, но шестерку сделаем совсем маленькой:
Результат 63 запишем, как и раньше, наискосок, но шестерку сделаем совсем маленькой:
× | 6 | 8 | 7 | 9 |
|
|
| 7 | |
|
|
| 6 |
|
|
|
|
| 3 |
Теперь умножим в разряде десятков 7 на 7. Получаем 49. Прибавляем сюда нашу «маленькую» шестерку: 49 + 6 = 55. Этот результат опять записываем наискосок:
× | 6 | 8 | 7 | 9 |
|
|
| 7 | |
|
| 5 | 6 |
|
|
|
| 5 | 3 |
Переходим к разряду сотен: 8∙7 + 5 = 61. Записываем:
× | 6 | 8 | 7 | 9 |
|
|
| 7 | |
| 6 | 5 | 6 |
|
|
| 1 | 5 | 3 |
И, наконец, в разряде тысяч получаем 6∙7 + 6 = 48:
× | 6 | 8 | 7 | 9 |
|
|
| 7 | |
4 | 6 | 5 | 6 |
|
4 | 8 | 1 | 5 | 3 |
Здесь мы еще перенесли «маленькую» четверку в разряде десятков тысяч вниз, чтобы получить окончательный ответ. Не правда ли, наши вычисления стали короче, а запись еще более компактной?
Не правда ли, наши вычисления стали короче, а запись еще более компактной?
Теперь возникает резонный вопрос. А как мы будем записывать эти вычисления в нашей тетрадке по математике, разлинованной в клетку? Будем ли мы писать «маленькие» цифры в отдельном ряду клеток или же втискивать их в тот же ряд клеток, где у нас записан ответ? Оба варианта не слишком хороши. Поэтому я предлагаю делать наши вычисления в столбик на отдельных листах бумаги. Для этого прекрасно подойдут обычные белые листы, какие используются для принтеров и копировальных машин. А тех, кому работать на линованной бумаге всё же привычнее, приглашаю воспользоваться листами с особой линовкой.
Лист со специальной линовкой для вычислений можно взять здесь (формат pdf).
Надо отметить, что в школе учат умножать «в столбик» несколько по-другому. Отличие состоит в том, что «маленькие» цифры не записывают на бумагу, а держат в уме — вероятно, по той именно причине, что в стандартных тетрадках в клетку их прото некуда записывать. На мой взгляд, это слишком усложняет процесс счета и только способствует ошибкам.
Переходим к умножению на двузначные числа. Пусть требуется вычислить
6879∙67.
Ну что ж, приступим.
6879∙67 =
6879∙(7 + 6∙10) =
6879∙7
+
6879∙6∙10 =
| 6 3 |
+ | 4 9 0 |
+ | 5 6 0 0 |
+ | 4 2 0 0 0 |
| + |
| 5 4 0 |
+ | 4 2 0 0 |
+ | 4 8 0 0 0 |
+ | 3 6 0 0 0 0 |
Здесь при умножении на 6 мы воспользовались тем же приемом, что и при умножении на 7, только к каждому получившемуся слагаемому приписали еще 0 из-за дополнительного умножения на 10. Сумму «желтых» слагаемых находим точно так же, как раньше мы находили сумму «зеленых» слагаемых:
Сумму «желтых» слагаемых находим точно так же, как раньше мы находили сумму «зеленых» слагаемых:
| × | 6 | 8 | 7 | 9 |
|
|
| 6 | 7 | |
| 4 | 6 | 5 | 6 |
|
| 4 | 8 | 1 | 5 | 3 |
4 | 5 | 4 | 5 |
|
|
4 | 1 | 2 | 7 | 4 |
|
Складываем получившиеся ряды «больших» цифр и получаем окончательный ответ (при этом «маленькие» цифры можно зачеркнуть, чтобы не мешались):
| × | 6 | 8 | 7 | 9 |
|
|
| 6 | 7 | |
| 4 | 6 | 5 | 6 |
|
| 4 | 8 | 1 | 5 | 3 |
4 | 5 | 4 | 5 |
|
|
4 | 1 | 2 | 7 | 4 |
|
| 1 |
|
|
|
|
4 | 6 | 0 | 8 | 9 | 3 |
Подобным же образом делается умножение на трехзначные числа. Например:
Например:
|
| × | 6 | 8 | 7 | 9 |
|
|
| 2 | 6 | 7 | |
|
| 4 | 6 | 5 | 6 |
|
|
| 4 | 8 | 1 | 5 | 3 |
| 4 | 5 | 4 | 5 |
|
|
| 4 | 1 | 2 | 7 | 4 |
|
1 | 1 | 1 | 1 |
|
|
|
1 | 3 | 7 | 5 | 8 |
|
|
| 1 | 1 | 1 |
|
|
|
1 | 8 | 3 | 6 | 6 | 9 | 3 |
Если в середине трехзначного числа стоит ноль, то запись выглядит так:
|
| × | 6 | 8 | 7 | 9 |
|
|
| 2 | 0 | 7 | |
|
| 4 | 6 | 5 | 6 |
|
|
| 4 | 8 | 1 | 5 | 3 |
1 | 1 | 1 | 1 |
|
|
|
1 | 3 | 7 | 5 | 8 |
|
|
| 1 | 1 |
|
|
|
|
1 | 4 | 2 | 3 | 9 | 5 | 3 |
Наконец, умножение круглых чисел (которые оканчиваются нулями) записывается в таком виде:
|
| × | 6 | 8 | 7 | 9 | 0 |
|
|
|
|
| 2 | 6 | 7 | 0 | 0 | ||
|
| 4 | 6 | 5 | 6 |
|
|
|
|
|
| 4 | 8 | 1 | 5 | 3 |
|
|
|
| 4 | 5 | 4 | 5 |
|
|
|
|
|
| 4 | 1 | 2 | 7 | 4 |
|
|
|
|
1 | 1 | 1 | 1 |
|
|
|
|
|
|
1 | 3 | 7 | 5 | 8 |
|
|
|
|
|
| 1 | 1 | 1 |
|
|
|
|
|
|
1 | 8 | 3 | 6 | 6 | 9 | 3 | 0 | 0 | 0 |
Из «бесконечного» сборника типовых упражнений
Умножение на однозначное число
Умножение на двузначное число
Умножение на трехзначное число
Умножение в столбик | Наука делать уроки
Самое главное правило, с которого мы начинаем изучать умножение в столбик:
Умножение в столбик на двузначное число
Пример: 46 умножить на 73
Этот пример можно записать в столбик.
Под числом 46 записываем число 73 по правилу:
Единицы записываем под единицами, а десятки под десятками
1Умножать начинаем с единиц.
3 умножим на 6. Получится 18.
- 18 единиц – это 1 десяток и 8 единиц.
- 8 единиц пишем под единицами, а 1 десяток запоминаем и прибавим к десяткам.
Теперь 3 умножим на 4 десятка. Получится 12.
12 десятков, да ещё 1, всего 13 десятков.
Сотен в этом примере нет, поэтому сразу на месте сотен пишем 1.
138 — это первое неполное произведение.
2 Умножаем десятки.7 десятков умножить на 6 единиц получится 42 десятка.
- 42 десятка это 4 сотни и 2 десятка.
- 2 десятка пишем под десятками. 4 запомним и прибавим к сотням.
7 десятков умножить на 4 десятка получится 28 сотен. 28 сотен, да ещё 4 получится 32 сотни.
- 32 сотни – это 3 тысячи и 2 сотни.
- 2 сотни пишем под сотнями, а 3 тысячи запомним и прибавим к тысячам.
Тысяч в этом примере нет, поэтому сразу на месте тысяч пишу 3.
3220 – это второе неполное произведение.
3Складываем первое и второе неполные произведения по правилу сложения в столбик.138 плюс 3220 получится 3358.
Читаем ответ: 46 умножить на 73 получится 3358
Работаем в столбик
Образец записи
(Кликните по картинке)
Компоненты действия умножения
(Кликните по картинке)
Ваша Помощница
— умная и нужная
шпаргалка
Кликните, чтобы скачать и затем распечатать
Образец рассуждения
во время записи
умножения в столбик
Внимательно просмотрите и примените в своих действиях!
Какие ошибки при умножении
можно сделать и
как их избежать
[Видео]
Внимательно просмотрите,
чтобы не совершать ошибок!
Правила для других случаев умножения
Умножение в столбик на однозначное число
youtube.com/embed/1c_GI_fTGMA?autohide=2&controls=1&disablekb=0&fs=1&start=0&loop=0&rel=0&showinfo=0&theme=light&modestbranding=1&wmode=transparent» frameborder=»0″ webkitallowfullscreen=»» mozallowfullscreen=»» allowfullscreen=»»/>
34 х 2
Этот пример можно записать в столбик.
Под числом 34 записываем число 2 по правилу:
Единицы записываем под единицами, а десятки, если они будут под десятками
1Умножать начинаем с единиц.2 умножим на 4. Получится 8.
2х4=8
8 пишем под единицами.
Теперь 2 умножим на 3десятка. Получится 6.
2х3=6
6 пишем под десятками.
Читаем ответ: 34 умножить на 2 получится 68.
Умножение в столбик на однозначное число с переходом через десяток
38 х 2
Этот пример можно записать в столбик.
Под числом 38 записываем число 2 по правилу:
Единицы записываем под единицами, а десятки, если они будут под десятками
1Умножать начинаем с единиц.2 умножим на 8. Получится 16.
- 16 единиц – это 1 десяток и 8 единиц.
- 8 единиц пишем под единицами. А 1 десяток запомним и прибавим к десяткам.
Теперь 2 умножим на 3 десятка. Получится 6.
6 десятков да ещё 1 всего 7 десятков.
7 пишем под десятками.
Читаем ответ: 38 умножить на 2 получится 76.
Умножение в столбик на однозначное число с переходом через десятки
68 х 2
Этот пример можно записать в столбик.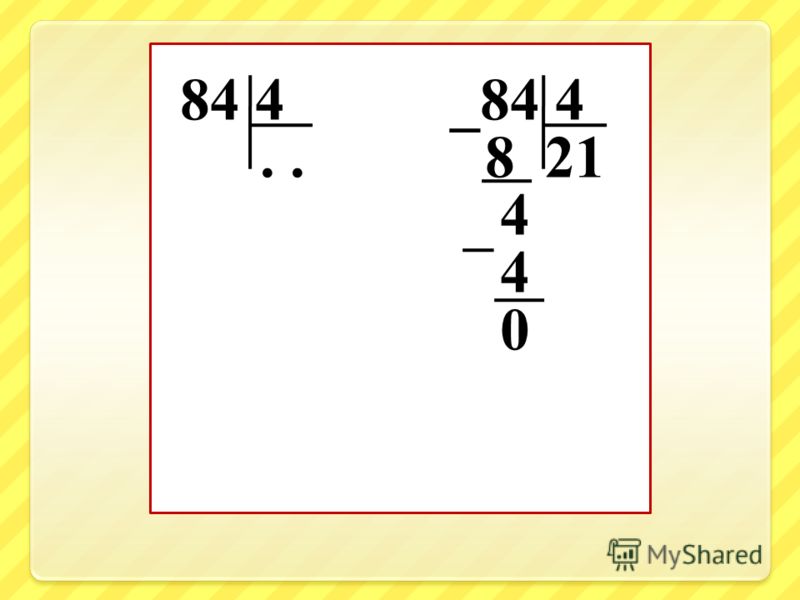
Под числом 68 записываем число 2 по правилу:
Единицы записываем под единицами, а десятки, если они будут под десятками
1Умножать начинаем с единиц.2 умножим на 8. Получится 16.
- 16 единиц – это 1 десяток и 6 единиц.
- 6 единиц пишем под единицами. А 1 десяток запомним и прибавим к десяткам.
Теперь 2 умножим на 6 десятков. Получится 12.
12 десятков да ещё 1 всего 13 десятков.
- 13 десятков – это 1 сотня да ещё 3 десятка.
- 3 десятка пишу под десятками. А 1 сотню запомним и прибавим к сотням.
Сотен в этом примере нет, поэтому сразу на месте сотен напишем 1.
Читаем ответ: 68 умножить на 2 получится 136.
Как делить в столбик | BeginPC.ru
В настоящее время современные технологии развиваются стремительными темпами, и все больше работы за нас выполняют компьютеры и различные другие электронные устройства. Тем не менее, умение выполнять арифметические операции без помощи калькулятора остаются все еще востребованными.
Ранее мы уже рассматривали, как складывать, вычитать и умножать в столбик на листе бумаги. Поэтому сегодня давайте освежим в памяти, а возможно кто-то узнает впервые алгоритм деления столбиком без калькулятора. В этом нет ничего сложного, главное внимательность и аккуратность.
Для начала запомним, что число которое делится называется делимое. Число на которое делят называют делителем, а результат деления частным. Чтобы было проще, давайте рассмотрим деление в столбик на конкретном примере и разделим 834 на 6. Первое что нам необходимо сделать, это записать их соответствующим образом.
Пишем делимое, затем правее него делитель и отделяем их друг от друга так называемым уголком. Все подготовительные операции выполнены и переходим непосредственно к делению в столбик.
Для этого необходимо в делимом двигаясь слева на право найти наименьшее число большее или равное делителю. Делитель у нас равен 6, а первая цифра в делителе равна 8 и она больше 6. Теперь необходимо найти сколько целых раз делитель помещается в неполном делимом, в данном случае всего один раз. Поэтому под делителем пишем 1, а под 8 записываем 6 проводим горизонтальную черту и находим их разность по правилам вычитания столбиком, то есть 2. Поскольку 2 меньше нашего делителя (6), то все сделано правильно, в противном случае, где то допущена ошибка.
Делитель у нас равен 6, а первая цифра в делителе равна 8 и она больше 6. Теперь необходимо найти сколько целых раз делитель помещается в неполном делимом, в данном случае всего один раз. Поэтому под делителем пишем 1, а под 8 записываем 6 проводим горизонтальную черту и находим их разность по правилам вычитания столбиком, то есть 2. Поскольку 2 меньше нашего делителя (6), то все сделано правильно, в противном случае, где то допущена ошибка.
Теперь сносим вниз следующую цифру исходного делимого (3) и проверяем чтобы получившееся число (23) было больше делителя (6). В данном случае это так. Снова находим сколько раз делитель помещается в неполном делимом, получается 3 раза. Поэтому под делителем записываем 3, а под делимым находим разность 23 и 18 (6*3), которая равна 5.
Дальше делаем все точно также, сносим вниз следующее число из делимого (4), получается число 54 и находим сколько раз в нем умещается делитель (6). Он умещается 9 раз, значит под делителем записываем 9, а под неполным делимым 54 (6*9). Поскольку 54 отнять 54 равно нулю и в делимом не осталось больше чисел, то деление закончено и частное равно 139. Можете проверить на калькуляторе или выполнив умножение в столбик 6 на 139.
Чтобы закрепить навык деления столбиком давайте рассмотрим еще один пример и разделим 1587 на 23. Согласно уже известному нам алгоритму находим в делимом наименьшее число большее или равное делителю, таким числом является 158. Делитель 23 умещается в неполном делимом 6 раз. Соответственно под делителем пишем 6, а под делимым 138 (23*6) и находим разность 158 и 138.
Поскольку 20 меньше делителя все сделано правильно, теперь сносим вниз следующее число (7) и находим сколько раз умещается делитель в получившемся числе 207. Он умещается 9 раз, а поскольку 207-207=0 и в делимом больше нет чисел, то деление в столбик законченно и ответ равен 69.
Как видите, ничего особо сложного нет, главное внимательность. Хотя внимательный читатель наверняка уже обратил внимание, что в обоих приведенных примерах делитель помещается в делимом целое число раз. Однако так бывает далеко не всегда, поэтому рассмотрим пример деления столбиком с остатком, для этого разделим 46 на 8.
Однако так бывает далеко не всегда, поэтому рассмотрим пример деления столбиком с остатком, для этого разделим 46 на 8.
Поскольку 4 меньше 8, то наименьшим неполным делимым является 46. В числе 46 делитель содержится 5 раз, следовательно под делителем пишем 5, а под делимым 40 (5*8).
Разность 46 и 40 равна 6. Число 6 меньше делителя, значит мы все сделали верно, но в делимом больше не осталось чисел, а разность не равна 0. Это значит, что разделить эти два числа без остатка нельзя. Чтобы найти остаток поступаем следующим образом. В разности ставим запятую, а к остатку приписываем 0. В остатке имеем число 60. Делитель умещается в нем 7 раз, значит пишем в разность 7 и вычитаем из 60 число 56 (8*7).
В остатке имеем 4, снова приписываем 0. Получается 40 и делитель умещается в нем 5 раз. В частное записываем 5 и вычитаем из остатка 40, получается 0.
Таким образом, мы разделили 46 на 8 столбиком и получили ответ 5,75. Теперь вы знаете, как делить в столбик без калькулятора. Кстати в Windows есть встроенный калькулятор «Пуск» ⇒ «Стандартные» ⇒ «Калькулятор», в котором всегда можно быстро выполнить необходимые вычисления.
Как объяснить ребенку деление столбиком во 2-3 классе
Как объяснить ребенку деление столбиком? Как дома самостоятельно отработать навык деления в столбик, если в школе ребенок что-то не усвоил? Делить столбиком учат во 2-3 классе, для родителей, конечно, это пройденный этап, но при желании можно вспомнить правильную запись и объяснить доступно своему школьнику то, что понадобится ему в жизни.
xvatit.com
Что должен знать ребенок 2-3 класса, чтобы научиться делить в столбик?
Как правильно объяснить ребенку 2-3 класса деление столбиком, чтобы в дальнейшем у него не было проблем? Для начала, проверим, нет ли пробелов в знаниях. Убедитесь, что:
- ребенок свободно выполняет операции сложения и вычитания;
- знает разряды чисел;
- знает назубок таблицу умножения.

Как объяснить ребенку смысл действия «деление»?
- Ребенку нужно объяснить все на наглядном примере.
Попросите разделить что-либо между членами семьи или друзьями. Например, конфеты, кусочки торта и т.п. Важно, чтобы ребенок понял суть — разделить нужно поровну, т.е. без остатка. Потренируйтесь на разных примерах.
Допустим, 2 группы спортсменов должны занять места в автобусе. Известно сколько спортсменов в каждой группе и сколько всего мест в автобусе. Нужно узнать, сколько билетов нужно купить одной и второй группе. Или 24 тетради нужно раздать 12 ученикам, сколько достанется каждому.
- Когда ребенок усвоит суть принципа деления, покажите математическую запись этой операции, назовите компоненты.
- Объясните, что деление – это операция противоположная умножению, умножение наизнанку.
Удобно показать взаимосвязь деления и умножения на примере таблицы.
Например, 3 умножить на 4 равно 12.
3 — это первый множитель;
4 — второй множитель;
12 — произведение (результат умножения).
Если 12 (произведение) разделить на 3 (первый множитель), получим 4 (второй множитель).
Компоненты при делении называются иначе:
12 — делимое;
3 — делитель;
4 — частное (результат деления).
Нам, взрослым, проще «по старинке» записать «уголком» — и дело с концом. НО! Дети еще не проходили деление в столбик, что делать? Как научить ребенка делить двузначное число на однозначное не используя запись столбиком?
Возьмем для примера 72:3.
Все просто! Раскладываем 72 на такие числа, которые легко устно разделить на 3:
72=30+30+12.
Все сразу стало наглядно: 30 мы можем разделить на 3, и 12 ребенок легко разделит на 3.
Останется только сложить результаты, т.е. 72:3=10 (получили, когда 30 разделили на 3) + 10 (30 разделили на 3) + 4 (12 разделили на 3).
72:3=24
Мы не использовали деление в столбик, но ребенку был понятен ход рассуждений, и он выполнил вычисления без труда.
После простых примеров можно переходить к изучению деления в столбик, учить ребенка правильно записывать примеры «уголком». Для начала используйте только примеры на деление без остатка.
Как объяснить ребенку деление в столбик: алгоритм решения
Большие числа сложно делить в уме, проще использовать запись деления столбиком. Чтобы научить ребенка правильно выполнять вычисления, действуйте по алгоритму:
- Определить, где в примере делимое и делитель. Попросите ребенка назвать числа (что на что мы будем делить).
213:3
213 — делимое
3 — делитель
- Записать делимое — «уголок» — делитель.
- Определить, какую часть делимого мы можем использоваться, чтобы разделить на заданное число.
Рассуждаем так: 2 не делится на 3, значит — берем 21.
- Определить, сколько раз делитель «помещается» в выбранной части.
21 разделить на 3 — берем по 7.
- Умножить делитель на выбранное число, результат записать под «уголком».
7 умножить на 3 — получаем 21. Записываем.
- Найти разницу (остаток).
На этом этапе рассуждений научите ребенка проверять себя. Важно, чтобы он понял, что результат вычитания ВСЕГДА должен быть меньше делителя. Если вышло не так, нужно увеличить выбранное число и выполнить действие еще раз.
- Повторить действия, пока в остатке не окажется 0.
Дальше можно взять пример посложнее, чтобы убедиться, что ребенок усвоил правильную запись и алгоритм рассуждений.
Как правильно рассуждать, чтобы научить ребенка 2-3 класса делить столбиком
Как объяснить ребенку деление 204:12=?
1. Записываем столбиком.
204 — делимое, 12 — делитель.
2. 2 не делится на 12, значит, берем 20.
3. Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
Чтобы разделить 20 на 12 берем по 1. Записываем 1 под «уголком».
4. 1 умножить на 12 получим 12. Записываем под 20.
5. 20 минус 12 получим 8.
Проверяем себя. 8 меньше 12 (делителя)? Ок, все верно, идем дальше.
6. Рядом с 8 пишем 4. 84 разделить на 12. На сколько нужно умножить 12, чтобы получить 84?
Сразу сложно сказать, попробуем действовать методом подбора.
Возьмем, например, по 8, но пока не записываем. Считаем устно: 8 умножить на 12 получится 96. А у нас 84! Не подходит.
Пробуем поменьше… Например, возьмем по 6. Проверяем себя устно: 6 умножить на 12 равно 72. 84-72=12. Мы получили такое же число, как наш делитель, а должно быть или ноль, или меньше 12. Значит, оптимальная цифра 7!
7. Записываем 7 под «уголок» и выполняем вычисления. 7 умножить на 12 получим 84.
8. Записываем результат в столбик: 84 минус 84 равно ноль. Ура! Мы решили правильно!
Итак, вы научили ребенка делить столбиком, осталось теперь отработать этот навык, довести его до автоматизма.
Почему детям сложно научиться делить в столбик?
Помните, что проблемы с математикой возникают от неумения быстро делать простые арифметические действия. В начальной школе нужно отработать и довести до автоматизма сложение и вычитание, выучить «от корки до корки» таблицу умножения. Все! Остальное — дело техники, а она нарабатывается с практикой.
Будьте терпеливы, не ленитесь лишний раз объяснить ребенку то, что он не усвоил на уроке, нудно, но дотошно разобраться в алгоритме рассуждений и проговорить каждую промежуточную операцию прежде, чем озвучить готовый ответ. Дайте дополнительные примеры на отработку навыков, поиграйте в математические игры — это даст свои плоды и вы увидите результаты и порадуетесь успехам чада очень скоро. Обязательно покажите, где и как можно применить полученные знания в повседневной жизни.
Уважаемые читатели! Расскажите, как вы учите ваших детей делить в столбик, с какими сложностями приходилось сталкиваться и какими способами вы их преодолели.
Онлайн калькулятор. Сложение, вычитание, умножение и деление столбиком.
Калькулятор вычисления суммы, разности, произведения и частного столбиком отобразит все этапы решения примера и даст подробное решение. Калькулятор может сложить, вычесть, умножить и разделить столбиком десятичные дроби и целые числа. Для записи десятичной дроби используйте точку либо запятую (например, 1.12 или 1,12).
Как складывать столбиком
Для того, чтобы сложит два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное сложение справа на лево, например, сложим столбиком 345 и 67.
345 + 67 = 412
110
+345
67
412
1) 5 + 7 = 12; 2 пишем, число 1 запишем над числом 4.
2) 4 + 6 = 10; 10 + 1 = 11; 1 пишем, 1 запишем над числом 3.
3) Под числом 3 нет слагаемого, поэтому просто прибавим 3 + 1 = 4
Получилось 412
Приведем еще один пример: 1567 + 761
1567 + 761 = 2328
1100
+1567
761
2328
1) 7 + 1 = 8, запишем 8.
2) 6 + 6 = 12; 2 пишем, 1 запишем над числом 5.
3) 5 + 7 = 12; 12 + 1 = 13; 3 пишем, 1 запишем над числом 1.
4) Под числом 1 нет слагаемого, поэтому просто прибавим 1 + 1 = 2
Как складывать столбиком десятичные дроби
Для того, чтобы сложить две десятичные дроби, необходимо записать одну десятичную дробь над другой, совместив их точки. Приведем пример: 123.345 + 46.02
123.345 + 46.02 = 169.365
+123.345
46.020
169.365
1) Запишем число 123.345 над числом 46.02
2) Под числом 5 нет слагаемого, поэтому просто запишем его внизу.
2) Далее сложим 2 и 4; 2 + 4 = 6; запишем 6 внизу.
3) 3 + 0 = 3; записываем 3.
4) Ставим точку
5) 3 + 6 = 9; записываем 9 внизу.
6) 2 + 4 = 6; записываем 6 внизу.
7) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Итак, у нас получилось 169.365
Приведем следующий пример: 123.99 + 12.99
123.99 + 12.99 = 136.98
001010
+123.99
12.99
136.98
1) 9 + 9 = 18; 8 пишем, 1 запишем над числом 9.
2) 9 + 9 = 18; 18 + 1 = 19; 9 пишем, 1 запишем над числом 3.
3) Ставим точку.
4) 2 + 3 = 5; 5 + 1 = 6; 6 запишем внизу
5) 2 + 1 = 3; 3 запишем внизу.
6) Так как под числом 1 нет слагаемого, просто сносим его вниз. Запишем число 1 внизу.
Ответ: 136.98
Для того чтобы сложить десятичную дробь с целым числом, необходимо сложить целую часть десятичной дроби с целым числом. Сложим, например, 23 и 0.34. У числа 23, после точки поставим столько нолей, сколько чисел после точки у десятичной дроби.
23 + 0.34 = 23.34
+23.00
0.34
23.34
1) 0 + 4 = 4. Запишем 4.
2) 0 + 3 = 3. Запишем 3.
3) Ставим точку
4) 3 + 0 = 3. Запишем 3
5) Под числом 2 нет слагаемого, поэтому просто сносим его вниз.
Ответ: 23.34
Как вычитать столбиком
Для того, чтобы вычесть два числа столбиком, необходимо записать большее число над меньшим и выполнить последовательное вычитание, например, вычтем столбиком 456 и 89.
456 — 89 = 367
..0
—456
89
367
1) Из 6-ти вычесть число 9 не получится, так как 6 меньше девяти, поэтому займем 1 у числа 5 и поставим над ним точку, получим вместо числа 6 число 16. Отнимем от 16 число 9; 16 – 9 = 7; запишем 7.
2) Так как мы заняли число 1 у числа 5, то теперь осталось число 4. Из числа 4 вычесть число 8 не получится, поэтому займем 1 у соседнего числа 4 и поставим над ним точку, получим вместо числа 4 число 14. Отнимем от числа 14 число 8 = 6. Запишем 6.
Отнимем от числа 14 число 8 = 6. Запишем 6.
3) Под числом 4 нет вычитаемого, поэтому отнимем от числа 4 число 1 (так как мы занимали 1-цу): 4 -1 = 3; запишем число 3.
Получилось 367.
Приведем еще один пример: 307 – 58
307 — 58 = 249
..0
—307
58
249
1) Из числа 7 вычесть число 8 не получится, так как 7 меньше 8, поэтому займем 1 у ноля. Поставим над нолем точку. Когда мы занимаем 1-цу у нуля, ноль становится числом 9! получим вместо 0 число 9. Однако у ноля не получится взять единицу, поэтому двигаемся влево и занимаем единицу у числа 3 и ставим над ним точку; отнимем от 17 число 8; 17 – 8 = 9; запишем 9.
2) Так как мы заняли число 1 у ноля, то теперь осталось число 9. Отнимем от числа 9 число 5 = 4. Запишем 4.
3) Под числом 3 нет вычитаемого, но мы помним, что мы заняли единицу у числа 3, поэтому 3-1 = 2. Запишем число 2.
Получилось 249.
Как вычитать столбиком десятичные дроби
Для того, чтобы отнять из десятичной дроби целое число, либо из целого числа вычесть десятичную дробь нужно у целого числа после точки записать столько нолей, сколько чисел после точки у десятичной дроби, затем записать большее число над меньшим.
Например вычтем столбиком из десятичной дроби 123.478 целое число 56
123.478 — 56 = 67.478
..00000
—123.478
56.000
67.478
Начинаем последовательно вычитать справа налево
1) 8 – 0 = 8. Запишем 8.
2) 7 – 0 = 7. Запишем 7.
3) 4 – 0 = 4. Запишем 4.
4) Ставим точку.
5) Из числа 3 не вычесть число 6, поэтому занимаем единицу у числа 2 и ставим над ним точку. 13 – 6 = 7. Запишем число 7.
6) Над числом 2 стоит точка, значит теперь там уже не число 2, а число 1. Из единицы число 5 не вычесть, поэтому занимаем единицу у числа 1 и ставим над ним точку. 11 – 5 = 6. Запишем число 6.
7) Над числом 1 стоит точка, следовательно, 1 – 1 = 0, поэтому на этом решение законченно.
Ответ: 67.478
Еще один пример на вычитание столбиком десятичной дроби из целого числа.
432 — 2.95
432 — 2.95 = 429.05
0..0.0
—432.00
2.95
429.05
1) Из ноля число 5 не вычесть, поэтому займем единицу у ноля и поставим над ним точку, далее, как мы уже знаем ставим точку над числом 2 и занимаем единицу. 10 – 5 = 5. Запишем число 5.
2) Над числом 0 стоим точка, следовательно, 0 превратился в число 9. 9 – 9 = 0. Запишем 0.
3) Над числом два стоит точка значит 2-1 = 1. Из числа 1 число 2 не отнять, поэтому занимаем единицу у числа 3 и ставим над ним точку. 11 – 2 = 9. Запишем число 9.
4) Над числом 3 стоит точка, 3 – 1 = 2. Так как нет вычитаемого, просто сносим число 2 вниз, тоже делаем и с числом 4.
Ответ: 429.05
Правила вычитания десятичной дроби из десятичной дроби, такие же как при сложении. Нам так же необходимо сначала совместить точки десятичных дробей и затем выполнить последовательное вычитание справа налево. Вот несколько примеров на вычитание десятичных дробей:
378.326 — 26.57 = 351.756
00.0.00
—378.326
26.570
351.756
0.07 — 0.009 = 0.061
000.0
—0.070
0.009
0.061
Как умножать столбиком
Для того, чтобы умножить одно число на другое необходимо записать первый множитель над вторым, причем не важно какой множитель больше первый или второй, но удобнее чтобы записать более компактное решение записать большее число над меньшим. Затем необходимо каждое число нижнего множителя умножить на каждое число верхнего справа налево, затем суммировать произведения.
На примере будет намного понятнее. Итак, умножим 367 на 12
367 × 12 = 4404
×367
12
734
3670
4404
1. Умножим число 2 на 367 и результат запишем с справа налево от числа 2.
Умножим число 2 на 367 и результат запишем с справа налево от числа 2.
1) 2 × 7 = 14. Запишем число 4, число 1 в уме.
2) 2 × 6 = 12; 12 + 1 = 13. Запишем 3, число 1 в уме.
3) 2 × 3 = 6; 6 + 1 = 7. Запишем число 7. На этом этапе мы получили число 734.
2. Умножим число 1 на 367 и результат запишем справа на лево начиная уже от числа 1 под первой строкой.
1) 1 × 7 = 7. Запишем число 7.
2) 1 × 6 = 6. Запишем число 6.
3) 1 × 3 = 3. Запишем число 3. На этом этапе мы получили число 367
3. Теперь нам необходимо сложить получившиеся два числа 734 и 367
1) Под числом 4 нет слагаемого, поэтом просто снесем его вниз. Запишем число 4.
2) 3 + 7 = 10. Запишем 0 и запомним число 1.
3) 7 + 6 + 1 = 14. Запишем число 4, число 1 в уме.
4) У числа три нет слагаемого, поэтому просто запишет число 3.
На этом решение закончено, получилось 4404.
Как умножать столбиком десятичные дроби
Десятичные дроби столбиком умножать очень просто. Прежде всего, уберем точки из десятичных дробей. Затем произведем умножение уже получившихся целых чисел, далее посчитаем количество чисел в первом и во втором множителе, сложим эти значения, результатом будет число равное количеству чисел после точки в получившемся произведении. На примерах все станет намного понятнее.
Умножим 0.2354 на 12.3997
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×123997
2354
495988
6199850
37199100
247994000
291888938
Теперь добавим точку в получившейся ответ. Так как в первом множителе 12.3997 после точки стоит 4 числа, и во втором множителе 0.2354 стоит 4 числа, тогда 4 + 4 = 8. Сдедовательно в ответе после точки будет 8 чисел.
2.91888938
×12.3997
0.2354
2.91888938
Умножим 49.265 на 0.0045
Уберем точки из десятичных дробей, чтобы было удобной умножать.
×49265
45
246325
1970600
2216925
Теперь добавим точку в получившейся ответ. Так как в первом множителе 49.265 после точки стоит 3 числа, а во втором множителе 0.0045 стоит 4 числа, тогда 3 + 4 = 7. Сдедовательно в ответе после точки будет 7 чисел.
0.2216925
×49.265
0.0045
0.2216925
Как делить столбиком
Как делить столбиком целые числа.
Деление столбиком с остатком, в данном материале рассматриваться не будет, если интересно, есть много информации по остатку от деления тут.
Разберем для начала как разделить большее число на меньшее в столбик (когда делимое больше делителя).
На примере будет намного нагляднее изучить данную тему. Итак, разделим 12 на 5
12 : 5 = 2.4
01205
01002.4
0020
0020
0000
При делении числа 12 на число 5 у нас получится конечная десятичная дробь. Кому интересно почитать что такое десятичные дроби — это можно сделать здесь.
1) Сколько раз число 5 помещается в числе 12? Правильно 2 раза. Поэтому первым делом умножим 2 на 5 получим 10.
2) Теперь отнимем из числа 12 число 10; 12 – 10 = 2. Запишем число 2.
3) В числе 12 нет больше чисел, поэтому поле числа 2 в ответе необходимо поставить точку. Целую часть ответа мы уже нашли! Двигаемся дальше.
4) Теперь будем находить дробную часть нашей десятичной дроби. Поставим ноль рядом с разностью. Получим число 20. Теперь снова думаем, сколько раз число 5 содержится в числе 20? Правильно 4 раза. 5 × 4 = 20.
5) Отнимем от числа 20 число 20; 20 – 20 = 0. Разность равна нулю, следовательно, результатом деления является конечная десятичная дробь.
Ответ: 2.4
Возьмем другой пример, где уже ответом будет являться бесконечная периодическая десятичная дробь. Разделим 7 на 3
Разделим 7 на 3
7 : 3 = 2.(3)
0703
0602.3
010
009
001
1) В числе 7 число 3 содержится 2 раза. То есть неполное частное деления числа 7 на число 3 равно числу 2. Умножим число 2 на делитель. 2 × 3 = 6.
2) Отнимем от числа 7 число 6; 7 — 6 = 1; В делимом больше нет чисел, поэтому ставим точку.
3) Начинаем вычислять ответ для дробной части. Для этого к получившейся разности добавим ноль, получим число 10. Неполное частное деления числа 10 на число 3 равно числу 3. Запишем число 3 после точки.
4) 3 × 3 = 9. Из числа 10 отнимем число 9; 10 – 9 = 1. На этом этапе необходимо завершить деление, так как мы уже получали число 1 при вычитании числа 6 из числа 7, следовательно, при дальнейшем решении примера мы снова и снова будем получать число три в виде неполного частного и этот процесс будет продолжаться бесконечно (2.333333333333333333333333333…). Такое повторение называется периодом бесконечной периодической десятичной дроби. Для краткости период записывают в скобках 2.(3)
Деление десятичных дробей в столбик примеры
Разделим 3.12 на 3.6
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 100
07120360
036001.97
03520
03240
002800
002520
000280
Разделим 9.4 на 45.1
Если числитель и знаменатель дроби умножить на одно и тоже число, то значение дроби не изменится, поэтому, чтобы было проще разделить одно число на другое, уберем запятую, домножив оба числа на 10
0940451
00000. 2084257206
2084257206
0940
0902
003800
003608
0001920
0001804
00001160
00000902
000002580
000002255
0000003250
0000003157
00000000930
00000000902
0000000002800
0000000002706
0000000000094
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Конвекторы величин |
| Конвертер единиц длины |
| Конвектор единиц скорости |
| Конвектор единиц ускорения |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
| Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Письменное умножение и деление
Большие числа удобно перемножать и делить письменно в столбик. Письменное умножение — это поразрядное умножение. Каждый разряд второго множителя умножается на первый множитель как одноразрядное число. В произведении поэтапного (разрядного) умножения первый разряд попадает в столбец того разряда второго множителя, на который умножают.
Правило. При умножении в столбик два множителя располагаются один под другим так, чтобы разряды чисел совпадали (находились в одном столбце). Слева ставится знак «х».
Если один из множителей или оба множителя оканчиваются нулями, то числа записываются так, чтобы значащие цифры наименьшего из разрядов находились в одном столбце. Нули переносятся в произведение и в поле записи поэтапных произведений не заносятся.
Поэтапные (разрядные) произведения складываются по разрядам и под чертой записывается результат. Слева от слагаемых произведений ставится знак «+».
Письменное умножение в столбик равноценно письменному умножению по разрядам в строку. При письменном умножении в строку применяются сочетательный и распределительный законы умножения (сумму заменяем слагаемыми и первый множитель умножаем на каждое из слагаемых).
Пример.
1 014 * 258 = 261 612
1 014 * 258 = 1 014 * (200 + 50 + 8) = 1 014 * 200 + 1 014 * 50 + 1014 * 8 = 202 800 + 50 700 + 8 112 = 261 612
Чтобы перемножить в столбик числа, оканчивающиеся нулями, нужно их подписать друг под другом так, чтобы первая справа значащая цифра первого множителя стояла под первой справа значащей цифрой второго множителя
.
Например: 1 014 * 258 = 261 612
- 1014 — первый множитель
- Х
- 258 — второй множитель
- ——— поэтапные произведения:
- 8112 — слагаемое (первое произведение)
- + 5070 — слагаемое (второе произведение)
- 2028 — слагаемое (третье произведение)
- ———
- 261612 — сумма (результат умножения)
Примеры записи умножении чисел, оканчивающихся нулями.
- 450
- Х
- 270
- ———
- 315 (45 * 7 = 315)
- +
- 90 (45 * 2 = 90)
- ———
- 121500
Внимание! Нули в конце множителей в поэтапном умножении не принимают участия, а сразу все нули множителей переносятся в результат вычислений.
Правильная запись:
Неправильная запись
Письменное деление многозначных натуральных чисел осуществляется и в строку, и в столбик по этапам.
Правило. При письменном делении двух натуральных чисел слева записывается делимое, а справа от него через вертикальную черту — делитель.
Под делимым в столбец записываются поэтапные произведения каждого разряда частного на делитель. После каждого поэтапного произведения проводим горизонтальную черту, под которой записывается разность делимого и произведения, которая должна быть всегда меньше делителя, если разряд частного вычислен верно. Дополнив разность следующим разрядом делимого, принимаем это число за следующее поэтапное делимое.
Деление по этапам производим до первого разряда заданного условием делимого. Если последняя разность 0 или число, меньшее делителя, то деление натуральных чисел окончено.
Частное по разрядам (от большего к меньшему) записывается под горизонтальной чертой под делителем. В частном должно быть столько же разрядов, сколько этапов деления.
Рассмотрим пример: 12 546 : 82
Производим деление первого этапа. Множитель (1) записываем как высший разряд частного. Вычисляем разность делимого и произведения первого этапа деления (125 — 82 = 43) и дописываем к ней справа один разряд из делимого, который стоит после наименьшего разряда числа, взятого для первого этапа деления. Полученное число (434) служит делимым второго этапа
Вычисляем разность делимого и произведения первого этапа деления (125 — 82 = 43) и дописываем к ней справа один разряд из делимого, который стоит после наименьшего разряда числа, взятого для первого этапа деления. Полученное число (434) служит делимым второго этапа
деления.
Делимое второго этапа делим на делитель (434 : 82), определяем следующий разряд в частном (5) и остаток после второго этапа деления (24). Дописываем к остатку следующий разряд делимого и выполняем третий этап деления (246 : 82). Определяем третье число в частном (3) и остаток (0).
Деление окончено после третьего этапа, следовательно, в частном — трех разрядное число (153).
Проще такое деление производить в столбик также в три этана (деление углом — это тоже поэтапное деление):
Делимое кратно 82, так как разделилось без остатка.
Основное свойство частного
Правило. Если делимое и делитель умножить или разделить на одно и то же натуральное число, то их частное не изменится.
Например:
12 : 4 = 3
умножим делимое и делитель на 5, получим:
60 : 20 = 3
Например:
625 : 125 = 5
разделим делимое и делитель на 25, получим:
125 : 5 = 5
Умножение и деление чисел в Excel
Умножение и деление в Excel легко, но для этого вам нужно создать простую формулу. Просто помните, что все формулы в Excel начинаются со знака равенства (=), и вы можете использовать панель формул для их создания.
Умножение чисел
Предположим, вы хотите выяснить, сколько воды в бутылках вам нужно для конференции с клиентами (общее количество участников × 4 дня × 3 бутылки в день) или возмещения командировочных расходов для деловой поездки (общее количество миль × 0. 46). Есть несколько способов умножать числа.
46). Есть несколько способов умножать числа.
Умножение чисел в ячейке
Для выполнения этой задачи используйте арифметический оператор * (звездочка).
Например, если вы введете в ячейке = 5 * 10 , в ячейке отобразится результат 50 .
Умножить числовой столбец на постоянное число
Предположим, вы хотите умножить каждую ячейку в столбце из семи чисел на число, содержащееся в другой ячейке.В этом примере число, на которое нужно умножить 3, содержится в ячейке C2.
Введите = A2 * $ B $ 2 в новом столбце вашей электронной таблицы (в приведенном выше примере используется столбец D). Обязательно включите в формулу символ $ перед B и перед 2 и нажмите ENTER.
Примечание. Использование символов $ сообщает Excel, что ссылка на B2 является «абсолютной», что означает, что при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2.Если вы не использовали символы $ в формуле и перетащили формулу в ячейку B3, Excel изменит формулу на = A3 * C3, что не сработает, потому что в B3 нет значения.
Перетащите формулу вниз в другие ячейки столбца.

Примечание. В Excel 2016 для Windows ячейки заполняются автоматически.
Умножение чисел в разных ячейках по формуле
Функцию ПРОДУКТ можно использовать для умножения чисел, ячеек и диапазонов.
Вы можете использовать любую комбинацию до 255 чисел или ссылок на ячейки в функции PRODUCT . Например, формула = ПРОДУКТ (A2, A4: A15,12, E3: E5,150, G4, h5: J6) умножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазоны (A4: A15, E3: E5 и h5: J6).
Делить числа
Предположим, вы хотите узнать, сколько человеко-часов ушло на завершение проекта (общее количество часов проекта ÷ общее количество людей в проекте) или фактический расход миль на галлон для вашей недавней поездки по пересеченной местности (общее количество миль ÷ общее количество галлонов).Есть несколько способов делить числа.
Делим числа в ячейке
Для выполнения этой задачи используйте арифметический оператор / (косая черта).
Например, если вы введете в ячейке = 10/5 , в ячейке отобразится 2 .
Важно: Обязательно введите в ячейку знак равенства ( = ), прежде чем вводить числа и оператор /; в противном случае Excel будет интерпретировать введенное вами значение как дату. Например, если вы введете 7/30, Excel может отобразить в ячейке 30 июля. Или, если вы введете 12/36, Excel сначала преобразует это значение в 12/1/1936 и отобразит 1 декабря в ячейке.
Например, если вы введете 7/30, Excel может отобразить в ячейке 30 июля. Или, если вы введете 12/36, Excel сначала преобразует это значение в 12/1/1936 и отобразит 1 декабря в ячейке.
Примечание: В Excel нет функции РАЗДЕЛИТЬ .
Разделите числа с помощью ссылок на ячейки
Вместо того, чтобы вводить числа непосредственно в формуле, вы можете использовать ссылки на ячейки, такие как A2 и A3, для ссылки на числа, которые вы хотите разделить и разделить.
Пример:
Пример может быть легче понять, если вы скопируете его на пустой рабочий лист.
Как скопировать пример
Создайте пустую книгу или рабочий лист.
Выберите пример в разделе справки.
Примечание. Не выбирайте заголовки строк или столбцов.
Выбор примера из справки
org/ListItem»>На листе выделите ячейку A1 и нажмите CTRL + V.
Чтобы переключиться между просмотром результатов и просмотром формул, возвращающих результаты, нажмите CTRL + `(серьезное ударение) или на вкладке Формулы нажмите кнопку Показать формулы .
Нажмите CTRL + C.
A | B | С | |
1 | Данные | Формула | Описание (результат) |
2 | 15000 | = A2 / A3 | Делит 15000 на 12 (1250) |
3 | 12 |
Разделите числовой столбец на постоянное число
Предположим, вы хотите разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которое вы хотите разделить 3, содержится в ячейке C2.
В этом примере число, на которое вы хотите разделить 3, содержится в ячейке C2.
A | B | С | |
1 | Данные | Формула | Константа |
2 | 15000 | = A2 / $ 2 | 3 |
3 | 12 | = A3 / 2 канадских доллара | |
4 | 48 | = A4 / 2 канадских доллара | |
5 | 729 | = A5 / 2 канадских доллара | |
6 | 1534 | = A6 / 2 канадских доллара | |
7 | 288 | = A7 / 2 канадских доллара | |
8 | 4306 | = A8 / C $ 2 |
Введите = A2 / $ C $ 2 в ячейке B2.Обязательно включите в формулу символ $ перед C и перед 2.
Перетащите формулу из B2 вниз в другие ячейки столбца B.
Примечание. Использование символов $ сообщает Excel, что ссылка на C2 является «абсолютной», что означает, что при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали символы $ в формуле и перетащили формулу в ячейку B3, Excel изменит формулу на = A3 / C3, что не сработает, потому что в C3 нет значения.
Нужна дополнительная помощь?
Вы всегда можете спросить эксперта в сообществе специалистов по Excel или получить поддержку в сообществе Answers.
См. Также
Умножьте столбец чисел на такое же число
Умножить на процент
Создайте таблицу умножения
Операторы расчета и порядок операций
Как разделить в Excel и обработать # DIV / 0! ошибка
В руководстве показано, как использовать формулу деления в Excel для деления чисел, ячеек или целых столбцов и как обрабатывать ошибки Div / 0.
Как и другие основные математические операции, Microsoft Excel предоставляет несколько способов деления чисел и ячеек. Какой из них использовать, зависит от ваших личных предпочтений и конкретной задачи, которую вам нужно решить. В этом руководстве вы найдете несколько хороших примеров использования формулы деления в Excel, которые охватывают наиболее распространенные сценарии.
Символ разделения в Excel
Распространенным способом деления является использование знака деления. В математике операция деления обозначается символом обелуса (÷).В Microsoft Excel символ разделения представляет собой косую черту (/).
При таком подходе вы просто пишете выражение типа = a / b без пробелов, где:
- a — это дивиденд — число, которое вы хотите разделить, и
- b — делитель — число, на которое делится делимое.
Как делить числа в Excel
Чтобы разделить два числа в Excel, введите знак равенства (=) в ячейку, затем введите число, которое нужно разделить, затем косую черту, затем число, на которое нужно разделить, и нажмите клавишу Enter, чтобы вычислить формула.
Например, чтобы разделить 10 на 5, введите в ячейку следующее выражение: = 10/5
На снимке экрана ниже показано еще несколько примеров простой формулы деления в Excel:
Когда формула выполняет более одной арифметической операции, важно помнить о порядке вычислений в Excel (PEMDAS): сначала скобки, затем возведение в степень (возведение в степень), затем умножение или деление в зависимости от того, что наступит раньше, а затем сложение или вычитание в зависимости от того, что наступит раньше.
Как разделить ячейку в Excel
Чтобы разделить две ячейки в Excel, используйте символ разделения точно так же, как показано в приведенных выше примерах, но вместо чисел укажите ссылки на ячейки.
Например:
- Чтобы разделить ячейку A2 на 5:
= A2 / 5 - Чтобы разделить ячейку A2 на ячейку B2:
= A2 / B2 - Чтобы последовательно разделить нескольких ячеек , введите ссылки на ячейки, разделенные символом деления.
 Например, чтобы разделить число в A2 на число в B2, а затем разделить результат на число в C2, используйте следующую формулу:
Например, чтобы разделить число в A2 на число в B2, а затем разделить результат на число в C2, используйте следующую формулу: = A2 / B2 / C2
Функция деления в Excel (QUOTIENT)
Скажу прямо: в Excel нет функции разделения.Всякий раз, когда вы хотите разделить одно число на другое, используйте символ деления, как объяснено в приведенных выше примерах.
Однако, если вы хотите вернуть только целую часть от деления и отбросить остаток, используйте функцию QUOTIENT:
ЧИСЛО (числитель, знаменатель)
Где:
- Числитель (обязательно) — делимое, т.е. число, которое нужно разделить.
- Знаменатель (обязательный) — делитель, т.е.е. число, на которое нужно разделить.
Когда два числа делят равномерно без остатка , символ деления и формула QUOTIENT возвращают одинаковый результат. Например, и = 10/5 , и = QUOTIENT (10, 5) возвращают 2.
Когда после деления остается остаток , знак деления возвращает десятичное число, а функция QUOTIENT возвращает только целую часть. Например, = 5/4 возвращает 1,25, а = QUOTIENT (5,4) возвращает 1.
3 вещи, которые вы должны знать о функции QUOTIENT
Как бы просто не выглядело, функция Excel QUOTIENT все же имеет несколько недостатков, о которых вы должны знать:
- Числитель , и знаменатель . Аргументы должны быть представлены в виде чисел, ссылок на ячейки, содержащие числа, или других функций, возвращающих числа.
- Если какой-либо из аргументов не является числовым, формула QUOTIENT возвращает #VALUE! ошибка.
- Если знаменатель равен 0, QUOTIENT возвращает ошибку деления на ноль (# DIV / 0!).
Как разделить столбцы в Excel
Разделить столбцы в Excel тоже просто. Это можно сделать, скопировав обычную формулу деления вниз по столбцу или используя формулу массива. Зачем использовать формулу массива для такой тривиальной задачи? Вы узнаете причину в мгновение ока 🙂
Зачем использовать формулу массива для такой тривиальной задачи? Вы узнаете причину в мгновение ока 🙂
Как разделить два столбца в Excel, скопировав формулу
Чтобы разделить столбцы в Excel, выполните следующие действия:
- Разделите две ячейки в самой верхней строке, например:
= A2 / B2 - Вставьте формулу в первую ячейку (скажем, C2) и дважды щелкните маленький зеленый квадрат в правом нижнем углу ячейки, чтобы скопировать формулу вниз по столбцу.Сделанный!
Поскольку мы используем относительные ссылки на ячейки (без знака $), наша формула деления будет изменяться в зависимости от относительного положения ячейки, в которую она копируется:
Наконечник. Аналогичным образом можно разделить две строки в Excel. Например, чтобы разделить значения в строке 1 на значения в строке 2, вы помещаете = A1 / A2 в ячейку A3, а затем копируете формулу вправо в необходимое количество ячеек.
Как разделить один столбец на другой с помощью формулы массива
В ситуациях, когда вы хотите предотвратить случайное удаление или изменение формулы в отдельных ячейках, вставьте формулу массива во весь диапазон.
Например, чтобы разделить значения в ячейках A2: A8 на значения в B2: B8 построчно, используйте эту формулу: = A2: A8 / B2: B8
Чтобы правильно вставить формулу массива, выполните следующие действия:
- Выберите весь диапазон, в который вы хотите ввести формулу (C2: C8 в этом примере).
- Введите формулу в строке формул и нажмите Ctrl + Shift + Enter, чтобы завершить ее. Как только вы это сделаете, Excel заключит формулу в {фигурные скобки}, указывая, что это формула массива.
В результате вы получите числа в столбце A, разделенные на числа в столбце B одним махом. Если кто-то попытается отредактировать вашу формулу в отдельной ячейке, Excel покажет предупреждение о том, что часть массива не может быть изменена.
Чтобы удалить или изменить формулу , вам нужно сначала выбрать весь диапазон, а затем внести изменения. Чтобы расширить формулу на новые строки, выберите весь диапазон, включая новые строки, измените ссылки на ячейки в строке формул, чтобы разместить новые ячейки, а затем нажмите Ctrl + Shift + Enter, чтобы обновить формулу.
Как разделить столбец на число в Excel
В зависимости от того, хотите ли вы, чтобы выходные данные были формулами или значениями, вы можете разделить числовой столбец на постоянное число, используя формулу деления или функцию Специальная вставка .
Разделите столбец на число по формуле
Как вы уже знаете, самый быстрый способ выполнить деление в Excel — использовать символ разделения. Итак, чтобы разделить каждое число в данном столбце на одно и то же число, вы помещаете обычную формулу деления в первую ячейку, а затем копируете формулу вниз по столбцу.Вот и все!
Например, чтобы разделить значения в столбце A на число 5, вставьте следующую формулу в A2, а затем скопируйте ее в любое количество ячеек: = A2 / 5
Как объяснено в приведенном выше примере, использование относительной ссылки на ячейку (A2) обеспечивает правильную настройку формулы для каждой строки. То есть формула в B3 становится = A3 / 5 , формула в B4 становится = A4 / 5 и т. Д.
Вместо того, чтобы указывать делитель непосредственно в формуле, вы можете ввести его в какую-либо ячейку, например, D2, и разделить на эту ячейку.В этом случае важно заблокировать ссылку на ячейку знаком доллара (например, $ D $ 2), сделав ее абсолютной ссылкой, потому что эта ссылка должна оставаться постоянной независимо от того, куда копируется формула.
Как показано на снимке экрана ниже, формула = A2 / $ D $ 2 возвращает точно такие же результаты, как = A2 / 5 .
Разделите столбец на одно и то же число с помощью специальной вставки
Если вы хотите, чтобы результаты были значениями, а не формулами, вы можете выполнить деление обычным способом, а затем заменить формулы на значения.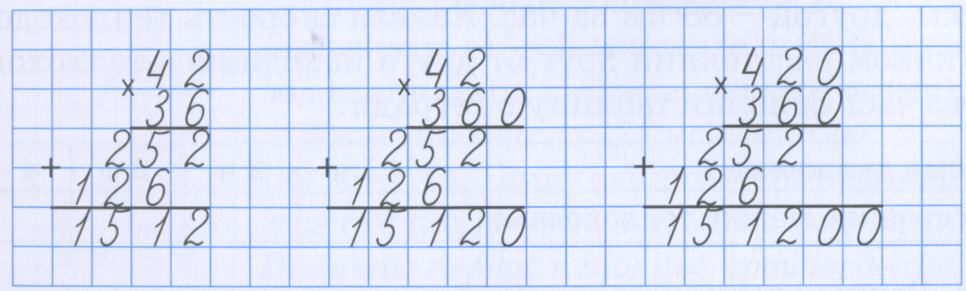 Или вы можете добиться того же результата быстрее с помощью опции Специальная вставка > Разделить .
Или вы можете добиться того же результата быстрее с помощью опции Специальная вставка > Разделить .
- Если вы не хотите отменять исходные числа, скопируйте их в столбец, в котором вы хотите получить результаты. В этом примере мы копируем числа из столбца A в столбец B.
- Поместите делитель в какую-нибудь ячейку, скажем D2, как показано на скриншоте ниже.
- Выберите ячейку делителя (D5) и нажмите Ctrl + C, чтобы скопировать ее в буфер обмена.
- Выделите ячейки, которые хотите умножить (B2: B8).
- Нажмите Ctrl + Alt + V, затем I, что является ярлыком для Специальная вставка > Разделить , и нажмите клавишу Enter.
Или щелкните правой кнопкой мыши выбранные числа, выберите Специальная вставка… из контекстного меню, затем выберите Разделить в разделе Операция и нажмите ОК.
В любом случае каждое из выбранных чисел в столбце A будет разделено на число в D5, и результаты будут возвращены в виде значений, а не формул:
Как разделить на процент в Excel
Поскольку проценты являются частями более крупного целого, некоторые люди думают, что для вычисления процента от данного числа вы должны разделить это число на проценты.Но это же заблуждение! Чтобы найти проценты, нужно умножать, а не делить. Например, чтобы найти 20% от 80, вы умножаете 80 на 20% и в результате получаете 16: 80 * 20% = 16 или 80 * 0,2 = 16.
В каких ситуациях вы делите число на процент? Например, чтобы найти X, если определенный процент от X равен Y. Чтобы прояснить ситуацию, давайте решим эту задачу: 100 — это 25% от какого числа?
Чтобы получить ответ, преобразуйте задачу в это простое уравнение:
X = Y / P%
Если Y равно 100, а P равно 25%, формула принимает следующий вид: = 100/25%
Поскольку 25% — это 25 частей от сотни, вы можете смело заменять процентное значение десятичным числом: = 100/0. 25
25
Как показано на скриншоте ниже, результат обеих формул будет 400:
Дополнительные примеры процентных формул см. В разделе Как рассчитать проценты в Excel.
Ошибка DIV / 0 Excel
Деление на ноль — это операция, для которой нет ответа, поэтому она запрещена. Всякий раз, когда вы пытаетесь разделить число на 0 или на пустую ячейку в Excel, вы получите ошибку деления на ноль (# DIV / 0!). В некоторых ситуациях эта индикация ошибки может быть полезной, предупреждая вас о возможных сбоях в вашем наборе данных.
В других сценариях формулы могут просто ждать ввода, поэтому вы можете заменить обозначения ошибок Excel Div 0 пустыми ячейками или своим собственным сообщением. Это можно сделать с помощью формулы ЕСЛИ или функции ЕСЛИОШИБКА.
Подавить ошибку # DIV / 0 с помощью IFERROR
Самый простой способ справиться с # DIV / 0! ошибка в Excel заключается в том, чтобы заключить формулу деления в функцию ЕСЛИОШИБКА следующим образом:
= ЕСЛИ ОШИБКА (A2 / B2; "")
Формула проверяет результат деления и, если она оценивается как ошибка, возвращает пустую строку («»), иначе результат деления.
Обратите внимание на два рабочих листа ниже. Какой из них эстетичнее?
Примечание . Функция ЕСЛИОШИБКА в Excel маскирует не только # ДЕЛ / 0! ошибок, но все другие типы ошибок, такие как # Н / Д, # ИМЯ ?, # ССЫЛКА !, # ЗНАЧЕНИЕ !, и т. д. Если вы хотите подавить конкретные ошибки DIV / 0, используйте формулу ЕСЛИ, как показано в следующий пример.
Обработка ошибки Excel DIV / 0 с помощью формулы IF
Чтобы замаскировать только ошибки Div / 0 в Excel, используйте формулу ЕСЛИ, которая проверяет, равен ли делитель (или не равен) нулю.
Например:
= ЕСЛИ (B2 = 0, "", A2 / B2)
или
= ЕСЛИ (B2 <> 0, A2 / B2, "")
Если делителем является любое число, отличное от нуля, формулы делят ячейку A2 на B2.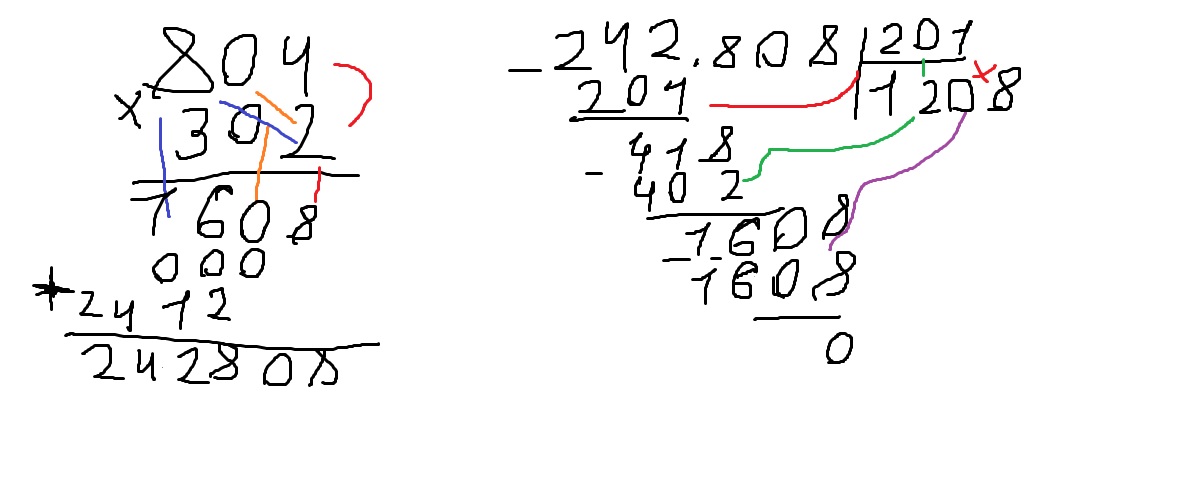 Если B2 равно 0 или пусто, формулы ничего не возвращают (пустая строка).
Если B2 равно 0 или пусто, формулы ничего не возвращают (пустая строка).
Вместо пустой ячейки вы также можете отобразить собственное сообщение, подобное этому:
= ЕСЛИ (B2 <> 0, A2 / B2, «Ошибка в вычислении»)
Как разделить с помощью Ultimate Suite для Excel
Если вы делаете первые шаги в Excel и еще не чувствуете себя комфортно с формулами, вы можете выполнить деление с помощью мыши.Все, что для этого требуется, — это установить наш Ultimate Suite в ваш Excel.
В одном из примеров, рассмотренных ранее, мы разделили столбец на номер с помощью специальной функции вставки Excel. Это потребовало большого количества движений мыши и двух ярлыков. Теперь позвольте мне показать вам более короткий способ сделать то же самое.
- Скопируйте числа, которые вы хотите разделить, в столбец «Результаты», чтобы предотвратить замену исходных чисел.
- Выберите скопированные значения (C2: C5 на скриншоте ниже).
- Перейдите на вкладку Инструменты Ablebits> > Группа Calculate и выполните следующие действия:
- Выберите знак разделения (/) в поле Operation .
- Введите число для деления в поле Значение .
- Нажмите кнопку Рассчитать .
Готово! Весь столбец делится на указанное число в мгновение ока:
Как и в случае с Excel Paste Special, результатом деления будет значений, , а не формул. Таким образом, вы можете безопасно переместить или скопировать вывод в другое место, не беспокоясь об обновлении ссылок на формулы. Вы даже можете переместить или удалить исходные числа, и ваши рассчитанные числа останутся в целости и сохранности.
Вот как вы делите в Excel с помощью формул или инструментов вычислений. Если вам интересно попробовать эту и многие другие полезные функции, включенные в Ultimate Suite for Excel, вы можете загрузить 14-дневную пробную версию.
Чтобы ближе познакомиться с формулами, обсуждаемыми в этом руководстве, загрузите наши примеры формул Excel Division.
Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Как сложить, вычесть, умножить или разделить несколько ячеек в Excel
Для выполнения основных математических операций не нужно разбирать калькулятор и вручную складывать ячейки, столбцы или строки.В Excel есть полезная функция, называемая формулами, которая позволяет выполнять как базовую математику, такую как сложение и вычитание, так и более сложные элементы, такие как поиск средних значений, или даже создавать собственные формулы с использованием сверхсовременных алгоритмов.
Сегодня мы рассмотрим различные варианты практического использования простых формул в Excel. В этом сценарии мы собираемся подсчитать счета, вычесть причитающуюся сумму, умножить счета в течение года и разделить их между тремя соседями по комнате каждый месяц.
1. Откройте книгу Excel. В этом примере мы воспользуемся простым подсчетом расходов и сложим их. Но на основе формулы, которую вы выбираете на шаге TKTK, вы можете так же легко вычесть, умножить или разделить ячейки для получения среднего значения.
2. Выберите ячейку, которую вы хотите использовать для отображения решения вашей простой формулы.
3. Для добавления решение простое. Нам просто нужно сообщить Excel, что мы добавляем, а затем определить, какие ячейки мы хотим добавить. Используйте эту формулу: = СУММ (D2: D7)
4. Вычесть не так просто, поскольку мы не можем вычесть несколько ячеек с помощью формулы одного и того же типа. Вместо этого мы должны вводить каждую ячейку вручную. Так, если бы мы хотели вычесть счет за сотовый телефон, например, из арендной платы, мы бы использовали эту формулу: = D5-D6
5. Для умножения формула в основном такая же, как вычитание. Чтобы умножить счет за телефон на 12, например, используйте эту формулу: = D6 * 12 (или вы можете умножить две ячейки в книге почти так же, как вы их вычитали, только звездочку вместо знака минус) .
Для умножения формула в основном такая же, как вычитание. Чтобы умножить счет за телефон на 12, например, используйте эту формулу: = D6 * 12 (или вы можете умножить две ячейки в книге почти так же, как вы их вычитали, только звездочку вместо знака минус) .
6. А для подразделения вы можете использовать следующую формулу: = D9 / 3
Как сложить, вычесть, разделить и умножить в Excel
Существуют различные арифметические функции, которые вы можете выполнять в Excel. В этом кратком руководстве я покажу вам, как складывать, вычитать, делить и умножать в Excel.
Прежде чем мы начнем, давайте посмотрим на символы, которые представляют основные арифметические функции в Excel:
- Символ ‘+’ используется для сложения / суммирования значений
- Символ ‘-‘ используется для вычитания значения
- Символ ‘/’ используется для деления значений
- Символ ‘*’ используется для умножения значений
Добавить значения в Excel
Для начала я покажу вам, как сложить / sum значений в Excel.В нашем примере мы суммируем числа 5 и 3:
(1) Сначала откройте электронную таблицу Excel, а затем дважды щелкните ячейку A1 , чтобы ввести свою функцию.
Для простоты я решил применить функцию сложения / суммирования в ячейке A1, но не стесняйтесь выбирать другую ячейку.
(2) Теперь введите: = 5 + 3
(3) Наконец, нажмите Введите . Результат вашей операции теперь будет отображаться в ячейке A1:
Вычесть значения в Excel
В этом примере мы выполним операцию вычитания 9-4:
(1) Сначала дважды щелкните в ячейке A1
(2) Затем введите: = 9-4
(3) Наконец, нажмите Введите . Результат вашей операции теперь будет отображаться в ячейке A1:
Результат вашей операции теперь будет отображаться в ячейке A1:
Значения деления в Excel
Теперь мы преформируем операцию деления на 12/3:
(1) Сначала дважды щелкните ячейку A1
(2) Затем введите: = 12/3
(3) Наконец, нажмите Введите , и вы получите:
Умножение значений в Excel
Здесь мы будем умножьте на числа 5 и 4 следующим образом:
(1) Чтобы начать, дважды щелкните ячейку A1
(2) Затем введите: = 5 * 4
(3) Наконец , нажмите Введите .Теперь вы увидите результат своей операции в ячейке A1:
Выполнение комбинации арифметических операций в Excel
Для начала давайте сохраним числа 22, 2 и 5 в ячейках A1, B1 и C1 соответственно.
Затем мы рассмотрим, как выполнить комбинацию следующих арифметических операций:
(1) Сложить и вычесть
(2) Вычесть и умножить
(3) Вычесть, умножить и разделить
Сложить и вычесть
Теперь давайте выполним следующую операцию 22-2 + 5:
(1) Сначала дважды щелкните ячейку A3 , чтобы ввести свои операции
Мы будем использовать ячейку A3 для заполнения результата нашей арифметической операции ( но не стесняйтесь использовать другую ячейку, если хотите).
(2) Затем введите: = A1-B1 + C1
(3) Наконец, нажмите Enter. Теперь вы увидите результат своей операции в ячейке A3:
Вычесть и умножить
Теперь мы будем вычитать и умножать следующим образом: (22-2) * 5
(1) Первоначально удваивается -Щелкните ячейку A3 , чтобы ввести свою функцию
(2) Затем введите: = (A1-B1) * C1
(3) Теперь нажмите Введите :
Вычесть, умножить и Разделить
Наконец, мы рассмотрим, как вычитать, умножать и делить следующим образом: (22-2) * 5-10/2
(1) Как и раньше, дважды щелкните ячейку A3 , чтобы ввести свою функцию
(2) Затем введите: = (A1-B1) * C1 — 10/2
(3) Наконец, нажмите Введите . Результат вашей операции будет отображаться в ячейке A3:
Результат вашей операции будет отображаться в ячейке A3:
Мы только что рассмотрели различные типы арифметических функций, которые вы можете выполнить в Excel.
Если вы хотите узнать больше о функции СУММ, посетите следующий пост о различных способах суммирования значений в Excel.
В общем, существует большое количество различных функций, которые вы можете выполнять в Excel, например, функция Max или функция VLOOKUP.
Excel XP: создание сложных формул
Урок 6: Создание сложных формул
/ ru / excelxp / создание простых формул / содержание /
Введение
К концу этого урока вы должны уметь:
- Создание сложных формул
- Заполнение формулы в другую ячейку
- Копирование и вставка формулы в другую ячейку
- Изменение формулы
- Создание абсолютной ссылки
Определение сложных формул
Простые формулы имеют одну математическую операцию. Сложные формулы включают более одной математической операции.
Порядок математических операций важен. Если вы вводите формулу, содержащую несколько операций, таких как сложение, вычитание и деление, Excel XP знает, как выполнять эти операции в определенном порядке. Порядок операций:
- Операции в скобках
- Экспоненциальные вычисления (в степени)
- Умножение и деление, в зависимости от того, что наступит первым
- Сложение и вычитание, в зависимости от того, что наступит раньше
Используя этот порядок, позвольте нам Посмотрите, как вычисляется формула 120 / (8-5) * 4-2 на следующем рисунке:
Давайте посмотрим на другой пример:
2 * (6-4) =?
Ответ 8 или 4? Если вы проигнорируете круглые скобки и вычислите в том порядке, в котором появляются числа, 2 * 6-4, вы получите неправильный ответ, 8.Чтобы получить правильный ответ, необходимо соблюдать порядок действий.
Чтобы вычислить правильный ответ:
- Вычислите операцию в скобках (6-4), где ответ равен 2.
- Умножьте ответ, полученный на шаге 1, который равен 2, на число 2 *, открывающее уравнение. Другими словами, умножьте 2 * 2.
- Ответ: 4.
При использовании формул со ссылками на ячейки результаты меняются каждый раз, когда числа редактируются .
В Excel никогда не выполняйте математические вычисления в уме и введите ответ в ячейку, в которой вы ожидаете получить ответ по формуле.
Определение сложных формул
Прежде чем двигаться дальше, давайте рассмотрим еще несколько формул, чтобы убедиться, что вы понимаете порядок операций, с помощью которых Excel вычисляет ответ.
| 5 * 3/2 | Умножьте 5 * 3 перед выполнением операции деления, потому что знак умножения стоит перед знаком деления.Ответ: 7,5 . |
| 5/3 * 2 | Разделите 5/3 перед выполнением операции умножения, потому что знак деления стоит перед знаком умножения. Ответ: 3,333333 . |
| 5 / (3 * 2) | Сначала выполните операцию в скобках (3 * 2) и разделите 5 на полученный результат. Ответ: 0,833333 . |
| 5 + 3-2 | Сложите 5 + 3 перед выполнением операции вычитания, потому что знак сложения стоит перед знаком вычитания.Ответ: 6 . |
| 5-2 + 3 | Вычтите 5-2 перед выполнением операции сложения, потому что знак вычитания стоит перед знаком сложения. Ответ: 6 . |
| 5-2 * 3 | Умножьте 2 * 3 перед выполнением операции вычитания, потому что знак умножения имеет более высокий порядок, чем знак вычитания.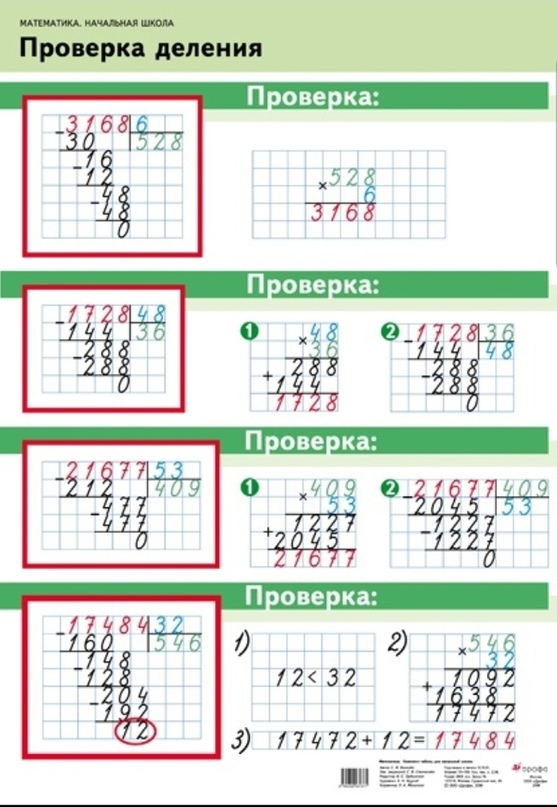 Ответ: -1 . Ответ: -1 . |
| (5-2) * 3 | Сначала выполните операцию в скобках (5-2), а затем умножьте на 3.Ответ: 9 . |
Создание сложных формул
Excel XP автоматически следует стандартному порядку операций в сложной формуле. Если вы хотите, чтобы сначала была вычислена определенная часть формулы, заключите ее в круглые скобки.
Если бы мы хотели, например, сложить содержимое ячеек B2 и B3, а затем взять этот ответ и умножить его на данные в ячейке A4, нам нужно было бы определить следующую формулу: = (B2 + B3) * A4 .
- Введите числа, которые вы хотите вычислить.
- Щелкните ячейку, в которой должна отображаться формула результат .
- Введите знак равенства (=), чтобы сообщить Excel, что формула определяется.
- Введите открывающую скобку или (.
- Щелкните первую ячейку для включения в формулу (например, ячейка B2).
- Введите знак сложения (+) , чтобы сообщить Excel, что добавление
- Щелкните вторую ячейку в формуле.Ссылка B3 показывает, где вы хотите получить результат.
- Завершите операцию B2 + B3, добавив закрывающую скобку, или).
- Введите следующий математический оператор или символ умножения (*) , чтобы сообщить Excel, что необходимо выполнить операцию умножения.
- Щелкните третью ячейку , которая будет включена в формулу, ячейка A4.
- Нажмите Введите или нажмите кнопку ввода в строке формул, чтобы завершить формулу.
Попробуйте изменить одно из значений в формуле и посмотрите, как изменится ответ на формулу.
Excel не всегда сообщит вам , если ваша формула содержит ошибку, поэтому вам нужно проверить все свои формулы. Чтобы узнать, как это сделать, прочитайте урок «Двойная проверка формул» в нашем руководстве по формулам Excel.
Чтобы узнать, как это сделать, прочитайте урок «Двойная проверка формул» в нашем руководстве по формулам Excel.
Заполнение формулами других ячеек
Иногда вы напишете формулу, которая будет использоваться в разных местах на листе. Например, электронная таблица может содержать несколько столбцов чисел.Каждый столбец будет содержать формулу, которая складывает все числа в нем. Вы можете написать формулу несколько раз, по одному разу в каждом столбце, или вы можете скопировать и вставить ее в каждый столбец. Формула заполнения Метод позволяет копировать формулу и одновременно заполнять ее во многих разных ячейках.
Указатель мыши принимает вид черного перекрестия при наведении на маркер заполнения или квадратную рамку в нижнем правом углу ячейки.
Чтобы использовать дескриптор заполнения для копирования формулы в окружающую ячейку:
- Щелкните ячейку, содержащую формулу, которую нужно скопировать.
- Поместите указатель мыши на маркер заполнения.
- Щелкните и удерживайте левую кнопку мыши, затем перетащите содержимое в ячейку, которая получит формулу заполнения.
- Отпустите кнопку мыши.
- Выберите опцию Копировать ячейки в раскрывающемся меню формулы заполнения.
Ссылки на ячейки в формуле автоматически обновляются, когда формула копируется в другие ячейки электронной таблицы.
Вы также можете скопировать и вставить формул в другие ячейки.Это обсуждается на следующей странице.
Копирование и вставка формул
Процесс копирования и вставки формулы идентичен процессу копирования и вставки текста.
Чтобы скопировать и вставить формулу:
- Выберите ячейку, содержащую формулу, которую вы хотите скопировать.
- Нажмите кнопку Копировать . Вокруг скопированных клеток появляются марширующие муравьи.
- Выберите ячейку, в которую будет вставлена скопированная формула.

- Нажмите кнопку ввода .Формула копируется в новое место.
Проверка формул
Вы можете изменить любую формулу, которая была ранее записана на листе.
Чтобы изменить формулу с помощью клавиатуры:
- Дважды щелкните ячейку, содержащую формулу, которую нужно изменить.
- Курсор теперь может перемещаться влево и вправо между значениями формулы в ячейке B5.
- Внесите необходимые изменения в формулу.
- Нажмите клавишу Enter или нажмите кнопку Enter, чтобы принять новую формулу.
Создание абсолютной ссылки
На предыдущих уроках мы видели, как ссылки на ячейки в формулах автоматически адаптируются к новым местоположениям, когда формула вставляется в разные ячейки.
Иногда при копировании и вставке формулы не требуется, чтобы одна или несколько ссылок на ячейки изменялись. Абсолютные ссылки решают эту проблему. Абсолютные ссылки на ячейки в формуле всегда относятся к одной и той же ячейке или диапазону ячеек в формуле. Если формула копируется в другое место, абсолютная ссылка остается прежней.
Абсолютная ссылка обозначается в формуле добавлением знака доллара ($). Он может предшествовать ссылке на столбец, ссылке на строку или и тем, и другим. Примеры абсолютных ссылок:
| $ A $ 2 | Столбец и строка не изменяются при копировании. |
| A $ 2 | Строка не изменяется при копировании. |
| $ A2 | Столбец не изменяется при копировании. |
Чтобы создать абсолютную ссылку:
- Введите числа, которые вы хотите вычислить (например, 34 567 в ячейке B2 и 1234 в ячейке B3).
- Создайте простую формулу (= B2 + B3).
- Чтобы создать абсолютную ссылку в формуле, вставьте значение $ перед B (ссылка на столбец) и 2 (ссылка на строку) в ссылке на B2, чтобы новая формула выглядела как = $ B $ 2 + B3 .
- Скопируйте и вставьте формулу в соседнюю ячейку. Теперь формула включает абсолютную ссылку на B2: = $ B $ 2 + D3.
Challenge
- Введите следующую информацию:
В ячейке A1 введите 12345 .
В ячейке A2 введите 15865 .
В ячейке B1 введите 9347 .
В ячейке B2 введите 11942 .
В ячейке C1 введите 19348 .
В ячейке C2 введите 17103 . - Создайте следующую простую формулу:
В ячейке A3, напишите формулу , чтобы сложить ячейки A1 и A2.
- Заполните формулу в ячейке A3 как в ячейке B3, так и в ячейке C3.
- Создайте следующую сложную формулу:
В ячейке A5, запишите формулу , которая делит ячейку A1 на сумму ячеек A3, B3 и C3.
- В формуле, определенной в ячейке A5, создает абсолютную ссылку на все ячейки и строки, указанные в следующей части формулы: сумма ячеек A3, B3 и C3.
- Скопируйте формулу и абсолютную ссылку в ячейку A5, а вставьте ее в ячейки B5 и C5.
- Обратите внимание, как формулы, отображаемые в ячейках A5, B5 и C5, отличаются друг от друга.
/ ru / excelxp / using-functions / content /
Как разделить в Excel
В Excel нет функции РАЗДЕЛЕНИЕ.Просто используйте косую черту (/), чтобы разделить чисел в Excel .
1. Приведенная ниже формула делит числа в ячейке. В качестве оператора деления используйте косую черту (/). Не забывайте, всегда начинайте формулу со знака равенства (=).
2. Приведенная ниже формула делит значение в ячейке A1 на значение в ячейке B1.
3. Excel отображает # DIV / 0! ошибка, когда формула пытается разделить число на 0 или пустую ячейку.
4. Приведенная ниже формула делит 43 на 8. Ничего особенного.
5. Вы можете использовать функцию ЧИСЛО в Excel, чтобы вернуть целую часть деления. Эта функция отбрасывает остаток от деления.
6. Функция МОД в Excel возвращает остаток от деления.
Посмотрите на снимок экрана ниже. Чтобы разделить числа в одном столбце на числа в другом столбце, выполните следующие действия.
7а. Сначала разделите значение в ячейке A1 на значение в ячейке B1.
7б. Затем выберите ячейку C1, щелкните в правом нижнем углу ячейки C1 и перетащите ее в ячейку C6.
Посмотрите на снимок экрана ниже. Чтобы разделить столбец чисел на постоянное число, выполните следующие шаги.
8а. Сначала разделите значение в ячейке A1 на значение в ячейке A8. Исправьте ссылку на ячейку A8, поместив символ $ перед буквой столбца и номером строки ($ A $ 8).
8б. Затем выберите ячейку B1, щелкните в правом нижнем углу ячейки B1 и перетащите ее в ячейку B6.
Объяснение: когда мы перетаскиваем формулу вниз, абсолютная ссылка ($ A $ 8) остается неизменной, а относительная ссылка (A1) изменяется на A2, A3, A4 и т. Д.
Если вы не являетесь героем формул, используйте Специальную вставку для деления в Excel без использования формул!
9. Например, выберите ячейку C1.
10. Щелкните правой кнопкой мыши и выберите «Копировать» (или нажмите CTRL + c).
11. Выберите диапазон A1: A6.
12. Щелкните правой кнопкой мыши и выберите «Специальная вставка».
13. Щелкните «Разделить».
14. Щелкните OK.
Примечание: чтобы разделить числа в одном столбце на числа в другом столбце, на шаге 9 просто выберите диапазон вместо ячейки.
Как разделить в Google Таблицах (числа, ячейки или столбцы)
Google Таблицы теперь являются популярным инструментом для работы с электронными таблицами для большинства людей. Это бесплатное приложение, с которым очень легко сотрудничать, и в нем есть несколько замечательных функций и возможностей.
Даже если вы хотите сделать что-то столь же простое, как хранение данных или простые вычисления, такие как умножение или деление, вы можете легко сделать это в Google Таблицах.
В этом руководстве. Я покажу вам несколько способов делить числа в Google Таблицах.
Вы можете легко разделить числа в Google Таблицах, используя встроенную формулу или оператор деления (как мы увидим на примерах).
Итак, приступим!
Разделить две ячейки в Google Таблицах
Если вы хотите разделить два числа в Google Таблицах (или две ячейки с числами), то есть несколько способов сделать это в Google Таблицах.
Использование функции РАЗДЕЛЕНИЕ
Деление в Google Таблицах — настолько обычная задача, что существует встроенная функция, которая позволяет вам разделить два числа или числа, которые находятся в двух ячейках.
Это функция РАЗДЕЛИТЬ (без оценок для угадывания)!
Предположим, вы хотите разделить значение в ячейке A1 на значение в ячейке B1.
Для этого можно использовать формулу DIVIDE:
= DIVIDE (A1, B1)
В приведенной выше формуле первым аргументом является делимое (число, которое необходимо разделить) и делитель ( число, на которое нужно разделить)
Я использовал ссылки на ячейки в приведенном выше примере, но вы также можете жестко указать значения в формуле.Например, вы также можете использовать следующую формулу:
= DIVIDE (1200,15)
Преимущество использования ссылок на ячейки заключается в том, что результат формулы становится динамическим. Это означает, что если я изменю значение в ячейке A1 или B1, формула обновится автоматически.
Также помните, что делитель не может быть 0. Если ваш делитель равен 0, вы получите ошибку деления — # DIV / 0!
Использование оператора DIVIDE
Еще один быстрый способ разделить числа в Google Таблицах — использовать оператор деления — косая черта (/)
Предположим, у вас есть данные, как показано ниже, и вы хотите разделить значение в ячейке A1 со значением в ячейке B1.
Для этого можно использовать приведенное ниже уравнение:
= A1 / B1
И если вы хотите быстро разделить числа (вместо ссылок на ячейки), вы также можете это сделать (как показано ниже формула):
= 1200/15
Также прочтите: Как умножать в Google Таблицах
Порядок приоритета при делении ячеек
При использовании арифметических операторов (таких как деление или умножение) в Google Таблицах важно знать порядок приоритета.
Позвольте мне попытаться объяснить это на примере.
Предположим, я использую следующую формулу:
= 1200/15 + 15
Можете ли вы угадать, каков будет результат?
Это будет 95.
Это происходит, поскольку в Google Таблицах существует порядок приоритета, в котором деление выполняется перед добавлением. Следовательно, сначала он делит 1200 на 15, где результат равен 80. Затем он добавляет 15 к этому результату, давая вам общий результат как 95.
Теперь нетрудно понять это в нашем простом примере, но это может привести к проблемам. при работе с большими сложными формулами.
В таких случаях лучше не беспокоиться о порядке приоритета, оставив вычисления в скобках (скобках).
Например, если вы хотите сначала выполнить сложение, а затем деление, вы можете использовать следующую формулу:
= 1200 / (15 + 15)
Это даст вам результат 40 (= 1200 / 30)
Разделение двух столбцов в Google Таблицах
В реальных сценариях вы не захотите открывать Google Таблицы для простого разделения.Вы можете легко сделать это с помощью калькулятора на своем смартфоне или с помощью простого поиска в Google.
Google Таблицы можно использовать для быстрого разделения чисел на столбцы и получения результата для сотен ячеек за секунду.
Например, предположим, что у вас есть набор данных, показанный ниже, и вы хотите вычислить деление, когда значение в столбце A делится на соответствующую ячейку в столбце B
Ниже приведена формула, которая будет делать это:
= ArrayFormula (A1: A20 / B1: B20)
Поскольку это формула массива, вам нужно только ввести эту формулу только в ячейку C1, и она даст вам результат, как показано выше.
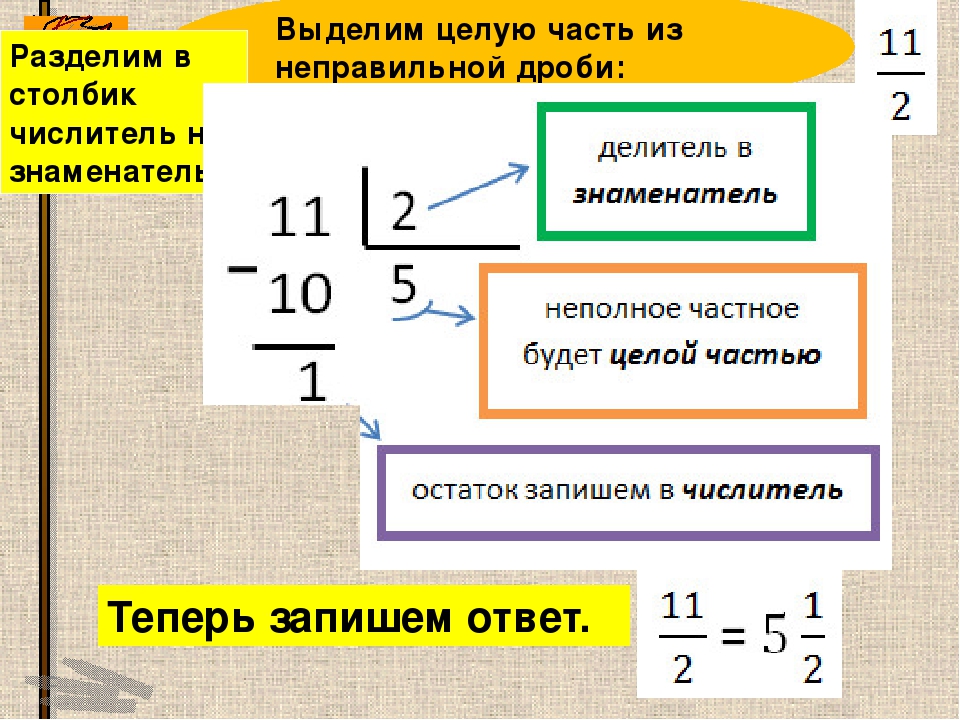 Результатом является неполное произведение.
Результатом является неполное произведение.

 Например, чтобы разделить число в A2 на число в B2, а затем разделить результат на число в C2, используйте следующую формулу:
Например, чтобы разделить число в A2 на число в B2, а затем разделить результат на число в C2, используйте следующую формулу: 