Как быстро разделить число на 5: простой способ

02

Февраль

Автор: Евгения Климкович

Рубрика: Математика

Большой привет от блога «ШколаЛа» всем, кто не хочет стоять на месте. Всем, кто хочет идти вперед совершенствоваться и развиваться. Всем, кто не только развивается сам, но и старается научить этому своих детей.

Давно известно, что отличным способом развития мышления являются вычисления в уме. Говорят, что несколько десятилетий назад в школах даже предмет такой был «Устный счет». Учили школяров прибавлять, вычитать, умножать и делить без использования спецприспособлений. И деление являлось одним из самых трудных действий.

Сегодня я и предлагаю научиться делить. Без применения калькулятора, компьютера и иных гаджетов. Абакус тоже не понадобится. Да что уж там, даже ручку с бумажкой отложим в сторонку. Будем учиться быстро делить на 5. Это довольно просто, если знать один секрет. Итак, давайте разбираться, как быстро разделить число на 5?

Деление таких чисел как 20, 45 или 35, а также других жителей таблицы умножения рассматривать не будем. Они делятся на 5 в уме молниеносно. Конечно, при условии твердого знания этой самой таблицы.

Мы замахнемся на что-нибудь посложнее. Нам бы чего побольше, покрупнее! Давайте возьмем такие:

• 185
• 380
• 267
• 1034

и попробуем их разделить.

И сразу вопрос. Скажите, что проще, умножить на 2 или разделить на 5? Конечно же, умножить на 2. Этим мы и воспользуемся.

Приступим.

Займемся числом 185. И прежде чем приступать к делению, умножим его на 2.

185 * 2 = 370

И что нам это дает? Да практически готовый ответ! Нужно просто отделить запятой крайнюю правую цифру полученного после умножения на 2 числа.

37,0

То есть наш результат 37.

185 : 5=37

Проверим себя с помощью калькулятора.

Получилось!

Тренируемся дальше, следующее на очереди 380. Действуем таким же способом.

380 * 2 = 760

76,0

380 : 5 = 76

Проверим.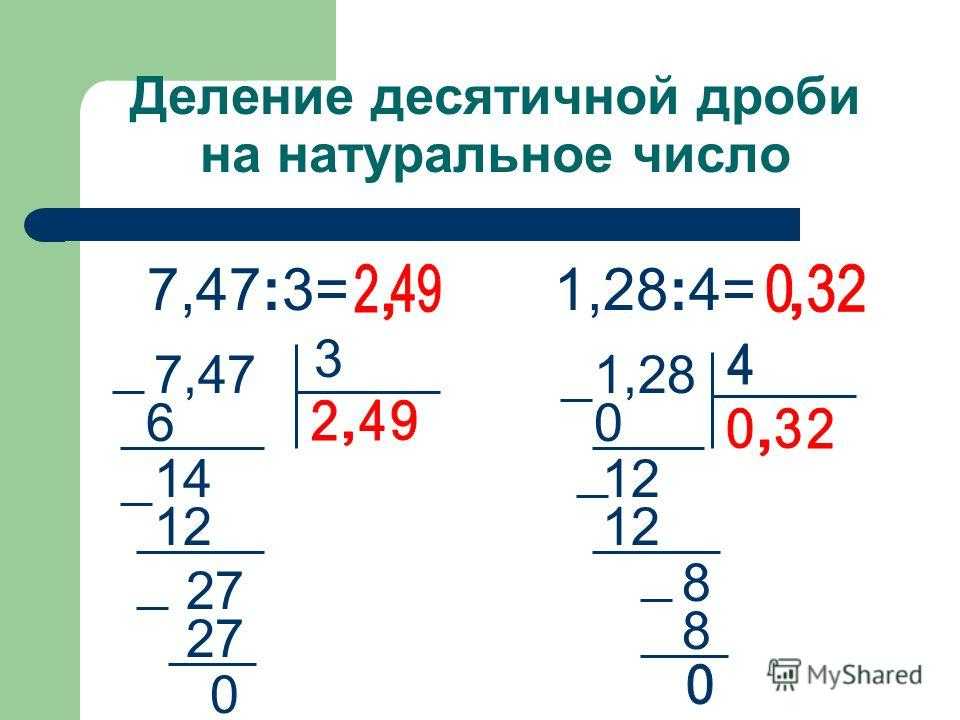

Верно!

На очереди 267. Попробуем.

267 * 2 = 534

53,4

267 : 5 = 53,4

Проверка!

Ура!

Ну и еще разок. 1034

1034 * 2 = 2068

206,8

1034 : 5 = 206,8

Ответственный момент! Проверим себя.

Все верно!

Работает способ! Нужно только тренироваться и тогда делить на пять вы будете ну очень быстро, что несомненно удивит окружающих. Предлагаю начать тренировку прямо сейчас.

Ниже вы видите примеры. Попробуйте их решить в уме. А чтобы проверить себя просто нажмите на картинку, и она покажет вам правильный ответ.

Ну как? Получилось? Молодцы!

«ШколаЛа» готова открыть вам и другие тайны обучения, так что подпишитесь на новости блога, чтобы не пропустить секретную информацию.

Не ленитесь, развивайтесь!

Евгения Климкович.

Понравилась статья? Поделись с друзьями:

Будь в курсе школьных событий!

Подпишись на новости блога!
Раз в неделю получай анонсы свежих статей на почту!

Нажимая на кнопку я даю согласие на обработку персональных данных и принимаю политику конфиденциальности.

Как быстро разделить число на 5?

Говорят: «Математика – гимнастика ума». Воистину, верные слова. Вычисления, производимые в уме, без калькулятора, карандаша и других «подручных инструментов», прекрасно развивают мозг. Кроме того, вы приобретаете уверенность в том, что в случае непредвиденных обстоятельств, спокойно обойдетесь собственными силами.

Еще несколько десятков лет назад в школах был такой предмет – «Устный счет», на занятиях школьники учились вычислять в уме – умножать, делить, складывать и вычитать числа. Из собственного опыта все мы знаем, что делить в уме намного сложнее, чем, например, умножать. Для того чтобы делить устно, нужно знать методику сокращенного деления и, естественно, таблицу умножения. Например, есть способ, который поможет вашему ребенку научиться быстро делить на 5.

Как это делается?

Метод быстрого деления на 5 очень прост. Естественно, он подразумевает, что ребенок таблицу умножения помнит «на зубок». Для примера мы не будем брать числа, которые в таблице умножения есть, и ваш ученик их хорошо помнит. Возьмем что-то более сложное. Например:

• 165
• 238
• 482
• 1026

Как мы помним, умножать легче, чем делить. А умножать на 2 – под силу практически всем школьникам. Так вот, чтобы быстро разделить любое число на 5, его нужно сначала умножить на 2! То, что получится в результате умножения, является почти ответом на вопрос: «Сколько будет, если разделить число на 5?» Только нужно в числе произведения последнюю цифру отделить запятой.

Проверим?

Берем число 165, умножаем его на 2, в результате получаем 330. Отделяем в этом числе последнюю цифру, то есть ноль, и получаем число 33. Именно это число и является результатом деления числа 165 на 5. Вот так просто, можете проверить на калькуляторе.

Продолжаем.

• 238х2 = 476.

47,6

238:5 = 47,6.

• 482х2 = 964.

96,4

482:5 = 96,4.

• 1026х2 = 2052.

205,2

1026:5 = 205,2.

Просто, как все гениальное.

И еще одно. Если уже мы говорим об устном счете, то для таких вычислений нужно тренировать память: это необходимо, чтобы удерживать в голове все расчеты.

Кстати, если у вашего школьника хорошо развита зрительная память, он может попробовать мысленно делить «в столбик». Этот метод не такой «скоростной», как предыдущий, но как вариант может использоваться.

Улучшить навыки счета поможет IQКлуб

Развить навыки счета, улучшить память, внимание, мышление, расширить кругозор вашего ребенка поможет интернет-сервис IQКлуб. Команда профессионалов, в которую вошли ученые, программисты, дизайнеры, педагоги, психологи, разработали специальные, очень увлекательные игры для детей. С учетом их возраста рассчитана нагрузка в обучающих программах.

Разработчики игр позаботились о том, чтобы они не содержали рекламы и платного контента. Интерактивное обучение, без сомнения, заинтересует современного ребенка. Его досуг будет интересным и, главное, полезным. А родители смогут контролировать процесс обучения в режиме онлайн.

Как же воспользоваться услугами сервиса IQКлуб?

1. Зарегистрируйтесь в системе.
2. Ваш ребенок проходит несложный, но занимательный тест.
3. Специальный алгоритм оценивает способности вашего малыша.
4. Для вашего ребенка формируется индивидуальная программа обучения.

Все! Заниматься можно в любом месте, где есть доступ к сети Интернет. Развивающие игры на сайте предназначены для детей от 3 до 14 лет. 13 тысяч родителей уже сотрудничают с новым интернет-сервисом IQКлуб, который имеет в своем арсенале более 90 полезных игр.

Калькулятор времени | Сложение, вычитание, умножение, деление Время

Базовый калькулятор

Поделись этим калькулятором и страницей

Калькулятор Используйте

Калькулятор времени для сложения, вычитания, умножения и деления времени в днях, часах, минутах и ​​секундах.

Калькулятор может складывать и вычитать отрезки времени или умножать и делить время на число или десятичную дробь. Ответы включают эквивалентное время в днях, часах, минутах или секундах.

Как рассчитать время

Ниже объясняется, как выполнять математические операции со временем. См. примеры сложения, вычитания, умножения и деления отрезков времени.

Как складывать время

Складывать дни, часы, минуты и секунды от наименьшей единицы времени к наибольшей.

1. Добавить секунды
2. Если общее количество секунд больше 59, вычтите 60 из секунд и перенесите 1 в минуты
3. Добавьте минуты, включая все перенесенные из расчета секунд
4. Если общее количество минут больше 59, вычтите 60 из минут и перенесите 1 в часы
5. Добавьте часы, включая перенесенные из расчета минут
6. Если общее количество часов больше 24, вычтите 24 из часов и перенесите 1 в дни
7. Добавьте дни, включая любые перенесенные из расчета часов

Добавление времени Пример задачи

Добавить 2 дня 21 часа 45 минут 39 секунд до 5 дней 10 часов 45 минут 22 секунды

2 дня

21 часа

45 минут

39 Seconds

& Plus;

5 дней

10 часов

45 минут

22 секунды

• 39секунды + 22 секунды = 61 секунда

 

2 дня

21 час

45 минут

39 секунд

+плюс;

5 дней

10 часов

45 минут

22 секунды

=

61 секунда

• 61 секунда — 60 = 1 секунда, перенести 1 в минуты
• 1 минута + 45 минут + 45 минут = 91 минута

перенос

1 минута

 

2 дня

21 час

45 минут

39 секунд

+ плюс;

5 дней

10 часов

45 минут

22 секунды

=

91 минута

1 секунда

• 91 минута — 60 = 31 минута, перевести 1 в часы
• 1 час + 21 час + 10 часов = 32 часа

перенос

1 час

1 минута

 

2 дня

21 час

45 минут

39 секунд

3 9;

5 дней

10 часов

45 минут

22 секунды

=

32 часа

31 минута

1 секунда

• 32 часа — 24 = 8 часов, перенос 1 на дни
• 1 день + 2 дня + 5 дней = 8 дней

Перенос

1 день

1 час

1 минута

2 Дни

21 часа

45 минут

39 секунд

& Plus;

5 дней

10 часов

45 минут

22 секунды

=

8 дней

8 часов

31 минута

1 секунда

• Завершено Добавление времени Математическая задача

 

2 дня

21 час

45 минут

39 секунд

+плюс;

5 дней

10 часов

45 минут

22 секунды

=

8 дней

8 часов

31 минута

1 секунда

Как вычесть время

Вычитание дней, часов, минут и секунд от наименьшей единицы времени к наибольшей.

1. Вычесть секунды
2. Если секунды, которые вы вычитаете, больше верхнего числа, заимствуйте 1 минуту из первых минут и добавьте 60 к первым секундам. Затем вычтите.
3. Вычесть минуты
4. Если количество минут, которые вы вычитаете, превышает максимальное число, заимствуйте 1 час от максимального количества часов и добавьте 60 к максимальному количеству минут. Затем вычтите.
5. Вычесть часы
6. Если часы, которые вы вычитаете, больше, чем верхнее число, заимствуйте 1 день из верхних дней и добавьте 24 к верхним часам. Затем вычтите.
7. Вычесть дни

Обратите внимание, что в любом случае, когда вам необходимо заимствовать, если следующая по величине единица равна 0, то заимствование производится из 2-й по величине единицы. Так же, как и при длинном вычитании, берите взаймы со следующего по величине разряда.

Время вычитания Пример задачи

Вычесть 2 дня 21 час 56 минут 18 секунд из 5 дней 0 часов 10 минут 13 секунд

 

5 дней

0 часов

10 минут

13 секунд

−

2 дня

21 час

56 минут

18 секунд

• Вычесть секунды
• 13 секунд меньше 18 секунд, поэтому заимствуйте 1 из первых минут
• 1 минута = 60 секунд, поэтому добавьте 60 секунд к 13, чтобы получить 73
• 73 секунды — 18 секунд = 55 секунд

одолжить

1 минута

5 дней

0 часов

9 минут

73 секунды

—

2 дня

21 часа

56 минут

18 секунд

& Equals;

55 секунд

• Вычесть минуты
• 9 минут меньше 56 минут, поэтому заимствуйте 1 из часов
• Есть 0 часов, поэтому займите 1 из дней
• 1 день = 24 часа и 1 час = 60 минут, поэтому добавьте 24 к часам, затем заимствуйте 1 из часов, чтобы получить 23
• Добавьте 60 минут к 9, чтобы получить 69
• 69 минут — 56 минут = 13 минут

borrow

1 day

1 hour

1 minute

 

4 days

23 hours

69 minutes

73 seconds

−

2 days

21 hours

56 minutes

18 секунд

=

13 минут

55 секунд

• Вычесть часы
• 23 часа — 21 час = 2 часа

borrow

1 day

1 hour

1 minute

 

4 days

23 hours

69 minutes

73 seconds

−

2 days

21 hours

56 minutes

18 секунд

=

2 часа

13 минут

55 секунд

• Вычесть дни
• 4 дня — 2 дня = 2 дня

borrow

1 day

1 hour

1 minute

 

4 days

23 hours

69 minutes

73 seconds

−

2 days

21 hours

56 minutes

18 секунд

=

2 дня

2 часа

13 минут

55 секунд

• Математическая задача на вычитание времени

5 дней

0 часов

10 минут

13 секунд

—

2 дня

21 часа

56 минут

18 секунд

& Equals;

2 дня

2 часа

13 минут

55 секунд

Как умножить время

Умножить дни, часы, минуты и секунды на кратное число, работая от наименьшей единицы времени к наибольшей.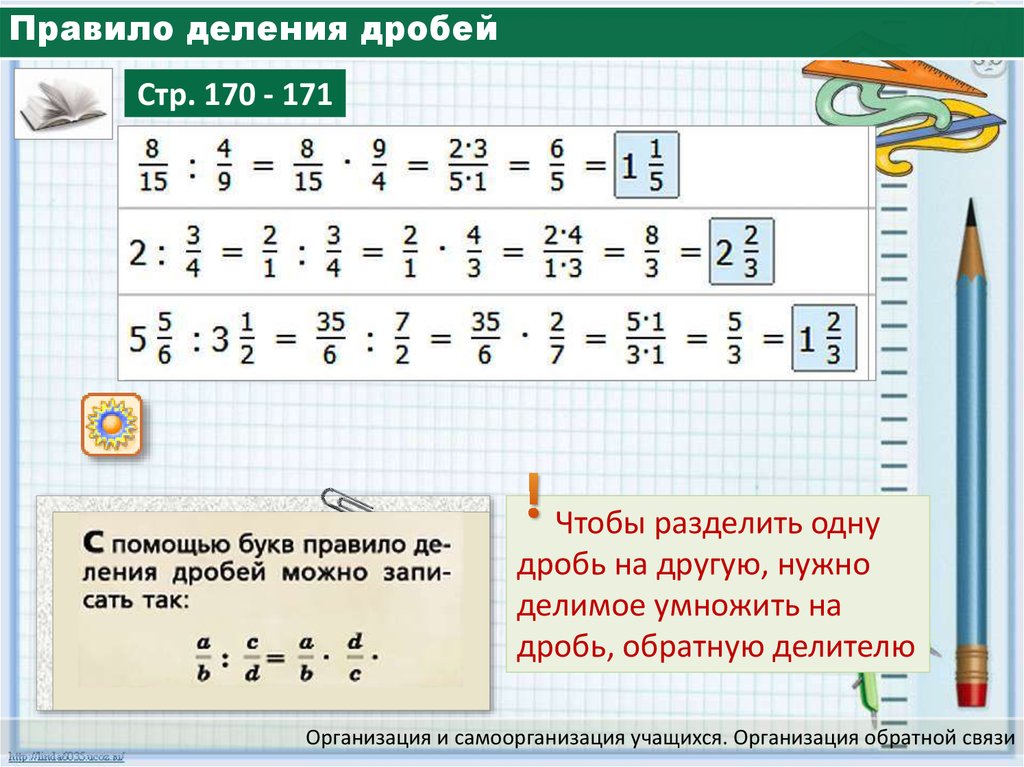

1. Умножить каждую единицу времени на кратное
2. Работая от наименьшей единицы времени к наибольшей, преобразовать лишние единицы времени в следующую более высокую единицу
3. Если секунды больше 59, разделите на 60, чтобы получить целое число и остаток
4. Сохраните остаток как общее количество секунд и добавьте целое число к минутам
5. Если минуты больше 59, разделите на 60, чтобы получить целое число и остаток
6. Сохраните остаток как общее количество минут и добавьте целое число к часам
7. Если часов больше 23, разделите на 24, чтобы получить целое число и остаток
8. Сохраните остаток как общее количество часов и добавьте целое число к дням

Умножение времени Пример задачи

Умножение 2 дня 10 часов 32 минуты 16 секунд на 5

2 дня

10 часов

32 минуты

16 секунд

• Умножение каждую единицу времени на 5

 

2 дня

10 часов

32 минуты

16 секунд

=

10 дней

50 часов

160 минут

80 секунд

• 80 секунд больше 59поэтому конвертируйте лишнее в минуты
• 80 разделить на 60 равно 1 с остатком 20
• Сохранить 20 секунд и перенести 1 на минуты
• 160 + 1 = 161 минута

перенос

1 минута

=

10 дней

50 часов

161 минута

20 секунд

• 161 минута больше 59, поэтому переведите лишнее в часы
• 161 разделить на 60 равно 2 с остатком 41
• Держите 41 секунду и переносите 2 на часы
• 50 + 2 = 52 часа

перенос

2 часа

1 минута

=

10 дней

52 часа

41 минута

20 секунд

• 52 часа больше 24, поэтому преобразуйте лишнее в дни
• 52 разделить на 24 равно 2 с остатком 4
• Хранить 4 часа и носить с собой 2 дня
• 10 + 2 = 12 дней

перенос

2 дня

2 часа

1 минута

=

12 дней

4 часа

41 минута

20 секунд

• Завершенная математическая задача на умножение времени

 

2 дня

10 часов

32 минуты

16 секунд

=

12 дней

4 часа

41 минута

20 секунд

Как разделить время

Разделите дни, часы, минуты и секунды на делитель, работая от наименьшей единицы времени к наибольшей.

1. Разделить каждую единицу времени на делитель
2. Затем, работая от наибольшей единицы времени к наименьшей, преобразуйте любые десятичные значения в целые числа, сдвигая десятичную сумму к меньшей единице времени
3. Если в днях есть десятичная дробь, сохраните целое число как общее количество дней и преобразуйте десятичную дробь в часы
4. Поскольку 1 день = 24 часа, умножьте десятичную дробь на 24 и прибавьте результат к часам
.
5. Если в часах есть десятичная дробь, сохраните целое число как общее количество часов и преобразуйте десятичную дробь в минуты
6. Поскольку 1 час = 60 минут, умножьте десятичную дробь на 60 и прибавьте результат к минутам
7. Если минуты имеют десятичную дробь, сохраните целое число как общее количество минут и преобразуйте десятичную дробь в секунды
8. Поскольку 1 минута = 60 секунд, умножьте десятичную дробь на 60 и прибавьте результат к секундам
9. Если в секундах есть десятичная дробь, вы обычно можете оставить это как окончательный ответ в зависимости от вашего приложения

Разделение времени Пример задачи

Разделить 4 дня 10 часов 13 минут 16 секунд на 4

 

4 дня

10 часов

13 минут

16 секунд

• Разделите каждую единицу времени на 4

 

4 дня

10 часов

13 минут

16 секунд

=

1 день

2,5 часа

3,25 минуты

4 секунды

• Работа от наименьшей единицы времени к наименьшей Преобразование любых десятичных значений в целые числа
• Часы — это не целое число, поэтому преобразуйте десятичную дробь в минуты
• 2,5 часа — это 2 часа плюс 0,5 часа
• Так как 1 час = 60 минут, 0,5 от 1 часа равняется 0,5 от 60 минут = 30 минут
• Хранить 2 часа и носить с собой 30 минут
• 30 + 3,25 = 33,25 минуты

перенос

30 минут

=

1 день

2 часа

33,25 минуты

4 секунды

• Минуты не являются целым числом, поэтому преобразуйте десятичную дробь в секунды
• 33,25 минуты равно 33 минутам плюс 0,25 минуты
• Так как 1 минута = 60 секунд, 0,25 от 1 минуты равняется 0,25 от 60 секунд = 15 секунд
• Сохранить 33 минуты и перенести 15 на секунды
• 15 + 4 = 19секунд

перенос

30 минут

15 секунд

=

1 день

2 часа

33 минуты

19 секунд

• Завершенная математическая задача на деление времени

 

4 дня

10 часов

13 минут

16 секунд

=

1 дней

2 часа

33 минуты

19 seconds

Time Conversion Units

1 day

24 hours

1,440 minutes

86,400 seconds

1 hour

60 minutes

3,600 seconds

1 minute

60 seconds

1 second

 

Цитируйте этот контент, страницу или калькулятор как:

Фьюри, Эдвард «Калькулятор времени | Сложение, вычитание, умножение, деление времени» на https://www. calculatorsoup.com/calculators/time/time-calculator.php из КалькуляторСуп, https://www.calculatorsoup.com — Онлайн калькуляторы

Подписаться на CalculatorSoup:

Как умножать и делить степени?

Показатель степени и степени используются для упрощения представления очень больших или очень малых чисел. Степень — это число или выражение, которое представляет собой многократное умножение одного и того же числа или множителя. Значение показателя степени — это количество раз, когда основание умножается само на себя.

Пример для показателей степени. Если нам нужно выразить 3 × 3 × 3 × 3 × 3 простым способом, мы можем записать это как 3 ⁵ , где 3 — основание, а 5 — показатель степени. Считается, что все выражение 3 ⁵ представляет мощность. Пример для степеней: 5 ³ = 5 в степени 3 = 5 × 5 × 5 = 125, 6 ⁴ = 6 в степени 4 = 6 × 6 × 6 × 6 = 1296. Показатель числа представляет сколько раз число умножалось само на себя. 3 умножается само на себя n раз, 3 × 3 × 3 × 3 × …n раз = 3 ^н . 3 ⁿ — сокращение от 3, возведенного в степень n. В результате показатели степени иногда называют степенью или, в некоторых случаях, индексами.

Общая форма показателей степени 

Показатель степени указывает, сколько раз нужно умножить число само на себя, чтобы получить желаемый результат. В результате любое число «b», возведенное в степень «p», может быть выражено как:

b ^p = {b × b × b × b × b × … × b} p раз

Здесь b — любое число, а p — натуральное число.

• Здесь b ^p также называется p ^th степенью b.
• «b» представляет основание, а «p» — показатель степени или степень.
• Здесь «b» умножается на «p» раз, и, таким образом, возведение в степень является упрощенным методом повторного умножения.

Некоторые основные правила экспонентов0860

Правило коэффициента ⇢ A ^N / A ^M = ^{N — M}

Правило мощности ⇢ ^N ) ^M = A ^N ) ^M = A ^N ) ^M = A ^N ) ^M = A ^N ) n = a ^n/m

Negative Exponent Rule ⇢ a ^-m = 1/a ^m

Zero Rule ⇢ a ⁰ = 1

One Rule ⇢ a ¹ = a

Как умножать и делить степени?

Решение:  

Экспоненты и степени используются для упрощения представления очень больших или очень малых чисел.

Деление показателей степени

Законы показателей степени упрощают процесс упрощения выражений. При делении показателей с одинаковым основанием основное правило — вычитание данных степеней. Это также известно как закон деления или свойство коэффициента экспоненты.

м ^{н ₁} ÷ м ^{н ₂} = m ^{n ₁} / m ^{n ₂} = m ^{(n ₁ – n ₂ )}

Первый случай: деление показателей степени с одинаковым основанием

Мы используем основное правило вычитания степеней для деления показателей степени с одинаковым основанием. Рассмотрим выражение m ^{n ₁} ÷ m ^{n ₂} , где «m» — общее основание, а показатели степени «n ₁ » и «n ₂ » — показатели степени. According to the ‘Quotient property of Exponents,’

m ^{n ₁} ÷ m ^{n ₂} = m ^{n ₁} / m ^{n ₂} = m ^{(n ₁ – n ₂ )}  

Пример: Разделить 3 ⁵ ÷ 3 ³  

Здесь, как мы видим, основания одинаковые, но разные мощности.

So the division law or Quotient law  : m ^{n ₁} ÷ m ^{n ₂}   =  m ^{n ₁} / m ^{n ₂} = м ^{(н ₁ – н ₂ )}  

Here, 3 ⁵ ÷ 3 ³

= 3 ⁵ /3 ³

= 3 ^(5-3)

= 3 ²   

Второй случай: деление показателей степени с разными основаниями

Мы применяем «степень свойства частного» для деления показателей степени с разными основаниями и одним и тем же показателем, который равен

(m/n) ^p = m ^p /n ^стр

Рассмотрим формулы m ^p ÷ n ^p , которые имеют разные основания, но один и тот же показатель степени.

Пример: Разделить: 15 ³ ÷ 3 ³ .

Это может быть решено с помощью «степени частного свойства»:

= 15 ³ ÷ 3 ³

= (15 / 3) ³

= 5 ³ .

Для умножения показателей степени 

Первый случай: при умножении показателей степени с одинаковым основанием 

В соответствии с этим правилом: степени или целые числа; это также известно как закон умножения показателей. При умножении двух выражений с одинаковым основанием мы можем использовать

m ^{n ₁} × m ^{n ₂} = m ^{(n ₁ + n ₂ )}  

Where m is the common base and n ₁ and n ₂ — это показатели степени.

Например, умножить 3 ³ × 3 ⁶ ?

Дано: 3 ³ × 3 ⁶  

Здесь основания одинаковы. Итак, мы будем использовать: m ^{n ₁} × m ^{n ₂} = m ^{(n ₁ + n ₂ )}  

Therefore, = 3 ⁽³⁺⁶⁾

= 3 ⁹

Второй случай: когда умножьте экспоненты с другими основаниями

, когда существует различные базы с теми же экспонентами, мы будем использовать формулу:

M ^{P9086. p = (m × n) p .}

Здесь m и n — разные основания, а p — показатель степени.

Пример: Умножьте 2 ³ × 4 ³

Данный: 2 ³ × 4 ³

ЗДЕСЬ. (m × n) ^p

= (2 × 4) ³

= 8 ³                        

Такими способами в разных случаях можно делить и умножать показатели степени.

Образец вопросов

Вопрос 1: Упростить или разделите 25 ⁴ /5 ⁴

Решение:

здесь. /n) ^p = m ^p /n ^p   

Therefore, = 25 ⁴ /5 ⁴

= (25/5) ⁴

= 5 ⁴

= 625

Вопрос 2: Найдите значение выражения, 15 ⁸ × 15 ³

Solution:

Given: 15 ⁸ × 15 ³

When multiplying two expressions with the same base but different exponent, 

m ^{n ₁} x M ^{N ₂} = M ^{(N ₁ + N + N + N + N + N + N + N . 0973 и n ₂ — показатели степени.}

, применив это правило,

мы получаем, = 15 ⁸ × 15 ³

= 15 ^{(8 + 3)}

= 15 ¹¹

4444444459 110860

44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444459. произведение (2x ³ y ⁵ ) и (3x ⁴ y ² )?

Решение:

Произведение  (2x ³ y ⁵ ) и (3x ⁴ y ² )

= (2x ³ y ⁵ ) × (3x ⁴ y ² )

= (2 × 3) × x ³ x ⁴ x x x x x x x x . ²                    

When multiplying two expressions with the same base, we can use m ^{n ₁} × m ^{n ₂} = m ^{(n ₁ + п ₂ )} 9Формула 0845, где m — общее основание, а n ₁ и n ₂ — показатели степени.

= 6x ³⁺⁴ × y ⁵⁺²

= 6x ⁷ y ⁷

Вопрос 4: Что представляет собой X ³ 2

. Вопрос 4: Что представляет собой x ³ 02

. 40855.

Решение:

Здесь дано: x ³ разделить на x ²  

здесь основания одинаковы, но показатели степени разные,

0859 n _¹ ÷ m ^{n ₂}    =  m ^{n ₁} / m ^{n ₂} = m ^{(n ₁ – n ₂ )}  

So write it as x ³ /x ²

= x ^{3 – 2}

= x ¹

= x

Вопрос 5: Оцените ³ × a ⁵ × A ^-6

Решение:

.