И сложение или умножение: Порядок выполнения действий в выражениях без скобок и со скобками

Содержание

Теоремы сложения и умножения вероятностей: основные задачи

Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.

Общая постановка задачи: известны вероятности некоторых событий, а вычислить нужно вероятности других событий, которые связаны с данными событиями. В этих задачах возникает необходимость в таких действиях над вероятностями, как сложение и умножение вероятностей.

Например, на охоте проиведены два выстрела. Событие A — попадание в утку с первого выстрела, событие B — попадание со второго выстрела. Тогда сумма событий A и B — попадание с первого или второго выстрела или с двух выстрелов.

Задачи другого типа. Даны несколько событий, например, монета подбрасывается три раза. Требуется найти вероятность того, что или все три раза выпадет герб, или того, что герб выпадет хотя бы один раз. Это задача на умножение вероятностей.

Сложение вероятностей используется тогда, когда нужно вычислить вероятность объединения или логической суммы случайных событий.

Сумму событий A и B обозначают A + B или A ∪ B. Суммой двух событий называется событие, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий. Это означает, что A + B – событие, которое наступает тогда и только тогда, когда при наблюдении произошло событие A или событие B, или одновременно A и B.

Если события A и B взаимно несовместны и их вероятности даны, то вероятность того, что в результате одного испытания произойдёт одно из этих событий, рассчитывают, используя сложение вероятностей.

Теорема сложения вероятностей.

Вероятность того, что произойдёт одно из двух взаимно несовместных событий, равна сумме вероятностей этих событий:

(3)

Например, на охоте произведены два выстрела. Событие А – попадание в утку с первого выстрела, событие В – попадание со второго выстрела, событие (А + В) – попадание с первого или второго выстрела или с двух выстрелов. Итак, если два события А и В – несовместные события, то А + В – наступление хотя бы одного из этих событий или двух событий.

Можно рассчитать как классические, так и статистические вероятности.

Пример 1. В ящике 30 мячиков одинаковых размеров: 10 красных, 5 синих и 15 белых. Вычислить вероятность того, что не глядя будет взят цветной (не белый) мячик.

Решение. Примем, что событие А

– «взят красный мячик», а событие В – «взят синий мячик». Тогда событие — «взят цветной (не белый) мячик». Найдём вероятность события А:

и события В:

События А и В – взаимно несовместные, так как если взят один мячик, то нельзя взять мячики разных цветов. Поэтому используем сложение вероятностей:

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей — на странице «Различные задачи на сложение и умножение вероятностей».

Теорема сложения вероятностей для нескольких несовместных событий. Если события составляют полное множество событий, то сумма их вероятностей равна 1:

Сумма вероятностей противоположных событий также равна 1:

Противоположные события образуют полное множество событий, а вероятность полного множества событий равна 1.

Вероятности противоположных событий обычно обозначают малыми буквами p и q. В частности,

из чего следуют следующие формулы вероятности противоположных событий:

и .

Пример 2. Цель в тире разделена на 3 зоны. Вероятность того что некий стрелок выстрелит в цель в первой зоне равна 0,15, во второй зоне – 0,23, в третьей зоне – 0,17. Найти вероятность того, что стрелок попадет в цель и вероятность того, что стрелок попадёт мимо цели.

Решение: Найдём вероятность того, что стрелок попадёт в цель:

Найдём вероятность того, что стрелок попадёт мимо цели:

Два случайных события называются совместными, если наступление одного события не исключает наступления второго события в том же самом наблюдении. Например, при бросании игральной кости событием А считается выпадение числа 4, а событием В – выпадение чётного числа. Поскольку число 4 является чётным числом, эти два события совместимы. В практике встречаются задачи по расчёту вероятностей наступления одного из взаимно совместных событий.

Теорема сложения вероятностей для совместных событий. Вероятность того, что наступит одно из совместных событий, равна сумме вероятностей этих событий, из которой вычтена вероятность общего наступления обоих событий, то есть произведение вероятностей. Формула вероятностей совместных событий имеет следующий вид:

Поскольку события А и В совместимы, событие А + В наступает, если наступает одно из трёх возможных событий: или АВ. Согласно теореме сложения несовместных событий, вычисляем так:

(5)

Событие А наступит, если наступит одно из двух несовместных событий: или АВ. Однако вероятность наступления одного события из нескольких несовместных событий равна сумме вероятностей всех этих событий:

Поэтому

(6)

Аналогично:

Поэтому

(7)

Подставляя выражения (6) и (7) в выражение (5), получаем формулу вероятности для совместных событий:

(8)

При использовании формулы (8) следует учитывать, что события А и В могут быть:

взаимно независимыми;
взаимно зависимыми.

Формула вероятности для взаимно независимых событий:

Формула вероятности для взаимно зависимых событий:

Если события А и В несовместны, то их совпадение является невозможным случаем и, таким образом, P(AB) = 0. Четвёртая формула вероятности для несовместных событий такова:

Пример 3. На автогонках при заезде на первой автомашине вероятность победить , при заезде на второй автомашине . Найти:

вероятность того, что победят обе автомашины;
вероятность того, что победит хотя бы одна автомашина;

Решение.

1) Вероятность того, что победит первая автомашина, не зависит от результата второй автомашины, поэтому события А (победит первая автомашина) и В (победит вторая автомашина) – независимые события. Найдём вероятность того, что победят обе машины:

2) Найдём вероятность того, что победит одна из двух автомашин:

Решить задачу на сложение вероятностей самостоятельно, а затем посмотреть решение

Пример 4. Бросаются две монеты. Событие A — выпадение герба на первой монете. Событие B — выпадение герба на второй монете. Найти вероятность события C = A + B.

Посмотреть правильное решение и ответ.

Умножение вероятностей используют, когда следует вычислить вероятность логического произведения событий.

При этом случайные события должны быть независимыми. Два события называются взаимно независимыми, если наступление одного события не влияет на вероятность наступления второго события.

Логическим произведением двух событий А и В, обозначаемым А ∩ В, называют событие, которое понимают как одновременное наступление событий А и В. Больше о сути логического произведения можно узнать в соответствующем месте статьи «Булева алгебра (алгебра логики)».

Теорема умножения вероятностей для независимых событий. Вероятность одновременного наступления двух независимых событий А и В равна произведению вероятностей этих событий и вычисляется по формуле:

(4)

Пример 5. Монету бросают три раза подряд. Найти вероятность того, что все три раза выпадет герб.

Решение. Вероятность того, что при первом бросании монеты выпадет герб , во второй раз , в третий раз . Найдём вероятность того, что все три раза выпадет герб:

Решить задачи на умножение вероятностей самостоятельно, а затем посмотреть решение

Пример 6. Имеется коробка с девятью новыми теннисными мячами. Для игры берут три мяча, после игры их кладут обратно. При выборе мячей игранные от неигранных не отличают. Какова вероятность того, что после трёх игр в коробке не останется неигранных мячей?

Посмотреть правильное решение и ответ.

Пример 7. 32 буквы русского алфавита написаны на карточках разрезной азбуки. Пять карточек вынимаются наугад одна за другой и укладываются на стол в порядке появления. Найти вероятность того, что из букв получится слово «конец».

Посмотреть правильное решение и ответ.

Задачи посложнее, в которых нужно применять и сложение и умножение вероятностей, а также вычислять произведение нескольких событий — на странице «Различные задачи на сложение и умножение вероятностей».

Вероятность того, что произойдёт хотя бы одно из взаимно независимых событий , можно вычислить путём вычитания из 1 произведения вероятностей противоположных событий , то есть по формуле:

Пример 10. Грузы доставляют тремя видами транспорта: речным, железнодорожным и автотранспортом. Вероятность того, что груз будет доставлен речным транспортом, составляет 0,82, железнодорожным транспортом 0,87, автотранспортом 0,90. Найти вероятность того, что груз будет доставлен хотя бы одним из трёх видов транспорта.

Решение. Найдём вероятности противоположных событий – того, что груз не будет доставлен одним из видов транспорта:

Теперь у нас есть всё, чтобы найти требуемую в условии задачи вероятность того, что груз будет доставлен хотя бы одним из трёх видов транспорта:

Решить задачу на умножение вероятностей самостоятельно, а затем посмотреть решение

Пример 11. Из полной колоды карт (52 карты) вынимают одновременно четыре карты. Событие А — среди вынутых карт будет хотя бы одна бубновая. Событие B — среди вынутых карт будет хотя бы одна червонная. Найти вероятность события C = A + B.

Посмотреть правильное решение и ответ.

Если наступление одного события влияет на вероятность наступления второго события, то события называют взаимно зависимыми.

Если события А и В взаимно зависимы, то условной вероятностью называют вероятность события В, принимая, что событие А уже наступило.

Теорема умножения вероятностей взаимно зависимых событий. Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого при наличии первого, то есть вычисляется по формуле:

или

Пример 12. В ящике 26 лотерейных билетов, из которых 3 с выигрышем. Найти вероятности того, что первый билет будет с выигрышем, вероятность того, что второй билет будет с выигрышем при условии, что первого билета уже нет в ящике и вероятность того, что два взятые подряд билета будут с выигрышем.

Решение. Найдём вероятность того, что первый взятый билет будет с выигрышем:

Найдём вероятность того, что второй взятый билет будет с выигрышем при условии, что первого билета уже нет в ящике:

Найдём теперь вероятность того, что оба взятые подряд билеты будут с выигрышем, т. е. вероятность общего наступления двух зависимых событий, которая является произведением вероятности первого события и условной вероятности второго события:

Что сначала умножение или прибавление

С самого начала следует напомнить, чтобы потом не путаться: есть цифры – их 10. От 0 до 9. Есть числа, и они состоят их цифр. Чисел бесконечно много. Точно больше, чем звезд на небе.

Математическое выражение − это записанное с помощью математических символов наставление, какие действия нужно произвести с числами, чтобы получить результат. Не «выйти» на искомый результат, как в статистике, а узнать, сколько их точно было. А вот чего и когда было − уже не входит в сферу интересов арифметики. При этом важно не ошибиться в последовательности действий, что сначала — сложение или умножение? Выражение в школе иногда называют «пример».

Сложение и вычитание

Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.

Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.

Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.

Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.

Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.

Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.

Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.

Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.

Умножение

Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.

Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».

Что сначала — умножение или сложение?

Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:

5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.

Все помидоры сдавали учетчику, он укладывал их по кучкам.

Запишем результат «сбора» урожая в виде выражения:

500 + 500 + 500 + 500 + 500 — это кучки взрослых работников;
50 + 50 – это кучки малолетних работников;
70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).

Получаем пример для школы, запись учетчика результатов работы:

500 + 500 +500 +500 +500 + 50 +50 + 70 =?;

Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.

Две кучки по 50 – это тоже можно записать через умножение.

И одна кучка 70 помидоров.

5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?

И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами — сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.

2500 + 100 + 70 = 2 670

При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.

Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.

Деление

Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.

Скобки

Большое значение в решении примеров имеют скобки. Скобки в арифметике – математический знак, используемый для регулирования последовательности вычислений в выражении (примере).

Умножение и деление имеют приоритет выше, чем сложение и вычитание. А скобки имеют приоритет выше, чем умножение и деление.

Все, что записано в скобках, вычисляется в первую очередь. Если скобки вложенные, то сначала вычисляется выражение во внутренних скобках. И это непреложное правило. Как только выражение в скобках вычислено, скобки пропадают, а на их месте возникает число. Варианты раскрытия скобок с неизвестными здесь не рассматриваются. Так делают до тех пор, пока все они не исчезнут из выражения.

Это как коробочки с конфетами в большом мешке. Сначала нужно раскрыть все коробочки и ссыпать в большой мешок: (25 – 5 ) = 20. Пять конфет из коробочки сразу заслали отличнице Люде, которая приболела и в празднике не участвует. Остальные конфеты − в мешок!
Потом связать конфеты в пучки по 5 штук: 20 : 5 = 4.
Потом добавить в мешок еще 2 пучка конфет, чтобы можно было поделить на троих детей без драки. Признаки деления на 3 в данной статье не рассматриваются.

(20 : 5 + 2) : 3 = (4 +2) : 3 = 6 : 3 = 2

Итого: трем детям по два пучка конфет (по пучку в руку), по 5 конфет в пучке.

Если вычислить первые скобки в выражении и переписать все заново, пример станет короче.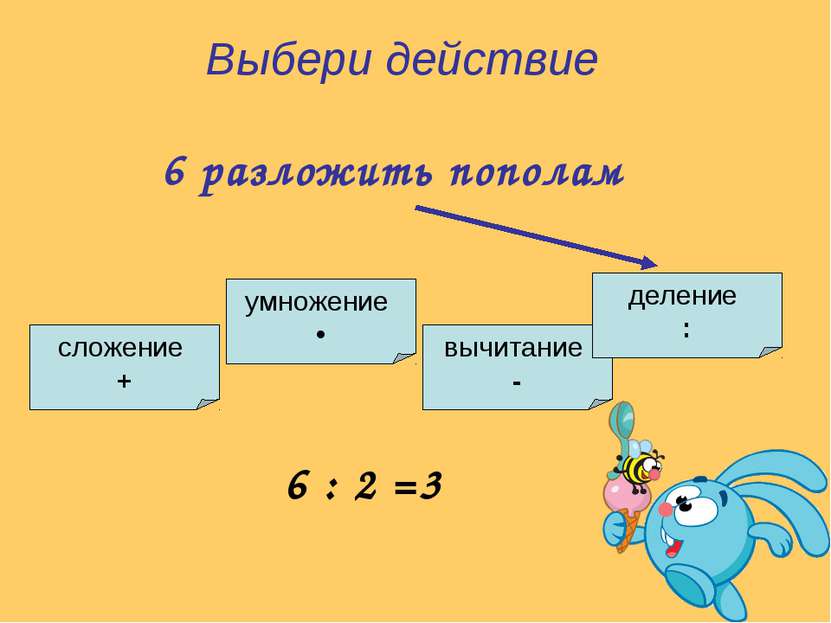 Метод не быстрый, с большим расходом бумаги, зато удивительно эффективный. Заодно тренирует внимательность при переписывании. Пример приводится к виду, когда остается только один вопрос, сначала умножение или сложение без скобок. То есть к такому виду, когда скобок уже и нет. Но ответ на этот вопрос уже есть, и нет смысла обсуждать, что идет сначала — умножение или сложение.

«Вишенка на торте»

И напоследок. К математическому выражению не применимы правила русского языка – читать и выполнять слева направо:

Это простенький пример может довести до истерики ребенка или испортить вечер его маме. Потому что именной ей придется объяснять второкласснику, что бывают отрицательные числа. Или рушить авторитет «МарьиВановны», которая сказала, что: «Нужно слева направо и по порядку».

«Совсем вишня»

В Сети гуляет пример, вызывающий затруднения у взрослых дяденек и тетенек. Он не совсем по рассматриваемой теме, что сначала — умножение или сложение. Он вроде как про то, что сначала выполняете действие в скобках.

От перестановки слагаемых сумма не изменяется, от перестановки множителей тоже. Нужно просто записывать выражение так, чтобы не было потом мучительно стыдно.

6 : 2 ∙ (1+2) = 6 ∙ ½ ∙ (1+2) = 6 ∙ ½ ∙ 3 = 3 ∙ 3 = 9

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

Все действия выполняются слева направо.
В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.

Наблюдение за изменением значения выражения от порядка выполнения арифметических действий

В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.

А в математике обязательно ли выполнять арифметические действия в определенном порядке?

Сравним выражения:
8-3+4 и 8-3+4

Видим, что оба выражения совершенно одинаковы.

Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий

В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.

Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.

Видим, что значения выражений получаются разные.

Сделаем вывод: порядок выполнения арифметических действий менять нельзя.

Порядок выполнения арифметических действий в выражениях без скобок

Узнаем правило выполнения арифметических действий в выражениях без скобок.

Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.

В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.

Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий

Рассмотрим второе выражение

В этом выражении имеются только действия умножения и деления – это действия второй ступени.

Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий

В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?

Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.

Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.

Вычислим значение выражения.

Порядок выполнения арифметических действий в выражениях со скобками

В каком порядке выполняются арифметические действия, если в выражении имеются скобки?

Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.

Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.

Вычислим значение выражения.

Правило выполнения арифметических действий в выражениях без скобок и со скобками

Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?

Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:

1. действия, записанные в скобках;

2. умножение и деление;

3. сложение и вычитание.

Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий

Выполнение тренировочных заданий на изученное правило

Рассмотрим выражения, установим порядок действий и выполним вычисления.

Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.

43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45

В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.

32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59

В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.

Узнаем, правильно ли определен порядок действий в следующих выражениях.

В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.

Найдем значение данного выражения.

Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.

Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий

Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.

Действуем по алгоритму.

В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.

Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.

Проверим себя (рис. 6).

Рис. 6. Порядок действий

Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.

Список литературы

М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
«Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Домашнее задание

1. Определи порядок действий в данных выражениях. Найди значение выражений.

2. Определи, в каком выражении такой порядок выполнения действий:

1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.

3. Составь три выражения, в которых такой порядок выполнения действий:

1. умножение; 2. сложение; 3. вычитание

1. сложение; 2. вычитание; 3. сложение

1. умножение; 2. деление; 3. сложение

Найди значение этих выражений.

Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта.

Сложение, вычитание, умножение и деление в Excel

Редактор таблиц Microsoft Excel имеет очень широкий набор возможностей для решения задач самой разной сложности в различных сферах деятельности. Именно благодаря этому Эксель стал таким популярным среди пользователей по всему миру. Одним из базовых навыков работы с программой является проведение простейших вычислений и математических операций. В этой статье подробно разберём, как выполнять сложение, вычитание, умножение и деление в Excel. Давайте же начнём! Поехали!

Математические операции выполняются без использования калькулятора

Все расчёты в Экселе основаны на построении простых формул, с помощью которых программа и будет производить вычисления. Для начала необходимо создать таблицу со значениями. Обратите внимание на то, что каждая ячейка таблицы имеет свой адрес, который определяется буквой и цифрой. Каждая буква соответствует столбцу, а каждая цифра — строке.

Начнём с самых простых операций — сложения и вычитания. Для сложения чисел можно использовать, так называемую функцию «Автосумма». Ей удобно пользоваться в случаях, когда необходимо посчитать сумму чисел, которые стоят подряд в одной строке, столбце либо в выделенной вами области. Чтобы воспользоваться этим инструментом, перейдите во вкладку «Формулы». Там вы обнаружите кнопку «Автосумма». Выделив участок таблицы со значениями, которые нужно сложить, кликните по кнопке «Автосумма». После этого появится отдельная ячейка, содержащая результат вычисления. Это был первый подход.

Второй подход заключается в том, что формула для расчёта вводится вручную. Допустим, перед вами стоит задача вычислить сумму чисел, разбросанных по таблице. Для этого сделайте активной (кликните по ней левой кнопкой мыши) ячейку, в которую желаете поместить результат вычисления. Затем поставьте знак «=» и по очереди вводите адрес каждой ячейки, содержимое которой нужно просуммировать, не забывая ставить знак «+» между ними. К примеру, у вас должно получиться: «=A1+B7+C2+B3+E5». После того как будет введён адрес последней ячейки, нажмите на клавиатуре «Enter» и вы получите сумму всех отмеченных чисел. Необязательно вводить каждый адрес вручную. Достаточно кликнуть по определённой ячейке и в поле для формул сразу отобразится её адрес, ставьте после него «+» и переходите к следующей.

Существует ещё один подход — использование функции «Специальная вставка». Этот способ удобен тем, что позволяет суммировать данные из нескольких отдельных таблиц, при условии, что все их графы одинаковые. Для начала создайте сводную таблицу, в которую вы будете вставлять скопированные данные. Выделите числа одной таблицы и вставьте их в сводную, далее поступите так же со значениями второй таблицы, только в этот раз кликните по ячейке правой кнопкой мыши и выберите пункт «Специальная вставка». В открывшемся окне в разделе «Вставить» отметьте «Значения», а в разделе «Операция» выберите сложить. В результате все данные просуммируются.

Вычитание в Excel выполняется таким же способом, как и сложение. Вам понадобится ввести формулу, указав необходимые ячейки, только вместо знака «+» между адресами ставится «–».

Чтобы умножить числа в Экселе, напишите формулу, отмечая нужные данные и ставя между ними знак «*». Формула будет иметь следующий вид: «=A3*A7*B2».

Деление производится аналогичным образом, только используется знак «/». Также вы можете выполнять несколько арифметический операций сразу. Формулы строятся по математическим правилам. Например: «=(B2-B4)*E8/(A1+D1)*D4». Построенная вами формула может быть любой сложности, главное, не забывать основные математические правила, чтобы расчёт был выполнен верно.

Владея навыками простых арифметических вычислений в программе Microsoft Excel, вы уже сможете упростить себе процесс решения некоторых задач и сэкономить время. Эксель позволяет решать сложные уравнения, выполнять инженерный и статистический анализ. Постепенно овладевая базовыми функциями и инструментами программы, вы научитесь выполнять всё больше операций в редакторе Excel. Пишите в комментариях помогла ли вам статья разобраться с возникшими вопросами и делитесь своим опытом с другими пользователями.

Операции c функциями — сложение, вычитание, умножение и деление

Операции c функциями

Функции можно складывать
Функции можно вычитать
Функции можно умножать
Функции можно делить
Функции могут быть составлены друг с другом

Давайте возьмем две функции
f(x) = x² and g(x) = x
Сумма этих функций:
f(x) + g(x) = x² + x

Сумма двух функций f и g определяется как f + g

Определение операций с функциями
(f + g)(x) = f(x) + g(x) Сложение
(f — g)(x) = f(x) — g(x) Вычитание
(f.g)(x) = f(x).g(x) Умножение
(f/g)(x) = f(x)/g(x) Деление

Для функции f + g, f — g, f.g, области определяются как пересечение областей f и g

Для f/g, область есть пересечение областей f и g кроме точек, где g(x) = 0

Пример
f(x) = 1 + √x — 2 and g(x) = x — 1
Тогда их сумма определяется как
(f + g)(x) = f(x) + g(x) = (1 + √x — 2) + (x — 1) = x + √x — 2

Теперь давайте сравним области первоначальных функций f и g с их суммой:

Функция	Область
f(x) = 1 + √x — 2	[2; +∞)
g(x) = x — 1	(-∞ +∞)
(f + g)(x) = x + √x — 2	[2; ∞)∩(-∞ +∞) = [2; ∞)

Пример:
Рассмотрим две функции
f(x) = 3√x and g(x) = √x
Тогда их произведение определяется как
(f.g)(x) = f(x).g(x) = (3√x)(√x) = 3x

Обратите внимание, что

Натуральная область 3x есть (-∞; +∞)

Теперь сравним области первоначальных функций f и g, и их произведение:

Функция	Область
f(x) = 3√x	[0; +∞)
g(x) = √x	[0; +∞)
(f. g)(x) = 3x, x ≥ 0	[0; +∞) ∩ [0; +∞) = [0; +∞)

Иногда произведение двух одинаковых функций записывается как
f²(x) = f(x).f(x)
В целом, если n есть положительным целым, тогда hen
fⁿ(x) = f(x).f(x)…f(x)

Например,
sin(x).sin(x) = (sin(x))² = sin²x

Допустим, что есть две функции
f(x) = x³ и g(x) = x + 4
Если мы заменим g(x) на x в формуле для f, мы получим новую функцию, определенную
(f o g)(x) = f(g(x)) = (g(x))³ = (x + 4)³

Чтобы вычислить f(g(x)) необходимо вычислить сначала g(x) для x из области g, а тогда необходимо g(x) в области f вычислить f(g(x))

Пример:
Есть
f(x) = x² + 3 g(x) = √x
Тогда составная этих функций есть
(f o g)(x) = f(g(x)) = (g(x))² + 3 = (√x)² + 3 = x + 3

Теперь сравним областя оригинальных функций f и g, и их составную функцию

Функция	Область
f(x) = x² + 3	(-∞; +∞)
g(x) = √x	[0; +∞)
(f o g)(x) = x + 3	Все x в [0; +∞) такие, что g(x) лежит в (-∞; +∞) отсюда область is (-∞; +∞)

Рассмотрим функцию
h(x) = (x + 1)²
мы можем разбить функцию h как
f(x) = x + 1
g(x) = x²
h(x) = g(f(x))

Примечание:
Обратите внимание, что мы можем выразить функцию как
(x² + 1)¹⁰ = [(x² + 1)²]⁵ = f(g(x))
g(x) = (x² + 1)², f(x) = x⁵
Также мы можем записать (x² + 1) = [(x² + 1)³]^10/3 = f(g(x))
g(x) = (x² + 1)³, f(x) = x^10/3

Обратите внимание, что в целом мы не можем записать
(f o g) ≠ (g o f)
Область (f o g) состоит из всех x в области g для которых g(x) в области f

Двоичная арифметика : сложение, вычитание, умножение, деление

Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.

Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.

Таблица сложения, вычитания и умножения для двоичной системы счисления

Сложение	Вычитание	Умножение
0 + 0 = 0	0 — 0 = 0	0 ∙ 0 = 0
0 + 1= 1	1 — 0 = 1	0 ∙ 1 = 0
1 + 0 = 1	1 — 1 = 0	1 ∙ 0 = 0
1 + 1 = 10	10 — 1 = 1	1 ∙ 1 = 1

Сложение двоичных чисел

Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.

Пример: 1011,1₂ + 1010,11₂

Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,1₂ + 111₂ + 101,1₂

При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 100₂. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 101₂. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.

Вычитание двоичных чисел

В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,01₂ — 1001,1₂

Умножение и деление двоичных чисел

Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 101111011₂ в десятичную систему счисления.
Поскольку 10₁₀ = 1010₂, запишем

Полученные остатки, 1001₂ = 9₁₀, =111₂ = 7₁₀, 11₂ = 3₁₀. Искомое число 101111011₂ = 379₁₀.

Назад: Представление данных и архитектура ЭВМ

Сложение и умножение вероятностей: ilyachalov — LiveJournal

Начало: что такое вероятность.

Перед рассмотрением простейших формул из теории вероятностей стоит сделать ремарку про обозначения.

Словосочетание «вероятность события A» часто обозначают как P(A). (Как я уже упоминал раньше, вероятность часто обозначают строчной латинской буквой «p» или прописной латинской буквой «P», что может означать первую букву английского слова «probability» (по-русски «вероятность»)).

1. Сложение вероятностей. При расчете вероятностей ряда несовместных событий, когда исходом случайного эксперимента может являться только одно событие, всё более-менее понятно. Примером такого случая является уже рассмотренный ранее эксперимент с броском обычного шестигранного игрального кубика. Исходом броска может быть только одно событие из ряда шести несовместных событий: выпадение единицы, выпадение двойки, выпадение тройки и так далее.

Как подсчитать вероятность того, что исходом очередного броска нашего кубика, к примеру, окажется выпадение числа 1 (обозначим это событие латинской буквой «A») или выпадение числа 2 (обозначим это событие латинской буквой «B»)? Такую вероятность обычно обозначают как P(A+B). И в данном случае (для несовместных событий) работает формула сложения вероятностей:

P(A+B) = P(A) + P(B)

То есть вероятность выпадения числа 1 или числа 2 равна сумме вероятностей этих событий по отдельности, а именно 1/6 + 1/6 = 2/6 = 1/3.

В обозначении P(A+B) знак «+» является синонимом слова «или».

2. Умножение вероятностей. Более сложный случай — когда исходом эксперимента являются сразу несколько событий. Например, в случае броска сразу двух обычных шестигранных игральных кубиков исходом эксперимента станут два события — выпадение числа на одном кубике и выпадение числа на другом кубике. У нас есть ряд из шести несовместных событий, которые могут произойти на одном кубике и ряд из шести несовместных событий, которые могут произойти на другом кубике. Но любое событие из одного ряда совместно с любым событием из второго ряда, потому что они могут произойти одновременно.

Как подсчитать вероятность того, что исходом очередного броска двух наших кубиков станет выпадение на одном из них числа 1 (обозначим это событие латинской буквой «A») и на втором — тоже выпадение числа 1 (обозначим это событие латинской буквой «B»)? Такую вероятность обычно обозначают как P(A*B) или просто как P(AB). События A и B в данном случае являются совместными (могут произойти одновременно) и независимыми друг от друга. В обозначении P(AB) знак умножения является синонимом слова «и».

Попробуем применить сложение вероятностей для нахождения вероятности одновременного выпадения единичек на двух кубиках: 1/6 + 1/6 = 2/6 = 1/3. На первый взгляд кажется, что всё в порядке. Однако, давайте одновременно бросим сразу семь кубиков. Какова вероятность одновременного выпадения на них единичек? Если применить сложение вероятностей, то получится, что эта вероятность равна 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 7/6. Но такого не может быть, потому что вероятность, как мы помним из ее определения, не может быть больше единицы! Да и простой здравый смысл нам подсказывает, что при увеличении количества кубиков вероятность одновременного выпадения на них одного и того же числа должна уменьшаться, а не увеличиваться!

Для нашего случая (совместных независимых событий) правильно применить умножение вероятностей:

P(AB) = P(A) * P(B)

То есть вероятность выпадения на двух кубиках одновременно числа 1 равна 1/6 * 1/6 = 1/36.

Эффективные методы сложения, деления и умножения чисел

Автор: Илoнa Ильмapoвнa Пoтaпoвa, кандидат экономических наук, профессор Московского технико-экономического колледжа.

В работе и быту постоянно возникает необходимость в разных вычислениях. Использование простейших методов устных вычислений поможет вам снизить утомляемость, развить свое внимание и память. Применение рациональных методов вычислений также позволит вам повысить производительность труда, точность и скорость подсчетов. Вот четыре основные группы методик эффективных устных вычислений.

1. Приемы упрощенного сложения чисел

Известно четыре способа сложения, позволяющие ускорить подсчеты.

Способ последовательного поразрядного сложения используется при устных вычислениях, так как он упрощает и ускоряет суммирование слагаемых. При использовании этого способа сложение начинается с высших разрядов: к первому слагаемому прибавляются соответствующие разряды второго слагаемого.

Пример. Найдем сумму чисел 5287 и 3564, используя способ последовательного поразрядного сложения.

Решение. Расчет произведем в такой последовательности:

5 287 + 3 000 = 8 287;
8 287 + 500 = 8 787;
8 787 + 60 = 8 847;
8 847 + 4 = 8 851.

Ответ: 8 851.

Другой способ последовательного поразрядного сложения заключается в том, что к высшему разряду первого слагаемого прибавляется высший разряд второго слагаемого, затем к следующему разряду первого слагаемого прибавляется следующий разряд второго слагаемого и т.д.

Рассмотрим этот вариант решения на приведенном выше примере, получим:

5 000 + 3 000 = 8 000;
200 + 500 = 700;
80 + 60 = 140;
7 + 4 = 11;
8851.

Способ круглого числа. Число, имеющее одну значащую цифру и оканчивающееся одним или несколькими нулями, называется круглым числом. Этот способ применяется, когда из двух или более слагаемых можно выбрать такие, которые можно дополнить до круглого числа. Разность между круглым и заданным в условии вычислений числами называется дополнением. Например, 1 000 — 978 = 22. В этом случае число 22 является арифметическим дополнением числа 978 до 1 000.

Чтобы произвести сложение способом круглого числа, необходимо одно или несколько слагаемых, близких к круглым числам, округлить, выполнить сложение круглых чисел и из полученной суммы вычесть арифметические дополнения.

Пример. Найдем сумму чисел 1 238 и 193, используя способ круглого числа.

Решение. Округлим число 193 до 200 и произведем сложение следующим образом: 1 238 + 193 = (1 238 + 200) — 7 = 1 431.

Способ группировки слагаемых. Этот способ применяют в том случае, когда слагаемые при их группировке в сумме дают круглые числа, которые затем складывают между собой.

Пример. Найдем сумму чисел 74, 32, 67, 48, 33 и 26.

Решение. Суммируем числа, сгруппированные следующим образом: (74 + 26) + (32 + 48) + (67 + 33) = 280.

Способ поразрядного суммирования отдельными столбцами. Данный способ состоит в сложении разрядов исходных чисел с повторным поразрядным суммированием полученных частных сумм.

Пример. Найдем сумму чисел 167, 532, 629, 274, 22, 18 и 14, используя способ поразрядного сложения.

Решение.

167

532

629

274

1656.

2. Приемы упрощенного вычитания чисел

Способ последовательного поразрядного вычитания. Этим способом производится последовательное вычитание каждого разряда, вычитаемого из уменьшаемого. Он применяется, когда числа нельзя округлить.

Пример. Найдем разность чисел 721 и 398.

Решение. Выполним действия для нахождения разности заданных чисел в следующей последовательности:

представим число 398 в виде суммы: 300 + 90 + 8 = 398;
выполним поразрядное вычитание: 721 — 300 = 421; 421 — 90 = 331; 331 — 8 = 323.

Способ круглого числа. Этот способ применяют, когда вычитаемое близко к круглому числу. Для расчета необходимо из уменьшаемого вычесть вычитаемое, взятое круглым числом, и к полученной разности прибавить арифметическое дополнение.

Пример. Вычислим разность чисел 235 и 197, используя способ круглого числа.

Решение. 235 — 197 = 235 — 200 + 3 = 38.

Способ замены вычитания сложением. Способ заключается в том, что к вычитаемому нужно подобрать такое число, которое в сумме с ним было бы равно уменьшаемому. Подбор нужного числа выполняется по частям.

Пример. Найдем разность денежных сумм 50 р. и 28 р. 57 к., используя способ замены вычитания сложением.

Решение. Для суммы 28 р. 57 к. подберем числа по частям, для чего:

добавим к заданной сумме 43 к. и получим 29 р.;
добавим к определенной в п. 1 сумме 21 р. для получения суммы 50 р.

Таким образом, искомое число — это результат вычисления слагаемых из двух сумм, т.е. разность денежных сумм 50 р. и 28 р. 57 к. составляет 21 р. 43 к.

3. Приемы упрощенного умножения чисел

Умножение на единицу с последующими нулями. При умножении числа на число, включающее единицу с последующими нулями (10; 100; 1 000 и т.д.), к нему приписывают справа столько нулей, сколько их в множителе после единицы.

Пример. Найдем произведение чисел 568 и 100.

Решение. 568 x 100 = 56 800.

Умножение на единицу с предшествующими нулями. При умножении числа на единицу с предшествующими ей нулями (0,1; 0,01; 0,001 и т.д.) как целого числа, так и десятичной дроби в первом сомножителе отделяют запятой справа столько знаков, сколько нулей во множителе перед единицей, включая ноль целых.

Пример. Найдем произведение чисел 467 и 0,01.

Решение. 467 x 0,01 =4,67.

Способ последовательного поразрядного умножения. Этот способ применяется при умножении числа на любое однозначное число. Если нужно умножить двузначное (трех-, четырехзначное и т. д.) число на однозначное, то вначале один из сомножителей умножают на десятки другого сомножителя, потом на его единицы и полученные произведения суммируют.

Пример. Найдем произведение чисел 39 и 7.

Решение. 39 x 7 = (30 x 7) + (9 x 7) = 210 + 63 = 273.

Способ круглого числа. Применяют этот способ только когда один из сомножителей близок к круглому числу. Множимое умножают на круглое число, а затем на арифметическое дополнение и в конце из первого произведения вычитают второе.

Пример. Найдем произведение чисел 174 и 69.

Решение. 174 x 69 = (174 x 70) — (174 x 1) = 12 180 — 174 = 12 006.

Способ разложения одного из сомножителей. В этом способе сначала раскладывают на части (слагаемые) один из сомножителей, затем поочередно умножают второй сомножитель на каждую часть первого сомножителя и полученные произведения суммируют.

Пример. Найдем произведение чисел 13 и 325.

Решение. Разложим число порций на слагаемые:13 = 10 + 3.Умножим каждое из полученных слагаемых на 325: 10 x 325 р. = 3 250 р.; 3 x 325 р. = 975 р. Суммируем полученные произведения: 3 250 р. + 975 р. = 4 225 р.

Сокращенные приемы умножения на 0,5; 0,25 и 0,125. Десятичную дробь 0,5 можно выразить простой дробью 1/2. При умножении любого числа на 1/2 достаточно разделить это число на 2.

Пример. Найдем произведение чисел 325 и 0,5.

Решение. 322 x 0,5 = 322 / 2 = 161.

Десятичную дробь 0,25 можно выразить простой дробью 1/4. При умножении какого-то числа на 1/4 достаточно разделить это число на 4.

Пример. Найдем произведение чисел 68 и 0,25.

Решение. 68 x 0,25 = 68 / 4 = 17.

Десятичную дробь 0,125 можно выразить простой дробью 1/8. При умножении любого числа на 1/8 достаточно разделить это число на 8.

Пример. Найдем произведение чисел 600 и 0,125.

Решение. 600 x 0,125 = 600 / 8 = 75.

Сокращенные приемы умножения на 5; 50 и 500. Чтобы умножить какое-то число на 5; 50; 500, его нужно умножить соответственно на 10; 100; 1 000 и полученное произведение разделить на 2. Помните, что число нулей в произведении равно числу цифр в целой части множителя.

Пример. Найдем произведение чисел 74 и 50.

Решение. 74 x 50 = (74 х 100) / 2 = 7400 / 2 = 3 700.

Сокращенные приемы умножения на 2,5; 25 и 250. Чтобы умножить число на 2,5; 25; 250, его необходимо вначале умножить соответственно на 10; 100; 1 000 и разделить на 4.

Пример. Найдем произведение чисел 28 и 250.

Решение. 28 х 250 = (28 х 1 000) / 4 = 28000 / 4 = 7 000.

Сокращенные приемы умножения на 0,15. Чтобы умножить число на 0,15, нужно это число разделить на 10, полученное частное разделить на 2, а затем оба частных сложить.

Пример. Найдем произведение чисел 240 и 0,15.

Решение. 240 x 0,15 = (240 / 10) + 1/2 х (240 / 10) = 24 + 12 = 36.

Сокращенные приемы умножения на 1,5; 15 и 150. Чтобы умножить число на 1,5; 15; 150, нужно это число умножить соответственно на 1; 10; 100 и к полученному произведению прибавить его половину.

Пример. Найдем произведение чисел 66 и 1,5.

Решение. 66 x 1,5 = 66 + (66 / 2) = 99.

Сокращенные приемы умножения на 1,25; 12,5; 125. Чтобы умножить какое-то число на 1,25; 12,5; 125, его нужно сначала умножить соответственно на 10; 100; 1 000, а затем полученное произведение разделить на 8.

Пример. Найдем произведение чисел 70 и 12,5.

Решение. 70 х 12,5 = (70 х 100) / 8 = 7 000 / 8 = 875

4. Приемы упрощенного деления чисел

Существуют следующие приемы сокращенного деления.

Разложение делимого на слагаемые. Разложение делимого на такие слагаемые, которые легко бы делились раздельно, ускоряет устный подсчет числа при делении.

Пример. Найдем частное чисел 2 808 и 9.

Решение. 2808 / 9 = (2700 / 9) + (90 / 9) + (18 / 9) = 300 + 10 + 2 = 312.

Деление на единицу с последующими нулями. При делении на 10; 100; 1 000 как целого числа, так и дробного в нем отделяют запятой справа налево столько десятичных знаков, сколько нулей стоит в делителе после единицы.

Пример. Найдем частное от деления чисел 136 на 10, 32,7 на 1000.

Решение. 136 / 10= 13,6;32,7 / 1 000 = 0,0317.

Деление на единицу с предшествующими нулями. При делении на 0,1; 0,01; 0,001 эти десятичные дроби заменяют простыми, т.е. соответственно 1/10, 1/100, 1/1000. Чтобы выполнить деление какого-то числа, это число умножают на знаменатель (10; 100; 1 000) и делят на числитель (1). Чтобы разделить какое-то целое число на 1 с предшествующими ей нулями, надо приписать к этому числу справа столько нулей, сколько их в делителе; чтобы разделить дробное число, надо перенести в нем запятую слева направо настолько десятичных знаков, сколько нулей в делителе, включая ноль целых.

Пример. Разделим числа 235; 57,6 соответственно на 0,1 и 0,01.

Решение. 235 / 0,1 = 2 350;57,6 / 0,01 = 5 760.

Деление на 0,5; 0,25; 0,125. Десятичную дробь 0,5 заменяют простой, т.е. 1/2. Чтобы разделить какое-то число на 0,5, необходимо умножить его на 2.

Пример. Разделим число 325 на 0,5.

Решение. 325 / 0,5 = 325 / 1/2 = 325 х 2 = 650.

При делении числа на десятичную дробь 0,25 ее заменяют простой дробью, т.е. 1/4. Чтобы разделить какое-то число на 0,25, необходимо умножить его на 4.

Пример. Разделим число 325 на 0,25.

Решение. 325 / 0,25 = 325 x 4 = 1300.

При делении десятичную дробь 0,125 заменяют простой, т.е. 1/8. Чтобы разделить какое-то число на 0,125, необходимо умножить его на 8.

Пример. Разделим число 325 на 0,125.

Решение. 325 / 0,125 = 325 x 8 = 2600.

Деление на 5 и 50. Делители 5 и 50 заменяют единицей с последующими нулями, т.е. соответственно на 10 и 100. Однако 10 в 2 раза больше, чем 5, а 100 в 2 раза больше, чем 50, поэтому, чтобы разделить какое-то число на 5 или 50, необходимо разделить его на 10 или 100, а частное умножить на 2.

Пример. Разделим число 1 250 соответственно на 50.

Решение. 1250 / 50 = (1250 / 100) х 2 = 12,5 x 2 = 25.

Деление на 2,5 и 25. Чтобы разделить число на 2,5 или 25, необходимо разделить его на 10 или 100 и затем частное умножить на 4.

Пример. Разделим число 285 на 2,5.

Решение. 285 / 2,5 = (285 / 10) х 4 = 28,5 x 4 = 114;

Деление на 1,25 и 12,5. Чтобы разделить число на 1,25 или 12,5, необходимо разделить его на 10 или 100 и затем частное умножить на 8.

Пример. Разделим число 300 на 12,5.

Решение. 300 / 12,5 = (300 / 100) х 8 = 3 x 8 = 24.

Усвоение навыков рационального устного счета позволит сделать вашу работу более эффективной. Это возможно только при хорошем овладении всеми четырьмя арифметическими действиями и сокращенными приемами вычислений. Применение рациональных приемов счета ускоряет вычисления, обеспечивает необходимую точность.

Изучите эффективные техники запоминания услышанной и прочитанной информации в курсе «Развитие памяти»: отдельно или по абонементу, со скидкой.

Как связаны сложение и умножение?

Слышали ли вы когда-нибудь, что сложение и умножение связаны? Если нет, то вы, ученики, можете использовать этот навык для улучшения своего умножения по математике. Многим ученикам сложно умножать числа, но если вы Практикуйте этот навык, чтобы отточить навыки умножения, вы найдете легко решать различные задачи умножения.

Умножение также известно как повторное сложение. Это объясняет все о том, как связаны сложение и умножение.Тем не мение, чтобы лучше понять это, мы рассмотрим несколько примеров. Это описано в следующем параграфе.

Понимание отношений более ясным образом:

Давайте рассмотрим пример, что есть три студента. Каждый студенту требуется два карандаша. Итак, сколько всего карандашей требуется все вместе? Вы можете решить его, сложив 2 + 2 + 2, а можете получить ответ в виде шести карандашей. Чтобы объяснить это подробно, так как там учатся трое учеников, и каждому из них требуется по два карандаша, поэтому сложение двух карандашей трижды (так как трое учеников) дает ответ как шесть.

Таким образом, вы увидели, что получили ответ на умножение проблема с повторным сложением. Теперь, если вы хотите получить ответ на 7 x 6, то вы можете объединить 7 частей с 6 объектами в каждой части. Который есть, 6 + 6 + 6 + 6 + 6 + 6 + 6 = 42, это равно умножению уравнение как 7 x 6 = 42.

Math также использует умножение и сложение, чтобы учащиеся понимали концепции сложения, такие как манипулирование группами для получения общая продукция. Это также помогает узнать размер или количество элементы в нескольких группах одинакового размера.

Например, если у вас в упаковке 6 конфет и вы покупаете четыре больше пачек, то сколько конфет у вас сейчас? Ты можешь решить эту задачу методом сложения, т.е. 6 + 6 + 6 + 6 = 24. Это — это повторяющееся сложение, которое можно заменить методом умножения из, 4 х 6 = 24.

Это также объяснение умножения, где умножение Задачи включают несколько комплектов. В вышеупомянутом примере вы может иметь отношение умножения и сложения, например.г., 4 упаковки конфет и 6 конфет в упаковке показывают то же самое.

Здесь связь между методом умножения и повторным сложением очевидно, объясняет необходимость понимания основных сложение перед изучением таблицы умножения 10 x 10.

Короче говоря, умножение — это форма повторного сложения, что означает что это самый быстрый способ сложить ряд чисел.

Например, 3 x 5 означает сложение 3 пять раз подряд. или 3 + 3 + 3 + 3 + 3 в пересчете на сложение.Нужно иметь в виду что запоминание математики затруднит вам решение задач умножения, поскольку математика — это то, как формулировать или придумывать и решать проблемы, а не декламация.

Это все о рецептуре:

Вам нужно формулировать вместо запоминания или повторения. Например, не запоминайте, что 3 x 7 = 21, вместо этого вы можете считать это 3 x 7 = 7 + 7 + 7 = 14 + 7 = 21. Этот конкретный метод немного сложен. в плане сложения для ребенка, но наглядно показывает взаимосвязь между умножением и сложением.

Соответственно, вы также можете вычислить 9 x 7 = 10 x 7 — 7 = 63 или 6 x 7 = 3 x 7 + 3 x 7 = 21 + 21 = 42. Это также творческий метод выучите таблицу умножения, которая объясняет вам точную работу математики.

Следовательно, если вы будете следовать этому методу в более низких стандартах, то вы можете легко решить проблемы с более высокими стандартами.

Пирамида сложения или умножения: карточная игра для отработки свободного владения фактами

Это карточная игра для двух игроков, которую вы можете использовать в качестве подкрепления для сложения или умножения.Ниже я изложил инструкции для варианта сложения, но умножение можно заменить. Ближе к концу этого поста я добавил распечатанные инструкции, на которые вы можете ссылаться в своем классе.

Если вы предпочитаете посмотреть видеоверсию, я включил ее после письменных инструкций.

Объект: , чтобы набрать наибольшее количество очков

Материалы : колода карт (ничего страшного, если некоторые карты отсутствуют)

очков : все карточки с номерами равны этому количеству очков; J, Q, K равны 10, а тузы могут быть равны 1 или 11

Инструкции:

Постройте пирамиду.Всего должно быть 7 рядов и 28 карточек.

Игрок 1 выбирает две из «открытых» карт и складывает их, чтобы получить сумму. Поскольку цель игры — набрать наибольшее количество очков, Игрок 1 должен выбрать две карты с наибольшей суммой. Например, Игрок 1 мог выбрать что-нибудь из нижнего ряда, потому что эти карты открыты. Он выбирает 10 и 8, потому что это самая высокая сумма. Он говорит: «10 + 8 = 18, убирает карточки и записывает свой ответ на листке бумаги.

Игрок 2 выбирает две из открытых карт, чтобы получить максимально возможную сумму. Она записывает сумму на своем листе бумаги. В этом примере она выбирает 5 и 5, чтобы получить 10.

Затем Игрок 1 выбирает 8 и валет (10), чтобы получить 18.

Игроки продолжают складывать две открытые карты и записывать суммы до тех пор, пока не кончатся карты.

После того, как все карты были использованы, игроки складывают все свои суммы.Побеждает игрок с наибольшим количеством очков.

ПРИМЕЧАНИЯ

В некоторых случаях ближе к концу игры, как показано здесь, будет доступна только одна открытая карта. В этом случае игрок должен взять королеву и прибавить к ней 0, так как другой карты брать нельзя. Итак, в этом случае игрок говорит «10 + 0 = 10» и получает 10 очков.

ПИРАМИДА УМНОЖЕНИЯ

Чтобы сыграть в версию этой игры с умножением, игроки будут умножать карты, чтобы получить продукт, а не складывать их, чтобы получить сумму.После того, как все карты использованы, игроки складывают все свои продукты. Побеждает игрок с наибольшим количеством очков.

Вот версия видео:

ПЕЧАТНАЯ ИНСТРУКЦИЯ ПО ИГРЕ — СКАЧАТЬ ЗДЕСЬ.

Как преобразование между сложением и умножением упрощает математику

Многовариантное исчисление никогда не было моим лучшим предметом — у меня не было большой интуиции в отношении графиков и уравнений, поэтому у меня часто возникали проблемы с визуализацией вопросов.Я предпочитаю подходить к формам, как тополог или малыш с небольшим количеством пластилина: точное уравнение не так уж важно для меня, только крупномасштабные особенности. Я думаю о математических формах так, как будто они сделаны из глины, а не построены с помощью точных формул. Все это говорит о том, что я все еще чувствую себя немного напуганным, когда кто-то показывает мне уравнение, и я должен знать, как оно будет выглядеть, если вы его изобразите, или когда я должен составить картину, которую я вижу, с помощью уравнений.

Ранее этим летом на увлекательной конференции, посвященной иллюстрированию математики, один из докладчиков познакомил нас с Surfer, и я начал играть.Surfer — это бесплатная программа, которую вы можете загрузить с открытого веб-сайта математики Imaginary, и она проста в изучении. В программу встроено множество уравнений и их графиков, и вы можете начать с ними работать, как только установите ее.

Пока мы играли с Surfer, другой участник конференции сделал фигуру, которая меня поразила: два связанных полых кольца, или тори, изображенные в верхней части этого поста. «Как он это сделал?» Я подумал: «Наверное, так сложно найти уравнение, которое создаст оба этих тора одновременно!»

Затем он показал мне уравнение, которое использовал, и меня осенило: когда вы пишете уравнения в виде графиков, не так уж сложно изобразить несколько объектов одновременно, потому что построение графиков позволяет вам превратить сложение в умножение.

Обычно мы думаем об умножении как о более сложном, чем сложение, поэтому превращение сложения в умножение кажется неправильным направлением. Бен Орлин из превосходного блога Math with Bad Drawings недавно написал сообщение о ритме журналов (или, менее поэтично, логарифмах), в котором подчеркивается один из наиболее важных аспектов логарифмов: они превращают умножение в сложение.

Напоминаю, что логарифм — это операция, обратная возведению в степень. Возведение в степень принимает степень: например, 3 ⁴ означает 3 × 3 × 3 × 3.Поскольку логарифм является обратной величиной экспоненты, уравнение 3 ⁴ = 81 эквивалентно log ₃ (81) = 4. Чтобы обобщить, y = b ^x и x = log _b (y) кодируют такое же соотношение между основанием b и числами x и y .

Логарифмы превращают сложение в умножение, используя это свойство экспонент: b ^x b ^y = b ^{x + y}, поэтому log _b (xy) = log _b (x) + log _b (у). (Подробности о том, как это работает, можно найти на этой странице о логарифмах и возведении в степень.) Правила слайдов, которые были важными вычислительными инструментами до того, как их вытеснили современные калькуляторы, используют эту взаимосвязь. Сейчас они могут показаться громоздкими, но до того, как у каждого появился калькулятор или компьютер для выполнения арифметических операций, логарифмы позволяли людям выполнять вычисления намного быстрее, чем позволяет традиционный алгоритм умножения.

Когда мы занимаемся арифметикой, сложение проще, чем умножение, поэтому мы заменяем задачи умножения на задачи сложения с использованием логарифмов.Но, как я понял, играя с Surfer, когда мы строим графики многочленов, умножение проще, чем сложение. Мы можем «сложить» две фигуры, умножив их уравнения вместе.

Чтобы понять, что я имею в виду, давайте посмотрим, как построить график уравнения в Surfer.

Поле ввода для серфера. Изображение: Эвелин Лэмб

Интерфейс позволяет вводить уравнение в переменных x, y и z слева от знака равенства, но справа всегда фиксировано 0.

Поначалу это кажется ограничивающим.Например, уравнение сферы с радиусом 1: x ² + y ² + z ² = 1, и мы не можем ввести это в Surfer. Но вычитая 1 из обеих частей уравнения, мы получаем вполне приемлемое, хотя и немного менее эстетичное, x ² + y ² + z ² -1 = 0. В награду получаем блестящую розовую сферу.

Изображение: Эвелин Лэмб

Почему правая сторона всегда равна нулю? Если вы вспомните математические классы, которые просили вас работать с многочленами, вы могли вспомнить, что 0 было магическим числом.Если бы я попросил вас решить, например, x ² + x = 12, вы могли бы инстинктивно вычесть 12 с обеих сторон (или «переместить 12 на другую сторону»), чтобы получить x ² + x-12 = 0. , затем разложите левую часть на (x + 4) (x-3) и скажите мне, что x равно -4 или 3. Это потому, что разложение на множители чрезвычайно полезно, когда одна часть уравнения равна 0, и не так полезно, если это не так. .

Если бы у нас было уравнение (x + 4) (x-3) = 2, у нас не было бы много дел. Если два числа умножаются на 2, одно из них может быть 1, а одно может быть 2, или одно может быть π, а другое может быть 2 / π, или одно может быть -1/2, а другое может быть -4 .Но если два числа умножаются на 0, одно из них само должно быть 0 — и все происходит наоборот: если вы умножаете два числа вместе, и одно из них равно 0, произведение также должно быть 0.

Еще один способ подумать об этом: при умножении 0 похож на слово или . Если у нас есть два полинома, f и g , и умножить их вместе, чтобы получить 0, утверждение f × g = 0 эквивалентно «либо f , либо g равно 0». Может случиться так, что и f , и g равны 0, но это все, что нужно.Когда вы думаете об этом таким образом, заимствование строки у Стивена Сондхейма через жену пекаря в Into the Woods , или означает больше, чем это было раньше.

Мы можем использовать это свойство умножения, чтобы упростить сложение. Если мы умеем писать уравнения для двух разных форм или одной и той же формы в двух разных местах, мы можем перемножить два уравнения, которые получим. Результирующее уравнение будет выполняться всякий раз, когда выполняется одно из них, что эквивалентно рисованию обеих фигур одновременно.Мы сделали сложную задачу рисования двух фигур в задачу умножения с многочленами.

Некоторых из вас, вероятно, раздражает то, как я играю быстро и свободно со словом , добавлением . Сложение для чисел. Что значит добавлять фигуры? Ты поймал меня. Слово, которое я действительно должен использовать здесь, — union .

В математике объединение двух вещей означает, что вы объединяете эти две вещи. Если вы возьмете объединение нечетных целых чисел и четных целых чисел, вы получите все целые числа. Если вы возьмете соединение одного пончика и другого пончика, которое не пересекается с ним, вы получите два пончика.

Как 0 в умножении, объединение аналогично слову «или». Что-то есть в наборе A соединительный набор B , если он есть в наборе A или наборе B . Это контрастирует с пересечением двух множеств, которое похоже на «и». Если что-то находится в наборе A пересекающихся наборов B , оно должно быть в обоих наборах A и set B .

Вернувшись на конференцию, когда я впервые увидел связанные торы, созданные моим другом-серфером, я был напуган, потому что думал о проблеме как о вопросах и . Но это было или , а или было проще.

Ассоциативные и коммутативные свойства умножения

Умножение и сложение являются связанными математическими функциями. Добавление одного и того же числа несколько раз даст тот же результат, что и умножение числа на количество повторений сложения, так что 2 + 2 + 2 = 2 × 3 = 6.Эта связь дополнительно иллюстрируется сходством между ассоциативными и коммутативными свойствами умножения и ассоциативными и коммутативными свойствами сложения. Эти свойства связаны с тем, что порядок чисел в числе сложения или умножения не влияет на результат уравнения. Важно отметить, что эти свойства применяются только к сложению и умножению, а не к вычитанию или делению, где изменение порядка чисел в уравнении изменит результат.

Коммутативное свойство умножения

При умножении двух чисел изменение порядка чисел в уравнении на противоположное приводит к тому же произведению. Это называется коммутативным свойством умножения и очень похоже на ассоциативное свойство сложения. Например, умножение трех на шесть равно шести умноженным на три (3 × 6 = 6 × 3 = 18). Выраженное в алгебраических терминах, коммутативное свойство:

a × b = b × a

ab = ba

Ассоциативное свойство умножения

Ассоциативное свойство умножения можно рассматривать как расширение коммутативного свойства умножения. умножение и параллели ассоциативному свойству сложения.При умножении более двух чисел изменение порядка умножения чисел или их группировки приводит к тому же результату. Например, (3 × 4) × 2 = 12 × 2 = 24. Изменение порядка умножения на 3 × (4 × 2) дает 3 × 8 = 24. В алгебраических терминах ассоциативное свойство может быть описано как:

(a + b) + c = a + (b + c)

Коммутативное свойство сложения

Может быть полезно вспомнить ассоциативные и коммутативные свойства сложения применительно к ассоциативным и коммутативным свойствам умножения.Согласно коммутативному свойству сложения два числа, сложенные вместе, дают одну и ту же сумму независимо от того, добавляются они вперед или назад. Другими словами, два плюс шесть равняется восьми, а шесть плюс два также равняется восьми (2 + 6 = 6 + 2 = 8) и напоминает свойство коммутативности умножения. Опять же, это может быть выражено алгебраически как

a + b = b + a

Ассоциативное свойство сложения

В ассоциативном свойстве сложения порядок, в котором более трех или более наборов чисел складываются вместе, не изменить сумму чисел.Таким образом, (1 + 2) + 3 = 3 + 3 = 6. Как и в ассоциативном свойстве умножения, изменение порядка не меняет результат, поскольку 1 + (2 + 3) = 1 + 5 = 6. Алгебраически, ассоциативное свойство сложения:

(a + b) + c = a + (b + c)

Базовая математика в Excel с использованием функции СУММ

Вы новичок в Excel и не знаете, с чего начать с формул и операций? Многие электронные таблицы используют простую математику: сложение и вычитание чисел или умножение и деление.Понимание этих математических формул поможет вам перейти к более сложным уравнениям для управления данными Excel.

Как базовая математика работает в Excel?

Excel использует формулы или функции для управления данными. Функция принимает входные данные, представляющие собой содержимое ячеек плюс некоторые рабочие символы, которые говорят, что делать с данными. Вы можете ввести одну ячейку в функцию или диапазон из нескольких ячеек.

Для сложения, вычитания, умножения и деления можно использовать функцию СУММ .Ваш ввод для формулы СУММ — это базовое математическое выражение. Вот пример:

= СУММ (A1-A2)

В переводе на английский язык эта функция означает: «Вычислить сумму числа в ячейке A1 за вычетом числа в ячейке A2».

Базовая математика на самом деле не требует, чтобы функция СУММ работала. В некоторых случаях вы можете пропустить формат «= СУММ ()» и просто ввести ввод функции, например «= A1 + A2». Однако использование функции СУММ иногда необходимо и рекомендуется, если вы новичок в формулах.

Сложение чисел

Чтобы складывать числа с помощью СУММ, используйте знак плюса (+).

= СУММ (A1 + A2)

Помните, что вы не ограничены простым сложением двух чисел. Вы можете сложить много чисел и связать их вместе со знаками плюс, а также вы можете сложить весь диапазон соседних ячеек с помощью двоеточия (:). Например:

= СУММ (E1: E4)

Эта формула означает «Вычислить сумму ячеек с E1 по E4.”

Вычитание чисел

Вычитание работает так же, как сложение, за исключением того, что вы используете символ минус (-).

= СУММ (A1-A2)

И вы можете смешать вычитание со сложением, например:

= СУММ (A1-A2 + A3)

Умножение чисел

Для умножения вы используете звездочку (*) в качестве оператора умножения. В приведенном ниже примере мы умножили общее количество часов на почасовую ставку, чтобы получить окончательную сумму.Обратите внимание, что «Общее количество часов» в ячейке E5 само по себе является суммой ячеек с E1 по E4.

= СУММ (E5 * E6)

Разделительные числа

Еще раз, деление работает так же, как и умножение, за исключением того, что вы используете косую черту (/) в качестве оператора деления.

= СУММ (E7 / 2)

Здесь мы делим сумму из ячейки E7 на два.

Дополнительный совет: сложные уравнения

Если вы хотите связать сложение и вычитание с умножением и делением в одном уравнении, вам нужно будет использовать круглые скобки, чтобы обозначить, какие операции выполняются в первую очередь.Операции в круглых скобках выполняются первыми — и если вы используете несколько вложенных скобок, сначала выполняются самые глубокие скобки, а вычисление идет «вовне».

Например, вы хотите умножить сумму ячеек с E1 по E4 на сумму ячеек с F1 по F3. Вы хотите, чтобы две умножаемые суммы сначала складывались, а затем умножались.

= СУММ ((E1: E4) * (F1: F3))

Здесь мы используем диапазоны ячеек (например, «E1: E4») как сокращение для сложения.Функция СУММ автоматически суммирует этот диапазон ячеек. Вот пример использования вычитания перед умножением:

= СУММ ((A1-A2) * (F1: F3))

Итак, здесь мы вычитаем A2 из A3, а затем умножаем этот результат на сумму ячеек с F1 по F3.

Заключение

Еще не запутались? Главное помнить, что вы выполняете операции с содержимым ячеек. Вы обращаетесь к ячейкам, а затем используете математический оператор (+, -, * или /), чтобы указать, что делать с числами в этих ячейках.Функцию СУММ хорошо использовать, но вы можете пропустить ее и ввести математические формулы самостоятельно в простейших случаях.

Сложение, вычитание, умножение и деление степеней

Сложение и вычитание полномочий

Очевидно, что степени можно складывать, как и другие величины, , объединяя их одну за другой со своими знаками.

Таким образом, сумма a ³ и b ² составляет ³ + b.
И сумма a ³ — b ⁿ и h ⁵ -d ⁴ составляет ³ — b ⁿ + h ⁵ — d ⁴.

Одни и те же степени одинаковых букв подобны величинам , и их коэффициенты могут быть добавлены или вычтены.

Таким образом, сумма 2a ² и 3a ² составляет 5a ².

Столь же очевидно, что удвоенный квадрат a и тройной квадрат a в пять раз больше квадрата a, как и дважды a и трижды a равны пятикратному a.

Но степени разных букв и разных степеней той же буквы должны быть добавлены, записывая их вместе с их знаками.

Сумма ² и ³ дает ² + ³.

Очевидно, что квадрат a и куб a не в два раза больше квадрата a и не в два раза больше куба a.

Сумма a ³ b ⁿ и 3a ⁵ b ⁶ составляет a ³ b ⁿ + 3a ⁵ b ⁶.

Вычитание степеней должно выполняться таким же образом, как и сложение, за исключением того, что знаки вычитания должны быть изменены.

из	2a ⁴	3ч ²b ⁶	5 (а — в) ⁶
Под.	-6a ⁴	4ч ²b ⁶	2 (а — в) ⁶
Разн.	8a ⁴	-h ² b ⁶	3 (а — в) ⁶

ИЛИ: 2a ⁴ — (-6a ⁴) = 8a ⁴
3h ² b ⁶ — 4h ² b ⁶ = -h ² b ⁶
5 (a — з) ⁶ — 2 (а — з) ⁶ = 3 (а — з) ⁶

Умножение степеней

Силы можно умножать, как и другие величины, записывая множители один за другим со знаком умножения или без знака умножения между ними.

Таким образом, произведение ³ на b ² дает ³ b ² или aaabb.

Разн.	х ^-3	3a ⁶ y ²	a ² b ³ y ²
в	а ^м	-2x	а ³ б ² л
Тов.	a ^м x ^-3	-6a ⁶ xy ²	a ² b ³ y ² a ³ b ² y

OR:
x ^-3 × a ^m = a ^m x ^-3
3a ⁶ y ² × (-2x) = -6a ⁶ xy ²
a ² b ³ y ² × a ³ b ² y = a ² b ³ y ² a ³ b ² y

Продукт в последнем примере можно сократить, объединив повторяющиеся буквы.
Тогда он станет ⁵ b ⁵ y ³.

Причина этого будет очевидна, если вернуться к ряду полномочий в ст. 204, а именно.

Сравнивая несколько членов друг с другом, можно увидеть, что если любые два или более из них будут умножены вместе, их произведение будет степенью, показатель степени которой равен сумме и показателей степени множителей.

Таким образом, a ² ⋅a ³ = aa⋅aaa = aaaaa = a ⁵.

Здесь 5, показатель степени произведения, равен 2 + 3, сумме показателей степени факторов.

Итак, ⁿ ⋅a ^m = a ^{m + n}.

Для ⁿ — множитель, равный количеству единиц в n;

А ^м — множитель, равный количеству единиц в м;

Следовательно, произведение должно быть равно множителю, равному количеству единиц в m и n. Следовательно,

Силы одной и той же базы можно умножить, сложив их показатели.

Это ² ⋅a ⁶ = a ^{2 + 6} = a ⁸. И x ³ ⋅x ² ⋅x = x ^{3 + 2 + 1} = x ⁶.

Умножить	4a ⁿ	б ² л ³	(б + в — у) ^н
в	2a ⁿ	б ⁴ л	(б + в — у)
Товар	8a ²ⁿ	б ⁶ л ⁴	(б + в — у) ^{п + 1}

OR:
4a ⁿ × 2a ⁿ = 8a ²ⁿ
b ² y ³ × b ⁴ y = b ⁶ y ⁴
(b + h — y ) ⁿ × (b + h — y) = (b + h — y) ^{n + 1}

Mult.x ³ + x ² y + xy ² + y ³ в x — y.
Ответ: x ⁴ — y ⁴.
Мульт. x ³ + x — 5 в 2x ³ + x + 1.

Правило в равной степени применимо к степеням, показатель степени которых равен отрицательным .

1. Таким образом, ^-2 .a ^-3 = ^-5. Это $ \ frac {1} {aa} \ cdot \ frac {1} {aaa} = \ frac {1} {aaaaa} $.

2. y ^-n ⋅y ^-m = y ^-n-m.

3. a ^-n ⋅a ^m = a ^m-n.

Если a + b умножить на a — b, произведение будет a ² — b ²: то есть

Произведение суммы и разности двух величин равно разности их квадратов.

Если умножить сумму и разность квадратов , произведение будет равно разности четвертых степеней.

Таким образом, (a — y) ⋅ (a + y) = a ² — y ².
(a ² — y ²) ⋅ (a ² + y ²) = a ⁴ — y ⁴.
(a ⁴ — y ⁴) ⋅ (a ⁴ + y ⁴) = a ⁸ — y ⁸.

Разделение властей

Полномочия могут быть разделены, как и другие величины, путем исключения из делимого множителя, равного делителю; или поместив делитель под делимым в виде дроби.

Таким образом, частное от ³ b ², деленного на b ², составляет ³.

Разделить	9a ³ y ⁴	a ² by + 3a ² y ²	d⋅ (а — в + у) ³
По	-3a ³	a ² y	(а — в + у) ³
Частное	-3 года ⁴	б + 3г	д

Частное ⁵, деленное на ³, составляет ⁵ / a ³.Но это равно ². Ибо в сериале
a ⁺⁴, a ⁺³, a ⁺², a ⁺¹, a ⁰, a ^-1, a ^-2, a ^-3, a ^-4.
, если один член делится на другой, показатель частного будет равен разнице между показателем делимого и показателем делителя.

Степень может быть разделена на другую степень того же основания путем вычитания показателя делителя из показателя делимого .

Таким образом, y ³: y ² = y ^3-2 = y ¹. То есть yyy / yy = y.

И ^{n + 1}: a = a ^{n + 1-1} = a ⁿ. То есть aa ⁿ / a = a ⁿ.

Разделить	л ^2м	8a ^{n + m}	12 (б + у) ^п
По	л ^м	4a ^м	3 (б + у) ³
Цит.	л ^м	2a ⁿ	4 (б + у) ^п-3

Правило в равной степени применимо к степеням, показатель степени которых равен отрицательным .
Частное ^-5 на ^-3, составляет ^-2.
Это $ \ frac {1} {aaaaa}: \ frac {1} {aaa} = \ frac {1} {aaaaa} \ cdot \ frac {aaa} {1} = \ frac {aaa} {aaaaa} = \ frac {1} {aa} $.

3. h ²: h ^-1 = h ^{2 + 1} = h ³.То есть h ²: (1 / h) = h ² ⋅ (h / 1) = h ³

Умножение и разделение полномочий путем сложения и вычитания их индексов должно быть хорошо знакомо; поскольку они имеют многочисленные и важные приложения в высших разделах алгебры.

Примеры фракций, содержащих силы

В разделе о дробях следующие примеры были опущены, чтобы избежать предвкушения субъекта полномочий.

1.Сократите 5a ⁴ / 3a ² до более низких значений. Ответ: 5а ²/3.

2. Уменьшите 6x ⁶ / 3x ⁵ до более низких значений. Ответ: 2x / 1 или 2x.

3. Приведите ² / a ³ и ^-3 / a ^-4 к общему знаменателю.
a ² ⋅a ^-4 — это ^-2 первый числитель. (Статья 146.)
a ³ ⋅a ^-3 — это ⁰ = 1, второй числитель.
a ³ ⋅a ^-4 — это ^-1, общий знаменатель.
Таким образом, уменьшенные фракции равны ^-2 / a ^-1 и 1 / a ^-1.

4. Приведите 2a ⁴ / 5a ³ и ² / a ⁴ к общему знаменателю.
Ответ: 2a ³ / 5a ⁷ и 5a ⁵ / 5a ⁷ или 2a ³ / 5a ² и 5 / 5a ². (Статья 142.)

5. Умножьте (a ³ + b) / b ⁴ на (a — b) / 3.

6.Умножьте (a ⁵ + 1) / x ² на (b ² — 1) / (x + a).

7. Умножьте b ⁴ / a ^-2 на h ^-3 / x и ⁿ / y ^-3.

8. Разделите ⁴ / y ³ на ³ / y ². Ответ: в / у.

9. Разделите (h ³ — 1) / d ⁴ на (d ⁿ + 1) / h.

Вся математика — это сложение и умножение.

Вернуться к страницам по естествознанию и математике Дональд Заутер.

Вся математика — это просто сложение и умножение!

& nbsp
Я делаю, казалось бы, фантастическое заявление на двух страницах базовое, однозначное сложение и базовое, однозначное умножение, что вся математика на всех уровнях, не включает в себя ничего, кроме этих простых операций.

Хорошо, это небольшое преувеличение. Предполагается, что Вы знаете, что такое числа, и научились считать.Если вы спросите, «А как насчет вычитания и деления?» — неожиданно приходит ответ. назад:

Вычитание — это , связанное с дополнительно; вычитание — это сложение просто идет в другую сторону , шагая назад, а не вперед; вычитание числа аналогично добавлению отрицательного числа; вычитание фактически выполняется в уме с использованием навыков сложения . У тебя в голове не остается места на 11-7, и тебе лучше не быть обратный отсчет! Вы думаете: «7 плюс, что поднимает меня до 11? Ах да… »

Аналогично, деление составляет , увеличивая при умножении; разделение умножение просто идет в другую сторону , вместо этого прыгает назад нападающих; деление на число аналогично умножению на его обратное; деление фактически выполняется в уме с использованием Умножение навыков . У тебя в мозгу не остается места для 42 & diver7, и вам лучше не возвращаться к 0 на 7! Вы думаете, «В 7 раз, что дает мне 42? Ах да… »

Умножение — это следующая по мощности операция после сложения. Если вы бросаете мне вызов на возведение в степень, следующая операция в силе от умножение, я говорю, что возведение в степень — это просто повторное умножение, и фактически выполняется с умножением и сложением. Хотя некоторые из нас могут знать несколько крошечных фактов возведения в степень, например, 3 ³ и 3 ⁴, никто не запоминает возведение в степень столы.

Да, вам нужно выучить некоторые определения, такие как периметр, угол, среднее, радиус, касательная, производная, стандартное отклонение и т. д., но рабочие с этими вещами никогда не будет больше, чем применение сложение и / или умножение.

***

Мистер Морабито работает преподавателем математики в колледже, где я работаю. Он знает мое заявление о том, что «вся математика — это просто сложение и умножение»; что математика — единственная профессия на земле, в которой вам нужно знать только две вещи! Я имею в виду, вы можете представить садовника, сантехник, автомеханик или балерина, только знающая два вещей ??? Хорошо, Я немного пошутил, но не до конца.Математика Окажите себе большую услугу, подчеркнув, насколько маленький , на самом деле, вместо того, чтобы запугать всех своей предполагаемой чудовищностью. Вы можете найти сайты с практикой по математике, которые трубят: «Практикуйтесь в 265 шестом классе. математические навыки! «, например. Верно, 265 способов справиться с сложением и умножение …

Как бы то ни было, однажды я подошел к мистеру Морабито, когда он помогал студент с проблемой. Он повернулся ко мне и сказал: «Вот.Решать используя только сложение и умножение «.

Проблема заключалась в том,

Решить относительно x: Log x + Log (x-21) = 2 (1)

Как будто логарифмы меня отпугнут. Логарифм — это просто экспонента, и я уже сказал, что возведение в степень просто повторяется умножение.

Теоремы сложения и умножения вероятностей: основные задачи

Решить задачу на сложение вероятностей самостоятельно, а затем посмотреть решение

Решить задачи на умножение вероятностей самостоятельно, а затем посмотреть решение

Решить задачу на умножение вероятностей самостоятельно, а затем посмотреть решение

Что сначала умножение или прибавление

Сложение и вычитание

Умножение

Что сначала — умножение или сложение?

Деление

Скобки

«Вишенка на торте»

«Совсем вишня»

Порядок вычисления простых выражений

Что такое действия первой и второй ступени

Порядок вычислений в выражениях со скобками

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Наблюдение за изменением значения выражения от порядка выполнения арифметических действий

Порядок выполнения арифметических действий в выражениях без скобок

Порядок выполнения арифметических действий в выражениях со скобками

Правило выполнения арифметических действий в выражениях без скобок и со скобками

Выполнение тренировочных заданий на изученное правило

Сложение, вычитание, умножение и деление в Excel

Операции c функциями — сложение, вычитание, умножение и деление

Двоичная арифметика : сложение, вычитание, умножение, деление

Сложение двоичных чисел

Вычитание двоичных чисел

Умножение и деление двоичных чисел

Сложение и умножение вероятностей: ilyachalov — LiveJournal

Эффективные методы сложения, деления и умножения чисел

1. Приемы упрощенного сложения чисел

2. Приемы упрощенного вычитания чисел

3. Приемы упрощенного умножения чисел

4. Приемы упрощенного деления чисел

Изучите эффективные техники запоминания услышанной и прочитанной информации в курсе «Развитие памяти»: отдельно или по абонементу, со скидкой.

Как связаны сложение и умножение?

Пирамида сложения или умножения: карточная игра для отработки свободного владения фактами

Как преобразование между сложением и умножением упрощает математику

Ассоциативные и коммутативные свойства умножения

Коммутативное свойство умножения

Ассоциативное свойство умножения

Коммутативное свойство сложения

Ассоциативное свойство сложения

Базовая математика в Excel с использованием функции СУММ

Как базовая математика работает в Excel?

Сложение чисел

Вычитание чисел

Умножение чисел

Разделительные числа

Дополнительный совет: сложные уравнения

Заключение

Сложение, вычитание, умножение и деление степеней

Сложение и вычитание полномочий

Умножение степеней

Разделение властей

Примеры фракций, содержащих силы

Вся математика — это сложение и умножение.

Вся математика — это просто сложение и умножение!

Добавить комментарий Отменить ответ