Двадцать задачек (по безумной, восхитительной геометрии) / Хабр

Предупреждение врача. Остерегайтесь этих головоломок. Побочные эффекты могут включать потерянное послеобеденное время, скомканные волосы и восклицания «А-а-а-х, вот как это делается» настолько громкие, что могут треснуть оконные стёкла.

Несколько месяцев назад я наткнулся в твиттере на математические головоломки Катрионы Ширер. Они сразу меня увлекли: каждая головоломка такая осязаемая, ручной работы, словно просит её решить. И на каждую вы можете легко потратить час времени, а то и больше.

Катриона разрешила мне подвесить вас на эти задачки — и поделилась 20 своими любимыми головоломками. Она даже удовлетворила моё любопытство и восхищение, дав интервью (см. в конце статьи).

Наслаждайтесь. И не говорите, что врач не предупреждал.

1. Сад часов

Какая часть каждого круга закрашена? (12 точек на равном расстоянии; единственная точка внутри круга — его центр)

«К сожалению, из эти шести моя любимая — единственная, которую я не придумала сама, — говорит Катриона, — это тёмно-синяя».

2. Опрокинутый квадрат

(Как по мне, это классика).

3. Это ловушка

В прямоугольной трапеции зелёная область на 6 больше, чем жёлтая. Чему равен x?

«Это „вторая версия” данной головоломки: она лучше, чем первая, которую я придумала».

4. Три квадратных тарелки

Длины сторон трёх квадратов — последовательные целые числа. Какова общая площадь?

«Эта мне очень нравится: на её основе я нарисовала много красивых узоров».

5. Красивая стрижка

Площадь левого нижнего квадрата 5. Какова площадь синего треугольника?

«Наверное, моя любимая за всё время. Выглядит просто невозможным! Здесь метод решения называется «стрижка», shearing (к сожалению, не в мою честь)».

6. Все люди рождены равными

«Ещё одна переделка, которую я предпочитаю оригиналу».

7. Полукруг турдакен

«Головоломки с углами гораздо труднее составлять. Ученики сказали, что это довольно простая задачка, но мои родители испытали большие трудности. Кажется, эта головоломка требует больше „знаний”, но сам процесс решения проще».

8. Степенные хорды

Какова площадь круга?

«В школе я не изучала теорему о пересекающихся хордах, поэтому люблю везде её использовать!»

9. Сказка о двух кругах

У этих правильных многоугольников одинаковый периметр. Найдите отношение площадей вписанных окружностей.

«Это следствие другой головоломки, но она мне нравится больше, чем оригинал!»

10. Doc Oct

У закрашенной области такое же значение, как у периметра правильного восьмиугольника. Каково значение?

«Думаю, это довольно чистая задачка, хотя выглядит как массовое разграбление головоломок Эда Сауталла».

11. Всё в квадрате

«Мне нравится то, что хотя вы здесь можете найти все стороны оранжевого треугольника (и я это сделала, когда решала), но на самом деле это не нужно — достаточно площади и гипотенузы».

12. Шип в улье

Два из правильных шестиугольников идентичны; у третьего площадь 10. Какова площадь красного треугольника?

«Довольно неплохо: мне нравится, что не нужно иметь дело с любой длиной стороны, которые почти наверняка ужасны».

13. Я видел равнобедренных

Все четыре треугольника равнобедренные. Найдите угол.

«Думаю, что формулировка этой задачки идеальна. Многие пропускают важную информацию и приходят к выводу, что есть бесконечное число решений!»

14. Зеленый против синего

На картинке больше зелёного цвета или синего (и на сколько)?

«Ещё одна из моих любимых».

15. Резцы по камню

Четыре равносторонних треугольника расположены вокруг квадрата с площадью 12. Какова закрашенная площадь?

«Тут самое лучшее — действительно хорошие решения по рассечению площади».

16. Едем, едем, уехалиугольник

Шесть одинаковых квадратов и меньший прямоугольник вписаны в этот правильный шестиугольник. Какую часть шестиугольника они занимают?

«Здесь ответ не такой красивый, но очень удивил меня. Думаю, из-за своей сложности эта задачка не получила такого распространения в твиттере, как другие!»

17. Только один факт

Какова площадь этого квадрата?

«Это одна из моих любимых, потому что сначала кажется, что информации недостаточно».

18. Стиральная машина

Какая часть большого квадрата закрашена?

«Здесь мне нравится сумбур квадратов, как они грохочут вокруг словно в стиралке. И ответ тоже удивительно красивый».

19. Летающие флаги

У квадратов одного цвета одинаковый размер. Какова площадь всех закрашенных областей?

«Это довольно просто, как только вы поймёте — но я поняла не сразу, поэтому простота ответа меня удивила».

20. Тигрогон

Какая часть фигуры закрашена? Шестиугольник правильный, с равномерно расположенными точками по периметру.

«Эту я редко публиковала. Но картинка напоминает мне Тигра Тони [с пачек быстрого завтрака Kellogg — прим. пер.]».

Закат над Квадратным городом

У левого квадрата площадь 4. Какова площадь правого квадрата?

«Мне нравится эта задачка, она напоминает закат над городом скверов.”

---

Если вы дочитали до этого места — возможно, через 6 месяцев после начала чтения — и ваш стол окружен скомканными бумагами и пустыми китайскими контейнерами для продуктов питания, то вам будет приятно почитать небольшое интервью с Катрионой.

Как вы пришли к разработке своих головоломок?

Я поехала в отпуск в Шотландское высокогорье, но забыла взять пальто, поэтому пришлось сидеть в домике в одиночестве, пока друзья гуляли на природе! Ничего не оставалось, кроме как машинально чертить линии на бумажке.

Не ожидала, что это превратится в хобби, но это немного затягивает, особенно когда люди присылают в ответ свои решения, которые мне нравятся. Почти всегда можно красиво сократить головоломку, что я пропустила.

Как проходит творческий процесс?

Всё начинается с рисования бессмысленных фигурок. В итоге получается целая страница перекрывающихся квадратов под разными углами или правильных (типа) пятиугольников с разными закрашенными частями, а потом я смотрю, есть ли там какая- то хорошая математика — отношения между длинами или площадями или углами.

Многие из ваших задачек нарисованы маркером на бумаге. Почему такой лоутек?

Я пробовала использовать Desmos и Geogebra, но не очень понравилось. По-моему, быстрее нарисовать вписанный круг вручную, после небольшого количества проб и ошибок, чем красиво строить его в геометрии программного обеспечения.

Кроме того, при использовании фломастера вы можете выдумывать вещи, потому что линии настолько толстые. Это хороший компромисс между тем, чтобы выглядеть «правильно», но также знать, что вы не можете просто вытащить линейку и измерить фигуру.

Одна из приятных вещей в геометрии — что она многое прощает. Я могу показать вам безнадёжный квадрат или круг, но этого достаточно, чтобы передать концепцию, потому что они так хорошо определены.

Некоторые из ваших головоломок дают самый минимум информации. Как вы находите эту границу, где диаграмма как раз определена?

Иногда этот минимум на самом деле подсказка, потому что он отправляет вас по одной дороге. Я предпочитаю давать чуть больше необходимого, поэтому есть несколько обманных маршрутов. Это также даёт большее разнообразие решений!

Было дело, я опубликовала пару невозможных головоломок: к счастью, кто-нибудь обычно указывает на это довольно быстро!

Я также публиковала задачки с массивным количеством излишней информации, потому что не видела хорошего решения, чтобы использовать только половину информации.

Советы для потенциальных создателей головоломок?

Отлично, тут мой синдром самозванца полностью проявится. Я определённо ещё новичок — я занимаюсь этим только с августа [статья опубликована в октябре 2018 года — прим. пер.]! С другой стороны, мне нравится создавать головоломки и читать решения даже больше, чем решать их самой.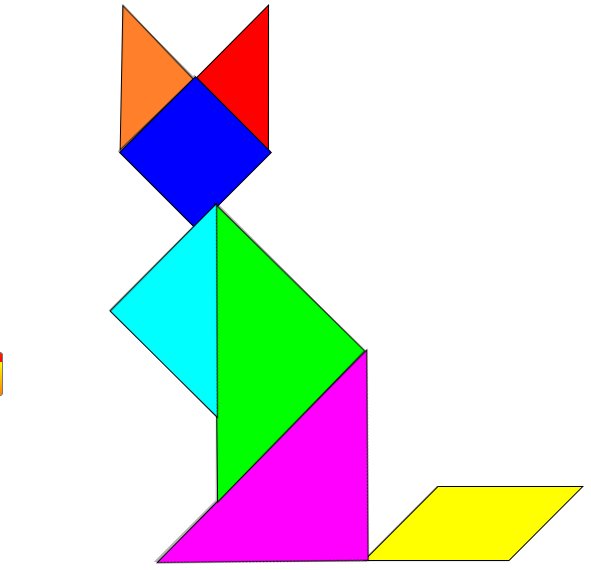

Основной целью головоломки должно быть развлечение — вот что отличает её от стандартной математической задачи. Таким образом, вам нужно по крайней мере два из трёх:

1. Красивая постановка задачи. Предоставьте минимум информации, чтобы читателю стало интересно, как вообще можно решить такую задачу. Или несколько дразнящих кусочков информации, каждый из которых якобы предлагает способ решения. Правильные многоугольники и круги — фантастические штуки, потому что скрывают огромное количество информации.
2. Красивый метод. Трюк или кратчайший путь, или внезапное озарение, которое всё упрощает. Это может быть не самый очевидный метод. Я видела много задачек, которые решаются с помощью алгебры или иррациональных чисел, или ужасных выражений с pi, а в конце всё внезапно сокращается — и я понимаю, что есть более простой способ.
3. Красивый ответ. Мало удовольствия работать над головоломкой, чтобы в конце получить некрасивый ответ.

В принципе, начните рисовать — найдите головоломку, которую вам понравилось решать, и подумайте, как можно её расширить или изменить некоторые элементы.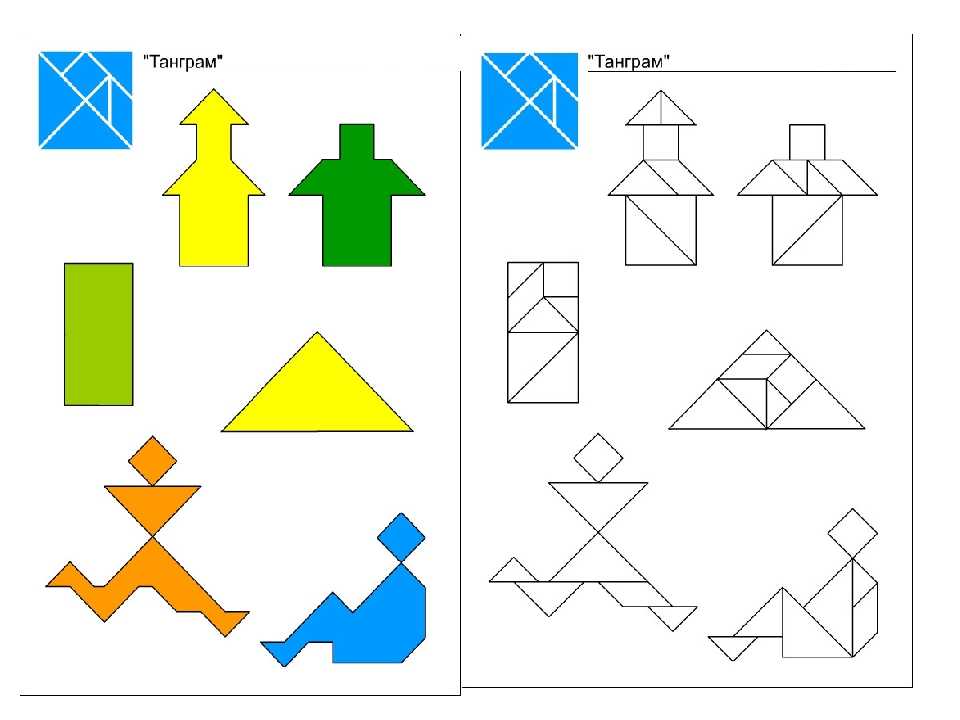

Если вдруг попадутся соотношения, которые вас удивляют, то с высокой вероятностью они удивят и других. Twitter — отличная платформа, так как люди могут публиковать в ответ собственные картинки.

«Плоские геометрические головоломки на складывание фигур»

муниципальное бюджетное общеобразовательное учреждение

«средняя общеобразовательная школа № 151»

Калининского района

 

 

 

СЕКЦИЯ МАТЕМАТИКИ

 

 

 

 

Ученик 5 «Б» класса

 

 

 

 

 

Плоские геометрические головоломки

 на складывание фигур

 

 

 

Научный руководитель:

Зайцева Наталья Валерьевна, учитель математики.

 

 

 

 

 

 

Новосибирск — 2019

Содержание

Введение…………………………………………………………………….

Глава 1. Головоломки и их виды………………………………………….

Глава 2. Мировые геометрические головоломки…………………………

Глава 3. Современные геометрические головоломки……………………

Глава 4. Практическое применение головоломок………………………..

Заключение………………………………………………………………….

Список литературы…………………………………………………………

    Приложения………………………………………………………………….

Введение

 

Однажды мне попалась в руки головоломка, которую принес в школу друг. Я долго не мог собрать нужную фигуру, хотя казалось, что это сделать легко. После долгих стараний я добился успеха. Чувства удовлетворения от своей работы и гордости переполняли меня. Тогда я заинтересовался геометрическими головоломками. В поисках новых головоломок я обнаружил, что мир их очень велик.

 Головоломки – игрушки на все времена. С самых давних пор умельцы изготавливали подобные забавы, отличающиеся многообразием вариантов решения. В наше время очень много людей  увлекается головоломками. Они любимы не только детьми, но и взрослыми. Это способ отвлечения от повседневных проблем и  направлены на развитие различных мыслительных процессов — сопоставление, обобщение, установление последовательности, определение отношений  «целое» — «часть».

Цель проекта:

•    Познакомиться с различными видами головоломок.

•    Пробудить у сверстников интерес к геометрическим головоломкам и занимательной математике.

•    Создать комплект головоломок «Танграм».

Задачи проекта:

•    Найти и изучить информацию по теме.

•    Рассмотреть различные виды головоломок.

•    Изучить историю происхождения некоторых мировых геометрических головоломок

•    Найти примеры более современных головоломок

 

 

Приступая к работе, я провёл опрос в 5-х классах. Я спросил, какие головоломки известны моим сверстникам и есть ли у них дома головоломки. Оказалось, что почти у каждого дома есть какая-нибудь головоломка. Наиболее популярны: Кубик Рубика, пазлы, тетрис, змейка, а так же мои сверстники любят проводить время за головоломками в компьютерных и мобильных играх.

 

 

 

 

 

 

 

 

Какие головоломки есть у одноклассников

 

 

В своей работе я решил рассматривать геометрические головоломки на складывание фигур.

  Прежде всего, геометрические головоломки призваны развивать логическое и пространственное мышление, воображение, внимание и зрительную память. Учат аккуратности и точности, умению анализировать. Воспитывают усидчивость и самостоятельность. Тренируют комбинаторные способности и сообразительность, подстегивают к творчеству. Головоломки полезны школьникам для подготовки к курсу геометрии.

Изучив различную литературу  о головоломках, я выявил наиболее интересные, на мой взгляд, мировые головоломки, существующие тысячелетия, а также придуманные относительно недавно. Некоторые из них я сделал своими руками и научился изображать силуэты людей, животных и различных предметов, т. е. творчески проводить время за игрой.

.

 

 

 

Глава 1

 Головоломки и их виды

Головоломка — непростая задача, для решения которой, как правило, требуется сообразительность, а не специальные знания высокого уровня.

Виды головоломок: общепринятая классификация головоломок отсутствует, можно лишь условно разделить их на несколько групп:

Ø Устные головоломки – задачи, полное условие которых может быть сообщено в устной форме не требующие для решения привлечения никаких дополнительных предметов (загадки, шарады).

Ø Головоломки с предметами — логические задачи с обычными бытовыми предметами (спичками, монетами, карточные головоломки).

Ø Печатные головоломки — напечатанные или нарисованные «картинки», в которых надо нарисовать какие-то символы по определенным правилам (кроссворды, ребусы).

Ø Механические головоломки — предметы, специально изготовленные как головоломки (кубик Рубика, змейка Рубика, пазлы, танграм).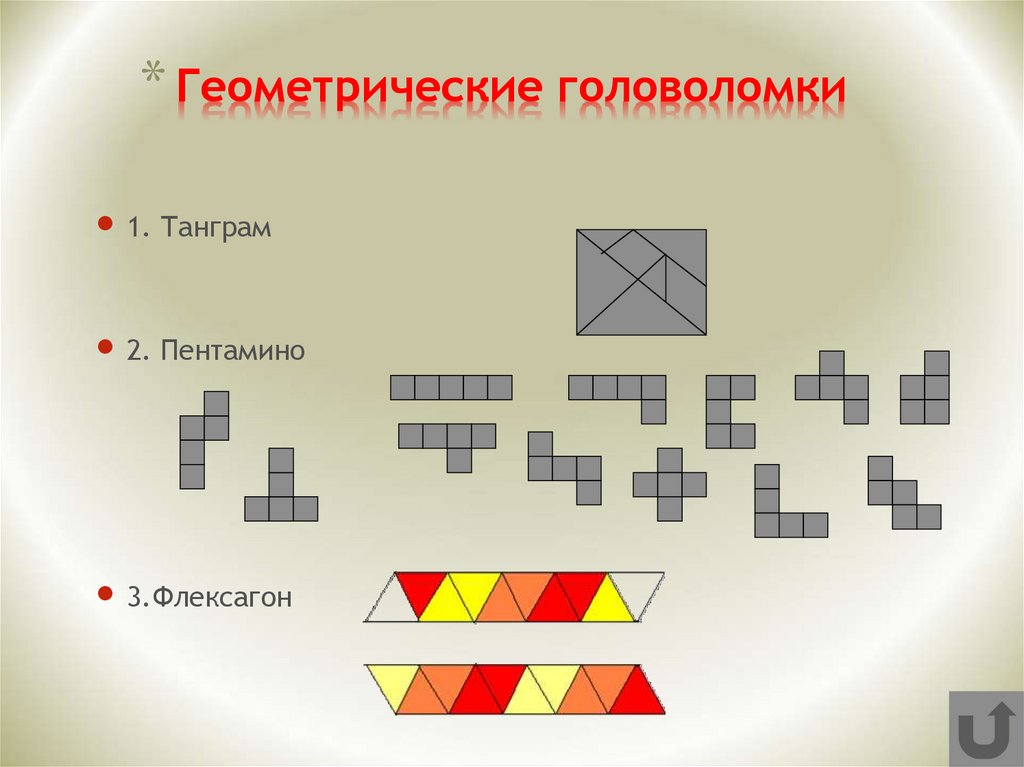

Американский коллекционер и специалист по головоломкам Джерри Слокум (Jerry Slocum) даёт следующее определение:

Механическая головоломка — это самостоятельный объект, состоящий из одной или более частей, содержащий задачу для одного человека, решаемую манипуляциями с помощью логики, рассуждений, озарения, везения и (или) терпения.

По ассортименту   головоломки на складывание фигур — это самый большой и старейший класс, к нему относятся около трети всех изобретаемых в мире механических головоломок. Задачей является собрать объект из составных элементов, чтобы он отвечал некоторым дополнительно заданным условиям. Механические головоломки этого класса в свою очередь можно разделить на плоскостные  и объёмные. Плоские головоломки представляют собой наиболее простой как для понимания, так и для решения тип механических головоломок.

Именно с составления задач на плоскости когда-то началась вся история головоломок.

 

Глава 2

Мировые геометрические головоломки

 

К мировым геометрическим головоломкам можно отнести следующие головоломки:

1. Колумбово яйцо — это овал, разрезанный на 10 частей — обычные треугольники, треугольники с одной округлой стороной и трапеции с одной округлой стороной, что позволяет составлять силуэты птиц, человека, животных, развивая наблюдательность и геометрическое воображение.

 

 

2. Волшебный круг — это круг, разделенный на 10 частей по принципу «каждый раз пополам», в результате чего в наших руках окажется несколько пар одинаковых по форме симметричных частей. Из них вы составляются силуэты человека, животных, растений, рыб и т.д., которые потом можно перенести на бумагу — дорисовать и раскрасить

 

 

3. Листик. Девять элементов головоломки «Листик» укладываются в рамку, напоминающую по форме схематичное изображение сердца или листа растения. Округлые и угловатые детали игрушки позволяют составлять всевозможные силуэты. Особенно хорошо из элементов этой головоломки получаются силуэты различных видов транспорта. Полученные изображения напоминают детские рисунки (собачки, птички, человечки).

 

4. Танграм (от китайского «семь дощечек мастерства») — головоломка, состоящая из семи танов (плоских геометрических  фигур), полученных делением квадрата на семь частей, которые складывают определённым образом для получения другой, более сложной, фигуры (изображающей человека, животное, предмет домашнего обихода, букву или цифру и т. д.). Фигура, которую необходимо получить, при этом обычно задаётся в виде силуэта или внешнего контура. При решении головоломки требуется соблюдать два условия: первое — необходимо использовать все семь фигур танграма, и второе — фигуры не должны перекрываться между собой.

Базовым элементом танграма является тан. Таны возможно получить при разрезании квадрата первоначально на два больших равных треугольника, далее согласно рисунка.  Минимальное количество базовых фигур равное семи приводит к гениальной простоте комбинаций.

Местом где была изобретена игра несомненно является Китай. Дата создания может быть определенна приблизительно 18 век. Первой известной древней книгой по танграму является «Собрание фигур из семи частей» (Китай 1803 г.). Издана она была на рисовой бумаге. Книги изданные в Европе были лишь отчасти оригинальны, а в своей основе имели китайские источники.

 

 

5. Монгольская игра — Одна из древних классических головоломок это квадрат, разделенный на части по принципу каждый раз пополам. Из получившихся таким образом одиннадцати фигур  вы сможете сложить стилизованные изображения предметов и животных (носорога, жирафа и др.)

 

 

 

 

6. Вьетнамская игра  – это круг, разделенный на семь частей. Все детали головоломки имеют обтекаемую форму, некоторые из них одинаковы по размеру, что позволяет сконструировать из замысловатых деталей силуэт какого-нибудь животного или птицы.

 

 

 7. Пентамино — одна из самых популярных мировых головоломок, пик популярности пришелся на конец 60-х годов.  Запатентовал головоломку “Pentomino” Соломон Вольф Голомб, математик и инженер, профессор

университета Южная Калифорния.

 Игра состоит из плоских фигур, каждая из которых состоит из пяти одинаковых квадратов (пять –«пента»), отсюда и название. Существуют еще

версия головоломок Тетрамино, состоящие из четырех квадратов, от этой игры и произошел известный компьютерный Тетрис.

 

 

8. Гексамино еще называют «Треугольные родственники Пентамино». Игра представляет собой 12 элементов, каждый из которых состоит из 6 равносторонних треугольников, причем составные части уже сами по себе напоминают знакомые предметы — уточку, факел, бабочку и т.д

 

 

9. Стомахион («приводящая в ярость»)

Игра стомахион была известна еще до нашей эры. Создателем ее считали Архимеда.

 В 1899 г. швейцарский историк Генрих Зютер обнаружил в книгохранилищах Берлина и Кембриджа арабскую рукопись «Книга Архимеда о разбиении фигуры стомахиона на 14 частей, находящихся в рациональных отношениях». Позже датский историк математики Гейберг подтвердил, что создателем игры является Архимед.

 Архимедова игра довольно сложна и предполагает некоторый опыт пространственного конструирования. Вместе с тем, эта игра – старинный способ подготовки к изучению геометрии.

 

 

10. Волшебный квадрат составлен из 7 элементов. С их помощью вы сможете составить стилизованные силуэты кораблей, животных, игрушек, домашней утвари. Незначительные перестановки дают возможность превращать фигуры одна в другую (мальчика — в собаку), создавать новые образы, придумывать им имена и названия

 

11. Головоломка Пифагора — это квадрат, разделенный на семь частей. Изобразительные возможности игры достаточно велики — можно создавать силуэты различной степени сложности и сложные геометрические фигуры, напоминающие предметы быта, животных, птиц и т.д

 

12. Сфинкс

В состав относительно несложной головоломки «Сфинкс» входит семь простых геометрических фигур.   В этой игре особенно удаются силуэты различных видов транспорта — ракеты, самолета, парусника, а также птиц.

 

 

 

 Глава 3

 Современные геометрические головоломки

 

Рассказы о головоломках, старых и не очень, можно найти в разных книгах. Одно их перечисление займет десятки страниц.

Приведу пример относительно новых головоломок, изобретенных в последние десятилетия. География их появления обширна, так как пристрастие к головоломкам не имеет границ.

 

1.Башня.

  Из 11 различных разверток куба надо построить симметричную относительно вертикали башню максимальной высоты, при этом внутри башни должно находиться наименьшее количество пустот. Элементы можно переворачивать.

2. Уголки

Из одиннадцати различных прямых уголков сложите квадрат. Уголки разрешено переворачивать.

 

 

3. Два квадрата

Из пяти изображенных в левой части рисунка элементов постройте квадрат наибольшего размера. Накладывать элементы друг на друга не разрешено, но их можно переворачивать. Эту головоломку в 1998 году привезли из Турции участники Чемпионата мира по решению головоломок. Как выяснилось, она была предложена на одном из соревнований турецких любителей головоломок.

 

Решив первую головоломку, попробуйте справиться с другой, но примите во внимание, что она имеет качественное отличие. Из шести элементов с правой части рисунка постройте квадрат наибольшего размера.

 

4. Капли дождя.

 В комплект этой оригинальной головоломки, выпущенной в 70-е годы, входит набор из 13 элементов, которые получены трансформациями каплеобразного элемента 1. Сам этот элемент используют в комплекте дважды, он является 13-м. Головоломку изобрели в Японии.

 

 

Глава 4

Практическое применение головоломок

 

Магнетический интерес к головоломкам возник очень давно и не пропадает до сих пор. Сейчас многие из них изготавливаются на производстве. Хороши они и тем, что их можно изготавливать самим.

 Знакомиться с играми нужно  постепенно:

Ø Рассмотреть набор, пробовать сочетать стороны и углы фигур.

Ø Заняться конструированием простых изображений: домиков, корабликов, грузовиков.

Ø Составить картинку. Сюжет из нескольких картинок.

Ø Ну а закономерным продолжением станет составление собственных схем.

После изучения различных головоломок, нужно перейти к практике и научиться увлекательно проводить время за игрой.

Для подробного рассмотрения я выбрал головоломку Танграм.  Эту головоломку я сделал сам из цветного картона. Суть игры заключается в конструировании на плоскости разнообразных предметных силуэтов, напоминающих животных, людей, предметы быта, транспорт, буквы, цифры, цветы и т.д. Например, в Танграме  насчитывают более 7 000 различных комбинаций. Самые распространенные из них — фигуры животных, птиц и человека.

Правила: 

Ø    В каждую собранную фигуру должны входить все элементы.

Ø    При составлении фигур элементы не должны налегать друг на друга.

Ø    Элементы фигур должны примыкать один к другому.

 

В результате игры получается плоскостное силуэтное изображение. Оно условно, схематично, но образ легко угадывается по основным характерным признакам предмета: его строению, пропорциональному соотношению частей и форме.

Для того чтобы сделать самим Танграм понадобится квадрат, который нужно разрезать по следующей схеме:

                

Дальше можно воспользоваться предложенными заданиями и сконструировать фигурки из деталей головоломки Танграм (Приложение 1)

 

 

Фигуры на следующих рисунках из тех, которые я научился делать сам по заданному силуэту.

   

 

 

Заключение

 

В своей работе я рассмотрел различные плоские геометрические головоломки. Исследовав их практическое применение , я пришёл к выводу, что комбинируя на плоскости элементы головоломок, можно создавать множество новых фигур, как геометрических, так и жанровых — очертания животных, людей, бытовых предметов и т. д. Мастерство игрока не имеет границ, и я буду ещё долго совершенствовать свои навыки с помощью геометрических головоломок.

Созданные, чтобы доставлять удовольствие, головоломки развивают, обогащая интеллектуально.

Однако далеко не все задачи решаются легко и непринужденно. Порой хочется забросить игрушку в дальний угол! Не складывается, не решается, не разбирается… Однако, если подумать, то именно терпеть головоломки учат в первую очередь. В жизни человеку придется не раз столкнуться с ситуациями, которые кажутся тупиковыми, из которых нет выхода. И первая реакция — отчаяние, упаднические настроения и гнев. Но ругаться на «жизнь» бессмысленно, проще глубоко вздохнуть, подумать и взяться за решение снова, но уже спокойно и выдержанно ища ответ.

 

Список используемой литературы.

1.     И.Ф. Шарыгин, Л.Н. Ерганжиева:  «Наглядная геометрия, 5-6 класс».

2.     Г. К. Муравин, О. В. Муравина:  «Математика, 5 класс».

3.     Л. П. Мочалов: «Головоломки»

4. В. Н. Белов, В. Н. Рыбинский. «Пленительные головоломки».

Интернет – ресурсы:

 

   http//www.yandex.ru/

    http//www.rambler.ru/

      http://ru.wikipedia.org/wiki/Танграм

Приложение

 

 

 

 

 

 

 

 

I. Паспорт проекта:

1	название проекта	Плоские геометрические головоломки на складывание фигур
2	фамилия, имя, отчество разработчика  проекта	Булыкин Роман Витальевич
3	класс	5 «Б»
4	название, номер учебного учреждения, где выполнялся проект	МБОУ «СОШ № 151», Калининский район, город Новосибирск
5	предметная область	математика
6	время разработки проекта	Январь 2019 – февраль 2019
7	Цели:	Познакомиться с различными видами головоломок. Пробудить у одноклассников интерес к геометрическим головоломкам и занимательной математике. Создать комплект головоломок «Танграм».
8	задачи	Найти и изучить информацию по теме. Рассмотреть различные виды головоломок. Изучить историю происхождения мировых геометрических головоломок «Танграм», «Колумбово яйцо», «Стомахион» и др. Найти примеры более современных головоломок.
9	тип проекта (по виду деятельности: поисковый, исследовательский, творческий, игровой и др.)	Поисковый, творческий
10	используемые технологии (мультимедиа, театрализация, телекоммуникации, программирование (с указанием среды разработки и языка программирования) и др. )	Мультимедиа,
11	форма продукта проекта	Мультимедийная презентация, Комплект головоломок
12	содержание
13	исследование(в исследовательском проекте)
14	область применения результата проекта	Конструирование и моделирование
15	результативность

 

 

25 веселых геометрических головоломок | Математика = Любовь

Ищете веселые и увлекательные геометрические головоломки? Вот коллекция из 25 бесплатных геометрических головоломок, которые я использовал в прошлом со своими учениками по математике в старшей школе. Большинство этих головоломок должны подходить для использования с людьми в возрасте от старшей начальной школы или средней школы до взрослых.

Любимыми геометрическими головоломками моих учеников определенно были головоломки с подвижными частями, которые нужно собирать, чтобы создавать различные геометрические фигуры. Головоломка с равносторонним треугольником и квадратная задача 1-4-5 пользуются успехом у студентов.

Если вы специально ищете геометрические головоломки для взрослых, я рекомендую печатные геометрические логические головоломки от Наоки Инабы, такие как головоломки Шикаку, лабиринты под углом, лабиринты с площадями, головоломки Санкаку и головоломки Дзукеи. Они доступны в виде печатных PDF-файлов для часов решения головоломок!

Если вы хотите, чтобы группа занималась решением какой-нибудь интересной геометрической задачи, я не могу не порекомендовать задание «Сделаем квадраты»!

25 забавных геометрических головоломок, которые стоит попробовать

color»> Головоломки Шикаку

Головоломки Шикаку — это японская логическая головоломка, основанная на геометрии. Цель головоломки шикаку состоит в том, чтобы разделить сетку на прямоугольники (и квадраты) так, чтобы число в каждом прямоугольнике относилось к площади этого прямоугольника.

Читать дальше

Пазл с парами

В этой головоломке с парами вам предстоит соединить шесть фигур в пары, чтобы сформировать три одинаковых по размеру и форме кусочка.

Подробнее

color»> Угловые лабиринты Наоки Инаба

Эти головоломки с угловым лабиринтом от Наоки Инабы заставляют учащихся найти путь в лабиринте, умея распознавать общие измерения углов. Нарисуйте путь через лабиринт от S до G. Каждый раз, когда вы проходите через пронумерованный круг, путь должен образовывать этот угол в градусах.

Читать далее

Подгонка фигур

В этой подгонке фигур от Ивана Московича головоломки задаются следующим вопросом: Сможете ли вы разместить шесть фигур на доске, не перекрывая друг друга? Звучит проще, чем есть!

Читать дальше

color»> Головоломка с конгруэнтными фигурами

В этой головоломке с конгруэнтными формами учащиеся получают кусочки двух цветов. Задача состоит в том, чтобы расположить кусочки двух цветов так, чтобы они образовали две конгруэнтные фигуры. Вы можете вращать части и переворачивать их, но не перекрывать их. Эта головоломка о конгруэнтных фигурах — творение гениального Эриха Фридмана.

Подробнее

Пазлы-лабиринты от Наоки Инабы

Пазлы-лабиринты от плодовитого японского создателя головоломок Наоки Инаба стали весьма популярны в Соединенных Штатах. Используйте свои знания области, чтобы найти недостающую информацию в каждой диаграмме.

Читать далее

Упражнение «Собери»

Упражнение «Строительство» — это совместная командная работа, которая побуждает учащихся к совместной работе, общению и логическому мышлению, когда они строят геометрический объект, чтобы удовлетворить набор заданных подсказок. Если вы хотите поработать над словарным запасом, это упражнение вводит/закрепляет такие слова, как «лицо» и «край».

Подробнее

border-width»/> Головоломки Санкаку

Головоломки Санкаку — это логическая головоломка, основанная на геометрии, в которой основное внимание уделяется нахождению площади треугольника. Цель каждой головоломки состоит в том, чтобы соединить три точки, чтобы сформировать треугольник с указанной площадью. Головоломки Санкаку созданы Наоки Инаба, плодовитым японским создателем головоломок.

Читать далее

Головоломка с драконом для отработки специальных правильных треугольников

Я нашел эту головоломку с драконом для отработки особых прямоугольных треугольников в Интернете и влюбился в нее. Каждый из треугольников является особым прямоугольным треугольником.

Подробнее

Задание на один большой квадрат

Я использовал это задание на один большой квадрат со своими студентами-тригонометристами, чтобы просмотреть 45-45-90 особых прямоугольных треугольников. Я нашел это задание в базе данных Open Curriculum Task. Мне нравилось слушать разговоры моих учеников, когда они боролись с этой проблемой. И я имею в виду «борьбу» в самом лучшем смысле!

Подробнее

Пазлы Zukei

color»> Пазлы Zukei — блестящее творение Наоки Инабы. Инаба бесплатно разместил эти головоломки на своем веб-сайте, но в них может быть немного сложно ориентироваться, так как все написано на японском языке. Можете ли вы соединить точки на каждой сетке, чтобы сформировать указанную геометрическую фигуру?

Читать далее

Загадка «Квадрат фигуры»

Мне нравится эта головоломка «Квадрат фигуры», потому что в ее решении задействована некоторая скрытая математика, которая может быть неочевидной на первый взгляд.

Подробнее

border-color number-border-width.border-width»/> Головоломка с равносторонним треугольником

Эта головоломка с равносторонним треугольником взята из первого тома Puzzle Box издательства Dover Publications. В конце концов я прикрепил магниты к задней части каждой части головоломки и повесил ее на доску для сухого стирания как свою u0022Puzzle of the Week.u0022

Подробнее

1-4-5 Square Challenge

The 1-4-5 Square Challenge — это на самом деле три испытания в одном. Сможете ли вы сделать квадрат, используя ровно 1 часть? А если ровно 4 штуки? А теперь настоящая задача: сможете ли вы составить квадрат, используя ровно 5 частей?

Читать дальше

color»> Пазл с квадратами

Соедините четыре предложенных прямоугольника так, чтобы получился идеальный квадрат. Части могут быть повернуты, но они не могут перекрываться.

Подробнее

Головоломки со счетом четырехугольников

Я думаю, что эти головоломки со счетом четырехугольников из книги «100 геометрических игр» Пьера Берлокена могли бы стать поводом для интересной беседы в классе.

Подробнее

color»> Квадрат в квадрате Пазл

Головоломка «Квадрат в квадрате» — творение гениального Петра Грабарчука. Вам даны шестнадцать прямоугольников. Среди этих прямоугольников только два могут быть помещены рядом друг с другом, чтобы образовать идеальный квадрат.

Подробнее

Пазл с 8 палочками

Сможете ли вы расположить восемь палочек так, чтобы они образовали ровно три квадрата одинакового размера?

Подробнее

color»> Головоломка с сеткой фигур

Цель головоломки с сеткой фигур состоит в том, чтобы разделить сетку на геометрические фигуры. Любые линии, которые вы рисуете, должны следовать либо линиям сетки, либо диагоналям квадратов сетки. Каждая фигура, которую вы рисуете, должна содержать ровно один значок фигуры внутри.

Читать далее

Части целого. Головоломка с равносторонним треугольником

Головоломка «Части целого» дает учащимся пять фигур, которые нужно сложить так, чтобы получился треугольник, три стороны которого имеют одинаковую длину. Другими словами, сформируйте равносторонний треугольник.

Подробнее

Пифагорейские головоломки

Ищете вызов? Проверьте эту страницу Make It Pythagorean Puzzles. Вставьте одну и ту же цифру (любым способом по вашему выбору) на каждую сторону треугольника, чтобы сформировать прямоугольный треугольник.

Читать дальше

Упражнение «Сделаем квадраты»

«Сделаем квадраты» — это отличное командообразующее занятие, описанное в «Руководстве по совместному обучению» Кагана. Студенты должны работать вместе, чтобы собрать свои палочки от эскимо, чтобы создать различное количество квадратов.

Подробнее

Пазл «Три из пяти»

Три из этих пяти фигурок соединяются вместе, образуя треугольник. Какие они?

Подробнее

Треугольная головоломка с индейкой

Сколько различных треугольников вы можете найти на этом изображении индейки на День Благодарения? Я наткнулся на эту треугольную головоломку с индейкой в ​​книге Мартина Гарднера.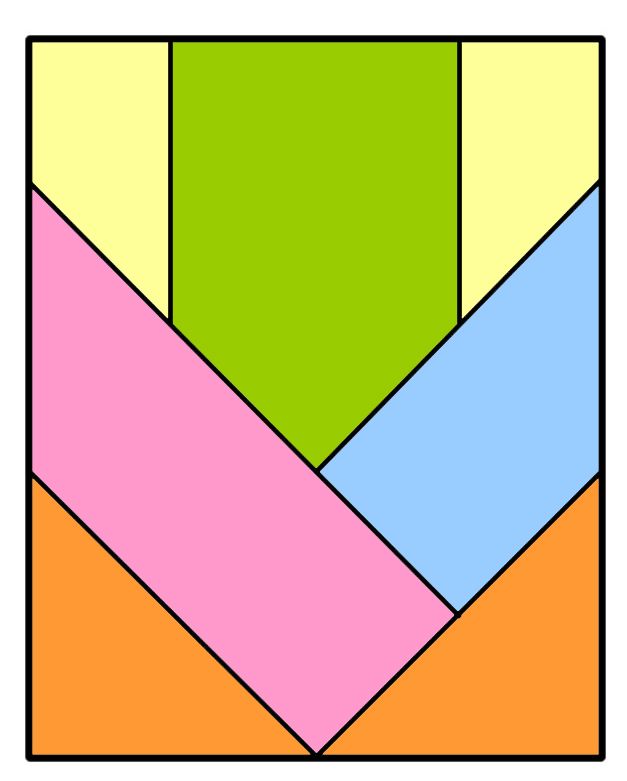

Читать дальше

Загадочная головоломка с треугольниками

Эта замысловатая головоломка с треугольниками существует уже более века u0026ndash; Сможете ли вы расположить эти восемь палочек так, чтобы получилось ровно четыре треугольника и два квадрата? Первоначальная головоломка должна была быть решена с помощью спичек, но я не думаю, что мне нужно объяснять, почему я не буду давать своим ученикам спички, чтобы играть с ними;

Подробнее

Дополнительные ресурсы для обучения геометрии

Опубликовано Опубликовано: 11 сентября 2022 г.  — Последнее обновление: 11 ноября 2022 г.

11 геометрических головоломок, которые сводят математиков с ума – Математика с плохими рисунками

Бен Орлин Катриона Ширер, мастер головоломок 15 апреля 2020 г. 7 апреля 2020 г. 4 Minutes

«Есть одна метазадача, — недавно размышлял математик Тимоти Гауэрс, — которая смутно стоит в моем списке дел, над которой нужно подумать».

Гауэрс, медалист Филдса 1998 года, совершил прорыв в комбинаторике. Чувак — профессор-исследователь Королевского общества в Кембриджском университете. Его список дел, без сомнения, представляет собой каталог глубоких и важных математических вопросов. Так что же это за мета-проблема не дает ему покоя?

«КАТРИОНА ШИРЕР ЭТО ДЕЛАЕТ???»

Катрина Ширер — учительница математики, чья учетная запись в Твиттере содержит самодельные геометрические головоломки. Но «головоломки», возможно, продают меньше их. Это головоломки, которые привлекают и привлекают математиков всех мастей.

Головоломки, вызывающие удивление с помощью заглавных букв и тройной пунктуации.

«Я не думаю, что когда-либо видел кого-то за всю свою жизнь, — говорит математик Майк Лоулер, — кто бы умел решать аккуратные геометрические задачи так, как это делает Катриона Ширер».

«Эти проблемы не могут просто прийти ей в голову, — настаивает Гауэрс. — У нее есть общая теория? Или хороший набор трюков? Или что?»

«Вчера я прочитал ее твит, — подхватил Джон Карлос Баэз, ведущий теоретик категорий, — где она сказала, что не так изобретательна, как думают некоторые люди: она снова и снова использует одни и те же приемы.

«Это, — заметил Баэз, — то же самое, что сказал Фейнман».

В ответ Катриона поделилась фрагментом видео из своей записной книжки. Это был еще один дразнящий проблеск ее плодородного мыслительного процесса:

Вот беглый просмотр моего блокнота, чтобы понять соотношение моих каракулей и головоломок. pic.twitter.com/Y5fbjqFzOO

— Катриона Ширер (@Cshearer41) 20 февраля 2020 г.

В любом случае, Катриона продолжает отклонять мои предложения связаться с издателями, но любезно выбирает любимые головоломки, чтобы поделиться ими здесь.

Итак, для вашего удовольствия: одиннадцать восхитительных экскурсов в геометрию.

 

1.
Транзит через Пурпурное Солнце Какова общая заштрихованная площадь?

«Это мой самый популярный твит, — говорит Катриона. «Есть много очень хороших ответов, но мне особенно нравится эта анимация, где различные возможности, кажется, обтекают одно фиксированное значение».

 

2.
Изумруд Ширера Четыре квадрата. Что за заштрихованная область?

«Это вопрос с подвохом, — говорит Катриона. Предупреждение о спойлере: «Одна из длин — это отвлекающий маневр — вам нужно только [отредактировано], чтобы иметь возможность ответить. На самом деле он был основан на более ранней головоломке, которую вы представили в своей первой коллекции».

 

3.
Пирамида с двумя гробницами Два квадрата внутри равностороннего треугольника. Какой угол?

«Есть много способов сделать это, — говорит Катриона. «Один из моих любимых — который я никогда бы не придумал сам — это тот, где верхняя часть головоломки мозаична для создания [спойлер отредактирован]».

Также обратите внимание: мои решения головоломок Катрионы одинаково утомительны и обычно сводятся к вычислениям в конце. Те, что в Твиттере, всегда великолепны, симметричны на уровне олимпийских гимнастов. Так что, это.

 

4.
Заходящее солнце, восходящая луна Какая часть прямоугольника закрашена?

«Это что-то вроде похмелья после всех тех головоломок с полукругами внутри прямоугольников, которые я собирал в декабре!» — говорит Катриона.

 

5.
Hex Hex Six Оба шестиугольника правильные. Какова длина розовой линии?

«Математика — уникальный (?) международный язык», — прокомментировал это один фанат. «Посмотрите, что слова ответов не на английском языке, но математические решения полностью понятны».

«Моя любимая вещь в Твиттере, — согласилась Катриона, — это возможность проводить математические расчеты с людьми по всему миру».

 

6.
Четыре, Три, Два Какова площадь этого треугольника?

«Я села рядом с кем-то на тренинге в Бирмингеме, — говорит Катриона, — который узнал мое имя в Твиттере и рассказал мне свой любимый геометрический факт: вписанная окружность в прямоугольный треугольник с целыми сторонами имеет целочисленный радиус. Мы потратили некоторые самые спокойные моменты дня, пытаясь выяснить все закономерности, и я собрал эту головоломку в поезде домой».

Забавное совпадение! Когда я преподавал в Бирмингеме, один из наших замечательных студентов рассказал об этом мне и другим преподавателям.

 

7.
Троицкая четверка Все четыре треугольника равносторонние. Какую часть прямоугольника они покрывают?

«Этот, — говорит Катриона, — на самом деле упоминается в последней книге Алекса Беллоса, которая, по-моему, очень крутая. Дизайн очень напоминает мне витраж в часовне. Мое любимое решение было от сына Майка Лоулера, просто потому, что (необычно для социальных сетей) мы видим весь мыслительный процесс, включая те моменты, где он застревает».

(Это, в общем, одна из восхитительных вещей в блоге Майка; это уникальный документ о математическом обучении и преподавании.)

8.
Падающее домино  Этот дизайн состоит из трех прямоугольников 2×1. . Какая его часть заштрихована?

«Это вдохновило Винсента Панталони, прославившегося Geometry Snack , на создание приятной побочной головоломки, — говорит Катриона. «В основном мне это нравится, потому что нечасто увидишь в дикой природе».