Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. | |||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Умножение дробей и смешанных чисел. Деление дробей и смешанных чисел. Примерно 6-класс (11-12 лет)Поделиться:
| ||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | |||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | ||||||
Умножение и деление алгебраических дробей
В этой статье мы продолжаем изучение основных действий, которые можно выполнять с алгебраическими дробями. Здесь мы рассмотрим умножение и деление: сначала выведем нужные правила, а затем проиллюстрируем их решениями задач.
Как правильно делить и умножать алгебраические дроби
Чтобы выполнить умножение алгебраических дробей или разделить одну дробь на другую, нам нужно использовать те же правила, что и для обыкновенных дробей.
Когда нам надо умножить одну обыкновенную дробь на другую, мы выполняем отдельно умножение числителей и отдельно знаменателей, после чего записываем итоговую дробь, расставив по местам соответствующие произведения. Пример такого вычисления:
23·47=2·43·7=821
А когда нам надо разделить обыкновенные дроби, мы делаем это с помощью умножения на дробь, обратную делителю, например:
23:711=23·117=227=1121
Умножение и деление алгебраических дробей выполняется в соответствии с теми же принципами. Сформулируем правило:
Определение 1Чтобы перемножить две и более алгебраические дроби, нужно перемножить отдельно числители и знаменатели. Результатом будет дробь, в числителе которой будет стоять произведение числителей, а в знаменателе – произведение знаменателей.
В буквенном виде правило можно записать как ab·cd=a·cb·d . Здесь a, b, c и d будут представлять из себя определенные многочлены, причем b и d не могут быть нулевыми.
Для того чтобы разделить одну алгебраическую дробь на другую, нужно выполнить умножение первой дроби на дробь, обратную второй.
Это правило можно также записать как ab:cd=ab·dc=a·db·c . Буквы a, b, c и d здесь означают многочлены, из которых a, b, c и d не могут быть нулевыми.
Отдельно остановимся на том, что такое обратная алгебраическая дробь. Она представляет из себя такую дробь, которая при умножении на исходную дает в итоге единицу. То есть такие дроби будут аналогичны взаимно обратным числам. Иначе можно сказать, что обратная алгебраическая дробь состоит из таких же значений, что и исходная, однако числитель и знаменатель у нее меняются местами. Так, по отношению к дроби a·b+1a3 дробь a3a·b+1 будет обратной.
Решение задач на умножение и деление алгебраических дробей
В этом пункте мы посмотрим, как правильно применять озвученные выше правила на практике. Начнем с простого и наглядного примера.
Пример 1Условие: умножьте дробь 1x+y на 3·x·yx2+5 , а потом разделите одну дробь на другую.
Решение
Сначала выполним умножение. Согласно правилу, нужно отдельно перемножить числители и знаменатели:
1x+y·3·x·yx2+5=1·3·x·y(x+y)·(x2+5)
Мы получили новый многочлен, который нужно привести к стандартному виду. Заканчиваем вычисления:
1·3·x·y(x+y)·(x2+5)=3·x·yx3+5·x+x2·y+5·y
Теперь посмотрим, как правильно разделить одну дробь на другую. По правилу нам надо заменить это действие умножением на обратную дробь x2+53·x·y :
1x+y:3·x·yx2+5=1x+y·x2+53·x·y
Приведем полученную дробь к стандартному виду:
1x+y·x2+53·x·y=1·x2+5(x+y)·3·x·y=x2+53·x2·y+3·x·y2
Ответ: 1x+y·3·x·yx2+5=3·x·yx3+5·x+x2·y+5·y ; 1x+y:3·x·yx2+5=x2+53·x2·y+3·x·y2 .
Довольно часто в процессе деления и умножения обыкновенных дробей получаются результаты, которые можно сократить, например, 29·38=672=112 . Когда мы выполняем эти действия с алгебраическими дробями, мы также можем получить сократимые результаты. Для этого полезно предварительно разложить числитель и знаменатель исходного многочлена на отдельные множители.
Если нужно, перечитайте статью о том, как правильно это делать. Разберем пример задачи, в которой нужно будет выполнить сокращение дробей.
Условие: перемножьте дроби x2+2·x+118·x3 и 6·xx2-1 .
Решение
Перед тем, как вычислять произведение, разложим на отдельные множители числитель первой исходной дроби и знаменатель второй. Для этого нам потребуются формулы сокращенного умножения. Вычисляем:
x2+2·x+118·x3·6·xx2-1=x+1218·x3·6·x(x-1)·(x+1)=x+12·6·x18·x3·x-1·x+1
У нас получилась дробь, которую можно сократить:
x+12·6·x18·x3·x-1·x+1=x+13·x2·(x-1)
О том, как это делается, мы писали в статье, посвященной сокращению алгебраических дробей.
Перемножив одночлен и многочлен в знаменателе, мы получим нужный нам результат:
x+13·x2·(x-1)=x+13·x3-3·x2
Вот запись всего решения без пояснений:
x2+2·x+118·x3·6·xx2-1=x+1218·x3·6·x(x-1)·(x+1)=x+12·6·x18·x3·x-1·x+1==x+13·x2·(x-1)=x+13·x3-3·x2
Ответ: x2+2·x+118·x3·6·xx2-1=x+13·x3-3·x2 .
В некоторых случаях исходные дроби перед умножением или делением удобно преобразовать, чтобы дальнейшие вычисления стали быстрее и проще.
Пример 3Условие: разделите 217·x-1 на 12·x7-x .
Решение: начнем с упрощения алгебраической дроби 217·x-1 , чтобы избавиться от дробного коэффициента. Для этого умножим обе части дроби на семь (это действие возможно благодаря основному свойству алгебраической дроби). В итоге у нас получится следующее:
217·x-1=7·27·17·x-1=14x-7
Видим, что знаменатель дроби 12·x7-x , на которую нам нужно разделить первую дробь, и знаменатель получившейся дроби являются противоположными друг другу выражениями. Изменив знаки числителя и знаменателя 12·x7-x , получим 12·x7-x=-12·xx-7 .
После всех преобразований можем наконец перейти непосредственно к делению алгебраических дробей:
217·x-1:12·x7-x=14x-7:-12·xx-7=14x-7·x-7-12·x=14·x-7x-7·-12·x==14-12·x=2·7-2·2·3·x=7-6·x=-76·x
Ответ: 217·x-1:12·x7-x=-76·x .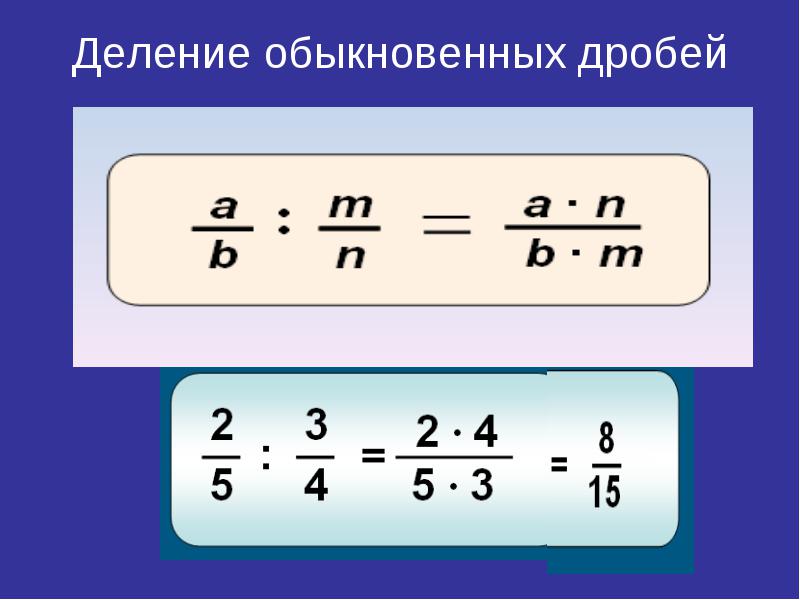
Как умножить или разделить алгебраическую дробь на многочлен
Чтобы выполнить такое действие, мы можем воспользоваться теми же правилами, что мы приводили выше. Предварительно нужно представить многочлен в виде алгебраической дроби с единицей в знаменателе. Это действие аналогично преобразованию натурального числа в обыкновенную дробь. Например, можно заменить многочлен x2+x−4 на x2+x−41 . Полученные выражения будут тождественно равны.
Пример 4Условие: разделите алгебраическую дробь на многочлен x+45·x·y:x2-16 .
Решение
Начнем с замены многочлена дробью, далее действуем согласно основному правилу.
x+45·x·y:x2-16=x+45·x·y:x2-161=x+45·x·y·1×2-16==x+45·x·y·1(x-4)·x+4=(x+4)·15·x·y·(x-4)·(x+4)=15·x·y·x-4==15·x2·y-20·x·y
Ответ: x+45·x·y:x2-16=15·x2·y-20·x·y.
Автор: Ирина Мальцевская
Преподаватель математики и информатики.
Кафедра бизнес-информатики Российского университета транспорта
Как умножить дроби? Определение, примеры, факты
Перекрестное умножение: введение
Мы обычно используем метод перекрестного умножения, чтобы найти неизвестные значения в любом алгебраическом уравнении. Давайте посмотрим на эти повседневные математические вопросы. Если один батончик стоит $\$$2, сколько будут стоить 10 таких батончиков?
Перекрестное умножение, как следует из названия, относится к умножению чисел, стоящих на перекрестных позициях.
Скрещиваем дроби $\frac{1}{10}$ и $\frac{2}{?}$.
$? \times 1= $\$$10$ $\times 2$
$? =$ $\$$20
Итак, 10 батончиков будут стоить $\$$20.
Давайте узнаем больше об этом методе и его применении.
Родственные игры
Что такое перекрестное умножение?
Для любого алгебраического уравнения типа $\frac{a}{b}=\frac{c}{d}$ , метод перекрестного умножения использует следующую формулу:
$a\times d = b\times c $
Чтобы скрестить умножить дроби, мы умножаем числитель первой дроби на знаменатель второй дроби и числитель второй дроби на знаменатель первой дроби.
Перекрестное умножение можно использовать для сравнения дробей, сложения или вычитания разных дробей, поиска неизвестного значения в выражении и сравнения отношений.
Связанные рабочие листы
Как перекрестно умножать дроби?
Давайте разберемся, как скрестить дроби на примере.
Мы знаем, что $\frac{3}{4} = \frac{6}{8}$
Перемножить дроби $\frac{3}{4}$ и $\frac{6}{8}$ .
Умножьте числитель первой дроби на знаменатель второй дроби.
Умножьте числитель второй дроби на знаменатель первой дроби.
Получаем
$3\times8=24$
$6\times4=24$
Итак, перемножая дроби $\frac{a}{b} = \frac{c}{d}$ , мы get $a\times d = b\times c$
Перекрестное умножение дробей для сравнения в отличие от дробей
Мы только что научились скрещивать умножающие дроби. Когда вы скрещиваете умножение дробей? В отличие от дробей можно сравнивать путем перекрестного умножения. Отличие от дробей — это дроби с разными знаменателями.
Пример :
Сравните $\frac{3}{7}$ и $\frac{5}{8}$ , используя перекрестное умножение.
Чтобы сравнить две дроби с разными знаменателями, мы делаем их знаменатели одинаковыми.
Мы делаем это, заменяя знаменатели произведением обоих знаменателей.
Итак, знаменатель обеих дробей становится $7 \times 8 = 56$
Теперь мы скрестим и умножим дроби , чтобы найти числители.
- Сначала умножаем числитель первой дроби на знаменатель второй дроби.
$3 \times 8 = 24$
Таким образом, первая дробь принимает вид: $\frac{24}{56}$
- Далее умножаем числитель второй дроби на знаменатель первой дроби.
$5 \times 7 = 35$
Таким образом, вторая дробь становится: $\frac{35}{56}$
Так как $\frac{24}{56} \lt \frac{35}{56} $ , можно сказать, что $\frac{3}{7} \lt \frac{5}{8}$.
Перекрестное умножение для сравнения отношений
Если два отношения равны, т.
е. $\frac{a}{b} = \frac{c}{d}$, (где b и d не равны нулю), то произведение после перекрестного умножения также равно.
- $\frac{a}{b} \lt \frac{c}{d}$, если $a\times d \lt b\times c$.
Пример: $\frac{1}{2} \lt \frac{3}{4}$, начиная с $4 \lt 6$.
- $\frac{a}{b} \gt \frac{c}{d}$, если $a \times d \gt b \times c$.
Пример: $\frac{1}{10} \gt \frac{1}{100}$ начиная со 100 $\gt 10$.
Мы можем использовать перекрестное умножение , чтобы найти значение переменной в уравнении, содержащем отношения. Давайте лучше поймем это на примере.
Пример : Если 8 подсвечников стоят $\$$40. Сколько будут стоить 12 таких подсвечников?
Стоимость 8 подсвечников = $\$$40
Стоимость 1 подсвечника $= \frac{40}{8}$ …………(i)
Пусть стоимость 12 подсвечники быть Икс.
Следовательно, стоимость 1 подсвечника составит $\frac{x}{12}$.
…………..(ii)
Приравнивая (i) и (ii), получаем
$\frac{40}{8} = \frac{x}{12}$
Перемножить, чтобы получить
$40 \times 12 = 8 \times x$
$\frac{480}{8}=$ x
x $=60$
Следовательно, стоимость 12 подсвечников составляет $\$$60.
Перекрестное умножение с одной переменной
Метод перекрестного умножения в основном используется для нахождения неизвестной переменной в уравнении. Давайте посмотрим на пример.
$\frac{4}{9} = \frac{x}{45}$
Когда мы пересекаем умножение:
$4 \times 45 = 180$ и $9 \times x = 9x$
Теперь, $9 x = 180$
x$ = \frac{180}{9} = 20$
Отсюда получаем $x = 20$
Решаемые примеры
1. Сравните дроби 57 и 49 перекрестным умножением.
Решение: Пересекая и умножая, мы находим
$5 \times 9 = 45$ и $4 \times 7 = 28$
Так как $45 \gt 28, 57$ больше, чем 49.
2. Джимми хочет найти значение x в заданном уравнении. Вы можете помочь ему?
$\frac{12}{15} = \frac{x}{10}$
Решение:
$\frac{12}{15} = \frac{x}{10} $ (дано)
При перекрестном умножении:
$12 \times 10 = 15 \times x$
$\frac{120}{15} =$ x
$8 = $ x
Итак, значение x равно 8.
3. Что больше, $\frac{7}{12}$ или $\frac{6}{11}$ ?
Решение :
Когда мы пересекаем умножение, мы находим
As, $77 \gt 72$
Следовательно, $\frac{7}{12} \gt \frac{6}{11}$.
Практические задачи
1Если дроби $\frac{4}{8}$ и $\frac{5}{x}$ равны, каково значение $x$?
40
5
15
10
Правильный ответ: 10
Поскольку данные дроби равны, мы можем перекрестно умножить и сказать, что $4x= 8 \times 5 = 40$
Таким образом, х $= $10
Если 4 кекса стоят $\$$12.
Сколько будут стоить 10 таких кексов?$\$30
$\$48
$\$40
$\$36
Правильный ответ: $\$30
Стоимость 4 кексов $\$$12.
Пусть стоимость 10 кексов равна x. Когда мы формулируем это как уравнение, мы имеем:
$\frac{12}{4} = \frac{x}{10}$
При перекрестном умножении мы получаем
$12 \times 10 = 4 \times x$
$\frac{120}{4} = x$
$30 = x$
Таким образом, стоимость 10 кексов составляет $\$$30.
Каково значение x, если $\frac{9}{11} = \frac{x}{33}$.
10
27
18
55
Правильный ответ: 27
$\frac{9}{11}= \frac{x}{33}$
При перекрестном умножении:
$ 9 х 33 = 11\times x$
$\frac{297}{11} = x$
$x = 27$
Итак, значение $x$ равно 27.
Часто задаваемые вопросы
Когда мы используем перекрестное умножение?
Мы используем метод перекрестного умножения для следующего:
- Процесс перекрестного умножения используется для сравнения дробей и отношений.
Используя эти , , мы можем оценить, равны ли они, больше или меньше. - Также используется для нахождения значений переменных в выражении.
Используя эти , , мы можем оценить, равны ли они, больше или меньше.2. Как используется перекрестное умножение для нахождения значения переменной?
Перекрестное умножение выполняется на числители и знаменатели дробей, которые присутствуют в обеих частях уравнения. Затем мы решаем уравнение, чтобы найти неизвестную переменную
Используем ли мы перекрестное умножение дробей?
Нет, при умножении дробей мы не крестим умножение. Чтобы умножить дроби, мы умножаем числители на числители и знаменатели.
Формулы умножения дробей | Список формул умножения дробей, которые необходимо знать
Пример 1: Решение: \(\frac{1}{5} \times \frac{1}{3}\)
Решение:
9 0005
\(\frac{1}{5} \times \frac{1}{3}\)
\(=\frac{1\times 1}{5 \times 3}\) Используя \(\ frac{a}{b}\times \frac{c}{d}=\frac{a.
c}{b.d}\)
\(=\frac{1}{15}\)
Пример 2: Решите: \(\frac{5}{10} \times \frac{6}{7}\)
Решение:
\(\ гидроразрыв{5} {10} \times \frac{6}{7}\)
\(=\frac{5\times 6}{10 \times 7}\) Используя \(\frac{a}{b}\ раз \frac{c}{d}=\frac{ac}{b.d}\)
\(=\frac{30}{70}\)
\(=\frac{30\div 10}{70 \дел 10}\)
\(=\frac{3}{7}\)
Пример 3: Решите: \(2\frac{7}{8} \times 3\frac{4}{5}\)
Решение:
\(2\ frac{7}{8} \times 3\frac{4}{5}\)
\(=\frac{23}{8} \times \frac{19}{5}\) As, \ (2\frac{7}{8}=\frac{2.8+7}{8}=\frac{23}{8}\) и \(3\frac{4}{5}=\frac{3.5+ 4}{5}=\frac{19}{5}\)
\(=\frac{23\times 9}{8 \times 5}\) Использование \(\frac{a}{b} \times \frac{c}{d}=\frac{a.
c}{b.d}\)
\(=\frac{437}{40}\)
Пример 4: Таблетка поливитаминов содержит \(\frac{1}{6}\) грамма цинка с . Врач Сэма прописал то же самое из-за множественных недостатков, которые у него были, и он должен был принимать \(4\frac{3}{4}\) таблеток в неделю. Каково общее количество цинка, которое Сэм употребил за неделю?
Решение:
Чтобы найти общее количество цинка, которое Сэм употребил за неделю, \(\frac{1}{6}\) нужно умножить на \(4\frac{3} {4}\) таблеток, что соответствует общему количеству Zinc Sam, которое необходимо употребить.
\(=4\frac{3}{4} \times \frac{1}{6}\)
\(=\frac{19}{4} \times \frac{1} {6}\)
\(=\frac{19\times 1}{4 \times 6}\) Используя \(\frac{a}{b}\times \frac{c}{d}= \frac{a.c}{b.d}\)
\(=\frac{19}{24}\)
Таким образом, потребление поливитаминов на неделю равно \(\frac{19}{24} \)
Пример 5: Салли хочет испечь хлеб, и у него есть \(\frac{2}{3}\)rd мешка муки.
Он использует \(\frac{3}{4}\)th муки из мешка. Сколько муки из всего мешка ушло на тесто?
Решение:
Салли использовал \(\frac{3}{4}\)th из \(\frac{2}{3}\)rd мешка муки. Чтобы рассчитать количество используемой муки, нам нужно умножить \(\frac{3}{4}\) и \(\frac{2}{3}\).
\(\frac{3}{4} \times \frac{2}{3}\)
\(=\frac{3\times 2}{4 \times 3}\) Использование \(\frac{a}{b}\times \frac{c}{d}=\frac{ac}{bd}\)
\(=\frac{6}{12}\)
\(=\frac{6\div 6}{12 \div 6}\)
\(=\frac{1}{2}\)
Следовательно, Салли использовал \(\frac {1}{2}\) всего мешка муки, чтобы испечь хлеб.
Пример 6: Вы хотите добавить в свой сад небольшой фонтан. Размеры фонтана и сада приведены ниже. Какова оставшаяся площадь сада?
Решение:
Длина сада \(=10\frac{1}{7}\) футов
Ширина сада \(=7\frac{3}{4}\) футов
Длина фонтана \(=6\frac{1}{2}\) ft
Ширина фонтана \(=4\frac{1}{4}\) ft
Общая площадь Сад можно найти по формуле площади прямоугольника.
Площадь прямоугольника \( = \) длина \( \times \) ширина
\(~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~=7\frac{3}{4} \times 10\frac{1}{7}\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=\frac{31}{4} \times \ frac{71}{7}\) As, \(7\frac{3}{4}=\frac{7.4+3}{4}=\frac{31}{4}\) и \(10\frac {1}{7}=\frac{10.7+1}{7}=\frac{71}{7}\)
\(~~~~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~=\frac{31\times 71}{4 \times 7}\) Используя \(\frac{a}{b}\times \frac{c }{d}=\frac{a.c}{b.d}\)
\(~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~~=\frac{221}{8}\) квадратный фут
Точно так же, используя формулу площади прямоугольника, мы можем найти общую площадь фонтана.
Площадь прямоугольника \( = \) длина \( \times \) ширина
\(~~~~~~~~~~~~~~~~~~~~~~~ ~~~~~~~~~=6\frac{1}{2} \times 6\frac{1}{4}\)
\(~~~~~~~~~~~~~ ~~~~~~~~~~~~~~~~~~~=\frac{13}{2} \times \frac{17}{4}\) As, \(6\frac{1 {2}=\frac{6.